Simulation of damage phenomena in metamaterials

Abstract

Los metamateriales se generan a partir de una red interrelacionada de celdas (caracterizadas por su geometría y conectividad) y pueden presentar un comportamiento a nivel macroscópico que difiere del que caracteriza a sus constituyentes más elementales. La modelización de la influencia que el daño y fractura de los elementos constituyentes tienen en las propiedades macroscópicas del metamaterial es de relevancia para su estudio mecánico. Alterando el comportamiento resistente a nivel elemento (variando su módulo elástico longitudinal), es posible aproximar el efecto del daño en la estructura completa. Es decir, se considera válida la sustitución del proceso de dañado y deformación plástica por una serie de estados intermedios contenidos en el régimen elástico lineal. En estos estados, la geometría del elemento permanece inalterada, y cada uno de ellos queda caracterizado por un valor del módulo elástico. En un proceso iterativo, los elementos que soportan tensiones superiores a las impuestas como fronteras, progresan a través de los diferentes estados, disminuyendo su módulo elástico, hasta que se consideran rotos y son eliminados de la estructura, pudiéndose alcanzar el colapso de la propia estructura. Al calcular, se desprecian los efectos másicos y se parte de un estado libre de tensiones residuales en cada iteración. Se presenta un algoritmo sencillo para simular el efecto del daño en estructuras de metamaterial, aplicable a cualquier programa de elementos finitos.

Palabras Clave: Metamateriales, Daño, Fractura

Metamaterials are generated from an interrelated set of cells and can present a macroscopic behaviour that differs from the one that characterizes its basic constituents. Modelling the influence that the damage and fracture of the elemental constituents have in the macroscopic properties of the metamaterial is relevant for its mechanical analysis. Altering the resistant behaviour of the elements (changing their longitudinal elastic modulus), it is possible to approximate the effect of the damage in the complete structure. It is considered as valid the substitution of the damage and plastic deformation phenomena by intermediate states contained in the linear elastic deformation regime. Each state is characterized by the elastic module of the element, whose geometry remains unmodified. In an iterative process, when the induced stress in the elements is greater than the one stablished as the limit, they progress through the different states, diminishing their elastic modulus until they are considered as fractured and are eliminated from the structure. Mass effects are ignored, and a stress-free structure is implemented to calculate each iteration. A simple algorithm is presented to simulate the effect of damage in metamaterial structures, applicable to any finite element software.

Keywords: Metamaterials, Damage, Fracture

1 INTRODUCCIÓN

Los metamateriales son materiales formados a partir de una red interrelacionada de celdas, caracterizadas por su geometría y conectividad [1]. Estas se ensamblan (tanto en el plano como en el espacio) para obtener las caras y/o vértices del sólido a generar. Las propiedades que presentan a nivel macroscópico pueden diferir de aquellas que caracterizan a sus constituyentes más elementales. El propio nombre sugiere este comportamiento, pues el prefijo meta-, derivado de la preposición ${\textstyle \mu \varepsilon \tau {\acute {\alpha }}}$, equivale a más allá [2], lo que indica que a partir de determinadas configuraciones de celda, es posible obtener propiedades anómalas [3] [4], como el comportamiento mecánico auxético [5] o índices de refracción negativos [6]. Este tipo de materiales no son extraños a la naturaleza, que presenta una amplia variedad, donde la distribución de celdas dentro del sólido y la propia estructura de cada celda varían desde disposiciones altamente regulares (honeycomb [7]) hasta completamente aleatorias (esponjas y espumas). Esto lleva a diferenciar entre metamateriales homogéneos (caracterizados por una distribución periódica de celdas) y no homogéneos (caracterizados por una distribución de celdas no periódica) [8]. En ciertos campos, como el electromagnetismo, es posible emplear provechosamente las propiedades de los metamateriales no homogéneos (como, por ejemplo, las espumas [9]), mientras que en otros, como el del diseño estructural, los homogéneos presentan cualidades que resultan más apropiadas [10]. Históricamente, la posibilidad de fabricar estos materiales ha ido ligada al desarrollo de técnicas de impresión 3D [11], que permite obtenerlos a partir de la idealización de la celda unidad y del uso de leyes topológicas que gobiernan las posiciones que toma. Esta tecnología está en continuo desarrollo, por lo que los métodos utilizados no están estandarizados [12].

El creciente interés por los metamateriales artificiales [13] se debe no solo a la dependencia de las propiedades macroscópicas de la celda de partida [14] [15], sino también a la capacidad de disminuir la densidad que presentan las estructuras de metamaterial frente a sólidos homogéneos fabricados a partir del mismo material base [16]. En el ámbito de la resistencia de materiales se utilizan predominante metamateriales homogéneos, lo que facilita la modelización de la respuesta a estados de cargas con capacidad de dañar y romper un número significativo de elementos.

Para conocer la respuesta mecánica y afrontar el problema de diseño, se precisa de un modelo que incluya los efectos derivados del fallo de los elementos constituyentes del metamaterial en su respuesta mecánica, ya que por construcción y debido a su dimensión respecto al metamaterial en conjunto, son más susceptibles de fallar. La evolución y acumulación de estos fallos lleva al colapso de la estructura. Por establecer una analogía con los materiales homogéneos, este proceso de evolución del efecto de daño desde el nivel fundamental hasta el macroscópico es similar al proceso de nucleación, crecimiento y propagación de grietas en roturas frágiles o al de formación, crecimiento y coalescencia de microvacíos en roturas dúctiles.

2 MÉTODO

2.1 Simplificación del efecto del daño

Tomando inspiración de diversos metamateriales presentes en la naturaleza, donde las aristas de cada celda son esbeltas, se toma como elemento de partida para generar las estructuras el elemento 1D barra-viga de dos nodos (beam), de sección cuadrada y constante.

Para simular el efecto del daño que genera una carga en la estructura de metamaterial, se acepta como válida la sustitución del proceso de dañado y deformación plástica a nivel elemento por una serie de estados intermedios en los que se implementan las hipótesis del régimen elástico lineal. Cada estado intermedio queda caracterizado por la geometría y el módulo de elasticidad del elemento ${\textstyle E}$, al que se le asignan valores decrecientes, desde el valor característico del material base, para el primer estado (cuando el elemento se encuentra dentro del régimen de deformación elástico), hasta que se anula (cuando se considera que el elemento ha fallado). La geometría se mantiene constante e igual a la del estado nominal, por lo que se está ignorando el proceso real de deformación propio de un sólido homogéneo metálico con cierta capacidad dúctil.

La disminución de los valores del módulo de elasticidad, a efectos de cálculo, es equivalente a alterar la geometría, ya que en la matriz de rigidez directa lineal del elemento, tanto el área ${\textstyle A}$ como el momento de inercia ${\textstyle I}$ van multiplicados en todos las componentes por ${\textstyle E}$. En los términos en los que ${\textstyle E}$ no aparece explícitamente, se puede relacionar con el módulo a cortadura ${\textstyle G}$, debido a que se trabaja con materiales isótropos.

Al aplicar una tensión, la variación de la geometría de la sección afecta de forma dispar a la distribución de área y a la de momento de inercia. Por tanto, el modificar en la misma proporción todos los términos a partir del cambio del valor de ${\textstyle E}$, supone una fuente de error. Que la modificación de ${\textstyle E}$ afecte a todo el elemento, mientras que, realmente, la variación del área de la sección se localiza mayoritariamente en una zona concreta del elemento y no tiene lugar (de manera significativa) a lo largo de toda su longitud, supone otra fuente de error. Cuanto menor sea el tamaño de los elementos, o mayor número de elementos se utilicen por arista, menor es la influencia de estos errores, ya que la reducción de ${\textstyle E}$ se localizada en una zona menos extensa de la estructura.

No se dispone de referencias en las que apoyarse para determinar con precisión los valores que debería tomar ${\textstyle E}$ en los diferentes estados, por ello se utiliza una distribución sencilla.

2.2 Evolución de los elementos

Una vez descrito el proceso basado en estados intermedios que sustituye a la deformación plástica y al crecimiento de grietas o microrroturas, es necesario establecer el número de estados con el que trabajar y el criterio para pasar de un estado al siguiente.

Con cero estados intermedios, al abandonar el régimen de deformación elástica, se considera que el elemento falla bruscamente sin ningún proceso intermedio previo, lo que no es realista si existe plasticidad y el crecimiento de las grietas es gradual. Esta simplificación del efecto del daño es excesiva para materiales dúctiles pero puede emplearse como primera aproximación en materiales con marcado carácter frágil. Al introducir más de un estado intermedio hasta alcanzar la rotura, en un caso general, al cargar la estructura y alcanzar el equilibrio, se obtienen tanto elementos dañados como fracturados, lo que genera una representación más fiel de la realidad. Se elige 10 como el número de estados intermedios y un rango de valores de ${\textstyle E}$ decrecientes, que comprende desde el módulo de elasticidad característico del material base hasta el 80% de ese valor, aparte del valor nulo.

Para establecer el criterio de paso de un estado al siguiente, se analizan las tensiones que soportan los elementos. Se supone el caso más sencillo, en el que las tensiones axiles son las más relevantes, siendo las cortantes despreciables frente a estas. Al trabajar con estructuras en el plano, el tensor de tensiones queda:

${\boldsymbol {\sigma }}={\begin{pmatrix}\sigma _{x}&0&0\\\\0&0&0\\\\0&0&0\\\end{pmatrix}}$

(1)

La tensión principal (${\textstyle \sigma _{1}}$), puede aproximarse como la suma de la tensión normal debida al momento flector y la tensión axil. A partir de los criterios de Rankine y de Treska, y siendo únicamente la tensión principal ${\textstyle \sigma _{1}}$ distinta de cero, se establece que el máximo de esta tensión sobre el elemento es el valor con el que se debe comparar para determinar si el elemento a estudiar, perteneciente a un estado intermedio (asociado a un ${\textstyle E_{Nk}}$), debería pasar al siguiente estado (asociado a ${\textstyle E_{Nk+1}}$), acercándolo así al fallo. Para el paso desde el estado inicial al primer estado de daño, la tensión con la que comparar ${\textstyle \sigma _{1}}$ es la tensión de fluencia del material base. Para las tensiones que establecen la frontera entre el resto de estados intermedios, se dispone un rango que comprende desde la tensión de fluencia, hasta un 130% de ese valor. A partir de estos razonamientos se impone (en MPa):

$E_{N}=10^{3}\cdot {\begin{pmatrix}70&68&67&66&65&64&63&62&61&60&57\end{pmatrix}}$

(2)

$\sigma _{N}={\begin{pmatrix}90&95&96&97&98&99&100&105&110&114&115\end{pmatrix}}$

(3)

La precisión de los valores no es crítica para el proceso, ya que el objetivo es determinar si el método permite representar en primera aproximación el comportamiento de las estructuras de estudio.

En la estructura de partida, todos los elementos están caracterizados por el mismo ${\textstyle E_{N1}}$ y la misma tensión ${\textstyle \sigma _{N1}}$.

Trabajar con más de un estado intermedio hace mandatorio el uso de un proceso iterativo, para que los elementos tengan la posibilidad de atravesar todos ellos. En cuanto a la transición entre diferentes estados, se aplican ciertas restricciones. Solo se puede pasar de un estado de daño, al inmediatamente posterior, independientemente de la tensión que esté soportando el elemento. No se puede ir hacia estados anteriores, ni se puede evitar pasar por alguno de los estados. Por lo tanto, para que un elemento falle, tiene que haber pasado antes por todos los estados.

2.3 Generación de las estructuras

La generación de las geometrías se lleva a cabo a partir del uso de simetrías y traslaciones de las posiciones de los nodos de la celda base. El material de partida utilizado es isótropo, con un módulo de elasticidad ${\textstyle E=70GPa}$ y un coeficiente de Poisson ${\textstyle \nu =0.3}$, representativo del ${\textstyle Al1080A}$. La sección de los elementos es cuadrada, de lado ${\textstyle l=0.5}$ ${\textstyle mm}$ constante.

Intentando acercar el proceso al utilizado en ensayos experimentales, en el que se utilizan superficies (tapas) en las caras del sólido (núcleo de metamaterial), se introducen elementos adicionales independientes de las celdas, que actúan como interfaces. El estado de carga no se impone sobre los nodos del núcleo, sino sobre las interfaces (a través de la aplicación de desplazamientos nodales). Como método de unión entre el núcleo y las interfaces se utilizan Multi Point Constrains (MPCs), estableciendo una unión entre mallas no conformes. Al trabajar con estructuras en el plano, se incorporan segmentos en vez de superficies, para que hagan de interfaz. Los elementos que forman estas interfaces no deben afectar a los resultados, por ello no se pasan por el algoritmo de modificación de ${\textstyle E}$, y sus propiedades son similares a las empleadas para el núcleo.

3 ALGORITMO

Se comienza definiendo la geometría de la celda de partida, que se utiliza para generar la estructura. Una vez construida la estructura, se impone el estado de carga. Para cada elemento se obtiene el máximo de ${\textstyle \sigma _{1}}$ y el valor de ${\textstyle E}$ (perteneciente a ${\textstyle E_{N}}$) que lo particulariza. Seguidamente, se compara ${\textstyle \sigma _{1}}$ máximo con el valor que se ha impuesto en el vector ${\textstyle \sigma _{N}}$ como frontera del estado intermedio que caracteriza al elemento. En caso de ser ${\textstyle \sigma _{1}}$ máximo mayor o igual al valor impuesto en ${\textstyle \sigma _{N}}$, el elemento en cuestión progresa al siguiente estado (deja de estar identificado por ${\textstyle E_{Nk}}$, y pasa a estarlo por ${\textstyle E_{Nk+1}}$), o es eliminado de la estructura (en el caso de que se encontrara en el último estado). En el caso opuesto, se mantiene el estado en el que se encontraba el elemento (sigue estando asociado a ${\textstyle E_{Nk}}$). Una vez analizados todos los elementos, se actualiza la estructura con las modificaciones pertinentes.

En todas las iteraciones se parte de la geometría nominal, en la que se han modificado los valores de ${\textstyle E}$ de aquellos elementos que presentan daño, y se han eliminado los que han fallado, pero no se tiene en cuenta el nivel de tensiones soportado por el elemento en iteraciones anteriores (se parte de una geometría libre de tensiones residuales), ni las deformaciones resultantes de esas tensiones. Es preciso mencionar que no se están teniendo en cuenta los efectos másicos, por lo que la tensión asociada al peso de los elementos no es un factor a considerar, lo que hace indiferente eliminar de la estructura aquellos elementos que han fallado o dejar las dos partes resultantes de la fractura en sus posiciones correspondientes.

Al modificar las propiedades de unos elementos y eliminar otros de la estructura, la redistribución de cargas provoca la activación de nuevos elementos, lo permite simular la evolución del efecto del daño.

3.1 Criterios de parada

En caso de que la redistribución de cargas no genere modificaciones de ${\textstyle E}$ en ningún elemento, se considera que la estructura ha alcanzado el equilibrio, ya que las tensiones soportadas son insuficientes para hacer evolucionar a estructura hacia un nuevo estado de daño. Como comportamiento contrapuesto aparece el fallo global de la estructura, lo que se deduce de la aparición de mecanismos (pues ya no se tiene una sola estructura, sino varias) que impiden que se pueda seguir iterando. Dada esta situación, se considera que la estructura ha colapsado, al ser el estado de carga impuesto excesivo. Estos dos criterios se obtienen como respuesta de la estructura al caso de carga. Cabe mencionar la posible aparición de elementos subapoyados formando mecanismos en el interior de la estructura, debido a que los elementos adyacentes han fallado. En esta situación, la estructura no ha colapsado, por ello, se debe continuar iterando. Para distinguir entre el colapso total y la aparición de mecanismos en el interior de la estructura, se eliminan los elementos asociados a los nodos que forman los mecanismos (pues no están trabajando) y se comprueba si los elementos restantes forman una estructura con todos los grados de libertad restringidos. Este proceso es a su vez iterativo, pues al quitar elementos, puede que otros que se encontraban apoyados, dejen de estarlo. Como último criterio, se limita el número máximo de iteraciones.

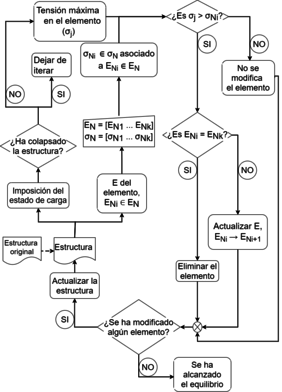
Figure 1: Diagrama del algoritmo.

4 RESULTADOS Y DISCUSIÓN

4.1 Análisis con estructuras jerárquicas

Se plantea una estructura jerárquica de triángulos equiláteros, basada en la geometría mostrada en la figura 2 y empleando dos niveles de jerarquización. La geometría y el caso de carga están basadas en [17]. Para cada lado de cada triángulo equilátero, se utiliza un solo elemento, de longitud ${\textstyle 1mm}$.

Figure 2: Primer nivel de jerarquización.

Como estado de carga, se restringe el desplazamiento vertical en la interfaz inferior, se impone un desplazamiento según esa misma dirección en la interfaz superior y se empotra el nodo de la esquina inferior izquierda.

Figure 3: Geometría de la estructura inicial.

Figure 4: Detalle de la geomatría de la estructura.

El modelo consta de 4.20224x10² elementos en el núcleo, tal y como se muestra en la figura 3, y para un desplazamiento impuesto de ${\textstyle 31\cdot 10^{-2}mm}$ requiere ${\textstyle 361}$ iteraciones hasta alcanzar el equilibrio. En la figura 4 se aprecia el detalle de la zona de la que se eliminan elementos de la estructura de manera deliberada, entorno al plano de simetría horizontal.

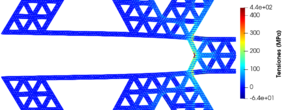
Figure 5: Detalle de la distribución de tensiones en la primera iteración.

En la figura 5 se observa que las tensiones máximas se obtienen en el extremo derecho de la zona de la que se han eliminado elementos deliberadamente, coincidiendo con el resultado obtenido en [17].

Figure 6: Distribución de tensiones una vez alcanzado el equilibrio.

Figure 7: Distribución de $E$ una vez alcanzado el equilibrio.

En la región en la que aparece la concentración de tensiones se da la rotura del primer elemento (lo que se podría equiparar con la nucleación de una grieta). Posteriormente, los elementos van fallando a través de dos frentes, hacia el centro de la estructura, uno por encima y otro por debajo del plano de simetría horizontal. Este avance es semejante al que presentaría un sólido homogéneo, debido al crecimiento de grietas.

Hasta alcanzar el equilibrio (figura 6), se produce el fallo de numerosos elementos, principalmente en la parte superior derecha, y en menor medida en la inferior derecha. En cuanto a los valores de ${\textstyle E}$ (figura 7), solo se han visto modificados en las inmediaciones de las posiciones en las que se ha producido el fallo de elementos. En el resto de la estructura, el valor de ${\textstyle E}$ se mantiene inalterado.

4.2 Análisis con estructuras cuadrangulares

La estructura se genera a partir de un cuadrado rotado 45º. Como caso de carga, en la interfaz inferior, los nodos quedan empotrados, mientras que en la superior se restringe el desplazamiento vertical, a la vez que se impone un desplazamiento horizontal, simulando así un caso de carga a cortadura. Para esta misma estructura, en [18] se calcula el fallo del primer elemento mediante procedimientos numéricos y experimentales, dándose este en ambos casos en la esquina inferior izquierda. El modelo consta de 1.323 elementos en el núcleo, y para un desplazamiento impuesto de ${\textstyle 11\cdot 10^{-2}mm}$ requiere ${\textstyle 72}$ iteraciones hasta alcanzar el equilibrio. El primer fallo aparece en la esquina inferior izquierda (figura 8), coincidiendo con el resultado obtenido en [18].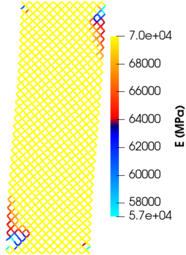

Figure 8: Aparición del fallo de los primeros elementos.

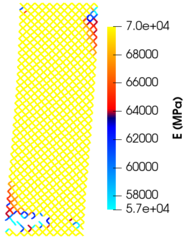
Figure 9: Distribución de $E$ una vez alcanzado el equilibrio.

Para la carga propuesta, hasta alcanzar el equilibrio, los elementos van fallando a través de un único frente, hacia el interior. Por otra parte, el efecto del daño no evoluciona significativamente en el resto de esquinas respecto de la iteración en la que se produjo el fallo de los primeros elementos (figura 9).

5 CONCLUSIONES

El método propuesto, aunque está basado en hipótesis que ignoran parte de la física del problema (omite el proceso de deformación plástica y no tiene en cuenta las tensiones residuales) genera resultados que, en primera aproximación, permiten estimar a partir de un sencillo algoritmo la aparición y propagación del efecto de daño en estructuras de metamaterial, a través del modelado de las condiciones necesarias para que se produzca la fractura a nivel elemento. Estableciendo una serie de alternativas, relativas a la situación en la que se puede encontrar cada elemento, en función de la tensión a la que está sometido y las condiciones de daño que presenta, se recogen los diferentes escenarios que tienen lugar de manera recurrente, por lo que implementando un proceso iterativo es posible obtener la evolución de la estructura. Como parámetros de control, se pueden elegir el número de estados intermedios hasta la rotura y el valor del módulo elástico y la tensión máxima que caracterizan cada estado. La selección de dichos valores permite acomodar el algoritmo a requerimientos específicos, lo cual le hace bastante versátil en cuanto a la posibilidad de representar diferentes materiales y tipos de rotura.

Los resultados obtenidos son consistentes con lo calculado mediante otros procediminetos, ya sea para la distribución de tensiones a obtener (caso de las estructuras jerárquicas triangulares, al comparar con [17]), o para la zona en la que se da el fallo del primer elemento (caso de las estructuras cuadrangulares, al comparar con [18]). En primera aproximación, se considera que el modelo genera resultados representativos del comportamiento real de las estructuras.

En conclusión, se presenta un algoritmo que permite simular el efecto de daño de forma sencilla en estructuras de metamaterial, que se puede implementar en cualquier programa de elementos finitos (sin necesidad de modificar su código) y cuyos resultados coinciden con los encontrados en la bibliografía.

BIBLIOGRAPHY

[1] Wartak, Marek S and Tsakmakidis, Kosmas L and Hess, Ortwin. (2011) "Introduction to metamaterials", Volume 67. Physics in Canada 1 30–34

[2] Kshetrimayum, Rakhesh S. (2004) "A brief intro to metamaterials", Volume 23. IEEE. IEEE potentials 5 44–46

[3] Lapine, M and Tretyakov, S. (2007) "Contemporary notes on metamaterials", Volume 1. IET. IET microwaves, antennas & propagation 1 3–11

[4] Bilotti, Filiberto and Sevgi, Levent. (2012) "Metamaterials: Definitions, properties, applications, and FDTD-based modeling and simulation", Volume 22. Wiley Online Library. International Journal of RF and Microwave Computer-Aided Engineering 4 422–438

[5] Ren, Xin and Das, Raj and Tran, Phuong and Ngo, Tuan Duc and Xie, Yi Min. (2018) "Auxetic metamaterials and structures: a review", Volume 27. IOP Publishing. Smart materials and structures 2 023001

[6] Smith, David R and Pendry, John B and Wiltshire, Mike CK. (2004) "Metamaterials and negative refractive index", Volume 305. American Association for the Advancement of Science. Science 5685 788–792

[7] Tancogne-Dejean, Thomas and Karathanasopoulos, Nikolaos and Mohr, Dirk. (2019) "Stiffness and Strength of Hexachiral Honeycomb-Like Metamaterials", Volume 86. Journal of Applied Mechanics 11

[8] Cui, Tie Jun and Smith, David R and Liu, Ruopeng. (2010) "Metamaterials". Springer

[9] Longhui He and Lianwen Deng and Yuhan Li and Heng Luo and Jun He and Shengxiang Huang and Hong Chen. (2018) "Wide-angle microwave absorption performance of polyurethane foams combined with cross-shaped metamaterial absorber", Volume 11. Results in Physics 769-776

[10] Kadic, Muamer and Bückmann, Tiemo and Schittny, Robert and Wegener, Martin. (2013) "Metamaterials beyond electromagnetism", Volume 76. IOP Publishing. Reports on Progress in physics 12 126501

[11] Yoon, Gwanho and Kim, Inki and Rho, Junsuk. (2016) "Challenges in fabrication towards realization of practical metamaterials", Volume 163. Elsevier. Microelectronic Engineering 7–20

[12] Gwanho Yoon and Inki Kim and Junsuk Rho. (2016) "Challenges in fabrication towards realization of practical metamaterials", Volume 163. Microelectronic Engineering 7-20

[13] Kelly, A. (2006) "Why engineer porous materials?", Volume 364. The Royal Society London. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 1838 5–14

[14] Liu, Yongmin and Zhang, Xiang. (2011) "Metamaterials: a new frontier of science and technology", Volume 40. Royal Society of Chemistry. Chemical Society Reviews 5 2494–2507

[15] Rodger M. Walser. (2001) "Electromagnetic metamaterials", Volume 4467. International Society for Optics and Photonics. Complex Mediums II: Beyond Linear Isotropic Dielectrics. SPIE 1 – 15

[16] Gibson, L.J. and Ashby, M.F. (1999) "Cellular Solids: Structure and Properties". Cambridge University Press

[17] Shekhawat, Ashivni. (2016) "Toughness and damage tolerance of fractal hierarchical metamaterials". arXiv preprint arXiv:1611.01719

[18] Turco, Emilio and Dell’Isola, Francesco and Rizzi, Nicola Luigi and Grygoruk, Roman and Müller, Wolfgang H and Liebold, Christian. (2016) "Fiber rupture in sheared planar pantographic sheets: numerical and experimental evidence", Volume 76. Elsevier. Mechanics Research Communications 86–90