Numerical solution of diffusion equation using a method of lines and generalized finite differences

Abstract

One of the greatest challenges in the area of applied mathematics continues to be the design of numerical methods capable of approximating the solution of partial differential equations quickly and accurately. One of the most important equations, due to the hydraulic and transport applications it has, and the large number of difficulties that it usually presents when solving it numerically is the Diffusion Equation.

In the present work, a Method of Lines applied to the numerical solution of the said equation in irregular regions is presented using a scheme of Generalized Finite Differences. A series of tests and numerical results are presented, which show the accuracy of the proposed method.

keywords Generalized Finite Differences, Method of Lines, Diffusion Equation, Irregular Regions

1 Introduction

When a substance is been transported with a speed equal to zero, i.e. no flow moves it, then, according to the transport equation [1], the initial profile of the substance should remain the same as time goes by, maintaining the substance concentration at each point in the fluid.

However, in practice, this does not happen due to molecular diffusion; this is due to the molecules are in constant motion, causing collisions and rebounds in different directions. The molecules will tend to separate, or diffuse, within the flow. In general, this movement moves from areas with a higher density of molecules to areas with a lower density.

Taking into account that the diffusive flux of a substance, ${\textstyle f(u)}$ in any part of a system is proportional to the gradient of its density, then it can be written as:

$f(u)=-\nu \nabla u(x,t)=-\nu {\frac {\partial }{\partial x}}u(x,t)$

(1)

where ${\textstyle \nu }$ represents the diffusion coefficient, which tells how easy a substance diffuses in a medium.

Since the change in total mass in a given interval ${\textstyle [x1,x2]}$ is due to the flux at the extreme points, then

${\frac {d}{dt}}\int _{x_{1}}^{x_{2}}u(x,t)dx=f(u(x_{1},t))-f(u(x_{2},t)).$

Assuming enough smoothness for the functions ${\textstyle u}$ and ${\textstyle f}$, the expression can be written as

$\int _{x_{1}}^{x_{2}}\left[{\frac {\partial }{\partial t}}u(x,t)+{\frac {\partial }{\partial x}}f(u(x,t))\right]dx=0$

Since this integral must be equal to zero for any ${\textstyle x_{1}}$ and ${\textstyle x_{2}}$ values, then the integrand must be identically zero. This is,

${\frac {\partial }{\partial t}}u(x,t)+{\frac {\partial }{\partial x}}f(u(x,t))=0,$

(2)

which is a formula know as a conservation law.

Replacing the flow equation (1) in the conservation law (2) it is possible to obtain,

${\frac {\partial }{\partial t}}u(x,t)+{\frac {\partial }{\partial x}}\left(-\nu {\frac {\partial }{\partial }}u(x,t)\right)=0$

which, making some pertinent derivations, takes the form

${\frac {\partial }{\partial t}}u(x,t)=\nu {\frac {\partial ^{2}}{\partial x^{2}}}u(x,t),$

(3)

which is known as the diffusion equation in a spatial dimension. This equation is also known as the heat equation, since heat diffuses in a similar way.

This same idea can be extended [2], following a similar process to the previous one, to define the diffusion equation in a plane as

${\frac {\partial }{\partial t}}u(x,y,t)=\nu \left({\frac {\partial ^{2}}{\partial x^{2}}}u(x,y,t)+{\frac {\partial ^{2}}{\partial y^{2}}}u(x,y,t)\right).$

(4)

For the case of interest of this work, it is important to obtain an approximation in generalized finite differences, for the spatial part, to the solution of the problem

${\frac {\partial }{\partial t}}u(x,y,t)=\nu \left({\frac {\partial ^{2}}{\partial x^{2}}}u(x,y,t)+{\frac {\partial ^{2}}{\partial y^{2}}}u(x,y,t)\right)\Omega \times [0,T]\nu \in I\!\!R,$ $u(x,y,0)=g(x,y)(x,y)\in \Omega ,$ $u(x,y,t)|_{\partial \Omega }=g(x,y,t)(x,y)\in \Omega t\in [0,T],$

Where ${\textstyle \Omega }$ is a simply connected planar domain, and its boundary, ${\textstyle \partial \Omega }$, is a positively oriented Jordan polygon, as the domain shown in Figure 1.

In this case, for the temporal discretization, a Method of Lines is proposed [3].

Figure 1: Example of an $\Omega$ domain.

2 Proposed Scheme

For the case of diffusion equation

${\frac {\partial }{\partial t}}u(x,y,t)=\nu \left({\frac {\partial ^{2}}{\partial x^{2}}}u(x,y,t)+{\frac {\partial ^{2}}{\partial y^{2}}}u(x,y,t)\right),$

it is possible to discretize the spatial derivatives applying a generalized finite differences method, for that it is convenient to considerate the approximation to the second order linear operator

$Lu=Au_{xx}+Bu_{xy}+Cu_{yy}+Du_{x}+Eu_{y}+Fu,$

(5)

where ${\textstyle A}$, ${\textstyle B}$, ${\textstyle C}$, ${\textstyle D}$, ${\textstyle E}$, and ${\textstyle F}$ are given functions. Within an arbitrary distribution of nodes, as the one presented on Figure 2, it is possible to approximate its value at a node ${\textstyle p_{0}=(x_{0},y_{0})}$ using values of ${\textstyle u}$ at some neighbor nodes ${\textstyle p_{i}=(x_{i},y_{i})}$, ${\textstyle i~=~1,2,\dots ,q}$ [4]. For this work, a finite difference scheme is applied at the node ${\textstyle p_{0}}$, which can be written as a linear combination as

$L_{0}=\Gamma _{0}u(p_{0})+\Gamma _{1}u(p_{1})+...+\Gamma _{q}u(p_{q})=\sum _{i=0}^{q}\Gamma _{i}u(p_{i}).$

(6)

where ${\textstyle \Gamma _{0},\Gamma _{1},\dots ,\Gamma _{q}}$ are adequate weighs.

Figure 2: Arbitrary distribution of $p_{0}$ and its neghbors.

According to [5,6], a finite difference scheme ${\textstyle L_{0}}$ is consistent with the linear operator ${\textstyle L}$ if the local truncation error ${\textstyle \tau }$ satisfies that

$\tau =\left[Lu\right]_{p_{0}}-[L_{0}u]_{p_{0}}\to 0$

(7)

as ${\textstyle p_{1}}$, ${\textstyle p_{2}}$, ${\textstyle \dots }$, ${\textstyle p_{q}\to p_{0}}$.

Using the six first terms of Taylor's series expansion, up to second order, of the consistency condition (7), it is possible to obtain the system

$\left({\begin{array}{lclc}1&1&...&1\\0&\Delta x_{1}&...&\Delta x_{q}\\0&\Delta y_{1}&...&\Delta y_{q}\\0&(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\0&\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\0&(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right)\left({\begin{array}{l}\Gamma _{0}\\\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right)=\left({\begin{array}{l}F(p_{0})\\D(p_{0})\\E(p_{0})\\2A(p_{0})\\B(p_{0})\\2C(p_{0})\\\end{array}}\right),$

(8)

where ${\textstyle \Delta x_{i}=x_{i}-x_{0}}$ and ${\textstyle \Delta y_{i}=y_{i}-y_{0}}$. In order to solve this linear system, it is possible to separate the first equation of the system (8)

$\sum _{i=0}^{q}\Gamma _{i}-F(p_{0})=0$

(9)

and then, the problem defined by

$\left({\begin{array}{lcl}\Delta x_{1}&...&\Delta x_{q}\\\Delta y_{1}&...&\Delta y_{q}\\(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right)\left({\begin{array}{l}\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right)=\left({\begin{array}{l}D(p_{0})\\E(p_{0})\\2A(p_{0})\\B(p_{0})\\2C(p_{0})\\\end{array}}\right),$

(10)

can be solved using the reduced Cholesky factorization of its normal equations, as in [7], namely

$M^{T}M\Gamma =M^{T}\beta ,$

where

$M=\left({\begin{array}{clc}\Delta x_{1}&...&\Delta x_{q}\\\Delta y_{1}&...&\Delta y_{q}\\(\Delta x_{1})^{2}&...&(\Delta x_{q})^{2}\\\Delta x_{1}\Delta y_{1}&...&\Delta x_{q}\Delta y_{q}\\(\Delta y_{1})^{2}&...&(\Delta y_{q})^{2}\\\end{array}}\right),\quad \Gamma =\left({\begin{array}{l}\Gamma _{1}\\\Gamma _{2}\\.\\.\\.\\\Gamma _{q}\\\end{array}}\right),\quad \beta =\left({\begin{array}{l}D(p_{0})\\E(p_{0})\\2A(p_{0})\\B(p_{0})\\2C(p_{0})\\\end{array}}\right).$

The value of ${\textstyle \Gamma _{0}}$ is then obtained from (9) assuming, for the case of the diffusion equation, ${\textstyle F(p_{0})=0}$.

Now, the scheme defined by (10) can be used to approximate the linear operator

$Lu=\nu \left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}\right)$

taking ${\textstyle A=C=\nu }$, and ${\textstyle B=D=E=0}$. The resulting ${\textstyle \Gamma _{i}}$ coefficients, define the Finite-Difference Scheme

$u_{0}^{k+1}=u_{0}^{k}+\sum _{i=0}^{q}\Gamma _{i}u_{i}^{k},$

(11)

for diffusion equation, where ${\textstyle k}$ represent the time level and ${\textstyle u_{i}^{k}}$ is the approximation to the solution in the point ${\textstyle p_{i}=(x_{i},y_{i})}$ at time ${\textstyle k\Delta t}$.

An important issue to be taken into account is the number of neighbors, ${\textstyle q}$, to use in the scheme. In this paper, 8 neighbor points were taken into account following the stencil shown in Figure 3.

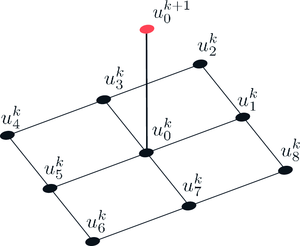
Figure 3: Centered stencil used in the scheme.

Once a discretization of the spatial operator is obtained, the problem of finding an approximation to the solution of the diffusion equation

${\frac {\partial u}{\partial t}}=L_{0},$

can be solved as a linear system of ordinary differential equations in time; which can be solved through a Runge-Kutta method. In the present work it is proposed to use Runge-Kutta [8] of order 2, 3, and 4 as follows:

Second order Runge-Kutta

$u^{k}=u^{k-1}+{\frac {\Delta t}{2}}\left(r_{1}+r_{2}\right),$

where

$r_{1}=u^{k-1},$

$r_{2}=u^{k-1}+{\frac {\Delta t}{2}}(r_{1}).$

Third order Runge-Kutta

$u^{k}=u^{k-1}+{\frac {\Delta t}{6}}\left(r_{1}+4r_{2}+r_{3}\right),$

where

$r_{1}=u^{k-1},$

$r_{2}=u^{k-1}+{\frac {\Delta t}{2}}(r_{1}),$

$r_{3}=u^{k-1}+\Delta t(2r_{2}-r_{1}),$

Fourth order Runge-Kutta

$u^{k}=u^{k-1}+{\frac {\Delta t}{6}}\left(r_{1}+2r_{2}+2r_{3}+r_{4}\right),$

where

$r_{1}=u^{k-1},$

$r_{2}=u^{k-1}+{\frac {\Delta t}{2}}(r_{1}),$

$r_{3}=u^{k-1}+{\frac {\Delta t}{2}}(r_{2}),$

$r_{4}=u^{k-1}+\Delta t(r_{3}),$

in all the cases, ${\textstyle k}$ represents the time level.

3 Numerical tests

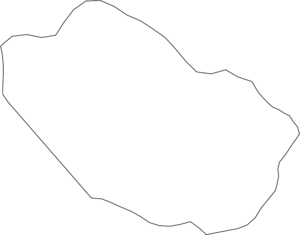
To show the performance of the proposed scheme, the problem of obtaining a numerical solution to diffusion equation on three different regions was proposed. The three regions, denoted as CAB, MID and UP, are non-rectangular planar domains and are shown on Figures 4a to 5.

(a) CAB region.	(b) MID region.
Figure 4

Figure 5: UP region.

All the regions were scaled to fit on ${\textstyle [0,1]\times [0,1]}$, and meshed with ${\textstyle 21\times {21}}$ nodes, following a variational procedure implemented in UNAMalla [9], then they were subdivided to obtain meshes with ${\textstyle 41\times {41}}$ nodes.

For all the regions, the initial and boundary conditions were taken from the closed form solution:

$g(x,y,t)=e^{(-2\pi ^{2}\nu t)}\cos(\pi x)\cos(\pi y)$

The time interval ${\textstyle [0,1]}$ was subdivided with different discretizations, the number of time steps was chosen to satisfy the classical Courant condition [10]:

$\Delta t={\frac {(\max(\Delta x))^{2}+(\max(\Delta y))^{2}}{2\nu }},$

where ${\textstyle \Delta x}$ and ${\textstyle \Delta y}$ are the spatial steps on each grid, taken from the meshes with ${\textstyle 41\times {41}}$ nodes, and ${\textstyle \nu =0.2}$.

The norm of the quadratic error, at a ${\textstyle k-}$th time level, can be computed as

$\|e^{k}\|_{2}={\sqrt {\sum _{i,j}(u_{i,j}^{k}-U_{i,j}^{k})^{2}A_{i,j}}}$

where ${\textstyle U_{i,j}^{k}}$ and ${\textstyle u_{i,j}^{k}}$ are the approximated and theoretical solutions, respectively, at the ${\textstyle i,j}$-th grid node, and ${\textstyle A_{i,j}}$ is the area of the polygon defined by the points ${\textstyle P_{i+1,j}}$, ${\textstyle P_{i,j+1}}$, ${\textstyle P_{i-1,j}}$ and ${\textstyle P_{i,j-1}}$.

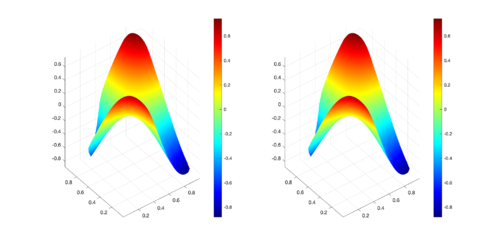
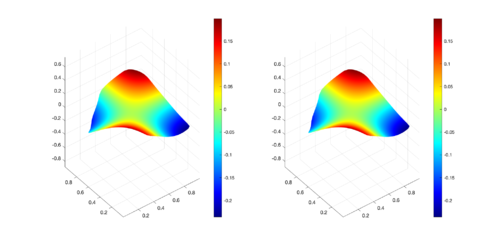
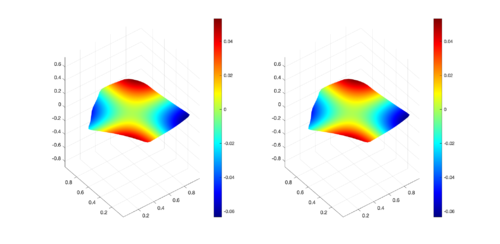
The set of Figures 6 to 9 presents a comparison of the numerical results obtained, for some time levels, with the proposed scheme using the fourth order Runge-Kutta approximation and the exact solution for CAB region. The approximation is presenten on the left, and the exact solution on the right.

Figure 6: Comparison between numerical results (left) and exact solution (right) for CAB region at $t=0$s.

Figure 7: Comparison between numerical results (left) and exact solution (right) for CAB region at $t=0.33$s.

Figure 8: Comparison between numerical results (left) and exact solution (right) for CAB region at $t=0.66$s.

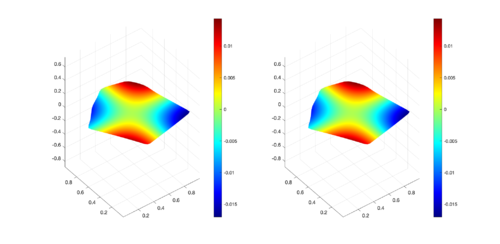
Figure 9: Comparison between numerical results (left) and exact solution (right) for CAB region at $t=1$s.

In a similar way, the sets of Figures 10 to 13, and 14 to 17 present the respective comparisons for the MID and the UP regions.

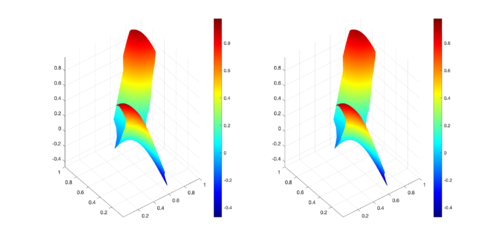
Figure 10: Comparison between numerical results (left) and exact solution (right) for MID region at $t=0$s.

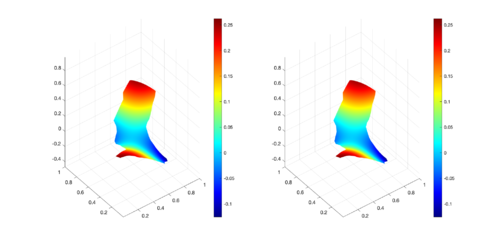
Figure 11: Comparison between numerical results (left) and exact solution (right) for MID region at $t=0.33$s.

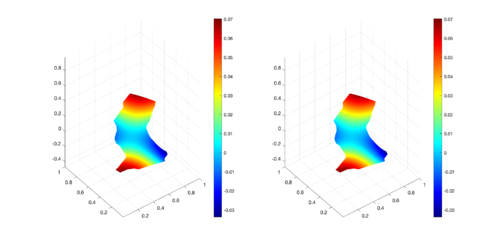
Figure 12: Comparison between numerical results (left) and exact solution (right) for MID region at $t=0.66$s.

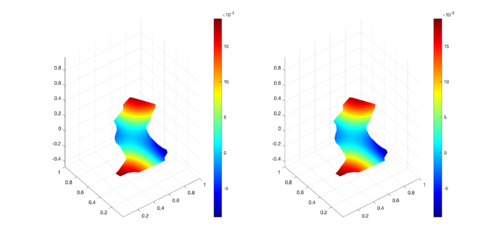
Figure 13: Comparison between numerical results (left) and exact solution (right) for MID region at $t=1$s.

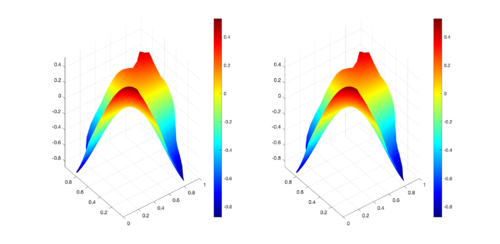
Figure 14: Comparison between numerical results (left) and exact solution (right) for UP region at $t=0$s.

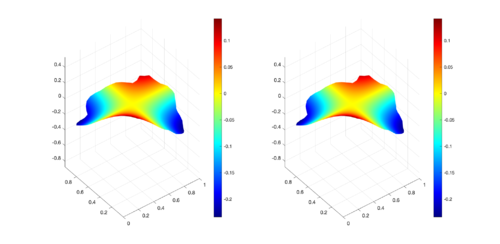
Figure 15: Comparison between numerical results (left) and exact solution (right) for UP region at $t=0.33$s.

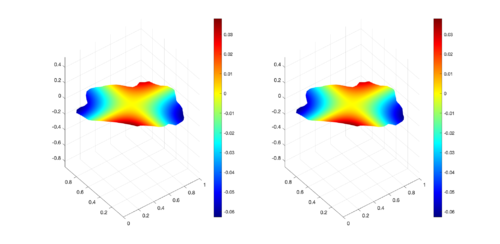
Figure 16: Comparison between numerical results (left) and exact solution (right) for UP region at $t=0.66$s.

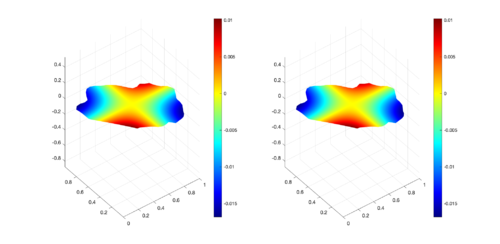
Figure 17: Comparison between numerical results (left) and exact solution (right) for UP region at $t=1$s.

Table 1 shows the results of the computed quadratic errores computed for all the test on CAB region. All the methods are reported with the following names: RKN, where N represents the Runge-Kutta order. Analogously, Tables 2 and 3 present the results for MID and UP regions respectively.

Table. 1 Computed $\|e^{k}\|_{2}$ for CAB.

CAB region
Method	time	$21\times {21}$nodes	$41\times {41}nodes$
RK2	$0.25$s	$1.1987E-04$	$2.6751E-05$
	$0.50$s	$4.5951E-05$	$1.0264E-05$
	$0.75$s	$1.7339E-05$	$3.8606E-06$
	$1.00$s	$6.5273E-06$	$1.4495E-06$
RK3	$0.25$s	$1.2515E-04$	$3.172E-05$
	$0.50$s	$4.7959E-05$	$1.2136E-05$
	$0.75$s	$1.8110E-05$	$4.5797E-06$
	$1.00$s	$6.8218E-06$	$1.7241E-06$
RK4	$0.25$s	$4.7901E-05$	$1.2122E-05$
	$0.50$s	$6.7934E-06$	$1.7169E-06$
	$0.75$s	$9.5131E-07$	$2.4025E-07$
	$1.00$s	$1.3353E-07$	$3.3712E-08$

Table. 2 Computed $\|e^{k}\|_{2}$ for MID.

MID region
Method	time	$21\times {21}$nodes	$41\times {41}nodes$
RK2	$0.25$s	$6.0947E-04$	$1.3452E-04$
	$0.50$s	$2.3585E-04$	$5.1647E-05$
	$0.75$s	$8.8078E-05$	$1.9274E-05$
	$1.00$s	$3.2834E-05$	$7.1847E-06$
RK3	$0.25$s	$6.0920E-04$	$1.3433E-04$
	$0.50$s	$2.3574E-04$	$5.1570E-05$
	$0.75$s	$8.8040E-05$	$1.9245E-05$
	$1.00$s	$3.2819E-05$	$7.1739E-06$
RK4	$0.25$s	$2.3575E-04$	$5.1571E-05$
	$0.50$s	$3.2817E-05$	$7.1734E-06$
	$0.75$s	$4.5586E-06$	$9.9644E-07$
	$1.00$s	$6.3330E-07$	$1.3843E-07$

Table. 3 Computed $\|e^{k}\|_{2}$ for UP.

UP region
Method	time	$21\times {21}$nodes	$41\times {41}nodes$
RK2	$0.25$s	$7.7062E-04$	$2.0092E-04$
	$0.50$s	$3.8002E-04$	$9.7678E-05$
	$0.75$s	$1.5808E-04$	$4.0295E-05$
	$1.00$s	$6.1880E-05$	$1.5696E-05$
RK3	$0.25$s	$7.7432E-04$	$2.0465E-04$
	$0.50$s	$3.8204E-04$	$9.9664E-05$
	$0.75$s	$1.5896E-04$	$4.1144E-05$
	$1.00$s	$6.2233E-05$	$1.6032E-05$
RK4	$0.25$s	$3.8188E-04$	$9.9622E-05$
	$0.50$s	$6.2129E-05$	$1.6005E-05$
	$0.75$s	$8.9096E-06$	$2.2853E-06$
	$1.00$s	$1.2497E-06$	$3.2014E-07$

4 Conclusions

It can be observed in the results presented in this work that the Line Method proposed for the solution of the diffusion equation produces satisfactory numerical solutions of the equation. In the tests carried out, no spurious oscillations or instabilities were perceived; Furthermore, it is shown that the approximations are more precise when using a fourth-order Runge-Kutta method.

It is possible to appreciate that with the presented discretizations, even with the second-order Runge-Kutta method, acceptable numerical results can be obtained. Additionally, the numerical results in Tables 1 to 3 show that a refinement of the spatial mesh can improve the approximations carried out with the method; as expected in this kind of methods. It is worth mentioning that, for all the tests, a minimum number of time steps was used, taking into account the classical theory for the diffusion equation, which makes the computational cost of this method low, since it does not require making very small temporary discretizations, as in other cases.

5 Acknowledgments

We want to thank AULA CIMNE-Morelia and CIC-UMSNH for the financial support for this work.

Special thanks to the ``Laboratorio de Matemáticas Aplicadas of the ``Facultad de Ciencias Físico-Matemáticas at ``Universidad Michoacana de San Nicolás de Hidalgo for lending their computational infrastructure.

BIBLIOGRAPHY

[1] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz and Juan Salvador Lucas-Martínez. (2018) "Aproximación de la Ecuación de Advección en Regiones Irregulares Utilizando un Método de Líneas y Diferencias Finitas Generalizadas", Volume 2. Revista Mexicana de Métodos Numéricos 2

[2] Victorita Dolean and Pierre Jolivet and Frédéric Nataf. (2015) "An Introduction to Domain Decomposition Methods: Algorithms, Theory, and Parallel Implementation". Society for Industrial and Applied Mathematics

[3] William Schiesser. (1991) "The Numerical Method of Lines". San Diego : Academic Press

[4] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz. (2015) "Numerical Solution of Advection Equations Using Structured Grids on Plane Irregular Regions With a Finite Differences Scheme", Volume 1. Boletón de la Sociedad Mexicana de Computación Científica y Sus Aplicaciones 3 29 - 32

[5] John C. Strikwerda. (2004) "Finite Difference Schemes and Partial Differential Equations". Society for Industrial and Applied Mathematics

[6] J. W. Thomas. (1995) "Numerical Partial Differential Equations: Finite Difference Methods", Volume 2. Springer

[7] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz. (2020) "A Study of the Stability for a Generalized Finite-Difference Scheme Applied to the Advection-Diffusion Equation", Volume 176. Mathematics and Computer in Simulations 301 - 311

[8] J. C. Butcher. (1969) "Conference on the Numerical Solution of Differential Equations", Volume 109. Springer 133 - 139

[9] UNAMalla. (2011) "An Automatic Package for Numerical Grid Generation"

[10] Michael B. Abbott and Andrew D. McCowan and Ian R. Warren. (1984) "Accuracy of Short-Wave Numerical Models", Volume 110. Journal of Hydraulic Engineering 10 1287 - 1301