Research on missile consumption in wartime with the airport runway as the target

DOI: XXXXX

ARTICLE

Research on Missile Consumption in Wartime with the Airport Runway as the Target

Qiaoyang Li^*, Guiming Chen, Ziqi Li, Lingliang Xu and Zengji Wei

Xi'an Research Institute of High-Tech, Xi’an, 710025, China

^*Corresponding Author: Qiaoyang Li. Email: liqiaoyang2019@163.com

Received: XXXX Accepted: XXXX

ABSTRACT To solve the problem of insufficient research on missile consumption in wartime with the airport runway as the target, this paper takes the airport runway as the target, taking the invalidation probability as the expected target, and adopting conventional missiles with submunitions. In combination with penetration and anti-missile countermeasures, this paper publicly proposes the consumption calculation method and model for the first time, and the multi-wave strikes strategy and calculation method are proposed either. The model is verified by combining the specific airport runway, fighter jet model and missile parameters. The experiment calculates the total consumption and the corresponding probability of destroying the target, as well as the total strike wave and the corresponding probability of destroying the target. The results prove the effectiveness and accuracy of the method and model, and provide an important basis for the sufficient amount of missiles to attack airport runways in wartime. KEYWORDS Airport runway; Consumption in Wartime; Conventional missile; Multi-wave strikes

1 Introduction

With the development of science and technology and the continuous improvement of weapons and equipment, modern warfare has increasingly shown the characteristics of high technology, high strength, and high synthesis. In a complex and changeable modern war, effectively weakening the enemy’s air military capabilities and sustained combat capabilities are of great significance to gaining the commanding heights of the war. As the main site of air raid operations, military airport is one of the key targets of the enemy. The airport runway is an important place for the fighter aircraft to take off, land, taxi and organize and guarantee aircraft activities. It is an important support for air operations and military training activities [1]. The airport runway area is large, while conventional missiles carrying submunitions are powerful, wide-ranging, accurate, and have a certain degree of intelligence [2], therefore, using conventional missiles carrying submunitions to attack airport runways is one of the important ways to block enemy airpower support and seize battlefield air supremacy. The research on missile consumption in wartime with the airport runway as the target provides an important basis for ensuring sufficient ammunition to strike the target in wartime.

At present, the related research on missile consumption in wartime with the airport runway as the target is highly confidential, and there are few published documents. When studying conventional missiles attacking airport runways, the main focus is on the impact of the aiming point on the invalidation probability with the known number of missiles[3]. Therefore, it is necessary to further study how to calculate the number of missiles that should be prepared based on the preset invalidation probability before the battle. For the research on the dispersion of sub-warheads of conventional missiles, analytical methods, statistical test methods, and simulation methods are generally used [4]. However, the analysis method cannot solve the randomness problem in the dispersion, and the statistical test method needs a large amount of data as support, which is difficult to solve. Therefore, in the dispersion study of submunitions, the simulation method is the most widely used.

Since the airport runway belongs to large military targets, it is difficult to successfully destroy it at one time. The attack on the airport usually requires multi-waves strikes [5]. How to rationally plan the various operational links of multi-wave strikes, clarify the tasks of each combat stage, and formulate scientific and reasonable multi-wave strike plans [6], which is conducive to improving the combat effectiveness of conventional missiles against the airport runway [7, 8].

The main innovations of this paper are as follows:

(1) This paper publicly proposes a method for calculating the missile consumption in wartime with the airport runway as the target for the first time.

(2) Different from the traditional research of judging whether the strike effect meets the invalidation probability when the number of missiles is known, the invalidation probability is used as a preset condition, and the minimum consumption that meets the condition is calculated through the gradual increase of the strike azimuth.

(3) Incorporate penetration and anti-missile countermeasures into the consumption calculation model.

(4) Through a large number of multi-wave strike simulation experiments, calculate the maximum and minimum consumption, strike waves and the probability of destroying the target.

The main structure of this paper is as follows: Section 1 introduces the related research work and the innovative points and structure of the paper; Section 2 establishes a missile consumption simulation model in wartime with the airport runway as the target; Section 3 verifies the model through simulation experiments for the specific airport runway, and the optimal consumption, strike wave and destruction probability are calculated; Section 4 summarizes the work and conclusions of the paper.

2 A Simulation Model of Missile Consumption in Wartime with the Airport Runway as Target

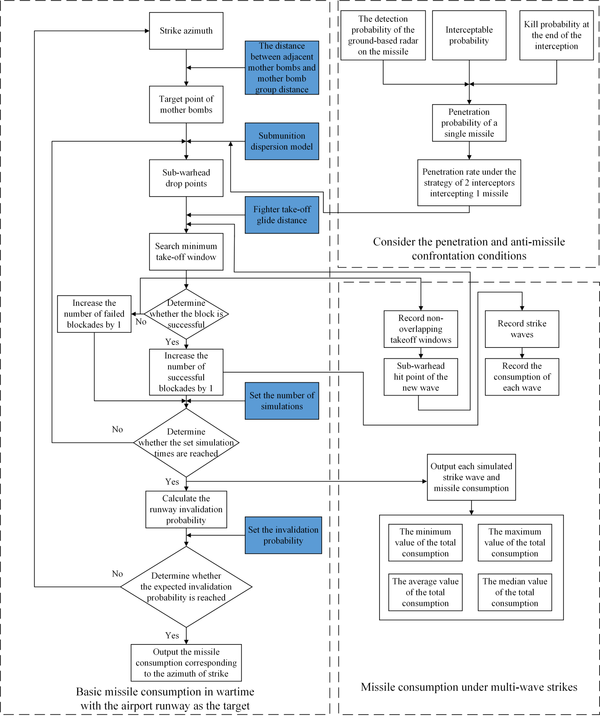
Figure 1 shows the simulation process of missile consumption in wartime with the airport runway as the target.

Figure 1: The simulation flow chart of missile consumption in wartime

with the airport runway as the target

The simulation model is based on the following basic assumptions:

(1) Defining the opposing parties: the missile striker is the red side, and the airport party is the blue side;

(2) Regardless of the changes in the guidance process of the missile of the red side, only the final guidance accuracy of the guidance method, that is, the circular error probable (CEP), is considered;

(3) Assume that there are no dumb bombs or failures in the missiles of the red side;

(4) The launch reliability and flight reliability of the missile of the red side are not considered;

(5) Assume that the crater area of the missile of the red side is equal to the average crater area and is a perfect circle;

(6) Assuming that the airport runway of the blue side is within range;

(7) Assume that the target of the blue side is consistent with the intelligence.

2.1 Basic Missile Consumption in Wartime with the Airport Runway as Target

Conventional missiles carrying submunitions are generally used to strike airport runways, and In the traditional simulation process, the invalidation probability of the runway is generally used to evaluate the runway strike effect [9,10]. In order to calculate the basic consumption of missiles in wartime, this paper takes the invalidation probability of the runway as the expected condition, that is, the input index. Then calculate the minimum consumption of missiles under the predetermined invalidation probability.

2.1.1 Traditional Simulation Model

Use simulation method to calculate the invalidation probability of the runway. That is, by simulating the drop points of mother bombs and the drop points of each sub-warhead, the craters formed by the sub-warheads on the runway are obtained, then determine whether the runway has the smallest window for the fighter to take off. If it exists, the blockade fails, otherwise the blockade is successful. In the same way, after M simulations, the number of successful simulation blockades is m. Then, the invalidation probability of the runway P is as follows.

(1)

Suppose a conventional missile with N sub-warheads is used to strike a single airport runway. For the i-th missile (i=1,2,...,N), its weapon parameters and target parameters are shown in Table 1.

Table 1: Weapon and target parameters table

Weapon parameters		Target parameters
Weapon accuracy	CEPi	Half length of the runway	A
The number of mother bombs	N	Half width of the runway	B
The throwing radius of the sub-warhead	Ri	Length of the minimum take-off window	a
Aiming points	(x0i,y0i)	Width of the minimum take-off window	b
The average crater area (corresponding to the airport level), r is the radius	r12	The airport level	Special grade
r22	Level I
r32	Level II
r42	Asphalt airport
The number of sub-warheads of each mother bomb	n

The schematic diagram of the airport runway is shown as Figure 2:

Figure 2: Schematic diagram of the airport runway

The mathematical model of the simulation process is as follows.

(1) The coordinate of the aiming point of the mother bomb

$\lbrace {\begin{array}{c}x_{i}=x_{0i}+{\frac {CEP_{i}}{1.17741002}}\times {\sqrt {-2ln({\alpha }_{1})}}cos(2\pi {\alpha }_{2})\\y_{i}=y_{0i}+{\frac {CEP_{i}}{1.17741002}}\times {\sqrt {-2ln({\alpha }_{1})}}sin(2\pi {\alpha }_{2})\end{array}}$

(2)

Where, α₁,α₂∈(0,1), are uniformly distributed random numbers.

(2) The coordinate of the drop point of the sub-warhead

Suppose the coordinate of the drop point of the k-th sub-warhead of the i-th mother bomb is (x_ik, y_ik).

$\lbrace {\begin{array}{c}Q_{1}=R_{i}{\sqrt {{\alpha }_{3}}}cos(2\pi {\alpha }_{4})\\Q_{2}=R_{i}{\sqrt {{\alpha }_{3}}}sin(2\pi {\alpha }_{4})\end{array}}$

(3)

Where, α₃,α₄∈(0,1), are uniformly distributed random numbers.

If

${\sqrt {Q_{1}{}^{2}+Q_{2}{}^{2}}}\leq R(i)$

(4)

Then

$\lbrace {\begin{array}{c}x_{ik}=xi+R_{i}{\sqrt {{\alpha }_{3}}}cos(2\pi {\alpha }_{4})\\y_{ik}=y_{i}+R_{i}{\sqrt {{\alpha }_{3}}}sin(2\pi {\alpha }_{4})\end{array}}$

(5)

If

${\sqrt {Q_{1}{}^{2}+Q_{2}{}^{2}}}\geq R(i)$

(6)

Then regenerate Q₁ and Q₂ to get the position of a sub-warhead in the scatter circle.

(3) Search for the smallest take-off window

Combining all craters with a radius of r, it is required that in a runway with a length of 2A and a width of 2B, there is no minimum take-off window of length a and width b. Here only consider the case that the fighter of the blue side takes off along the long side of the runway.

(4) Perform multiple simulations to ensure that the invalidation probability is basically stable

In this way, we record all simulation results, the total number of runway blockades U₁ and the total number of simulations U₀, the invalidation probability of the runway P is:

$P={\frac {U_{1}}{U_{0}}}$

(7)

2.1.2 Improved Simulation Model

First, define the missile strike azimuth $\varphi$ as the angle between the line of a set of aiming points and the long side of the runway, as shown in Figure 3; if the azimuth is 0, as shown in Figure 4.

Figure 3: Schematic diagram of strike azimuth

Figure 4: Schematic diagram of 0-degree strike azimuth

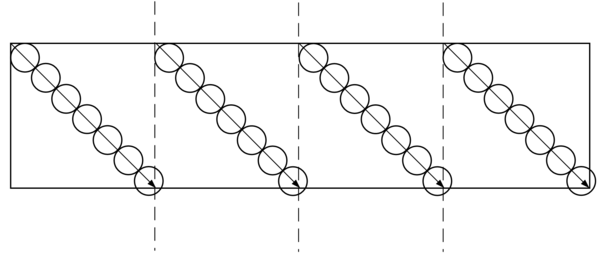
The selection of the aiming point for hitting the airport runway is shown in Figure 5. Among them, the distance between adjacent mother bombs of each group of mother bombs and the mother bomb group distance are both inputable values, as shown in Figure 6.

Figure 5: Schematic diagram of aiming point selection

$\lbrace {\begin{array}{c}x_{i}=x_{0i}+{\frac {CEP_{i}}{1.17741002}}\times {\sqrt {-2ln({\alpha }_{1})}}cos(2\pi {\alpha }_{2})\\y_{i}=y_{0i}+{\frac {CEP_{i}}{1.17741002}}\times {\sqrt {-2ln({\alpha }_{1})}}sin(2\pi {\alpha }_{2})\end{array}}$

Figure 6: Schematic diagram of the distance between adjacent mother bombs

and mother bomb group distance

Description:

(1) It is required to achieve full coverage of the end sprinkling circle in the direction of the arrow, and the radius of the circle is R_i, that is, the throwing radius of the sub-warhead;

(2) The center of each circle is the desired aiming point.

The normal simulation process takes the number of missiles as the input and the invalidation probability as the output, the goal of this paper is to take the invalidation probability as the input and the consumption as the output. And if the strike azimuth $\varphi$ is fixed, the number of missiles can be directly determined.

Therefore, the improved simulation process is as follows. Set different strike azimuths in steps from small to large (that is, determine the number of corresponding missiles), calculate the invalidation probability at different azimuths, and stop the increment if the set invalidation probability is reached, and the azimuth angle and the number of missiles are the best azimuth angle and the minimum missile consumption required.

2.2 Missile Consumption under the Penetration

In the actual combat process, the blue target will not be undefended, so it is necessary to consider the penetration process of the red missile [11-14], calculate the missile's penetration probability, and then calculate the consumption of the red missile under the condition of a single penetration.

The penetration probability of a single missile is

$p=1-p_{1}p_{2}p_{3}$

(8)

Where: p₁ is the detection probability of the blue ground-based radar on the red missile [15-18]; p₂ is the interceptable probability; p3 is the kill probability of the blue missile on the red ballistic missile [19-22].

2.2.1 The Detection Probability of the Blue Ground-Based Radar on the Red Missile

(1) Calculation of signal-to-noise ratio $\left(S/N\right)$

The search radar equation is

$R_{s}={\left[p_{Av}A{\frac {T_{f}}{\Omega }}{\frac {\sigma E_{i}(n)}{4\pi KT_{0}F_{n}(S/N)L}}\right]}^{1/4}$

(9)

The parameter explanation in the equation is shown in Table 2.

Table 2: Parameter explanation table

Parameter	Explanation
$R_{s}$	Radar detection range
$p_{Av}$	Antenna transmit average power
$A$	Radar effective area
$T_{f}$	Time to scan the entire airspace
$\Omega$	Solid angle spanned the entire airspace
$\sigma$	Target radar cross-sectional area
$E_{i}(n)$	Video pulse cumulative efficiency
K	Boltzmann constant (1.38*1023J/K)
$T_{0}$	Standard room temperature (Generally 2900K)
$F_{n}$	Noise figure
$\left(S/N\right)$	Signal-to-noise ratio
L	System loss

Equation (9) can be converted to

$R_{s}^{4}={\frac {c\sigma }{(S/N)\Omega }}$

(10)

c is the parameter that determines the performance of the radar, which can be obtained from equation (10)

$(S/N)={\frac {c\sigma }{R_{s}^{4}\Omega }}$

(11)

(2) Calculation of detection probability

The equation of detection probability is

$P_{x}={\int }_{y_{0}}^{\infty }E(y)dy$

(12)

Where: $E(y)$ is the distribution density of the mixture of signal and noise of the pulse group in one scan.

$y_{0}$ is the determined value of detection, when the false alarm is justified as $i={10}^{-6}$ , $y_{0}$ can be approximated as

$y_{0}=4.75{\sqrt {n}}+n$

(13)

Where: n is the pulse accumulation number of one scan.

Under certain circumstances, $E(y)$ has the following expression

$E(y)={\frac {n(S/N)+1}{(n-2){\left[n(S/N)\right]}^{n-1}}}e^{-{\frac {y}{n(S/N)+1}}}{\int }_{0}^{\frac {(S/N)y}{n(S/N)+1}}t^{n-2}e^{-t}dt$

(14)

Substituting equation (7) into equation (5), and the probability of false alarms is very small, so generally approximate results can be obtained

Failed to parse (syntax error): p_1=�\frac{n(S/N)+1}{n(S/N)}{�}^{n-1}e^{-\frac{y_0}{n(S/N)+1}}

(15)

2.2.2 Interceptable Probability

$p_{2}=\lbrace {\begin{array}{cc}1&t_{a}>t_{r}+t+t_{f1}\\0&t_{a}\leq t_{r}+t+t_{f1}\end{array}}$

(16)

Where: $t_{a}$ is the flight time of the red missile being tracked steadily to the vicinity of the blue missile interception zone; $t_{r}$ is the process time from the blue radar stably tracking the red ballistic missile to the identification, judgment, task assignment and determination of the predicted interceptor to the preparation for launch; $t$ is the flight time of the blue missile from launch to the near boundary of the interception zone; $t_{f1}$ is the reaction time from when the blue missile receives the launch order to the first missile.

Equation (9) is equivalent to

$p_{2}=\lbrace {\begin{array}{cc}1&R_{s}>R_{0}\\0&R_{s}\leq R_{0}\end{array}}$

(17)

Where: $R_{s}$ is the radar detection range, $R_{0}$ is the critical range.

2.2.3 The Killing Probability of the Blue Missile to the Red Ballistic Missile at the End of Interception

The blue side's probability of detonating the red missile's re-entry warhead is

$p_{3}=1-e^{-{\overline {m}}p_{c}}=1-e^{-{\frac {249}{R_{L}^{2}{sin}^{2}q_{r}}}}$

(18)

Where: $R_{L}$ is the radius of the blind zone; $q_{r}$ is the angle between the relative speed of the red and blue missiles and the line between them.

2.2.4 Consumption under penetration strategy

Combining equation (8), it can be obtained that the penetration probability of a single tactical ballistic missile of the red side against two missiles of the blue side is

$q^{'}={\left(1-p\right)}^{2}$

(19)

Based on the following assumptions:

(1) The blue side adopts the strategy of 2 interception and 1 for the red side missiles;

(2) The different mother bombs of the red side can be regarded as facing different small targets, so the overall penetration rate of all the red side missiles can be regarded as $q^{'}$ .

Therefore, to calculate the consumption in the case of penetration, it is necessary to randomly remove $1-q^{'}$ of the sub-warheads of all the mother bombs in the strike planning in the simulation in Section 2.1 (that is, the total number of missiles successfully striking the runway is the number of missiles under the determined attack azimuth angle multiplied by $q^{'}$ ). Repeat the process of searching the minimum take-off window and calculating the invalidation probability in section 2.1.

2.3 Consumption under the Multi-Wave Strikes

In combat, the red missile will be intercepted by the blue anti-missile defense system under a single wave of strikes. Therefore, multi-wave strikes are required to achieve the established blockade rate requirement.

In Figure 7, the red box represents the minimum take-off window searched for when evaluating the results after the first wave of strikes.

Figure 7: Schematic diagram of the minimum take-off window

Assuming the penetration rate is $q^{'}$ , in a simulated multi-wave strike,

(1) The total number of red missiles in the first wave of strikes is $number_{1}$ . Next, judge whether there is a minimum take-off window after the first wave of strikes. If it does not exist, there is no need to conduct multi-wave strikes. The strike wave is recorded as 1, the consumption of the red missiles is denoted as $N=number_{1}$ ;

(2) If there is a minimum take-off window, search and count the total number of non-overlapping windows. The result is marked as $number_{2}$ . The window arrangement and number results are non-unique. Just consider a random result here. If there is a minimum take-off window $number_{2}$ , the total number of red missiles in the second wave of strikes is $number_{2}$ , and the aiming point of each missile's simulated strike is the geometric center of the minimum take-off window. After $q^{'}$ penetration (round the result), the evaluation is carried out. Judge whether there is a take-off window, if not, the consumption of the red missile is recorded as $N=number_{1}+number_{2}$ ;

(3) If there is a minimum take-off window, continue to strike and search according to (2);

……

(4) Finally get the number of strike waves, the number of waves of the red missile and the total consumption of the red missile;

(5) Carry out multiple multi-wave strikes simulations to find the strike wave and missile consumption for each simulation. Finally, output the minimum, maximum, average, and median of the total consumption.

3 Simulation Experiment

3.1 Experimental Process

According to the simulation model and process, based on the C# development environment, a simulation software is developed to facilitate rapid simulation and calculation of results.

Select the I-level airport runway in a certain area as the strike target, suppose the fighter model is F-16 [22-25], combined with the parameters of a certain type of missile, the weapon parameters, target parameters and simulation parameters are shown in Table 3.

Table 3: Experimental data table

Weapon parameters		Target parameters		Simulation parameters
Weapon accuracy CEP/m	60	Length of the runway/m	3000	The minimum invalidation probability	0.75
The throwing radius of the sub-warhead/m	80	Width of the runway/m	50	Increasing azimuth	5°
The average radius of the crater (the airport level：Level I)/m	2.5	Length of the minimum take-off window/m	533	The distance between adjacent mother bomb/m	533
The number of sub-warheads of each mother bomb	30	Width of the minimum take-off window/m	20	Mother bomb group distance/m	533

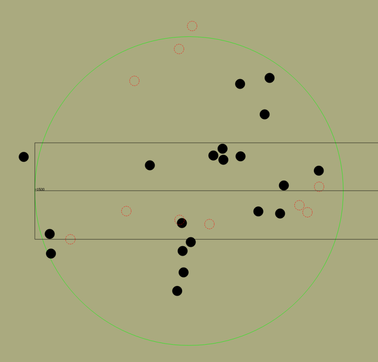
When setting up the penetration and anti-missile countermeasure module, assuming that the anti-missile system is the "Patriot" and its supporting system [26, 27], the final penetration probability of a single missile is 0.8. Combine formula (19) to perform a single-wave penetration simulation to obtain a simulation diagram. Since the original simulation diagram is too slender, the local interception is explained, as shown in Figure 8.

Figure 8: A partial diagram of a single-wave penetration simulation

As shown in Figure 8, the green circle represents the sub-warhead throwing circle, the black solid circle represents the crater left after the sub-warhead strikes the airport, and the red dotted circle represents the sub-warhead that was successfully intercepted.

Based on the single-wave penetration simulation, 1000 multi-wave penetration simulations were performed respectively. The results are shown in Table 4.

Table 4: Multi-wave penetration simulation table

Number of simulations	The first wave consumption	The second wave consumption	The third wave consumption	The fourth wave consumption	The fifth wave consumption	The sixth wave consumption	The total consumption	The total strike wave
1	6	3	3	1			13	4
2	6	4					10	2
3	6	4					10	2
4	6	3	1				10	3
5	6	3	1				10	3
6	6	8	1				15	3
7	6	6	1				13	3
8	6	3	1				10	3
9	6	4	3	1			14	4
10	6	5	1				12	3
11	6	7	2	1			16	4
12	6	5	1				12	3
13	6	7	2				15	3
14	6	4	2	1	1		14	5
15	6	1	1	1			9	4
16	6	4	2				12	3
17	6	7	5	2			20	4
18	6	4	1				11	3
19	6	4	2				12	3
20	6	6					12	2
21	6	3	1				10	3
22	6	3					9	2
23	6	7	2	1			16	4
24	6	3	2				11	3
25	6	7	1				14	3
26	6	5	1				12	3
27	6	4	2	2	1	1	16	6
28	6	5					11	2
29	6	6	1				13	3
30	6	5	1	1			13	4
……
998	6	5	1	1			13	4
999	6	3	1	1	1		12	5
1000	6	4	4	1	1		16	5

3.2 Analysis of Experimental Results

Through 1000 multi-wave penetration strike simulations, the minimum total consumption is 6, the maximum is 20, the average is 12, and the median is 12. It can be concluded that to strike the set target airport runway, it is necessary to prepare at least about 6 missiles and at most about 20 missiles.

The following is a further analysis of the experimental results, the frequency, percentages and cumulative percentages of different total consumption in 1000 simulation experiments are counted, and Table 5 is obtained. For a more intuitive comparison, the histogram of the frequency of the total consumption and the percentage graph of the total consumption are made, as shown in Figure 9 and Figure 10 respectively.

Table 5: Statistics of total consumption after 1000 simulations

Total consumption	Frequency	Percentage	Cumulative percentage
6	5	0.005	0.005
7	12	0.012	0.017
8	47	0.047	0.064
9	80	0.080	0.144
10	148	0.148	0.292
11	157	0.157	0.449
12	161	0.161	0.610
13	138	0.138	0.748
14	111	0.111	0.859
15	55	0.055	0.914
16	41	0.041	0.955
17	33	0.033	0.988
18	8	0.008	0.996
19	2	0.002	0.998
20	2	0.002	1.000

$\lbrace {\begin{array}{c}Q_{1}=R_{i}{\sqrt {{\alpha }_{3}}}cos(2\pi {\alpha }_{4})\\Q_{2}=R_{i}{\sqrt {{\alpha }_{3}}}sin(2\pi {\alpha }_{4})\end{array}}$

Figure 9: Histogram of the frequency of the total consumption

${\sqrt {Q_{1}{}^{2}+Q_{2}{}^{2}}}\leq R(i)$

Figure 10: Percentage graph of the total consumption

It can be seen from Table 5 and Figure 9 that the total number of consumption of 10, 11, 12, 13 and 14 have the most occurrences, all exceeding 100 times, and they account for 71.5% of the total number of simulations. And from Table 5 and Figure 10, if the striker prepares 14 missiles, there is an 85.9% chance of destroying the target airport runway; if the striker prepares 15 missiles, there is a 91.4% chance of destroying the target airport runway.

The frequency, percentages, and cumulative percentages of different total waves in 1000 simulation experiments are calculated, and Table 6 is obtained. Make the histogram of the frequency of the total wave and the percentage graph of the total wave, as shown in Figure 11 and Figure 12 respectively.

Table 6: Statistics of the total wave after 1000 simulations

Total consumption	Frequency	Percentage	Cumulative percentage
1	5	0.005	0.005
2	263	0.263	0.268
3	489	0.489	0.757
4	188	0.188	0.945
5	42	0.042	0.987
6	10	0.010	0.997
7	2	0.002	0.999
8	1	0.001	1.000

$\lbrace {\begin{array}{c}x_{ik}=xi+R_{i}{\sqrt {{\alpha }_{3}}}cos(2\pi {\alpha }_{4})\\y_{ik}=y_{i}+R_{i}{\sqrt {{\alpha }_{3}}}sin(2\pi {\alpha }_{4})\end{array}}$

Figure 11: Histogram of the frequency of the total wave

${\sqrt {Q_{1}{}^{2}+Q_{2}{}^{2}}}\geq R(i)$

Figure12: Percentage graph of the total wave

It can be seen from Table 6 and Figure 11 that the total wave number of 3 appears the most, which is 489, reaching 48.9% of the total number of simulations. From Table 6 and Figure 12, it can be seen that with sufficient missiles, the striker has a 94.5% probability of destroying the target airport runway within 4 waves.

4 Conclusion

To solve the problem of insufficient research on missile consumption in wartime with the airport runway as the target, this paper takes the airport runway as the target, taking the invalidation probability as the expected target, and adopting conventional missiles with submunitions. In combination with penetration and anti-missile countermeasures, this paper publicly proposes the consumption calculation method and model for the first time, and the multi-wave strikes strategy and calculation method are proposed either. The model is verified by combining the specific airport runway, fighter jet model and missile parameters. In the end, under the target airport and related parameters given in this paper, if 14 missiles are prepared, there is an 85.9% probability of destroying the target airport runway; if 15 missiles are prepared, there is a 91.4% probability of destroying the target airport runway; There is a 94.5% probability that the target airport runway will be destroyed within 4 waves with sufficient missiles. In the next step, combined with the maintenance rate and timeliness, the model is further optimized.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant 71601180.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Sennaroglu, Bahar, Celebi, Gulsay, Varlik. (2018). A military airport location selection by ahp integrated promethee and vikor methods. Transportation research, Part D. Transport and environment.

2. Li, X., Luo, M., Wang, M. (2008). Composite strike method of conventional missile. Tactical Missile Technology.

3. Zhen, Z., Feng, jiang. (2017). A Study on Aim Points Selection Method for Attacking Airport Runway. Informatization Research, 43(01), 19-21+28.

4. Gao, X. (1989). Application of computer-simulation in the study of bomblet dispersion. Acta Armamentarii.

5. Wang, T., Yang, P., Ouyang, H. (2011). Investigation into multi-time missile warfare based on markov chain. Tactical Missile Technology, 4, 20-22.

6. Guangzhi, B., Bin, Z., Shuai, S. (2014). Aimpoints Selection Method Multiwave Attack Runway with Ballistic Missiles. Fire Control & Command Control, 39(11), 66-64+71.

7. Zhang, K., Liu, Y. C., Guan, S. Y. (2002). Investigation into the problem of evaluating combat effectiveness for missile weapon systems. Journal of Astronautics.

8. Kim, J., Kim, W. (2020). Simulation analysis on the effectiveness of missile defense. Journal of Peace Research, (4).

9. Ma, B., Zhou, C. Lou, L., Zhang, T. (2004). Automatic assessment of the attacked airports based on image analysis. Journal of Huazhong University of ence and Technology, 07, 13-15.

10. Miao, Q. G., Liu, J., Ning, S. T. (2012). Battle damage assessment of airport based on fuzzy comprehensive evaluation. Systems Engineering and Electronics, 34(7), 1395-1399.

11. Zou, H. (2019). Application of iterative learning algorithm based on data driving to the evaluation of missile penetration capability. Shipboard Electronic Countermeasure.

12. Feng, L. P., Fan, Z. E., Nie, Y. F. (2020). Simulation on terminal penetration trajectory of anti-ship missile under interception conditions. DEStech Transactions on Engineering and Technology Research.

13. Zhang, X. Y., Song, G. B. (2006). Design and realization of anti-ship missile penetration simulation system based on HLA. Journal of System Simulation, 08, 2350+2354.

14. Xia, J., Xie, L. Y., Wang, X. Q. (2008). Research on optimal penetration strategies of ballistic missile. Journal of Ballistics, 20(08), 65-68.

15. Feng, D. J., Wang, X. S., Liu, J. Q. (2010). Jamming effect analysis of chaff cloud on ground-based radar and its application. Modern Radar, 32(06), 22-26.

16. Zhou, Y., Wang, X. S., Wang, G. Y., Wang, L. D., Liu, Y. H. (2003). Fuzzy evaluation on radar jamming effect based on ballistic missile penetration. Systems Engineering and Electronics, 07, 807-809.

17. Zhao, F., Li, D., Wang, X. S., Xiao, S. P. (2006). Missile defense radar simulation system. Journal of System Simulation, 05, 1190-1194.

18. Yin, L., Liu, H., Zhao, X., Shufang, L. I. (2018). Research on AN/TPY-2 radar range and jamming based on radar equation. Systems Engineering and Electronics, 40(01), 50-57.

19. Lee, J. S. (1973). Optimal sam defense system: an application of optimal control concept to operations research. IEEE Transactions on Automatic Control, 18(5), 485-489.

20. Hecht, Jeff. (2010). Is there any way to defend against a ballistic missile?. New Scientist, 206(2762), 12-12.

21. Dutta, D. (2014). Probabilistic analysis of anti-ship missile defence effectiveness. Defence Science Journal, 64(2), 123-129.

22. Bethe, H. A., Garwin, R. L., Gottfried, K., Kendall, H. W. (1984). Space-based ballistic-missile defense. Scientific American, 4(4), 39-49.

23. Ron, N. (2006). How organizations learn: post-flight reviews in an F-16 fighter squadron. Organization Studies, 27(8), 1069-1089.

24. Jones, D. (2014). This systems architect builds the most advanced F-16 combat simulators. IEEE Spectrum, 51(6), 24-24.

25. Farhat, C., Geuzaine, P., Brown, G. (2003). Application of a three-field nonlinear fluid–structure formulation to the prediction of the aeroelastic parameters of an F-16 fighter. Computers & Fluids, 32(1), 3-29.

26. Holland, O. T., Wallace, S. E. (2012). Using agents to model the kill chain of the ballistic missile defense system. Naval Engineers Journal, 123(3), 141-151.

27. Marshall, E. (1991). Patriot's effectiveness challenged. Science, 254(5033), 791-791.