Siphon pipe parameter optimization of the toilet using CFD-DEM coupling method

Abstract

The computational fluid dynamics (CFD) and discrete element method (DEM) coupling method is used to simulate the flushing process of the toilet and this paper analyzes the influence of different structural parameters of siphon pipe on the flushing performance of the toilet. And through the adjusted-parameters toilet, tlushing experments were carried out to verify the simulations. Meanwhile the orthogonal test of different structural parameters of siphon pipes were conducted to study the flushing Performance. The research results show that the CFD-DEM coupling method can be used to study the regularity of the toilet flushing performance. The toilet can get the better flushing performance when the tilt angle of the angle of inclination is 50°, the curvature width and length are 50 mm and 220 mm, the width and height of the secondary water seal are 100 mm and 25 mm and pipe diameter is 53 mm. The method in this paper can provide a new idea for the study and design of the flushing performance of the toilet.

Keyword: CFD-DEM, flushing performance, structural parameters, coupling method, adjusted-parameters toilet

1. Introduction

Toilets are essential necessities in our daily life and water consumption of toilets is large among a variety of sanitary equipment [1]. The toilet flushing performance is an important index of quality assessment. And thus, constantly improving the flushing performance of the toilet has been the goal for researchers and workers in sanitary ware industry.

So far, there are two main research methods for the toilet flushing performance: simulation research and experimental research. In simulation research, CFD method was widely used by most scholars to complete the simulation of the toilet flushing process, which can only consider water flow rule [2,3]. In the experimental research, it is convenient for us to get a quantitative flushing effect, but it is not easy to get the complete flow field data [4-6]. In fact, the complex flushing process of toilet contains the interactions of flow-solids and solids-walls besides the movement process of water flow. All these factors have a certain impact on the flushing performance of the toilet. Therefore, the exploration of a new method considering the movement process of solids in the flushing process will be an important part in the study of the toilet flushing performance.

In order to incorporate the movement process of solids into the flushing process of the toilet, it is necessary for us to seek a computational model to simulate the comprehensive fluid and solid systems. And the CFD-DEM coupling method right provides a computational method for the complex model. The basic idea is that the computational fluid dynamics is used to calculate the flow of fluid, and DEM is used to calculate the force and movement of particles. The advantage of the CFD-DEM coupling method is that it can not only really simulate the flow rule of flow field, but also can take the particles’ shapes, collision, movement path and adhesion of particles into account. More importantly, it has been applied widely in many fields such as geology, sands flow, drainage machinery and so on [7-9]. In this paper, the CFD-DEM coupling method is used to study and simulate the flushing process of the toilet. Further, we verify the simulation rule by physical simulation experiments. At the same time, the orthogonal test is used to study different structural parameters of siphon pipes. All these research contents can provide references for the flushing performance analysis of the toilet and the design of siphon pipes.

2. Theory

2.1 CFD theory

The flushing process of the toilet is a typical process of fluid flow. The process of fluid flow must observe the continuity equation and the law of conservation of momentum, they can be expressed as follows:

${\frac {\partial \rho }{\partial t}}+{\frac {\partial \rho u_{i}}{\partial x_{i}}}=0$

(1)

${\frac {\partial \rho u_{i}}{\partial t}}+{\frac {\partial \rho u_{i}u_{j}}{\partial x_{j}}}=\rho f_{i}-{\frac {\partial p}{\partial x_{i}}}+{\frac {\partial }{\partial x_{j}}}\left(\mu {\frac {\partial u_{i}}{\partial x_{j}}}\right)$

(2)

The flushing process of the toilet contains the flow of free liquid surface. So far, the Volume of Fluid (VOF) method is widely used to solve the free liquid surface. VOF method is a computational method proposed by Hirt and Nichols for dealing with complex problems of free liquid surface [10]. The advantage of this method is that it can represent the complex change process of free surface by only a function. The mode of VOF based on the fluid volume method is widely used in dealing with stratified flow, free-surface flow and sloshing, and it also gets effective practice in the study for the flushing process of the toilet [2].

In the mode of VOF, different fluid components all observe the same momentum equation. In the calculation, the volume fraction of the components of different fluids in each computational element of flow field can all be stored, and the sum of the volume fractions of all phases in each control body is one. For ease of expression, assuming the volume fraction of the $j$ phase in $i$ element is $a_{j}$, three different cases are as follows:

(1) When $a_{j}=0$, it means that the j phase in i element is empty;

(2) When $a_{j}=1$, it means that the j phase in i element is completely full;

(3) When $0<a_{j}<1$, it means that there are j phase and other phases in i element.

The model of VOF can capture the interface information between different phases by the continuity equation of the volume fraction for one or more phases, such as take i phase as an example and it can be expressed as follows:

${\frac {\partial a_{i}}{\partial t}}+{\overset {\rightarrow }{v}}\cdot \nabla a_{i}=$${\frac {S_{a_{i}}}{{\rho }_{i}}}+{\frac {1}{{\rho }_{i}}}\sum _{j=1}^{n}\left({\dot {m}}_{ji}-\right.$$\left.{\dot {m}}_{ij}\right)$

(3)

where ${\dot {m}}_{ji}$ means the mass transport from $j$ phase to i phase and ${\dot {m}}_{ij}$ means the mass transport from $i$ phase to $j$ phase.

Generally speaking, the value of the item on the right is 0. When the equation of the volume fraction is not based on the principal phase, the volume fraction of the principal phase can be calculated by the following formula:

$\sum _{i=1}^{n}a_{i}=1$

(4)

when there are only two phases in the whole system, the density of each element can be calculated by the following formula:

$\rho =a_{2}{\rho }_{2}+(1-a_{2}){\rho }_{1}$

(5)

By the calculation of a single momentum equation in all regions, the results are shared by all phases. The volume fraction of the phase expressed by momentum equation can be expressed by the following formula:

${\frac {\partial }{\partial t}}(\rho {\overset {\rightarrow }{v}})+$$\nabla \cdot (\rho {\overset {\rightarrow }{v}}{\overset {\rightarrow }{v}})=$$-\nabla p+\nabla \cdot \left[\mu (\nabla {\overset {\rightarrow }{v}}+\nabla {\overset {\rightarrow }{v}}^{T})\right]+\rho {\overset {\rightarrow }{g}}+{\overset {\rightarrow }{F}}$

(6)

2.2 DEM Theory

DEM is a new computational method proposed by Cundall and Track [11], which can be used to solve the laws of motion and mechanical properties of complex discrete systems, and it is first applied effectively in geomechanics. DEM has been playing an important role in many fields such as granular engineering since it was proposed [12,13]. Its basic idea is to divide a discontinuity into a series of individuals with many rigid elements, and make all rigid elements satisfy the equations of motion. Then, the equations of motion of all rigid elements are calculated by time-step iteration method to get the global motion state of the discontinuity. The calculation principle of discrete element method can be expressed by the following formula:

${\ddot {x}}_{j}(T)=\partial {\dot {x}}_{j}(T)/\partial T={\left(\sum F(T)\right)}_{j}/m_{j}$

(7)

${\ddot {\theta }}_{j}(T)=\partial {\dot {\theta }}_{j}(T)/\partial T={\left(\sum M(T)\right)}_{j}/I_{j}$

(8)

where $x_{j}$ is the translational shift of $j$ unit, $\sum F(T)$ is the resultant force of j unit, $M_{j}$ is the sum of $j$ unit’s quality, $\theta _{j}$ is the angular shift of $j$ unit, $\sum M(T)$ is the resultant moment of $j$ unit.

A new shift of the unit can be obtained by the difference method or Euler method, and the new contact force and torque can be generated. Then it returns to formulas (7) and formulas (8) to update the calculation to get the motion information of all units. In the flushing process of the toilet, the solid particles in the flow field will be affected by many effect for the gravity of the particles themselves, the contact-impact force between the particles and the inner wall of siphon pipes, the fluid drag force, the fluid buoyancy, the pressure-gradient force, the false mass force and the lift force. The related results show that the drag force is the main interaction force between fluid and particles, and the effect of the false mass force and the lift force on particles can be ignored [14].

The motion of particles in the flow field can be expressed in two forms: translational motion and rotational motion. For any particle $i$, the equation of translational motion can be expressed by the following formula:

$m_{i}{\frac {d{\mbox{v}}_{i}}{dt}}=m_{i}{\mbox{g}}+{\mbox{F}}_{b}+{\mbox{F}}_{c}+{\mbox{F}}_{d}+{\mbox{F}}_{p}$

(9)

where $m_{i}$ is the mass of particle $i$; $v_{i}$ is the speed of particle $I,\,F_{b}$ is the buoyancy of particle $I,\,F_{c}$ is the contact-impact resultant force of particle $I,\,F_{d}$ is the drag force of particle $I,\,F_{P}$ is the pressure-gradient force of particle $i$.

The buoyancy force of particles in the fluid $F_{b}$ can be expressed by the following formula:

${\mbox{F}}_{b}=\rho gV_{p}$

(10)

The contact-impact force of particles $F_{c}$ can be expressed by the following formula:

${\mbox{F}}_{c}={\mbox{F}}_{cni}+{\mbox{F}}_{cti}+{\mbox{F}}_{dni}+$${\mbox{F}}_{dti}$

(11)

where $F_{cni}$ is the normal contact force of particles, $F_{cti}$ is the tangential contact force of particles, $F_{dni}$ is the normal damping force of particles and $F_{dti}$ is the tangential damping force of particles.

The magnitude of contact-impact force depends on the contact model when calculating, the contact-impact force is from between particles and between particles and the inner walls of siphon pipes. Hertz-Mindlin’s no slip model is used to describe this contact-impact behavior. The basic idea for Hertz-Mindlin’s no slip model is to use Hertz contact theory to calculate the normal force and Mindlin-Deresiewicz contact model to calculate the tangential contact force[15]. In this paper, spherical particles are used to study the flushing process of the toilet, the free resistance model is used to study the drag force model, and this model can be expressed by the following formula:

${\mbox{F}}_{d}=0.5C_{D}\rho A\vert v\vert v$

(12)

where $C_{D}$ is the drag coefficient, $\rho$ is the fluid density, ${\textstyle A}$ is the projected area of particles, ${\textstyle |v|}$ is the variable size of speed and ${\textstyle v}$ is the relative speed.

The drag coefficient ${\textstyle C_{D}}$ can be expressed by the following formula:

$C_{D}=\lbrace {\begin{array}{c}24/Re\,\,Re\leq 0.5\\24(1.0+0.25Re^{0.687})/Re\,\,0.5<Re\leq 1000\\0.44\,\,Re>1000\end{array}}$

(13)

where ${\textstyle Re}$ is the Reynolds number. The pressure-gradient force can be expressed by the following formula:

${\mbox{F}}_{p}=-V_{i}\nabla p_{s}$

(14)

where ${\textstyle V_{i}}$ is the volume of particle ${\textstyle i}$ and $\nabla p_{s}$ is the static pressure gradient.

For any particle ${\textstyle i}$, the equation of rotational motion in the flow field can be expressed by the following formula:

$I_{i}{\frac {d{\mbox{ω}}_{i}}{dt}}=\sum _{i=1}^{n}\left({\mbox{T}}_{i}\right)$

(15)

where ${\textstyle I_{i}}$ is the moment of inertia of particles, ${\textstyle \omega _{i}}$ isthe angular speed of particles and ${\textstyle T_{i}}$ is the torque of particles.

2.3 CFD-DEM coupled method

CFD-DEM coupling method is a numerical analysis method for multiphase flow problems of particles and fluids. It has been widely used in many fields. Its basic idea is to model the fluid as a continuous medium and calculate it in the CFD method，and DEM and Newton's second law are combined to calculate the motion of particles which are considered to be a discrete phase.

The flushing process of the toilet consists of two parts: one is the flow of water flow, the other is the movement of particles under the effect of water flow. In the process of the flow of water flow, water flow is considered to be a continuous phase, it can be calculated by solving the continuity equation and N-S equation. In the process of particle motion, particles are considered to be a discrete phase, the force and motion of particles can be calculated by Newton's second law. The data for the process of the flow of water flow and particle motion can be transmitted through the interface card.The coupling process for the flushing process of the toilet in FLUENT and EDEM is shown in Figure 1 [16-18].

Figure 1. The calculation process of CFD-DEM coupled method

According to Figure 1, in the calculation, FLUENT first calculates the flow field of an interpolation time period, and transmits the flow field information of the interpolation point to EDEM at an interpolation time interval. EDEM reads the flow field information from FLUENT, then adds various field forces to the motion equation of particles by the interface plug-in (API) and start to calculate the forces and motion of particles in the corresponding interpolation time interval. After EDEM completes the calculation in the interpolation time period, FLUENT starts to update the flow field in the next interpolation time period in circulation. The interpolation time period is the time interval of data transmission, and the value is taken the smaller and the calculation error is the smaller. The minimum interpolation time interval is a FLUENT calculation time step, that is the time step is the smaller, the calculation accuracy is the higher.

The flow field information transmitted from FLUENT to EDEM includes velocity field, volume fraction field (or density field) and pressure-gradient field. The main reason why the volume fraction field or density field need to be transmitted is that the calculation domain contains two kinds of mediums: water flow and air in the flushing process of the toilet, the field forces (buoyancy force and drag force) of particles in different mediums are different. Therefore, it is necessary to distinguish the properties of mediums in various locations in fluid domain. The interface plug-in between FLUENT and EDEM is compiled by Visual Studio development tool through API. The contents of the interface plug-in include reading the flow field information, distinguishing the properties of mediums in calculation domain, calculating field forces and setting the interpolation time interval for a transient calculation. In this paper, the effect of water flow on particles is mainly considered, and it is a one-way coupling method.

3. Simulation and experimental conditions

3.1 Simulation parameter settings

3.1.1 CFD parameter settings

In this paper, the flushing process of a siphon jet toilet with different structural parameters of siphon pipes is studied by CFD-DEM coupling method. According to the structural characteristics of the toilet model and considering the calculation time and accuracy, the hybrid grid is used to mesh, that is, the water tank part with regular structure is divided into structured grids to reduce the number of grids, and the unstructured grids are used to mesh in other areas to reduce the difficulty of meshing. The number of grids is about 2.3 million (Figure 2a).

In the CFD calculation of the flushing process, the pressure base solver is used for a transient solution. The VOF model is used to calculate the multiphase flow, and the air is setted as the first phase, water is setted as the second phase. The Realizable $k$-epsilon model is chosen for the turbulence model and the standard wall function is applied to deal with the near-wall. Pressure-velocity coupling method adopts SIMPLE algorithm, the momentum equation is discretized by second-order upwind, and turbulent kinetic energy, turbulent kinetic energy dissipation rate and transient equation are discretized by first-order upwind. According to the actual situation of the flushing process, a pressure inlet boundary condition and two pressure outlet boundary conditions are setted up, as shown in Figure 2. In Figure 2b, the red part is water, the blue part is air, and the water in the water tank is 5.5 L. The computation time step of FLUENT is 0.0002 s, the computation time is 6.6 s, and the maximum iteration step is 20 steps.

(a)	(b)
Figure 2. (a) The assembled grid model. (b) The setting of boundary conditions

3.1.2 DEM parameter settings

The solid medium in the flushing process is polypropylene spherical particles with a radius of 8.75 mm, a density of 890 kg/m$^{3}$, a flushing quantity of 130, and the wall material of the toilet is ceramic. The formation of particles is set up by the secondary development of the granular factory, that is all water tested balls are generated at the water seal position of the toilet at the beginning of the calculation, and this ensures that the initial state of the water tested balls is the same in each test in order to avoid the influence of the randomness of particle formation on the flushing results. Considering that the contact force between particles and between particles and the inner walls of the toilet, it is necessary to determine the contact parameters between particles and between particles and the walls. In this paper, a high-speed camera is used to measure the contact parameters. Detailed parameter settings are shown in Table 1. The computation time step of EDEM is setted as $2\times 10^{-6}$ s.

Table 1. The setting of EDEM parameters

Material properties	Poisson ratio	Density（kg/m$^{3}$）	Shear modulus（Pa）
Particles	0.41	890	3.2e+08
Pipe wall	0.22	2300	9.06e+10Pa
Collision attributes	Restitution coefficie	Static friction coefficient	Rolling friction coefficient
particles-particles	0.6282	0.12	0.0486
particles-walls	0.7823	0.2	0.0306

3.1.3 Structure parameter setting of siphon pipes

In this paper, the influence of structural parameters of siphon pipes on the flushing performance of the toilet is studied. In order to better analyze, the structures of siphon pipes is divided, which are shown in Figure 3.

Figure 3. The division of structural parameters of siphon pipes

In Figure 3, the structure size of siphon pipes is characterized by six parameters: $R$, $L_{1}$, $H_{1}$, $L_{2}$, $H_{2}$ and $D$. $R$ is the inclination angle of A-B section of siphon pipes, $H_{0}$ is the water seal height of of siphon pipes, $L_{1}$ is the length of radian change, $H_{1}$ is the height of radian change, $L_{2}$ is the length of E-F section of secondary water seal, $H_{2}$ is the height of secondary water seal, and $D$ is the diameter of siphon pipes. $R$, $L_{1}$, $H_{1}$, $L_{2}$, $H_{2}$ and $D$ are named as inclination angle, curvature width, curvature length, secondary water seal width, secondary water seal height and pipe diameter, respectively. All these parameters are both connected and independent, when one of them is changed, the other parameters remain unchanged. In order to explore the effect of six parameters on the flushing performance, six tests are carried out, and the detailed parameters are shown in Table 2.

Table 2. The structure parameters of siphon pipes

NO.	$R$（°）	$L_{1}$ （mm）	$H_{1}$ （mm）	$L_{2}$ （mm）	$H_{2}$ （mm）	$D$ （mm）
1	36,40,44,48,52,56	55	210	90	30	50
2	48	45,50,55,60,65,70	210	90	30	50
3	48	65	170,190,210,230,250	90	30	50
4	48	65	210	60,70,80,90,100,110	30	50
5	48	65	210	90	10,20,30,40,50,60	50
6	48	65	210	90	30	44,47,50,53,56,59

3.2 Experimental platform

In order to study the influence of structural parameters of siphon pipes on the flushing performance, a set of experimental platform with adjustable structural parameters of siphon pipes need to be builded. The simulation model used in the numerical calculation is based on a siphon jet toilet. Therefore, the building of the physical experimental platform is also based on it, and the improved toilet model is shown in Figure 4. In this experimental platform, the shape of siphon pipes can be adjusted arbitrarily within a certain range, and the water volume in the water tank can be controlled automatically through a flowmeter. The structural parameters of the siphon pipes are consistent with the parameters in the simulation experiment, and the water volume in the water tank is 5.5 L. It should be noted that the influence of siphon pipe diameter on the flushing performance has not been studied in the experiment, this is because the siphon pipe diameter is related to the basin structure of the toilet, when the basin structure is determined, the pipe diameter is also determined, and the siphon pipe diameter is 50 mm in this experiment. In addition, because of the size limitation of the toilet model, there are only three values of the curvature length parameters are studied. In the experiment, the material properties and quantity of solid granular medium are the same as those in the simulation, and each experiment is carried out six times, then the average value is taken as the quantity of flushing balls.

Figure 4. Experimental platform of toilet

3.3 Definition of flushing capacity

In order to analyze quantitatively the flushing performance of the toilet and consider synthetically the relationship between the quantity of flushing balls and the amount of water in the flushing process, the flushing capacity is defined as the evaluation index of the flushing performance of the toilet, and the flushing capacity can be expressed by the following formula:

$P={\frac {V_{B}}{V_{W}}}$

(16)

where $V_{B}$ is the volume of all tested water balls that are washed away and $V_{W}$ is the volume of water used in the flushing process. According to the formula of the flushing capacity, the flushing capacity can be understood as the volume of tested water balls that are washed away by a unit volume of water.

4. The discussion of flushing performance

4.1 Verification of simulation law

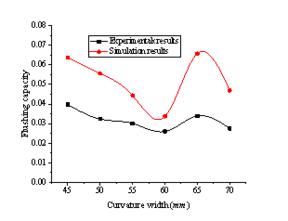
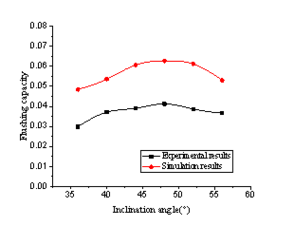
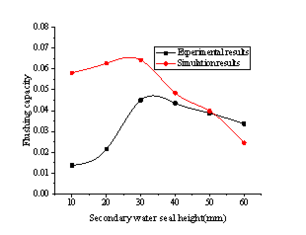
The relationship between the flushing capacity of the toilet and structural parameters of siphon pipes can be obtained by studying the flushing process of different siphon pipe structural parameters using CFD-DEM coupling method. In order to verify the reliability of the simulation law, the experiments under the same structural parameters are carried out, and the simulation law is compared with the experimental law, the results are shown from Figure 5 to Figure 9.

Figure 5. Comparison of inclination angle

Figure 6. Comparison of curvature width

Figure 7. Comparison of curvature length

Figure 8. Comparison of secondary water seal width

Figure 9. Comparison of secondary water seal height

As are shown from Figure 5 to Figure 9, the experimental results and the simulation results have the same change rule, and only the absolute values are different. And the difference are mainly reflected in the value of the flushing capacity in the simulation, which is larger than that in the experiment. On the one hand, it is caused by the inconsistency of physical experiment model and simulation calculation model, on the other hand, it is also affected by the accuracy of coupling algorithm in simulation calculation. Although the simulation law and the experimental law are different in the absolute value, the factors that cause the difference all have the same effect on the absolute value of flushing capacity under all parameters, and as a whole, it can reflect the range of structural parameters with better flushing performance. Therefore, it is practicable to study the regularity of the flushing performance of structural parameters of different siphon pipes. The numerical simulation method is not limited by the fixed size of model, it can study the flushing process in a wider range of structural parameters. And it is also convenient to obtain data which is not easy to get in physical experiments, and it is helpful to further study the flushing mechanism and reduce the development cycle and cost.

Because of the size limitation of experimental platform, there is no study about the effect of diameter change of siphon pipes on the flushing performance. Therefore, we can use CFD-DEM method to simulate the flushing process under different diameters. The simulation results are shown in Figure 10.

Figure 10. The influence of siphon pipe diameter on the flushing performance

According to Figure 10，the flushing capacity increases gradually and the flushing performance of the toilet increases gradually with the pipe diameter increases from 44 mm to 53 mm. When the pipe diameter increases from 53 mm to 56 mm, the flushing performance of the toilet remains unchanged, it is mainly because all the tested water balls are washed out under the diameters of these two pipes. When the pipe diameter is increased to 59 mm, the flushing capacity begins to decline. It is mainly because the pipe diameter is the larger, the siphon strength is the lower and the flushing force is the smaller under the same water consumption condition, which also shows that the bigger is not the better under the same flushing water consumption condition, and the reasonable pipe diameter is helpful to get better flushing and water-saving comprehensive properties. When the diameters of the pipe are 53mm and 56mm, the flushing performance of the toilet is better. In addition, the diameter of the siphon pipe is the smaller, the velocity of water flow is the higher in the pipe, and the siphon negative pressure is the lower, but the flushing capacity is lower, which also shows that the flushing performance can not be judged directly by the velocity and the negative pressure in the pipe under the condition of the pipe diameter changes, and it is necessary to combine the punching balls test.

4.2 The study of orthogonal experiment

In order to explore the influence of the structural parameters of each siphon pipe on the flushing performance, and to find a better combination of the structural parameters of siphon pipes, an orthogonal test was carried out in this paper. According to the experimental part, the pipe diameter of the toilet is related to the structure of the basin wall. When the diameter of siphon pipes changes, the model of the basin wall also changes. If the orthogonal experiment is carried out, many different models of the toilet need to be made, which greatly increases the development cycle and cost. According to the above research, CFD-DEM coupling method can better reflect the change rule of the flushing capacity of the toilet, and we can use the simulation method to carry out the numerical analysis when it is not easy to carry out an experimental research. Therefore, we can use the simulation method to carry out the orthogonal test.

There are six parameters to be considered in the structure of siphon pipes, each parameter is taken at three levels, and the $L_{18}$（$3^{7}$）orthogonal table is selected for the test, a total of 18 experiments are required. The parameter settings and results of orthogonal test are shown in Table 3.

Table 3. The parameter settings of orthogonal test

Test number	Factors						Flushing capacity
	A	B	C	D	E	F
	$R$（°）	$L_{1}$ （mm）	$H_{1}$ （mm）	$L_{2}$ （mm）	$H_{2}$ （mm）	$D$ （mm）
1	48	45	200	90	20	47	0.0561
2	48	50	210	100	25	50	0.0648
3	48	65	220	110	30	53	0.0628
4	50	45	200	100	25	53	0.0663
5	50	50	210	110	30	47	0.0434
6	50	65	220	90	20	50	0.0526
7	52	45	210	90	30	50	0.0413
8	52	50	220	100	20	53	0.0663
9	52	65	200	110	25	47	0.0439
10	48	45	220	110	25	50	0.0622
11	48	50	200	90	30	53	0.0510
12	48	65	210	100	20	47	0.0434
13	50	45	210	110	20	53	0.0653
14	50	50	220	90	25	47	0.0582
15	50	65	200	100	30	50	0.0633
16	52	45	220	100	30	47	0.0515
17	52	50	200	110	20	50	0.0663
18	52	65	210	90	25	53	0.0663
Average value 1	0.0567	0.0571	0.0578	0.0543	0.0583	0.0494
Average value 2	0.0582	0.0583	0.0541	0.0593	0.0603	0.0584
Average value 3	0.0560	0.0554	0.0589	0.0573	0.0522	0.0630
Range	0.0022	0.0030	0.0048	0.0050	0.0081	0.0136

The range reflects the influence of each structural parameter change of siphon pipes on the flushing capacity, and the bigger range indicates that the structural parameters will cause a bigger change on the flushing capacity in the experiment, so the maximum row of range indicates that the level of its structural parameters is the most important factor affecting the flushing performance of the toilet. According to Table 3, the size relation of range is $F>E>D>C>B>A$, therefore, the order of the influence of the structural parameters of siphon pipes on the flushing capacity is from primary to secondary is pipe diameter, secondary water seal height, secondary water seal width, curvature length, curvature width and inclination angle. The optimized combination parameter of orthogonal test is $A_{2}B_{2}C_{3}D_{2}E_{2}F_{3}$, but the parameter combination don’t contain that one in the orthogonal test table. Therefore, it needs to be verified by experiments. The flushing capacity of the optimized combination scheme obtained by simulation method is 0.0663. Compared with the results of the orthogonal test, the flushing capacity of the fourth, eighth, seventeenth and eighteenth groups are all 0.0663, which is the same as that one in the optimized scheme. That is, all the solid particles are flushed out. Therefore, it is not yet able to determine whether the flushing capacity under the optimized parameters of the scheme is the optimal. In order to further determine the flushing performance between the optimized scheme and the fourth, eighth, seventeenth and eighteenth groups, the quantity of flushing balls is increased from 130 to 150, then the above five combination parameters are re-tested, and the results of the experiments are shown in Figure 11.

Figure 11. The flushing capacity under different groups

According to Figure 11, the flushing capacity is the biggest under the optimized scheme, this indicates that the best flushing capacity can be obtained when the inclination angle is 50°, the curvature width is 50 mm, the curvature length is 220 mm, the secondary water seal width is 100 mm, the secondary water seal height is 25 mm and the pipe diameter is 53 mm.

5. Conclusions

According to the above analysis, the following conclusions can be obtained:

1. CFD-DEM coupling method can be used to reflect the overall changing tendency of the flushing performance of the toilet, but the absolute value is different. Therefore, CFD-DEM coupling method can be used to study the regularity of the flushing performance of the toilet. When the experimental method is not easy, the simulation method can be used to analyze qualitatively the flushing performance of the toilet.
2. Better flushing performance of the toilet can be obtained when the inclination angle is 50°, the curvature width is 50 mm, the curvature length is 220 mm, the secondary water seal width is 100 mm, the
3. It is worth to further study about how to use CFD-DEM coupling method for quantitative analysis of the toilet flushing performance.

Acknowledgements

The authors gratefully acknowledged the support from National Natural Science Foundation of China (51775113). Fujian university-industry cooperation project (2017H6002). Research start-up funds of FuJian University of Technology (GY-Z160139). Fuzhou Science and technology project (2020-GX-16). No part of this paper has published or submitted elsewhere. The authors declared that they have no conflicts of interest to this work. All authors have seen the manuscript and approved to submit to your journal.

References

[1] Shi-Yi Z., Zi-Jian L., Zhi-Wei P. Optimized design of toilet siphon pipeline based on fluent and its validated test. Journal of System Simulation, 20:4412, 2008.

[2] Wang Y., Xiu G., Tan H. Cad and Cae analysis for siphon jet toilet. In International Conference on Optics in Precision Engineering and Nanotechnology, ICOPEN 2011, Elsevier, Singapore, p. 472, March 23-25, 2011.

[3] Mahecha J., López O., Ardila O. Computational study of the dynamics of the flow in a gravity-driven toilet. In ASME 2012 Fluids Engineering Division Summer Meeting Collocated with the ASME 2012 Heat Transfer Summer Conference and the ASME 2012 International Conference on Nanochannels, Microchannels and Minichannels, p. 1319, 2012.

[4] An I.Y., Lee Y.L., Kim J.-H. A study of the characteristics of a super water-saving toilet with flexible trapway by measuring accumulated flow rate. Journal of Mechanical Science and Technology, 28:3067-3074, 2014.

[5] An I.Y., Lee Y.L., Jung E.D., Cho W.S. A study on performance optimization of a toilet by measuring accumulated flow rate of a trapway. Journal of Mechanical Science and Technology, 28:1319-1326, 2014.

[6] Cheng W.S., Lee R.T., Liu C.H., Hsia C.W. A study on evacuation performance of siphon‐type water closets. AIP Conference Proceedings, 1225, 75, 2010.

[7] Chen J., Wang Y., Li X., He R., Han S., Chen Y. Reprint of erosion prediction of liquid-particle two-phase flow in pipeline elbows via CFD-DEM coupling method. Powder Technology, 282:25-31, 2015.

[8] Park K.M., Yoon H.S., Kim M.I. CFD-DEM based numerical simulation of liquid-gas-particle mixture flow in dam break. Communications in Nonlinear Science and Numerical Simulation, 59:105, 2018.

[9] Akhshik S., Behzad M., Rajabi M. CFD-DEM simulation of the hole cleaning process in a deviated well drilling: the effects of particle shape. Particuology, 25:72-82, 2016.

[10] Hirt C.W., Nichols B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 39(1):201-225, 1981.

[11] Cundall P.A., Strack O.D.L. A discrete numerical model for granular assemblies. Geotechnique, 29(1):47-65, 1979.

[12] De Bono J.P., Mcdowell G.R. An insight into the yielding and normal compression of sand with irregularly-shaped particles using DEM. Powder Technology, 271:270-277, 2015.

[13] Li Z., Tong X., Qiu Y. The research of particle sieving under a creative mode of vibration. Journal of Vibroengineering, 19(6):4172-4184, 2017.

[14] Habib M.A., Badr H.M., Ben-Mansour R., Said S.A.M. Numerical calculations of erosion in an abrupt pipe contraction of different contraction ratios. International Journal for Numerical Methods in Fluids, 46(1):19-35, 2004.

[15] Mindlin R.D., Deresiewicz H. Elastic spheres in contact under varying oblique forces. Journal of Applied Mechanics, 20:327-327-344, 1953.

[16] Chu K.W., Wang B., Yu A.B., Vince A. CFD-DEM modelling of multiphase flow in dense medium cyclones. Powder Technology, 193(3):235-247, 2009.

[17] Chu K.W., Kuang S.B., Yu A.B., Vince A. Particle scale modelling of the multiphase flow in a dense medium cyclone: effect of fluctuation of solids flowrate. Minerals Engineering, 33:34-45, 2012.

[18] Chaumeil F., Crapper M. Using the DEM-CFD Method to predict Brownian particle deposition in a constricted tube. Particuology, 15:94-106, 2014.