Numerical implementation for conception of strut and tie models in reinforced concrete structures

Abstract

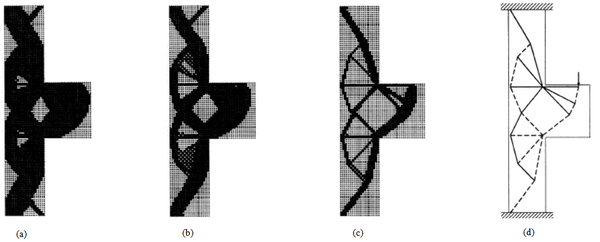
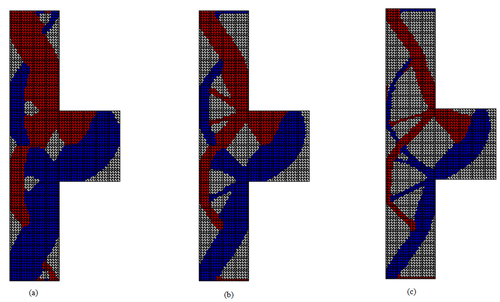
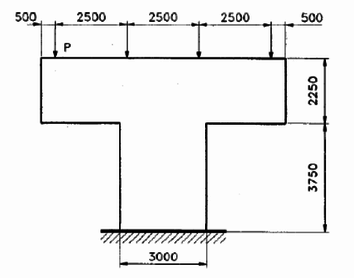
The Strut-and-Tie Model can be na excellent alternative for the design of reinforced concrete structural elements submitted to plane stress state and for regions with geometric or static discontinuity, replacing empirical procedures with a rational design methodology. To make the design of the model less dependent on the designer's experience, this article aims to combine the topological optimization technique ESO (Evolutionary Structural Optimization) with the Finite Element Method for the automatic generation of strut-and-tie models. The evolution criterion of the adopted topological optimization method considers the elimination of less stressed elements in terms of stress, from an elastic-linear analysis. In this context, it is possible to obtain optimized solutions of complex problems involving structural concrete. Three numerical examples are presented to prove and validate the formulations and techniques implemented whose strut-and-tie models present a good agreement in relation to the answers found in precursor scientific works on the subject.

Keywords: Strut-and-tie model, finite element method, topological optimization, reinforced concrete

Resumo

O Modelo de Bielas e Tirantes pode ser uma excelente alternativa para o dimensionamento de elementos estruturais em concreto armado submetidos a estado plano de tensão e para regiões que apresentem descontinuidade de ordem geométrica ou estática, substituindo procedimentos empíricos por uma metodologia racional de projeto. Para tornar a concepção do modelo menos dependente da experiência do projetista, o presente artigo tem como objetivo aliar a técnica de otimização topológica ESO (Evolutionary Structural Optimization) ao Método dos Elementos Finitos para geração automática dos modelos de bielas e tirantes. O critério de evolução do método de otimização topológica adotado considera a eliminação de elementos menos solicitados em termos de tensão, a partir de uma análise elástico-linear. Nesse contexto, é possível obter soluções otimizadas de problemas complexos envolvendo o concreto estrutural. São apresentados três exemplos numéricos para comprovação e validação das formulações e técnicas implementadas, cujos modelos de bielas e tirantes obtidos apresentam boa concordância em relação às respostas encontradas em trabalhos científicos precursores sobre o tema.

Palavras-chave: Modelo de bielas e tirantes, método dos elementos finitos, otimização topológica, concreto armado

1. Introdução

Para regiões ou elementos estruturais nos quais a Hipótese de Bernoulli não descreva adequadamente o comportamento estrutural ou distribuição de tensões, pode-se recorrer a outras alternativas de dimensionamento, tais como o Método dos Elementos Finitos (MEF) e o Modelo de Bielas e Tirantes (MBT). Nessas regiões, denominadas na literatura de ‘Regiões D’ (Descontinuity), as tensões de cisalhamento são significativas e a distribuição de deformações é não linear. Como exemplo, citam-se elementos estruturais como vigas-parede, consolos, sapatas, nós de pórticos, blocos rígidos de fundação sobre estacas, furos em vigas e dentes Gerber.

Estudos pioneiros envolvendo o MBT tiveram origem no início do século XX. Ritter e Morsch propuseram, a partir de resultados experimentais, a analogia clássica do modelo de treliças para o dimensionamento a cisalhamento de vigas fletidas de concreto armado. Segundo esse modelo, admite-se a substituição da viga original por uma treliça equivalente definida a partir da distribuição de tensões. As barras tracionadas representam campos de tensão de tração (tirantes), enquanto as barras comprimidas representam campos de tensão de compressão (bielas).

Foi a partir dos trabalhos desenvolvidos por Schlaich et al. [1], entretanto, que o tema ganhou forte impulso. Além das vigas inicialmente analisadas, esses pesquisadores estenderam a aplicação do modelo de bielas e tirantes a outros tipos de elementos estruturais. Abordaram temas como procedimentos para definição das regiões com e sem descontinuidade, geração dos modelos de treliças no interior do contínuo de concreto, cálculo dos esforços internos, diretrizes para verificação das tensões nas bielas e regiões nodais e cálculo e detalhamento da armadura necessária.

Entretanto, a não unicidade do modelo topológico, torna a concepção dependente da experiência e da sensibilidade estrutural do projetista para representar o fluxo interno de tensões. Sendo a armadura calculada e distribuída conforme o modelo topológico definido para o elemento estrutural de concreto armado, a correta definição desse não somente gera economia como também está relacionada à segurança.

A otimização topológica (OT) é comumente vista como um método computacional para lançar estruturas a partir da distribuição ótima de material em uma determinada região do espaço. Neste artigo, isso é feito através de uma combinação do Método dos Elementos Finitos, de um modelo para o comportamento do material e de técinas de otimização. Ou seja, o domínio de projeto é discretizado em uma malha refinada de elementos finitos, de modo que se possa analisar seu comportamento e, então, é distribuído material de forma racionalizada através de algoritmos de otimização.

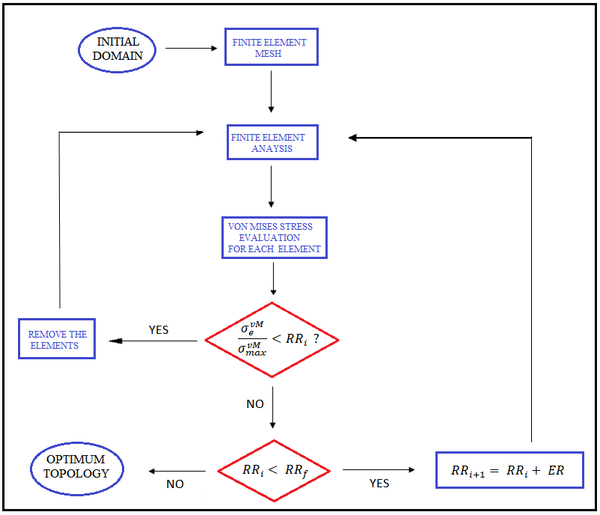
É nesse contexto que se insere o objetivo deste trabalho, isto é, fornecer uma ferramenta eficaz e confiável para a geração automática do modelo de bielas e tirantes via OT, definindo a melhor configuração a ser adotada para a análise. Será adotada uma técnica de otimização de layout, proposta inicialmente por Xie e Steven [2] denominado Otimização Estrutural Evolucionária (Evolutionary Structural Optimization – ESO). A essência do método consiste na remoção gradual de regiões menos solicitadas, com base num critério de penalidade baseado em tensões equivalentes de von Mises. Isto é, elementos com tensões abaixo de um determinado limite são removidos da malha a cada iteração num processo denominado “hard-kill”. Dessa forma, é possível obter uma estrutura ótima para um dado volume remanescente.

Para a realização do objetivo principal pode-se destacar os seguintes objetivos específicos: implementação de um elemento finito triangular de três nós para análise em estado plano de tensão; implementação de uma rotina de otimização topológica dentro de um Programa de Elementos Finitos. A escolha do elemento triangular de três nós para a análise numérica de estruturas em estado plano de tensões, deve-se ao fato de que esse elemento requer uma discretização do contínuo bastante detalhada, permitindo assim definir as regiões de compressão e tração do modelo bielas e tirantes com mais refinamento. Uma vez que, em algumas etapas das análises a técnica de evolução utilizada no processo de otimização topológica na estrutura plana de concreto consiste em eliminar o elemento o da malha de elementos finitos, por isso a exigência de uma malha bem refinada, em consequência um elemento mais pobre em termos das funções de forma.

2. Formulação do elemento finito triangular linear

Para geração do modelo de bielas e tirantes considerando análise linear, foi implementado a técnica ESO que é uma alternativa ao rigor matemático de métodos clássicos de otimização. O algoritmo baseia-se em uma análise via MEF e, como o presente estudo trata de elementos estruturais de concreto armado submetidos a estado plano de tensões, foi necessária, portanto, a implementação de um elemento finito bidimensional, cuja formulações é descrita neste item.

O elemento finito implementado neste trabalho é o elemento triangular de três nós e dois graus de liberdade por nó, denominado Constant Strain Triangle (CST), usado na simulação numérica pelo MEF, baseado em deslocamentos. No caso da análise linear, o material é considerado homogêneo, isotrópico e linear.

Segundo o Princípio dos Trabalhos Virtuais (PTV), aplicando-se um campo de deformação virtual compatível ao elemento triangular tem-se: ${\textstyle \delta W_{int}=\delta W_{ext}}$, isto é, o trabalho virtual externo é igual ao trabalho virtual interno. O trabalho virtual interno, ${\textstyle \delta W_{int}}$, pode ser escrito como:

${\textstyle \delta W_{int}={\underset {V}{\displaystyle \int \!\int \!\int }}{\sigma }_{ij}\delta {\epsilon }_{ij}dV}$

(1)

onde ${\textstyle \delta }$ é o operador variacional, ${\sigma }_{ij}$ é o estado tensional real em um ponto qualquer no elemento, e ${\textstyle \delta {\epsilon }_{ij}}$ é o estado de deformação virtual em um ponto qualquer no elemento. A partir do tensor de deformação de Green-Lagrange e desprezando-se as tensões no plano de normal na direção $z$, chega-se à Eq. (2) para trabalho virtual interno, onde $t$ é a espessura do elemento triangular

$\delta W_{int}=t{\underset {A}{\int \!\int }}\left[\delta u_{,x}{\sigma }_{x}+\delta v_{,y}{\sigma }_{y}+(\delta u_{,y}+\delta v_{,x}){\tau }_{xy}\right]dA.$

(2)

Para o elemento triangular de três nós é usual adotar as funções de interpolação em coordenadas naturais, as quais podem ser escritas como:

$N_{1}={\xi }_{1}=\xi ={\frac {\left(y_{2}-y_{3}\right)}{2A}}x+$${\frac {\left(x_{3}-x_{2}\right)}{2A}}y+{\frac {(y_{3}-y_{2})x_{2}-(x_{3}-x_{2})y_{1}}{2A}}$	(3a)
$N_{2}={\xi }_{2}=\eta ={\frac {\left(y_{3}-y_{1}\right)}{2A}}x+$${\frac {\left(x_{1}-x_{3}\right)}{2A}}y+{\frac {(x_{3}-x_{1})y_{1}-(y_{3}-y_{1})x_{1}}{2A}}$	(3b)
$N_{3}={\xi }_{3}=1-\xi -\eta$	(3c)

onde $x_{1}$, $x_{2}$, $x_{3}$, $y_{1}$, $y_{2}$, $y_{3}$ são as coordenadas cartesianas do elemento e $A$ sua área.

Definindo o vetor de deslocamentos nodais por $q={\left\{{\begin{array}{cccccc}u_{1}&u_{2}&u_{3}&v_{1}&v_{2}&v_{3}\end{array}}\right\}}^{T}$ e representando as funções de interpolação em coordenadas naturais pelo vetor coluna ${\Phi }^{T}=\left({\begin{array}{ccc}N_{1}&N_{2}&N_{3}\end{array}}\right)$, definem-se as equações aproximadas dos deslocamentos associados aos deslocamentos nodais q que podem ser escritas na forma matricial conforme a Eq. (4)

$\left\{{\begin{array}{c}u\\v\end{array}}\right\}=\left[{\begin{array}{cc}{\Phi }^{T}&{O}^{T}\\{O}^{T}&{\Phi }^{T}\end{array}}\right]q{\mbox{.}}$

(4)

Na Eq. (4), $O$ é um vetor coluna nulo com três termos. Sendo os deslocamentos $u$ e $v$ funções dos deslocamentos nodais, os seus variacionais podem ser escritos a partir da seguinte expressão: ${\textstyle \delta a=\delta q^{T}\left({\frac {\partial a}{\partial q}}\right)}$ , sendo ${\textstyle {\textbf {q}}}$ o vetor dos deslocamentos nodais, ${\textstyle \partial }$ o operador diferencial e $a$ substituído por $u$ e $v$ Substituindo esses variacionais na Eq. (2) chega-se ao trabalho virtual de um elemento triangular dado pela equação a seguir

$\delta W_{int}=\delta {\textbf {q}}^{T}t{\underset {A}{\int \!\int }}\left[{\frac {\partial u_{,x}}{\partial {\textbf {q}}}}{\sigma }_{x}+{\frac {\partial v_{,y}}{\partial {\textbf {q}}}}{\sigma }_{y}+\left({\frac {\partial u_{,y}}{\partial {\textbf {q}}}}+{\frac {\partial v_{,x}}{\partial {\textbf {q}}}}\right){\tau }_{xy}\right]dA.$

(5)

sendo ${\textstyle {\textbf {f}}_{ext}}$ o vetor de forças externas nas direções dos graus de liberdade do elemento triangular, o trabalho virtual externo é dado por ${\textstyle \delta W_{ext}=\delta {\textbf {q}}^{T}{\textbf {f}}_{ext}}$, onde ${\textstyle {\textbf {f}}_{ext}}$ é o vetor de forças externas aplicadas diretamente na direção dos graus de liberdade do elemento, e as forças nodais equivalentes obtidas a partir do carregamento externo atuando no contorno do elemento. Da condição ${\textstyle \delta W_{ext}=\delta W_{int}}$ tem-se:

$\delta {\textbf {q}}^{T}t{\underset {A}{\int \!\int }}\left[{\frac {\partial u_{,x}}{\partial {\textbf {q}}}}{\sigma }_{x}+{\frac {\partial v_{,y}}{\partial {\textbf {q}}}}{\sigma }_{y}+\left({\frac {\partial u_{,y}}{\partial {\textbf {q}}}}+{\frac {\partial v_{,x}}{\partial {\textbf {q}}}}\right){\tau }_{xy}\right]dA=$$\delta q^{T}f_{ext}$

(6)

Como a expressão acima deve ser válida para qualquer campo de deslocamento virtual ${\textstyle \delta {\bf {q}}}$, segue que ${\textstyle {\textbf {f}}_{int}-{\textbf {f}}_{ext}={\mbox{0}}}$, onde ${\textstyle {\textbf {f}}_{int}}$ é o vetor de forças internas definido por:

$f_{int}=t{\underset {A}{\int \!\int }}\left[{\frac {\partial u_{,x}}{\partial {\textbf {q}}}}{\sigma }_{x}+{\frac {\partial v_{,y}}{\partial {\textbf {q}}}}{\sigma }_{y}+\left({\frac {\partial u_{,y}}{\partial {\textbf {q}}}}+{\frac {\partial v_{,x}}{\partial {\textbf {q}}}}\right){\tau }_{xy}\right]dA$

(7)

A Eq. (7) pode ser escrita na forma matricial como:

${\textbf {f}}_{int}=t{\underset {A}{\int \!\int }}\left[{\begin{array}{c}{\sigma }_{x}{\Phi }_{,x}+{\tau }_{xy}{\Phi }_{,y}\\{\sigma }_{y}{\Phi }_{,y}+{\tau }_{xy}{\Phi }_{,x}\end{array}}\right]{\mbox{ }}dA$

(8)

Utilizando o método de Newton-Rapshon na solução do problema ${\textstyle {\textbf {f}}_{int}-{\textbf {f}}_{ext}={\mbox{0}}}$ é necessária a determinação da derivada dessa expressão em relação aos deslocamentos nodais, obtendo assim a matriz de rigidez tangente. Sendo ${\textstyle {\textbf {f}}_{ext}}$ constante em relação aos deslocamentos nodais, a matriz de rigidez tangente é dada por ${\textstyle {\textbf {K}}=\partial {\textbf {f}}_{int}/\partial {\textbf {q}}}$, que, após manipulações algébricas, pode ser escrita de acordo com a Eq. (9)

${\textbf {K}}=t{\underset {A}{\int \!\int }}\left[{\begin{array}{c}{\Phi }_{,x}{\left({\frac {\partial {\sigma }_{x}}{\partial {\textbf {q}}}}\right)}^{T}+{\Phi }_{,y}{\left({\frac {\partial {\tau }_{xy}}{\partial {\textbf {q}}}}\right)}^{T}\\{\Phi }_{,y}{\left({\frac {\partial {\sigma }_{y}}{\partial {\textbf {q}}}}\right)}^{T}+{\Phi }_{,x}{\left({\frac {\partial {\tau }_{xy}}{\partial {\textbf {q}}}}\right)}^{T}\end{array}}\right]dA$

(9)

onde, $\Phi _{,x}$ e $\Phi _{,y}$ são as derivadas das funções de forma com relação a $x$ e $y$, respectivamente, ${\sigma }_{x}$ e ${\sigma }_{y}$ são as tensões normais nas direções x e y, respectivamente, ${\tau }_{xy}$ é a tensão cisalhante, ${\bf {q}}$ é o vetor de deslocamento nodal, $t$ é a espessura e $A$ a área do elemento.

Na Eq. (9), a derivada da tensão normal na direção $x$ em relação aos deslocamentos nodais é dada por:

${\frac {\partial {\sigma }_{x}}{\partial q}}={\frac {\partial {\sigma }_{x}}{\partial {\epsilon }_{x}}}{\frac {\partial {\epsilon }_{x}}{\partial q}}+$${\frac {\partial {\sigma }_{x}}{\partial {\epsilon }_{y}}}{\frac {\partial {\epsilon }_{y}}{\partial q}}$

(10)

As derivadas das deformações lineares em relação aos deslocamentos nodais são dadas pelas Eqs. (11) e (12)

${\frac {\partial {\epsilon }_{x}}{\partial q}}={\frac {\partial u_{,x}}{\partial q}}=$$\left[{\begin{array}{c}{\Phi }_{,x}\\O\end{array}}\right]$	(11)
${\frac {\partial {\epsilon }_{y}}{\partial q}}={\frac {\partial v_{,y}}{\partial q}}=$$\left[{\begin{array}{c}O\\{\Phi }_{,y}\end{array}}\right]$	(12)

Substituindo as Eqs. (11) e (12) na derivada da tensão normal na direção x em relação aos deslocamentos nodais (Eq. (10)), tem-se:

${\frac {\partial {\sigma }_{x}}{\partial q}}={\frac {E}{1-{\nu }^{2}}}\left[{\begin{array}{c}{\Phi }_{,x}\\\nu {\Phi }_{,y}\end{array}}\right]$

(13)

De forma análoga à descrita para tensão normal na direção $x$, pode-se chegar às Eqs. (14) e (15) para as derivadas em relação aos deslocamentos nodais das outras tensões atuantes no elemento

${\frac {\partial {\sigma }_{y}}{\partial q}}={\frac {E}{1-{\nu }^{2}}}\left[{\begin{array}{c}\nu {\Phi }_{,x}\\{\Phi }_{,y}\end{array}}\right]$	(14)
${\frac {\partial {\tau }_{xy}}{\partial q}}={\frac {E}{2(1+\nu )}}\left[{\begin{array}{c}{\Phi }_{,y}\\{\Phi }_{,x}\end{array}}\right]$	(15)

A seguir são determinadas as derivadas das funções de forma em relação aos eixos $x$ e $y$.

${\Phi }_{,x}={\Phi }_{,\xi }{\xi }_{,x}+{\Phi }_{,\eta }{\eta }_{,x}=$$\left\{{\begin{array}{c}1\\0\\-1\end{array}}\right\}{\frac {y_{2}-y_{3}}{2A}}+\left\{{\begin{array}{c}0\\1\\-1\end{array}}\right\}{\frac {y_{3}-y_{1}}{2A}}={\frac {1}{2A}}\left\{{\begin{array}{c}y_{2}-y_{3}\\y_{3}-y_{1}\\y_{1}-y_{2}\end{array}}\right\}$	(16)
${\Phi }_{,y}={\Phi }_{,\xi }{\xi }_{,y}+{\Phi }_{,\eta }{\eta }_{,y}=$$\left\{{\begin{array}{c}1\\0\\-1\end{array}}\right\}{\frac {x_{3}-x_{2}}{2A}}+\left\{{\begin{array}{c}0\\1\\-1\end{array}}\right\}{\frac {x_{1}-x_{3}}{2A}}={\frac {1}{2A}}\left\{{\begin{array}{c}x_{3}-x_{2}\\x_{1}-x_{3}\\x_{2}-x_{1}\end{array}}\right\}$	(17)

Na representação isoparamétrica, as coordenadas cartesianas $x$ e $y$ são relacionadas com as coordenadas paramétricas $\xi$ e $\eta$. Então, para mudança do domínio de integração $dA=dxdy$ para $d\xi d\eta$ utiliza-se a relação $dA=det{\mbox{J}}d\xi d\eta$ onde ${\bf {J}}$ é a matriz jacobiano da transformação das coordenadas $x$ e $y$ para as coordenadas paramétricas $\xi$ e $\eta$ dada pela equação seguir. Dessa forma, $det{\bf {J}}=2A$

${\mbox{J}}=\left[{\begin{array}{cc}x_{,\xi }&y_{,\xi }\\x_{,\eta }&y_{,\eta }\end{array}}\right]$

(18)

3. Otimização estrutural evolucionária

A técnica ESO surge como uma alternativa ao rigor matemático de métodos clássicos de otimização. Apresenta uma base teórica simples cujo fundamento consiste na inserção de vazios na estrutura através da eliminação gradual dos elementos menos solicitados do domínio durante o processo de evolução. Portanto, para se obter a configuração ótima deve-se agregar ao estudo um nível de análise estrutural dependente de um domínio discreto, o que torna o emprego do MEF uma etapa do algoritmo de otimização.

Neste trabalho a representação matemática técnica ESO baseia-se no conceito de tensão, isto é, o nível máximo de tensão na estrutura, obtido por análises via MEF, é tomado como um indicador do nível de eficiência de cada elemento. Elementos com baixo nível de tensão são, portanto, sistematicamente removidos da estrutura. A cada iteração novos elementos ineficientes são eliminados da malha e o procedimento se repete até que o campo de tensão atuante em todo o domínio seja praticamente constante e muito próximo da tensão admissível do material ou que seja atingida a restrição de volume mínimo.

O critério de remoção é feito comparando-se a tensão de von Mises de cada elemento com a tensão de von Mises máxima existente em toda a estrutura. Portanto, no fim de cada iteração todos os elementos que atendem à Eq. (19) serão eliminados. A forma de retirada do elemento ocorre atribuindo-se baixos valores para seu módulo de elasticidade longitudinal ($E=10^{-12}$). Desse modo, evita-se o remalhamento da estrutura

${\sigma }_{e}^{\upsilon M}<RR_{i}.{\mbox{ }}{\sigma }_{Max}^{\upsilon M}$

(19)

onde:

${\textstyle {\sigma }_{e}^{vM}}$= tensão de von Mises no elemento analisado;

$RRi$= razão de rejeição na i-ésima iteração ($0<RRi<1,0$);

${\textstyle {\sigma }_{Max}^{vM}}$= máxima tensão de von Mises da iteração.

A razão de rejeição é usada para retardar o processo de remoção do elemento. O ciclo de remoção ocorre até que não possam mais ser removidos elementos para um dado valor de $RRi$. Quando isto ocorre, um estado de equilíbrio é alcançado. O processo evolucionário é redefinido adicionando-se à $RRi$ uma razão de evolução, $ER$. A razão de rejeição é atualizada de acordo com a Eq. (20)

$RR_{i+1}=RR_{i}+ER$

(20)

O valor inicial da razão de rejeição ($RR_{0}$) é definido de forma empírica pelo usuário. Entretanto, segundo Querin [3], para garantir melhor convergência, os valores de $RR_{0}$ e $ER$ devem ser de aproximadamente 1%. O processo se repete enquanto a estrutura não atingir o volume final, $VF$, definido pelo usuário, ou seja:

$VR<(1-VF){\mbox{ }}.{\mbox{ }}VT$

(21)

onde $VR$ é o volume retirado acumulado até aquela iteração, $VF$ é o volume final expresso em percentual (por exemplo, $VF=0,4$ implica que a retirada de elementos cessará quando o volume da estrutura atingir 40% do seu volume total inicial) e $VT$ o volume inicial total da estrutura.

Matematicamente, o ESO pode ser escrito como:

Failed to parse (syntax error): \mbox{D }(j)=\left\{ \begin{array}{c} \mbox{D}_0,\\ \mbox{0,} \end{array}\begin{array}{c} se\\ se \end{array}\begin{array}{c} j\\ j \end{array}\begin{array}{c} \in \\ \in \end{array}\begin{array}{c} \Gamma \\ \Gamma \, {}' \end{array}\right./math> |} | style="text-align: right;vertical-align: center;width: 5px;text-align: right;white-space: nowrap;"|(22) |} onde: <math>{\bf D}(j) = matriz constitutiva do ponto ${\textstyle j\in \,\Omega }$; ${\bf {D}}_{0}$ = matriz constitutiva inicial; $\Omega =\Gamma +\Gamma '$ = domínio da estrutura; $\Gamma =\left\{\Omega /\left({\frac {{\sigma }_{e}^{vM}}{{\sigma }_{m{\acute {a}}x}^{vM}}}\right)\geq {\mbox{RR}}_{i}\right\}$ conjunto dos elementos que não serão removidos. $\Gamma \,{}'=\left\{\Omega /\left({\frac {{\sigma }_{e}^{vM}}{{\sigma }_{m{\acute {a}}x}^{vM}}}\right)<{\mbox{RR}}_{i}\right\}$, conjunto dos elementos que serão removidos. Portanto, o algoritmo ESO apresenta a seguinte marcha, representada no fluxograma da Figura 1: 1º Passo: discretização do domínio e aplicação das condições de contorno e ações prescritas; 2º Passo: análise da estrutura via MEF e cálculo das tensões principais e tensões de von Mises em cada elemento; 3º Passo: retirar os elementos que satisfaçam a Eq. (19), dentro de um limite pré-definido de volume (p%); 4º Passo: repetir os passos 2 e 3 até que seja atingido o equilíbrio; 5º Passo: acréscimo da razão de rejeição conforme a Eq. (20) e iniciar nova retirada de elementos repetindo os passos 2, 3 e 4. Figura 1. Fluxograma do algoritmo ESO em nível de tensão 4. Critério de escoamento do von Mises O critério de remoção é baseado na tensão de von Mises de cada elemento na i-ésima iteração, que em termos de tensões principais pode ser calculada conforme a Eq. (23): ${\sigma }_{e}^{vM}={\frac {\sqrt {2}}{2}}{\sqrt {{\left({\sigma }_{1}-{\sigma }_{2}\right)}^{2}+{\left({\sigma }_{2}-{\sigma }_{3}\right)}^{2}+{\left({\sigma }_{3}-{\sigma }_{1}\right)}^{2}}}$ (23) Para o caso de estado plano de tensão, com ${\sigma }_{3}=0$ ${\sigma }_{vM}^{2}={\sigma }_{1}^{2}-{\sigma }_{1}{\sigma }_{2}+$${\sigma }_{2}^{2}$ (24) 5. Exemplos numéricos Neste item são apresentadas algumas aplicações considerando o método ESO implementado. São feitas análises elástico-lineares em estruturas submetidas a estado plano de tensão. O material é considerado homogêneo e isotrópico. Para cada exemplo são definidas as propriedades mecânicas do material e o domínio inicial de projeto. Além disso, são especificados os seguintes parâmetros: $RR$ (razão de rejeição), $ER$ (razão de evolução), $VF$ (volume final desejado), $VI$ (volume máximo retirado por iteração), $VR$ (volume total retirado até uma dada iteração), número da iteração e malha de elementos finitos adotada. Nesse item podem ser feitos os agradecimentos às instituições de fomento à pesquisa, às empresas privadas patrocinadoras do trabalho, aos pesquisadores e profissionais que auxiliaram na execução dos ensaios e fornecimento de dados e materiais. 5.1 Estrutura de Michell O primeiro exemplo a ser apresentado trata-se de uma viga simplesmente apoiada submetida a uma carga concentrada conforme indicado na Figura 2a, comumente chamada na literatura de estrutura de Michell. A solução analítica é mostrada na Figura 2b. O material adotado foi o aço, cujo módulo de elasticidade $E=200$GPa, coeficiente de Poisson $\nu =0.3$ e espessura igual a 1mm. Figura 2. (a) Domínio inicial para estrutura de Michell. (b) Solução analítica O domínio foi discretizado numa malha de elementos triangulares de $96\times 40$. O processo evolucionário teve início com uma razão de rejeição ($RR$) de 1% e uma razão de evolução ($ER$) de 0,75%. O volume retirado ($VR$) de 60% do volume inicial e o volume máximo retirado por iteração ($VI$) de 1,75%. As Figura 3a, 3b e 3c apresentam a evolução da estrutura, enquanto que a Figura 3d ilustra o modelo de bielas e tirantes obtido, onde as bielas estão representadas em azul e os tirantes em vermelho. Figura 3. (a) Iteração 22, $RR=2,5\%$, $VR=5,6\%$. (b) Iteração 69, $RR=4,75\%$, $VR=18,6\%$. (c) Iteração 175, $RR=10,75\%$, $VR=60,0\%$. (d) Modelo de bielas e tirantes 5.2 Consolo curto Este exemplo apresenta um consolo curto projetado para suportar uma carga pontual de 500kN. A Figura 4 traz as dimensões da estrutura em milímetros. O módulo de elasticidade do concreto foi tomado igual a $E=28567$ MPa, coeficiente de Poisson $\nu =0,15$ e a espessura assumida como sendo igual a 300mm. Figura 4. Consolo Curto (Liang et al. [4]) Este exemplo foi estudado por Liang et al. [4] e Almeida et al. [5]. A Figura 5 apresenta a evolução da estrutura e o correspondente modelo de bielas e tirantes sugerido pelos autores, no qual as bielas estão representadas por linha pontilhada e os tirantes por linha cheia. Figura 5. (a), (b), (c) Processo evolucionário. (d) Modelo de bielas e tirantes (Liang et al. [4]) No presente trabalho a estrutura foi modelada usando uma malha com 5664 elementos triangulares de três nós com 25 mm de lado. Para obter a topologia ótima apresentada na Figura 6, os parâmetros adotados foram: $RR=0,01$, $ER=0,05$, $VF=45\%$, $VI=0,05$. Os campos de compressão (bielas) são representados em azul e os campos de tração (tirantes) em vermelho. Figura 6. (a) Iteração 25, $RR=11,0\%$, $VR=15,0\%$. (b) Iteração 31, $RR=11,0\%$, $VR=35,0\%$. (c) Iteração 47, $RR=16,0\%$, $VR=55,0\%$ 5.3 Pilar de ponte Este exemplo foi proposto por Liang et al. [6] e estudado também por Almeida et al. [7]. Trata-se de um pilar de ponte projetado para suportar quatro cargas concentradas de 2750kN transferidas por quatro vigas de aço-concreto. O pilar tem espessura de 1,5m e é admitido como sendo engastado na fundação. A geometria, condições de contorno e ações do problema estão indicados na Figura 7, com dimensões em milímetros e kN. Figura 7. Domínio de projeto do pilar de ponte (Liang et al. [6]) O domínio foi discretizado numa malha refinada com 12260 elementos finitos triangulares. As propriedades do material isotrópico utilizado são módulo de elasticidade $E=28,6$GPa e coeficiente de Poisson $\nu =0,15$. O processo evolucionário teve início com uma razão de rejeição ($RR$) igual a 4% e uma razão de evolução ($ER$) de 2%. O volume final desejado igual a 48% do volume inicial e taxa de retirada de material por iteração ($VI$) igual a 1,75%. A Figura 8 apresenta o MBT alcançado. As regiões em vermelho e azul indicam, respectivamente, regiões de tração, tirantes, e regiões de compressão, bielas. Figura 8. (a) Modelo de bielas e tirantes obtido no presente trabalho - Iteração 164, $RR=18\%$, $VR=52\%$. (b) Topologia ótima proposta por Liang et al. [6] 6. Conclusões O objetivo do artigo é a apresentação de uma formulação numérica para verificar o fluxo de tensões em estruturas bidimensionais para geração automática do modelo de bielas e tirantes que auxiliem o projetista na concepção e posterior dimensionamento de estruturas de concreto armado. O algoritmo de otimização topológica ESO foi, portanto, utilizado com esse propósito. O uso do Método dos Elementos Finitos, considerando análise linear elástica, se torna conveniente devido ao critério de remoção adotado para o ESO. Assim, um domínio estendido é inicialmente discretizado numa malha refinada de elementos finitos e, iterativamente, o algoritmo conduz à configuração ótima que representa o modelo de bielas e tirantes procurado. Finalmente, pode-se afirmar que os exemplos numéricos apresentados estão de acordo com os resultados encontrados na literatura científica, o que validam a efetividade da formulação implementada. Para o dimensionamento, alerta-se para o fato de que o modelo de bielas e tirantes deve atender aos procedimentos impostos por códigos normativos, principalmente no que se refere à utilização de armadura mínima, que podem ser maiores que os tirantes concebidos. Agradecimentos Os autores agradecem à CAPES, CNPq, FAPEMIG, Fundação Gorceix e PROPEC/UFOP pelo apoio financeiro e suporte necessários para realização desta pesquisa. Referências [1] Schlaich J., Schäfer K., Jennewein M. Toward a consistent design of structural concrete. PCI Journal, 32(3):75-150, 1987. [2] Xie Y.M., Steven G.P. A simple evolutionary procedure for structural optimization. Computers & Structures, 49(5):885-896, 1993. [3] Querin O.M., Evolutionary structural optimization stress based formulation and implementation. PhD dissertation, University of Sydney, 1997. [4] Michell A.G.M. The limits of economy of material in frame-structures. Philosophy Magazine, 8:589–597, 1904. [5] Liang Q.Q., Xie Y.M., Steven G.P. Topology optimization of strut-and-tie models in reinforced concrete structures using an evolutionary procedure. ACI Structural Journal, 97(2):322–330, 2000. [6] Almeida V.S., Simonetti H.L., Neto L.O. Comparative analysis of strut-and-tie models using Smooth Evolutionary Structural Optimization. Engineering Structures, 56:1665–1675, 2013a. [7] Liang Q.Q., Uy B., Steven G.P. Performance-based optimization for strut-and-tie modeling of structural concrete. Journal of Structural Engineering, 128(6):815-823, 2002.