Operational influence of the nature of the damping considered in the adjustment of the structural response model on the results of the scale factors for operational modal analysis

Resumen

La consideración del supuesto de amortiguamiento viscoso como hipótesis de partida en el análisis dinámico de estructuras, puede introducir un error apreciable en los cálculos, ya que la energía disipada por la estructura en su oscilación, en ese caso, es dependiente de la frecuencia, mientras experimentalmente se pone de manifiesto lo contrario, si se atiende al amortiguamiento estructural o histerético.

Los modos de vibración obtenidos en el análisis modal operacional no están escalados, al ser desconocida la magnitud de la excitación sobre la estructura. Por ello es necesario recurrir a procedimientos de cálculo adicionales, como el método del cambio de masa, para determinar los factores de escala de cada modo. Sin embargo, todas las variantes de este método, en el estado del arte actual, han sido deducidas en la situación no amortiguada.

En este trabajo se analiza la influencia de la desviación de los resultados para los factores de escala, obtenidos mediante un análisis con amortiguamiento viscoso, frente a sus homólogos determinados bajo la consideración de amortiguamiento histerético o estructural, independiente de la frecuencia, cuyos resultados ajustan mucho mejor con el comportamiento experimental de la estructura.

Palabras clave: Análisis modal, amortiguamiento histerético y viscoso, factores de escala

Abstract

The consideration of the assumption of viscous damping as a starting hypothesis in the dynamic analysis of structures can introduce a substantial error in the calculations. This is due to the energy dissipated by the structure in its oscillation being frequency dependent under that premise, while experimentally the opposite becomes apparent, when structural or hysteretic damping is taken into account.

The modes of vibration obtained in the operational modal analysis are not scaled, since the magnitude of the excitation on the structure is unknown. For this reason it is necessary to resort to additional calculation procedures, such as the mass change method, to determine the scale factors of each mode. However, all variants of this method, in the current state of the art, have been deduced in the undamped situation.

In this paper we analyze the influence of the deviation of the results for the scale factors, obtained by means of a viscous damping analysis, compared to that same deviation determined under the consideration of hysteretic or structural damping, independent of the frequency, whose results align much better with the experimental behavior of the structure.

Keywords: Modal analysis, hysteretic and viscous damping, scaling factor

1. Introducción

En el análisis modal experimental (AME) tradicional es necesario conocer tanto la respuesta del sistema estructural como la excitación del mismo, con el objeto de poder relacionarlos a través de las funciones de respuesta en frecuencia (FRF) y extraer de ellas los parámetros modales que caracterizan el comportamiento dinámico de la estructura [1,2].

Por otra parte, en el análisis modal operacional (AMO) solo se registra la respuesta del sistema, mientras que la magnitud de la excitación es desconocida [3, 4], por lo que no se pueden determinar las FRF del sistema y los modos de vibración obtenidos no están escalados [5, 6]. A fin de determinar los factores de escala de cada modo, es necesario recurrir a un método adicional.

Una primera clasificación de estos métodos de escalado de los modos de vibración, sería la siguiente:

1) Procedimientos fundamentados en la modificación del comportamiento dinámico de la estructura. Existen diversas variantes, que consisten en modificar la masa y/o la rigidez del sistema estructural, para relacionar los resultados obtenidos en sendos análisis operacionales: el de la estructura original y la modificada [7].

2) Ajuste de un modelo de elementos finitos de la estructura analizada utilizando los parámetros modales obtenidos en el AMO [8, 9].

3) Procedimientos basados en la estimación de la matriz de masa de la estructura [10]. Las propiedades inerciales de la estructura (definidas por la matriz de masa), se pueden calcular de forma precisa para utilizarla en el análisis dinámico, de la misma forma que su conocimiento se emplea en el análisis estático (esto no tiene nada que ver con la masa modal, que merece una mención aparte, ya que es una propiedad dinámica relacionada con la proporción en la que la masa de la estructura participa en la vibración de cada modo).

4) Procedimientos fundamentados en añadir a la estructura original, un sistema de vibración secundaria (actuador electro hidráulico), para analizar la respuesta conjunta [11].

1.1. El método del cambio de masa en el AMO

Este método pertenece a la primera de las categorías mencionadas en el apartado anterior, está basado en un procedimiento de ensayo más completo, mediante la realización de dos ensayos AMO -por una parte- sobre la estructura modificada -y por otra- sobre la estructura original sin modificar [7,12]. La modificación se lleva a cabo añadiendo masas puntuales en los grados de libertad donde los modos de vibración son conocidos.

Parloo et al. proponen que el factor de escala que relaciona los modos de vibración normalizados y no normalizados [7], Φ = α ψ, sea determinado introduciendo un cambio de masa, definido mediante la matriz de cambio de masa [Δm] y aplicando la expresión

${\alpha }={\sqrt {\frac {{\rm {2}}\Delta {\rm {\omega }}}{{\rm {\omega }}\cdot \left\{{\rm {\psi }}\right\}^{\rm {T}}\cdot \left[{\rm {\Delta m}}\right]\cdot \left\{{\rm {\psi }}\right\}}}}$

(1)

en la que

${\Delta \omega }={\omega }_{0}-{\omega }_{1},\qquad {\omega }={\frac {{\omega }_{0}+{\omega }_{1}}{2}}$

(2)

y $\omega _{0}$, $\omega _{1}$ son las frecuencias naturales del modo considerado, antes y después de la aplicación del cambio de masa.

Por su parte, Brincker y Andersen proponen utilizar el valor medio de los factores de escala [12]. A diferencia del caso anterior, se determina el valor medio del factor de escala calculado con los modos no modificados y modificados (por efecto de la alteración de las propiedades de masa). Es decir, a partir de

${\alpha }_{00}={\sqrt {\frac {\left({\omega }_{0}^{2}-{\omega }_{1}^{2}\right)}{{\omega }_{1}^{2}\cdot \left\{{\psi }_{0}\right\}^{T}\cdot \left[{\Delta m}\right]\cdot \left\{{\psi }_{0}\right\}}}}$

(3)

y junto con

${\alpha }_{11}={\sqrt {\frac {\left({\omega }_{0}^{2}-{\omega }_{1}^{2}\right)}{{\omega }_{1}^{2}\cdot \left\{{\psi }_{1}\right\}^{T}\cdot \left[{\Delta m}\right]\cdot \left\{{\psi }_{1}\right\}}}}$

(4)

se determina el valor medio de los mismos

${\alpha }={\frac {{\alpha }_{00}+{\alpha }_{11}}{2}}$

(5)

Las ventajas del AMO, se convierten en inconvenientes en su aplicación a través del método de cambio de masa, por ejemplo en el caso de los puentes. En los que para realizar las sucesivas operaciones de modificación de masa (en general más de una) y su posterior medición, es necesario interrumpir el tráfico rodado [13].

En la elección entre ambos tipos de análisis dinámicos: AMO y AME, resulta preferible este último, siempre y cuando se trate de pequeñas estructuras que se pueden ensayar en laboratorio, o para grandes estructuras que pueden ser excitadas artificialmente sin problemas significativos.

En un trabajo anterior [13], se han determinado el modelo de respuesta y sus parámetros modales, que caracterizan el comportamiento dinámico de la estructura analizada en este trabajo: el Puente de la Cartuja. Estos datos se consideran de referencia, para su comparación con otros simulados numéricamente, habiéndose ajustado aquellos para un amortiguamiento histerético. De esta forma, la estructura del puente ha sido modelizada con el objeto de someterlo a una serie de simulaciones numéricas.

Una vez que se dispone de los parámetros modales experimentales de la estructura, antes de realizar la modificación de masa, es muy conveniente calcular la distribución de la masa propia del puente, su conocimiento permitirá disponer de un cambio de masa relativo en todos los g.d.l. muy similar, al objeto de reducir los errores introducidos por los cambios en los modos de vibración.

La influencia del amortiguamiento en el comportamiento estructural, y su estimación con la mayor exactitud posible, ha cobrado gran importancia en los últimos años; y por ello ha sido objeto de gran interés. En [14] se utiliza la variación en el factor de amortiguamiento como el parámetro principal para la localización del daño estructural. En Montalvão y Silva se presenta un método alternativo para la identificación del factor de amortiguamiento, resultante de un análisis centrado en la energía disipada por ciclo de vibración [15]. Este procedimiento es efectivo en el caso de estructuras poco amortiguadas y que presenten sus modos de vibración razonablemente separados. Sin embargo, su determinación se realiza para modos de vibración individuales, a diferencia del presente trabajo en el que se consideran todos los modos de vibración comprendidos dentro de un determinado rango de frecuencias de interés.

En este trabajo, se ha simulado la matriz de FRF para amortiguamiento viscoso, y mediante un análisis de regresión [16, 17], se ha ajustado la misma, sin y con modificación de masa. Con el objeto de comparar estos resultados con los procedimientos más utilizados en el estado del arte actual [7, 12] para obtener factores de escala, frente a los valores de referencia, obtenidos bajo el supuesto de un amortiguamiento histerético; para analizar su correspondencia entre ellos.

2. Modelización del amortiguamiento

La Tabla 1 muestra la ecuación diferencial del movimiento para un sistema de un grado de libertad (g.d.l.) para una excitación p_(t) dependiente del tiempo y armónica.

Tabla 1. Características de la modelización mediante amortiguamiento viscoso e histerético

ECUACIÓN DIFERENCIAL DEL MOVIMIENTO (1 g.d.l.): $m{\ddot {y}}+f_{D}+ky=p(t)$
PARÁMETROS REPRESENTATIVOS	MODELIZACIÓN DEL AMORTIGUAMIENTO
	VISCOSO	HISTERÉTICO
FUERZA DISIPATIVA O DE AMORTIGUAMIENTO $f_{D}$	$f_{D}=c{\dot {y}}$	$f_{D}=h/\omega {\dot {y}}=\eta {\bf {K}}/\omega {\dot {y}}\qquad \Leftrightarrow \qquad f_{d}=k(1+i\eta )y$
PROPIEDADES	Proporcional a la velocidad	Proporcional a la velocidad Inversamente prop. frec.	Unión de fuerzas elásticas y de amortiguamiento: Propor. a la amplitud del desplaz. En fase con la velo. (la cte. imag. i coloca la fuerza en fase con la velo.)
ENERGIA DISIPADA POR CICLO $E_{D}$	$E_{D}=\pi Y^{2}c\omega$	$E_{D}=\pi Y^{2}h$
PROPIEDADES	Función de la frec. y se incrementa linealmente con ella Propor. al cuadrado de la amplitud del mov.	Independiente de la frecuencia Propor. al cuadrado de la amplitud del mov.

En ella se representan también las dos formas más comunes de modelizar el amortiguamiento o disipación de energía en las estructuras. Así, el primero de ellos, se relaciona con la velocidad a través del amortiguamiento viscoso lineal equivalente por

$f_{D}=c\;{\dot {y}}$

(6)

Esta forma constituye la modelización más simple del amortiguamiento, ya que la ecuación diferencial del movimiento asociada es lineal, por tanto su resolución de forma analítica es accesible.

Por otra parte, la fuerza disipativa para amortiguamiento independiente de la frecuencia (histerético) se modeliza como

$f_{D}=h\,/\omega \;{\dot {y}}=\eta \,K\,/\,\omega \;{\dot {y}}$

(7)

suponiéndola también proporcional a la velocidad, pero inversamente proporcional a la frecuencia.

La energía disipada ${\bf {E}}_{D}$ para ambos tipos de amortiguamiento en un ciclo de vibración viene dada por las expresiones indicadas en la Tabla 1. La correspondiente al amortiguamiento viscoso es dependiente de la frecuencia, y se incrementa linealmente con la frecuencia de excitación ${\boldsymbol {\omega }}$. Sin embargo, experimentalmente se comprueba que la energía disipada en los esfuerzos cíclicos oscilatorios sobre los metales estructurales es independiente de la frecuencia.

Este tipo de amortiguamiento independiente de la frecuencia, surge en los sistemas estructurales como consecuencia de las acciones externas, que dan lugar a acciones elásticas restauradoras. Las cargas alternativas producen un cierto retardo entre las deformaciones y las cargas.

Así mismo, en la Tabla 1 se presenta también un resumen de las características en la modelización mediante amortiguamiento viscoso e histerético sobre un sistema estructural; para el caso del segundo se indican dos expresiones equivalentes para la fuerza disipativa f_D o de amortiguamiento, el término de la derecha es el resultado de sustituir la respuesta estacionaria (también armónica) para la velocidad , en la ecuación diferencial del movimiento.

De esta forma, este segundo término k (1+i η) y de la ecuación diferencial del movimiento, representa la unión de fuerzas elásticas y de amortiguamiento. Se puede afirmar que incorpora las propiedades de rigidez del sistema; habitualmente se lo conoce como rigidez compleja del sistema.

Por otra parte (Tabla 1), c representa el coeficiente de amortiguamiento, i la unidad compleja, el coeficiente η surge como una fracción de la rigidez k del sistema, conocido como factor de pérdida de amortiguamiento histerético: η = h/k ; finalmente, el parámetro h resultante es una constante, que tiene dimensiones de rigidez, y depende del material, conocido como coeficiente de amortiguamiento histerético.

La ecuación diferencial del movimiento expresada de esta última forma para varios g.d.l., y suponiendo que el mecanismo disipativo es histerético, adopta la forma:

$\left[\;M\,\right]\,\;\left\{\,{\ddot {y}}(t)\right\}\;\;+\;\,\left[\;\left[\,K\,\right]+i\,\left[\,H\,\right]_{}^{}\right]_{}^{}\,\;\left\{\,y(t)\right\}\;\;=\;\left\{\,F(t)\right\}$

(8)

Con los mismos significados de sus términos (para un g.d.l.) vistos en párrafos anteriores; estableciendo aquí la analogía para varios g.d.l. y representando aquellos en mayúsculas; de esta forma la matriz [K]+i[H] puede considerarse como una matriz de rigidez compleja, donde la parte imaginaria representa un desfase de π/2.

Para una función de excitación armónica dependiente del tiempo, la ecuación diferencial presenta una resolución analítica aceptable; sin embargo para un F_(t) arbitrario (o p_(t) en el caso de un sistema de 1 g.d.l.), su resolución matemática en el dominio del tiempo se vuelve muy compleja; ya que puede contener muchos componentes armónicos de diferentes frecuencias (análisis de Fourier). Por tanto, para esta modelización del amortiguamiento su análisis es más factible en el dominio de la frecuencia.

Por otra parte, entre las ventajas del amortiguamiento histerético estarían:

• Se ajusta de una forma más exacta al comportamiento exhibido por la mayoría de las estructuras reales.

• El análisis de sistemas de varios g.d.l. de forma analítica, es mucho más simple.

A su vez, para el amortiguamiento viscoso, el proceso disipativo íntegro, se está representando a través del uso de un elemento lineal equivalente, en el sentido de que, las ecuaciones diferenciales del movimiento resultantes en la modelización de un sistema estructural que incorpora esta tipología de amortiguamiento pueden ser resueltas para cualquier tipo de excitación de entrada p_(t) ; esta es la principal ventaja del amortiguamiento viscoso, y el motivo de su amplia utilización en toda clase de documentación científico-técnica.

Es en resonancia (ω = ω_n), donde la respuesta del sistema es más sensible al amortiguamiento. En [18-20] se muestra que la respuesta suministrada por el amortiguamiento histerético es idéntica a la ofrecida por el amortiguamiento viscoso si las razones de amortiguamiento de ambos están relacionados por

$\eta =2\xi \beta$

(9)

Y la razón de frecuencias β = ω/ω_n , entre la frecuencia de excitación y la natural del sistema, alcanza un valor unidad (β = 1), por tanto en resonancia

$\eta =2\xi$

(10)

entonces la respuesta con ambos tipos de amortiguamiento se hace idéntica, así como la energía disipada E_D (Figura 1). Sin embargo, fuera de resonancia (β ≠ 1), tanto las amplitudes como los ángulos de fase difieren entre sí.

Figura 1. Evolución de la energía disipada ED en un ciclo de vibración, frente a la frecuencia de excitación ω

En la frecuencia de resonancia se produce otra diferencia singular entre el amortiguamiento independiente de la frecuencia y el viscoso. La resonancia en amplitud y en ángulo de fase coinciden para el primero, mientras que en el segundo hay un cierto desfase produciéndose para la resonancia en amplitud a una frecuencia un poco menor que la de resonancia. Estas diferencias sin ser significativas, representan una fuente de cierta dificultad en la conciliación de datos físicos.

3. Modificación de la matriz FRF del sistema estructural

La introducción aquí de este apartado, se hace necesaria para el posterior análisis mediante simulaciones numéricas de las FRF. El problema de la determinación de los nuevos parámetros modales de un sistema dinámico, después de realizar modificaciones en el modelo de respuesta del mismo, se analiza en [21], en el dominio de la frecuencia, la relación entre fuerzas externas y desplazamientos viene dada por

${X}_{{0}\,\left({\omega }\right)}={H}_{{0}\left({\omega }\right)\,}\,{F}_{\left({\omega }\right)}$

(11)

donde X_0(ω) es la respuesta del sistema en los g.d.l. indicados, H_0(ω) la matriz de FRF original, de la estructura sin modificar y F_(ω) la excitación externa.

La matriz ΔB_(ω) de modificación de la rigidez dinámica, a utilizar para describir las alteraciones realizadas en la estructura original [22] tiene la forma

${\Delta B}_{\left({\omega }\right)}=-{\omega }^{2}{\Delta M}$

(12)

Es importante hacer notar que la expresión anterior es válida para amortiguamiento histerético o viscoso indistintamente, siempre y cuando las modificaciones que se realicen a la estructura solo afecten a las propiedades inerciales (es decir solo a la masa, no a la rigidez ni al amortiguamiento).

Así es posible predecir la nueva respuesta de la estructura modificada H_(ω) y las modificaciones de masa ΔB_(ω) previstas en la misma [21] para ambas modificaciones del amortiguamiento.

${H}_{\left({\omega }\right)\,}=\left[\;{I}+{H}_{{0}\left({\omega }\right)\,}\,{\Delta B}_{\left({\omega }\right)}\right]^{\;-1}\,{H}_{{0}\left({\omega }\right)\,}$

(13)

siendo I la matriz identidad. Esta operación repetida en el rango de frecuencias de interés, constituye una tercera dimensión de las matrices.

De esta forma es posible predecir la respuesta de la estructura frente a una modificación de masa sin necesidad de realizar un ensayo experimental mediante el método de modificación de masa. Y así determinar los factores de escala de los modos de vibración mediante simulaciones numéricas, con una exactitud muy alta, ya que permite tener en cuenta las diferencias entre los modos de vibración modificados y no modificados.

Para conseguir resultados válidos mediante el método del cambio de masa, es necesario alcanzar una modificación mínima en la masa de la estructura, en general un incremento en torno a un 5% representa una modificación razonable [7,12].

Experiencias previas en ensayos de estructuras civiles, y en particular en aplicaciones a puentes, permiten asegurar que ya se alcanzan buenos resultados con modificaciones de masa que produzcan desviaciones de frecuencia de un 1 o 2% [23].

Esta última expresión (13) posee algunas características más idóneas, con referencia a la establecida inicialmente en [21]:

• La influencia del segundo sumando en la operación de inversión es reducida, al estar constituido por la matriz FRF original, afectada por unas modificaciones pequeñas frente a la estructura real de partida; asumiendo entonces un comportamiento favorable de la matriz de identidad I con respecto a la operación de inversión, resulta poco probable que la matriz H_(ω) resultante esté mal condicionada.

• Es suficiente con invertir la matriz una sola vez.

4. Características del puente analizado

El puente de La Cartuja, está ubicado en el Meandro de San Jerónimo, en Sevilla (España) [24, 25]. Su tipología estructural se corresponde con la de un puente de tipo viga cajón continua de sección variable (el canto varía desde los 6 m hasta los 1.92 m, siendo de 3 m en la zona central), con tablero ortótropo de 11 m de ancho, completamente metálico [13].

En su día se convirtió en el puente más esbelto del mundo, con una relación luz/canto de 56.6, este valor es posible alcanzarlo gracias a:

• La continuidad de la viga del puente.

• Los vanos laterales relativamente cortos.

• Y las ménsulas ubicadas en el tablero y en los estribos, que trasmiten reacciones negativas a la infraestructura (Figura 2).

Figura 2. Alzado general del Puente de la Cartuja

Cada 4.25 m se han dispuesto marcos de rigidización transversal a lo largo de la viga principal, de esta forma se divide la misma en 56 dovelas. El peso en acabado del puente es de 1869 t, equivalente a 714 kp/m² (Figuras 2 y 3).

Figura 3. Vista en primer término, del vano principal central del Puente de la Cartuja

5. Análisis de resultados

Teniendo en cuenta la expresión η = 2 ξ (10), se ha simulado la matriz de FRF para amortiguamiento viscoso, tal y como se ha mencionado en el apartado 1.1.

En la modelización del esqueleto resistente del Puente de la Cartuja se han utilizado 56 dovelas de 4.25 m cada una (Figuras 2 y 4); 57 secciones transversales en total (al igual que en el proyecto constructivo del mismo). El efecto del arrastre del esfuerzo cortante sobre estas, se ha tenido en cuenta en el modelo.

Figura 4. Modelización del Puente de la Cartuja: viga cajón continua de sección variable, con tablero ortótropo

Para poder aplicar el método del cambio de masa descrito en [7,12] se ha simulado la respuesta dinámica del puente sometida a un incremento de masa del 5%, mediante el procedimiento descrito en el apartado 3. Esta modificación de masa se aplica sobre la directriz del tablero mediante masas puntuales.

Al ser la viga del puente de canto variable, su masa por unidad de longitud no es constante (la modificación del 5% es con respecto a la masa total). Por lo que la modificación en cada tramo es distinta, pero manteniendo la misma proporción de cambio; al objeto de evitar errores entre los modos de vibración de la estructura, sin modificar y modificada. El desplazamiento de frecuencia conseguido con esta modificación inercial es del 2.41%, sobradamente válido.

En [16,17] se describe la alternativa empleada para estimar los modos de vibración en un modelo incompleto, como el presente, utilizando complementos residuales móviles (en la parte real e imaginaria de la respuesta) basado todo ello en técnicas de optimización. Con estos procedimientos se ha tenido en cuenta el efecto de los modos fuera del rango de frecuencias de interés en el análisis.

Los procedimientos citados en [16,17] se idearon para amortiguamiento independiente de la frecuencia (histerético), pero con modificaciones menores, son efectivas para el caso general de amortiguamiento viscoso.

La Tabla 2 muestra un resumen de los resultados obtenidos. Los factores de escala de referencia correspondientes al ajuste independiente de la frecuencia (histerético), se han obtenido a partir de los parámetros modales que caracterizan el comportamiento dinámico del puente analizado, en un trabajo anterior [13].

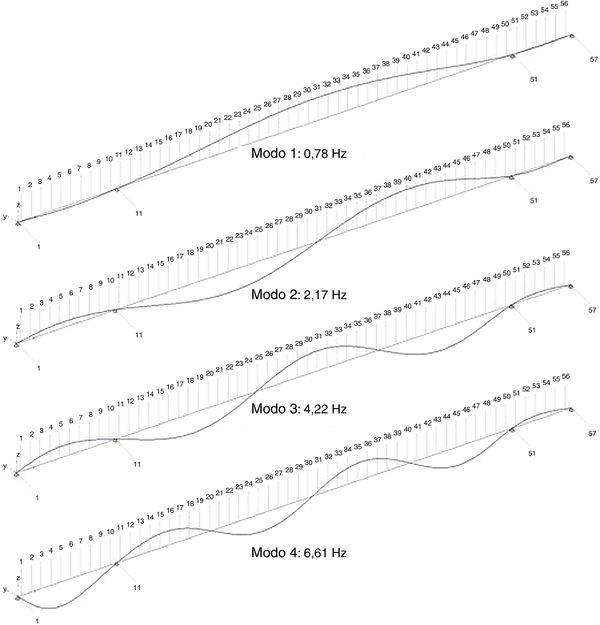
Se han extraído los 6 primeros modos en flexión vertical, y los 4 primeros en flexión horizontal (Figuras 5 y 6). La Tabla 2 muestra los resultados de los factores de escala correspondientes a ellos, mediante: simulaciones numéricas (ajuste viscoso), y estimaciones, utilizando el método de cambio de masa, en concreto las propuestas [7,12]. La desviación de los factores de escala α, con respecto a los de referencia α_ref, se calcula mediante la expresión

(14)

Frente a los obtenidos mediante una modelización del amortiguamiento como viscoso en la respuesta del sistema. También se ha determinado la media de la desviación en cada caso, así como la desviación típica correspondiente.

Figura 5. Flexión vertical: primeros cuatro modos de oscilación

Las propuestas citadas en el Apartado 1.1 [7,12], son las más utilizadas en el estado del arte actual, y dentro de él con las que además se obtienen mejores resultados; sin embargo es necesario hacer notar que estas expresiones fueron deducidas en la situación de no amortiguamiento.

Tabla 2. Resultados de los factores de escala: estimaciones y simulaciones numéricas

Modo nº	MAGNITUDES de REFERENCIA Ajuste histerético (indepen. de la frecuencia)	ESTIMACIONES Método del cambio de masa				SIMULACIONES NUMÉRICAS
		Propuesta Prof. Parloo [7]		Propuesta Prof. Brincker y Andersen [12]		Ajuste viscoso
			Δ [%]		Δ [%]		Δ [%]
1	0.4571-0.0014i	0.4460-0.0014i	2.42	0.4572-0.0014i	0.01	0.4580-0.0014i	0.19
2	0.4702-0.0022i	0.4585-0.0021i	2.49	0.4699-0.0022i	0.06	0.4708-0.0022i	0.13
3	0.4151+0.0015i	0.4100+0.0015i	1.23	0.4202+0.0015i	1.23	0.4150+0.0015i	0.02
4	0.4439-0.0002i	0.4505-0.0002i	1.37	0.4617-0.0002i	3.89	0.4415-0.0002i	0.55
5	0.4266-0.0038i	0.4272-0.0038i	1.76	0.4379-0.0039i	0.68	0.4306-0.0039i	0.93
6	0.4266-0.0066i	0.4124-0.0064i	3.31	0.4230-0.0065i	0.84	0.4268-0.0066i	0.03
7	0.4571+0.0019i	0.4667+0.0019i	2.10	0.4784+0.0020i	4.65	0.4571+0.0019i	0.00
8	0.4713-0.0048i	0.4764-0.0049i	1.08	0.4890-0.0050i	3.76	0.4713-0.0048i	0.00
9	0.4239+0.0024i	0.4049+0.0023i	4.47	0.4153+0.0024i	2.02	0.4246+0.0024i	0.16
10	0.3960-0.0032i	0.3930-0.0032i	0.80	0.4028-0.0033i	1.66	0.3965-0.0032i	0.12
Media de la desviación [%]			2.30		1.92		0.21
Desviación típica de la diferencia σΔ [%]			1.39		1.54		0.29

Finalmente, en el margen derecho de la Tabla 2, se muestran los resultados simulados numéricamente para un ajuste viscoso, utilizando las técnicas de optimización citadas en párrafos previos, que se obtienen con el programa informático Gams: sistema de modelado para la programación matemática y la optimización [26].

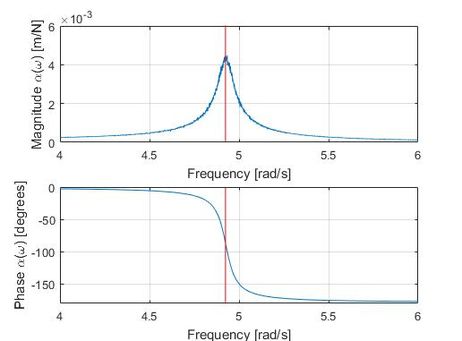
En la sección 32 del puente, muy próxima a la posición intermedia en el vano central, y también a la clave del mismo, se muestra, en el dominio de la frecuencia (Figura 7), una de las componentes α_jk(ω) de la matriz de FRF (magnitud y fase) para un g.d.l. vertical, y en la situación de partida: con un ajuste independiente de la frecuencia para el amortiguamiento. Nótese la coincidencia en la misma frecuencia de la resonancia en magnitud y ángulo de fase, como era de esperar.

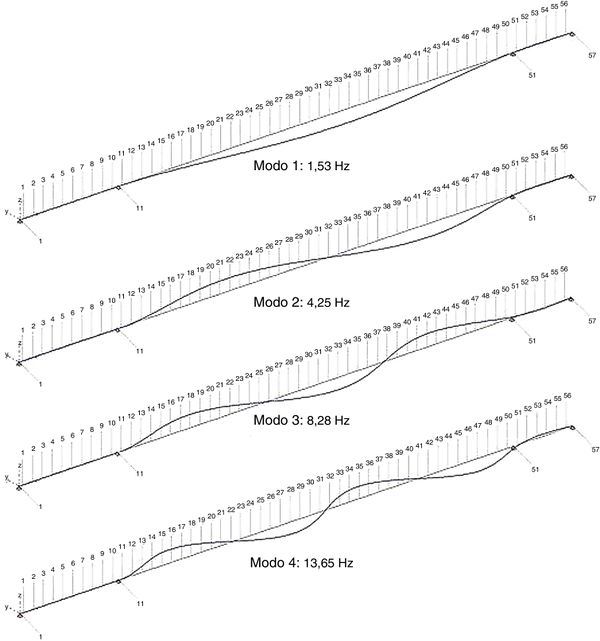
Figura 6. Flexión horizontal: primeros cuatro modos de oscilación

Figura 7. Componente αj,k(ω) de la matriz FRF (magnitud y fase), de la diagonal principal, correspondiente a un g.d.l. vertical en la sección 32 del puente

6. Conclusiones

A la vista de los resultados se observa que la desviación frente a las magnitudes de referencia es mayor en el caso [7], frente a [12], en donde se tiene en cuenta la alteración en los modos de vibración por la modificación de masa; la desviación típica o estándar crece muy poco en este último caso, por lo que se considera irrelevante.

Teniendo en cuenta la totalidad de la respuesta para su ajuste en el dominio de la frecuencia, y considerando amortiguamiento viscoso, la desviación de los factores de escala, se reduce en un orden de magnitud. Sin embargo todavía aparece una diferencia muy reducida frente al comportamiento experimental real de la estructura, con un amortiguamiento independiente de la frecuencia (histerético):

• Del análisis de resultados se observa que las FRF se ajustan mucho mejor para un modelo con amortiguamiento independiente de la frecuencia frente a su homólogo viscoso (primera etapa del proceso de optimización descrito en [16]). Valores representativos para una FRF: 250 iteraciones en 0.7 s (hist.), frente a 373 iteraciones en 1.26 s (visc.).

• Con los resultados de la etapa anterior, al proceder el ajuste de la matriz modal, la función objetivo final alcanza valores más óptimos, (más reducidos): 10.43710^-3 (hist.) frente a 17.57110^-3 (visc.), (segunda etapa del proceso de optimización descrito en [17]). Asimismo, para el ajuste de la matriz modal han sido necesarias 397 iteraciones realizadas en 1.2 s (hist.), frente a 488 iteraciones realizadas en 1.53 s (visc.).

• Los errores asociados con cada frecuencia en las que se mide la respuesta (variables ε_Ri y ε_Ii , [16]), son también más reducidas al final del proceso iterativo para amortiguamiento independiente de la frecuencia (histerético).

Referencias

[1] Cunha A.,Caetano E. From Input-Output to Output-Only Modal Identification of Civil Engineering, in Proceedings of the 1nternational Operational Modal Analysis Conference (IOMAC), 1-22, 2005.

[2] Coppotelli G. On the Estimate of the FRFs from Operational data, Mechanical Systems and Signal Processing, 23:288-299, 2008.

[3] Ibrahim S., Brincker R., Asmussen J. Modal Parameter Identification from Responses of General Unknow Random Inputs, Proceedings of The 14^th International Modal Analysis Conference (IMAC), 446-452, 1996.

[4] Batel M. Operational Modal Análisis – Another Way of Doing Modal Testing. Sound and Vibration. august:22-27, 2002.

[5] D. Bernal, Modal Scaling from Known Mass Perturbations, Journal of Engineering Mechanics, 130 9 (2004), 1083-1088.

[6] M.M. Khatibi; M.R. Ashory, A. Malekjafarian, Scaling of Mode Shapes Using Mass-Stiffness Change Method. Proceedings of the International Operational Modal Analysis Conference (IOMAC), Copenhagen, 679-706, 2009.

[7] E. Parloo, P. Verboven, P. Guillaume, M. Van Overmeire, Sensitivity-based operational mode shape normalization, Mechanical Systems and Signal Processing (MSSP) 16 (5) (2002) 757-767.

[8] J.E. Mottershead, M.I. Friswell, Model updating in structural dynamics: A survey, Journal of Sound and Vibration 165 (2) (1993) 347–375.

[9] C.E. Ventura, J.F. Lord, M. Turek, R. Brincker, P. Andersen, E. Dascotte, Fem updating of tall buildings using ambient vibration data., en: Proceedings of the sixth International Conference on Structural Dynamics (EURODYN), Paris, France, 2005.

[10] D. Bernal, B. Gunes, Damage localization in output-only systems: a flexibility based approach, en: Proceedings of the International Modal Analysis Conference (IMAC) XX, Los Angeles, California, 2002.

[11] J. Porras, J. de Sebastián, C. Casado, A. Lorenzana, Modal mass estimation from output-only data using oscillator assembly, Mechanical Systems and Signal Processing 26 (2011) 15–23.

[12] R. Brincker and P. Andersen, A Way of Getting Scaled Mode Shapes in Output Only Modal Analysis, In Proc. Of the International Modal Analysis Conference (IMAC) XXI, paper 141, 1-5, February 2003.

[13] L.M. Villa G., Comparación entre la estimación de parámetros modales de estructuras a partir de análisis modal clásico y operacional con modificaciones de masa, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 33(3-4), pp. 188–196, (2017). http://dx.doi.org/10.1016/j.rimni.2016.04.003

[14] A method for the localization of damage in a CFRP plate using damping, D. Montalvão, A.M.R. Ribeiro, J. Duarte-Silva, Mechanical Systems and Signal Processing, 23 (2009) 1846–1854. http://dx.doi.org/10.1016/j.compstruct.2012.10.050

[15] An alternative method to the identification of the modal damping factor based on the dissipated energy, D. Montalvão, J.M.M. Silva, Mechanical Systems and Signal Processing 54-55 (2015) 108–123. http://dx.doi.org/10.1016/j.ymssp.2014.08.025

[16] L.M. Villa G., Aplicación de Técnicas de Optimización para la Determinación de Parámetros Modales a través de las Funciones de Respuesta en Frecuencia, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, Vol. 23, Nº 4, pp. 395-414, (2007).

[17] L.M. Villa G., Cálculo de la Matriz Modal de un Sistema Dinámico a partir de las Constantes Modales Utilizando Técnicas de Optimización, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, Vol. 24, Nº 1, pp. 13-23, (2008).

[18] R.W. Clough y J. Penzien, Dynamics of structures, 2ª ed., MacGraw-Hill, Singapur 1993.

[19] N. M. Mendes Maia, J. M. Montalvão e Silva, Theoretical and Experimental Modal Análisis, Research Studies Press Ltd., 1997.

[20] A.K. Chopra. Dinámica de Estructuras, 4ª ed., México, Pearson, 2014.

[21] A. Sestieri, Structural Dynamic Modification, In Academy Proceedings in Engineering Sciences (Sadhana), Vol. 25, Part 3, 247-259, June 2000.

[22] X.Q. Zhu, S.S. Law . Time Domain Identification of Moving Loads on Bridge Deck. Journal of Vibration and Acoustics, Volume 125, Number 2 (April 2003), pp. 187-198.

[23] E. Parloo, B. Cauberghe, F. Benedettini, R. Alaggio y P. Guillaume, Sensitivity-based Operational Mode Shape Normalisation: Application to a Bridge, Mechanical Systems and Signal Processing (MSSP) 19 (2005) 43-55.

[24] F. Asensio Cerver, Bridges, Atrium, Barcelona, 1992.

[25] Sevilla: Puentes del 92, Colegio de Ingenieros de Caminos, Canales y Puertos de Andalucía (Sección de Publicaciones), 1992.

[26] E. Castillo, J. A. Conejo, P. Pedregal, R. García, N. Alguacil, Building and Solving Mathematical Programming Models in Engineering and Science, Research Studies Press Ltd., 2001.