Optimization Study For The Cross-Section Of A Concrete Gravity Dam: Genetic Algorithm Model And Application.

Abstract

Concrete gravity dams have trapezoidal shape in their cross section and shall guarantee the global stability against acting loads like hydrostatic and uplift pressures through his gravitational actions (self-weight and others). This study focuses on the shape optimization of concrete gravity dams using genetic algorithms. The cross section of dam is considered as the objective function and design variables are the geometric parameters of the gravity dam. The optimum cross-section design of concrete gravity dams is achieved by the Genetic Algorithm (GA) in Matlab. Sliding, overturning and floating constraints are considered. In order to assess the efficiency of the pro-posed methodology for gravity dam optimization, an example, the Belo Monte gravity dam as a real-world structure has been selected and the optimization of the dam subject to usual load condition has been achieved.

Keywords : optimization, concrete, gravity dams, genetic algorithm, real example, design.

1 Introduction

Concrete gravity dams are hydraulic structures widely used as water reservoir to hydroelectric power plants in general. These structures have trapezoidal shape in their cross section and shall guarantee the global stability against acting loads like hydrostatic and uplift pressures through his gravitational actions (self-weight and others). Hence, finding a proper shape design minimization of the dam's cross-section area can remarkably reduce the construction costs [3].

For stability requirements, the dam must be safe against overturning and sliding. Moreover, the safe stresses in the concrete of the dam or in the foundation material shall not be exceeded. The potential failure plans as concrete-foundation contact, horizontal plans through the dam body or through the foundation, can be considered, according to the rupture mechanisms identified by the geotechnical model [11].

In order to assure the structural global stability and the allowable stress criteria for the concrete gravity dam design, as discussed in Gutstein [19] and [20], a trial and error procedure process is

usually carried out from a preliminary cross section defined in the design initial phases, followed by stability and stress analysis studies. Then, if the chosen cross section does not meet the security criteria, it shall be modified and analyzed again; if safety criteria are being met with a little effort, a new study can be conducted with the purpose of optimizing the design.

To achieve this purpose, several alternative schemes with various patterns should be selected and modified to obtain a number of feasible shapes. Therefore, the proper shape of dam considering the economy and safety of design, structural considerations, etc. is selected as the final shape. In order to reliably achieve an optimal shape for dams instead of this trial and error procedure, optimization techniques have been effectively utilized [24], [23] and [34].

Genetic Algorithms (GA) are heuristic search approaches that are applicable to a wide range of optimization problems. This flexibility makes them attractive for many optimization problems in practice. They represent one branch of the field of study called evolutionary computation, in that they imitate the biological processes of reproduction and natural selection to solve for the fittest solutions [7].

GA can solve a broad class of engineering problems encountered in practice, possessing a large number of design parameters (integer, discrete, continuous and integer/discrete-continuous) and a large number of constraints. It has been highly successful as one of evolutionary computation techniques in searching for a broad class of stacking sequence, size, topology optimization problems for composite structures [29], [30], [31] and [18].

Designing and constructing concrete gravity dams must be in a way that not only realize sustained conditions, but also impose the minimum production costs. The major imposed cost in such dams is expenses of excessive use of concrete [35].

Optimizing this cost requires cross-section optimization. The main aim of this paper is to present and discussed an optimization study for concrete gravity dams based on GA’s method and Matlab application. The present work brings a simple implementation using GA in Matlab for usual load condition, contrasting with the complexity presented in [3], [2], [35], [24], [23] and [14] which bring approaches with high complexity computational methods.

The dam's geometry and the load effects over it must be considered in its design analisys procedure. In order to reduce the computational cost of the optimization process, the stopping criteria is limited to satisfactory values. To demonstrate the efficiency of GAs in finding the

optimum design of concrete gravity dams, the shape optimization of a real dam from Belo Monte Hydropower is presented as an example for normal conditions.

2 Stability Analysis of Concrete Gravity Dams

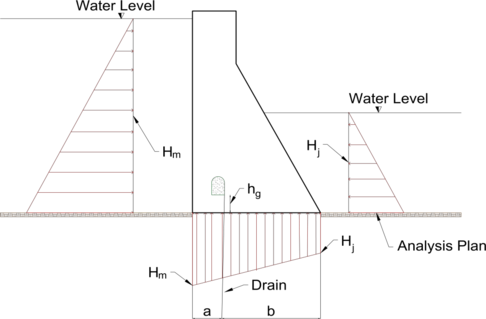
In this study is used usual loading combination. Therefore, normal design reservoir elevation, with appropriate loads and uplift. Figure 1 shows the usual loads acting in a dam considering drain. Water pressure is the most major external load acting on such a dam. The horizontal water pressure, exerted by the weight of the water stored on the upstream side on the dam can be estimated from rule of hydrostatic pressure distribution.

Figure 1. Concrete Gravity Dam Cross-Section and Imposed Forces.

For uplift determination, considering drain reduction, Hdm is adopted as shown in Equation 1.

𝐻𝑑𝑚 =

𝐻𝑗 +

1

File:Review 819849654054-picture-x0000 s3247.svg 3 ∗ (𝐻𝑚 − 𝐻𝑗) 𝑓𝑜𝑟 𝐻𝑗 > ℎ𝑔

(1)

1

{ℎ𝑔 + 3 ∗ (𝐻𝑚 − ℎ𝑔) 𝑓𝑜𝑟 𝐻𝑗 < ℎ𝑔

hg is the height, Hm upstream water, Hj downstream water and Hdm is uplift height with drain

reduction. To guarantee security for a dam, the dam cross section is verified against floating, overturning and sliding.

Floating safety factor has the function to guarantee the stability of structure against the forces that tend to make the body float. It is calculated by Equation 2 [12].

𝐹𝑆𝐹 =

∑ 𝑉

∑ 𝑈 (2)

Where FSF is safety factor against floating, should be greater than 1.3. ΣV is resultant vertical

force and ΣU is total uplift force.

The overturning of a gravity dam may be calculated by dividing the total resisting moments by the total moments tending to cause overturning about the downstream toe, it is defined as the ratio between the resisting moments and overturning moments [33].

∑ 𝑀𝑟

𝐹𝑆𝑂 =

∑ 𝑀𝑜

(3)

FSO is the safety factor against overturning, should be greater than 1.5. Mr are moments resisting

and Mo moments overturning.

A dam will fail in sliding at its base, or at any other level, if the horizontal forces causing sliding are greater than the resistance available to it at that level. The resistance against sliding may be due to friction alone, or due to friction and shear strength of the joint. The sliding stability is based on a safety factor as a measure of determining the resistance of the structure against sliding [32].

𝐹𝑆𝑆 =

µ ∑ 𝑉

∑ 𝐻 (4)

FSS is the safety factor against sliding which should also be greater than 1.0. µ is coefficient of

friction, ΣV is total vertical force acting on dam and ΣH is total horizontal force acting on dam.

3 Geometrical Model of Concrete Gravity Dams And Problem Formulation

In order to assign the geometrical model of concrete gravity dams, the shape can be defined using four parameters. Based on the model of concrete gravity dam depicted in Figure 2, the cross-section of concrete gravity dam studied is defined by the four parameters given by Equation 5

𝑋 = {ℎ𝑏, 𝑏𝑐 , 𝑏𝑥 , ℎ𝑡} (5)

Figure 2. Geometrical model of concrete gravity dam

Where bc is a parameter required to defined crest of gravity dam. Also, the downstream slope is specified by the bx and ht design variables and hb is the dam’s height.

The process of evaluating the overall stability of a concrete dam, makes use of the static equations to evaluate the equilibrium of rigid body of the part. In order to automate the calculation of the global stability of a concrete gravity dam, an evaluation program was developed in the Matlab language. This program will be used as a starting point of the research.

The evaluation program has the ability to calculate overall stability and dam stress from the dimensions and conditions provided by the designer. This algorithm returns the values of the safety factors, calculated by equations 2,3 and 4.

After completing the calculations, the program displays the values obtained for FSF, FSO and FSS with a message indicating whether these values meet the design criteria, or whether the study section should be resized.

Gravity dam optimization problem is explained in this section. The cross-sectional area of the dam is considered as an objective function to be minimized. An optimization problem subjected to design constraints can be expressed as follows:

Find 𝑋𝐿 ≤ 𝑋 ≤ 𝑋𝑈 Minimize 𝑓(𝑋) Subject to 𝑔(𝑋) ≤ 0

Where f and g are the objective function and the constraints, respectively. XL and XU are the lower bound and the upper bound of the design variables, X , respectively [23].

The objective function is the function you want to optimize. For standard optimization algorithms, this is known as the objective function. In this optimization problem of concrete gravity dams, the cross-section area of gravity dam body is considered as objective function, f(X), that should be minimized. The cross-section area of concrete gravity dam can be determined as follows:

𝑓(𝑋) = 𝑓(𝐴) = (ℎ𝑏 ∗ 𝑏𝑐 ) +

(𝑏𝑥 − 𝑏𝑐) ∗ (ℎ𝑏 − ℎ𝑡)

(6)

2

Where f(A) is cross-section area, and hb, bc, bx and ht are design variables showed in figure 2.

In the present study, the behavior and stability constraints are considered as the problem constraints, g(X). The behavior constraints consist on the safety factor against floating, overturning and sliding, calculated by equations 2, 3 and 4.

1.3 − 𝐹𝑆𝐹 ≤ 0

1.5 − 𝐹𝑆𝑂 ≤ 0

1.0 − 𝐹𝑆𝑆 ≤ 0

4 The Optimization Algorithm (Optdam)

4.1 Genetic Algorithm (GA)

Genetic algorithm (GA) is a method for solving both constrained and unconstrained optimization problems that is based on natural selection, the process that drives biological evolution. It is an optimization and search technique based on the principles of genetics and natural selection [21]. An individual is any point to which you can apply the fitness function [1].

The value of the fitness function for an individual is its score. A population is an array of individuals. At each iteration, the genetic algorithm performs a series of computations on the current population to produce a new population. Each successive population is called a new generation. The best fitness value for a population is the smallest fitness value for any individual in the population [15].

To create the next generation, the genetic algorithm selects certain individuals in the current population, called parents, and uses them to create individuals in the next generation, called children. Typically, the algorithm is more likely to select parents that have better fitness values [28].

A GA allows a population composed of many individuals to evolve under specified selection rules to a state that maximizes the fitness (minimizes the cost function). The genetic algorithm repeatedly modifies a population of individual solutions [27].

Evolution is the basis of Genetic Algorithms. The current variety and success of species is a good reason for believing in the power of evolution. Species are able to adapt to their environment. They have developed to complex structures that allow the survival in different kinds of environments. Mating and getting offspring to evolve belong to the main principles of the success of evolution. These are good reasons for adapting evolutionary principles to solving optimization problems [25].

It presumes that the potential solution of a problem is an individual and can be represented by a set of parameters. These parameters are regarded as the genes of a chromosome and can be structured by a string of values in binary form. A positive value, generally known as fitness value, is used to reflect the degree of “good-ness” of the chromosome for solving the problem, and this value is closely related to its objective value [26].

At each step, the genetic algorithm selects individuals at random from the current population to be parents and uses them to produce the children for the next generation. They combine survival of the fittest among string structures with a structured yet randomized information exchange search algorithm with some of innovative flair of human search [16]. Over successive generations, the population evolves toward an optimal solution.

It can be applied to solve a variety of optimization problems that are not well suited for standard optimization algorithms, including problems in which the objective function is discontinuous, nondifferentiable, stochastic, or highly nonlinear. The genetic algorithm can address problems of mixed integer programming, where some components are restricted to be integer-valued [10].

The genetic algorithm differs from a classical, derivative-based, optimization algorithm in two main ways. First, classical algorithms generate a single point at each iteration. The sequence of points approaches an optimal solution, GA generates a population of points at each iteration and the best point in the population approaches an optimal solution. The second difference is that classical algorithms selects the next point in the sequence by a deterministic computation, instead, GA selects the next population by computation which uses random number generators.

4.2 Penalty Function

In generic search methods, most applications of GAs to constraint optimization problems have used the penalty function approach of handling constraints. The penalty function approach involves a number of penal-ty parameters which must be set right in any problem to obtain feasible solutions [22].

It's applied constraint handling method for genetic algorithms. It uses the penalty function in Equation 7, where infeasible solutions are compared based only on their constraint violation [8].

𝑓(𝑥⃗), 𝑖𝑓 𝑔𝑗(𝑥⃗) ≥ 0 ∀𝑗= 1,2, … 𝑚,

𝐹(𝑋⃗) = {

𝑚

𝑓𝑚𝑎𝑥 + ∑ 𝑅𝑗〈𝑔𝑗 (𝑥⃗)〉 𝑂𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

𝑗=1

(7)

Where g(x) denotes the absolute value of the operand, if the operand is negative and returns a

value zero, otherwise. The parameter Rj is the penalty parameter of the jh inequality constraint. The purpose of a penalty parameter Rj is to make the constraint violation g(x) of the same order of magnitude as the objective function value f(x) [9].

The parameter fmax is the objective function value of the worst feasible solution in the population. Thus, the fitness of an infeasible solution not only depends on the amount of constraint violation, but also on the population of solutions at hand. However, the fitness of a feasible solution is always fixed and is equal to its objective function value.

4.3 Optdam

Bearing in mind the importance of studying dams and application for evolutionary computing methods of optimization, the aim now is to comment on the Optdam program developed in Matlab. This program allows finding an optical dam’s cross section. The program was developed to cover general cross sections of dams in terms of geometry as showed in figure 2.

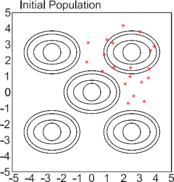
The GA in Matlab, as well as other GAs, begins by creating a random initial population Figure 3, and then creates a sequence of new populations. At each step, the algorithm uses the individuals in the current generation to create the next population [16].

Figure 3. Initial Population

After initial population, GA scores each member of the current population by computing its fitness value, scales the raw fitness scores to convert them into a more usable range of values, then selects members, called parents, based on their fitness. Some of the individuals in the current population that have lower fitness are chosen as elite [17]. These elite individuals are passed to the next population. Produces children from the parents. Hence, children are produced either by making random changes to a single parent, mutation, or by combining the vector entries of a pair of parents, crossover. Therefore, GA replaces the current population with the children to form the next generation [5] and [6]. The schematic diagram illustrates the process of creating the next generation Figure 4.

Figure 4. Creating the next generation

Resuming, the GA in Matlab uses three main types of rules at each step to create the next generation from the current population.

• Selection rules select the individuals, called parents, that contribute to the population at the next generation.

• Crossover rules combine two parents to form children for the next generation.

• Mutation rules apply random changes to individual parents to form children.

The algorithm stops when one of the stopping criteria is met. Figure 5 shown the convergence process. The GA parameters of Optdam program are shown in table 1. In Figure 6 are shown a flowchart illustrating the GA in program.

Figure 5. Convergence Process

Table 1 GA Information

GA Parameters

Parameters Adopted Population type Double vector Population size 100

Fitness scaling Rank

Elite count 40

Cross-over fraction 0.8

Mutation function Constraint dependent Cross-over function Constraint dependent Migration direction forward Migration fraction 0.2

Migration interval 20

Initial penalty 10

Penalty factor 100

Maximum number of generations 100

Stall generations 50

Function tolerance 10-6

Constraint tolerance 10-3

5 Example

Figure 6. Optdam

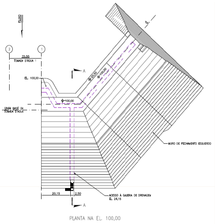
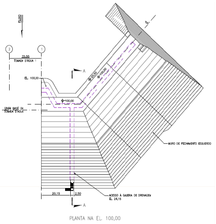
In order to investigate the computational efficiency of the proposed GA optimization method for the shape optimization of concrete gravity dams, Belo Monte side wall dam, located 52 km Transamazônica Highway southwest of Altamira, Pará, Brazil, is considered as a real-world structure. The dam structure is 80 m high with a crest length of 100 m and its construction consumed about 2392400 m³ concrete. The initial design of Belo Monte dam is shown in Figure 7.

Figure 7. Belo Monte’s Dam

Analyzing the initial design of Belo Monte dam, the safety against floating, overturning and sliding was calculated with the evaluated program.. The results of the usual load case, geometry parameters and water level are shown in Table 2.

Table 2 Dam Information

Safety factors

Factor Design criteria request Achieved values FSF 3.00 4.52

FSO 1.50 2.08

FSS 1.00 1.32

Geometry parameters

Parameter Value Unit

Cross section area 2392.4 m²

Concrete volume 2392400 m³

Water parameters

Parameter	Value	Unit
Upstream water	70.5	m
Downstream water	0	m

In the present study, four variables are considered for creating the trapezoidal dam geometry. The lower and upper bounds of design variables required for the optimization process can be determined using some preliminary design methods. These bounds are shown in Table 3. Also, for finding the optimum shape of the dam, the properties of concrete, water and foundation as shown in Table 4 are considered.

Table 3 Variables

Belo Monte’s design variables

Design variable Lower bound (m) Upper bound (m) h 75 80

bc 2 10

bx 16 56

ht 2 10

Table 4 Materials

The properties of materials

Material Properties Value Concrete’s Elasticity Modulus 240.00 MPa Concrete resistance 25.00 MPa

Poison’s ratio of concrete 0.2 - Mass density of concrete 2500 Kg/m³ Speed of pressure wave 1440 m/s Wave reflection coefficient 0.9 -

Rock friction angle π/5 rad

Partial friction safety factor	1	-
Internal friction coefficient	0.7	-
Elasticity modulus of rock	27.580	MPa
Poison’s ratio of foundation rock	0.2	-

6 Results

The optimum design of the gravity dam for Belo Monte’s dam using GA is given in Table 5. By comparing the solution obtained for the dam with the GA can significantly reduce the concrete volume of dam.

Table 5 Optimization Results

Optimum designs of the dam obtained by Optdam (GA)

Design variable h	Value 80	Unit m
bc	6	m
bx	43	m
ht	7	m
FSF	4.5062	-
FST	1.5001	-
FSD	1.0030	-
Cross section area	1830.5	m²
Concrete savings	56190	m³
Concrete savings percentage	23.49	%

Figure 8 shown the genealogy of individuals. Lines from one generation to the next are red to indicate mutation children, blue to indicate cross-over children and black to indicate elite individuals. It is noted that the number of children arising from mutation and cross-over are well higher than the number of elite individuals, which suggests that premature convergence is not

occurring, premature convergence is not desirable and characterized by a high number of elite individuals [4].

Figure 8. Genealogy

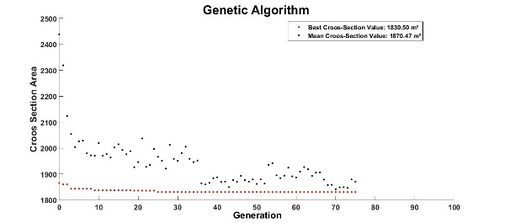
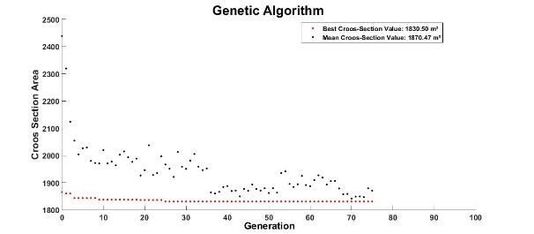
The graph in Figure 9 presents the best cross section area value of the objective function in each generation versus the number of the generation. The best values and mean values are highlighted for each iteration. It can be concluded that the methodology presents too much robustness in the resolution of the problem (reduction of area), already in the first iteration, in its best solution, have acceptable results.

It is noted that as the iterations progress, the mean values obtained are approaching the best values, this is due to the GA’s natural selection excludes the values of lesser fitness and starts to work only with the values that best fit adapt to the solution of the problem.

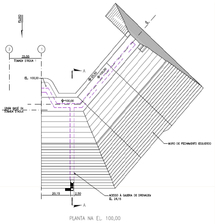
In order to limit the computational cost, the number of iterations and stall generation was limited to a hundred and fifty respectively, showing a valid criterion, since an optimal section could be obtained with an even smaller number of iterations. In Figure10 it can see the optimized cross section within the pre-optimization section, emphasizing the area savings obtained by Optdam.

Figure 9. Stop Criterion

Figure 10. Optimized Section

7 Conclusions

An efficient optimization procedure is introduced to find the optimal shapes of concrete gravity using genetic algorithm in Matlab software. The concrete gravity dam body is treated as a two- dimensional structure involving the geometry.

An example of a Belo Monte’s dam was presented. The GA optimum solution obtained for the dam reveal that Belo Monte’s dam could be design with a more economic cross-section. Results demonstrated the ability of these algorithms for this type of continuous optimization problem.

Status of optimally designed dam for the algorithm is also provided for better assessment of safety factors. It is shown that all the constraints are completely satisfied.

This research provides useful optimization formulations for trapezoidal concrete gravity dams and can be extended to other dams. The final result is a robust genetic algorithm program for shape optimization of concrete gravity dams, that is simple from a mathematical point of view and is able to work with trapezoidal dams under different load and bounder conditions. The proposed method reduces the cross-section area and consequently the volume of dam up to 20% with very low computational effort..

8 Acknowledgments

The research described in this paper was financially supported by the Federal Institute of Education, Science and Technology of Goias.

9 References

[1] Ackley, David H. (1987). "The model." In A Connectionist Machine for Genetic Hillclimbing, pp. 29-70. Springer, Bos-ton, MA.

[2] Ali, Pr Dr Ahmed AM, Pr Dr Rafa HS Al-Suhaili, and Shamil AK Behaya. (2014) "A genetic algorithm optimization model for the gravity dam section under seismic excitation with reservoir-dam-foundation interactions." Amer J Eng Res 3, no. 6: 143-53.

[3] Baghlani, Abdolhossein, Mohsen Sattari, and Mohammad Hadi Makiabadi. (2014) "Application of genetic program-ming in shape optimization of concrete gravity dams by metaheuristics." Cogent Engineering 1, no. 1: 982348.

[4] Bento, Eduardo Prevedello, and Nelson Kagan. (2008) "Algoritmos genéticos e variantes na solução de problemas de configuração de redes de distribuição." Sba: Controle & Automação Sociedade Brasileira de Automatica 19, no. 3: 302-315.

[5] Conn, Andrew R., Nicholas IM Gould, and Philippe Toint. (1991) "A globally convergent augmented Lagrangian algo-rithm for optimization with general constraints and simple bounds." SIAM Journal on Numerical Analysis 28, no. 2: 545-572.

[6] Conn, Andrew R., Nicholas IM Gould, and Philippe Toint. (1991) "A globally convergent augmented Lagrangian algo-rithm for optimization with general constraints and simple bounds." SIAM Journal on Numerical Analysis 28, no. 2: 545-572.

[7] Carr, Jenna. (2014) "An introduction to genetic algorithms." Senior Project 1: 40.

[8] Deb, Kalyanmoy. (2000) "An efficient constraint handling method for genetic algorithms." Computer methods in ap-plied mechanics and engineering 186, no. 2-4: 311-338.

[9] Deb, K. (1995) "Optimization for Engineering Design: Algorithms and Examples Prentice- Hall." New Delhi.

[10] Deep, Kusum, Krishna Pratap Singh, Mitthan Lal Kansal, and C. Mohan. (2009) "A real coded genetic algorithm for solving integer and mixed integer optimization problems." Applied Mathematics and Computation 212, no. 2: 505-518.

[11] Durieux, Johan Hendrik. (2009). "Development of a practical methodology for the analysis of gravity dams using the non-linear finite element method." PhD diss., University of Pretoria.

[12] ELETROBRÁS CENTRAIS ELÉTRICAS BRASILEIRAS. (2003). "Critérios de projeto

civil de usinas hidrelétricas."

[13] Ghaffari, Yousef, Fereshteh Nouri Zonouz, Vahid Mahdavifar, Ramin Taghinezhad, and Vafa Soltangharaei. (2018). "Shape Optimization of Gravity Dams Using Genetic Algorithm." PhD diss., MSc. Thesis, University of Tabriz, Tabriz, Iran.

[14] Ghaffari, Yousef et al. (2018). Shape Optimization of Gravity Dams Using Genetic Algorithm. Tese de Douto-rado. MSc. Thesis, University of Tabriz, Tabriz, Iran.

[15] Gen, Mitsuo, and Runwei Cheng. (2000). Genetic algorithms and engineering optimization. Vol. 7. John Wiley & Sons.

[16] Goldberg, David E., and John H. Holland. (1988) "Genetic algorithms and machine learning." Machine learning 3, no. 2: 95-99.

[17] Guide, MATLAB User’S. (1998) "The mathworks." Inc., Natick, MA 5: 333.

[18] Gurba, W. (2001) "Probabilistic Methods of Composite Structures Optimization." PhD diss., Ph. D. Thesis, Cracow Uni-versity of Technology, Krakówm (in Polish).

[19] Gutstein, Daniela. (2011). "Projeto de estruturas de barragens de gravidade de concreto por meio de métodos computa-cionais: visão geral e metodologia."

[20] Gutstein, Daniela. (2003). "Estudo das tensões em fundações de barragens de gravidade de concreto pelo método de elementos finitos."

[21] Haupt, Randy L., Sue Ellen Haupt, and Sue Ellen Haupt. (1998) Practical genetic algorithms. Vol. 2. New York: Wiley.

[22] Homaifar, Abdollah, Charlene X. Qi, and Steven H. Lai. "Constrained optimization via genetic algorithms." Simulation 62, no. 4 (1994): 242-253.

[23] Khatibinia, M., H. Chiti, A. Akbarpour, and H. R. Naseri. (2016) "Shape optimization of concrete gravity dams consid-ering dam–water–foundation interaction and nonlinear effects." Iran University of Science & Technology 6, no. 1: 115-134.

[24] Khosravi, Sh, and M. Khatibinia. (2016). "Optimal Shape Design of Concrete Gravity Dams Including." Iranian Journal of Structural Engineering 3, no. 2.

[25] Kramer, Oliver. (2017). Genetic algorithm essentials. Vol. 679. Springer.

[26] Man, Kim-Fung, Kit-Sang Tang, and Sam Kwong. (1996) "Genetic algorithms: concepts and applications [in engineer-ing design]." IEEE transactions on Industrial Electronics 43, no. 5: 519-534.

[27] Michalewicz, Zbigniew, and Stephen J. Hartley. (1996) "Genetic algorithms+ data structures= evolution programs." Mathematical Intelligencer 18, no. 3: 71.

[28] Mitchell, Melanie. (1998).An introduction to genetic algorithms. MIT press.

[29] Muc, A. (1997) "Transverse shear effects in discrete optimization of laminated compressed cylindrical shells." Compo-site structures 38, no. 1-4: 489-497.

[30] Muc, A. W. Gurba, (2001) Genetic algorithms and finite element analysis in optimization of composite structures, Composite Structures, vol. 54, ss. 275-81.

[31] Muc, A. (2018) Evolutionary design of engineering constructions, Latin American Journal of Solids and Structures.

[32] Usace, Manual Engineer. (1995) "Gravity dam design." ENGINEER 20020626: 116.

[33] USBR - United States Bureau of Reclamation (1976). “Design of gravity dams”. Denver:

United States Depart-ment of the Interior – Bureau of Reclamation.

[34] Vianna, Luis Claudio Coelho. (2003). "Otimização de seções transversais de concreto armado: aplicação a pórticos." PhD diss., Universidade de São Paulo.

[35] Yazd, Hamidreza Golkar Hamzee, Seyed Jafar Arabshahi, Mojtaba Tavousi, and Abbas Alvani. (2015) "Optimal de-signing of concrete gravity dam using Particle Swarm Optimization Algorithm (PSO)." Indian Journal of Science and Technology 8, no. 12: 1.