| Line 59: | Line 59: | ||
El criterio de fluencia del modelo Mohr-Coulomb proviene de la ley de fricción de Coulomb, la cual establece que el estado general de esfuerzos es formulado mediante las funciones de fluencia (Ecuaciones 1 y 2). Dichas funciones de fluencia están en términos de los esfuerzos principales: ''i''=1,2,3; ''j''=2,3,1; ''k''=3,2,1. Además, se incorporan los dos parámetros de resistencia al corte: ángulo de fricción (''Φ'') y cohesión del material (''c''). | El criterio de fluencia del modelo Mohr-Coulomb proviene de la ley de fricción de Coulomb, la cual establece que el estado general de esfuerzos es formulado mediante las funciones de fluencia (Ecuaciones 1 y 2). Dichas funciones de fluencia están en términos de los esfuerzos principales: ''i''=1,2,3; ''j''=2,3,1; ''k''=3,2,1. Además, se incorporan los dos parámetros de resistencia al corte: ángulo de fricción (''Φ'') y cohesión del material (''c''). | ||
| − | <math display="inline">{f}_{ia}=\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) +</math><math>\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) \mathrm{sin}\,\phi -c\, \mathrm{cos}\,\varphi \, \leq 0</math> | + | {| class="formulaSCP" style="width: 100%; text-align: center;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{f}_{ia}=\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) +</math><math>\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) \mathrm{sin}\,\phi -c\, \mathrm{cos}\,\varphi \, \leq 0</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
| + | |} | ||
| − | <math display="inline">{f}_{ib}=\frac{1}{2}\left( {\sigma }_{k}^{'}-\, {\sigma }_{j}^{'}\right) +</math><math>\frac{1}{2}\left( {\sigma }_{k}^{'}-\, {\sigma }_{j}^{'}\right) \mathrm{sin}\,\phi -c\, \mathrm{cos}\,\varphi \, \leq 0</math> | + | {| class="formulaSCP" style="width: 100%; text-align: center;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{f}_{ib}=\frac{1}{2}\left( {\sigma }_{k}^{'}-\, {\sigma }_{j}^{'}\right) +</math><math>\frac{1}{2}\left( {\sigma }_{k}^{'}-\, {\sigma }_{j}^{'}\right) \mathrm{sin}\,\phi -c\, \mathrm{cos}\,\varphi \, \leq 0</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| + | |} | ||
Por otro lado, la formulación del comportamiento elastoplástico perfecto en el modelo está dado por la interacción entre la tasa de deformación elástica y la tasa de deformación plástica (Ec. 8). Dicha interacción parte de la forma básica de la ley de Hooke (Ec. 9), donde ''D<sup>e</sup>'' representa la matriz de rigidez del material. | Por otro lado, la formulación del comportamiento elastoplástico perfecto en el modelo está dado por la interacción entre la tasa de deformación elástica y la tasa de deformación plástica (Ec. 8). Dicha interacción parte de la forma básica de la ley de Hooke (Ec. 9), donde ''D<sup>e</sup>'' representa la matriz de rigidez del material. | ||
| − | <math display="inline">\overset{\cdot}{\overline{\epsilon }}+{\overset{\cdot}{\overline{\epsilon }}}^{e}\, +</math><math>{\overset{\cdot}{\overline{\epsilon }}}^{p}</math> | + | {| class="formulaSCP" style="width: 100%; text-align: center;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\overset{\cdot}{\overline{\epsilon }}+{\overset{\cdot}{\overline{\epsilon }}}^{e}\, +</math><math>{\overset{\cdot}{\overline{\epsilon }}}^{p}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
| + | |} | ||
| − | <math display="inline">{\overset{\cdot}{\sigma }}^{'}={D}^{e}{\overset{\cdot}{\overline{\epsilon }}}^{e}=</math><math>{D}^{e}\left( \overset{\cdot}{\overline{\epsilon }\, -}{\overset{\cdot}{\overline{\epsilon }}}^{e}\right)</math> | + | {| class="formulaSCP" style="width: 100%; text-align: center;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{\overset{\cdot}{\sigma }}^{'}={D}^{e}{\overset{\cdot}{\overline{\epsilon }}}^{e}=</math><math>{D}^{e}\left( \overset{\cdot}{\overline{\epsilon }\, -}{\overset{\cdot}{\overline{\epsilon }}}^{e}\right)</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
| + | |} | ||
Debido la sobreestimación de la dilatancia del suelo en la teoría de plasticidad asociada relativa el modelo Mohr-Coulomb plantea una función de potencial plástico, ''g. ''[13]. Además, en el caso particular ''g'' ≠ ''f'' este modelo describe la plasticidad no asociada del material. De esta manera, el modelo Mohr-Coulomb plantea funciones de potencial plástico a las que se les adiciona el parámetro del ángulo de dilatancia, <math display="inline">\psi</math> (Ecs. 10 y 11). Dicho parámetro, se requiere para modelar los incrementos de deformación volumétrica plástica del suelo. | Debido la sobreestimación de la dilatancia del suelo en la teoría de plasticidad asociada relativa el modelo Mohr-Coulomb plantea una función de potencial plástico, ''g. ''[13]. Además, en el caso particular ''g'' ≠ ''f'' este modelo describe la plasticidad no asociada del material. De esta manera, el modelo Mohr-Coulomb plantea funciones de potencial plástico a las que se les adiciona el parámetro del ángulo de dilatancia, <math display="inline">\psi</math> (Ecs. 10 y 11). Dicho parámetro, se requiere para modelar los incrementos de deformación volumétrica plástica del suelo. | ||
| − | <math display="inline">{g}_{ia}=\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) +</math><math>\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) \mathrm{sin}\,\psi</math> | + | {| class="formulaSCP" style="width: 100%; text-align: center;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{g}_{ia}=\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) +</math><math>\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) \mathrm{sin}\,\psi</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{g}_{ib}=\frac{1}{2}\left( {\sigma }_{k}^{'}-\, {\sigma }_{j}^{'}\right) +</math><math>\frac{1}{2}\left( {\sigma }_{j}^{'}-\, {\sigma }_{k}^{'}\right) \mathrm{sin}\,\psi</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
| + | |} | ||
| − | |||
Con base en la anterior consideración, las deformaciones plásticas pueden ser descritas mediante la ecuación 3; donde corresponde al multiplicador plástico. Cuando λ=0 el comportamiento será puramente elástico mientras que λ>0 denota un comportamiento netamente plástico. | Con base en la anterior consideración, las deformaciones plásticas pueden ser descritas mediante la ecuación 3; donde corresponde al multiplicador plástico. Cuando λ=0 el comportamiento será puramente elástico mientras que λ>0 denota un comportamiento netamente plástico. | ||
| − | <math display="inline">{\overset{\cdot}{\overline{\epsilon }}}^{p}=\Lambda \frac{\partial g}{\partial {\sigma }^{'}}</math> | + | {| class="formulaSCP" style="width: 100%; text-align: center;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{\overset{\cdot}{\overline{\epsilon }}}^{p}=\Lambda \frac{\partial g}{\partial {\sigma }^{'}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
| + | |} | ||
Teniendo en cuenta todas las ecuaciones anteriores se obtiene la relación entre los esfuerzos efectivos y las tasas de deformación para el comportamiento elastoplástico [16]. El modelo Mohr-Coulomb es considerado el modelo constitutivo más utilizado en la Ingeniería Geotécnica, debido a su simplicidad y fácil medición de sus parámetros. | Teniendo en cuenta todas las ecuaciones anteriores se obtiene la relación entre los esfuerzos efectivos y las tasas de deformación para el comportamiento elastoplástico [16]. El modelo Mohr-Coulomb es considerado el modelo constitutivo más utilizado en la Ingeniería Geotécnica, debido a su simplicidad y fácil medición de sus parámetros. | ||
Revision as of 15:43, 8 November 2018
Abstract
In geotechnical engineering one of the challenges is the soil characterization. Nevertheless, currently it exists computational tools, which permits estimate the soil behaviour from information obtained in the laboratory. This document addresses the numerical modelling of triaxial tests set with Ko consolidation during its shear stage by means of single element test tool. The work methodology was based on the stress paths comparison between lab data and numerical simulations with three different constitutive models: (i) Mohr-Coulomb, (ii) Cam-Clay Modified, (iii) Hypoplastic. Such stress paths were obtained in drained and undrained conditions. The soil material corresponds to a porous collapsible clay from Brasilia (Brazil). Results show the calibration of the parameters for each constitutive model. Besides, presents the stress-strain curves until achieving the critical state condition in the simulations. Finally, it was established the constitutive model that presents the best fitting to the real behaviour of this kind of material, under specific conditions for advanced triaxial tests.
Keywords: Anisotropic Consolidation, Constitutive Models, Single Element Test, Triaxial Test.
Resumen
En la ingeniería geotécnica uno de los mayores desafíos es la caracterización de del suelo. Sin embargo, en la actualidad existen herramientas computacionales que permiten estimar el comportamiento del suelo a partir de parámetros medidos en laboratorio. Este documento aborda la modelación numérica de la etapa de corte de una serie de ensayos triaxiales con consolidación Ko usando una herramienta tipo single element test. La metodología de trabajo se basó en la comparación de las trayectorias de esfuerzos entre datos de laboratorio y simulaciones numéricas ejecutadas con tres modelos constitutivos diferentes: (i) Mohr-Coulomb, (ii) Cam-Clay Modificado, (iii) Hipoplástico. Dichas trayectorias fueron obtenidas durante la etapa de corte en condiciones drenadas y no drenadas. El material de estudio corresponde a una arcilla porosa colapsable proveniente de la cuidad de Brasilia (Brasil). Los resultados exhiben el proceso de calibración de los parámetros de cada una de las leyes constitutivas para las simulaciones numéricas. Asimismo, muestran las curvas esfuerzo-deformación hasta alcanzar el estado crítico del suelo durante las simulaciones. Finalmente, se estableció el modelo constitutivo que presenta mejor ajuste al comportamiento real de este tipo de material bajo condiciones específicas de ensayos triaxiales avanzados.
Palabras clave: Ensayo Triaxial, Consolidación Anisotrópica, Single Element Test, Modelos Constitutivos.
1. Introducción
Los suelos son materiales cuyo comportamiento es elastoplástico no lineal [1]. Sin embargo, su rango elástico se evidencia, únicamente, a bajas deformaciones [2]. Por lo tanto, el comportamiento de los suelos se representa matemáticamente mediante modelos constitutivos que involucran la respuesta de los mismos frente a solicitaciones de carga y deformación. A lo largo del tiempo, dichos modelos se han implementados para materiales y condiciones específicas [3].
Así pues, la implementación de modelos constitutivos en programas de computador se ha convertido en una herramienta versátil que permite aproximar el comportamiento de algunos tipos de suelo sin recurrir a ensayos de laboratorio. No obstante, dichos programas están formulados con modelos constitutivos que son simplificaciones de la realidad y, por consiguiente, no existe un programa que reemplace la caracterización física, mecánica y dinámica de dichos materiales [4]. Dentro de la industria computacional los modelos constitutivos más representativos y con mayor aceptación para evaluar el comportamiento de las arcillas son: Mohr-Coulomb, Cam-Clay Modificado e Hipoplástico.
Diversos trabajos se han desarrollado con el fin de identificar el modelo constitutivo que mejor represente el comportamiento del suelo. [5] desarrollaron simulaciones numéricas para dos tipos de muestras de suelo recuperadas en la cuidad de Bogotá (Colombia). La primera fue tomada cerca del Aeropuerto El Dorado a tres metros de profundidad; mientras que la segunda fue extraída a 40 m de profundidad en el sector El Polo de la misma ciudad. Más tarde, [6] presentaron una alternativa basada en el método single element test para calibrar modelos constitutivos. Su trabajo incorporó simulaciones numéricas de tres modelos diferentes para suelos con estructura cementada. Por otra parte, [7] realizaron modelaciones numéricas para evaluar el proceso de consolidación Ko en cámaras triaxiales. Dichas modelaciones fueron ejecutadas con tres modelos constitutivos diferentes y mediante un single element test.
El objetivo de este artículo es presentar los resultados de unas simulaciones numéricas que incorporan las trayectorias de esfuerzos de unos ensayos triaxiales con consolidación Ko drenados y no drenados. Dichas modelaciones fueron ejecutadas con tres modelos constitutivos diferentes. La estructura del documento está compuesta por seis secciones. La primera es la introducción del trabajo realizado. La segunda es el marco teórico de los modelos constitutivos usados en las simulaciones. La tercera sección describe el suelo analizado. La cuarta sección muestra el proceso de calibración de los parámetros de cada uno de los modelos constitutivos. La quinta sección corresponde a los resultados de las simulaciones numéricas y su comparación con los datos de laboratorio. Por último, en la sexta sección se resaltan los hallazgos más importantes del trabajo mediante las conclusiones.
2. Antecedentes
2.1 Modelos constitutivos en geomateriales
Un modelo constitutivo es una formulación matemática que permite describir el desempeño físico de un suelo como un material ideal [8]. Por lo tanto, el objetivo de un modelo constitutivo es establecer el comportamiento del suelo durante la aplicación de cargas o deformaciones con base en teorías como la de la elasticidad, plasticidad, viscoplasticidad, micro fractura y fatiga de manera combinada o separada [9]. Además, debido a que los suelos son materiales naturales es necesario incorporar dentro de dichas teorías factores como el tiempo, el esfuerzo de fluencia y la densidad. Así pues, la formulación de un modelo constitutivo representa una hipótesis simplificada de la realidad y que adopta parámetros según el material para el que fue calibrado [10].
2.1.1 Modelo Mohr-Coulomb
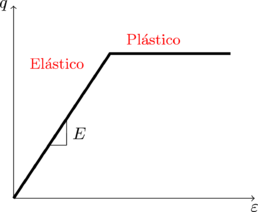
Es un modelo elastoplástico perfecto que es usado para realizar una primera aproximación al comportamiento del suelo. Así pues, este modelo es la base para la calibración y verificación de simulaciones numéricas, ya que provee soluciones analísticas a dichos problemas [11]. Su comportamiento linear elástico se basa en la ley de Hooke y su concepto de plasticidad perfecta está basada en el criterio de envolvente de falla [12]. El modelo Mohr-Coulomb no representa el comportamiento elastoplástico progresivo, sino que es un modelo que en su etapa inicial considera al suelo como un material elástico y posteriormente plástico perfecto (Figura 1). Este modelo es capaz de simular el comportamiento de suelos granulares sueltos y de suelos finos normalmente consolidados [13].
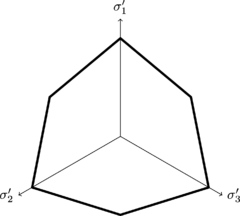
Dentro del concepto de plasticidad del modelo está implícito el desarrollo de deformaciones irreversibles; por lo que en la búsqueda de determinar si se ha alcanzado el rango elástico en un estudio se acude al uso de una función de fluencia f. Dicha función está estrechamente relacionada con el esfuerzo y la deformación. La condición f=0 advierte el inicio del rango plástico y puede ser presentada como una superficie de fluencia fija en el espacio de los esfuerzos principales [14]. De esta manera, los estados de esfuerzo que se encuentran dentro de la superficie de fluencia fija, tendrán un comportamiento exclusivamente elástico y sus deformaciones serán reversibles. Por otro lado, cuando los esfuerzos son iguales o mayores a las fronteras descritas dentro de la superficie, sus deformaciones serán elásticas y plásticas [15]. Además, cuando se cumple la condición f=0 para todas las funciones de fluencia en conjunto, la superficie de fluencia del material puede ser representada como un cono hexagonal en el espacio de los esfuerzos principales. La Figura 2 muestra la anterior condición.
El criterio de fluencia del modelo Mohr-Coulomb proviene de la ley de fricción de Coulomb, la cual establece que el estado general de esfuerzos es formulado mediante las funciones de fluencia (Ecuaciones 1 y 2). Dichas funciones de fluencia están en términos de los esfuerzos principales: i=1,2,3; j=2,3,1; k=3,2,1. Además, se incorporan los dos parámetros de resistencia al corte: ángulo de fricción (Φ) y cohesión del material (c).
|
|
(1) |
|
|
(2) |
Por otro lado, la formulación del comportamiento elastoplástico perfecto en el modelo está dado por la interacción entre la tasa de deformación elástica y la tasa de deformación plástica (Ec. 8). Dicha interacción parte de la forma básica de la ley de Hooke (Ec. 9), donde De representa la matriz de rigidez del material.
|
|
(3) |
|
|
(4) |
Debido la sobreestimación de la dilatancia del suelo en la teoría de plasticidad asociada relativa el modelo Mohr-Coulomb plantea una función de potencial plástico, g. [13]. Además, en el caso particular g ≠ f este modelo describe la plasticidad no asociada del material. De esta manera, el modelo Mohr-Coulomb plantea funciones de potencial plástico a las que se les adiciona el parámetro del ángulo de dilatancia, (Ecs. 10 y 11). Dicho parámetro, se requiere para modelar los incrementos de deformación volumétrica plástica del suelo.
|
|
(5) |
|
|
(6) |
Con base en la anterior consideración, las deformaciones plásticas pueden ser descritas mediante la ecuación 3; donde corresponde al multiplicador plástico. Cuando λ=0 el comportamiento será puramente elástico mientras que λ>0 denota un comportamiento netamente plástico.
|
|
(7) |
Teniendo en cuenta todas las ecuaciones anteriores se obtiene la relación entre los esfuerzos efectivos y las tasas de deformación para el comportamiento elastoplástico [16]. El modelo Mohr-Coulomb es considerado el modelo constitutivo más utilizado en la Ingeniería Geotécnica, debido a su simplicidad y fácil medición de sus parámetros.
2.1.2 Modelo Cam-Clay Modificado
Roscoe et al. (1958) [17] desarrollaron en la Universidad de Cambridge un modelo elastoplástico que incorpora la ley de flujo asociado para suelos cohesivos. El modelo es conocido actualmente como Cam-Clay. Dicho modelo incluyó el concepto de superficie de fluencia, con el fin de establecer el nivel de esfuerzos en el que las deformaciones volumétricas son recuperables. Sin embargo, [18] simplificaron la forma de dicha superficie de fluencia dando origen al modelo Cam-Clay Modificado (Figura 3).
La formulación de este modelo parte propiedades mecánicas que se obtienen a través de ensayos de laboratorio. Los parámetros que conforman el modelo Cam-Clay son el módulo de elasticidad del suelo (E), la relación de Poisson (ν), la pendiente de la línea de estado crítico (M), la pendiente de la línea de normal consolidación (λ) y el factor de compresibilidad de carga y descarga (κ). Este modelo, al igual que los demás modelos elastoplásticos, tiene presente que las deformaciones plásticas del suelo se muestran de forma ortogonal a la línea del estado crítico [19]. La función de fluencia de este modelo está definida por la ecuación 4, siempre y cuando se cumple la condición f = 0. De esta manera, se obtiene una superficie de fluencia en forma de elipse en el espacio p´- q bajo una trayectoria de esfuerzos η.
|
|
(8) |
En el espacio p´- q la parte superior de la elipse intercepta la línea de estado crítico (LEC). Dicho parámetro es fundamental para establecer el fin de la regla de flujo asociado y, gráficamente, la altura de la elipse que representa la superficie de fluencia del material. Paralelamente, en el momento en que el suelo supera el esfuerzo de fluencia (p´0) comenzará a presentar un comportamiento de endurecimiento. Además, el material experimentará un aumento gradual de la línea de estado límite (LEL), provocando una expansión de la superficie de fluencia y un incremento de las deformaciones volumétricas. Por lo tanto, mediante el modelo Cam-Clay se tienen en cuenta aspectos como el historial de esfuerzos del suelo y la teoría de estado crítico. Sin embargo, este modelo es utilizado principalmente para representar el comportamiento de suelos finos y no de suelos granulares.
2.1.3 Modelo Hipoplástico
La formulación del modelo hipoplástico se remonta a los estudios realizados por [20] en la Universidad de Karlsruhe. Más tarde fue modificado por [21], [22], [23]. No obstante, ellos se centraron en el análisis de suelos granulares. Por tal razón, [24] realizó una modificación para suelos cohesivos e incluyó a este modelo el comportamiento no lineal del suelo y el efecto del tiempo en las deformaciones del material. Dentro de los resultados de dicho autor se destaca la ecuación constitutiva hipoplástica para arcillas (ecuación 5).
(9)
Donde define el tensor de velocidad de esfuerzos; ℒ y N son tensores constitutivos de cuarto y segundo orden, respectivamente; D representa el tensor de elongación; finalmente, y representan los factores de barotropía y picnotropía mediante cantidades escalares que simulan la dependencia del comportamiento mecánico del suelo con base en su densidad y estados de esfuerzo. Los tensores ℒ y N de la ecuación 5 están interrelacionados y actúan como una regla de flujo hipoplástica; por lo que su modificación no es un proceso simple. Debido a esta condición se incluyó la función tensorial (ecuación 6).
(10)
Al reemplazar la ecuación 6 en la ecuación 5 se tiene:
(11)
Por otro lado, si se sustituye y en la ecuación 16 se obtiene una solución trivial que, también, puede ser determinada eliminando el tensor . Así pues, se alcanza una condición . Dicha condición corresponde al estado crítico del suelo. A partir de la anterior formulación se modificó la ecuación base del modelo de hipoplasticidad, a través de la definición de una la regla de flujo bajo la condición de estado crítico e independencia del tensor ℒ. A partir de lo anterior, el tensor N se define:
(12)
La cantidad escalar, o también llamada grado de no-linealidad, permanece para la condición de estado límite; donde m corresponde a un tensor de segundo orden con regla de flujo hipoplástico y D es un tensor de cuarto orden hipoelástico. Al igualar la ecuación 7 y ecuación 8 se obtiene la ecuación de hipoplasticidad generalizada (ecuación 9).
(13)
Por lo tanto, gracias a las formulaciones anteriores, el modelo Hipoplástico permite simular apropiadamente el comportamiento no lineal tanto de suelos granulares como de suelos finos.
3. Metodología
3.1 Descripción geológica y geotécnica del material
El distrito Federal de Brasilia se caracteriza por tener un suelo conformado, en su gran parte, por una capa de arcilla porosa plegable. Asimismo, dicho terreno corresponde a un depósito de suelo tropical residual altamente intemperizado o también denominado laterítico (Figura 4). A lo largo del perfil típico del suelo se evidencia una baja presencia de sílice y un alto grado de hierro y aluminio, debido a procesos de lixiviación en las capas superiores [6]. Por otro lado, el material exhibe una estructura metaestable a causa de su alta porosidad y tipo de cementación. Además, la estructura del material se ve afectada al aumentar su porcentaje de humedad y variación de su estado de esfuerzos. Así pues, el suelo de Brasilia es susceptible al fenómeno del colapso [25].
Los materiales de estudio corresponden a suelos provenientes del campo experimental de la Universidad de Brasilia (UnB). De allí se recuperaron tres muestras inalteradas a diferentes profundidades; la primera entre los 3.00 y 3.30 m de profundidad, la segunda entre 6.00 y 6.30 m de profundidad y la tercera 8.70 y 9.00 m de profundidad. La Figura 5 presenta la estratificación del campo experimental y la Tabla 1 describe dicho perfil.
| Profundidad | Caracterización |
| 0.00 – 8.80 m | Horizonte de suelo residual laterítico, que experimentó procesos de intemperismo, constituido por una arcilla arenosa roja oscura (0 m a 5 m) y una arcilla gravo-arenosa roja oscura (5 m a 8.8 m) (arcilla porosa) |
| 8.80 – 10.30 m | Horizonte de transición, compuesto de un suelo laterítico (8.8 m a 9.8 m) y pocas estructuras relictas (9.8 m a 10.3 m). |
| 10.30 – 15.00 m | Horizonte de suelo saprolítico constituido por intercalaciones de cuarzo (10.3 m a 11.3) y un limo arcilloso rojo (11.3 m a 15.0 m). |
La Tabla. 2 presenta los valores de obtenidos a partir de los ensayos de caracterización física del material. Dichos parámetros corresponden a humedad natural (ω) medido según la norma ASTM D2216 [26], límites de consistencia estimados de acuerdo con el procedimiento de la norma ASTM D 4318 [27] y el peso unitario del suelo estimado a través del método de la parafina.
| Muestra | Profundidad (m) | γ (kN/m3) | LL (%) | LP (%) | IP (%) | ω (%) |
| 1 | 3.00 – 3.30 | 26.5 | 56.4 | 31.2 | 25.2 | 34.8 |
| 2 | 6.00 – 6.30 | 26.6 | 59.8 | 34.6 | 25.2 | 32.3 |
| 3 | 8.70 – 9.00 | 26.3 | 66.8 | 36.4 | 30.4 | 30.0 |
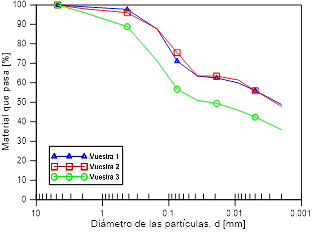
Por otra parte, se estableció la distribución de tamaño de partículas según el procedimiento de la norma ASTM D422 [28] (Figura 6). A partir del análisis granulométrico se encontró que el contenido de partículas finas para la muestra uno y la muestra dos son semejantes. Por lo tanto, las curvas de ambas muestras se comportan de forma unimodal. Asimismo, se identificó que en el tamiz No 200 (0.075 mm) pasa una gran cantidad de material fino; lo que comprueba que el suelo es arcilloso. Paralelamente, se evidenció que la muestra tres presenta una mayor cantidad de arenas finas respecto a las dos primeras muestras. Además, se encontró que en dicha muestra más del 50% pasa el tamiz No. 200.
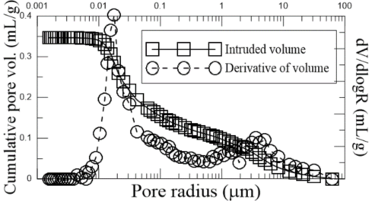
Por otra parte, se realizaron ensayos de porosimetría mediante el método de intrusión de mercurio, como complemento a las curvas de distribución de tamaño de partículas. Lo anterior, con el fin de establecer la distribución y el tamaño de los poros de la arcilla de Brasilia (Figura 7). El ensayo de porosimetría consiste en la inyección mercurio a presión a través de los vacíos del suelo [29]. Según la presión con la que entra el mercurio se estima la presión capilar dentro los poros y, posteriormente, se calcula el tamaño de los mismos. Una vez trazada la curva de resultados es posible identificar la presencia de micro y macro poros mediante los puntos de inflexión.
3.2 Ensayos triaxiales con consolidación Ko
El ensayo triaxial es utilizado para evaluar la resistencia al corte, el comportamiento esfuerzo deformación, la generación de presión de poros y la respuesta contractante o dilatante de los suelos bajo condiciones axisimétricas de esfuerzos y drenaje controlados [30]. En este ensayo, un espécimen de suelo con forma cilíndrica es cubierto con una membrana de látex dentro de una cámara a presión y, posteriormente, es sometido a un proceso de carga o incremento de esfuerzos. En los ensayos triaxiales se pueden variar las presiones que actúan sobre el espécimen de suelo en las tres direcciones ortogonales. Lo anterior, permite realizar mediciones sobre sus propiedades mecánicas de forma completa.
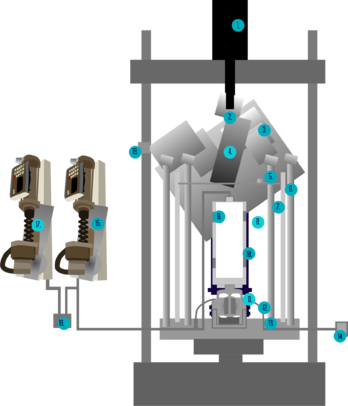
El equipo triaxial que se utilizó en esta investigación está conformado por una cámara de acrílico reforzada por tres cilindros metálicos; una prensa de compresión 5 kN que permite variar la velocidad de aplicación de carga axial mediante un dispositivo de accionamiento mecánico; dos controladores de presión y volumen GDS con 1 MPa y 200 cm3 de capacidad; tres sensores de deformación local tipo LVDT (dos axiales y uno radial) y un sistema para saturar o drenar la muestra por medio de dos discos porosos. Además, el aparato cuenta con un sistema de adquisición de datos automatizado. De esta manera, el dispositivo fue adaptado de tal forma que no se presentaran deformaciones laterales y así simular el comportamiento del suelo en reposo. La Figura 8 presenta el esquema dicho de equipo.
Por otro lado, se desarrolló un plan experimental que incluyó ensayos triaxiales con consolidación Ko en condiciones drenadas y no drenadas; es decir, tipo CKoD y CKoU (Figura 9). Así pues, durante el plan experimental se realizaron dos ensayos CKoD y un CKoU, cada uno con tres puntos. Además, dichos ensayos se ejecutaron sobre especímenes obtenidos de cada una de las muestras de arcilla porosa extraídas del campo experimental de la UnB.
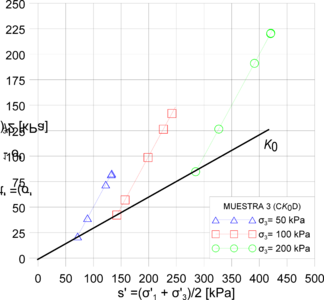
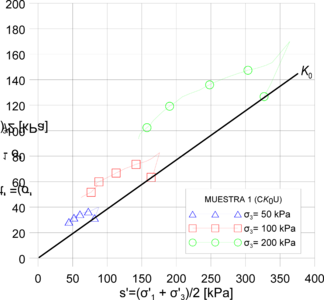
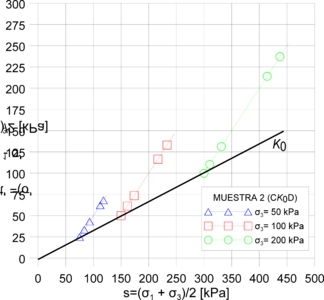
Asimismo, se establecieron las trayectorias de esfuerzo durante las etapas de consolidación y corte mediante las invariantes de esfuerzo tipo Cambridge (espacio p´- q) y MIT (espacio t´- s´). Las Figuras 10 y 11 muestran las dichas trayectorias de esfuerzo. Allí se encontró, durante la etapa de consolidación, que el valor del coeficiente de tierras en reposo (Ko) oscila entre 0.47 y 0.53. Por otra parte, se estableció que el valor de la pendiente de la línea de estado crítico (LEC) está 1.12 y 1.25.
4. Resultados y análisis
Los single element program son herramientas útiles para simular pruebas de laboratorio mediante una computadora. Dichos programas cuentan con una amplia gama de opciones para seleccionar las condiciones del ensayo. Por lo tanto, allí se puede fijar las condiciones de drenaje e implantar la velocidad de aplicación de la carga o de la de deformación de la misma manera que se realiza en el laboratorio.
Uno de los single element program más comunes es el Incremental Driver, el cual fue creado por [31]. La formulación de incremental driver fue hecha en Fortran y es de uso libre. No obstante, este trabajo utiliza una herramienta desarrollada por [32] [33], denominada Triax. Dicho programa simula del comportamiento de suelos mediante el de ecuaciones constitutivas elásticas, elastoplásticas e hipoplásticas. De esta manera, Triax permite evaluar el comportamiento de la arcilla porosa aplicando diferentes modelos constitutivos. Además, facilita la calibración de los modelos constitutivos usando datos obtenidos en laboratorio.
Se utilizaron tres modelos constitutivos diferentes para replicar el comportamiento de la arcilla porosa de Brasilia mediante simulaciones numéricas. Sin embargo, el desarrollo de las pruebas computacionales requirió la calibración previa de todos los parámetros en cada modelo. Dichas calibraciones se realizaron mediante un proceso iterativo, en el que se ajustaron los parámetros principales de cada uno de los modelos constitutivos, a partir de las propiedades mecánicas presentadas en la sección 3. La metodología para calibrar los parámetros de los tres modelos constitutivos se basó en el procedimiento propuesto por [34] [35].
4.1 Calibración parámetros modelo Mohr – Coulomb
Los parámetros del modelo de Mohr-Coulomb representan las propiedades mecánicas reales del suelo, y su principal característica es que la resistencia del material depende del esfuerzo de confinamiento. Además, este modelo permite establecer el estado de esfuerzos límite del material mediante un procedimiento gráfico en el que se establece la envolvente de dalla del suelo. La calibración de los parámetros (Φ, c, E, υ) del modelo de Mohr-Coulomb es relativamente simple; no obstante, se debe tener el estado de esfuerzos al que está sometido el suelo.
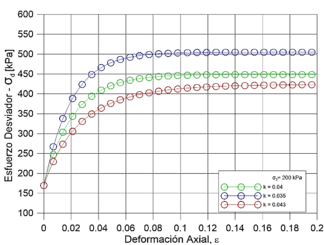
La cohesión (c) y el ángulo de fricción (Φ) se calibraron a partir del valor del esfuerzo máximo desviador (q) medido en los ensayos de laboratorio. Así pues, dichas propiedades fueron identificadas previamente y únicamente se ajustaron para dar una mejor aproximación a los resultados experimentales. Por otra parte, la calibración de E se realizó con base en un proceso iterativo en que se tomó como punto de partida el valor de módulo secante al 50% de q. No obstante, la calibración la calibración de la relación de Poisson (υ) se realizó mediante la variación de valores típicos reportados en la literatura por [37] Budhu (2015) para suelos con características semejantes a las del material de estudio. La Figura 9 muestra la metodología de calibración del modelo Mohr-Coulomb. Del mismo modo, la Tabla 3 presenta los resultados de la calibración del modelo.
| Muestra | Tipo de ensayo | Φ
° |
c
(kPa) |
E
(MPa) |
υ
( ) |
| 1 | CK0U | 29.50 | 0 | 11.50 | 0.44 |
| 2 | CK0D | 32.30 | 10.20 | 11.55 | 0.30 |
| 3 | CK0D | 29.00 | 22.10 | 11.70 | 0.31 |
4.2 Calibración parámetros modelo Cam-Clay
La estimación de los parámetros del modelo Cam-Clay requiere una caracterización elástica y plástica del comportamiento mecánico del suelo. Lo anterior se debe a que el modelo involucra el potencial plástico del material y una regla de flujo asociada [38] (Wood, 1991). En consecuencia, la respuesta elástica (es decir, aquella dentro de la superficie de fluencia) es establecida por medio del módulo de corte G y el módulo de deformación volumétrica K. Sin embargo, dichos parámetros se pueden obtener mediante pruebas triaxiales convencionales en condiciones drenadas y no drenadas [39] (Bedin et al., 2012).
Por otra parte, la respuesta plástica se puede obtener utilizando los parámetros M y λ. Dichos parámetros representan la pendiente de la línea de estado crítico (LEC) y la pendiente de la línea de consolidación normal (LCN). Por esta razón, es necesario desarrollar pruebas edométricas y triaxiales, simultáneas, para obtener dichos parámetros. No obstante, los parámetros para las primeras iteraciones del modelo Cam-Clay se recopilaron a partir de los resultados obtenidos durante plan experimental (M) a través de LEC y la calibración del modelo Mohr- Coulomb (G) mediante la ecuación 10.
(14)
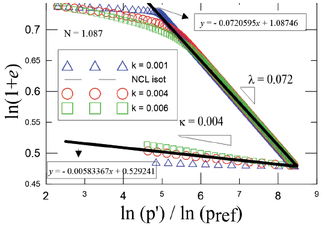
En consecuencia, los parámetros plásticos para calibrar el modelo Cam-Clay se generaron a partir de simulaciones de ensayos edométricos (Figura 12). De esta manera, se identificaron las pendientes de los tramos de carga (λ) y descarga (κ) de la curva de consolidación. Asimismo, se encontraron otros parámetros que son necesarios para la calibración del modelo Hipoplástico y que se mencionarán más adelante. La Tabla 3 presenta los valores de los parámetros obtenidos en la calibración.
| Muestra | Tipo de ensayo | G
(MPa) |
M | κ | λ |
| 1 | CK0U | 4.29 | 0.900 | 0.004 | 0.072 |
| 2 | CK0D | 4.02 | 0.980 | 0.090 | 0.100 |
| 3 | CK0D | 4.62 | 0.980 | 0.087 | 0.097 |
4.3 Calibración modelo Hipoplástico
El proceso de calibración de los parámetros N, λ y κ se realizó mediante la simulación del ensayo edométrico (Figura 12), tal y como ya se mencionó previamente. Es importante señalar que el modelo Hipoplástico predice los anteriores parámetros únicamente en el espacio e vs ln p'. Por lo tanto, durante esta calibración se evaluó el comportamiento de la Superficie de Estado Límite (SEL). Dicha superficie también se puede representar en el espacio 3D compuesto por las invernantes de esfuerzo y la relación de vacíos.
El parámetro r se puede definir directamente como la relación entre el módulo volumétrico y el módulo de corte del material, los cuales están en función de E y υ. Dichos valores se obtuvieron a partir de iteraciones numéricas en condiciones isotrópicas y asumiendo que el suelo está normalmente consolidado. Sin embargo, dado que el modelo predice una degradación gradual de la rigidez al corte, [40] Ruge et al., (2016) recomiendan realizar un estudio paramétrico para encontrar un valor apropiado del parámetro r. Este enfoque es válido porque no existe interrelación con otros parámetros del modelo [41] (Ruge, 2014). La Figura 13 muestra la calibración del parámetro r.
El ángulo de fricción crítico (Φc) fue obtenido a partir de la pendiente de la línea de estado crítico del suelo. En esta fase, el material presenta deformaciones cortantes sin experimentar deformaciones volumétricas y variaciones en el estado de esfuerzos efectivo. Para encontrar el parámetro Φc, se ejecutó una regresión lineal usando los puntos de estado crítico de las pruebas triaxiales hechas en laboratorio. La Tabla 4 muestra los parámetros calibrados para el modelo Hipoplástico.
| Muestra | Tipo de ensayo | Φc
° |
λ | k | N | r |
| 1 | CK0U | 20 | 0.28 | 0.21 | 1.40 | 0.06 |
| 2 | CK0D | 20 | 0.06 | 0.03 | 1.10 | 0.13 |
| 3 | CK0D | 20 | 0.09 | 0.04 | 1.20 | 0.11 |
4.4 Simulaciones numéricas
Después de realizar la calibración de los parámetros, se procedió a realizar las simulaciones numéricas. Lo anterior, tuvo como propósito establecer cuál de los tres modelos constitutivos presenta mejor ajuste a la respuesta esfuerzo-deformación y a las trayectorias de esfuerzo reportadas en los datos experimentales. De esta manera, se ingresaron los datos (input) al programa mediante un archivo de texto simple y que debe ser guardado con la extensión. inp. A continuación, se presenta el procedimiento de construcción y la estructura del archivo input para la evaluación del modelo hipoplástico de la muestra tres en condiciones drenadas bajo un esfuerzo de confinamiento de 200 kPa.
Inicialmente, se ingresan a los valores iniciales que se encuentra sometida la muestra; es decir, esfuerzo medio de consolidación anisotrópica, esfuerzo desviador y tasa de deformación (p, q, epax). El signo negativo indica que la trayectoria es a compresión.
Posteriormente, se establecen el tipo de ensayo que se desea realizar y el valor de la deformación axial (en porcentaje), a la que el usuario desea finalizar la simulación.
Por último, hace referencia al tipo de modelo constitutivo que se quiere fallar el espécimen numérico, seguido de las propiedades del mismo como se evidencia.
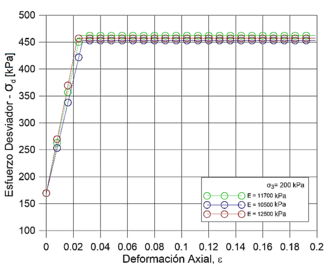
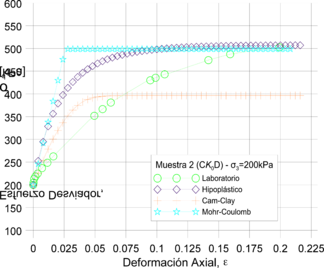
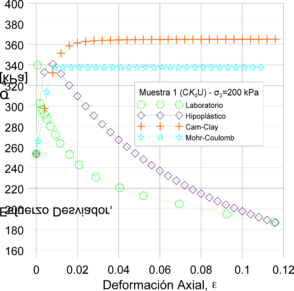
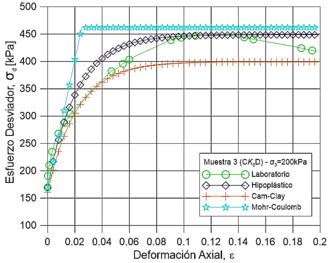
De esta manera, se obtuvieron las curvas esfuerzo-deformación que comparan el comportamiento de cada uno de los modelos respecto al comportamiento real de las muestras (Figura 14). Los resultados revelaron en términos de resistencia máxima que tanto el modelo Mohr-Coulomb como el modelo Hipoplástico presentan valores de esfuerzo último cercanos a los reportados en los ensayos de laboratorio. No obstante, se encontró que condiciones no drenadas el modelo con mejor ajuste a los datos de laboratorio es el Hipoplástico. Además, únicamente el modelo hipoplástico representó el comportamiento no lineal del suelo. Los anteriores planteamientos se establecieron con base en la similitud que tienen las curvas de los datos de los modelos y el ensayo triaxial.
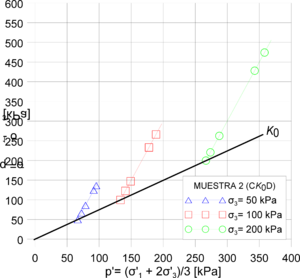
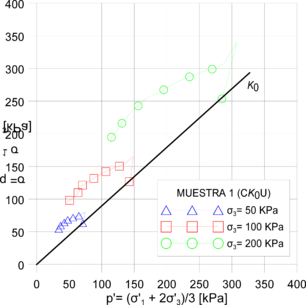
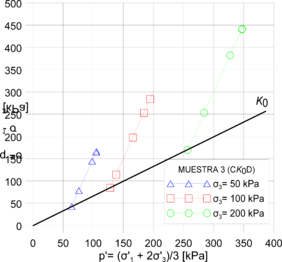
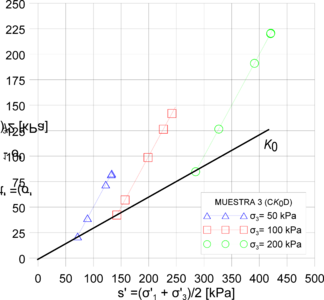
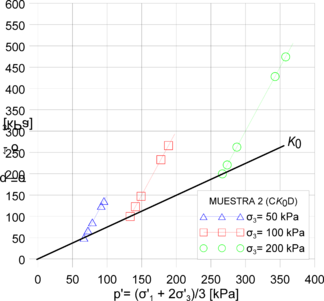
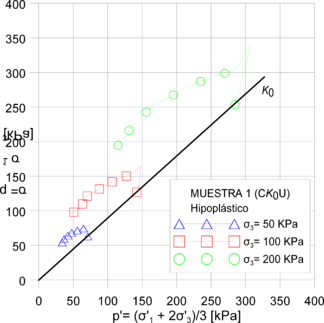
Por otra parte, se calcularon las trayectorias de esfuerzo Cambridge y MIT (Figuras 15 y 16). Se encontró que todos los modelos replican la tendencia de los ensayos drenados. No obstante, el modelo Hipoplástico fue el único que reportó trayectorias no drenadas cercanas a las presentadas en la Figura 10 (izq.). Por lo tanto, se encontró que el modelo Hipoplástico es el modelo con valores de estado crítico más próximos a los obtenidos mediante los ensayos de laboratorio, pese que el modelo Cam-Clay incorpora el valor de la M directamente. La precisión del modelo Hipoplástico, en la evaluación del comportamiento de la arcilla porosa de Brasilia, se debe a que dicho modelo contempla la no linealidad del material y replica fielmente su resistencia máxima. La Tabla 5 presenta el contraste entre los resultados obtenidos en las simulaciones numéricas contra los obtenidos en laboratorio.
| Modelo | Muestra | qmáx
(kPa) |
c'
(kPa) |
Φ'
° |
M |
| Mohr-Coulomb | 1 | 348.52 | 0 | 29.50 | 1.13 |
| 2 | 498.38 | 10.20 | 32.30 | 1.17 | |
| 3 | 453.96 | 22.10 | 29.00 | 1.20 | |
| Cam-Clay | 1 | 365.83 | 0 | 34.58 | 1.40 |
| 2 | 396.34 | 11.25 | 27.70 | 1.10 | |
| 3 | 499.26 | 23.54 | 30.00 | 1.20 | |
| Hipoplástico | 1 | 341.35 | 0 | 28.84 | 1.15 |
| 2 | 502.56 | 11.25 | 28.84 | 1.15 | |
| 3 | 450.62 | 23.10 | 28.84 | 1.15 | |
| 1 | 340.02 | 0 | 27.21 | 1.12 | |
| Laboratorio | 2 | 500.73 | 11.01 | 32.78 | 1.16 |
| 3 | 450.22 | 23.04 | 28.73 | 1.25 |
Figura 15. Resultados trayectorias de esfuerzo: (izq.) Cambridge muestra 1 modelo Hipoplástico; (der.) Cambridge muestra 2 modelo Hipoplástico; (inf.)
5. Conclusiones
Este documento se aborda la modelación numérica de una serie de ensayos triaxiales, realizados sobre arcilla porosa colapsable, mediante el uso de modelos constitutivos diferentes en el programa Triax. En este estudio se ejecutó un plan experimental en laboratorio, con el fin de establecer las propiedades físicas y mecánicas del suelo. Además, se realizó una serie de simulaciones numéricas en las que inicialmente se calibraron los parámetros de los modelos constitutivos y, posteriormente, se compararon los datos experimentales con los resultados de dichas simulaciones. De esta manera, estableció el modelo constitutivo que mejor se ajusta al comportamiento real de material. Las conclusiones prácticas y académicas son las siguientes:
1. Los valores del coeficiente de tierras en reposo (Ko) obtenidos mediante los ensayos triaxiales con consolidación anisotrópica cumplen en las tres muestras con el criterio 1-senΦ' establecido por [42]. Asimismo, se lograron replicar dichas condiciones de consolidación en las simulaciones numéricas. Así pues, las simulaciones numéricas se pueden usar como una alternativa en ingeniería geotécnica para la evaluación del comportamiento anisotrópico de cualquier tipo de suelo.
2. Los parámetros calibrados mediante las simulaciones numéricas, obedecen a un patrón similar, a para suelos arcillosos porosos colapsables. Sin embargo, se evidenciaron diferencias de dichos parámetros entre los tres modelos constitutivos pese a que se modeló el mismo tipo de suelo.
3. Los resultados del modelo Mohr-Coulomb y Cam-Clay mostraron un comportamiento elástico lineal, el cual no obedece al comportamiento esfuerzo-deformación real del suelo estudiado. Sin embargo, el modelo Hipoplástico presentó un buen ajuste a la no linealidad del material. Por lo tanto, el modelo Hipoplástico representa mejor el rango elástico de la arcilla porosa de Brasilia.
4. Al modificar los parámetros de los modelos Mohr-Coulomb e Hipoplástico, durante la etapa de calibración de los mismos, se evidenció que los resultados de las simulaciones no variaban significativamente. Sin embargo, al modificar levemente los parámetros del modelo Cam-Clay se observó un cambio abrupto en la forma de la curva esfuerzo-deformación de la simulación. De esta manera, se encontró que los parámetros constitutivos que rigen el modelo Cam-Clay son altamente sensibles al momento de evaluar el comportamiento del suelo mediante este modelo. Asimismo, se evidenció que debido a la cantidad de parámetros en los otros dos modelos es necesario cambiar significativamente los valores de sus parámetros, para observar alteraciones representativas en las curvas esfuerzo-deformación.
Referencias bibliográficas
[1] Atkinson, J. H. ‘Non-linear soil stiffness in routine design’, Géotechnique. Thomas Telford Ltd, 50(5), pp. 487–508. doi: 10.1680/geot.2000.50.5.487. 2000.
[2] Camacho-Tauta, J. Evaluation of the small-strain stiffness of soil by non-conventional dynamic testing methods. PhD. Thesis, Universidade de Lisboa. 2011.
[3] Robin, V. et al. An effective constitutive model for lime treated soils. Computers and Geotechnics, 66, pp. 189–202. doi: 10.1016/j.compgeo.2015.01.010. 2015.
[4] Runesson, K. Constitutive Modelling of Engineering Materials -Theory and Computation. 7th edn. Göteborg: Chalmers University of Technology. 2006.
[5] Mendoza, C. and Lizcano, A. Comportamiento Anisotrópico de la Arcilla de Bogotá. in XIII Congreso Colombiano de Geotecnia. Manizales: Universidad Nacional de Colombia. 2010.
[6] Mendoza, C., Farias, M. and da Cunha, R. P. Validación de modelos constitutivos avanzados de comportamiento mecánico para la arcilla estructurada de Brasilia. Obras y proyectos. Universidad Católica de la Santísima Concepción, (15), pp. 52–70. doi: 10.4067/S0718-28132014000100005. 2014.
[7] Ruge, J.C. et al. Numerical Simulations of Ko Triaxial Tests on Collapsible Porous Clay’, Geotechnical Engineering Journal of the SEAGS & AGSSEA. 2018.
[8] Kolymbas, D. Introduction to hypoplasticity. 1st edn. A.A. Balkema. 2000.
[9] Desai, C.S. Constitutive Modeling for Geologic Materials: Significance and Directions. International Journal of Geomechanics. American Society of Civil Engineers, 5(2), pp. 81–84. doi: 10.1061/(ASCE)1532-3641(2005)5:2(81). 2005
[10] Rios, S. et al. Simplifying calibration of bonded elasto-plastic models. Computers and Geotechnics. Elsevier, 73, pp. 100–108. doi: 10.1016/J.COMPGEO.2015.11.019. 2016.
[11] Abbo, A.J. et al. A C2 continuous approximation to the Mohr–Coulomb yield surface. International Journal of Solids and Structures. Pergamon, 48(21), pp. 3001–3010. doi: 10.1016/J.IJSOLSTR.2011.06.021. 2011.
[12] Camacho-Tauta, J., Molina-Gómez, F. A. and Reyes-Ortiz, O. Simulation of traffic loading on an embankment by the finite element method with different soil models. in Rinaldi, V. A. (ed.) Six International Symposium on Deformation Characteristics of Geomaterials. Buenos Aires, pp. 737–744. doi: 10.3233/978-1-61499-601-9-737. 2015.
[13] Nieto-Leal, A., Camacho-Tauta, J. and Ruiz Blanco, E.F. Determinación de parámetros para los modelos elastoplásticos Mohr-Coulomb y Hardening Soil en suelos arcillosos’, Revista Ingenierías Universidad de Medellín, 8(15), pp. 75–91. 2009.
[14] Nieto-Leal, A. and Kaliakin, V.N. Improved shape hardening function for bounding surface model for cohesive soils. Journal of Rock Mechanics and Geotechnical Engineering. Elsevier, 6(4), pp. 328–337. doi: 10.1016/J.JRMGE.2013.12.006. 2014.
[15] Kaliakin, V. N. and Dafalias, Y. F. Simplifications to the bounding surface model for cohesive soils. International Journal for Numerical and Analytical Methods in Geomechanics. John Wiley & Sons, Ltd, 13(1), pp. 91–100. doi: 10.1002/nag.1610130108. 1989.
[16] Smith, I.M., Griffiths, D.V. and Margetts, L. Programming the Finite Element Method. 5th edn. New York: Wiley. 2013.
[17] Roscoe, K.H., Schofield, A.N. and Wroth, C.P. On The Yielding of Soils. Géotechnique. Thomas Telford Ltd, 8(1), pp. 22–53. doi: 10.1680/geot.1958.8.1.22. 1958.
[18] Roscoe, K.H. and Burland, J.B. On the Generalised Stress-Strain Behaviour of Wet Clays. in Engineering Plasticity, pp. 535–609. 1968.
[19] Camacho-Tauta, J.F., Reyes-Ortiz, O.J. and Bueno Pumarejo, P.B. Utilización del modelo Cam-Clay modificado en suelos cohesivos de la sabana de Bogotá. Ciencia e Ingeniería Neogranadina. Universidad Militar Nueva Granada, (14), pp. 1–13. 2004.
[20] Kolymbas, D. Ein nichtlineares viskoplastisches Stoffgesetz für Böden. Karlsruher Institut für Technologie. 1978.
[21] Wu, W. Hypoplastizität als mathematisches Modell zum mechanischen Verhalten granularer Stoffe. Karlsruher Institut für Technologie.1992.
[22] Wolffersdorff, P.A. A hypoplastic relation for granular materials with a predefined limit state surface. Mechanics of Cohesive-frictional Materials. John Wiley & Sons, Ltd., 1(3), pp. 251–271. 1996
[23] Niemunis, A. Extended hypoplastic models for soils. Politechnika Gdańska. 2002.
[24] Mašín, D. A hypoplastic constitutive model for clays. International Journal for Numerical and Analytical Methods in Geomechanics, 29(4), pp. 311–336. doi: 10.1002/nag.416. 2005.
[25] Ruge, J.C., da Cunha, R.P. and Rondón, H. Simulación de pruebas de carga en pilotes usando un modelo constitutivo hipoplástico. Revista EIA, 11(21), pp. 171–183. 2014.
[26] ASTM International (2010a) ASTM D2216 Standard Test Methods for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass. 2010.
[27] ASTM International (2010b) D4318 - Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. 2010.
[28] ASTM International (2007) D422 - Standard Test Method for Particle-Size Analysis of Soils, Annual Book of ASTM Standards. 2007.
[29] Ruge, J.C. et al. Implications of the atmosphere-soil interaction for the design of earth retaining structures. E3S Web of Conferences. Edited by P. Delage et al. EDP Sciences, 9, p. 12002. doi: 10.1051/e3sconf/20160912002. 2016.
[30] Fratta, D., Aguettant, J. and Roussel-Smith, L. Introduction to Soil Mechanics Laboratory Testing. 1st edn. CRC Press. 2007.
[31] Niemunis, A. Incremental Driver - User Manual. 1st edn. 2007.
[32] Mašín, D. Clay hypoplasticity with explicitly defined asymptotic states. Acta Geotechnica 8, No. 5, 481-496. 2013.
[33] Mašín, D. Coupled thermohydromechanical double structure model for expansive soils. ASCE Journal of Engineering Mechanics 143, No. 9. 2017.
[34] Suchomel, R. and Mašín, D. Spatial variability of soil parameters in an analysis of a strip footing using hypoplastic model. in Benz, T. and Steinar, N. (eds) Numerical Methods in Geotechnical Engineering. 7th edn. NORWAY: CRC Press/Balkema, pp. 383–388. 2010.
[35] Budhu, M. Soil Mechanics Fundamentals (Metric Version). 1st edn. Wiley. 2015.
[36] Wood, D.M. Soil Behaviour and Critical State Soil Mechanics. 1st ed. Cambridge University Press. 1991.
[37] Bedin, J. et al. Gold tailings liquefaction under critical state soil mechanics. Géotechnique. Thomas Telford Ltd, 62(3), pp. 263–267. doi: 10.1680/geot.10. P.037. 2012.
[38] Ruge, J.C. Análise do comportamento de cortina de estacas executada em solo poroso metaestável mediante o uso de um modelo constitutivo hipoplástico considerando a resposta não saturada. PhD. Thesis. Universidade de Brasília. 2014.
[39] Jaky, J. The coefficient of earth pressure at rest. In Hungarian “A nyugalmi nyomas tenyezoje”’, Journal Society Hungarian Engineering and Architecture, pp. 355–358. 1944.
Document information
Published on 22/01/20
Accepted on 14/11/19
Submitted on 06/11/18
Volume 36, Issue 1, 2020
DOI: 10.23967/j.rimni.2019.11.003
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?