| Line 130: | Line 130: | ||
{| style="margin: 1em auto 1em auto;border: 1pt solid black;border-collapse: collapse;font-size: 85%;" | {| style="margin: 1em auto 1em auto;border: 1pt solid black;border-collapse: collapse;font-size: 85%;" | ||
|- style="border: 1pt solid black;" | |- style="border: 1pt solid black;" | ||
| − | | style="border-top: 1pt solid black;border-left: none;border-bottom: 1pt solid black;border-right: none;text-align: center;"<br/>Simulação | + | | style="border-top: 1pt solid black;border-left: none;border-bottom: 1pt solid black;border-right: none;text-align: center;"|<br/>Simulação |
| style="border-top: 1pt solid black;border-left: none;border-bottom: 1pt solid black;border-right: none;text-align: center;"|PCM | | style="border-top: 1pt solid black;border-left: none;border-bottom: 1pt solid black;border-right: none;text-align: center;"|PCM | ||
| style="border-top: 1pt solid black;border-left: none;border-bottom: 1pt solid black;border-right: none;text-align: center;"|T<sub>pc</sub> [<sup>o</sup>C] | | style="border-top: 1pt solid black;border-left: none;border-bottom: 1pt solid black;border-right: none;text-align: center;"|T<sub>pc</sub> [<sup>o</sup>C] | ||
Revision as of 16:16, 15 March 2017
Estudo numérico do processo de fusão de PCMs em cavidade cilíndrica
J.J. Estrazulas, R.C. Oliveski
FTEC - Caxias do Sul, RS BRAZIL
Received: 11 January 2016
Accepted: 19 September 2016
Published: July 2017
Resumo
Inúmeras aplicações residenciais, comerciais e industriais tem seu rendimento aumentado quando um sistema de armazenamento de energia térmica é incorporado. Os PCMs (Phase Change Materials), devido ao seu alto calor latente de fusão, são materiais que representam uma alternativa viável à implementação de sistemas de armazenamento de energia térmica. Este trabalho apresenta um estudo numérico do processo de fusão de PCMs da família RT (Rubitherm Technologies GmbH) em cavidades cilíndricas. O estudo foi realizado através de simulação numérica por CFD (Computational Fluid Dynamics), com o software ANSYS Fluent. O modelo numérico adotado é bidimensional e foi validado com resultados numéricos e experimentais da literatura, obtendo-se boa aproximação. Para os PCMs aqui estudados, aumentando-se a temperatura de 10 oC para 20 oC e de 10 oC para 30 oC, acima da temperatura de mudança de fase, para frações líquidas entre 0,4 e 0,8, a redução média dos tempos de fusão é de, aproximadamente, 55,8% e 71,8%, respectivamente.
Palavras-chave: Armazenamento térmico, phase change materials, PCM, CFD.
Numerical study of PCMs melting process in cylindrical cavity
Abstract
Several residential, commercial and industrial applications have their efficiency increased when a thermal energy storage system is incorporated. The PCMs (Phase Change Materials), due to their high latent heat of fusion, are materials that represent a viable alternative to the implementation of thermal energy storage systems. This paper presents a numerical study of RT (Rubitherm Technologies GmbH) PCMs family fusion process in cylindrical cavities. The study was conducted through a CFD (Computational Fluid Dynamics) numerical simulation, with ANSYS Fluent software. The numeric model adopted is two-dimensional and has been validated with numerical and experimental results of literature, achieving a good approximation. For PCMs here studied, increasing the temperature from 10 oC to 20 oC and 10 oC to 30 oC, above the phase change temperature, for liquid fractions between 0.4 and 0.8, the average reduction of fusion time is approximately 55.8% and 71.8 %, respectively.
Keywords: Thermal storage, phase change materials, PCM, CFD.
1 Introdução
O contínuo crescimento da emissão de gases na atmosfera, decorrente do aumento da população mundial e os altos custos dos combustíveis fósseis e da energia elétrica são os motivos básicos para uma utilização mais eficiente da energia em todas as áreas da atividade humana. Edifícios comerciais e apartamentos residenciais são os consumidores de energia mais intensivos. Nos Estados Unidos, 41,1% de toda a energia primária consumida no ano de 2010, foi demandada por consumidores residenciais e comerciais, sendo o aquecimento, refrigeração e iluminação as maiores demandas [1]. Já na Europa, os edifícios residenciais consomem 40% de toda a energia [2]. No Brasil, estes setores consomem 13,7% de toda a energia primária [3]. A busca de novas tecnologias para diminuir a crescente preocupação com os problemas ambientais atuais, com a possível carência de energia, seu alto custo e os pesados investimentos necessários à criação de novas centrais de geração de energia tem constituído um dos principais problemas científicos nas últimas três décadas. O aspecto central deste problema é a necessidade de armazenamento de energia, térmica ou elétrica, com a finalidade de cobrir as lacunas existentes entre a geração de energia e o seu respectivo consumo. Estas lacunas podem ser de ordem temporal e de demanda [4].
Os métodos usados para armazenamento térmico de energia (TES-Thermal Energy Storage) são classificados em armazenamento térmico de energia por calor sensível (SHTES-Sensible Heat Thermal Energy Storage) e armazenamento térmico de energia por calor latente (LHTES - Latent Heat Thermal Energy Storage). Os SHTES dependem do aumento ou redução do calor sensível de um material. Já os LHTES dependem da capacidade do material em armazenar energia em uma condição praticamente isotérmica, com estreita faixa de variação. Estes tipos de sistemas utilizam PCMs (Phase Change Materials) e oferecem como vantagem, além da temperatura constante durante os ciclos de armazenamento e liberação da energia, maior capacidade de armazenamento e menor volume quando comparados aos SHTES [5]. Os LHTES constituem uma técnica eficaz, tanto para fins de aquecimento quanto refrigeração, porque eles são capazes de prover uma alta densidade de armazenamento de energia. Quando comparados com os SHTES, os LHTES requerem menor peso e volume de material para uma determinada quantidade de energia [4].
De acordo com Zhou et al. [6], a maioria dos PCMs sofrem de um problema comum que é a baixa condutividade térmica, com valores ao redor de 0,2 W/mK para os materiais parafínicos e 0,5 W/mK para os hidratos de sal e materiais eutéticos. Esta baixa condutividade aumenta o tempo dos processos de carga e descarga de um LHTES que utiliza PCM como meio de armazenamento térmico. Al-Abidi et al. [7] destacam que a maioria das técnicas propostas para a melhoria na condutividade térmica tem sido baseadas na introdução de aletas metálicas, nas mais variadas formas e configurações, nos tanques que armazenam os PCMs. Este fato é devido à simplicidade deste tipo de implementação, com facilidade de fabricação e baixo custo. Outras estratégias abordadas na pesquisa de Agyenim et al. [4] abrangem o uso de múltiplos tubos metálicos, a agitação através da inserção de bolhas, o uso de anéis metálicos, o uso de multitubos e escovas de carbono, o encapsulamento do PCM em material polimérico (microencapsulamento), o uso de uma matriz metálica ou de grafite, o uso de esferas metálicas ou de material poliolefínico, a adição de flocos de grafite e a compactação do PCM em painéis planos ou na forma de barras. Em alguns casos, como no acréscimo de anéis metálicos ao PCM, a condutividade térmica foi aumentada em 10 vezes.
Outro problema apresentado por alguns PCMs é o subresfriamento, ou seja, quando o PCM não se solidifica imediatamente após sua temperatura estar abaixo da temperatura de mudança de fase. Neste caso a solidificação do PCM só é conseguida levando-se a sua temperatura bem abaixo da temperatura de mudança de fase, para iniciar a cristalização do material e liberar o calor latente nele armazenado. A técnica mais comum para solucionar este problema é a incorporação de aditivos especiais, denominados ¨nucleadores¨, aos PCMs. A limitação atualmente existente é que estes ¨nucleadores¨ somente são eficazes numa faixa de temperatura entre 10 a 20 K acima ou abaixo da temperatura de mudança de fase [8,9].
Como mencionado anteriormente, os LHTES são utilizados para o armazenamento de energia térmica e no controle e manutenção da temperatura. Dentre as aplicações dos PCMs nestes campos, destacam-se: atenuação do aquecimento de baterias de íons de lítio e de dispositivos móveis; tubos de calor e dissipadores de calor, para refrigeração de componentes eletrônicos; refrigeração comercial (caminhões) e residencial (freezers); embalagens para produtos farmacêuticos ou derivados do sangue; roupas para uso em regiões com temperaturas extremas; conforto térmico residencial (através do uso de PCM microencapsulado na argamassa de paredes, placas de PCM instaladas no piso, forro ou sótão); fogões solares e secadores de grãos; aquecimento solar de água.
Diversos pesquisadores focaram seus esforços no estudo de geometrias cilíndricas. Murray e Groulx [10], por exemplo, analisaram experimentalmente o processo de transferência de calor durante consecutivos ciclos carga/descarga de PCM visando aplicação em sistema de aquecimento solar de água. Eles demonstraram que o aumento da taxa de escoamento do líquido de transferência térmica (HTF), durante o processo de carga, resulta em fusão significativamente mais rápida. Por outro lado, durante o processo de descarga, um aumento do escoamento não afeta o tempo requerido para a solidificação do PCM.
Longeon et al. [11] estudaram, de forma numérica e experimental, a influência do ponto de entrada do fluido de transferência térmica (HTF) no tempo de fusão/solidificação do PCM RT 35 em um trocador de calor tipo casco-tubo. Os autores concluíram que o melhor rendimento do sistema era obtido executando a entrada do HTF pelo topo do trocador de calor durante o processo de carga e pela base durante o processo de descarga.
Zeng et al. [12] analisaram experimentalmente a fusão de PCM com propriedades térmicas incrementadas através da adição de nanopartículas (NePCM). Estes concluíram que o aumento de condutividade térmica obtido com a adição de nanopartículas reduz drasticamente os processos de convecção no PCM, não se traduzindo em redução no tempo de fusão do mesmo.
Al-Abidi et al. [13] investigaram numericamente os processos de solidificação do PCM RT 82 em um trocador de calor composto por três tubos verticais concêntricos, sendo o PCM armazenado no tubo intermediário, dotado de diferentes configurações de aletas e espessura destas aletas. Eles concluíram que o número de aletas e o comprimento delas influenciam diretamente na redução dos tempos de solidificação, ao passo que a espessura das aletas não tem efeito sobre o processo de solidificação.
Tay et al. [14]) executaram análise experimental do processo de fusão de PCM em tanque cilíndrico vertical dotado de tubos de cobre que executavam a circulação do fluido de transferência térmica e também da recirculação do PCM já liquefeito, processo ao qual estes autores deram o nome de “dynamic melting”. Com a adoção deste tipo de técnica, os autores demonstraram que a condutividade térmica pode ser duplicada, sendo este efeito comparável ao conseguido com a adição de aletas ao sistema.
Kalaiselvam et al. [15] avaliaram, tanto de forma experimental como numérica, os processos de fusão e solidificação de três PCMs parafínicos. Na etapa de solidificação, os processos numéricos resultaram em um tempo 11% inferior aos obtidos experimentalmente. Já durante o processo de fusão, os tempos obtidos numericamente foram 16,11% inferiores aos coletados nos testes.
Observa-se que pesquisadores tem feito esforços no sentido de apresentar estratégias de solução de problemas envolvendo PCMs. No entanto, devido à diversidade de PCMs disponíveis, vários destes materiais não foram ainda estudados detalhadamente, seja de forma numérica ou experimental.
Apesar da potencialidade da utilização dos PCMs na área de armazenamento térmico de energia, eles ainda apresentam deficiências e lacunas que vem sendo analisadas pelos pesquisadores, resultando em técnicas que visam o aprimoramento das características destes materiais e maior previsibilidade nos cálculos de capacidade térmica, tempos de fusão, solidificação e demais parâmetros necessários à correta aplicação dos PCMs. Dentre as deficiências dos PCMs pode-se citar a baixa condutividade térmica, a instabilidade de alguns PCMs ao longo dos ciclos de carga/descarga e a ausência de pesquisas detalhando inúmeros PCMs comercialmente disponíveis no mercado mundial.
Este trabalho visa contribuir para a diminuição desta lacuna, estudando detalhadamente a mudança de fase de quatro diferentes PCMs da família RT [16] em cavidades cilíndricas. Assim, os objetivos específicos são: (a) implementar numericamente o modelo matemático de mudança de fase; (b) validar a metodologia e o modelo matemático com resultados da literatura; (c) avaliar e (d) comparar o processo de fusão de diferentes PCMs quando submetidos a diferentes temperaturas acima da sua temperatura de mudança de fase (Tpc).
2 Metodologia
2.1 Abordagem Numérica
A dinâmica de fluidos computacional (CFD) é o conjunto de ferramentas numéricas e computacionais utilizadas para resolver, visualizar e interpretar a solução das equações de balanço de momento, massa e energia. Tal ferramenta utiliza técnicas numéricas para solucionar problemas de engenharia, física e muitas outras áreas, já que esse tipo de simulação computacional é capaz de predizer fenômenos físicos e físico-químicos que ocorrem em um dado escoamento. Essa ferramenta vem sendo cada vez mais utilizada no desenvolvimento de produtos de consumo, aplicações industriais, aeroespaciais e de defesa. Em qualquer aplicação que envolva o escoamento de gases, escoamento de líquidos ou transferência de calor, a análise por CFD possibilita a inovação e novos patamares de eficiência para produtos e processos. Atualmente existem diversos softwares comerciais de CFD disponíveis no mercado. Dentre os mais conhecidos destacam-se o ANSYS CFX, o ANSYS Fluent, o Star-CD e o Flow-3D, entre outros.
O presente estudo foi desenvolvido utilizando-se os softwares CFD ANSYS Fluent (para as simulações numéricas), ANSYS CFX (para o pós-processamento dos resultados) e ANSYS ICEM (para a criação da malha computacional), todos disponíveis no Laboratório de Simulação Numérica do Programa de Pós-Graduação em Engenharia Mecânica da UNISINOS.
2.2 Definição do problema
2.2.1 Definição dos parâmetros geométricos
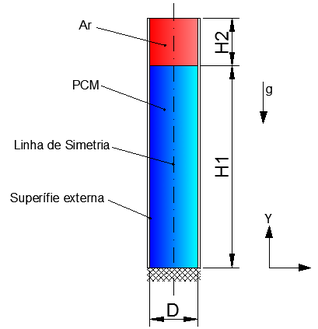
A geometria estudada consiste de uma cavidade cilíndrica vertical, conforme apresentado na Figura 1, a qual também indica que a aceleração da gravidade está em sentido oposto ao eixo Y. Nesta geometria o diâmetro (D) é de 30 mm e a altura H1 (=170 mm) representa a quantidade de PCM dentro do cilindro no tempo inicial (t=0). A altura H2 (=40 mm) é a folga necessária para compensar a dilatação térmica do PCM. Assim, durante o processo de aquecimento, ocorre um deslocamento ascendente da interface PCM-ar, sem que haja escape de PCM. A fase sólida é mostrada em cor azul e o ar, na parte superior (aberta ao ambiente), é mostrado em cor vermelha. Na base do cilindro está representada sua condição adiabática.
2.2.2 Seleção do material
A empresa alemã Rubitherm dispõe de uma grande variedade de PCMs, denominados RT. Cada RT apresenta uma temperatura de mudança de fase que varia de -9 oC até 100 oC. O valor da temperatura de mudança de fase é indicado depois das letras RT, conforme mostrado na Tabela 1.
As análises propostas para este trabalho compreendem o estudo numérico do processo de fusão dos PCMs relacionados na Tabela 1, quando submetidos a temperaturas de 10, 20 e 30 oC acima de suas respectivas temperaturas de mudança de fase (Tpc), ou seja com ΔT=10, 20 e 30 ºC.
A escolha dos PCMs a serem estudados numericamente foi feita visando possíveis aplicações de mercado. Assim sendo, os RTs selecionados foram: o RT 4, pois pode ser utilizado para aplicações de conservação e transporte de alimentos ou produtos farmacêuticos; o RT 35 e RT 55 são de interesse na área de aquecimento solar de água e, por fim, o RT 82 também foi acrescentado, pois pode ser utilizado em algumas aplicações industriais.
| PCM | Temperatura
de Fusão [°C] |
Calor Latente de Fusão.
L±7,5% [kJ kg-1] |
Condutiv. Térmica
k [W m-1 K-1] |
| RT 4 | 2 – 4 | 182 | 0,2 |
| RT 35 | 29 – 36 | 170 | 0,2 |
| RT 55 | 51 – 57 | 172 | 0,2 |
| RT 82 | 77 - 85 | 176 | 0,2 |
Na Tabela 2 são apresentados as simulações e detalhes do tipo de PCM, constante C (conhecida como ¨mushy zone¨, que corresponde à região do PCM que está em processo de mudança de fase) e o ∆T investigados. Para estas simulações serão analisadas a influência da temperatura sobre a velocidade do processo de fusão dos PCMs. Vale destacar que a constante C é detalhada no modelo matemático, Seção 3.3.
Simulação |
PCM | Tpc [oC] | C [kg m-3 s-1] | ∆T [oC] |
| 1- 3 | RT 4 | 2-4 | 107 | 10, 20 e 30 |
| 4- 6 | RT 35 | 29-36 | 107 | 10, 20 e 30 |
| 7- 9 | RT 55 | 51-57 | 107 | 10, 20 e 30 |
| 10- 12 | RT 82 | 77-85 | 107 | 10, 20 e 30 |
As simulações foram feitas utilizando as especificações técnicas de cada PCM (temperaturas de fusão e solidificação, calor latente de fusão, massas específicas nos estados sólido e líquido, condutividade térmica e viscosidade dinâmica). Um detalhamento das propriedades termodinâmicas e de como a massa específica de cada PCM é interpolada consta no Apêndice B.
2.2.3 Modelo matemático
As equações de conservação utilizadas no modelamento de um sistema com PCM, através da técnica de modelagem entalpia-porosidade, são [17]:
|
|
(1) | |
|
|
(2) | |
|
|
(3) | |
|
|
(4) |
onde é a fração volumétrica do PCM na enésima célula computacional, podendo assumir três condições: se a enésima célula não contém o PCM; se a enésima célula está cheia de PCM; se a enésima célula contém a interface entre o PCM e um ou mais fluidos existentes no domínio computacional; é a massa específica, k é a condutividade térmica, μ é a viscosidade dinâmica, é o termo fonte da quantidade de movimento, é o vetor velocidade, T é a temperatura, h é entalpia específica e p é a pressão.
A entalpia do material é definida como a soma da entalpia sensível (Eq.(5)) e da variação de entalpia devida à mudança de fase (γL), sendo, href a entalpia de referência na temperatura de referência (Tref), Cp o calor específico, L a entalpia de fusão (calor latente do material) e a fração líquida durante a mudança de fase que ocorre em uma faixa de temperatura Ts < T < Tl, definida pela seguinte relação [17]:
|
|
(5) | |
|
|
(6) |
A técnica entalpia-porosidade, analisada por Brent e Voller (1988), trata a região de mudança de fase (parcialmente solidificada), como se fosse um meio poroso. A porosidade em cada célula é definida como igual à fração líquida naquela célula. Em regiões totalmente solidificadas a porosidade é igual a zero, o que extingue as velocidades nestas regiões. O termo fonte ( ) da equação da quantidade de movimento (Eq.(2)) toma a seguinte forma:
|
|
(7) |
onde A( é a “função porosidade” definida por Brent e Voller (1988).
|
|
(8) |
onde é uma pequena constante para evitar a divisão por zero, recebendo valor de e C é a constante que reflete o processo cinético e a morfologia da região de mudança de fase. Entre outros, esta constante foi estudada por Brent e Voller [18] e Shmueli et al. [17]. Estes pesquisadores demonstraram que C controla, efetivamente, o grau de penetração de massa na região de mudança de fase e, desta maneira, conduz a um processo de fusão (ou solidificação) mais rápido ou mais lento, dependendo do valor adotado. Normalmente estes valores variam entre 105 à 1010 e dependem da geometria utilizada. A constante C, também conhecida como “mushy zone”, foi assumida igual a 107, mesmo valor utilizado por Shmueli et al. [17].
2.2.4 Validação numérica
Para a validação do modelo numérico utilizou-se os resultados de Shmueli et al. [17]. Estes autores investigaram a fusão do PCM RT 27 em cavidade cilíndrica vertical, mostrada na Figura 1, e compararam diversas simulações com os resultados experimentais de Katsman et al. [19].
O problema consiste em manter a temperatura da superfície externa 10 oC acima da temperatura média de fusão do PCM. A parte superior da geometria cilíndrica é exposta ao ar ambiente e a parte inferior foi considerada adiabática. As propriedades do RT 27, cuja temperatura de mudança de fase é 27 oC, são apresentadas na Tabela 3.
| Estado: | Cp
[J kg-1] |
k
[W m-1 K-1] |
ρ
[kg m-3] |
L
[kJ kg-1] |
μ
[Pa s] |
| Sólido
|
2500 | 0,2 | 870 | 170 | - |
| Líquido | 2500 | 0,2 | 870 em 299K
781,5 em 310K 750 em 343K |
--- | -1,137439x10-8T3 + 1,1788188x10-5T2 – 0,004111388T + 0,4857203 |
Na simulação executada, a temperatura inicial de todo o sistema foi definida como 22 oC, ou seja, o PCM está ligeiramente sub-resfriado, de forma a garantir que esteja em estado sólido no início da simulação. Foi assumido que ambas as fases, sólida e líquida, do PCM são homogêneas e isotrópicas e que o processo de fusão é simétrico em relação ao eixo central (Figura 1). Adicionalmente foi considerado que a fase líquida do PCM e o ar são fluidos Newtonianos, incompressíveis e o regime de escoamento laminar foi assumido para ambos.
2.2.5 Definição dos Parâmetros Computacionais
Para realizar as simulações foi utilizado o software ANSYS Fluent. As condições de contorno adotadas foram as mesmas especificadas no trabalho de Shmueli et al. [17]. Para descrever a interface entre o PCM e o ar, a qual se desloca com o tempo, sem interpenetração dos dois fluidos, o modelo de “volume de fluido” ou VOF foi utilizado na simulação.
As condições de contorno para as velocidades são de não-deslizamento e não-penetração em todos os contornos sólidos. A parede externa da geometria cilíndrica foi mantida a uma temperatura constante de 38oC (10 oC acima da temperatura máxima de fusão do RT 27, que é de 28 oC) e na superfície inferior foi considerada a condição adiabática. No contorno superior, exposto à atmosfera ambiente, a condição de pressão de saída (Pressure Outlet) foi utilizada e a temperatura ambiente assumida foi de 38 oC.
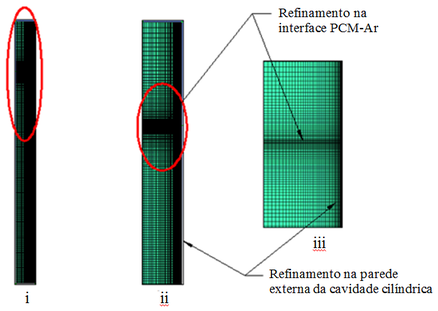
A geração da malha computacional constitui uma etapa determinante no processo de análise numérica. Uma malha pobre, ou seja, com poucos elementos, faz com que o processo numérico não represente com a acurácia necessária os diferentes processos físicos que ocorrem durante a mudança de fase do PCM. Por outro lado, deve-se ter sempre em conta que, quanto maior o número de volumes de controle de uma malha, tanto maior será o custo computacional, em termos de tempo de processamento e de capacidade de equipamentos. A malha computacional mostrada na Figura 2 foi criada seguindo as recomendações do trabalho de Shmueli et al. [17], tendo cada um de seus elementos 0,5 mm de lado, com um total de 13.652 elementos.
Foi adotado um refinamento em duas regiões distintas: junto à parede externa do cilindro e junto à interface entre o PCM e o ar. Estes refinamentos têm como objetivo, respectivamente, capturar de forma mais detalhada os efeitos de condução e convecção nos instantes iniciais da simulação e melhor acompanhar o deslocamento da interface, a qual ocorre em função do aumento de volume do PCM.
Na validação numérica foi utilizado passo de tempo (Δt) de 0,01 s e os critérios de convergência (CC) para continuidade e as componentes de velocidade foram de 10-3, sendo de 10-6 para a energia, ambos calculados com dupla precisão. Vale destacar que estes critérios de convergência foram os mesmos utilizados por Shmueli et al. [17].
Visando confirmar que o ∆t e os critérios de convergência (CC) adotados não implicavam em erro para o processo numérico, foram executadas as simulações detalhadas na Tabela 4, variando estes parâmetros.
Tabela 4. Simulações com variação de ∆t e CC.
| Simulação | Constante
C [kg m-3 s-1] |
Passo de
tempo ∆t [s] |
CC
Contin. e Veloc. |
CC
Energia |
| A | 107 | 0,01 | 10-3 | 10-6 |
| B | 107 | 0,01 | 10-6 | 10-8 |
| C | 107 | 0,002 | 10-3 | 10-6 |
| D | 107 | 0,002 | 10-6 | 10-8 |
Na Tabela 5 são apresentados os resultados das simulações de fração líquida para as 4 simulações da Tabela 4. Os resultados indicam que, mesmo com o uso de passo de tempo e critérios de convergência mais refinados como os usados nas simulações B, C e D, os resultados são praticamente os mesmos obtidos com os critérios adotados na simulação A. Os desvios médios obtidos para os resultados das frações líquidas das simulações B, C e D, em relação aos obtidos na simulação A foram, respectivamente, 0,35%, 0,63% e 0,26%. Se forem tomados apenas os resultados obtidos após 2 min estes mesmos desvios ficam em 0,06%, 0,05% e 0,02%. Tais constatações permitem afirmar que os parâmetros utilizados para o ∆t e CC nesta validação numérica (os mesmos da simulação A) são válidos e resultam em velocidades de fusão que reproduzem, com bom grau de precisão, os dados experimentais de Katsman [19].
| Simulação A | Simulação B | Simulação C | Simulação D | ||||
| Tempo [min] | Fração
Líquida |
Fração
Líquida |
Desvio
[%] |
Fração
Líquida |
Desvio
[%] |
Fração
Líquida |
Desvio
[%] |
| 0,167 | 0,044239 | 0,045346 | 2,50 | 0,046819 | 5,51 | 0,045670 | 3,13 |
| 2 | 0,164532 | 0,166829 | 1,40 | 0,168182 | 2,17 | 0,164612 | 0,05 |
| 4 | 0,236794 | 0,236769 | -0,01 | 0,236921 | 0,05 | 0,236669 | -0,05 |
| 6 | 0,297303 | 0,297392 | 0,03 | 0,297170 | -0,04 | 0,297167 | -0,05 |
| 8 | 0,336182 | 0,336224 | 0,01 | 0,336340 | 0,05 | 0,336330 | 0,04 |
| 10 | 0,375469 | 0,374736 | -0,20 | 0,374837 | -0,17 | 0,375104 | -0,10 |
| 12 | 0,409504 | 0,411161 | 0,40 | 0,411253 | 0,43 | 0,410346 | 0,21 |
| 14 | 0,445273 | 0,444849 | -0,10 | 0,445006 | -0,06 | 0,445186 | -0,02 |
| 16 | 0,478774 | 0,480461 | 0,35 | 0,479022 | 0,05 | 0,478816 | 0,01 |
| 18 | 0,511701 | 0,511500 | -0,04 | 0,511609 | -0,02 | 0,511792 | 0,02 |
| 20 | 0,541824 | 0,542962 | 0,21 | 0,543028 | 0,22 | 0,542620 | 0,15 |
| 22 | 0,570371 | 0,570318 | -0,01 | 0,570325 | -0,01 | 0,570367 | 0,00 |
| 24 | 0,6004645 | 0,600446 | 0,00 | 0,600478 | 0,00 | 0,600549 | 0,01 |
A presente validação consistiu em uma análise do tipo transiente em um espaço planar bidimensional. Para solução do problema foram adotados os seguintes modelos: volume de fluido (VOF) como modelo multifásico, escoamento laminar como modelo de viscosidade e modelo de solidificação e derretimento (solidification & melting). Os resultados parciais da validação foram salvos a cada 600 passos de tempo e o número máximo de iterações para atingir a convergência, em cada passo de tempo, foi definido como 1000.
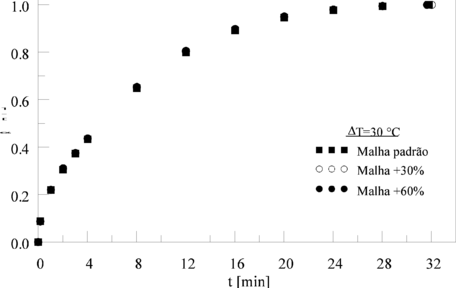
Além da malha padrão, foram executadas simulações com malhas adicionais, contendo um número de elementos 30% e 60% acima da malha padrão. As curvas mostradas na Figura 3 representam a fração líquida do PCM para as três malhas citadas. Os resultados obtidos com a malha padrão apresentaram um desvio máximo de 0,5% em relação aos obtidos com a malha mais refinada, significando que ela está adequada ao uso nas simulações deste trabalho.
Destaca-se que os resultados apresentados na Figura 3 referem-se a ∆T = 30 oC. Esta condição implica em processos térmicos e fluidodinâmicos mais intensos do que aqueles obtidos com ∆T = 10 oC, exigindo assim malhas computacionais mais refinadas. Portanto, uma vez feita a validação da malha computacional com o processo mais intenso, os menos intensos também estão assegurados.
3 Resultados e Discussão
Nesta seção serão apresentados os resultados da validação numérica e do estudo dos PCMs selecionados.
3.1 Validação numérica
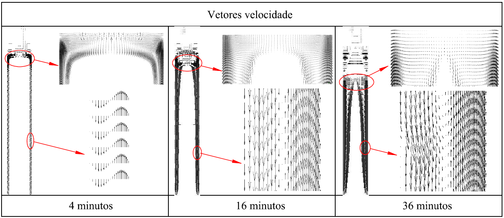
A Figura 4 mostra vetores velocidade em diferentes instantes de tempo e permite confirmar as observações feitas por Sparrow e Broadbent [20], ratificadas no trabalho de Shmueli et al. [17]. No início do processo a transferência de calor ocorre por condução da parede externa da geometria cilíndrica para a fase sólida do PCM, através de uma finíssima camada de PCM líquido. Na medida em que o processo de fusão avança, a convecção natural no PCM líquido se torna dominante, o que pode ser observado através dos vetores velocidade mostrados, os quais indicam intensidade da velocidade local. A evolução destes processos vai alterando o formato do PCM sólido, inicialmente cilíndrico, para cônico, e, paulatinamente, vai reduzindo o volume da fase sólida.
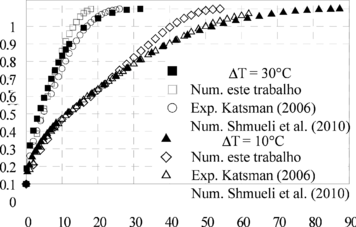
Na Figura 5 são apresentados os resultados de fração líquida quando o RT 27 é submetido a temperaturas de 10oC e 30oC acima de sua Tpc. Observa-se boa convergência entre os resultados numéricos de Shmueli et al. [17] e os obtidos na validação numérica do presente trabalho, tanto para ∆T = 10 oC quanto para ∆T = 30 oC. Comparando-se os resultados numéricos, do presente trabalho e de Shmueli et al. [17]) com os resultados experimentais de Katsman [19], pode se observar que: (a) para ∆T = 30 oC, os três resultados são muito semelhantes, qualitativa e quantitativamente, até a fração líquida de, aproximadamente, 0,8. Acima deste valor, a diferença média é de, aproximadamente, 7 % e (b) para ∆T = 10 oC, os resultados numéricos e experimentais apresentam valores muito próximos até fração líquida de 0,7. Acima deste valor, os resultados experimentais e numéricos, tanto de Shmueli quanto do presente trabalho, apresentaram, aproximadamente, 12% de desvio máximo entre eles. No entanto, apesar das diferenças máximas de 7 e 12 %, deve-se lembrar que este é um processo transiente e que estas diferenças ocorrem apenas em curto intervalo de tempo. Se considerado o tempo total do processo, a diferença média é de 2,5 e 6,1% para ∆T de 10 e 30 oC, respectivamente, o que pode ser considerado bastante razoável para processos de mudança de fase, principalmente para pequenos ∆T (10 ºC), quando o processo de investigação, tanto numérico quanto experimental, se torna cada vez mais exigente . Shmueli et al. [17] testou vários valores para a constante C. O uso da constante C=107 foi o que apresentou resultados mais próximos dos obtidos experimentalmente.
Ainda em relação à Figura 5, tomando-se como parâmetro de comparação o tempo necessário para atingir uma fração líquida de 0,6 com ∆T = 10oC (24 min), constata-se que o aumento para ∆T = 20oC reduz este tempo em 53,9% (11,06 min) e, usando-se ∆T = 30oC, este mesmo tempo é reduzido em 70,8% (7,02 min). Outra observação importante é que o tempo de fusão total, observado no processo numérico, foi reduzido em 66,7%, quando se eleva o ΔT = 10 °C para 30 °C. Este valor ficou muito próximo dos 63,6%, observados nos experimentos de Katsman [19].
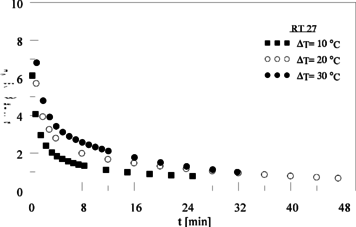
Na Figura 6 são apresentados os perfis de fluxo de calor do RT 27 para ΔT de 10 oC, 20 oC e 30 oC, com C=107. Observa-se que o fluxo de calor é intenso nos instantes iniciais do processo de fusão, quando a troca térmica é dominada pelo processo de condução, e decresce exponencialmente na medida em que há um incremente do processo de convecção no PCM já liquefeito. Além disso, no tempo de 8 min, por exemplo, também pode-se observar que, quanto maior é o ΔT maior é o fluxo de calor, correspondendo assim às expectativas para este tipo de processo.
3.2 Resultados obtidos com a análise dos PCMs
Os resultados apresentados nesta seção referem-se aos 12 tipos de PCMs citados apresentados na Tabela 2. Foi avaliada a influência da temperatura em relação aos tempos de fusão e também sobre fluxo de calor, considerando ΔT de 10 oC, 20 oC e 30 oC acima da Tpc de cada PCM. Para a comparação das simulações são investigados os tempos necessários para atingir as frações líquidas de 0,4, 0,6 , 0,8 e 1,0.
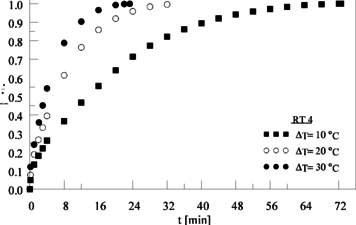
A Figura 7 apresenta a variação da fração líquida em função do tempo para o PCM RT 4, quando submetido a ΔT de 10 oC, 20 oC e 30 oC. Tomandose como referência inicial o tempo necessário para que o RT 4 atinja a fração líquida de 0,6 (~18 min), com ΔT = 10 oC, observa-se que o aumento do ΔT para 20 oC e 30 oC faz com que este tempo seja reduzido em 57% e 72,7%, totalizando, aproximadamente, 7,74 min e 4,93 min, respectivamente.
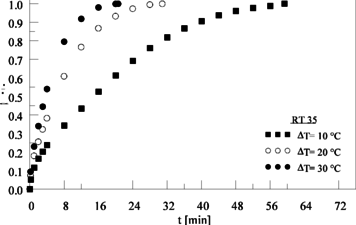
A variação da fração líquida com o tempo, para o PCM RT 35, é mostrada na Figura 8 quando este é submetido a ΔT de 10 oC, 20 oC e 30 oC. O tempo necessário para atingir a fração líquida de 0,6 é de 19,4 min. 7,8 min e 4,9 min, apresentando redução de 59,8% e de 74,6%, respectivamente, em relação ao tempo obtido com ΔT de 10 oC.
Na Tabela 6 é apresentado um sumário dos tempos de fusão para a fração líquida de 0,6, assim como outras características dos PCM estudados. Observa-se que o incremento do ΔT de 10 oC para 20 oC reduz o tempo de fusão, em média, em 56,6%. Já o incremento no ΔT de 10 oC para 30 oC, reduz em 72,1% o tempo de fusão médio.
| PCM | L
[kJ kg-1] |
Tempo para atingir α=0,6 [min] | Redução de Tempo [%] | |||
| DT=10oC | DT=20oC | DT=30oC | de DT=10oC | de DT=10oC | ||
| para DT=20oC | para DT=30oC | |||||
| RT 4 | 182 | 18,05 | 7,74 | 4,93 | 57,1% | 72,7% |
| RT 27 | 179 | 24,00 | 11,06 | 7,02 | 53,9% | 70,8% |
| RT 35 | 170 | 19,40 | 7,80 | 4,90 | 59,8% | 74,7% |
| RT 55 | 172 | 23,70 | 10,75 | 6,60 | 54,6% | 72,2% |
| RT 82 | 176 | 17,50 | 7,40 | 5,20 | 57,7% | 70,3% |
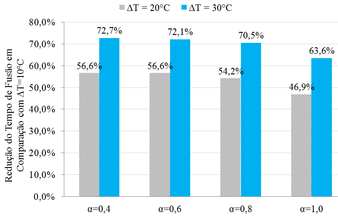
Na Figura 9 são apresentadas as reduções médias obtidas nos tempos de fusão dos diversos PCMs para as frações líquidas de 0,4, 0,6, 0,8 e 1,0 (fusão completa). Estes resultados mostram que, para frações líquidas entre 0,4 e 0,8, as reduções percentuais obtidas nos tempos de fusão, situam-se em patamares muito próximos, sendo que as reduções médias são de 55,8% e 71,8%, quando incrementado o ΔT= 10 oC para 20 oC e de 20 oC para 30 oC, respectivamente. Para α=1,0 e ΔT=30 oC a redução média de 63,6% aproximou-se bastante do observado experimentalmente para o RT 27 (66,7%), conforme Figura 5.
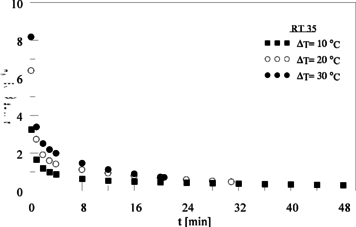
No que diz respeito ao fluxo de calor (q¨), o comportamento verificado para os PCMs estudados foi similar ao mostrado na Figura 6, ou seja, o fluxo de calor é intenso nos instantes iniciais, quando a troca térmica é dominada pelo processo de condução e decai exponencialmente na medida em que o efeito convectivo avança. A Figura 10 apresenta o comportamento do fluxo de calor do RT 35 em função do tempo, para diferentes ΔT.
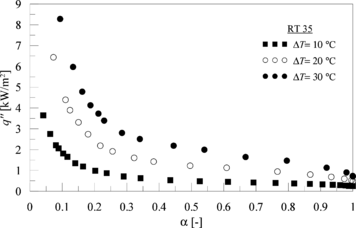
Na Figura 11 é apresentado o resultado do comportamento do fluxo de calor em função da fração líquida variando ΔT, para o RT 35. Vale destacar que também aqui constatou-se que há similaridade do comportamento do fluxo de calor para todos os PCMs estudados, ou seja o fluxo de calor decresce exponencialmente na medida em que o PCM se liquefaz.
Na Tabela 7 são apresentados os valores do fluxo de calor dos PCMs estudados (em t=10 s) e os incrementos obtidos quando o ΔT é aumentado de 10 °C para 20 °C e também para 30 °C. Os incrementos no fluxo de calor variaram entre 51,7% e 74,1% (aumentando o ΔT de 10 °C para 20 °C) e entre 98,1% a 124,3% (aumentando o ΔT de 10 °C para 30 °C).
| PCM | L
[kJ kg-1] |
q”máx [kW m-2] | Redução de Tempo [%] | |||
| DT=10oC | DT=20oC | DT=30oC | de DT=10oC | de DT=10oC | ||
| para DT=20oC | para DT=30oC | |||||
| RT 4 | 182 | 4,65 | 7,21 | 9,21 | 55,1% | 98,1% |
| RT 35 | 170 | 3,70 | 6,44 | 8,30 | 74,1% | 124,3% |
| RT 55 | 172 | 4,18 | 6,34 | 8,43 | 51,7% | 101,7% |
| RT 82 | 176 | 3,83 | 6,66 | 8,47 | 73,9% | 121,2% |
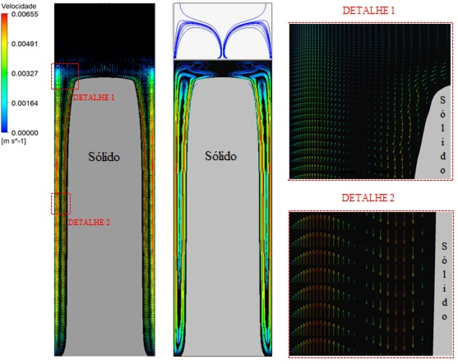
Em termos de características de escoamento, todos os processos de fusão analisados são muito similares. Estes são representados na Figura 12(a-b), para o RT 4, com ΔT=10 ºC no t=10 min. Com o aquecimento da parede vertical, o PCM, inicialmente sólido, muda de fase e passa a aumentar sua temperatura para valores acima da temperatura de fusão. Em decorrência disso, forças de empuxo se tornam presentes, decorrentes da variação da massa específica.
Nas Figuras 12(a-b) são apresentados os campos de velocidade e de linhas de corrente. Com o aumento da temperatura junto à parede vertical, e consequente redução da massa específica, ocorre um escoamento ascendente do PCM líquido. Esta condição pode ser verificada na Figura 12(a), sendo melhor visualizada nos Detalhes 1 e 2. Nestes detalhes também é possível identificar o escoamento descente junto à parcela sólida, em consequência da conservação da massa. Também é possível verificar a região cisalhante entre os escoamentos ascendente e descendente, onde a velocidade é zero. A possibilidade de visualização deste detalhe indica que o grau de refinamento da malha computacional está adequado para representar o processo. Já na Figura 12(b), onde estão representadas linhas de corrente, além da região referente à parcela sólida, pode-se observar duas regiões distintas com recirculação: a do PCM líquido (junto à parede lateral) e a do ar (no topo do domínio computacional). Neta última observa-se duas recirculações bem definidas, as quais são decorrentes do arrasto provocado pela recirculação do PCM líquido na interface entre os dois fluidos, indicando que ali também a malha computacional está adequada para o processo analisado.
4 Conclusões
Este trabalho teve como objetivo investigar numericamente o processo de fusão de diferentes tipos de PCMs em cavidades cilíndricas, inicialmente validando a metodologia e o modelo matemático com resultados da literatura e, posteriormente, avaliando e comparando o processo de fusão de diferentes PCMs quando submetidos a diferentes temperaturas acima da sua temperatura de mudança de fase (Tpc).
A implementação do modelo numérico foi validada com resultados para PCM RT 27. Estes foram confrontados com resultados numéricos e experimentais da literatura, apresentando boa aproximação. Assim sendo, a metodologia, modelo matemático, malha computacional e demais parâmetros utilizados foram considerados aptos para os estudos das simulações.
Foram simulados os processos de fusão de quatro diferentes PCMs considerando-se três ΔT (10, 20 e 30 ºC) acima da temperatura de fusão destes PCMs, totalizando 12 diferentes simulações. Para estas simulações as conclusões obtidas foram que o incremento do ΔT, de 10 oC para 20 oC, ocasiona uma redução média geral nos tempos de fusão de 55,8% para atingir frações líquidas entre 0,4 e 0,8. Já o aumento do ΔT de 10 oC para 30 oC resulta em uma redução média geral do tempo de fusão de 71,8%, para a mesma faixa de frações líquidas. As reduções de tempo médias obtidas para atingir a fusão completa dos PCMS (fração líquida 1,0) foram de 46,9% (de ΔT de 10 oC para 20 oC) e de 63,6% (de ΔT de 10 oC para 30 oC). Este último resultado mostrou-se similar ao obtido experimentalmente por Katsman [19], no qual a redução de tempo para fusão completa do RT 27 foi de 66,6% (de ΔT de 10 oC para 30 oC).
No que diz respeito ao fluxo de calor (q¨), verificou-se que a utilização de ΔT mais elevado propicia um forte incremento no fluxo de calor inicial, contribuindo no processo de troca térmica e reduzindo o tempo de fusão do PCM.
Apêndice A
Símbolo |
Significado | Unidade |
| C | Constante Mushy Zone | kg m-3 s-1 |
| CC | Critério de convergência | - |
| cp | Calor específico do fluido a pressão constante | J kg-1 K-1 |
| D | Diâmetro do cilindro de PCM | mm |
| Dm | Diâmetro médio | mm |
| g | Aceleração da gravidade | m s-2 |
| h | Entalpia específica | J kg-1 |
| hs | Entalpia sensível | J kg-1 |
| href | Entalpia de referência | J kg-1 |
| H1 | Altura da cavidade estudada contendo PCM | mm |
| H2 | Altura da cavidade estudada contendo ar | mm |
| k | Condutividade térmica | W m-1 K-1 |
| L | Calor latente de fusão | J kg-1 |
| p | Pressão | Pa |
| q | Taxa de transferência de calor | W |
| q" | Fluxo de calor | W m-²] |
| Termo fonte de momento | Pa m-1 | |
| t | Tempo | s |
| T | Temperatura | oC, K |
| Ts | Temperatura do PCM na fase sólida | oC, K |
| Tl | Temperatura do PCM na fase líquida | oC, K |
| Tpc | Temperatura de mudança de fase | oC, K |
| V | Volume | m3 |
| Vetor velocidade | m/s | |
| αn | Fração líquida na enésima célula computacional | - |
| α(t) | Fração líquida do PCM em um instante ¨t¨ | - |
| ∆ | Variação | - |
| Constante numérica (0,001) | - | |
| ρ | Massa específica | kg m-3 |
| μ | Viscosidade dinâmica | Pa s |
| Fração líquida | - |
Apêndice B. Propiedades dos PCMs estudados
Para a execução deste trabalho foram consideradas as características técnicas disponíveis no website da empresa Rubitherm Technologies GmbH (www.rubitherm.com), abaixo transcritas.
| Propriedade | RT 4 | RT 35 | RT 55 | RT 82 |
| Temperatura de Fusão [oC] | 2-4 | 29-36 | 51-57 | 77-85 |
| L [kJ kg-1] | 182 (-5 a 10 oC) | 170 (26 a 41 oC) | 172 (48 a 63 oC) | 176 (70 a 85 oC) |
| cp [kJ kg-1 K-1] | 2 | 2 | 2 | 2 |
| K [W m-1 K-1] | 0,2 | 0,2 | 0,2 | 0,2 |
| Expansão volumétrica [%] | 12,5 | 12,5 | 14 | 12,5 |
| Flash point [oC] | 110 | 167 | >200 | >200 |
Através de contatos feitos via e-mail, com a direção da empresa Rubitherm, foram coletados, adicionalmente, os seguintes dados:
| Propriedade | RT 4 | RT 35 | RT 55 | RT 82 |
| r (sólido) [kg m-3] | 880,0 (-15 oC) | 860,0 (15 oC) | 880,0 (15 oC) | 880,0 (15 oC) |
| r (início da fusão) [kg m-3] | 870,0 (2 oC) | 850,0 (29 oC) | 870,0 (51 oC) | 870,0 (77 oC) |
| r (término da fusão) [kg m-3] | 870,0 (4 oC) | 781,5 (36 oC) | 870,0 (57 oC) | 870,0 (85 oC) |
| r (líquido) [kg m-3] | 770,0 (15 oC) | 770,0 (45 oC) | 770,0 (80 oC) | 770,0 (90 oC) |
| r (dado adicional) [kg m-3] | 700,0 (40 oC) | 700,0 (70 oC) | 700,0 (100 oC) | 700,0 (100 oC) |
| PCM | Temp. de Referência | Viscosidade Cinética | Viscosidade Dinâmica |
| [oC] | [mm2 s-1] | [mPa s] | |
| RT 4 | 40 | 2,6 | 1,82 |
| RT 35 | 70 | 3,3 | 2,31 |
| RT 55 | 100 | 3,8 | 2,66 |
| RT 82 | 100 | 4,5 | 3,15 |
Referências
| [1] | U.S. Department Of Energy. Building Energy Data Book. Disponível em http://buildingsdatabook.eren.doe.gov/TableView.aspx?table=1.1.3. Acesso em 22 de março de 2015. |
| [2] | European Comission. Statistical Pocketbook 2014. Disponível em: http://ec.europa.eu/transport/facts-fundings/statistics/pocketbook-2014_en.htm. Acesso em 22 de março de 2015. |
| [3] | Ministério De Minas E Energia. Balanço Energético Nacional – Ano Base 2013. Disponível em: https://ben.epe.gov.br/BENRelatorioFinal2013.aspx. Acesso em 22 de março de 2015. |
| [4] | Agyenim, F., Hewitt, N., Eames, P., Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renewable and Sustainable Energy Reviews, v. 14, p. 615-628, 2010. |
| [5] | Pielichowska, K., Pielichowski, K. Phase change materials for termal energy storaga. Progress in Materials Science, v. 65, p. 67-123, 2014. |
| [6] | Zhou, D., Zhao, C.Y., Tian, Y. Review on termal energy storage with phase change materials in building applications. Applied Energy, v. 92, p. 593-605, 2012. |
| [7] | Al-Abidi, A.A., Mat, S.B., Sopian, K., Sulaiman, M.Y., Lim, C.H., Mohammad, A.T.A. Review of thermal energy storage for air conditioning systems. Renewable and Sustainable Energy Reviews, v. 16, p. 5802-5819, 2012. |
| [8] | Oró, E., Gracia, A., Castell, A. Farid, M.M., Cabeza, L.F. Review on phase change materials (PCMs) for cold termal energy storage applications. Applied Energy, v. 99, p. 513-533, 2012. |
| [9] | Mehling, H., Cabeza, L. F. Heat and cold storage with PCM: An up to date introduction into basics and applications. 1. ed. Berlin: Springer, 2008. |
| [10] | Murray, R. E., Groulx, D. Experimental study of the phase change and energy characteristics inside a cylindrical latent heat energy storage system: Part 1 consecutive charging and discharging. Renewable Energy, v. 62, p. 571-581, 2014. |
| [11] | Longeon, M., Soupart A., Fourmigué, J.F., Bruch, A., Marty, P. Experimental and numerical study of annular PCM storage in the presence of natural convection. Applied Energy, v. 112, p. 175-184, 2013. |
| [12] | Zeng, Y., Fan, L.W., Xiao, Y.Q., Yu, Z.T., Cen, K.F. An experimental investigation of melting of nanoparticle-enhanced phase change materials (NePCMs) in a bottom-heated vertical cylindrical cavity. International Journal of Heat and Mass Transfer, v. 66, p. 111-117, 2013. |
| [13] | Al-Abidi, A.A., Mat, S.B., Sopian, K., Sulaiman, M.Y., Mohammad, A.T. Numerical study of PCM solidification in a triplex tube heat exchanger with internal and external fins. International Journal of Heat and Mass Transfer, v. 61, p. 684-695, 2013. |
| [14] | Tay, N.H., Bruno F., Belusko, M. Experimental investigation of dynamic melting in a tube-in-tank PCM system. Applied Energy, v. 104, p. 137-148, 2013. |
| [15] | Kalaiselvam, S., Veerappan, M., Aaron, A.A., Iniyan, S. Experimental and analytical investigation of solidification and melting of PCMs inside cylindrical encapsulation. International Journal of Thermal Sciences, v. 47, p. 858-874, 2008. |
| [16] | Rubitherm. Disponível em http://www.rubitherm.de/english/index.htm. Acesso em: 07 de maio de 2014. |
| [17] | Shmueli, H., Ziskind, G., Letan, R. Melting in a vertical cylindrical tube: Numerical investigation and comparison with experiments. International Journal of Heat and Mass Transfer, v. 53, p. 4082-4091, 2010. |
| [18] | Brent, A.D., Voller, V.R. Enthalpy-porosity technique for modeling convection-diffusion phase change – application to the melting of a pure metal. Numerical Heat Transfer, v. 13, p. 297-318, 1988. |
| [19] | Katsman, L. Investigation of phase change in cylindrical geometry with internal fins. M.Sc. Thesis, Heat Transfer Laboratory, Department of Mechanical Engineering, Ben-Gurion University of the Negev, Beer-Sheva, Israel, 2006. |
| [20] | Sparrow, E.M., Broadbent, J.A. Inward melting in a vertical tube which allows free expansion of the phase-change medium, ASME Journal of Heat Transfer, v. 104, p. 309-315, 1982. |
Document information
Published on 03/01/18
Accepted on 19/09/16
Submitted on 11/01/16
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.5.001
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?