VanessaSoule (talk | contribs) |
VanessaSoule (talk | contribs) |
||
| Line 277: | Line 277: | ||
|} | |} | ||
| − | En las tres olas, es posible identificar que el riesgo de mortalidad por COVID–19 | + | En las tres olas, es posible identificar que el riesgo de mortalidad por COVID–19: |
| − | |||
* Disminuye en municipios con mayor grado de escolaridad. (Ver Figura [[#img-4|4]]) | * Disminuye en municipios con mayor grado de escolaridad. (Ver Figura [[#img-4|4]]) | ||
* Aumenta en municipios con población ocupada con ingresos de hasta 2 salarios mínimos. (Ver Figura [[#img-5|5]]) | * Aumenta en municipios con población ocupada con ingresos de hasta 2 salarios mínimos. (Ver Figura [[#img-5|5]]) | ||
Revision as of 08:22, 8 December 2023
1 Introducción
Los primeros casos de la enfermedad COVID-19 en México, se detectaron a finales de febrero de 2020 desencadenando un brote de contagios que aumentó drásticamente a medida que la pandemia avanzaba, [1]. Es crucial tener en cuenta que nunca se pudo conocer el número real de personas infectadas, esto debido tanto a portadores asintomáticos, como a la falta de registro de enfermos que no asistieron a clínicas, centros de salud u hospitales[2] en busca de atención médica.
Es importante observar que el acceso a servicios de calidad en salud, educación, empleo y vivienda depende en gran medida del nivel socioeconómico de las personas. Estudios realizados en México han proporcionado evidencia concluyente de que la mayor concentración de patologías complejas y exceso de mortalidad se encuentra en las regiones o grupos donde prevalecen elevados niveles de marginación y exclusión social [3]. En todo el territorio mexicano, se observan notables contrastes entre distintas zonas geográficas, grupos étnicos y estratos socioeconómicos. Dada la relación entre estas disparidades y el alto índice de contagios y muertes causadas por las condiciones de salud predominantes, que a menudo facilitan la transmisión del virus en personas con comorbilidades, es esencial analizar el impacto de la pandemia desde una perspectiva que englobe tanto los aspectos sociales como los económicos y los médicos.
El objetivo de este estudio es identificar factores socioeconómicos que pudieran tener influencia en el riesgo de mortalidad por COVID-19. Lo anterior a un nivel de desagregación geográfica municipal. Para alcanzar esta meta, se utiliza la teoría de regresión múltiple, en donde se busca modelar el riesgo de mortalidad por COVID-19 como función lineal de muchas variables socioeconómicas. En este caso, la etapa clave sería la selección de variables.
El artículo se organiza de la siguiente manera, en la Sección 3 se da un breve resumen de la teoría de regresión múltiple. Las fuentes de información utilizadas, así como la manera en la que se construyó la variable dependiente para el modelo de regresión múltiple, se describen en la Sección 4. En la Sección 5, se identifica que el tamaño de la población en los municipios de México es muy heterogéneo y se presenta una solución para que esto no afecte el ajuste de los modelos de regresión. La Sección 6, presenta la forma en la que se construyeron las variables que nos permitirán incluir los factores socioeconómicos en el modelo y en la Sección 8 se presenta el ajuste de los modelos, así como las variables que contribuyen a explicar el riesgo de mortalidad. Finalmente, en la Sección 9 se presentan las conclusiones.
2 Modelo de regresión
La teoría de regresión puede consultarse en los libros clásicos [4] y [5]. Para una visión aplicada en donde se usa el paquete estadístico R, [6], ver el libro [7]. A continuación, se brinda una descripción muy breve de la teoría de regresión lineal múltiple enfocándonos en las herramientas que se usarán más adelante.
Un modelo de regresión es un modelo matemático que, de manera muy general, busca alcanzar dos objetivos 1) entender o identificar la relación que existe entre una variable dependiente y un conjunto de variables independientes y 2) predecir los valores de la variable dependiente usando las variables independientes. Estos dos objetivos generalmente se contraponen debido a que modelos más simples suelen ser más fáciles de interpretar, pero modelos con pocas variables suelen no capturar la complejidad de los datos (o predecir) como modelos con más variables. Adicionalmente, añadir demasiadas variables puede llevar a un sobreajuste, donde el modelo se ajusta demasiado bien a los datos de entrenamiento, pero no es capaz de describir datos nuevos. En muchos casos, se busca un equilibrio entre la simplicidad del modelo, su capacidad de predicción y la interpretación que nos brinda del fenómeno que buscamos entender; por lo que es indispensable tener claro lo que se busca en cada problema que se quiera analizar. En este trabajo lo que se desea es alcanzar el primer objetivo.
El modelo de Regresión Lineal Múltiple (RLM) puede ser escrito en forma matricial como:
|
|
(1) |
en donde es un vector aleatorio, es decir, sus elementos son variables aleatorias. El vector representa los coeficientes de regresión y son parámetros que se asumen como constantes desconocidas. Cada elemento de es un coeficiente parcial de regresión que refleja el cambio en la variable dependiente por unidad en la variable independiente . Cabe mencionar que en términos generales, la columna de unos dentro de nuestro conjunto de variables independientes, no se considera una variable independiente en el sentido tradicional, ya que no representa una característica específica del conjunto de datos original. Sin embargo, en el contexto del modelo de regresión lineal, se le trata como una variable adicional que permite al modelo ajustar la ordenada al origen. Por lo tanto, aunque no es una variable en el sentido típico, se incluye en la matriz de variables independientes para facilitar el ajuste del modelo.
Los supuestos básicos de la RLM se centran en el vector aleatorio , conocido como el vector de errores del modelo. Los supuestos son: 1) la esperanza de los errores, , es cero, 2) su varianza es constante () y 3) los errores son independientes entre sí. Adicionalmente, se tiene un supuesto distribucional que nos permitirá realizar pruebas de bondad de ajuste del modelo de RLM, i.e. pruebas estadísticas para determinar que tan bien describe el modelo a la variable dependiente. El supuesto distribucional 4) es el error que sigue una distribución normal con media cero y varianza . Considerando los supuestos básicos y que se conoce de antemano la matriz de variables independientes , es fácil observar que la relación media entre la variable dependiente e independientes está dada por .
2.1 Estimación
El análisis de RLM nos da herramientas para, primero, estimar y a continuación determinar que tan bien nuestro modelo ajusta los datos. Para estimar los coeficientes del modelo, lo más sencillo es utilizar el método de mínimos cuadrados, aquí se busca determinar el vector que minimiza la distancia
|
|
(2) |
Derivando con respecto a , igualando a cero y simplificando se llega a
|
|
(3) |
Multiplicando ambos lados de la ecuación (3), por la inversa de , se obtiene el estimador para por mínimos cuadrados:
|
|
(4) |
La matriz existe si las columnas de (las variables independientes) son linealmente independientes. Por lo tanto, el modelo ajustado de regresión queda definido como .
2.2 Comparación de modelos
Es sencillo definir una medida del error en la estimación, ésta es simplemente la suma del cuadrado de los errores en la estimación, i.e. . También se puede demostrar que la varianza de la variable dependiente, se divide en la cantidad de variabilidad en las observaciones explicada por el modelo de regresión, más el error en la estimación, i.e.
|
|
A partir de la descomposición de la varianza, se obtiene el coeficiente de determinación
|
|
que indica la proporción de la varianza de los datos, efectivamente explicada por el modelo. La muy bien podría usarse para comparar modelos de RLM, sin embargo en el caso de modelos anidados (modelos donde las variables independientes de un modelo son un subconjunto de las variables independientes de otro modelo) es fácil verificar que modelos con un mayor número de variables siempre producen mayores valores de , por lo que la no es una estadística recomendable para comparar modelos, obviamente lo que se busca es un modelo con el menor número de variables y que describa bien los datos. Estos modelos son más fáciles de interpretar, manejar y mantener.
Para resolver el problema con la , una alternativa es comparar modelos usando el criterio de información de Akaike (AIC), [8]. El AIC se basa en el cálculo de la estadística
|
|
en donde la parte izquierda es una medida de falta de ajuste del modelo, es el número de observaciones y es una penalización por el número de variables independientes que se incluyen en el modelo. Al comparar modelos, se prefieren modelos con menor AIC.
La manera obvia para elegir el mejor modelo es hacer todas las regresiones posibles (todas las posibles combinaciones de variables independientes) y para cada regresión calcular el . Sin embargo, el número de regresiones posibles con variables independientes es . Si tenemos variables independientes sería necesario ajustar modelos, lo que quizá sea factible pero sería computacionalmente muy demandante. Sin embargo, si se tienen 30 variables, el número de modelos a considerar es de , lo que ya no es viable. Por lo anterior, las estrategias más utilizadas para seleccionar variables son los métodos de selección paso a paso. Estas estrategias consisten en agregar o eliminar una variable cada vez, comparando el modelo actual con el siguiente basándonos en el AIC (aunque podrían usarse otros criterios). Este tipo de métodos tiene 3 posibilidades:
Forward: Selecciona paso a paso hacia adelante. Empieza con el modelo más simple y va agregando una a una las variables hasta que el modelo deje de mejorar. Backward: Selecciona paso a paso hacia atrás. Empieza con el modelo que incluye a todas las variables y elimina una a una, hasta que el modelo deje de mejorar. Both: Selecciona paso a paso en ambas direcciones. Es una combinación de los dos métodos anteriores.
La librería MASS, [9], del paquete estadístico R, implementa estás técnicas vía la función stepAIC.
3 Los Datos
Fundamentalmente, se contó con dos fuentes de información:
- La base de datos de la Secretaría de Salud del Gobierno de México SINAVE/SISVER, [10]. Esta base de datos registra información de todas aquellas personas que acudieron a alguna clínica, centro de salud u hospital público o privado por sospecha de haberse contagiado de COVID-19. Esta información se tiene a nivel paciente, pero obviamente no tiene información de identificación.
- La base de datos del Censo de Población y Vivienda 2020 del INEGI, [11]. El Censo contiene información detallada sobre varias características de la población y de sus viviendas en todo el país. Puede descargarse en el sitio de INEGI y el nivel de desagregación puede ser manzana, AGEB, localidad, municipio, estado o nacional.
Inicialmente, se intentó unir la información de ambas bases de datos a nivel localidad (considerando sólo a la CDMX), pero fue imposible pues las claves de localidad en la base SINAVE/SISVER no corresponden con las mismas claves en las bases de datos del INEGI. En cambio, a nivel municipal existía suficiente homogeneidad entre ambas bases de datos para poder unirlas: ambas bases de datos cuentan con la clave de estado y clave de municipio de INEGI, además existe coincidencia de más del 98% en estas variables de ambas bases de datos.
3.1 Variable dependiente: riesgo de mortalidad
La última versión de la base SINAVE/SISVER, que se descargó para este trabajo, fue la del 16 de marzo del 2022. En esta actualización, se contaba con información de casos totales, incluyendo positivos, sospechosos y negativos. Para obtener nuestra base de datos de trabajo, se filtraron los casos positivos a COVID-19 ( observaciones). La evolución del número de casos positivos por mes se presenta en la Figura 1.
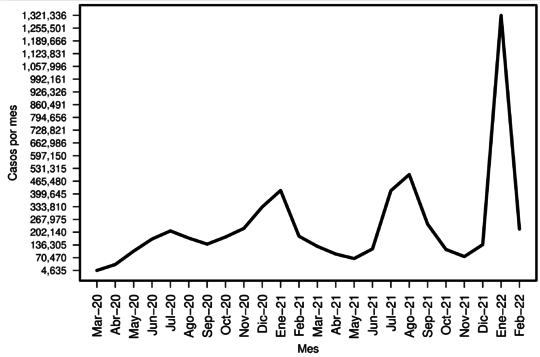
|
| Figura 1: Evolución mensual del número de casos positivos a COVID-19. |
Es fácil apreciar que hasta marzo del 2022, México había sido impactado por cuatro olas de la pandemia por COVID-19. Estas sucedieron en los meses:
- Primera ola: junio, julio y agosto del 2020.
- Segunda ola: diciembre de 2020, enero y febrero del 2021.
- Tercera ola: julio, agosto y septiembre del 2021.
- Cuarta ola: diciembre de 2021, enero y febrero del 2022.
Lo anterior, considerando el mes en donde se observó el pico de contagios, junto con el anterior y el posterior.
Como se mencionó en la introducción, el objetivo de este trabajo se centra en describir el riesgo de mortalidad por COVID-19, esto es
|
|
en donde es el número de defunciones ocasionadas por el COVID-19 y es el número de casos positivos a COVID-19. En la Figura 2, se muestra la evolución mensual del riesgo de mortalidad.
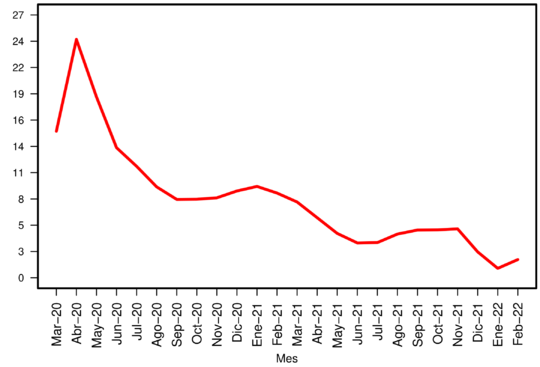
|
| Figura 2: Evolución del riesgo de mortalidad por COVID-19. |
Observando las Figuras 1 y 2 notamos que durante la primera ola de la pandemia había relativamente pocos casos, pero la mortalidad fue la más alta que se observó durante toda la pandemia. En cambio, en la cuarta ola se dio el mayor pico en el número de casos y la menor mortalidad. Recordemos que al principio de la pandemia el conocimiento que se tenía de esta nueva enfermedad era mínimo, incluso algunos sectores de la población no le dieron relevancia. A medida que pasaron los meses, el conocimiento que existía de la enfermedad iba creciendo, e incluso a finales del año 2020 empezó la vacunación contra el COVID-19. Considerando con cuidado que estos factores iban evolucionando en el tiempo, se pensó que la mejor estrategia sería modelar el riesgo de mortalidad en cada una de las primeras tres olas de la pandemia, para finalmente intentar predecir lo que sucedería en la cuarta ola.
Filtrando la información para cada ola de la pandemia y obteniendo el porcentaje de fallecimientos por COVID-19, en cada municipio de la República Mexicana, se obtuvieron cuatro bases de datos. Cada una con aproximadamente registros. Dependiendo de la ola que se esté analizando, el número de municipios en donde se observaron casos positivos a COVID-19 cambia. En la primera ola, se observaron casos positivos en un total de municipios, en la segunda y en la tercera ola . Cada base de datos, además del porcentaje de fallecimientos por COVID-19 en cada municipio, tiene la clave de estado y de municipio de cada registro. Estas variables nos dan la oportunidad de unir estas bases de datos con la información del INEGI.
Es importante mencionar que la base SINAVE/SISVER cuenta con variables como la fecha de inicio de síntomas, fecha de fallecimiento, el sexo, edad, tipo de paciente (hospitalizado o ambulatorio), comorbilidades (9 variables dicotómicas que indican si el paciente padecía o no cierta comorbilidad) entre muchas variables más. Sin embargo, para alcanzar los objetivos delineados en este trabajo, las variables relevantes fueron fecha de inicio de síntomas (para determinar la ola de la pandemia a la que el paciente pertenece) y la fecha de fallecimiento (para crear una variable dicotómica con la información de los fallecimientos).
4 Número de habitantes en los municipios de México
La República Mexicana está integrada por municipios de los cuales, según la sección anterior, presentaron al menos algún caso positivo a COVID-19. Analizando el tamaño de la población de los municipios del país, se observó gran heterogeneidad. Por ejemplo, existe un municipio con sólo 81 habitantes y otro con 1,922,523. Debido a que se busca identificar la relevancia de diversos factores socioeconómicas para describir el riesgo de mortalidad, por COVID-19, en los municipios de México, lo anterior representa una dificultad ya que las conclusiones del análisis podrían estar dictadas mayormente por la disparidad entre el tamaño de la población de los municipios y no por el efecto de las variables socio-económicas.
Para resolver el problema identificado en el párrafo anterior, se dividió a los municipios en grupos de acuerdo al número de habitantes. Primero, se aplicó la función logaritmo al tamaño de la población, generando una distribución normal. Después, se usaron cuantiles para obtener 5 grupos, cada uno compuesto por municipios con aproximadamente el mismo tamaño poblacional. Al agregar esta información a la base de datos con los porcentajes de fallecimientos por COVID-19 (de las 3 olas de la pandemia), se observó que la distribución normal se mantiene. En la Figura 3 se muestra en colores los 5 grupos, notando que el grupo con mayor densidad, es decir, el grupo que presenta más casos positivos son los municipios medianos (grupo 3 - municipios entre 9 mil y 19 mil habitantes).
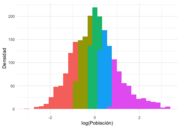
|
|

|
| (a) 1ra ola | (b) 2da ola | (c) 3ra ola |
| Figura 3: Distribución del tamaño de los municipios (con base logarítmica) en donde se observaron casos positivos en cada ola de la pandemia. | ||
Esto nos ayudará a que las conclusiones del análisis, para los municipios del mismo tamaño, sean comparables entre las tres olas de la pandemia. Además, podremos identificar las variables significativas específicas en cada grupo poblacional.
5 Factores socioeconómicos
En la sección anterior, se describe el esfuerzo realizado para lograr que el tamaño de la población de los municipios no tenga impacto en las conclusiones que se pudieran obtener. Con el mismo objetivo, se construyen las variables socioeconómicas que se incluirían en nuestros modelos de RLM.
De manera general, para construir las variables independientes, primero se extrajeron los subtotales a nivel municipal del Censo, a continuación se calculó la proporción de cada una y se multiplicó por cien para tener porcentajes. Por ejemplo, para obtener el porcentaje de analfabetas por municipio, primero, se tomó la población total de 15 años o más analfabeta, segundo, se dividió entre la población total de 15 años o más y finalmente se multiplicó por cien. Se hizo algo similar para la población económicamente activa, la población sin seguridad social, etc. En otros casos, cuando era claro que no habría impacto del tamaño de la población de los municipios, simplemente se tomó el sub-total a nivel municipal directamente de la base de datos del Censo: grado promedio de escolaridad, promedio de hijos nacidos vivos, promedio de ocupantes en viviendas particulares habitadas, etc. Las variables socioeconómicas construidas a partir de variables del Censo, junto con sus nombres mnemotécnicos, consideradas en el análisis se describen en la Tabla 1 (18 variables).
Las 18 variables se pegaron a las bases de datos con el porcentaje de fallecimientos por municipio y para cada una de las tres olas de la pandemia.
| 1) Grado promedio de escolaridad de la población de 15 años o más (GPEST) | 2) % Población económicamente activa de la población de 15 años o más (PEA) | 3) % Población sin seguridad social (SSS) |
| 4) Promedio de ocupantes por vivienda (POV) | 5) Promedio de hijos nacidos vivos (PHNV) | 6) % Población habla lengua indígena (PHLI) |
| 7) % Población con analfabetismo (ANALF) | 8) % Ocupantes en viviendas particulares sin drenaje ni excusado (SDE) | 9) % Ocupantes en viviendas particulares sin energía eléctrica (SEE) |
| 10) % Ocupantes en viviendas particulares sin agua entubada (SAE) | 11) % Ocupantes en viviendas particulares con piso de tierra (VPT) | 12) % Viviendas particulares con hacinamiento (VHAC) |
| 13) % Población en localidades con menos de 5000 habitantes (P5000) | 14) % Población masculina (POBMAS) | 15) % Población de 60 años y más (P60YM) |
| 16) % Población ocupada con ingresos de hasta 2 salarios mínimos (P2SM) | 17)% Población con diabetes (PDIAB) | 18) % Población con obesidad (POBES) |
6 Análisis exploratorio
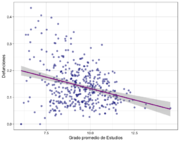
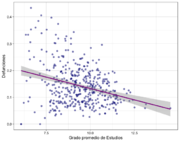
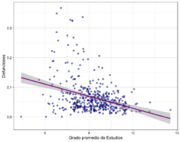
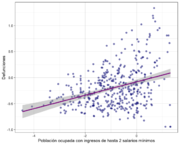
Una vez construidas nuestras bases de datos de trabajo, se realizó un análisis descriptivo exploratorio para detectar posibles asociaciones entre variables. A continuación se muestran un par de diagramas de dispersión en donde se presenta el porcentaje de fallecimientos por COVID-19 en los municipios del país contra el grado promedio de escolaridad y la población ocupada.
|
|
|
| (a) 1ra ola | (b) 2da ola | (c) 3ra ola |
| Figura 4: Porcentaje de fallecimientos () Vs grado promedio de escolaridad () a nivel municipal. | ||
|
|
|
| (a) 1ra ola | (b) 2da ola | (c) 3ra ola |
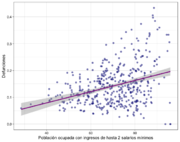
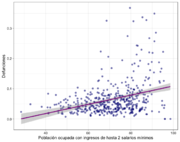
| Figura 5: Porcentaje de fallecimientos () Vs población ocupada con ingresos de hasta 2 salarios mínimos. () a nivel municipal. | ||
En las tres olas, es posible identificar que el riesgo de mortalidad por COVID–19:
- Disminuye en municipios con mayor grado de escolaridad. (Ver Figura 4)
- Aumenta en municipios con población ocupada con ingresos de hasta 2 salarios mínimos. (Ver Figura 5)
- Aumenta en municipios con mayor porcentaje viviendas con hacinamiento (no se muestra la gráfica).
- Aumenta en municipios con mayor promedio de ocupantes por vivienda (no se muestra la gráfica).
7 Ajuste de modelos y selección de variables
Con el objetivo de describir el riesgo de fallecimiento por COVID-19, en cada municipio del país, se ajustaron 15 modelos de RLM. Estos 15 modelos consideran a los 5 grupos de municipios construidos a partir del número de habitantes en cada municipio, así como las 3 olas de la pandemia (ver Figura 3). Adicionalmente, para identificar a las variables socioeconómicas que pudieran tener mayor relevancia para describir el riesgo de fallecimiento, también se realizó una selección de variables. La estrategia fue la de selección hacia adelante y hacia atrás, buscando la combinación de variables que minimizará el criterio de información de Akaike (AIC). Los resultados se muestran en la Tabla 2 para la primera ola, Tabla 3 segunda ola y Tabla 4 para la tercera ola.
| Grupos de acuerdo al tamaño de los municipios | |||||
| Variables | (1) | (2) | (3) | (4) | (5) |
| PDIAB | –0.692 (0.375) | ||||
| PEA | 0.306 (0.180) | –0.179 (0.120) | |||
| SSS | 0.110 (0.065) | 0.094 (0.042) | |||
| P60YM | 0.899 (0.379) | 0.588 (0.207) | |||
| POBES | 0.303 (0.160) | 0.677 (0.183) | |||
| PHNV | –7.612 (4.096) | ||||
| GPEST | –2.757 (1.302) | –3.849 (1.340) | |||
| PHLI | –0.104 (0.034) | ||||
| SDE | 1.126 (0.297) | 0.695 (0.224) | –0.531 (0.132) | ||
| SEE | –1.575 (0.925) | –1.340 (0.383) | –0.370 (0.191) | ||
| VHAC | 0.223 (0.072) | ||||
| ANALF | –0.605 (0.221) | 0.491 (0.150) | |||
| POBMAS | –2.197 (1.061) | ||||
| SAE | 0.293 (0.161) | 0.133 (0.084) | |||
| POV | –3.862 (1.166) | ||||
| P2SM | 0.348 (0.137) | 0.343 (0.111) | 0.204 (0.064) | 0.116 (0.039) | |
| Constant | –0.634 (10.633) | 21.505 (26.381) | 111.978 (55.307) | 1.721 (9.905) | 11.755 (4.120) |
| Observations | 429 | 428 | 428 | 428 | 429 |
| R | 0.060 | 0.089 | 0.084 | 0.054 | 0.214 |
| Adjusted R | 0.047 | 0.076 | 0.071 | 0.043 | 0.201 |
| Residual Std. Error | 26.479 | 21.779 | 17.019 | 12.608 | 6.613 |
| F Statistic | 4.506 | 6.847 | 6.435 | 4.837 | 16.365 |
| Note: | p0.1; p0.05; p0.01 | ||||
| Grupos de acuerdo al tamaño de los municipios | |||||
| Variables | (1) | (2) | (3) | (4) | (5) |
| POBES | 0.373 (0.158) | 0.247 (0.148) | 0.345 (0.185) | 0.330 (0.114) | |
| PHNV | 10.915 (4.571) | 12.035 (2.228) | |||
| VHAC | –0.245 (0.134) | –0.224 (0.072) | |||
| GPEST | 8.816 (2.547) | –3.906 (1.097) | –4.129 (1.302) | ||
| SSS | –0.228 (0.125) | 0.340 (0.049) | |||
| PEA | 0.234 (0.130) | ||||
| ANALF | 1.271 (0.346) | –0.440 (0.232) | |||
| PHLI | –0.093 (0.031) | ||||
| POV | –7.590 (3.607) | 7.875 (2.616) | –2.501 (1.454) | ||
| SDE | –0.425 (0.150) | ||||
| SAE | –0.388 (0.169) | 0.124 (0.069) | |||
| P2SM | 0.526 (0.217) | ||||
| P5000 | 0.078 (0.024) | 0.053 (0.025) | |||
| P60YM | 0.420 (0.254) | 1.269 (0.305) | |||
| POBMAS | –1.839 (1.073) | ||||
| Constant | –111.784 (42.096) | 50.139 (10.600) | 117.604 (56.096) | –41.898 (14.969) | –8.235 (5.528) |
| Observations | 444 | 444 | 443 | 444 | 444 |
| R | 0.072 | 0.029 | 0.047 | 0.093 | 0.214 |
| Adjusted R | 0.055 | 0.023 | 0.034 | 0.083 | 0.201 |
| Residual Std. Error | 29.452 | 23.999 | 17.433 | 12.719 | 8.196 |
| F Statistic | 4.213 | 4.408 | 3.594 | 9.005 | 16.939 |
| Note: | p0.1; p0.05; p0.01 | ||||
| Grupos de acuerdo al tamaño de los municipios | |||||
| Variables | (1) | (2) | (3) | (4) | (5) |
| POBES | –0.400 (0.141) | 0.319 (0.101) | |||
| PDIAB | 0.684 (0.398) | ||||
| ANALF | 0.526 (0.181) | –0.632 (0.229) | |||
| PHNV | 3.295 (2.324) | 7.694 (0.896) | |||
| POBMAS | 2.310 (0.716) | –1.610 (0.503) | |||
| VPT | –0.276 (0.152) | –0.121 (0.072) | |||
| GPEST | –2.631 (0.711) | –5.201 (1.106) | –3.481 (0.594) | ||
| PEA | 0.170 (0.105) | 0.206 (0.082) | |||
| SSS | 0.218 (0.067) | 0.299 (0.071) | 0.240 (0.045) | 0.184 (0.027) | |
| P60YM | 0.369 (0.234) | 0.139 (0.076) | |||
| POV | 3.762 (1.971) | 3.522 (1.899) | |||
| SAE | –0.209 (0.079) | 0.090 (0.036) | |||
| SDE | –0.121 (0.078) | –0.371 (0.073) | |||
| VHAC | 0.317 (0.183) | –0.253 (0.114) | –0.240 (0.078) | ||
| PHLI | 0.056 (0.038) | ||||
| P2SM | 0.162 (0.093) | 0.154 (0.093) | |||
| P5000 | 0.079 (0.020) | ||||
| Constant | –115.367 (34.148) | 6.903 (11.829) | 29.754 (15.378) | 65.262 (25.185) | –16.417 (2.180) |
| Observations | 462 | 461 | 461 | 461 | 461 |
| R | 0.064 | 0.082 | 0.141 | 0.274 | 0.253 |
| Adjusted R | 0.052 | 0.070 | 0.129 | 0.254 | 0.245 |
| Residual Std. Error | 22.685 | 14.747 | 14.246 | 8.737 | 4.864 |
| F Statistic | 5.186 | 6.789 | 12.378 | 14.086 | 30.866 |
| Note: | p0.1; p0.05; p0.01 | ||||
En todos los casos, se aprecia que los coeficientes de determinación, las de los modelos, son muy pequeñas. Es importante mencionar, que estamos trabajando datos reales y que el objetivo de este proyecto es identificar variables socioeconómicas que pudieran estar relacionadas con el riesgo de mortalidad en los municipios de México. Por lo tanto, nos concentramos sólo en los coeficientes de las variables seleccionadas por el AIC en cada caso.
Los coeficientes de regresión estimados son las pendientes del modelo de RLM, expresión 1, veamos como interpretarlos en un par de casos. Para la primera ola, si en algún municipio, de los grupos 2 ó 3, el grado promedio de escolaridad aumentara en 1 año. Entonces, las defunciones disminuirían en 2.76 % y 3.85 % respectivamente. Observando ahora los municipios en el grupo 4 en las tres olas, si el porcentaje de la población de 60 años y más aumentará en 1 %, entonces las defunciones aumentarían 0.59 % en la primera ola, 1.27 % en la segunda ola y 0.37 % en la tercera ola. Finalmente, es interesante observar que durante la tercera ola y para los municipios más grandes (grupo 5), si aumentara el promedio de hijos nacidos vivos en uno, entonces el porcentaje de defunciones aumentaría en 7.7%
Analizando los 15 modelos ajustados, se identificó que uno de los factores socio-económicos más relevantes fue el grado promedio de estudios y se observa que municipios con mayor grado de escolaridad presentaron menor riesgo de mortalidad por COVID-19. Principalmente, en municipios de los grupos 2, 3 y 4 donde se tiene una población mayor a 3,419 habitantes y menor a 45,399. A continuación, se determinó que las variables relacionadas con el empleo también influyeron fuertemente pero en un modo negativo. Es decir, si el porcentaje población económicamente activa aumentara en los municipios medianos (al menos en la segunda y tercera ola), entonces aumentaría el riesgo de fallecer. En el caso de los municipios con el porcentaje de población ocupada con ingresos de hasta 2 salarios mínimos más grandes, se observó un alto riesgo de mortalidad en la primera ola de la pandemia. Durante este periodo, muchas personas quedaron sin ingresos, principalmente las que vivían de la economía informal, que por lo mismo no contaban con seguridad social para atenderse; y aunado a la ignorancia y desconocimiento del virus, causando un alto grado de mortalidad, [2].
Para tener una visión global, se construyó la Tabla 5 que muestra las variables socioeconómicas que tuvieron algún grado de asociación (positiva o negativa) con el porcentaje de fallecimientos por COVID-19 en al menos dos modelos de cada ola de la pandemia.
| Variables – Fechas | 1ra ola (Junio 2020 - Agosto 2020) | 2da ola (Diciembre 2020 - Febrero 2021) | 3ra ola (Julio 2021 - Septiembre 2021) |
| Grado promedio de escolaridad de la población de 15 años o más | ✓ | ✓ | ✓ |
| % Población económicamente activa de la población de 15 años o más | ✓ | ✓ | |
| % Población sin seguridad social | ✓ | ✓ | ✓ |
| Promedio de ocupantes por vivienda | ✓ | ✓ | |
| Promedio de hijos nacidos vivos | ✓ | ✓ | |
| % Población habla lengua indígena | |||
| % Población con analfabetismo | ✓ | ✓ | ✓ |
| % Ocupantes en viviendas particulares sin drenaje ni excusado | ✓ | ✓ | |
| % Ocupantes en viviendas particulares sin energía eléctrica | ✓ | ||
| % Ocupantes en viviendas particulares sin agua entubada | ✓ | ✓ | ✓ |
| % Ocupantes en viviendas particulares con piso de tierra | |||
| % Viviendas particulares con hacinamiento | ✓ | ✓ | |
| % Población en localidades con menos de 5000 habitantes | ✓ | ||
| % Población masculina | ✓ | ||
| % Población de 60 años y más | ✓ | ✓ | ✓ |
| % Población ocupada con ingresos de hasta a 2 salarios mínimos | ✓ | ✓ | ✓ |
| % Población con diabetes | |||
| % Población con obesidad | ✓ | ✓ | ✓ |
Un primer detalle, que es fácil apreciar, es que el número de variables socio-económicas significativas fue aumentando conforme iba evolucionando la pandemia, a pesar de que el conocimiento acerca de la enfermedad aumentaba así como la vacunación. Esto puede deberse al aumento de casos positivos de COVID–19 que hubo en la segunda y tercer ola con respecto a la primera, Figura 1.
Los factores socioeconómicos fueron sumamente importantes para determinar como sería la evolución del paciente llegando a fallecer en algunos casos si no se contaba con algún servicio de salud, por eso la variable del porcentaje de población sin seguridad social resultó muy significativa, sobre todo en los municipios con mucha población. De la misma forma, si el promedio de hijos nacidos vivos es alto o en localidades con menos de 5,000 habitantes (que por lo general son zonas marginadas), se corre un mayor riesgo de fallecer por COVID-19. Si consideramos las condiciones de vivienda, las personas que residen en viviendas sin agua entubada resultan más afectadas en esta pandemia, principalmente en municipios donde la población es muy grande. Esto obviamente, pues el virus se transmite al tener contacto con él (mientras más grande la población mayor es el riesgo) siendo indispensable tener agua para lavarse las manos y sin ella, aumenta el riesgo.
Por lo que podemos concluir que las variables socioeconómicas más significativas e influyentes en las defunciones por estar presente en las 3 olas de contagios fueron el grado promedio de estudios, la población sin seguridad social, la población analfabeta, el porcentaje de ocupantes en viviendas sin agua entubada, la población de 60 años y más, la población ocupada con ingresos de hasta 2 salarios mínimos, y la población con obesidad. Las cuales influyeron para un mayor o menor número de defunciones de acuerdo a cada ola de la pandemia y a cada grupo poblacional.
8 Conclusiones
Analizando la Pandemia por COVID–19, sin considerar las condiciones de salud de la población, los datos ajustados con 15 modelos de RLM muestran que los factores socioeconómicos sí influyen en el riesgo de mortalidad por COVID-19, dependiendo la ola de la pandemia que se analice y el tamaño del municipio donde se encuentre una persona. De forma concisa, se identificó que el factor socioeconómico con mayor influencia es el grado promedio de estudios, ya que a mayor grado de escolaridad la probabilidad de fallecer por COVID-19 es menor. Principalmente en los municipios medianos (entre 3,419 y 45,399 habitantes) en donde el riesgo de mortalidad disminuiría, en promedio, 3.75% si se aumentara en una unidad el grado promedio de estudios.
En el trabajo de tesis que da origen a este artículo, también se hizo una predicción del riesgo de mortalidad para los municipios grandes de la cuarta ola de la pandemia. En este caso, se utilizó el modelo obtenido para los municipios grandes en la tercer ola. Esto no se presenta pues el objetivo principal era el de identificar factores socio-económicos que influyen en el riesgo de fallecer por COVID-19 que es el que se describe en este texto.
La pandemia representa un problema complejo ya que las condiciones entre cada ola fueron cambiando en el tiempo, sin embargo, las condiciones sociales y económicas no cambian a la misma velocidad. Por lo cual se necesitan enfocar esfuerzos en mejorar la educación a nivel nacional y la situación general en la que vive la población para que tenga una mejor resiliencia ante cualquier adversidad.
BIBLIOGRAFÍA
[1] Suárez V and Suarez Quezada M and Oros Ruiz S and Ronquillo De Jesús E. (2020) "Epidemiología de COVID-19 en México: del 27 de febrero al 30 de abril de 2020", Volume 220. Rev Clin Esp 8 463-471
[2] Universidad de California en San Francisco "La respuesta de México al Covid-19: Estudio de caso" https://globalhealthsciences.ucsf.edu/sites/globalhealthsciences.ucsf.edu/files/la_respuesta_de_mexico_al_covid_esp.pdf
[3] González-Pérez, Guillermo J.and Vega–López María G. and Romero-Valle, Samuel and Vega-López, Agustin and Cabrera-Pivaral, Carlos E. (2008) "Exclusión Social e Inequidad en Salud en México: Un análisis socio–espacial", Volume 10. Revista de salud pública. Revista de salud pública 1
[4] Montgomery, D. and Peck, E.A. and Vining, G.G. (2012) "Introduction to linear regression analysis". Wiley
[5] Allen M. P. (1997) "Understanding Regression Analysis". Plenum Press
[6] R Core Team. (2022) "R: A Language and Environment for Statistical Computing". R Foundation for Statistical Computing
[7] Wesberg, S. (1980) "Applied Linear Regression". Wiley, 4 Edition
[8] Akaike, H. (1974) "A new look at the statistical model identification", Volume 19. IEEE Transactions on Automatic Control 6 716-723
[9] W. N. Venables and B. D. Ripley. (2002) "Modern Applied Statistics with S". Springer, Fourth Edition
[10] Secretaría de Salud, Gobierno de México. (2020) "Datos Abiertos Dirección General de Epidemiología" https://www.gob.mx/salud/documentos/datos-abiertos-152127
[11] INEGI. (2021) "Principales resultados por localidad (ITER). Censo de Población y Vivienda 2020" https://www.inegi.org.mx/programas/ccpv/2020/default.html#Datos_abiertos
Document information
Published on 13/12/23
Submitted on 29/10/23
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?