(Created page with " <div id="_GoBack" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> <big>'''INTERFASE GID PER A LA GENERACIÓ PARAMÈTRICA DE GEOMETRIES TRENADES P...") |
|||
| Line 1: | Line 1: | ||
| + | ==Interfase GiD per a la generació paramètrica de geometries trenades per a l’apantallament de cables coaxials== | ||
| − | + | '''R. Méndez''', '''R. Isanta''', '''R. Otín''', '''O. Fruitos''' | |
| − | + | ||
| − | + | Centre Internacional de Mètodes Numèrics a l’Enginyeria - CIMNE Barcelona, Spain | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Centre Internacional de Mètodes Numèrics a l’Enginyeria | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | == | + | ==1 Introducció== |
<span style="text-align: center; font-size: 75%;">En aquest informe tècnic es presenta un programa que genera automàticament geometries trenades per a l’apantallament (shielding) de cables coaxials i que s’integra en l’entorn GiD. L’objectiu general d’aquest treball és desenvolupar una eina numèrica capaç de </span><span style="text-align: center; font-size: 75%;">generar la geometria inicial de la simulació electromagnètica. Aquesta simulació electromagnètica té com a propòsit calcular la transferència d’impedància d’aquests trenats d’apantallament. La transferència d’impedància és una</span><span style="text-align: center; font-size: 75%;"> magnitud que caracteritza l’eficàcia d’aquest apantallament. Una baixa transferència indica un bon apantallament. El desenvolupament d’aquesta eina numèrica ajudarà a optimitzar el disseny de trenats (com menys material, més bon apantallamen</span><span style="text-align: center; font-size: 75%;">t) i per arribar a comprendre bé la física del problema. A més a més, l’avantatge d’emprar una eina numèrica basada en el mètode dels elements finits en lloc de càlculs analítics és que se serà capaç d’aplicar per materials i geometries generals</span><span style="text-align: center; font-size: 75%;"> i al mateix temps complexes. L’eina que es vol costumitzar es diu ERMES (Electric Field Regularized Maxwell Equations with Singularities), i és un codi d’elements finits que empra GiD [1] com a pre i post processador. Fins al moment de la elaboració del present inform</span><span style="text-align: center; font-size: 75%;">e, s’està desenvolupant l’eina de generació de geometria per separat d’ERMES [4]. </span> | <span style="text-align: center; font-size: 75%;">En aquest informe tècnic es presenta un programa que genera automàticament geometries trenades per a l’apantallament (shielding) de cables coaxials i que s’integra en l’entorn GiD. L’objectiu general d’aquest treball és desenvolupar una eina numèrica capaç de </span><span style="text-align: center; font-size: 75%;">generar la geometria inicial de la simulació electromagnètica. Aquesta simulació electromagnètica té com a propòsit calcular la transferència d’impedància d’aquests trenats d’apantallament. La transferència d’impedància és una</span><span style="text-align: center; font-size: 75%;"> magnitud que caracteritza l’eficàcia d’aquest apantallament. Una baixa transferència indica un bon apantallament. El desenvolupament d’aquesta eina numèrica ajudarà a optimitzar el disseny de trenats (com menys material, més bon apantallamen</span><span style="text-align: center; font-size: 75%;">t) i per arribar a comprendre bé la física del problema. A més a més, l’avantatge d’emprar una eina numèrica basada en el mètode dels elements finits en lloc de càlculs analítics és que se serà capaç d’aplicar per materials i geometries generals</span><span style="text-align: center; font-size: 75%;"> i al mateix temps complexes. L’eina que es vol costumitzar es diu ERMES (Electric Field Regularized Maxwell Equations with Singularities), i és un codi d’elements finits que empra GiD [1] com a pre i post processador. Fins al moment de la elaboració del present inform</span><span style="text-align: center; font-size: 75%;">e, s’està desenvolupant l’eina de generació de geometria per separat d’ERMES [4]. </span> | ||
| Line 123: | Line 60: | ||
<span id='_Toc255810303'></span> | <span id='_Toc255810303'></span> | ||
| − | == | + | ==2 Generació dels trenats== |
<span id='_Toc255810304'></span> | <span id='_Toc255810304'></span> | ||
| − | === | + | ===2.1 Informació genèrica=== |
<span style="text-align: center; font-size: 75%;">Alguns paràmetres del disseny del cable són comunes per a forats circulars i romboïdals. A continuació es comenta i representa sobre un exemple cada un d’ells.</span> | <span style="text-align: center; font-size: 75%;">Alguns paràmetres del disseny del cable són comunes per a forats circulars i romboïdals. A continuació es comenta i representa sobre un exemple cada un d’ells.</span> | ||
| Line 172: | Line 109: | ||
<span id='_Toc255810305'></span> | <span id='_Toc255810305'></span> | ||
| − | === | + | ===2.2 Forats circulars=== |
<span style="text-align: center; font-size: 75%;">Els paràmetres específics per als forats circulars són un: el seu diàmetre. En la finestra d’entrada de dades: Hole D.</span> | <span style="text-align: center; font-size: 75%;">Els paràmetres específics per als forats circulars són un: el seu diàmetre. En la finestra d’entrada de dades: Hole D.</span> | ||
| Line 196: | Line 133: | ||
<span id='_Toc255810306'></span> | <span id='_Toc255810306'></span> | ||
| − | === | + | ===2.3 Forats romboïdals=== |
<span style="text-align: center; font-size: 75%;">Els paràmetres específics per als forats romboïdals són dos: la seva diagonal principal (paral·lela a l’eix del cable) i la seva altra diagonal (perpendicular a l’eix del cable). Els assignem els noms '''a''' i '''b'''.</span> | <span style="text-align: center; font-size: 75%;">Els paràmetres específics per als forats romboïdals són dos: la seva diagonal principal (paral·lela a l’eix del cable) i la seva altra diagonal (perpendicular a l’eix del cable). Els assignem els noms '''a''' i '''b'''.</span> | ||
| Line 220: | Line 157: | ||
<span id='_Toc255810307'></span> | <span id='_Toc255810307'></span> | ||
| − | === | + | ===2.4 Forats romboïdals tipus 2=== |
<span id='OLE_LINK1'></span><span style="text-align: center; font-size: 75%;">Els paràmetres per a aquest mòdul són els més comuns amb pel què fa referència a les dades proporcionades per fabricants. Els paràmetres són els següents:</span> | <span id='OLE_LINK1'></span><span style="text-align: center; font-size: 75%;">Els paràmetres per a aquest mòdul són els més comuns amb pel què fa referència a les dades proporcionades per fabricants. Els paràmetres són els següents:</span> | ||
| Line 252: | Line 189: | ||
<span id='_Toc255810308'></span> | <span id='_Toc255810308'></span> | ||
| − | === | + | ===2.5 Forats romboïdals tipus 2- Simetria=== |
<span style="text-align: center; font-size: 75%;">Aquest mòdul és idèntic a l’anterior. La única diferència resideix en la geometria de sortida, que serà la mínima que permet aprofitar les simetries del problema.</span> | <span style="text-align: center; font-size: 75%;">Aquest mòdul és idèntic a l’anterior. La única diferència resideix en la geometria de sortida, que serà la mínima que permet aprofitar les simetries del problema.</span> | ||
| Line 258: | Line 195: | ||
<span id='_Toc255810309'></span> | <span id='_Toc255810309'></span> | ||
| − | === | + | ===2.6 Arxius Batch=== |
<span style="text-align: center; font-size: 75%;">Per a crear la geometria es genera un arxiu batch amb les instruccions GiD que permeten la seva creació.</span> | <span style="text-align: center; font-size: 75%;">Per a crear la geometria es genera un arxiu batch amb les instruccions GiD que permeten la seva creació.</span> | ||
| Line 276: | Line 213: | ||
<span id='_Toc255810310'></span> | <span id='_Toc255810310'></span> | ||
| − | == | + | ==3 Tutorial 1: Ús de l’eina== |
<span style="text-align: center; font-size: 75%;">Iniciar GiD i carregar el ''Problem type'' '''Braided wires 1.5.1'''</span> | <span style="text-align: center; font-size: 75%;">Iniciar GiD i carregar el ''Problem type'' '''Braided wires 1.5.1'''</span> | ||
| Line 384: | Line 321: | ||
<span id='_Toc255810311'></span> | <span id='_Toc255810311'></span> | ||
| − | == | + | ==4 Tutorial 2: Simulació amb ERMES partint de Braided Wires 1.5.1== |
<span style="text-align: center; font-size: 75%;">En aquest apartat, s’explicarà l’ús que es fa de la geometria generada per l’eina de creació paramètrica dins del programa electromagnètic ERMES en un cas concret de càlcul. Aquest càlcul correspon a un exemple que es mostra al paper [2] i serveix per comparar el comportament de l’eina de generació de geometries acoblada amb el càlcul pel mètode dels elements finits que realitza ERMES respecte dels resultats obtinguts en [2].</span><span style="text-align: center; font-size: 75%;">A la següent figura es mostra el patró del teixit desenvolupat en un pla (extret de [2]).</span> | <span style="text-align: center; font-size: 75%;">En aquest apartat, s’explicarà l’ús que es fa de la geometria generada per l’eina de creació paramètrica dins del programa electromagnètic ERMES en un cas concret de càlcul. Aquest càlcul correspon a un exemple que es mostra al paper [2] i serveix per comparar el comportament de l’eina de generació de geometries acoblada amb el càlcul pel mètode dels elements finits que realitza ERMES respecte dels resultats obtinguts en [2].</span><span style="text-align: center; font-size: 75%;">A la següent figura es mostra el patró del teixit desenvolupat en un pla (extret de [2]).</span> | ||
| Line 398: | Line 335: | ||
<span id='_Toc255810312'></span> | <span id='_Toc255810312'></span> | ||
| − | === | + | ===4.1 Ús de la eina de generació de geometria=== |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 420: | Line 357: | ||
<span id='_Toc255810313'></span> | <span id='_Toc255810313'></span> | ||
| − | === | + | ===4.2 Assignació de materials=== |
<span style="text-align: center; font-size: 75%;">A continuació (figura 22) es mostra l’assignació de materials al model. En verd s’ha informat el material vacuum en per modelar l’aire que envolta el model i que marca el límit del problema. En blau es dibuixa la part corresponent als forats on no hi ha el trenat. El material té les mateixes característiques que en el cas del vacuum. En lila, el material poliuretano que treballa de dielèctric. Finalment, el material de color blanc és coure. Aquest és el que apantalla i també es troba en el nucli del cable coaxial.</span> | <span style="text-align: center; font-size: 75%;">A continuació (figura 22) es mostra l’assignació de materials al model. En verd s’ha informat el material vacuum en per modelar l’aire que envolta el model i que marca el límit del problema. En blau es dibuixa la part corresponent als forats on no hi ha el trenat. El material té les mateixes característiques que en el cas del vacuum. En lila, el material poliuretano que treballa de dielèctric. Finalment, el material de color blanc és coure. Aquest és el que apantalla i també es troba en el nucli del cable coaxial.</span> | ||
| Line 434: | Line 371: | ||
<span id='_Toc255810314'></span> | <span id='_Toc255810314'></span> | ||
| − | === | + | ===4.3 Assignació de densitat de corrent=== |
<span style="text-align: center; font-size: 75%;">El següent pas és l’assignació de densitats de corrent a l’aire que envolta el cable coaxial, justament al llarg de la capa “vacuum” anteriorment mencionada. En aquest cas es tracta d’un valor arbitrari ja que es vol trobar la transferència d’impedància que passa al nucli. S’aplica a una </span><span style="text-align: center; font-size: 75%;">superfície que està en pla XY, perpendicular a la direcció Z d’assignació de la densitat de corrent.</span> | <span style="text-align: center; font-size: 75%;">El següent pas és l’assignació de densitats de corrent a l’aire que envolta el cable coaxial, justament al llarg de la capa “vacuum” anteriorment mencionada. En aquest cas es tracta d’un valor arbitrari ja que es vol trobar la transferència d’impedància que passa al nucli. S’aplica a una </span><span style="text-align: center; font-size: 75%;">superfície que està en pla XY, perpendicular a la direcció Z d’assignació de la densitat de corrent.</span> | ||
| Line 450: | Line 387: | ||
<span id='_Toc255810315'></span> | <span id='_Toc255810315'></span> | ||
| − | === | + | ===4.4 Selecció de les superfícies d’integració=== |
<span style="text-align: center; font-size: 75%;">Per poder determinar la transferència d’impedància al nucli, és necessari integrar els valors de camp elèctric i d’intensitat de les superfícies que es troben pintades en groc i en verd a la figura 25. D’aquesta manera es pot calcular les impedàncies de les dues </span><span style="text-align: center; font-size: 75%;">superfícies i trobar la relació entre ambdues impedàncies. Per calcular aquestes integrals és necessari prémer el botó assign de la finestra de la figura 24 i seleccionar les superfícies pintades de verd i de groc a la dreta de la figura 25</span><span style="text-align: center; font-size: 75%;">. </span> | <span style="text-align: center; font-size: 75%;">Per poder determinar la transferència d’impedància al nucli, és necessari integrar els valors de camp elèctric i d’intensitat de les superfícies que es troben pintades en groc i en verd a la figura 25. D’aquesta manera es pot calcular les impedàncies de les dues </span><span style="text-align: center; font-size: 75%;">superfícies i trobar la relació entre ambdues impedàncies. Per calcular aquestes integrals és necessari prémer el botó assign de la finestra de la figura 24 i seleccionar les superfícies pintades de verd i de groc a la dreta de la figura 25</span><span style="text-align: center; font-size: 75%;">. </span> | ||
| Line 468: | Line 405: | ||
<span id='_Toc255810316'></span> | <span id='_Toc255810316'></span> | ||
| − | === | + | ===4.5 Paràmetres de càlcul=== |
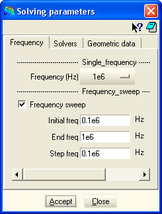
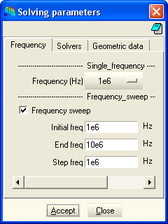
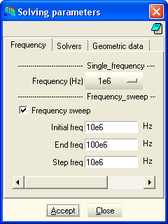
<span style="text-align: center; font-size: 75%;">En la figura 26 es mostren les diferents pestanyes dels paràmetres de càlcul que s’han d’assignar al programa ERMES per tal de calcular el model de forma adequada. En el cas de la pestanya de d’esquerra, es tracta de l’assignació del rang de freqüències que escombra el programa</span><span style="text-align: center; font-size: 75%;">. </span> | <span style="text-align: center; font-size: 75%;">En la figura 26 es mostren les diferents pestanyes dels paràmetres de càlcul que s’han d’assignar al programa ERMES per tal de calcular el model de forma adequada. En el cas de la pestanya de d’esquerra, es tracta de l’assignació del rang de freqüències que escombra el programa</span><span style="text-align: center; font-size: 75%;">. </span> | ||
| Line 498: | Line 435: | ||
<span id='_Toc255810317'></span> | <span id='_Toc255810317'></span> | ||
| − | === | + | ===4.6 Paràmetres de càlcul=== |
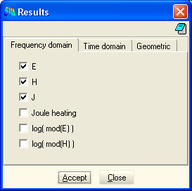
<span style="text-align: center; font-size: 75%;">El següent pas és seleccionar els paràmetres que es desitja obtenir de ERMES. En aquest cas és important que estiguin seleccionats el camp elèctric i la densitat elèctrica en la pestanya de domini de la freqüència. En cas de no seleccionar algun d’aquest dos resultats que es volen, el programa no podrà extreure la informació necessària per obtenir la transferència d’impedància.</span> | <span style="text-align: center; font-size: 75%;">El següent pas és seleccionar els paràmetres que es desitja obtenir de ERMES. En aquest cas és important que estiguin seleccionats el camp elèctric i la densitat elèctrica en la pestanya de domini de la freqüència. En cas de no seleccionar algun d’aquest dos resultats que es volen, el programa no podrà extreure la informació necessària per obtenir la transferència d’impedància.</span> | ||
| Line 516: | Line 453: | ||
<span id='_Toc255810318'></span> | <span id='_Toc255810318'></span> | ||
| − | === | + | ===4.7 Malla=== |
<span style="text-align: center; font-size: 75%;">Els elements amb què treballa el programa ERMES són els tetraedres. En aquest cas s’ha buscat que hi hagi una malla molt fina en les superfícies objecte de ser integrades el programa per obtenir-ne la impedància. En la resta del model la malla és força uniforme. En aquest cas el nombre de nodes ascendeix a 10275 i el nombre d’elements a 52121. </span> | <span style="text-align: center; font-size: 75%;">Els elements amb què treballa el programa ERMES són els tetraedres. En aquest cas s’ha buscat que hi hagi una malla molt fina en les superfícies objecte de ser integrades el programa per obtenir-ne la impedància. En la resta del model la malla és força uniforme. En aquest cas el nombre de nodes ascendeix a 10275 i el nombre d’elements a 52121. </span> | ||
| Line 530: | Line 467: | ||
<span id='_Toc255810319'></span> | <span id='_Toc255810319'></span> | ||
| − | === | + | ===4.8 Resultats obtinguts=== |
<span style="text-align: center; font-size: 75%;">A continuació es mostren alguns dels resultats que el programa escriu als arxius amb extensió “.info”. Es tractra dels resultats de les integrals que efectua el programa en les 2 superfícies que s’han assignat anteriorment. </span> | <span style="text-align: center; font-size: 75%;">A continuació es mostren alguns dels resultats que el programa escriu als arxius amb extensió “.info”. Es tractra dels resultats de les integrals que efectua el programa en les 2 superfícies que s’han assignat anteriorment. </span> | ||
| Line 548: | Line 485: | ||
<span id='_Toc255810320'></span> | <span id='_Toc255810320'></span> | ||
| − | === | + | ===4.9 Càlcul de la impedància transferida en funció de la freqüència=== |
<span style="text-align: center; font-size: 75%;">Pel què fa a l’aplicació en Matlab, genera un llistat de la impedància transferida respecte de la freqüència. A continuació es reprodueixen el resultats obtinguts per l’exemple cas d’estudi.</span> | <span style="text-align: center; font-size: 75%;">Pel què fa a l’aplicació en Matlab, genera un llistat de la impedància transferida respecte de la freqüència. A continuació es reprodueixen el resultats obtinguts per l’exemple cas d’estudi.</span> | ||
| Line 628: | Line 565: | ||
<span id='_Toc255810321'></span> | <span id='_Toc255810321'></span> | ||
| − | == | + | ==5. Referències bibliogràfiques== |
<span style="text-align: center; font-size: 75%;">[1] [http://www.gidhome.com www.gidhome.com] </span> | <span style="text-align: center; font-size: 75%;">[1] [http://www.gidhome.com www.gidhome.com] </span> | ||
Revision as of 16:30, 26 January 2017
Interfase GiD per a la generació paramètrica de geometries trenades per a l’apantallament de cables coaxials
R. Méndez, R. Isanta, R. Otín, O. Fruitos
Centre Internacional de Mètodes Numèrics a l’Enginyeria - CIMNE Barcelona, Spain
1 Introducció
En aquest informe tècnic es presenta un programa que genera automàticament geometries trenades per a l’apantallament (shielding) de cables coaxials i que s’integra en l’entorn GiD. L’objectiu general d’aquest treball és desenvolupar una eina numèrica capaç de generar la geometria inicial de la simulació electromagnètica. Aquesta simulació electromagnètica té com a propòsit calcular la transferència d’impedància d’aquests trenats d’apantallament. La transferència d’impedància és una magnitud que caracteritza l’eficàcia d’aquest apantallament. Una baixa transferència indica un bon apantallament. El desenvolupament d’aquesta eina numèrica ajudarà a optimitzar el disseny de trenats (com menys material, més bon apantallament) i per arribar a comprendre bé la física del problema. A més a més, l’avantatge d’emprar una eina numèrica basada en el mètode dels elements finits en lloc de càlculs analítics és que se serà capaç d’aplicar per materials i geometries generals i al mateix temps complexes. L’eina que es vol costumitzar es diu ERMES (Electric Field Regularized Maxwell Equations with Singularities), i és un codi d’elements finits que empra GiD [1] com a pre i post processador. Fins al moment de la elaboració del present informe, s’està desenvolupant l’eina de generació de geometria per separat d’ERMES [4].
Per calcular la impedància de transferència, ERMES necessita la geometria de GiD del trenat d’apantallament. La generació d’aquestes geometries és, de lluny, la tasca que més temps consumeix en el temps total de procés de computació.Aquest és el motiu pel qual necessitem un programa capaç de fer aquestes geometries automàticament. En aquest document es presenta un mòdul bàsic que genera tubs perforats. En un futur, aquest programa s’estendrà a la generació de geometries trenades reals.
El generador presentat aquí, està completament integrat dins de GiD i té una interfase amigable. Després d’introduir els paràmetres del tub perforat en una finestra, es crea la geometria. Llavors, aquesta geometria està preparada per ser emprada per ERMES. El llenguatge TCL-TK i els TKWITGETS han estat emprats per fer les finestres on l’usuari interactua, mentre la generació de la geometria és gestionada amb un codi C++ i importada a GiD com a arxiu batch.
Aquesta interfase permet la creació de la geometria simplificada d’un cable trenat. Per aquest motiu es proporciona a l’usuari unes finestres on definir els paràmetres d’aquest trenat, que posteriorment es definiran.
Es proposen diferents opcions per a la creació de la geometria.
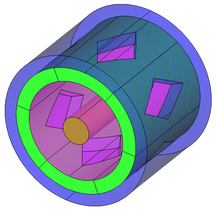
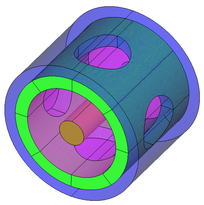
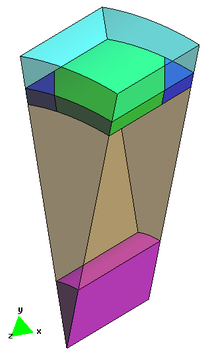
- 1. La primera simplificació geomètrica del trenat consisteix en una superfície cilíndrica perforada, corresponent a les zones no cobertes per el trenat. De moment poden definir-se forats tant circulars com romboïdals (aquests últims sempre que tinguin una diagonal alineada amb l’eix del cable).
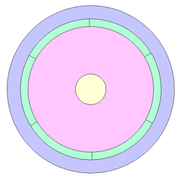
La geometria obtinguda consta de vàries parts: el recobriment (en verd), el nucli (en marró), el dielèctric (en rosa), els forats (en blau clar) i la zona de definició d’excitacions de contorno (en blau fosc).
Figura 1 - Exemple de geometria amb forat romboidal
Figura 2 - Exemple de figura amb forat circular
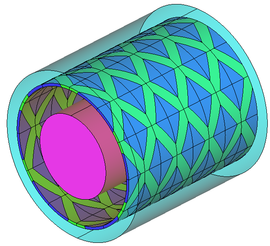
- 2. La segona opció és bastant més fidel a la realitat. En ella es crea una geometria simplificada del propi trenat.
A l’igual que en l’apartat anterior, la geometria consta d’un recobriment (en verd), un nucli (en rosa), un dielèctric (en marró), forats (en blau fosc) i una zona de definició d’excitacions de contorn (en blau clar).
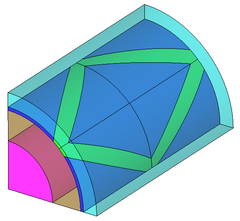
- 3. La tercera i última opció permet la creació d’una geometria com la anterior. No es genera tot el model sinó la mínima part que permet l’aplicació de propietats de simetria al problema.
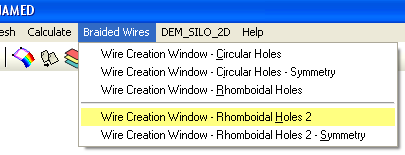
Per a usar aquesta interfase n’hi ha prou amb carregar el Problem type Braided wires 1.5.1. Apareixerà a continuació una nova pestanya de menú amb els diferents mòduls o opcions.
2 Generació dels trenats
2.1 Informació genèrica
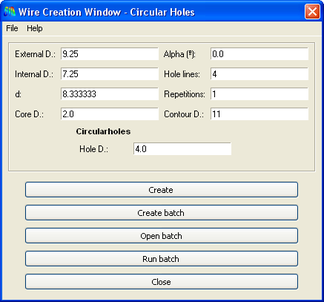
Alguns paràmetres del disseny del cable són comunes per a forats circulars i romboïdals. A continuació es comenta i representa sobre un exemple cada un d’ells.
- * External D.: Diàmetre extern del recobriment.
- * Internal D.: Diàmetre intern del recobriment.
- * d: Longitud de cada porció periòdica.
- * Core D: Diàmetre del nucli.
- * Alpha: Angle format per la línia de forats (Hole line).
- * Hole lines: Número de línies de forats.
- * Repetitions: Repeticions de la porció periòdica.
- * Contour D.: Diàmetre del cilindre de contorn.
Figura 6 - Vista lateral de la peça generada mitjançant la finestra de la figura 5
2.2 Forats circulars
Els paràmetres específics per als forats circulars són un: el seu diàmetre. En la finestra d’entrada de dades: Hole D.
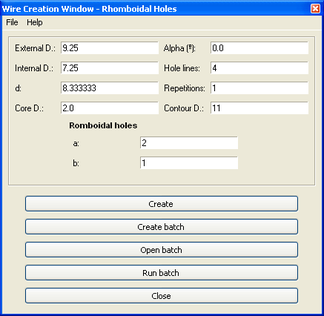
2.3 Forats romboïdals
Els paràmetres específics per als forats romboïdals són dos: la seva diagonal principal (paral·lela a l’eix del cable) i la seva altra diagonal (perpendicular a l’eix del cable). Els assignem els noms a i b.
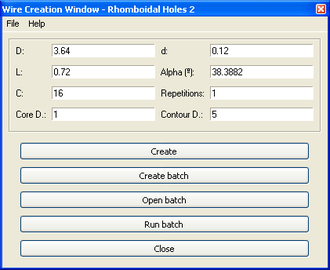
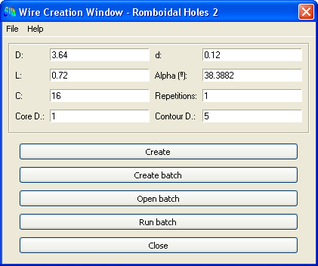
2.4 Forats romboïdals tipus 2
Els paràmetres per a aquest mòdul són els més comuns amb pel què fa referència a les dades proporcionades per fabricants. Els paràmetres són els següents:
- * D: Diàmetre intern del recobriment.
- * L: Amplada de les vetes.
- * C: Nombre de vetes.
- * Core D: Diàmetre del nucli.
- * d: Gruix del cable de recobriment.
- * Alpha: Angle de la veta respecte de l’eix principal del cable.
- * Repetitions: Repeticions de la porció periòdica.
- * Contour D.: Diàmetre del cilindre de contorn.
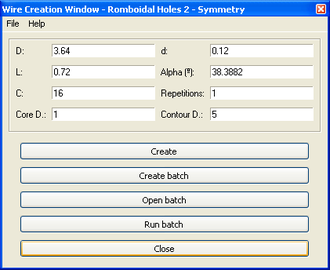
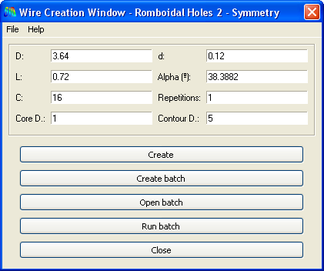
2.5 Forats romboïdals tipus 2- Simetria
Aquest mòdul és idèntic a l’anterior. La única diferència resideix en la geometria de sortida, que serà la mínima que permet aprofitar les simetries del problema.
2.6 Arxius Batch
Per a crear la geometria es genera un arxiu batch amb les instruccions GiD que permeten la seva creació.
És possible editar aquest arxiu batch una vegada generat i abans d’executar-lo. Per a aquest motiu existeixen els botons “Create batch”, “Open batch” i “Run Batch”.
3 Tutorial 1: Ús de l’eina
Iniciar GiD i carregar el Problem type Braided wires 1.5.1
Apareix una nova pestanya de menú “Braided Wires”. En ella seleccionem Wire Creation Window – Romboidal Holes 2.
Usarem les següents dades per a crear la geometria corresponent a l’exemple descrit a la referència [2]:
:* Radi intern del recobriment:
|
7,28 mm
6 16 0,12 mm 38,39 º |
Per tant els paràmetres corresponents en la Wire Creation Window seran:
:* D:
|
7.28
0.72 16 5 |
:* d:
|
0.12
38.39 º 1 8 |
Podem polsar el botó “Create” per a obtenir la següent geometria:
Si es vol una longitud major de cable s’ha de modificar el paràmetre Repetitions. La següent figura mostra la mateixa geometria per a un valor de 8 de tal paràmetre:
Si en lloc de crear directament la geometria volem modificar directament polsant “Create batch” creem l’arxiu batch per a crear dita geometria, que podem obrir polsant “Open batch”.
Una vegada fetes les modificacions en l’arxiu batch el guardem i tanquem, i polsem la tecla “Run batch”. Amb això es genera en el GiD la geometria modificada.
4 Tutorial 2: Simulació amb ERMES partint de Braided Wires 1.5.1
En aquest apartat, s’explicarà l’ús que es fa de la geometria generada per l’eina de creació paramètrica dins del programa electromagnètic ERMES en un cas concret de càlcul. Aquest càlcul correspon a un exemple que es mostra al paper [2] i serveix per comparar el comportament de l’eina de generació de geometries acoblada amb el càlcul pel mètode dels elements finits que realitza ERMES respecte dels resultats obtinguts en [2].A la següent figura es mostra el patró del teixit desenvolupat en un pla (extret de [2]).
4.1 Ús de la eina de generació de geometria
A partir d’aquest moment, es carrega el Problem type d’ERMES i comença l’assignació de les diferents condicions de contorn electromagnètiques.
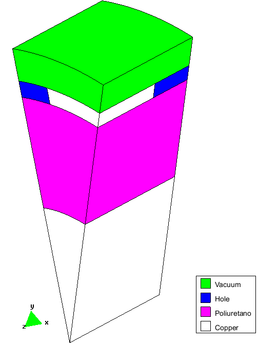
4.2 Assignació de materials
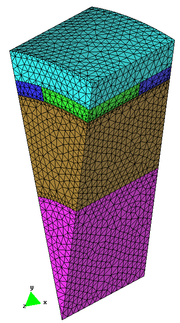
A continuació (figura 22) es mostra l’assignació de materials al model. En verd s’ha informat el material vacuum en per modelar l’aire que envolta el model i que marca el límit del problema. En blau es dibuixa la part corresponent als forats on no hi ha el trenat. El material té les mateixes característiques que en el cas del vacuum. En lila, el material poliuretano que treballa de dielèctric. Finalment, el material de color blanc és coure. Aquest és el que apantalla i també es troba en el nucli del cable coaxial.
4.3 Assignació de densitat de corrent
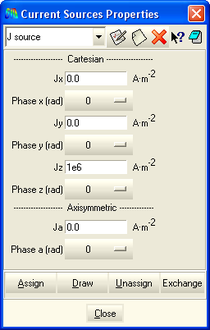
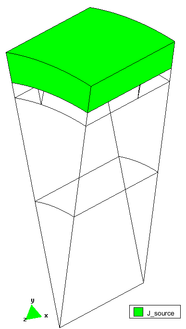
El següent pas és l’assignació de densitats de corrent a l’aire que envolta el cable coaxial, justament al llarg de la capa “vacuum” anteriorment mencionada. En aquest cas es tracta d’un valor arbitrari ja que es vol trobar la transferència d’impedància que passa al nucli. S’aplica a una superfície que està en pla XY, perpendicular a la direcció Z d’assignació de la densitat de corrent.
Figura 23 – Finestra d’introducció de paràmetres de densitats de corrent
Figura 24 - Assignació de densitats de corrent
4.4 Selecció de les superfícies d’integració
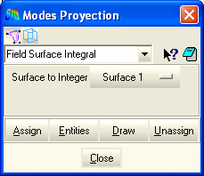
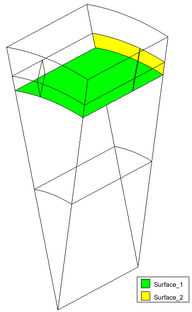
Per poder determinar la transferència d’impedància al nucli, és necessari integrar els valors de camp elèctric i d’intensitat de les superfícies que es troben pintades en groc i en verd a la figura 25. D’aquesta manera es pot calcular les impedàncies de les dues superfícies i trobar la relació entre ambdues impedàncies. Per calcular aquestes integrals és necessari prémer el botó assign de la finestra de la figura 24 i seleccionar les superfícies pintades de verd i de groc a la dreta de la figura 25.
4.5 Paràmetres de càlcul
En la figura 26 es mostren les diferents pestanyes dels paràmetres de càlcul que s’han d’assignar al programa ERMES per tal de calcular el model de forma adequada. En el cas de la pestanya de d’esquerra, es tracta de l’assignació del rang de freqüències que escombra el programa.
..
En les imatges que es mostren a continuació, hi ha dos rangs diferents de freqüències: De 1 a 10 MHz i de 10 a 100 MHz. Aquest estudi pretén conèixer la variació de l’apantallament en funció de les freqüències de les senyals d’interferència.
4.6 Paràmetres de càlcul
El següent pas és seleccionar els paràmetres que es desitja obtenir de ERMES. En aquest cas és important que estiguin seleccionats el camp elèctric i la densitat elèctrica en la pestanya de domini de la freqüència. En cas de no seleccionar algun d’aquest dos resultats que es volen, el programa no podrà extreure la informació necessària per obtenir la transferència d’impedància.
4.7 Malla
Els elements amb què treballa el programa ERMES són els tetraedres. En aquest cas s’ha buscat que hi hagi una malla molt fina en les superfícies objecte de ser integrades el programa per obtenir-ne la impedància. En la resta del model la malla és força uniforme. En aquest cas el nombre de nodes ascendeix a 10275 i el nombre d’elements a 52121.
4.8 Resultats obtinguts
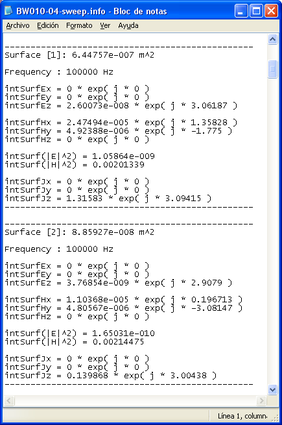
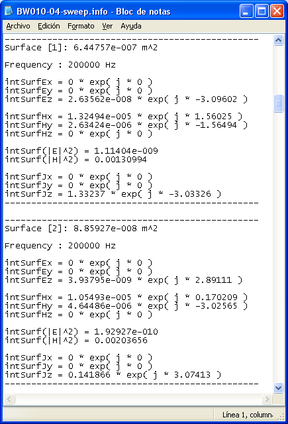
A continuació es mostren alguns dels resultats que el programa escriu als arxius amb extensió “.info”. Es tractra dels resultats de les integrals que efectua el programa en les 2 superfícies que s’han assignat anteriorment.
A més a més de generar aquests arxius, el programa ordena aquesta informació en format de matriu per poder treballar posteriorment mitjançat una aplicació en Matlab®. Concretament es generen 2 arxius (Surf1.dat i Surf2.dat), un per a cada superfície.
4.9 Càlcul de la impedància transferida en funció de la freqüència
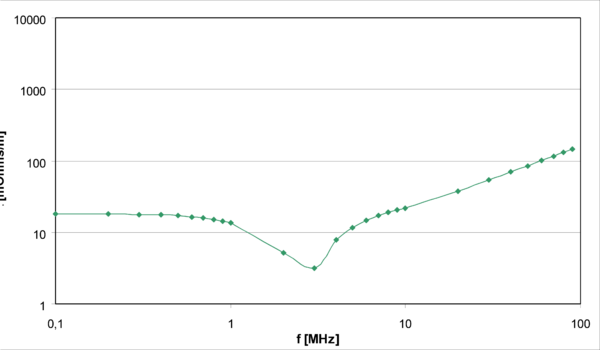
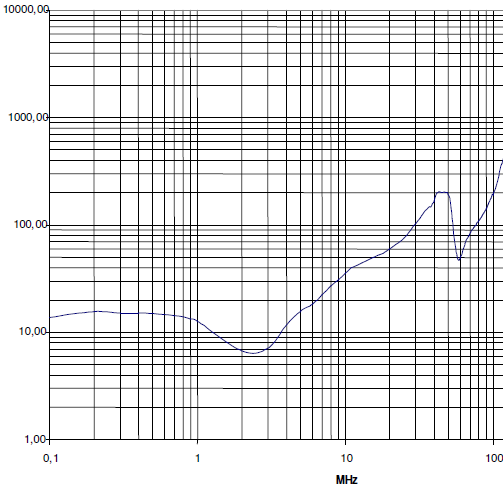
Pel què fa a l’aplicació en Matlab, genera un llistat de la impedància transferida respecte de la freqüència. A continuació es reprodueixen el resultats obtinguts per l’exemple cas d’estudi.
f = 0.100000 MHz |Zt| = 18.024440 mOhms/m
f = 0.200000 MHz |Zt| = 18.008985 mOhms/m
f = 0.300000 MHz |Zt| = 17.826732 mOhms/m
f = 0.400000 MHz |Zt| = 17.467782 mOhms/m
f = 0.500000 MHz |Zt| = 16.981435 mOhms/m
f = 0.600000 MHz |Zt| = 16.400470 mOhms/m
f = 0.700000 MHz |Zt| = 15.743705 mOhms/m
f = 0.800000 MHz |Zt| = 15.025441 mOhms/m
f = 0.900000 MHz |Zt| = 14.258094 mOhms/m
f = 1.000000 MHz |Zt| = 13.453255 mOhms/m
f = 1.000000 MHz |Zt| = 13.453186 mOhms/m
f = 2.000000 MHz |Zt| = 5.211261 mOhms/m
f = 3.000000 MHz |Zt| = 3.158555 mOhms/m
f = 4.000000 MHz |Zt| = 7.882612 mOhms/m
f = 5.000000 MHz |Zt| = 11.715349 mOhms/m
f = 6.000000 MHz |Zt| = 14.656036 mOhms/m
f = 7.000000 MHz |Zt| = 16.966087 mOhms/m
f = 8.000000 MHz |Zt| = 18.856751 mOhms/m
f = 9.000000 MHz |Zt| = 20.491335 mOhms/m
f = 10.000000 MHz |Zt| = 21.985356 mOhms/m
f = 10.000000 MHz |Zt| = 21.985552 mOhms/m
f = 20.000000 MHz |Zt| = 37.434550 mOhms/m
f = 30.000000 MHz |Zt| = 54.032300 mOhms/m
f = 40.000000 MHz |Zt| = 69.801426 mOhms/m
f = 50.000000 MHz |Zt| = 85.175696 mOhms/m
f = 60.000000 MHz |Zt| = 100.468521 mOhms/m
f = 70.000000 MHz |Zt| = 115.614677 mOhms/m
f = 80.000000 MHz |Zt| = 130.471740 mOhms/m
f = 90.000000 MHz |Zt| = 144.948986 mOhms/m
A continuació es mostren dues gràfiques. La gràfica 2 és la que mostra els valors experimentals publicats en la referència [2]. La gràfica 1 és la obtinguda mitjançant ERMES. Es tracta de gràfiques de la impedància transferida vs. freqüència.
La correspondència és millor per a valors de freqüència inferiors a 50 MHz ja que el programa no captura la oscil·lació experimental entre els valors 50 i 100 MHz. En termes generals, la tendència d’ambdues corves és similar. No obstant, es posa de manifest és que en la vall que apareix en el gràfic 1 és més pronunciada que en el cas del gràfic 2 i que aquesta està desplaçada a la dreta. Les discrepàncies observades són degudes bàsicament al modelitzat dels forats que presenta la geometria analitzada ja que Braided Wires realitza els forats de forma cilíndrica i en el cas de la geometria real les parets dels forats són normals a la superfície on es localitzen. És a dir, que en el cas dels forats de la geometria real el diàmetre de la part exterior dels forats té una mida més gran que en la part interna dels forats. En la geometria que prové de Braided Wires ambdós tamanys són iguals.
5. Referències bibliogràfiques
[1] www.gidhome.com
[2] F. Calluso, M. Casti, G. Ferrero, L. Zanero, “A Fast, Accurate, and Sensitive Method for Calculating Surface Transfer Impedance”.
[3] R. Méndez, R. Isanta, R. Otín, O. Fruitos, “GiD interface for the parametric generation of simplified braided-wire shields geometries” (Accepted)
[4] R. Otin, J. Verpoorte, and H. Schippers, “A Finite Element Model for the Computation of the
Transfer Impedance of Cable Shields”. IEEE Transactions on Electromagnetic Compatibility. Submitted.
Document information
Published on 01/01/2009
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?