Parallel computing for reducing time in security constrained optimal power flow analysis

Revision as of 15:51, 20 October 2022

Abstract

This paper presents a novel approach for solving the security-constrained optimal power flow (SCOPF) optimization problem using parallel Computing. In this approach, switched shunt banks, generation power ramp, and demand response are considered in the SCOPF by maximizing the market surplus during regular operation and for a set of contingencies of branches and generators. The optimization problem is solved using the Nonlinear Interior Point Method. The contingency assessment is paralleled in multiple CPU cores to decrease the computation time. Additionally, the test systems used in ARPA-GO competition were used and compared with the ARPA benchmark results to assess the proposed algorithm. The numerical results show this method is suitable for fast SCOPF using paralleling Computing.

keywords High-Performance Computing $\cdot$ Interior-point method, Reliability $\cdot$ Security Constraint Optimal Power Flow (SCOPF)

Received: date / Accepted: date

1 Introduction

Power systems must operate in energy equilibrium in a secure, reliable, economical, and sustainable way; commonly contrary issues. Hence, tools to optimize the planning, maintenance, and operation of electrical networks are required. The optimal power flow (OPF) is a well-known problem [1] where the power balance and generation, thermal and voltage limits among other constraints are considered. However, the solution of this formulation could be non-optimal or insecure if contingencies occur in the grid. To securely operate considering the multiple contingencies that could arise, the OPF needs to be reformulated considering security constraints. This reformulation is known as Security Constraint Optimal Power Flow (SCOPF). According to [2], an improvement of 5 in the efficiency of the SCOPF algorithm can save between 619$ in the U.S and it can also save between 2687$ in the world. Illustrating, these savings are close to 1x10¹ of the 2021 annual investment in the power sector [3].

To increase the performance of the SCOPF algorithm many advantages are obtained. However, in order to employ SCOPF during real-time operation, the solution of this optimization problem needs to be computationally efficient given the well-known issues of OPF such as non-convexity [4], network size, integer-mixed variable decisions, among others. Therefore, to reduce the solution time of SCOPF algorithms, two approaches have been proposed. For one hand, to select a set of critical contingencies [5,6]. For other hand, to simplify the problem using a linear approximation [Mithun2010].

Given the uncertainty in reducing the number of contingencies or using linear approximations during the planning and operation of the next-generation energy systems, a robust SCOPF assessment is required [7], However, this kind of algorithm presents a high computational cost. New approaches emerge to face this challenge, such as the use of reinforced learning (artificial intelligence algorithms) to operate networks during contingencies [8] or paralleling the Computing of the SCOPF by employing High-Performance Computing (HPC), both to reduce the computation cost. The issue with reinforced learning is that an artificial agent needs to be trained for each network with known states, therefore HPC is commonly used for different applications for power systems. For instance, in [9] an embedded computer is used to partially solve power flows paralleling the Newton-Raphson algorithm. In [10,11] a hybrid CPU-GPU approach to solving power flows using Parallel Computing is employed. Finally, in [12] a Multi-CPU/Core Computing Environment is used for contingency analysis showing an acceleration ratio of 2.69x10¹ compared with sequential processing. However, the OPF is not considered.

Based on the reported benefits of employing HPC in power systems applications [13,14], in this paper a novel SCOPF analysis using parallel computing is addressed. This approach maximizes the market surplus during regular operation and contingencies, considering network constraints of power generation and load ramps. Also, generators’ active and reactive capacity, lines and transformers thermal limits, switchable shunts, voltage security limits, and price responsive demand are considered. The main contributions of this paper are summarized as follows:

A novel SCOPF algorithm is proposed to run in parallel. This algorithm is divided in two main stages, first one where a OPF is solved for a base case optimizing the market surplus, and a second one where each contingency is solved in parallel in order to obtain the conditions to operate the system in a secure condition. The contingency assessment is performed by solving an OPF with both power generation and demand costs equal to zero and using the OPF base case results as initial points. This algorithm can provide a rapidly and reliable solution for optimal and secure operation of power networks
For the SCOPF algorithm, the fixed switchable shunts are modeled as generators with an active power equal to zero and no cost, and the responsive demand is modeled as generators injecting negative power with constant power factor. This novel modeling can improve the optimal operation of modern power systems
The SCOPF algorithm can run on a multi-node cluster platform. The ARPA-GO platform was used to eval the effectiveness of the SCOPF algorithm using large and realistic networks

This paper is organized as follows: in Background the theoretical background of OPF is introduced. 3 presents the proposed methodology to compute SCOPF using parallel computing, followed by Results, where the algorithm is assessed for different study cases. Finally, in Conclusion, conclusions are addressed.

2 Background

The fundamental OPF problem is formulated to minimize the cost of generation subject to equality constraints of bus power balance and inequality constraints of maximum and minimum active and reactive power generation, minimum and maximum bus voltages and thermal transmission constraints, including transformers and lines. This formulation is shown below, where it is stated to minimize:

(1)

subject to

(2)

(3)

(4)

(5)

(6)

(7)

(8)

where ${\textstyle P_{g_{i}}}$ is the active power generated by the generator ${\textstyle i}$ , ${\textstyle f}$ is the cost function, ${\textstyle N_{gen}}$ is the number of generators, ${\textstyle P_{i}}$ is the injected power at bus ${\textstyle i}$ , ${\textstyle E}$ is the absolute value of bus voltage, ${\textstyle P_{g_{i}}^{0}}$ is the generating power at prior condition, ${\textstyle \Delta P_{g_{i}}^{d}}$ , ${\textstyle \Delta P_{g_{i}}^{d}}$ are the down and up generator ramps, ${\textstyle N_{bus}}$ is the number of buses, ${\textstyle S_{ij}}$ is the power flow by branch, ${\textstyle Y_{ik}}$ is the branch admittance between bus ${\textstyle i}$ and ${\textstyle k}$ , ${\textstyle P_{g}^{min}}$ and ${\textstyle P_{g}^{max}}$ are generators limits, ${\textstyle E_{i}^{min}}$ and ${\textstyle E_{i}^{max}}$ are bus voltage limits, ${\textstyle S_{ij}^{max}}$ is the branch thermal limit. Finally, ${\textstyle u}$ is the vector of decision and state variables, bus angles ${\textstyle \left(\theta \right)}$ and voltages, and active and reactive generator power.

2.1 Shunt Banks

The switched shunt banks are used to securely optimize the grid operation. These banks are composed of blocks with fixed steps resulting in an equivalent shunt susceptance as follows:

(9)

Where ${\textstyle b_{ii}}$ is the resulting shunt susceptance at bus ${\textstyle i}$ , ${\textstyle a}$ is the block, ${\textstyle b_{a}}$ is the susceptance step size, ${\textstyle k}$ is the current step position, and ${\textstyle N_{a}}$ is the number of shunt blocks.

2.2 Demand Response

The demand response allows to increase or decrease the load with an associated cost to enhance the SCOPF. The demand response is subject to:

(10)

Where ${\textstyle t}$ is the fraction of current load and ${\textstyle t_{min}}$ and ${\textstyle t_{max}}$ are the maximum and minimum fraction of load, respectively. Hence, the resulting active and reactive parts of the load are:

(11)

(12)

where ${\textstyle P_{l_{i}}}$ , ${\textstyle Q_{l_{i}}}$ are the active and reactive demands at bus ${\textstyle i}$ , respectively, and ${\textstyle P_{l_{i}}^{0}}$ , ${\textstyle Q_{l_{i}}^{0}}$ are the active and reactive demand at a primary operating point. Additionally, the loads can be subject to ramp limits as follows:

(13)

Where ${\textstyle \Delta P_{l_{i}}^{rd}}$ , ${\textstyle \Delta P_{l_{i}}^{ru}}$ are the down and upper ramp limits, respectively.

2.3 Cost functions

Polynomial and piecewise linear cost functions are used for an OPF assessment if convex functions are assumed [15]. For piecewise linear functions, a helper cost (auxiliary) variable ${\textstyle y}$ is added for each segment of the function, and the following constraints are included in the formulation of OPF:

(14)

where ${\textstyle j}$ is the segment of the piecewise function, ${\textstyle x}$ is the generator output power or demand, ${\textstyle m}$ is the slope, and ${\textstyle x_{j},c_{j}}$ is the sequence of points of the segment, respectively. Commonly a piecewise function with one segment is replaced by a polynomial of grade one.

3 SC-OPF Proposal

In this section, the proposed algorithm for solving the SCOPF using paralleling computing is addressed. In this algorithm, switched shunt banks, demand response, and piecewise cost functions for loads and generators are considered. Systems operating in island mode are outside of the scope of this SCOPF algorithm.

3.1 SCOPF formulation

The proposed formulation is based on 01_OPF_Statement as shown in 02_OPF_Statement_ARPA. In this formulation, the cost for normal operation (base case) and during a contingency (case k) are taken into account using the cost function ${\textstyle f_{0}}$ for the base case, ${\textstyle f_{k}}$ for each considered contingency, and the helper cost variables ${\textstyle y}$ . In the SCOPF, the set of constraints must be fulfilled for the base case and contingencies. In this way, it is stated:

To Maximize

{P_{g_{i}},u,P_{l_{i}}}{f_{0}\left(P_{g_{i}},u,P_{l_{i}}\right)+\sum _{n=1}^{N_{gen}+N_{l}}y_{n}+\sum _{k=1}^{K}\left(f_{k}\left(P_{g_{i}},u,P_{l_{i}}\right)+\sum _{n=1}^{N_{gen}+N_{l}}y_{n}\right)}{}{}

(15)

Subject to

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

The demand response is modeled by assuming loads as generators injecting negative power and adding three constraints to the SCOPF. The first constraint is an inequality to model the minimum and maximum fraction of response load. The second one is an inequality to model the load ramps. The last constraint is equality to guarantee the ratio between reactive and active power demand response. For switched shunt banks, the algorithm is run in two stages. In the first one, the shunt banks are assumed as generators with inequalities of maximum and minimum reactive power ${\textstyle \left(Q_{s}\right)}$ and with equality constraints of active power equal to zero. In the second stage, the reactive power ${\textstyle \left(Q_{s}\right)}$ is approximate to the close shunt bank position, as shown in the following subsection. With that selected shunt block position, the resulting shunt impedance adds to the branch, and the OPF is back run, eliminating the assumed shunt as generators. Hence, the Nonlinear Interior Point Method based on Matpower formulation [15] solves the OPF problem for the base case and contingencies.

3.2 Shunt Banks

The relation between switchable shunt bank block position and susceptance for the second stage of the OPF is shown in SB_Table. Hence, for the base case and each contingency the shunt susceptance position is selected according to injected power obtained to model the shunt bank as a generator with active power equal to zero.

Table. 1 Susceptance value for each shunt block position
${\textstyle x_{sh}^{1}}$	$x_{sh}^{2}$	$x_{sh}^{Na}$	$\sum S_{h}$
0	0		$S_{0,0,\cdots }$
0	1		$S_{0,1,\cdots }$
0			$S_{0,\cdots ,\cdots }$
0	$k_{2}$		$S_{0,k_{2},\cdots }$
1	0		$S_{1,0,\cdots }$
1	1		$S_{1,1,\cdots }$
1			$S_{1,\cdots ,\cdots }$
1	$k_{2}$		$S_{1,k_{2},\cdots }$
	0		$S_{\cdots ,0,\cdots }$
	1		$S_{\cdots ,1,\cdots }$
	$k_{2}$		$S_{\cdots ,k_{2},\cdots }$
$k_{1}$	0		$S_{k_{1},0,\cdots }$
$k_{1}$	1		$S_{k_{1},1,\cdots }$
$k_{1}$			$S_{k_{1},\cdots ,\cdots }$
$k_{1}$	$k_{2}$		$S_{k_{1},k_{2},\cdots }$

3.3 Paralleling Strategy

As the set of contingencies does not depend on each other, those can be computed in parallel. The proposed paralleling strategy to solve SCOPF is shown in LC_OPF_Strategy_One and can be summarized in the following steps:

The base case OPF is run modeling the switchable shunt as generators
Fix the shunt bank position adding the equivalent shunt susceptance to each branch and run the OPF
Read contingency set and update limits of voltage and branch current ratings for contingencies
Update the ramp limits of generation and demand power using the ${\textstyle P_{g_{i}}^{0},P_{g_{i}}^{0}}$ of the base case
Assign to each contingency a core of the available CPUs to execute in parallel steps 1 and 2. In summary, in this step the secure operation conditions for each contingency is assessed, solving the OPF problem of 02_OPF_Statement_ARPA assuming generation and demand cost as zero, in other words, ${\textstyle y_{n}}$ =0. Hence, the optimization problem is reduced to remove both the helper cost variables and the piecewise restrictions.

In step 5 is exploited the capabilities of parallel computing running each contingency as an OPF without cost variables. With this novel approach, it is guaranteed that during a contingency the power network operates fulfilling all security constraints (power balance, limits of loads, generators, voltage, branches, among others).

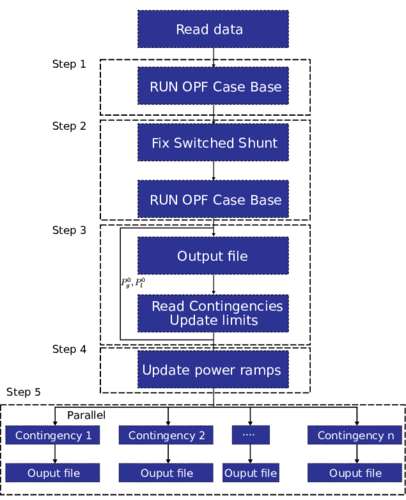
Figure 1: Proposed paralleling strategy to solve SCOPF

During both the read data and read contingencies stages, a comparison between the ramps of generators and loads and the maximum and minimum allowable power is performed to delete over-defined inequalities.

4 Case of Study

The validation of the proposed parallel algorithm is performed using the data-set and the scoring method formulated by the ARPA-GO challenge [16]. The algorithm was implemented in Python using the following open-source libraries:

Pandas: For management data
Scipy: For sparse matrix operations
pypardiso: Python interface to the Intel MKL Pardiso library to solve sparse linear systems of equations
mpi4py: Python bindings for the Message Passing Interface (MPI) standard, to exploit multiple processors on workstations or clusters

4.1 Influence of number of CPU cores

To assess the influence of several cores in the elapsed time to solve SCOPF, the case model C2T2N00617 scenario 185 of the ARPA-GO Competition data set was used. This is a system of 617 buses, 853 branches, and 108 contingencies. The CPU used was a Ryzen 3600 with 12 threats and a frequency base of 3.6 GHz . In 01_core_time is shown the elapsed time by the number of cores employed, where can be appreciated an exponential decay according to the number of cores. While comparing the ten threats with two threats, a speedup close to 5X was achieved.

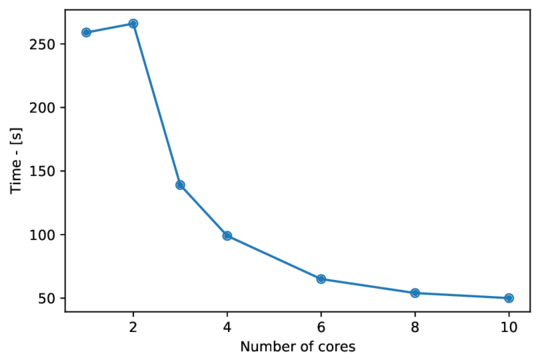
Figure 2: Elapsed time to solve SCOPF for the C2T2N00617-185 ARPA system using a different number of CPU-threats

The benefits obtained with the proposed algorithm and the reported by ARPA-e Benchmark were 1.50314x10⁶ USD and 1.50807x10⁶ USD, respectively. That shows a similar performance between the two algorithms.

4.2 Fixed demand and generation

To evaluate the influence of demand response and dispatchable generators on the benefit, a sensitivity analysis is performed executing the SCOPF with different levels of dispatchable load and generation. For that, a share of generation and demand are modeled as fixed elements injecting or consuming power. The 02_Demand_Load shows the results obtained for different ratios of fixed demand and generation. A fixed value of 1 means that all loads or generators (1x10² ) are non-responsive or non-dispatchable. On the contrary, a fixed value of 0 means that all generators are dispatchable or all demands are responsive. As expected, for this case, the higher benefit was obtained to fix on 1 of the total elements of demand and generation. The lowest benefit was to fix a non-demand response of 1x10² of the total loads and fixing the non-dispatchable generator at 6x10¹ . Overall, for the case model C2T2N00617-185 the demand response costs present a stronger influence on the benefit than the generation costs, demonstrating the potential benefits of the proposed SCOPF algorithm.

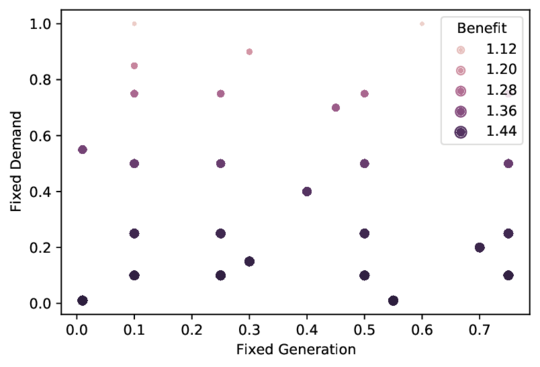
Figure 3: Influence of fixed loads and generators on the benefit (1x10⁶ USD)for the case model C2T2N00617-185

4.3 Large Size Systems

For assessing large size systems, the ARPA-GO competition platform was employed. This platform consists of a multi-node cluster with six nodes, each with 24 cores (a total of 144 cores) using the operating system Centos 7.4. MPI is used to manage the cluster. In 03_Comparision the benefit obtained for different ARPA-GO models using the ARPA-Benchmark results and the proposed SCOPF algorithm is shown. The number of contingencies for each model are 966, 500, 2540, 401, and 1023 respectively. The results show a similar performance between the two algorithms. For cases larger than 14000 buses, the algorithm shows slow convergence, and the platform interrupts the execution because the time limit was exceeded.

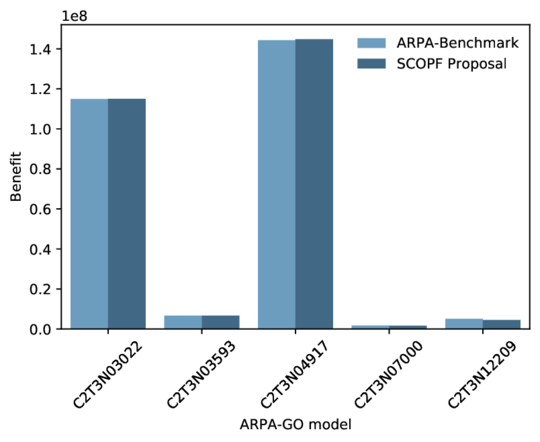
Figure 4: Benefit Comparison between ARPA-Benchmark and the proposed SCOPF for different scenarios

5 Conclusion

In this paper, an enhanced security constraints optimal power flow algorithm is proposed to be used in Paralleling Computing. This algorithm considers demand response, generator ramps limits, and switchable shunt banks during normal operation and contingencies based on the standard OPF formulation. The algorithm was assessed using python scripts and open libraries with the ARPA-GO competition data sets on a desktop and in a multi-node cluster. The tests performed show how the algorithm becomes more efficient according to the increase in the number of cores, and the SCOPF has shown convergence for systems of 12000 buses. However, in larger cases, the algorithm presents numerical error convergences. Finally, the algorithm was developed to support the secure online operation of power systems using multiple CPUs to reduce the execution time.

Conflict of interest

The authors declare that they have no conflict of interest.

BIBLIOGRAPHY

[1] Maskar, Mukund B and Thorat, A.R. and Korachgaon, Iranna. (2017) "A review on optimal power flow problem and solution methodologies". 2017 International Conference on Data Management, Analytics and Innovation (ICDMAI). IEEE 64–70

[2] Cain, Mb and O'Neill, Rp and Castillo, A. (2012) "History of Optimal Power Flow and Formulations (OPF Paper 1)". FERC Staff Tech. Pap. December 1–36

[3] International Energy Agency. (2021) "World Energy Investment 2021". World Energy Investment 2021. OECD

[4] Low, Steven H. (2014) "Convex Relaxation of Optimal Power Flow—Part I: Formulations and Equivalence", Volume 1. IEEE. IEEE Transactions on Control of Network Systems 1 15–27

[5] Majidi-Qadikolai, Mohammad and Baldick, Ross. (2016) "Integration of Contingency Analysis With Systematic Transmission Capacity Expansion Planning: ERCOT Case Study", Volume 31. Institute of Electrical and Electronics Engineers Inc. IEEE Transactions on Power Systems 3 2234–2245

[6] Valencia-Zuluaga, Tomas and Agudelo-Martinez, Daniel and Arango-Angarita, Dario and Acosta-Urrego, Camilo and Rivera, Sergio and Rodriguez-Medina, Diego and Gers, Juan. (2021) "A Fast Decomposition Method to Solve a Security-Constrained Optimal Power Flow (SCOPF) Problem Through Constraint Handling", Volume 9. Institute of Electrical and Electronics Engineers Inc. IEEE Access 52812–52824

[7] Moreira, Alexandre and Street, Alexandre and Arroyo, Jose M. (2015) "An Adjustable Robust Optimization Approach for Contingency-Constrained Transmission Expansion Planning", Volume 30. Institute of Electrical and Electronics Engineers Inc. IEEE Transactions on Power Systems 4 2013–2022

[8] Marot, Antoine and Donnot, Benjamin and Dulac-Arnold, Gabriel and Kelly, Adrian and O'Sullivan, Aïdan and Viebahn, Jan and Awad, Mariette and Guyon, Isabelle and Panciatici, Patrick and Romero, Camilo. (2021) "Learning to run a Power Network Challenge: a Retrospective Analysis" 112–132

[9] Rodriguez, Diego F. and Alvarez, David L. and Gomez, Diego and Gers, Juan M. and Rivera, Sergio. (2021) "Low-Cost Analysis of Load Flow Computing Using Embedded Computer Empowered by GPU". 2021 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT). IEEE 1–5

[10] Araújo, Igor and Tadaiesky, Vincent and Cardoso, Diego and Fukuyama, Yoshikazu and Santana, Ádamo. (2019) "Simultaneous parallel power flow calculations using hybrid CPU-GPU approach", Volume 105. Elsevier BV. International Journal of Electrical Power & Energy Systems 229–236

[11] Wang, Zhenqi and Wende-von Berg, Sebastian and Braun, Martin. (2021) "Fast parallel Newton–Raphson power flow solver for large number of system calculations with CPU and GPU", Volume 27. Elsevier. Sustainable Energy, Grids and Networks 100483

[12] Zhou, Mike and Feng, Donghao. (2019) "Parallel Contingency Analysis for Multi-CPU/Core Computing Environment", Volume 52. Elsevier B.V. IFAC-PapersOnLine 4 105–110

[13] Khaitan, Siddhartha Kumar. (2016) "A survey of high-performance computing approaches in power systems", Volume 2016-Novem. 2016 IEEE Power and Energy Society General Meeting (PESGM). IEEE 1–5

[14] Rodriguez, Diego and Gomez, Diego and Alvarez, David and Rivera, Sergio. (2021) "A Review of Parallel Heterogeneous Computing Algorithms in Power Systems", Volume 14. Multidisciplinary Digital Publishing Institute. Algorithms 10 275

[15] Zimmerman, Ray D. and Murillo-Sanchez, Carlos E. and Thomas, Robert J. (2009) "MATPOWER's extensible optimal power flow architecture". 2009 IEEE Power & Energy Society General Meeting. IEEE 1–7

[16] . (2019) "ARPA-E Grid Optimization Competition"

@@ Line 128: / Line 128: @@
 | style="text-align: center;" | <math>b_{ii} = \sum _{a=1}^{N_a} b_a x_{ak} </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (1)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (9)
 |}
@@ Line 144: / Line 144: @@
 | style="text-align: center;" | <math>t_{min} \leq t \leq t_{max} </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (2)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (10)
 |}
@@ Line 156: / Line 156: @@
 | style="text-align: center;" | <math>P_{l_i}  = P_{l_i}^0  t_i </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (3)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (11)
 |}
@@ Line 166: / Line 166: @@
 | style="text-align: center;" | <math>Q_{l_i}  = Q_{l_i}^0  t_i </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (4)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (12)
 |}
@@ Line 178: / Line 178: @@
 | style="text-align: center;" | <math>P_{l_i}^0-\Delta P_{l_i}^{d}  \leq P_{l_i} \leq P_{l_i}^0+\Delta P_{l_i}^{u}  </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (5)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (13)
 |}
@@ Line 194: / Line 194: @@
 | style="text-align: center;" | <math>y \ge m_j \left(x-x_j \right)+c_j </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (14)
 |}
@@ Line 205: / Line 205: @@
 ===3.1 SCOPF formulation===
-The proposed formulation is based  on 01_OPF_Statement as shown in 02_OPF_Statement_ARPA. In this formulation, the cost for normal operation (base case) and during a contingency (case k) are taken into account using the cost function <math display="inline">f_0</math> for the base case, <math display="inline">f_k</math> for each considered contingency, and the helper cost variables <math display="inline">y</math>. In the SCOPF, the set of constraints must be fulfilled for the base case and contingencies.
+The proposed formulation is based  on 01_OPF_Statement as shown in 02_OPF_Statement_ARPA. In this formulation, the cost for normal operation (base case) and during a contingency (case k) are taken into account using the cost function <math display="inline">f_0</math> for the base case, <math display="inline">f_k</math> for each considered contingency, and the helper cost variables <math display="inline">y</math>. In the SCOPF, the set of constraints must be fulfilled for the base case and contingencies. In this way, it is stated:
+To Maximize
 {| class="formulaSCP" style="width: 100%; text-align: left;"
@@ Line 215: / Line 216: @@
 | style="text-align: center;" | <math>      {P_{g_i},u,P_{l_i}}{ f_0\left(P_{g_i},u,P_{l_i} \right)+\sum_{n=1}^{N_{gen}+N_{l}} y_n+\sum_{k=1}^{K} \left( f_k\left(P_{g_i},u,P_{l_i}\right)+\sum_{n=1}^{N_{gen}+N_{l}} y_n\right)}{}{} </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (15)
 |}
+Subject to
 {| class="formulaSCP" style="width: 100%; text-align: left;"
@@ Line 225: / Line 228: @@
 | style="text-align: center;" | <math>     {P_i-\operatorname{Re}\left(E_i \sum_{k=1}^{N_{bus}} Y_{ij} E_j \right)}{=0}{i=1,\ldots,N_{bus}}</math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (16)
 |}
@@ Line 235: / Line 238: @@
 | style="text-align: center;" | <math>     {Q_i-\operatorname{Im}\left(E_i \sum_{k=1}^{N_{bus}} Y_{ij} E_j \right)}{=0}{i=1,\ldots,N_{bus}}</math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (17)
 |}
@@ Line 245: / Line 248: @@
 | style="text-align: center;" | <math>     { P_{l_i}^{0} t_{min}\leq P_{l_i}}{\leq P_{l_i}^{0} t_{max} \quad}{i=1,\ldots,N_{l}}</math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (18)
 |}
@@ Line 255: / Line 258: @@
 | style="text-align: center;" | <math>     {P_{l_i}^0-\Delta P_{l_i}^d \leq  P_{l_i} }{\leq P_{l_i}^0+\Delta P_{l_i}^u}{i=1,\ldots,N_{l}} </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (19)
 |}
@@ Line 266: / Line 269: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (20)
 |}
@@ Line 277: / Line 280: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (21)
 |}
@@ Line 288: / Line 291: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (22)
 |}
@@ Line 299: / Line 302: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (23)
 |}
@@ Line 310: / Line 313: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (24)
 |}
@@ Line 321: / Line 324: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (25)
 |}
@@ Line 332: / Line 335: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (26)
 |}
@@ Line 343: / Line 346: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (27)
 |}
@@ Line 354: / Line 357: @@
   </math>
 |}
-| style="width: 5px;text-align: right;white-space: nowrap;" | (6)
+| style="width: 5px;text-align: right;white-space: nowrap;" | (28)
 |}