(Tag: Visual edit) |
|||
| Line 1: | Line 1: | ||
| − | + | <span id="_GoBack"></span> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <span | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==1 Introducción== | ==1 Introducción== | ||
| Line 85: | Line 23: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Tabla 1.''' Resistencia en direcciones principales en función del caso de carga y resistencia a la cortadura interlaminar (valores medios) [3-5] | + | <span style="text-align: center; font-size: 75%;">'''Tabla 1.''' Resistencia en direcciones principales en función del caso de carga y resistencia a la cortadura interlaminar (valores medios) [3-5]</span></div> |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
Revision as of 14:13, 15 October 2022
1 Introducción
Los elementos estructurales están frecuentemente sometidos a cargas aplicadas perpendicularmente a su superficie, que ocasionan que los mismos flecten. A nivel de laboratorio, los ensayos de flexión son básicos ya que permiten comprobar la integridad estructural del material cuando éste se encuentra sometido a esfuerzos de tracción, compresión y cortadura de forma simultánea. En particular, los ensayos de tres puntos se utilizan ampliamente en la caracterización mecánica de los materiales debido la amplia información que proporcionan y a su relativa simplicidad. Para este tipo de ensayos, existen ecuaciones bien documentadas que permiten realizar el análisis de materiales con igual respuesta ante cargas de tracción y de compresión cuando estos trabajan a flexión [1,2].
Parte de la investigación realizada por miembros del grupo de investigación COMES (Mecánica de los Medios Continuos e Ingeniería de Estructuras) de la Universidad de Castilla La-Mancha se ha orientado al estudio de la influencia del distinto comportamiento a tracción y a compresión de materiales estructurales no convencionales sometidos a ensayos de flexión de tres puntos [3-5]. Para ello, se ha desarrollado un modelo analítico lineal basado en los principios de elasticidad y equilibrio. De esta forma, las ecuaciones que gobiernan el problema describen la desviación de la fibra neutra y la no simetría de la distribución de tensiones normales y tangenciales. Además, el modelo define el umbral teórico que permite estimar si el modo de fallo inicial del material será debido a los esfuerzos de flexión o de cortadura.
Durante la investigación previa, se ha planteado revisar la validez de estas ecuaciones experimentalmente mediante ensayos con materiales compuestos avanzados. Los materiales compuestos son de interés para el diseño y fabricación de estructuras resistentes cada vez más ligeras, lo que es crucial en distintas aplicaciones. Muestra de ello son la industria del transporte, la eólica o la deportiva donde los materiales compuestos de matriz polimérica a la que se le añaden determinados refuerzos son ampliamente utilizados. Hasta el momento, el modelo analítico ha sido validado experimentalmente mediante ensayos con CFRP (polímeros reforzados con fibra de carbono) [6]. Así se han estudiado tanto laminados unidireccionales como cross-ply fabricados a partir de capas de fibra de carbono pre-impregnadas con resina epoxi (prepreg). En estos estudios se ha comprobado que el modo de fallo inicial depende directamente de la relación entre la distancia entre apoyos y el espesor de la probeta, donde la iniciación del daño producido experimentalmente se ha observado por medio de microscopía óptica. En todos los casos las mediciones experimentales han concordado con las estimaciones analíticas, habiéndose mostrado la validez del modelo analítico expuesto.
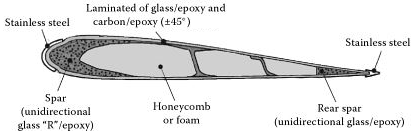
En este trabajo se toma como base la experiencia del grupo de trabajo en el campo del modelado, análisis y experimentación ante cargas de flexión de materiales compuestos unidireccionales y cross-ply con distinto comportamiento a tracción y a compresión. Como continuación, se aplica el modelo desarrollado al análisis de laminados angle-ply formados por la agrupación de capas unidireccionales con las fibras orientadas a ±45°, los cuales son muy utilizados en la industria aeronáutica (ver Figura 1). Es necesario definir las configuraciones de estudio para intentar reducir al máximo el acople entre los esfuerzos de flexión y los de torsión, lo que se logra utilizando un número elevado de capas alternas [7].
En el caso de la realización de ensayos uniaxiales, los laminados ±45º angle-ply formados por una gran cantidad de capas alternantes suelen desarrollar pseudo-ductilidad debido principalmente a la tendencia que tienen las fibras a alinearse con la dirección de carga y a la fluencia de la matriz. Este comportamiento genera de forma general altos niveles de deformación antes del fallo total del material. El mecanismo responsable del mismo que con frecuencia ha sido analizado en la literatura existente ante la presencia de cargas uniaxiales [9,10], podría ser también de gran importancia ante casos de carga de flexión. Una de las propuestas de este trabajo es observar este fenómeno en los experimentos de tres puntos, ya que la sección transversal de las probetas de ensayo estará sometida a cargas de tracción en su zona inferior y de compresión en su parte superior simultáneamente.
2 Material y Equipamiento
El material utilizado para el desarrollo de este trabajo ha sido cedido por la empresa Airbus desde su sede de Illescas (Toledo), el cual es un material pre-impregnado (prepreg) de matriz epoxi reforzado con fibras de carbono unidireccionales denominado M21E/34%/UD268/IMA-12K. Este prepreg tiene aplicación directa en la industria aeronáutica, en concreto en la estructura primaria del Airbus A350 XWB. Las propiedades obtenidas en la caracterización del mismo [3,5] se presentan en las Tablas 1 y 2, en las cuales se muestran los valores medios del módulo de Young , coeficiente de Poisson y tensión de rotura que exhibe una capa en direcciones principales, donde los superíndices y se refieren a los casos de carga de tracción y compresión respectivamente. Además, el material presenta la resistencia a la cortadura interlaminar [3] que se muestra en la Tabla 1. A partir de las propiedades del material en direcciones principales ante cargas de tracción y compresión se pueden obtener, utilizando la teoría clásica de placas laminadas y el criterio de fallo de Tsai-Hill [11], los valores aparentes del módulo de elasticidad y tensión de rotura que presentan las capas ±45° cuando están cargadas uniaxialmente ( , , y ).
| [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] |
| 2600.90 | 1356.20 | 56.07 | 200.00 | 103.93 | 46.65 |
| [GPa] | [GPa] | [GPa] | [GPa] | [GPa] | ||
| 177.56 | 97.03 | 11.84 | 7.46 | 5.15 | 0.39 | 0.03 |
Los equipos necesarios para la realización del trabajo son una prensa de platos calientes para curado de material compuesto, una máquina universal de ensayos con un útil de flexión en tres puntos incorporado, un microscopio electrónico de barrido para observar el daño producido en las probetas y la medición de deformaciones tanto con galgas extensométricas como mediante un equipo de Correlación Digital de Imagen (DIC).
3 Procedimiento
La metodología de trabajo plantea la aplicación de la técnica de la sección homogeneizada, desarrollada en trabajos anteriores [3-5], al problema de un laminado formado por agrupaciones de capas a ±45° sometido a flexión de tres puntos. Este modelo analítico permite tener en cuenta en sus estimaciones la diferente repuesta del material ante cargas de tracción y de compresión. La comprobación desde el punto de vista experimental de las predicciones analíticas vertidas permitirá estimar el grado de acierto del modelo desarrollado. Para ello, se propone la fabricación propia de los laminados en una prensa de platos calientes a partir de material pre-impregnado unidireccional CFRP. A partir de ellos, se mecanizarán probetas de forma prismática con sección transversal de base mm y altura mm, para ensayarlas en un útil de flexión de tres puntos con una distancia entre apoyos igual a mm.
3.1 Modelo analítico
Para abordar la complejidad analítica derivada del diferente comportamiento a tracción y a compresión del material, se utiliza la técnica de la sección homogeneizada con el fin de unificar la respuesta elástica en la sección transversal y así analizar el problema por medio de la teoría clásica para vigas esbeltas sometidas principalmente a flexión [12]. Se asume una desviación de la fibra neutra (FN) con respecto al plano medio de la probeta, la cual dividirá a la sección en dos regiones estando la inferior traccionada y la superior comprimida. Si se numeran estas dos regiones de abajo a arriba y se toma la posición de la FN como origen de coordenadas verticales , aplicando la nomenclatura seguida en trabajos anteriores las coordenadas que limitan las zonas traccionada y comprimida son , e . Igualmente, se puede definir el ratio que relaciona los módulos de elasticidad a tracción y a compresión como . De tal forma que la posición de la FN se puede obtener resolviendo la ecuación que obliga a que el momento estático de la sección homogeneizada sea igual a cero. Trabajando en la sección más desfavorable con los valores máximos de las tensiones normales debidas al momento flector y de las tensiones tangenciales debidas al esfuerzo cortante, la condición límite para que la probeta desarrolle modos de fallo a tracción o una apertura interlaminar se puede obtener relacionando dichos valores máximos. Teniendo en cuenta que la tensión normal de rotura ante cargas de tracción es más limitante que la resistencia a compresión , si se cumple la relación la probeta presentará un fallo debido a la máxima tensión normal desarrollada en la zona de tracción y si presentará como primer fallo una apertura interlaminar en la posición de la FN.
3.2 Desarrollo experimental
En este trabajo se propone estudiar dos laminados diferentes con un alto número de capas para reducir al máximo el acople entre los esfuerzos de flexión y de torsión. Se plantea analizar probetas [+45 -45]6S y [+452 -452]3S, que según el criterio analítico explicado deben iniciar el fallo experimentalmente a tracción debido al momento flector. Los dos casos de estudio poseen 24 capas formando agrupaciones de ±45º, siendo la principal diferencia entre ellos la alternancia que presentan en su orientación. De tal forma que el primer laminado actuará como un material formado por 24 capas que invierten su signo de forma continua y con paso igual al espesor de una capa . Mientras tanto, la segunda configuración aparentemente se comportará como un laminado de 12 capas que alternan el signo de su orientación con paso igual . Esto debería dar lugar a que, según predice la teoría clásica de laminados [11], los dos desarrollen una primera zona similar de comportamiento elástico lineal. Sin embargo tras la etapa lineal es esperable que ambas configuraciones muestren una respuesta mecánica distinta. En el primer laminado el efecto de la reorientación de las fibras en la dirección de la carga se espera sea más acusado que en el segundo, al actuar aparentemente la configuración [+45 -45]6S como un laminado con un número de capas doble que el caso [+452 -452]3S y reduciéndose así en este último el número de capas que contribuyen al efecto “tijera” que genera la pseudo-ductilidad.
Una vez fabricados los laminados, se realiza sobre ellos ensayos de flexión de tres puntos en probetas con forma de prisma rectangular cuya dimensión es ligeramente diferente a la propuesta debido al proceso manual de corte. Las principales limitaciones de los especímenes están impuestas sobre su longitud y ancho que son elegidos para adecuarse a los requerimientos dimensionales impuestos por el útil de flexión y para conseguir un modo de fallo homogéneo en toda la sección. Mientras tanto el espesor de la probeta viene determinado por el número de capas del laminado, que ha sido elegido lo suficientemente grande para poder despreciar la aparición de momentos torsores en el estudio. Durante los ensayos se registran la carga aplicada en la sección central, así como el mapa de desplazamientos y deformaciones tomados en el plano lateral de la probeta mediante un equipo DIC. Además, la utilización de galgas extensométricas en la cara inferior de la sección central de la probeta permite asegurar la veracidad de las deformaciones adquiridas mediante comparación de los valores obtenidos mediante los dos tipos de técnicas. La localización del inicio y evolución del daño se realiza mediante observación visual directa y utilizando recursos microscópicos.

(a) |

(b) |
4 Resultados y Discusión
Tras llevar a cabo los ensayos de flexión, en los dos laminados propuestos las capas inferior y superior son las que más se deforman debido al momento flector. Al ser la resistencia a la tracción en la dirección de la carga más pequeña que su tensión de rotura a compresión, el daño se inicia en la capa inferior de la probeta. Este resultado confirma experimentalmente la predicción realizada utilizando el modelo analítico propuesto. No sólo aparece una única grieta inicialmente, si no que varias microgrietas surgen en su vecindad al mismo tiempo. Después de la iniciación del daño, la capa inferior pierde su capacidad de soportar carga y las capas restantes deben continuar soportando el incremento de la carga externa. Entonces se produce un efecto “dominó” en el que las capas inferiores pasan a ser alternativamente las más deformadas a tracción y van presentando grietas similares a las descritas anteriormente. A medida que el daño se va propagando de abajo a arriba, las capas que ya han fallado tienden a separase debido al aumento del ángulo inducido en la probeta. A modo de ejemplo, en la Figura 2a se muestra una imagen tomada durante el ensayo de una probeta [+45 -45]6S, en la que se puede ver la rotura de las capas inferiores donde se inicia el daño debido a la máxima tensión de tracción sufrida. Así mismo el modo de fallo explicado se puede observar en la Figura 2b, realizada con microscopía electrónica de barrido sobre la zona crítica de interés.
5 Conclusiones
Tanto a nivel científico como tecnológico existe interés en conocer la respuesta a flexión de los materiales poliméricos reforzados para conseguir soluciones estructurales con características mecánicas comparables a las de los materiales metálicos pero con un menor peso. Debido al comportamiento no convencional de los materiales compuestos, es deseable estimar cuál es la influencia en los parámetros relevantes de la distinta respuesta del material ante cargas de tracción y de compresión.
Los materiales compuestos presentan generalmente diferente comportamiento tensión-deformación bajo cargas de tracción y de compresión. El efecto de esta característica se ha examinado en términos de la flexión en tres puntos en materiales compuestos formados por capas de CFRP. Usando la técnica de la sección homogeneizada se ha estudiado el problema considerando una respuesta homogénea del material. Teniendo en cuenta la diferente respuesta de material a tracción y a compresión, se muestra la descripción analítica que permite determinar si la probeta presenta modos de fallo iniciales debidos al momento flector o al esfuerzo cortante. La coincidencia con las observaciones experimentales muestran la capacidad del modelo analítico para definir laminados cuya respuesta de flexión y primer fallo pueden ser controlados previamente.
Agradecimientos
Este trabajo ha sido financiado por el Ministerio de Economía y Competitividad mediante el proyecto de referencia DPI2016-77715-R.
Referencias
[() ] UNE-EN 2562:1997: Aerospace series. Carbon fibre reinforced plastics. Unidirectional laminates. Flexural test parallel to the fibre direction (1997).
[2] UNE-EN ISO 14130:1999: fibre-reinforced plastic plastic composites. Determination of apparent interlaminar shear strength by shortbeam method (1999).
[3] M.C.Serna Moreno, A.Romero Gutiérrez, J.L.Martínez Vicente. Composite Structures,146, pág. 62–68 (2016).
[4] M.C.Serna Moreno, A.Romero Gutiérrez, J.L.Martínez Vicente. Composite Structures, 136, pág. 706–711 (2016).
[5] M.C.Serna Moreno, A.Romero Gutiérrez, J.L.Martínez Vicente. Materials Science and Engineering: IOP Conf. Series, 139, article 012047, 8 pages (2016), DOI:10.1088/1757-899X/139/1/012047.
[6] Callister WD. Materials Science and Engineering: An Introduction. John Wiley & Sons Inc; 2007.
[7] J.C. Halpin. Primer on composite materials analysis, Lancaster, PA: Technomic Publishing Co Inc (1992).
[8] Fuente: http://www.compositesworld.com/blog/23, Composites World, 26/06/2016.
[9] J.D. Fuller, M.R. Wisnom. Composites Part A, 69, pág. 64–71 (2015).
[10] J.D. Fuller, M.R. Wisnom. Composites Science and Technology, 112, pág. 8–15 (2015).
[11] R.M.Jones. Mechanics of Composite Materials, Taylor & Francis, ISBN: 1-56032-712-X (1999).
[12] J.A.Garrido, A.Foces. Resistencia de Materiales, Secretariado de Publicaciones. Universidad de Valladolid (1994).
Document information
Published on 14/10/18
Accepted on 14/10/18
Submitted on 14/10/18
Volume 02 - Comunicaciones Matcomp17 (2018), Issue Núm. 4 - Comportamiento en servicio de los materiales compuestos (2), 2018
DOI: 10.23967/r.matcomp.2018.10.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?