Research on dynamic characteristics of three-shafts ring-plate magnet gear

Revision as of 11:43, 1 September 2022

Abstract

Dynamic characteristic analysis is the key step to improve the transmission performance of eccentric permanent magnet gear. The study of this step can not only analyze the dynamic force process of each transmission part, but also improve the operation stability and bearing capacity of eccentric permanent magnet gear. Taking three-shaft ring-plate magnet gear (TRMG) as the research object, based on its operation mechanism and dynamic model, this paper establishes the balance equation of force and torque of each part of TRMG. Through the combination of electromagnetic finite element simulation and mathematical analysis method, the force of the input shaft and the supporting shaft in the TRMG motion process is solved. By improving the TRMG power input mode, the dynamic performance of TRMG is optimized, and the stability of transmission structure is improved. The feasibility of this new transmission mode is verified by multi-body dynamics analysis.

Keywords: Ring-plate permanent magnet gear, multiple crank mechanism, dynamic model, optimization and improvement

1. Introduction

Ring plate transmission device is a structure based on K-H type planetary gear transmission with small tooth difference. It has the advantages of compact structure, large transmission ratio, strong bearing capacity, and high transmission efficiency.

Chen et al. [1] first developed a mechanical three-ring reducer (TRR) transmission device, which moved the rolling bearings from the inside of the cycloid wheel in K-H-V small tooth difference reducer to the outside, greatly dispersed the payload of the rolling bearings, and effectively extended service life of rolling bearings.

TRR drives the eccentric rotation of the ring plate by two eccentric shafts and the fixed axis of the inner rotor rotates, so that the center point of the inner rotor must be in line with the center points of the eccentric shafts on both sides of the TRR. As a result, when the rotation angle of one eccentric shaft is 0° or 180°, the transmission trajectory of the other eccentric shaft is uncertain, so that the ring plate cannot run smoothly for a whole week. Therefore, TRR sets three ring plates, which are installed at 120° each other. When one ring plate is in uncertain motion, the other two ring plates can drive it through the position smoothly.

However, due to the large number of TRR ring plates and a small number of eccentric shafts, the eccentric shafts of TRR bear a large inertia force and radial force, which leads to large vibration and noise during the operation of TRR [2,3], and its mechanical gears are prone to tooth surface bonding, pitting, falling off and surface crushing [4-6]. Although scholars have studied the transmission structure, vibration frequency, and elastic deformation of TRR to improve its operating stability [7-11], due to the special structure of TRR, the inertia force and radial force borne by its eccentric shafts are still large.

In Ge et al. [12], a three-shaft ring-plate Magnet Gear (TRMG) is proposed for contactless transmission by using the air-gap magnetic field of permanent magnet gear, which can not only solve the problems of mechanical gear damage caused by TRR, because the three eccentric shafts of TRMG are arranged around the inner rotor at 120° each other, the uncertainty of ring plate movement caused by collinearity between the center of the eccentric shafts and the center of the inner rotor can also be avoided, and the number of ring plates can be reduced to one, so that the radial force and inertia force of the eccentric shaft of TRMG are much smaller than those of TRR [13].

Due to the multi-field coupling transmission mode of TRMG (the coupling of air-gap magnetic field and mechanical structure), the transmission analysis of its dynamic process is complicated, so the current research on TRMG is still in the static electromagnetic analysis stage [14-17]. However, the key theoretical steps to realize the practical application of TRMG are to analyze the dynamic transmission process of TRMG, and judge its motion stability and calculate the dynamic force status of each transmission shaft.

Therefore, combining the theory of electromagnetic field with the theory of rigid body dynamics, the electromagnetic drive equation and mechanical balance equation of TRMG components are established in this paper. By analyzing the dynamic characteristics of TRMG transmission structure, the stability during operation of TRMG and the force of each eccentric shaft are calculated, and the problems such as mechanical stuck of the structure and operation uncertainty are judged. Finally, by changing the power input mode of the transmission structure, the stability of the transmission structure is further improved and it has the possibility of practical application.

2. TRMG motion mechanism

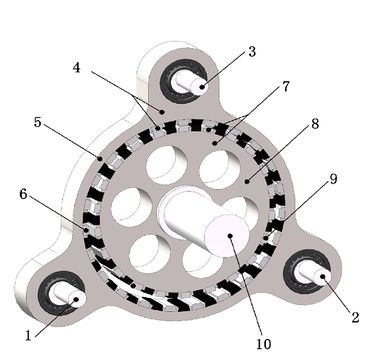
Figure 1 shows the mechanical structure of TRMG. In Figure 1, shaft 1, shaft 2, and shaft 3 are eccentric high-speed shafts, which are connected with ring-plate permanent magnet ring 4 through rolling bearings; the ring-plate permanent magnet ring 4 is composed of a ring plate (outer yoke) 5 and outer ring permanent magnet 6, and are located outside the low-speed permanent magnet ring 7; the low-speed permanent magnet ring 7 is composed of an inner yoke 8 and inner ring permanent magnet 9. In general, the difference between ring-plate permanent magnet ring and low-speed permanent magnet ring is 1 pair of magnetic pole pairs.

1-3: Eccentric high-speed shaft. 4: Ring-plate permanent magnet ring. 5: Ring plate. 6: Outer ring permanent magnet. 7: Low-speed permanent magnet ring. 8: Inner yoke. 9: Inner ring permanent magnet. 10: Low-speed shaft

Figure 1. TRMG mechanical structure diagram

In Figure 1, the eccentricity of eccentric high-speed shafts is equal to the eccentricity from ring-plate permanent magnet ring to low-speed permanent magnet ring. Set the radius of low-speed permanent magnet ring and ring-plate permanent magnet ring respectively is ${\textstyle r_{1}}$ and ${\textstyle r_{2}}$ respectively, and the eccentricity of the high-speed shaft is ${\textstyle r}$ , then: ${\textstyle r=r_{2}-r_{1}}$ .

When anyone high-speed shaft shown in Figure 1 drives the ring-plate permanent magnet ring to move, the outer ring permanent magnet rotates around the inner ring permanent magnet. Due to the change of the relative position of the two permanent magnets, the inner ring permanent magnet embedded in the low-speed permanent magnet ring rotates around its axis under the change of magnetic field force. Set the center of low-speed permanent magnet ring as ${\textstyle {\mbox{O}}_{1}}$ , the center of ring-plate permanent magnet ring as ${\textstyle {\mbox{O}}_{2}}$ , and the revolution angle speed of ring-plate permanent magnet ring as ${\textstyle \omega }$ , then the angular acceleration of ${\textstyle {\mbox{O}}_{2}}$ around ${\textstyle {\mbox{O}}_{1}}$ is ${\textstyle {\alpha }_{{\mbox{O}}2}={\omega }^{2}r}$ , whose direction is from ${\textstyle {\mbox{O}}_{2}}$ to ${\textstyle {\mbox{O}}_{1}}$ .

3. TRMG kinetic model and equilibrium equation

3.1 TRMG force analysis model

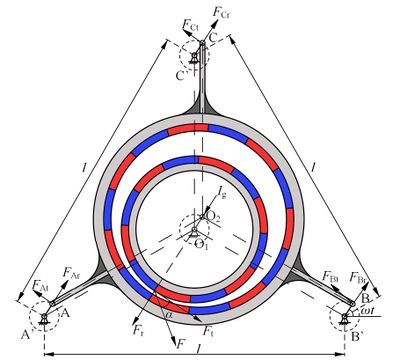
Figure 2 is the force analysis model of Figure 1.

Figure 2. TRMG force analysis model

In Figure 2, crank AA', crank BB' and crank CC' represent eccentric high-speed shaft 1, 2 and 3, respectively. $F_{r}$ and $F_{t}$ are the radial electromagnetic force and tangential electromagnetic force of low-speed permanent magnet ring and ring-plate permanent magnet ring respectively; $F_{Ar}$ , $F_{At}$ , $F_{Br}$ , $F_{Bt}$ , $F_{Cr}$ and $F_{Ct}$ are the radial force and tangential force of each eccentric high-speed shaft acting on the ring-plate bearing seat hole through rolling bearing; ${\textstyle I_{g}}$ is the inertial force on the ring-plate permanent magnet ring; ${\textstyle t}$ is crank rotation time and ${\textstyle l}$ is the rack spacing.

3.2 TRMG electromagnetic force analysis

Establish the low-speed permanent magnet ring section $XO_{1}$ Y rectangular coordinate system. Set up $\beta$ Is the included angle along the $x$ -direction at a point on the circumference of the inner ring permanent magnet rotor surface. Set up $B$ is the air-gap magnetic density at any point on the surface of the low-speed permanent magnet ring, $B_{x}$ and $B_{y}$ are components along with the $x$ and $y$ directions respectively, $B_{t}$ and $B_{r}$ are components along with the tangential and radial directions, respectively, then:

(1)

where $i$ is the TRMG transmission ratio.

Set up the tangential and radial electromagnetic force of the unit area of the low-speed permanent magnet ring are $f_{t}$ and $f_{r}$ . According to the Maxwell stress tensor method, it can be:

{\begin{array}{c}\displaystyle f_{t}={\frac {1}{{\mu }_{0}}}B_{r}\left(\beta ,t\right)B_{t}\left(\beta ,t\right)\\\displaystyle f_{r}={\frac {1}{2{\mu }_{0}}}\left[B_{r}^{2}\left(\beta ,t\right)-B_{t}^{2}\left(\beta ,t\right)\right]\end{array}}

(2)

where ${\mu }_{0}$ is the permeability of vacuum.

Set up the tangential and radial electromagnetic force of the low-speed permanent magnet ring are $F_{t}$ and $F_{r}$ respectively, then:

{\begin{array}{c}\displaystyle F_{t}=\oint f_{t}ds{=}{\frac {r_{1}L}{{\mu }_{0}}}{\int }_{0}^{2\pi }\left[B_{r}^{}\left(\beta ,t\right)B_{t}^{}\left(\beta ,t\right)\right]d\beta \\\displaystyle F_{r}=\oint f_{r}ds={\frac {r_{1}L}{2{\mu }_{0}}}{\int }_{0}^{2\pi }\left[B_{r}^{2}\left(\beta ,t\right)-B_{t}^{2}\left(\beta ,t\right)\right]d\beta \end{array}}

(3)

According to Eq. (3), $F_{r}$ and $F_{t}$ can be obtained as long as the surface air-gap magnetic density $B$ of the low-speed permanent magnet ring is obtained.

By taking the torque of tangential electromagnetic force, the electromagnetic torque ${\textstyle T}$ of the low-speed permanent magnet ring can be obtained:

(4)

3.3 Force analysis of each shaft with TRMG single-shaft input

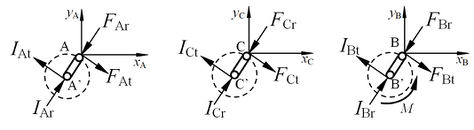
If crank BB' is used as the input shaft, and crank AA' and crank CC' are used as support shafts, the force model of each shaft is shown in Figure 3.

Figure 3. Force model of TRMG shafts

In Figure 3, $M$ is input torque, and $I_{Ar}$ , $I_{At}$ , $I_{Br}$ , $I_{Bt}$ , $I_{Cr}$ , and $I_{Ct}$ are the radial and tangential forces acting on A', B', and C' of the ring-plate permanent magnet ring through the rolling bearing, respectively.

The static equilibrium equations of ring-plate permanent magnet ring, input shaft B, and support shafts A and C can be obtained from the theoretical mechanical rigid body force and moment balance equations, respectively

{\begin{array}{c}F_{At}+F_{Bt}+F_{Ct}=F_{t}\\F_{Ar}+F_{Br}+F_{Cr}=F_{r}-I_{g}\\F_{Ar}\sin(\omega t-30{\mbox{°}})-F_{Br}\cos(\omega t-60{\mbox{°}})+F_{Bt}\sin(\omega t-60{\mbox{°}})+F_{Cr}\cos \omega t=\displaystyle {\frac {{\sqrt {3}}r_{2}}{l}}\cdot F_{t}\end{array}}

(5)

If $F_{a}$ , $F_{b}$ , and $F_{c}$ are set as the radial additional force acting on the ring-plate permanent magnet ring by the rolling bearing of each shaft respectively, then:

(6)

In Eq. (6), $F'_{Ar}$ , $F'_{Br}$ , and $F'_{Cr}$ are respectively the radial force of support shafts A, C and input shaft B acting on the ring-plate permanent magnet ring through the rolling bearing under the ideal condition, and:

(7)

In Eq. (7), the inertia force ${\textstyle I_{g}=m{\alpha }_{{O}2}{=}m{\omega }^{2}r}$ , where ${\textstyle m}$ is the weight of ring-plate permanent magnet ring.

According to Eq. (7), the difference between $F_{Ar}$ , $F_{Br}$ , and $F_{Cr}$ are proportional to the additional force applied.

If the contact stiffness of the rolling bearings of input shaft and the support shafts is $K$ , and the ring-plate permanent magnet ring generates angle by the radial additional force is ${\textstyle \alpha }$ , then the coordination conditions of the body displacement and its deformation can be obtained:

(8)

According to Eq. (8), the difference between the tangential force of crank BB' (input shaft) and the tangential electromagnetic force of low-speed permanent magnet ring (output shaft) in TRMG can lead to deviation from the ideal state during the operation of ring-plate.

Combine Eq. (8) with Eqs. (3)-(7), it can be obtained:

(9)

(10)

(11)

(12)

(13)

According to Eq. (10), when the structural parameters of TRMG permanent magnets remain unchanged, $F_{Bt}$ is proportional to the input torque $M$ and inversely proportional to the eccentricity of the high-speed shaft $r$ .

It can be seen from Eqs. (11)-(13):

(1) The radial force of each shaft in TRMG is composed of tangential and radial electromagnetic force of low-speed permanent magnet ring and the tangential force of input shaft.

(2) When $\omega t$ is equal to 0° or 180°, that is, when the crank AA' and the crank BB' are collinear with the connecting rod AB, $F_{Cr}$ is larger than $F_{Ar}$ and $F_{Br}$ , indicating that the crank CC' drives the crank AA' and the crank BB' to move through ring-plate and making them pass through the collinear position smoothly.

(3) Since the expressions of $F_{Ar}$ , $F_{Br}$ and $F_{Cr}$ contain trigonometric functions of input tangential force and tangential electromagnetic force, the impact load of input shaft and support shafts can be reduced by reducing their amplitudes, to slow down the extrusion and elastic deformation caused by impact load and increase the service life of rolling bearings.

4. TRMG dynamic model simulation

To obtain the force relationship curve of each moving part in TRMG, Ansys Maxwell is used to analyzing the magnetic field force between the low-speed permanent magnet ring and the ring-plate permanent magnet ring, to determine the radial and tangential electromagnetic force in TRMG. $F_{\mbox{t}}$ and $F_{\mbox{r}}$ are then put into MATLAB force analysis program, and the force curve of each motion shaft is determined.

4.1 Analysis of TRMG electromagnetic characteristics

Set rated power is $P=1{\mbox{kW}}$ rated output speed of low-speed permanent magnet ring is $n_{\mbox{o}}=70{\mbox{r/min}}$ , transmission ratio is $i=22$ , torque density is $T_{\mbox{d}}=148{\mbox{kN}}\cdot {\mbox{m/m}}^{\mbox{3}}$ , flux leakage coefficient is 0.2. The static and dynamic electromagnetic fields that calculate the function of Ansys Maxwell are used to analyze the finite element structure of TRMG and TRMG parameters are optimized according to improved torque characteristics. Finally, TRMG electromagnetic model parameters as shown in Table 1 can be obtained.

Table 1. TRMG electromagnetic model parameters

Symbol	Description	Value (Unit)
${\textstyle p_{i}}$	Pole pairs of inner permanent magnet	${\textstyle 22}$
${\textstyle p_{o}}$	Pole pairs of outer permanent magnet	${\textstyle 23}$
${\textstyle r_{1}}$	Inner radius of outer yoke iron	${\textstyle 96}$ (mm)
${\textstyle r_{2}}$	Outer radius of outer permanent magnet ring	${\textstyle 100}$ (mm)
${\textstyle r_{3}}$	Inner radius of outer permanent magnet ring	${\textstyle 94}$ (mm)
${\textstyle r_{4}}$	Outer radius of inner permanent magnet ring	${\textstyle 90}$ (mm)
${\textstyle r_{5}}$	Inner radius of inner permanent magnet ring	${\textstyle 84}$ (mm)
${\textstyle r_{6}}$	Outer radius of inner yoke iron	${\textstyle 88}$ (mm)
${\textstyle h_{i}}$	Inner yoke iron thickness	${\textstyle 15}$ (mm)
${\textstyle h_{o}}$	Outer yoke iron thickness	${\textstyle 15}$ (mm)
${\textstyle r}$	Eccentricity	${\textstyle 3}$ (mm)
${\textstyle L}$	Axial length	${\textstyle 30}$ (mm)
${\textstyle M_{m}}$	Magnetization	- ${\textstyle 890}$ (kA/m)
${\textstyle {\mu }_{0}}$	Vacuum permeability	${\textstyle 4\pi \times 10^{-7}}$

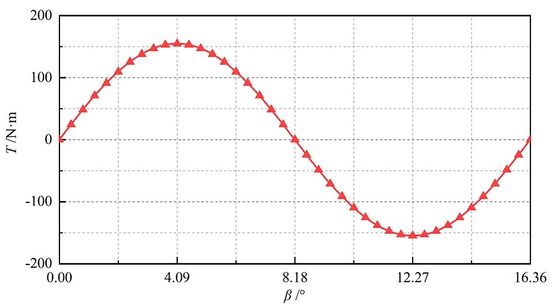
Figure 4 shows TRMG electromagnetic torque curve based on the parameters in Table 1 by ANSYS.

Figure 4. Relationship between

and

As can be seen from Figure 4, the electromagnetic torque curve of low-speed permanent magnet ring is a sine wave. When it rotates 1/2 and 3/2 magnetic pole angles, the maximum output electromagnetic torque is $T_{\max }=148{\mbox{kN}}\cdot {m}$ . In this paper, the load torque is 125N·m.

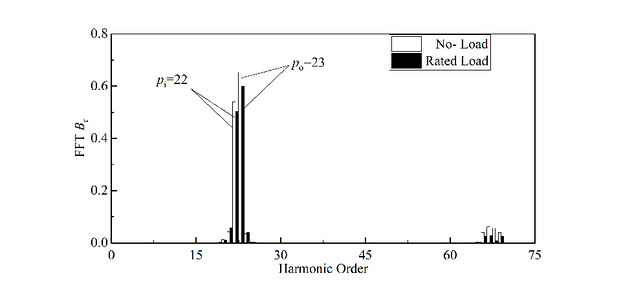
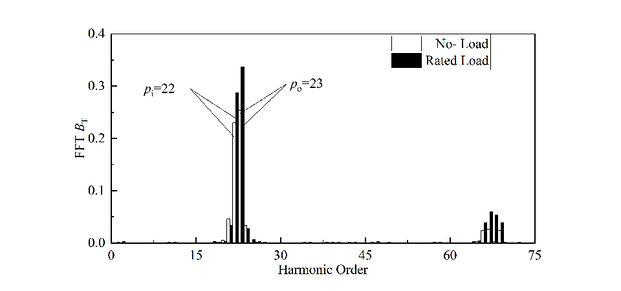
Figures 5 and 6 show the harmonic comparison of radial and tangential air-gap magnetic density of TRMG under no-load and load after Fourier decomposition.

As can be seen from Figure 5, the radial air-gap flux density waveform of TRMG is mainly composed of 22nd harmonic and 23rd harmonic, among which the 23rd and 22nd harmonic of no-load (about 0.65t and 0.55t) are larger than the loaded harmonic (about 0.59t and 0.51t). As can be seen from Figure 6, the 23rd and 22nd harmonics (about 0.25t and 0.23t) of TRMG tangential air-gap flux density in no load are less than the loaded harmonics (about 0.34t and 0.29t).

Figure 5. The spectrum of radial electromagnetic force

Figure 6. The spectrum of tangential electromagnetic force

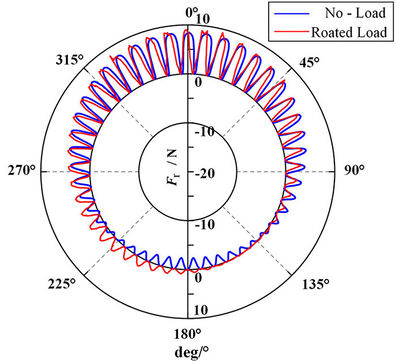
Combined with Eqs. (3) and (4), the variation of radial electromagnetic force acting on low-speed permanent magnet ring with no-load and rated load can be obtained, as shown in Figure 7.

Figure 7. The distribution curve of radial electromagnetic force

As can be seen from Figure 7, the positive direction of ${\textstyle F_{r}}$ deviates from the center of the circle, while the negative direction of ${\textstyle F_{r}}$ points to the center of the circle. Therefore, the smaller side of the air-gap between permanent magnets attracts each other, while the larger side repays each other. The average radial electromagnetic force under no-load and rated load is 535N and 441N respectively. The tangential electromagnetic force is small at no-load, and most of the air-gap magnetic field generated by TRMG acts on the radial magnetic field force, making the radial magnetic field force larger at no-load.

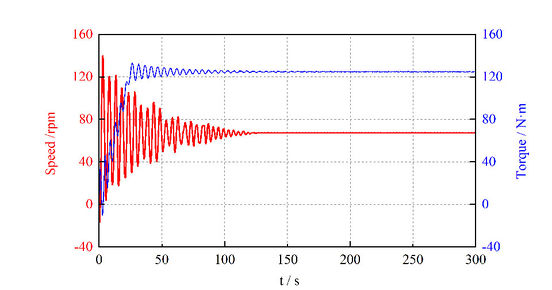
Figure 8 shows the dynamic characteristic curve of low-speed permanent magnet ring under rated load.

Figure 8. Dynamic characteristic of low-speed permanent magnet ring

According to the transmission ratio and Maxwell stress tensor method, the input torque ${\textstyle M=5.64}$ N·m, and the tangential and radial electromagnetic force received by the low-speed permanent magnet ring is $F_{t}=1378$ N and $F_{r}=441$ N, respectively.

4.2 TRMG each shaft force analysis

Suppose that the force of shaft A, shaft B and shaft C on the ring-plate bearing hole through the rolling bearing is $F_{A}$ , $F_{B}$ and $F_{C}$ , respectively, then:

{\begin{array}{c}F_{A}={\sqrt {F_{Ar}^{2}+F_{At}^{2}}}\\F_{B}={\sqrt {F_{Br}^{2}+F_{Bt}^{2}}}\\F_{C}={\sqrt {F_{{C}r}^{2}+F_{{C}t}^{2}}}\end{array}}

(14)

According to TRMG mechanical analysis model, TRMG dynamic force is analyzed in MATLAB, and $F_{t}=1378$ N and $F_{r}=441$ N are replaced into the equation to obtain the change curves of force of input shaft and support shafts in Figure 9.

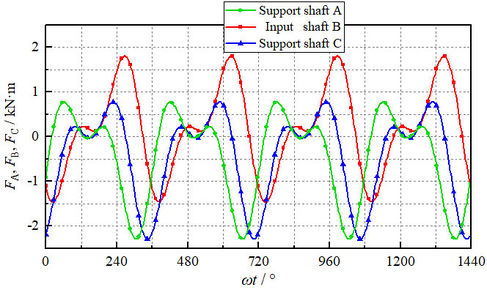
Figure 9. Change curves of

,

and

under single shaft driving

Figure 9 shows that:

(1) When the cranks rotate, the force of the input shaft and the support shafts change periodically, and the varying degree of support shaft A and C is the same. According to Eq. (9), $F_{At}$ and $F_{Ct}$ are 0, shaft A and C are only TRMG connection structures, and both transmission process are the same, so the bearing force trends is the same.

(2) When the cranks rotate, the force of the input shaft and the support shafts can make fluctuate in addition to periodic change. For example, when $\omega t=120{\mbox{°}}$ , the change of $F_{B}$ produces fluctuation.

Because in Figure 9, when $\omega t=120{\mbox{°}}$ , crank BB' and crank CC' are collinear with connecting rod BC. At this time, due to $F_{A}$ is small and it fails to pass smoothly through the collinear position, resulting in the fluctuation of $F_{B}$ .

When $\omega t=180{\mbox{°}}$ , although the crank AA' and crank BB' are collinear with the connecting rod AB, $F_{C}$ is large at this time, which enables to pass through the collinear position smoothly, so $F_{B}$ does not fluctuate at this time. Similarly, the same is true for $F_{A}$ and $F_{C}$ fluctuations.

5. TRMG multi-shafts drive mode

Due to TRMG's low operating efficiency driven by a single shaft, the force range of the rolling bearing is large and has large fluctuations, leading to low service life. The power is input and studied by three cranks of TRMG at the same time.

5.1 Force analysis of TRMG with multi-shafts drive

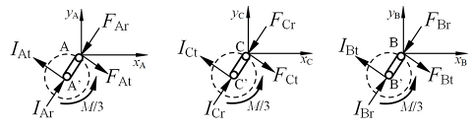
Figure 10 is a schematic diagram of the force acting on each shaft in the multi-shafts drive.

Figure 10. TRMG force analysis under multi-shafts driving

As can be seen from Figure 10, since the support cranks are changed to input cranks, the force between the input cranks is the same. At this time, the static balance equations of input crank AA', BB' and CC' are:

(15)

{\begin{array}{c}F_{Ar}{=}\displaystyle {\frac {r_{1}L}{6{\mu }_{0}}}{\int }_{0}^{2\pi }\left[B_{r}^{2}\left(\beta ,t\right)-B_{t}^{2}\left(\beta ,t\right)\right]d\beta -\displaystyle {\frac {1}{3}}I_{g}+\displaystyle {\frac {{\sqrt {3}}M}{108r}}-\displaystyle {\frac {M}{54r}}\sin 2\omega t-\displaystyle {\frac {M}{9r}}\sin(\omega t-30{\mbox{°}})\sin \omega t-\\-\displaystyle {\frac {M}{18r}}\sin(2\omega t-60{\mbox{°}})-\displaystyle {\frac {{\sqrt {3}}r_{2}r_{1}L}{3l{\mu }_{0}}}\sin(\varphi -30{\mbox{°}}){\int }_{0}^{2\pi }\left[B_{r}^{}\left(\beta ,t\right)B_{t}\left(\beta ,t\right)\right]d\beta \end{array}}

(16)

{\begin{array}{c}F_{Br}{=}\displaystyle {\frac {r_{1}L}{6{\mu }_{0}}}{\int }_{0}^{2\pi }\left[B_{r}^{2}\left(\beta ,t\right)-B_{t}^{2}\left(\beta ,t\right)\right]d\beta \displaystyle {\frac {1}{3}}I_{g}+{\frac {M}{18r}}\sin(2\omega t-120{\mbox{°}})-\displaystyle {\frac {M}{9r}}\sin \omega t\cdot \cos(\omega t-60{\mbox{°}})-\\-\displaystyle {\frac {{\sqrt {3}}M}{36r}}+\displaystyle {\frac {M}{18r}}\sin 2\omega t-\displaystyle {\frac {{\sqrt {3}}r_{2}r_{1}L}{3l{\mu }_{0}}}\cos(\omega t-60{\mbox{°}}){\int }_{0}^{2\pi }\left[B_{r}^{}\left(\beta ,t\right)B_{t}^{}\left(\beta ,t\right)\right]d\beta \end{array}}

(17)

{\begin{array}{c}F_{Cr}{=}\displaystyle {\frac {r_{1}L}{6{\mu }_{0}}}{\int }_{0}^{2\pi }\left[B_{r}^{2}\left(\beta ,t\right)-B_{t}^{2}\left(\beta ,t\right)\right]d\beta -\displaystyle {\frac {1}{3}}I_{g}+\displaystyle {\frac {{\sqrt {3}}M}{9r}}{\cos }^{2}\omega t+\displaystyle {\frac {M}{18r}}\sin 2\omega t+\\+\displaystyle {\frac {{\sqrt {3}}r_{2}r_{1}L}{3l{\mu }_{0}}}\cdot \cos \omega t{\int }_{0}^{2\pi }\left[B_{r}^{}\left(\beta ,t\right)B_{t}\left(\beta ,t\right)\right]d\beta \end{array}}

(18)

By comparing Eqs. (16)-(18) and Eqs. (11)-(13), it can be seen that the difference between TRMG tangential electromagnetic force and the input tangential force is reduced by using the multi-shafts drive, thus reducing the magnitude and amplitude of $F_{Ar}$ , $F_{Br}$ and $F_{Cr}$ .

5.2 Force relationship curve of TRMG each shaft by multi-shafts

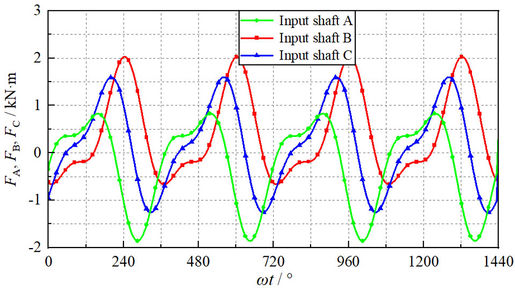
By substituting Eqs.(16)-(18) into MATLAB transmission force analysis program, the force variation curves of input shafts A, B, and C shown in Figure 11 can be obtained.

Figure 11. Change curves of

,

and

under multi-shafts driving

In order to make a more intuitive comparison between the performance of multi-shafts and single shaft drive, the performance comparison of TRMG under multi-shafts and single shaft drive is shown in Table 2.

Table 2. Performance comparison of TRMG multi-shafts vs single shaft drive.

Parameter Comparison	Single shaft drive	Multi-shafts drive
$F_{A}$ maximum value	$2.2$ (kN)	$1.6$ (kN)
$F_{A}$ oscillation wave	$0.5$ (kN)	$0$ (kN)
$F_{B}$ maximum value	$1.8$ (kN)	$2.1$ (kN)
$F_{B}$ oscillation wave	$0.3$ (kN)	$0$ (kN)
$F_{C}$ maximum value	$2.2$ (kN)	$1.6$ (kN)
$F_{C}$ oscillation wave	$0.5$ (kN)	$0$ (kN)

From Table 2, after TRMG adopts multi-shafts drive when the cranks rotate, the force on shaft B increases slightly ( $0.3$ kN), but the force on shaft A and shaft C decreases significantly ( $0.6$ kN). As can be seen from Figures 10 and 11, the force acting on each shaft is more average. This is because after changing to multi-shafts drive, the eccentric magnetic field force of the magnetic force device can be greatly reduced due to the symmetrical distribution of the magnetic force device of the input shafts relative to the TRMG, thus the force acting on each input shaft is more uniform and the stress environment of each shaft can be effectively alleviated.

In addition, the vibration of $F_{A}$ , $F_{B}$ , and $F_{C}$ is eliminated after changing to multi-shafts drive, and the vibration problem of each shaft is solved. Thus, the stress condition of rotary bearings can be significantly improved and their service life can be prolonged.

6. TRMG multibody dynamics analysis

To further verify the correctness of established TRMG torque balance equation and determine the feasibility of multi-shafts drive TRMG scheme, through ADAMS multi-body dynamics simulation software is used to analyze the values of $F_{A}$ , $F_{B}$ , and $F_{C}$ in multi-shafts drive TRMG, and the results are compared with the calculated data.

Table 3 shows the constraint allocation of mechanical devices in the TRMG multi-body dynamics simulation model.

Table 3. Constraint allocation of TRMG model

Part - Part	Constraint
Input shaft A- Ground	Rotating
Input shaft B- Ground	Rotating
Input shaft C- Ground	Rotating
Input shaft A- Ring-plate permanent magnet ring	Rotating
Input shaft B- Ring-plate permanent magnet ring	Rotating
Input shaft C- Ring-plate permanent magnet ring	Rotating
Low-speed permanent magnet ring - Output shaft	Fixed
Output shaft - Ground	Rotating

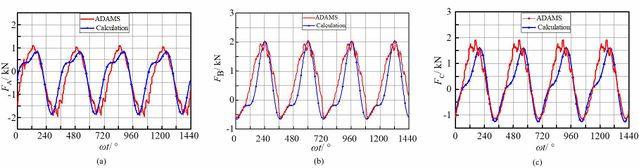
According to the analysis results of the TRMG dynamics model, input shafts A, B, and C are given input speed $n=1200$ r/min, and the output shaft is given load torque of 124N·m.The multi-body dynamics simulation and analytical calculation data curves of the forces acting on input shafts A, B, and C are obtained, as shown in Figure 12.

Figure 12.

,

and

> theory and multi-body dynamics distribution curves

As can be seen from Figure 12:

(1) When multi-body dynamics analysis of multi-shafts driven TRMG is adopted, the numerical changes of $F_{A}$ , $F_{B}$ , and $F_{C}$ tend to be more sinusoidal, and their results are always greater than those of analytical analysis.This is because the multi-body dynamic analysis needs to consider the material properties of the structure, the moment of inertia, the distribution of constraints, and other factors, and also takes the coupling relationship between components into account, which makes the running process of each shaft in the simulation more stable, and finally leads to the large results of $F_{A}$ , $F_{B}$ , and $F_{C}$ , and the changes tend to be more sinusoidal.

(2) When using the multi-body dynamic analysis and analytical analysis, the variation trend of $F_{A}$ , $F_{B}$ , and $F_{C}$ in the two analysis results is roughly the same, and the deviation of their amplitude is within a reasonable range (about 10%). Thus, it can be further confirmed that the established TRMG torque balance equation is correct. In addition, $F_{A}$ , $F_{B}$ , and $F_{C}$ of the two analyses all changed periodically without significant fluctuation, which confirmed the feasibility of a multi-shafts TRMG drive scheme.

7. Conclusions

(1) Combined of electromagnetism theory and rigid body statics theory, TRMG mechanical balance equation is established, and FEM and mathematical analytical method are combined to solve the force acting on each shaft, Finally, the validity of TRMG model is verified by multi-body dynamics method.

(2) Compared with the single-shaft drive mode, TRMG adopts multi-shafts drive, which can make the force on each drive shaft more even, eliminate the shock caused by the single-shaft drive, greatly improve the force condition of the rolling bearing, and prolong the service life of the rolling bearing.

(3) The established TRMG mathematical model has universality, which provides a certain mathematical basis for in-depth study of multi-shafts ring-plate transmission structure and magnetic gear structure with large torque.

Acknowledgments

This work was funded by the National Natural Science Foundation of China (Grant No.51375063), and also sponsored by the Natural Science Research Project of Liaoning Province Education Department (Grant No.JDL2020001) and partly funded by the Technological Innovation Research Foundation Project of Dalian (Grant No.2018J12SN071).

References

[1] Chen Z.Y., Liu Z.W., Wang Z.D., Guo S.L. Three-ring type deceleration (or increase) transmission device. CN85106692, 1987.

[2] Song Y., Tian G., Zhang J., Liu M., Liu J. Prediction for dynamic characteristics of ring-plate planetary indexing cam mechanism. Transactions of Tianjin University, 15:249-254, 2009.

[3] Yang B., Liu Y., Zhong Z. Experimental research on noise source identification of ring-plate pin-cycloid planetary reducer. ICLEM 2010: Logistics for Sustained Economic Development, 1596-1601, 2010.

[4]. Liu M., Song Y., Zhang C., Tian G. Force analysis of rollers of ring-plate-type planetary indexing cam mechanism. China Mechanical Engineering, 19(16):1912-1915, 2008.

[5] Jafarizadeha M.A., Hassannejadb R., Ettefaghb M.M., Chitsazb S. Asynchronous input gear damage diagnosis using time averaging and wavelet filtering. Mechanical Systems and Signal Processing, 22:172-201, 2008.

[6] Wang W.Q., Ismail F., Golnaraghi M.F. Assessment of gear damage monitoring techniques using vibration measurements. Mechanical Systems and Signal Processing, 15(5):905-922, 2001.

[7] Shin J.H., Kwon S.M. On the lobe profile design in a cycloid reducer using instant velocity center. Mechanism and Machine Theory, 41:596-616, 2006.

[8] Liu W., Lin T., Xie Y. Vibration characteristic analysis and experimental research of double-ring gear reducer. China Mechanical Engineering, 20(10):1192-1196, 2009.

[9] Ce Z.J.S.Y.Z., Xianju M. Statics analysis of three-ring gear reducer by finite element method. Transactions of the Chinese Society for Agricultural Machinery, 38(3):141-143, 2007.

[10] Zhang J., Song Y.M., Zhang C. Elasto-dynamic analysis of ring-plate gear reducer with small tooth number difference. Journal of Mechanical Engineering, 44(2):118-123, 2008.

[11] Lei Z.C.L.L.Z., Bin Y. Study on double-crank reducer with external gear board. Transactions of the Chinese Society for Agricultural Machinery, 39(8):149-152, 2008.

[12] Ge Y., Liu D., Wang D. Research on three-shaft ring-plate permanent magnetic gear variable speed transmission device. 2021 IEEE International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), pp. 66-70, 2021.

[13] Ge Y., Liu D. Analysis of structure and starting characteristics of three-shaft ring-plate permanent magnet gear. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 37(4), 44, 2021.

[14] Molokanov O., Dergachev P., Dergachev S., Kuznetsova E., Kurbatov P. A novel double-rotor planetary magnetic gear. IEEE transactions on magnetics, 54(11):1-5, 2018.

[15] Ge Y.J., Nie C.Y., Xin Q. A three dimensional analytical calculation of the air-gap magnetic field and torque of coaxial magnetic gears. Progress In Electromagnetics Researc, 131:391-407, 2012.

[16] Davey K., McDonald L., Hutson T. Axial flux cycloidal magnetic gears. IEEE Transactions on Magnetics, 50(4):1-7, 2014.

[17] Deng Z., Nas I., Dapino M.J. Torque analysis in coaxial magnetic gears considering nonlinear magnetic properties and spatial harmonics. IEEE Transactions on Magnetics, 55(2):1-11, 2019.