Revision as of 13:23, 28 June 2022 (view source) Rimni (talk | contribs) ← Older edit		Revision as of 13:28, 28 June 2022 (view source) Rimni (talk | contribs) (→‎5. Application of the rod counting method to the Mandelbrot fractal) Newer edit →
Line 337:		Line 337:
	Using the described method of counting rods on a Mandelbrot fractal generated in GeoGebra and whose profile with the different sizes of rods used is shown in [[#img-5|Figure 5]] and the counting results are described in  [[#table-4|Table 4]].		Using the described method of counting rods on a Mandelbrot fractal generated in GeoGebra and whose profile with the different sizes of rods used is shown in [[#img-5|Figure 5]] and the counting results are described in  [[#table-4|Table 4]].
−	With the results of  [[#table-4|Table 4]], the linear approximation is made, following the Richardson method, which gives us the function of the straight line that best fits the set of points and which is (Eq.[[#eq-4|(4)]]):	+	<div id='img-5'></div>
−		+	{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;"
−	<span id="eq-4"></span>	+
−	{| class="formulaSCP" style="width: 100%; text-align: left;"	+
−	|-	+
−	|	+
−	{| style="text-align: left; margin:auto;width: 100%;"	+
	|-		|-
−	| style="text-align: center;" | <math>h\left(x\right)=1.15397x+3.49872 \;\; \Rightarrow \;\; D_{Br} = 1.15397 </math>	+	|[[Image:Review_986628909362-Fig5-Chaos.png|357px|The different sizes of rods used to enclose the Mandelbrot fractal are shown, in a perimeter measurement using the rod counting method. The different lengths of the rods were (in cm): a) 0.2, b) 0.15, c) 0.1, d) 0.08, d) 0.06 and e) 0.04.]]
−	|}	+	|- style="text-align: center; font-size: 75%;"
−	| style="width: 5px;text-align: right;white-space: nowrap;" | (4)	+	| colspan="1" | '''Figure 5:''' The different sizes of rods used to enclose the Mandelbrot fractal are shown, in a perimeter measurement using the rod counting method. The different lengths of the rods were (in cm): a) 0.2, b) 0.15, c) 0.1, d) 0.08, d) 0.06 and e) 0.04.
	|}		|}
		+
	<div class="center" style="font-size: 75%;">'''Table 4'''. Results of rod counting measurements on a Mandelbrot fractal</div>		<div class="center" style="font-size: 75%;">'''Table 4'''. Results of rod counting measurements on a Mandelbrot fractal</div>
Line 389:		Line 385:
−	<div id='img-5'></div>	+	With the results of  [[#table-4|Table 4]], the linear approximation is made, following the Richardson method, which gives us the function of the straight line that best fits the set of points and which is (Eq.[[#eq-4|(4)]]):
−	{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;"	+
		+	<span id="eq-4"></span>
		+	{| class="formulaSCP" style="width: 100%; text-align: left;"
	|-		|-
−	|[[Image:Review_986628909362-Fig5-Chaos.png|357px|The different sizes of rods used to enclose the Mandelbrot fractal are shown, in a perimeter measurement using the rod counting method. The different lengths of the rods were (in cm): a) 0.2, b) 0.15, c) 0.1, d) 0.08, d) 0.06 and e) 0.04.]]	+	|
−	|- style="text-align: center; font-size: 75%;"	+	{| style="text-align: left; margin:auto;width: 100%;"
−	| colspan="1" | '''Figure 5:''' The different sizes of rods used to enclose the Mandelbrot fractal are shown, in a perimeter measurement using the rod counting method. The different lengths of the rods were (in cm): a) 0.2, b) 0.15, c) 0.1, d) 0.08, d) 0.06 and e) 0.04.	+	|-
		+	| style="text-align: center;" | <math>h\left(x\right)=1.15397x+3.49872 \;\; \Rightarrow \;\; D_{Br} = 1.15397 </math>
		+	|}
		+	| style="width: 5px;text-align: right;white-space: nowrap;" | (4)
	|}		|}

---

Revision as of 13:28, 28 June 2022

Abstract

In this work, the “rod counting” method is reviewed in comparison with the “box counting” method applied to linear measurements on irregular figures. Both methods are applied in measurements of fractal dimension of some knowing fractals. Results shows that the “rod counting” method is more accurate in linear measurements. Later the method is applied in a Mandelbrot fractal figure to measure its perimeter fractal dimension.

Keywords: Rod counting, box counting, Mandelbrot fractal, fractal dimension, ImageJ

1. Introduction

When Benoit Mandelbrot initially refers to the method of Lewis Fry Richardson [1,2,3] on the measurements of the coast lines (${\textstyle L}$) of Britain or borders of Germany, Spain, etc., he does so using the idea of “a compass opening” or rods of the same size (${\textstyle s}$) in a first measurement, and that later, changes the size of the rods to measure the coastline or border again (Richardson's method).

Then, when plotting these results wit ${\textstyle \ln(L)}$ on the vertical axis and ${\textstyle \ln(s)}$ on the horizontal axis, it is described a straight line when a linear fit of the measurements is made and the Hausdorff-Besicovitch dimension is related with the slope of the line.

Mandelbrot also refers to the fact that the measurements made in 2-H, in the case of self-similarity, coincide with the Hausdorff-Besicovitch dimension [2]. However, the comparison that Mandelbrot makes in his 1967 article [1], for linear measurements he does with variants of the Koch curve and whose statistical self-similarity is the Hausdorff-Besicovitch fractal dimension.

The fractal dimension method are used in medicine to study breast cancer, but the use of this technique is done by analysing the contour of an image generated in a mammography and periodically reviewing the evolution of the disease through the revision of the perimeter of the updated images [4,5]. The same procedure is used for recognition of plants [6] through the study of their leaves (analysis of the contour and veins).

The “box counting” method has been used to measure the fractal dimension of areas as well as lengths, this consists of building a box with side ``${\textstyle \xi _{k}}$ and counting the points that remain inside the box, the relation of powers for any dimension is (Eq. (1)):

${\displaystyle N\approx {\frac {L}{\xi _{k}}}\;\;{;}\;\;N\approx {\frac {A}{\xi _{k}^{2}}}\;\;{;}\;\;N\approx {\frac {V}{\xi _{k}^{3}}}\;\;\Rightarrow \;\;N\propto {\frac {1}{\xi _{k}^{D}}}}$

(1)

where ${\textstyle L}$ is the perimeter length ${\textstyle \xi _{k}}$ is the scale, ${\textstyle A}$ is the area, ${\textstyle V}$ is the volume, ${\textstyle N}$ is the number of “rods”, “boxes” or “cubes” used, and “D” is the Hausdorff-Besicovitch dimension.

Applying the relationship only for longitudinal measurements, let us compare the results given by the measurement made using boxes (Box Counting) with that made through rods (Rod Counting). The measurements for the counting of boxes will be carried out with the “ImageJ” application [7] that is part of a “SciJava OSS” free software project using the “FracLac” plugin and the counting of rods with the “GeoGebra” app [8].

The box counting technique has been reviewed by some authors and an optimization algorithm has been proposed [9], however the results obtained when applying the procedure are close to the rod counting method, but the latter being simpler in its implementation.

2. Calculation of the fractal dimension with the Richardson method

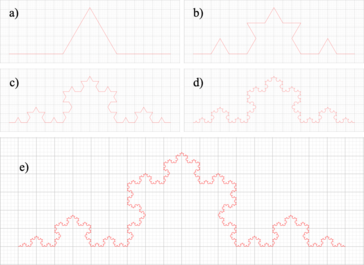
To carry out this comparison we will use the Koch curve, whose Hausdorff-Besicovitch fractal dimension is known (${\textstyle D=1.26186}$), [10,11]. Figure 1 shows five moments of construction of the Koch curve, which was generated in GeoGebra [8].

Figure 1. Koch curve generated in GeoGebra

Arranging these construction moments in Table 1 following the methodology proposed by Richardson, we obtain the straight line whose slope is the Hausdorff-Besicovitch fractal dimension [1], [12]-[18].

L. Rod ${\textstyle \left(a_{k}\right)}$	Scale ${\textstyle \left(\xi _{k}=a_{k}/a_{1}\right)}$	N. Rods ${\textstyle N(\xi _{k})}$	${\displaystyle P_{k}\left(\ln(1/\xi _{k}),\ln(N)\right)}$
3	1	4	${\displaystyle P_{1}\left(0,1.38629\right)}$
1	1/3	16	${\displaystyle P_{2}\left(1.09861,2.77259\right)}$
1/3	1/9	64	${\displaystyle P_{3}\left(2.19732,4.15888\right)}$
1/9	1/27	256	${\displaystyle P_{4}\left(3.2954,5.54518\right)}$
1/27	1/81	1024	${\displaystyle P_{5}\left(4.39445,6.93147\right)}$

Linear fit of the data in the last column of Table 1 leads us to the linear function (Eq.(2)):

${\displaystyle f\left(x\right)=1.26186x+1.38629}$

(2)

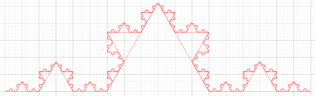
where it is observed that the slope of this function is the fractal dimension calculated based on the Hausdorff-Besicovitch description for Koch's curve, but obtained with Richardson's procedure (Figure 2).

Figure 2. Fractal dimension of Koch's curve measured following Richardson's method with the “rod” sizes equals to the original size used in every step of construction

Geometric fractals of a) Hilbert's curve, b) Koch 85's curve and c) the Cantor middle-thirds set were also generated in GeoGebra [8], whose fractal dimensions were calculated with the rod counting method, which are shown in Table 2. These figures were generated and measured since their fractal dimension are calculated with the perimeter or contour procedure. There are other fractal figures that can be generated, such as the Sierpinsky's triangle and carpet and some others, but since areas are generated in these elements, it is more convenient to use the box counting method there.

	(a) Hilbert's curve fractal ${\displaystyle h\left(x\right)=2.041x+1.2403}$
	L. Rod ${\textstyle \left(a_{k}\right)}$	Scale ${\textstyle \left(\xi _{k}=a_{k}/a_{1}\right)}$	N. Rods ${\textstyle N\left(\xi _{k}\right)}$	${\displaystyle P_{k}\left(\ln \left(1/\xi _{k}\right),\ln \left(N\right)\right)}$
	4	1	3	${\displaystyle P_{1}\left(0,1.0986\right)}$
	2	0.5	15	${\displaystyle P_{2}\left(0.6931,2.7081\right)}$
	1	0.25	63	${\displaystyle P_{3}\left(1.3863,4.1431\right)}$
	0.5	0.125	255	${\displaystyle P_{4}\left(2.0794,5.5413\right)}$
	0.25	0.625	1023	${\displaystyle P_{5}\left(2.7726,6.9305\right)}$
	0.125	0.0313	4095	${\displaystyle P_{6}\left(3.4657,8.3175\right)}$
	0.0625	0.0156	16383	${\displaystyle P_{7}\left(4.1589,9.7040\right)}$
	0.0313	0.0078	65535	${\displaystyle P_{8}\left(4.8520,11.0903\right)}$
	(b) Koch 85's curve fractal ${\displaystyle m\left(x\right)=1.785x+1.386}$
	4.1392	1	4	${\displaystyle P_{1}\left(0,1.3863\right)}$
	1.9037	0.4599	16	${\displaystyle P_{2}\left(0.7767,2.7726\right)}$
	0.8755	0.2115	64	${\displaystyle P_{3}\left(1.5535,4.1589\right)}$
	0.4027	0.0973	256	${\displaystyle P_{4}\left(2.3301,5.5452\right)}$
	0.1852	0.0447	1024	${\displaystyle P_{5}\left(3.1068,6.9315\right)}$
	0.0852	0.0206	4096	${\displaystyle P_{6}\left(3.8833,8.3178\right)}$
	0.0392	0.0095	16384	${\displaystyle P_{7}\left(4.6596,9.7041\right)}$
	(c) Cantor middle-thirds set fractal ${\displaystyle n\left(x\right)=0.6309x+0.6931}$
	0.3333	1	2	${\displaystyle P_{1}\left(0,0.6931\right)}$
	0.1111	0.3333	4	${\displaystyle P_{2}\left(1.0986,1.3863\right)}$
	0.037	0.1111	8	${\displaystyle P_{3}\left(2.1972,2.0794\right)}$
	0.0123	0.037	16	${\displaystyle P_{4}\left(3.2958,2.7726\right)}$
	0.0041	0.0123	32	${\displaystyle P_{5}\left(4.3944,3.4657\right)}$

3. Application of the box counting method

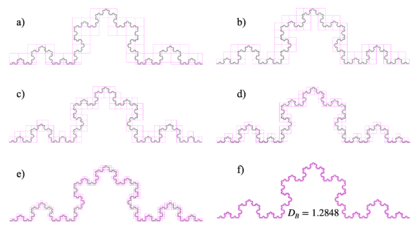
Let's calculate the fractal dimension again for Figure 1e, but using the “ImageJ” application [7] through the “FracLac” plugin. For this was generated an image in jpg, png or bmp format with only the Koch's curve, to be able to carry out the procedure in the aforementioned software. Figure 3 shows the result obtained [4]-[12].

Figure 3. Fractal dimension ${\displaystyle D_{B}=1.2848}$ calculated using the “FracLac” plugin of “ImageJ” app

The image shown has different sizes of the “boxes” and in the smaller one (Figure 3f) the fractal dimension that was obtained and that shows a difference with the one calculated directly from (Figure 1e) with the procedure carried out in Table 1, this difference of the fractal dimensions is ${\textstyle \Delta D_{B}=0.02294}$.

4. Application of the counting method with non-ideal rod sizes

If it is carry out the same procedure of “counting rods”, but with dimensions (scales) of each rod different from those known for its construction, this is to have a generalized method applicable to any figure, the following measurements shown in the Figure 4 and calculations are made in the Table 3.

In Figures 4e and 4f approximations of the fit were taken for rod sizes of 0.1 and 0.05 respectively and thus show that this is not exact, given the differences between the magnitudes of the sides of the “ideal” Koch's curve and the magnitude of the rod used.

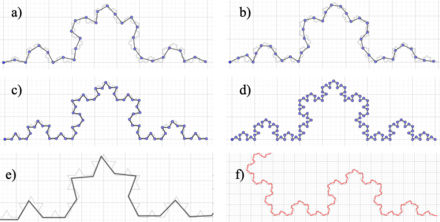
Figure 4. Rod sizes used. (a) 0.5. (b) 0.4. (c) 0.3. (d) 0.2. (e) 0.1. (f) 0.05

L. Rod (${\textstyle a_{k}}$)	Scale ${\textstyle \left(\xi _{k}=a_{k}/a_{1}\right)}$	N. Rods ${\textstyle N\left(\xi _{k}\right)}$	${\displaystyle P_{k}\left(\ln \left(1/\xi _{k}\right),\ln \left(N\right)\right)}$
0.5	1	30	${\displaystyle P_{1}\left(0,3.4012\right)}$
0.4	0.8	37	${\displaystyle P_{2}\left(0.22314,3.61092\right)}$
0.3	0.6	64	${\displaystyle P_{3}\left(0.51083,4.15888\right)}$
0.2	0.4	128	${\displaystyle P_{4}\left(0.91629,4.85203\right)}$
0.1	0.2	256	${\displaystyle P_{5}\left(1.60944,5.54518\right)}$
0.05	0.1	515	${\displaystyle P_{6}\left(2.30259,6.24417\right)}$

The linear fit for the set of points ${\textstyle P=\{P_{1},P_{2},P_{3},P_{4},P_{5},P_{6}\}}$ of Table 3 which was obtained from Figure 4 is given by Eq. (3) with a fractal dimension of ${\textstyle D_{B}=1.25966}$

${\displaystyle g\left(x\right)=1.25966x+3.46763}$

(3)

This measurement generates a difference with respect to the original measurement of ${\textstyle \Delta D_{B}=0.0022}$, that is, an order of magnitude with respect to the difference that exists between the “box counting” and the original measurement. This shows that the “rod counting” procedure is a better approximation than the “box counting” in longitudinal measurements of the fractal dimension. Figure 4 shows approaches to the six moments of construction of the adjustment to the Koch curve.

It can also be seen that even when both Eqs.(2) and (3) do not have the same slopes, those straight lines obtained are “relatively close” to parallelism.

5. Application of the rod counting method to the Mandelbrot fractal

Using the described method of counting rods on a Mandelbrot fractal generated in GeoGebra and whose profile with the different sizes of rods used is shown in Figure 5 and the counting results are described in Table 4.

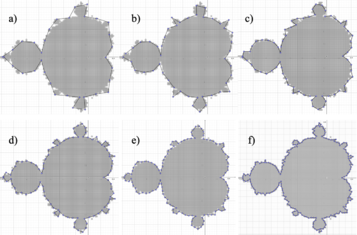
Figure 5: The different sizes of rods used to enclose the Mandelbrot fractal are shown, in a perimeter measurement using the rod counting method. The different lengths of the rods were (in cm): a) 0.2, b) 0.15, c) 0.1, d) 0.08, d) 0.06 and e) 0.04.

L. Rod (${\textstyle a_{k}}$)	Scale ${\textstyle \left(\xi _{k}=a_{k}/a_{1}\right)}$	N. Rods ${\textstyle N\left(\xi _{k}\right)}$	${\displaystyle P_{k}\left(\ln \left(1/\xi _{k}\right),\ln \left(N\right)\right)}$
0.2	1	33	${\displaystyle P_{1}\left(0,3.49651\right)}$
0.15	0.8	47	${\displaystyle P_{2}\left(0.28768,3.85015\right)}$
0.1	0.6	71	${\displaystyle P_{3}\left(0.69315,4.26268\right)}$
0.08	0.4	97	${\displaystyle P_{4}\left(0.91629,4.57471\right)}$
0.06	0.2	132	${\displaystyle P_{5}\left(1.20397,4.88280\right)}$
0.04	0.1	213	${\displaystyle P_{5}\left(1.60944,5.36129\right)}$

With the results of Table 4, the linear approximation is made, following the Richardson method, which gives us the function of the straight line that best fits the set of points and which is (Eq.(4)):

${\displaystyle h\left(x\right)=1.15397x+3.49872\;\;\Rightarrow \;\;D_{Br}=1.15397}$

(4)

For this same fractal, the box counting procedure is used, in the FracLac plugin of the ImageJ application [4], whose result is shown in figure (6) with a (slope of the straight line), which, as can be seen, has a difference with respect to the calculated with the counting of rods.

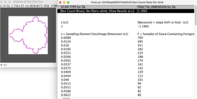
Figure 6: Results of processing perimeter of Mandelbrot's fractal with the box counting method, in the “FracLac” plugin of “ImageJ” app, ${\displaystyle D_{Bb}=1.1965}$

6 Discussion about rod counting method.

In table 5 results of calculation by rod counting and box counting are shown and compared with the the theoretical calculations reported [10]-[12], also results obtained by [9] are shown in the last column of table 5 for comparison. The penultimate row of the table 5 refers to the calculated Koch's snowflake fractal with non-regular sizes.

Table. 5 Comparison of measurements made on different fractal figures using different procedures. The last column takes into a count results given by [9] .

Geometry	Theoretical	Rod C.	B. Count.	E. B. Count.
Koch Snowflake	1.2620	1.26186	1.2848	1.267
Hilbert´s curve	2.0000	2.04097	1.8984	1.974
Koch 85' curve	1.7850	1.78505	1.7032	1.788
Cantor Set	0.6310	0.63093	0.8082	- -
Koch NIS	1.2620	1.25966	1.2848	1.267
Mandelbrot	- -	1.15397	1.1965	- -

The application of the “box counting” method implies the measurement of the area of an object, however this same procedure, without any change, is used in the measurement of lengths, but there are differences in the results obtained, as shown in table 5, when compared with the theoretical results.

In column 4 of table 5 an area method is used and even when this area collapse to a line, this procedure shows a numerical difference with respect to a perimeter method.

Based on these differences, it is proposed to use the “rod counting” for longitudinal measurements, the “box counting” method is used to measure areas, as well as for the measurement of 3D distributions, the “cube counting” is used.

Taking into account the existing software, the ImageJ application gives us the possibility to efficiently measure the fractal dimension of areas, but it does not have a plugin to perform linear measurements. This is why GeoGebra, even though it is not designed for that purpose, has tools that enable the application of the “rod counting” method in an orderly manner.

7 Conclusions.

• It was possible to show that there is a numerically evaluable difference between the counting of boxes and the counting of rods for linear (perimeter) measurements.

• The method of counting rods and boxes is applied to the fractal of the Koch curve and whose differences with respect to the Hausdorff-Besicovitch result give us ${\textstyle \Delta D_{Bb}=0.02294}$ and ${\textstyle \Delta D_{Br}=0.0022}$, where it refers to the counting of boxes and rods respectively.

• Both measurement methods are applied to the Mandelbrot fractal, in a perimeter measurement, and it is established that ${\textstyle D_{Bb}=1.1965}$ (box count), and that ${\textstyle D_{Br}=1.15397}$ (rod count) which is considered as the correct one, because it is a linear measurement.

Therefore, it is established that in the linear measurements made on fractals, the counting of rods provides a better approximation to the result of applying the Hausdorff-Besicovitch definition than those obtained with the counting of boxes, even with “non-standardized” rod sizes.

Thus, if the objective is to have a better description of the surrounding reality, the method used to describe the fractal geometry that is generated must be in accordance with the measurement made, to measure lines, the counting of rods, to measure areas, the counting of boxes and to measure volumes, the counting of cubes.

BIBLIOGRAPHY

[1] B. Mandelbrot, “The fractal geometry of nature”, W. H. Freeman 1982. [2] B. Mandelbrot, “Self-affine and Fractal dimension”, Physica Scripta, vol. 32(4), 1985, pp. 257-260. [3] B. Mandelbrot, “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension”, Science, 156(3775), pp. 636-638, DOI: 10.1126/science.156.3775.636 [4] Santos E., Souza F. and Ambrosío P. “Fractal dimension for characterization of focal breast lesion”, Conference WCCM XI, July 20 - 25, 2014, Barcelona, Spain. DOI: 10.13140/2.1.4186.9441 [5] Maipas S, Nonni A, Politi E, et al. (November 24, 2018) The Goodness-of-fit of the Fractal Dimension as a Diagnostic Factor in Breast Cancer. Cureus 10(11): e3630. doi:10.7759/cureus.3630 [6] Martinez B. de Oliveira Plotze R. Falvo M. and de Castro M. “Fractal dimension applied to plant identification”, Information Sciences, Elsevier, vol 178(12), 2008, pp 2722-2733. [7] ImageJ “Processing and Analysis in Java” https://imagej.nih.gov [8] Geogebra, “GeoGebra to teach and learn Mathematics” www.geogebra.org [9] Gun-Baek So, Hye-Rim So, Gang-Gyoo Jin, “Enhancement of the Box-Counting Algorithm for fractal dimension estimation”, Pattern Recognition Letters, Volume 98, 2017, Pages 53-58, http://dx.doi.org/10.1016/j.patrec.2017.08.022 [10] H. Strogatz, ``Nonlinear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering, Westview Press, Boulder CO. USA, 2nd edition (2015). [11] R. Devaney “A first course in chaotic dynamical systems theory and experiment” CRC Press, Florida USA, 2nd edition (2020). [12] D. Gatzouras and S. Lalley, “Hausdorff and box dimensions of certain self-affine fractals”, Indiana University Mathematics Journal, vol. 41(2), 1992, pp. 533-568. [13] A. Husain, J. Reddy, D. Bisht and M. Sajid “Fractal dimension of coastline of Australia”, Nature Scientific Report, 2021, doi.org/10.1038/s41598-021-85405-0 [14] C. Schneider, W. Rasband and K. Eliceiri “NIH Image to ImageJ: 25 years of image analysis”, Nature Methods 9, 2012, pp. 671–675. [15] P. Shanmugavadivu and V. Sivakumar, “Fractal dimension-bound spatiotemporal analysis of digital mammograms”, The European Physics Journal Special Topics, vol. 225, pp. 137-146. [16] B. Bárány, M. Hochman and A. Rapaport, “Hausdorff dimension of planar self-affine measures”, Inventiones Mathematicae. vol. 16, 2019, pp. 601–659. [17] H. Christensen, and O. Driver, “The fractal nature of clouds in global storm-resolving models”, ArXiv:2108.08565v1, 19 Aug 2021.

[18] C. Acosta, O. Carvente and F. Peñuñuri, “Fractal dimension measured over areas and perimeters using Box Counting technique applied over a Mandelbrot figures”, RIMNI, Vol. 38(1), 2022, doi.org/10.23967/j.rimni.2022.03.007