Analisys of interlaminar stresses in composite laminates by finite difference method

Revision as of 09:47, 3 May 2022

A. Solis^a, S. Sánchez-Sáez^a, E. Barbero^a

^a Departmento de Mecánica de Medios Continuos y Teoría de Estructuras, Universidad Carlos III de Madrid, Leganés, 28925, España

Análisis de las tensiones fuera del plano en laminados mediante diferencias finitas

Historia del artículo: Recibido 5 de Mayo 2017 En la versión revisada 5 de Mayo 2017 Aceptado 31 de Mayo 2017 Accesible online 21 de Junio 2017	En este trabajo se han determinado las componentes del tensor de tensiones completo que caracteriza el estado tensional que aparece en un laminado simétrico de material compuesto sometido a una carga uniaxial en su plano. Cobran, en este estudio, especial interés las componentes de tensión fuera del plano de aplicación de la carga y que son responsables de la aparición de mecanismos de daño que pueden originar el fallo del laminado como la delaminación y la rotura transversal por cortadura. Utilizando argumentos de simetría y la consideración de borde libre de tensiones como condición de contorno en tensiones, se construye un esquema de diferencias finitas que permite resolver las ecuaciones de equilibrio interno y obtener una solución físicamente válida. De esta manera, este planteamiento permite mejorar la aproximación que se consigue mediante el uso de elementos tipo lámina propia de planteamientos bidimensionales. Con el modelo desarrollado se han evaluado las tensiones fuera del plano para distintas secuencias de apilamiento, estudiando los valores máximos y mínimos de las distintas componentes de tensiones interlaminar al variar la orientación de estos laminados.
Palabras clave: Tensiones interlaminares Laminado simétrico Efecto de borde Diferencias finitas

Analisys of interlaminar stresses in composite laminates by finite difference method

Keywords: Interlaminar stress Symmetric laminate Edge effect Finite difference method	In this work, full stress tensor components regarding stress state for a simmetrical composite laminate under uniform uniaxial extension have been determined. Off-plane stresses are specially meaningful due to the fact that they are responsible for failure mechanisms such as delamination and shear stress cracking. A finite difference scheme has been used to solve internal equilibrium equations subjected to stress-free boundary conditions along boundary lines; moreover symmetry considerations have been made. In such way, we get an improvement in solutions in contrast with results obtained following bidimensional reasoning and using laminate based elements. Off-plane stresses for differents ply-sequences have been evaluated and maximum and minimum values for different fibers orientations were explored.

1 Introducción

Las estructuras de materiales compuestos de tipo laminado son especialmente sensibles a las tensiones fuera del plano debido a que las propiedades resistentes y de rigidez en la dirección del espesor del laminado son inferiores a las propiedades en el plano. Tensiones en dirección del espesor aparecen incluso aunque las cargas estén contenidas en el plano del laminado, por ejemplo, en puntos cercanos a un borde libre asociadas a las diferencias en el comportamiento entre dos láminas adyacentes con diferentes orientaciones y a la necesidad de verificar la condición de contorno. Estas tensiones pueden ser muy relevantes en la estimación de la carga de rotura de un laminado, por lo que una reducción de las mismas puede incrementar la resistencia del laminado.

Asociados al efecto de borde libre hay dos modos de fallo controlados por diferentes componentes del tensor de tensiones. Uno de los modos de fallo más críticos en los laminados es la delaminación que es controlado por la componente normal en dirección del espesor [1] o por tensiones tangenciales [2]. Este modo de fallo es responsable de una pérdida significativa de capacidad resistente de la estructura frente a cargas de compresión [2]. Otro de los modos de fallo es el fallo por cortadura que origina fisuras transversales, controlado en este caso por las componentes a cortadura interlaminar del tensor de tensiones. Determinar las componentes de tensión fuera del plano es por tanto de gran relevancia, así como estimar sus valores relativos para determinar el posible modo de fallo que puede aparecer.

El uso de modelos bidimensionales para abordar el estudio de estructuras de tipo laminado, como puede ser la teoría del laminado, no permite el cálculo de tensiones fuera del plano y, por tanto, puede hacer que se produzca un fallo prematuro en la estructura con resultados catastróficos. Los modelos tridimensionales aplicados de forma general a un problema arbitrario resultan a menudo complejos de abordar. Una aproximación muy extendida es el empleo del método de los elementos finitos [3-4], el cual requiere un gran afinamiento de la malla para recoger el fenómeno de concentración de tensiones. Otras metodologías son el método de los elementos de contorno [5] o las diferencias finitas [6]. Una alternativa es la estimación de las tensiones interlaminares mediante consideraciones de equilibrio que junto a hipótesis simplificativas permite resolver casos de carga simples y laminados simétricos.

El problema de las tensiones fuera del plano asociado a efectos de borde ha sido muy estudiado en la literatura (ver por ejemplo, los trabajos [7] y [8] que realizan una revisión sobre el estado del arte de este problema) desde los trabajos pioneros de Pipes y Pagano en 1970 [6]. Se han estudiado diferentes secuencias de apilamiento: 0/90, 90/0, +45/-45, cuasi-isótropos, etc [3-5]. Los resultados muestran que las tensiones interlaminares se ven modificadas significativamente con la secuencia de apilamiento. Por tanto, se hace necesario un estudio sistemático de diferentes orientaciones y secuencia de apilamiento que engloble las orientaciones empleadas por diferentes autores.

En este trabajo se analizan las tensiones interlaminares en laminados simétricos, evaluando la influencia de la orientación de las láminas considerando varias secuencias de apilamiento. Se emplea un modelo basado en diferencias finitas, que se contrasta con resultados de la literatura cientifica obtenidos mediante una metodología diferente [3].

2 Descripción del modelo

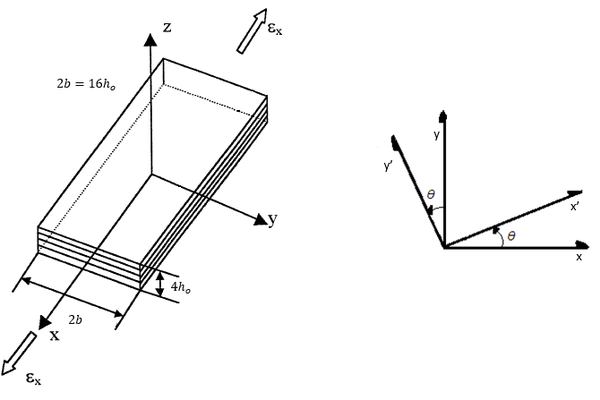
Se ha analizado el problema de un laminado simétrico respecto del plano ‘xy’ compuesto por 4 láminas con secuencia de apilamiento ±ð sometido a un estado de carga uniaxial en sus bordes, Figura 1. El laminado tiene un ancho ${\textstyle 2b}$ , con ${\textstyle b=}$ $8{h}_{0}$ , siendo ${\textstyle {h}_{0}}$ el espesor de una lámina.

Figura 1. Sistema de ejes geométricos para el laminado y relación con los ejes principales de ortotropía de cada lámina. El plano z=0 corresponde al plano de simetría del laminado

El laminado está constituido por láminas con comportamiento lineal elástico con simetría ortótropa. La ecuación constitutiva de la lámina en los ejes x- y- z se puede expresar como:

\left({\begin{matrix}{\begin{matrix}{\sigma }_{x}\\{\sigma }_{y}\\{\sigma }_{z}\end{matrix}}\\{\begin{matrix}{\tau }_{yz}\\{\tau }_{xz}\\{\tau }_{xy}\end{matrix}}\end{matrix}}\right)=

Failed to parse (syntax error): \left( \begin{matrix}\begin{matrix}\overline{{C}_{11}}&\overline{{C}_{12}}&\overline{{C}_{13}}\\\overline{{C}_{12}}&\overline{{C}_{22}}&\overline{{C}_{23}}\\\overline{{C}_{13}}&\overline{{C}_{23}}&\overline{{C}_{33}}\end{matrix}&\begin{matrix}0&0&\overline{{C}_{16}}\\0&0&\overline{{C}_{26}}\\0&0&\overline{{C}_{36}}\end{matrix}\\\begin{matrix}0&0&0\\0&0&0\\\overline{{C}_{16}}&\overline{{C}_{26}}&\overline{{C}_{36}}\end{matrix}&\begin{matrix}\overline{{C}_{44}}&\overline{{C}_{45}}&0\\\overline{{C}_{45}}&\overline{{C}_{55}}&0\\0&0&\overline{{C}_{66}}\end{matrix}\end{matrix}\right) \left( \begin{matrix}\begin{matrix}{\epsilon }_{x}\\{\epsilon }_{y}\\{\epsilon }_{z}\end{matrix}\\\begin{matrix}{\gamma }_{yz}\\{\gamma }_{xz}\\{\gamma }_{xy}\end{matrix}\end{matrix}\right) \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 1)

Las componentes de la matriz de rigidez son función de las constantes elásticas del material y del ángulo de orientación ð de las direcciones de ortotropía.

En un estado de carga uniaxial, el equilibrio de tensiones predice que las componentes del tensor de tensiones son independientes de la coordenada ‘x’ en puntos suficientemente alejados de la zona de aplicación de la carga (principio de Saint-Venant).

La independencia de las tensiones con respecto a ‘x’ se traduce en independencia también con respecto a ‘x’ de las componentes del tensor de deformaciones. Asumiendo pequeños desplazamientos y pequeñas deformaciones las relaciones de compatibilidad se escriben:

Failed to parse (syntax error): \begin{matrix}{\epsilon }_{x}={u}_{,x}\\{\epsilon }_{y}={v}_{,y}\\\begin{matrix}{\epsilon }_{y}={v}_{,y}\\{\gamma }_{yz}={w}_{,y}+{v}_{,z}\\\begin{matrix}{\gamma }_{xz}={u}_{,z}+{w}_{,x}\\{\gamma }_{xy}={u}_{,y}+{v}_{,x}\end{matrix}\end{matrix}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 2)

Dado que existe simetría de cargas y geométrica en el laminado bajo estudio, el campo de desplazamiento que resulta de la integración de la ecuación (2) deberá tener la siguiente forma funcional:

Failed to parse (syntax error): {\textstyle \begin{matrix}u={\epsilon }_{x}x+U(y,z)\\v=V(y,z)\\w=W(y,z)\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 3} )

Donde ε_x es la deformación impuesta sobre el laminado bajo estudio. La forma del campo de desplazamientos dada en la ecuación (3) proporciona así un campo de tensiones tal que:

Failed to parse (syntax error): {\sigma }_{ij}={\sigma }_{ij}\left( U,V,W\right) ={\sigma }_{ij}\left( y,z\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 4)

Lo que muestra que las componentes de tensiones y deformaciones de este problema dependen sólo de las coordenadas ‘y‘ y ‘z‘. Con estas consideraciones las ecuaciones de equilibrio interno se reducen a:

Failed to parse (syntax error): \begin{matrix}\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}=0\\\frac{\partial {\sigma }_{y}}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}=0\\\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_{z}}{\partial z}=0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 5)

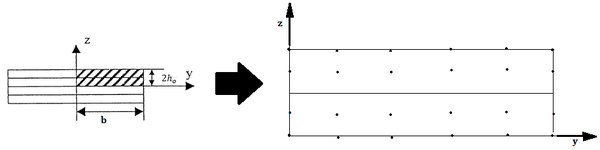
Por tanto, es posible estudiar sólo la parte del laminado contenida en el primer cuadrante (parte izquierda de la Figura 2):

Figura 2. Corte transversal del laminado en el plano ‘yz’

En los bordes del laminado, deberán verificarse las condiciones de contorno de bordes libres de tensiones:

Failed to parse (syntax error): \begin{matrix}{\sigma }_{y}={\tau }_{yz}={\tau }_{xy}=0\, \, en\, \, y=b\\{\sigma }_{z}={\tau }_{yz}={\tau }_{xz}=0\, \, en\, \, z=2{h}_{o}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 6)

Para resolver el problema, se ha considerado útil definir las siguientes variables adimensionales:

${\textstyle {\overline {y}}={\frac {y}{b}};\quad {\overline {z}}={\frac {z}{{h}_{o}}};\quad {\overline {U}}=}$ ${\frac {U}{{h}_{o}}};\quad {\overline {V}}={\frac {V}{b}};\quad {\overline {W}}={\frac {W}{{h}_{o}}};\quad R=$ Failed to parse (syntax error): \frac{b}{{h}_{o}}\quad \quad \quad \quad (\, \, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 7)

Combinando las expresiones anteriores es posible formular las ecuaciones que deben verificar las componentes del campo de desplazamientos en cada punto del dominio, ecuacion 8

Failed to parse (syntax error): \begin{matrix}R\overline{{C}_{26}}{\overline{V}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{36}}+\overline{{C}_{45}}\right) {\overline{W}}_{,\overline{y}\overline{z}}+\overline{{C}_{66}}{\overline{U}}_{,\overline{y}\overline{y}}+{R}^{3}\overline{{C}_{45}}{\overline{V}}_{,\overline{z}\overline{z}}+{R}^{2}\overline{{C}_{55}}{\overline{U}}_{,\overline{z}\overline{z}}=0\\R\overline{{C}_{22}}{\overline{V}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{23}}+\overline{{C}_{44}}\right) {\overline{W}}_{,\overline{y}\overline{z}}+\overline{{C}_{26}}{\overline{U}}_{,\overline{y}\overline{y}}+{R}^{3}\overline{{C}_{44}}{\overline{V}}_{,\overline{z}\overline{z}}+{R}^{2}\overline{{C}_{45}}{\overline{U}}_{,\overline{z}\overline{z}}=0\\\overline{{C}_{44}}{\overline{W}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{45}}+\overline{{C}_{36}}\right) {\overline{U}}_{,\overline{y}\overline{z}}+{R}^{2}\left( \overline{{C}_{23}}+\overline{{C}_{44}}\right) {\overline{V}}_{,\overline{y}\overline{z}}+{R}^{2}\overline{{C}_{33}}{\overline{W}}_{,\overline{z}\overline{z}}=0\end{matrix}\quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 8)\,

Mientras que en los puntos del contorno se deberán verificar las condiciones dadas por las ecuaciones 9 y 10:

Failed to parse (syntax error): \begin{matrix}\, \overline{{C}_{22}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{23}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{26}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{12}}{\epsilon }_{x}\\\frac{1}{R}\overline{{C}_{44}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{44}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{45}}{\overline{U}}_{,\overline{z}}=0\\\overline{{C}_{26}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{36}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{66}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{16}}{\epsilon }_{x}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 9)\,

Failed to parse (syntax error): \, \begin{matrix}\, \overline{{C}_{23}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{33}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{36}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{13}}{\epsilon }_{x}\\\frac{1}{R}\overline{{C}_{44}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{44}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{45}}{\overline{U}}_{,\overline{z}}=0\\\frac{1}{R}\overline{{C}_{45}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{45}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{55}}{\overline{U}}_{,\overline{z}}=0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 10)\,

Para resolver el sistema descrito se emplea un esquema de diferencias finitas que discretizando el dominio mediante un esquema de puntos discretos como el mostrado en la parte derecha de la Figura 2, permita obtener el campo de desplazamientos, deformaciones y tensiones del problema tridimensional completo. Para preservar la continuidad de los desplazamientos y de las tensiones fuera del plano entre dos láminas orientadas con diferentes orientaciones, la discretización se hace de forma que la interfase entre las láminas quede confinada entre dos filas de puntos materiales.

Para construir el esquema de diferencias finitas se utilizan fórmulas de diferencias centradas para las derivadas segundas y fórmulas de diferencias centradas y regresivas para las derivadas primeras. Asímismo se tienen en cuenta para escribir las ecuaciones de campo, las siguientes relaciones de simetría:

Failed to parse (syntax error): \begin{matrix}{U}_{,z}\left( y,0\right) =0\\{V}_{,z}\left( y,0\right) =0\\W\left( y,0\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 11)\, \,

Failed to parse (syntax error): \begin{matrix}{U}_{,y}\left( 0,z\right) =0\\V\left( 0,z\right) =0\\{W}_{,y}\left( 0,z\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 12)\, \,

También para impedir los desplazamientos como sólido rígido se imponen las siguientes condiciones:

Failed to parse (syntax error): \begin{matrix}U\left( 0,z\right) =U\left( 0,0\right) =0\\\, V\left( 0,0\right) =0\, \, \\W\left( 0,0\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 13)

Así con todos estos elementos se construye un sistema algebraico del tipo ${\textstyle Ax=}$ $b$ . De esta manera, para un dominio discretizado con N puntos, se tiene un sistema con los siguientes elementos:

Un vector de incógnitas que representa las componentes de los desplazamientos en los puntos del dominio:

Failed to parse (syntax error): x=\left( \begin{matrix}\begin{matrix}{U}_{1}\\{V}_{1}\\{W}_{1}\end{matrix}\\\begin{matrix}\begin{matrix}{U}_{2}\\{V}_{2}\\{W}_{2}\end{matrix}\\\begin{matrix}\ldots \\\begin{matrix}{U}_{N}\\{V}_{N}\\{W}_{N}\end{matrix}\end{matrix}\end{matrix}\end{matrix}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 14)

Una matriz que contiene los coeficientes que multiplican a cada una de las incógnitas y que están expuestos en las ecuaciones (8), (9) y (10).

Y un vector que contiene los términos independientes, descritos nuevamente en las ecuaciones (8), (9) y (10).

Conviene notar que la estructura del sistema algebraico de ecuaciones a resolver se puede escribir también:

Failed to parse (syntax error): A\left( \frac{x}{{\epsilon }_{x}}\right) =\left( \frac{b}{{\epsilon }_{x}}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 15)

Dada la estructura del vector b se tiene que:

Failed to parse (syntax error): \frac{b}{{\epsilon }_{x}}\not =f\left( {\epsilon }_{x}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 16)

Esto implica que es posible obtener los desplazamientos de los puntos de la malla por unidad de deformación axial y obtener, gracias a la linealidad de los operadores involucrados, y a partir de éstos, las deformaciones y las tensiones también por unidad de deformación. Para obtener el valor real de las variables, para un nivel de deformación aplicado, basta por tanto multiplicar los resultados obtenidos por dicho valor.

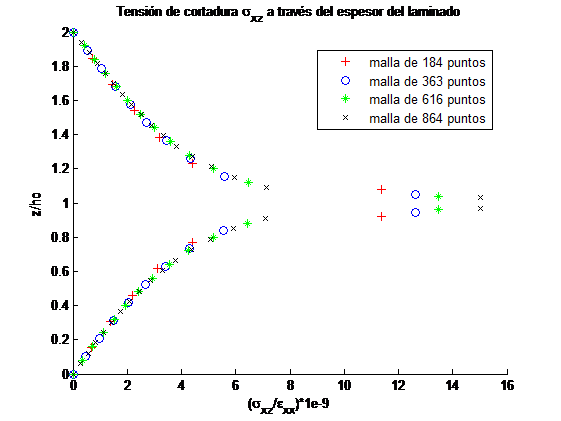
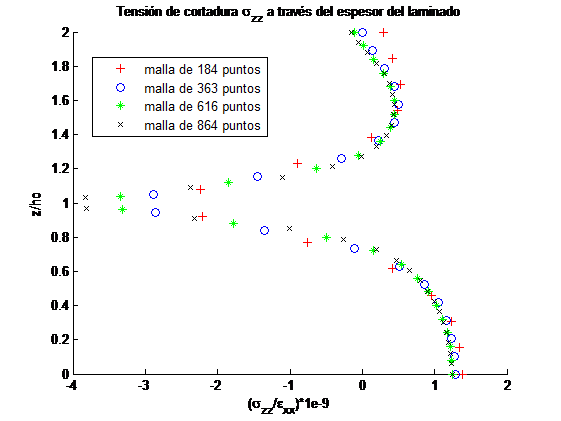
Se ha realizado un análisis de sensibilidad de los resultados del modelo al tamaño de malla. Para ello se ha estudiado un laminado con una relación geométrica b=8h_o. Se ha seleccionado un laminado con dos secuencias de apilamiento [-45/45]_S y [0/-45/90/45]_S de un material cuyas propiedades mecánicas se han tomado de la literatura [3]. Se han considerado cuatro mallas de 184, 363, 616 y 864 puntos.

Tabla 1. Propiedades mecánicas del material utilizado en el análisis de sensibilidad [3].

E₁₁

(GPa)

E₂₂

E₃₃

(GPa)

G₁₂

(GPa)

G₁₃

G₂₃

(GPa)

ν₁₂

ν₁₃

ν₂₃

137.9

14.5

5.86

0.21

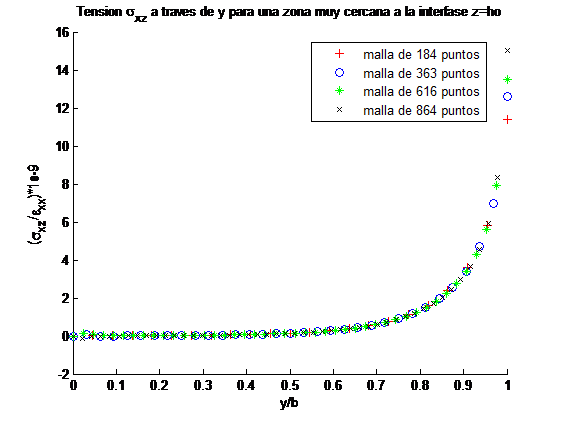
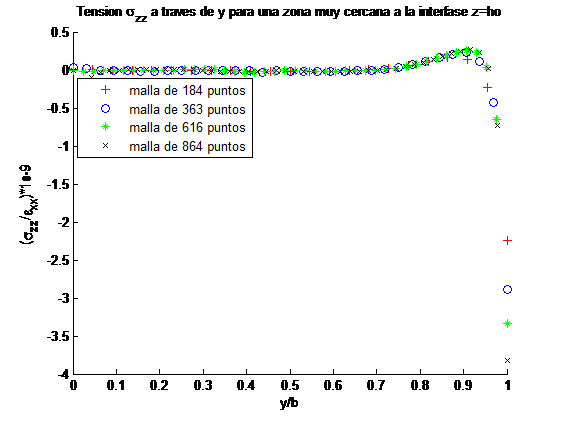
Se han analizado las tensiones fuera del plano del laminado a lo largo del ancho de la interfase entre cada lámina y la distribución de estas tensiones a lo largo del espesor en el borde libre para los dos laminados analizados. En las Figuras 3 y 4 se muestran los resultados correspondientes al laminado [-45/45]_S, para el otro laminado los resultados son semejantes. Como era de esperar, las tensiones fuera del plano son prácticamente nulas durante alrededor de un 50% del ancho del laminado para el caso representado en la Figura 3. La distancia al borde libre en la que las tensión cae a cero es igual al espesor del laminado [5,6]. La tensión ${\textstyle {\sigma }_{xz}\,}$ crece al acercarse a la interfase entre dos láminas con orientaciones diferentes, figura 4a, mientras que la tensión ${\textstyle {\sigma }_{zz}}$ cambia de signo conforme se acerca a la interfase, figura 4b.

La variación de las tensiones es independiente del número de puntos de la malla, recogiendose con más precisión los incrementos de las tensiones al aumentar el número de puntos.

Los resultados muestran que considerar una malla de 616 puntos es suficiente dado que el incremento en la precisión que se consigue con una malla más fina es prácticamente despreciable.

a)

b)

Figura 3. Tensiones fuera del plano a través del ancho en la interfase para distintas mallas en el laminado [-45/45]_S, a) tensión

, b) tensión

a)

b)

Figura 4. Tensiones fuera del plano a través del espesor en el borde libre para distintas mallas en el laminado [-45/45]_S a) tensión

, b) tensión

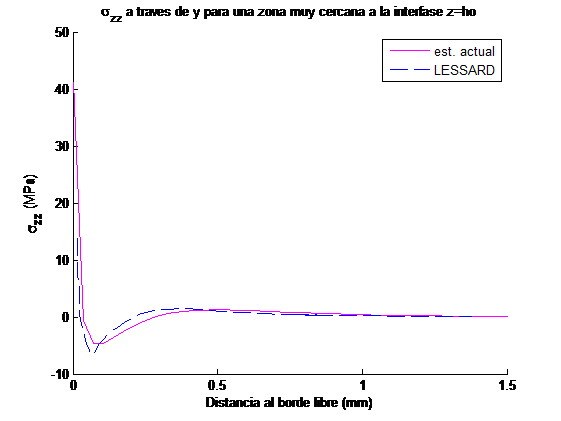
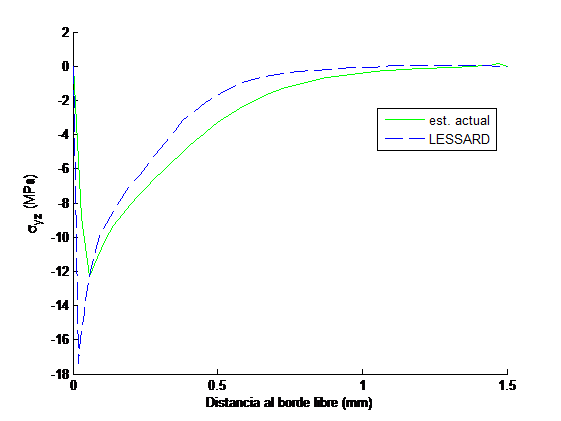
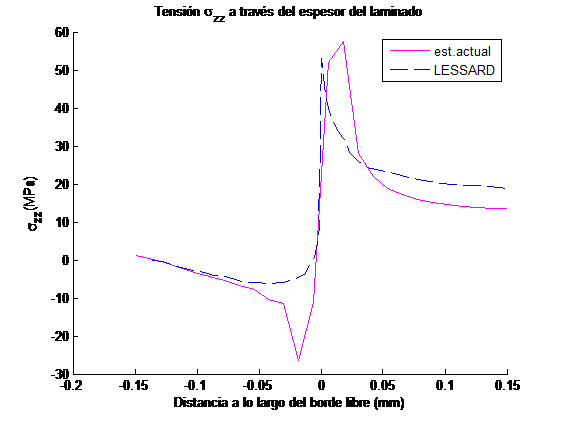
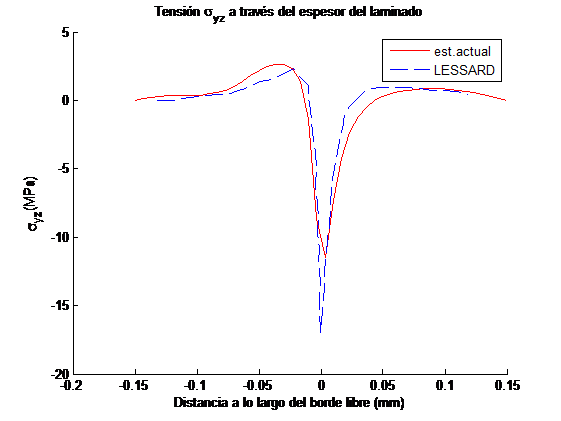
Con objeto de verificar los resultados que proporciona el esquema empleado para el análisis de las tensiones fuera del plano, se ha realizado una comparación con los mostrados por Lessard et al. [3] para dos secuencias de apilamiento ${\textstyle {[0/90]}_{s}}$ y ${\textstyle {[90/0]}_{s}}$ . Las propiedades del material analizado son las mismas que las mostradas en la Tabla 1. A modo de ejemplo se muestran sólo los resultados del primero de los laminados.

Se han estudiado las tensiones ${\textstyle {\sigma }_{zz}}$ y ${\textstyle {\sigma }_{yz}}$ a lo largo del ancho del laminado en la interfase de láminas con distinta orientación (Figuras 5 y 6), y a lo largo del espesor en el borde libre (Figuras 7 y 8), y se han comparado con las curvas análogas del artículo de Lessard et al. [3] para una deformación axial aplicada de un 1%.

Conviene recordar que la tensión ${\textstyle {\sigma }_{yz}}$ a lo largo del espesor en el borde libre se anula por condición de contorno. Así que las gráficas representadas para esta tensión a lo largo del espesor, figura 8, corresponden a los valores que se han estimado en una zona interior del laminado muy cercana al borde libre (en concreto en los nodos inmediatamente anteriores a los situados en el borde libre).

Figura 5. Tensión

a través del ancho en la interfase. Laminado [0/90]_S

Figura 6. Tensión σ_yz a través del ancho en la interfase. laminado [0/90]_S

Figura 7. Tensión

a través del espesor del laminado. a) laminado [0/90]_S

Figura 8. Tensión σ_yz a través del espesor del laminado. Laminado [0/90]_S

Se observa que los resultados obtenidos mediante el modelo desarrollado reproducen las tendencias mostradas en [3] y aproximan razonablemente los valores extremos de las curvas. Las variaciones de las tensiones interlaminares observadas en la figura 5 y 6 también son semejantes a las observadas por otros autores [4 y 9].

3 Resultados

Con el modelo desarrollado se ha estudiado la variación del valor de las tensiones interlaminares en laminados sometidos a una carga uniaxial en su plano, considerando diferentes secuencias de apilamiento en las que se ha variado la orientación de las láminas. Se ha analizado la respuesta de cuatro secuencias de apilamiento, dos con 4 láminas [ð³/−ð³]ð y [2ð³/−ð³]ð , y otros dos con 6 láminas [ð³₂/−ð³]ð y [ð³/2ð³/−ð³]ð . En todos los casos se ha analizado la variación de la orientación entre 0º y 90º. Estas secuencias de apilamiento se han definido de la siguiente forma, por ejemplo para una orientación de θ=30º, los laminados considerados serán [30/−30]ð y [60/−30]ð los de 4 láminas, y [30₂/−30]ð y [30/60/−30]ð los de 6 láminas.

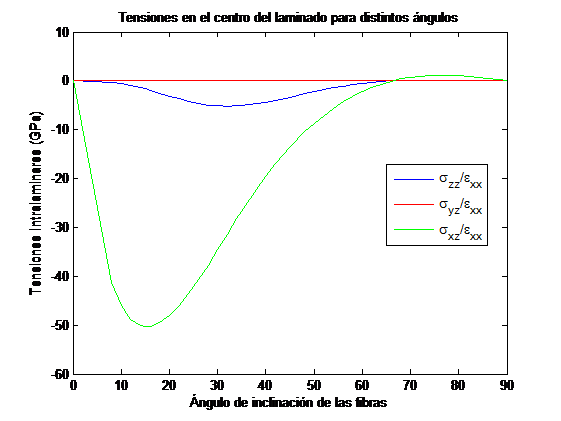
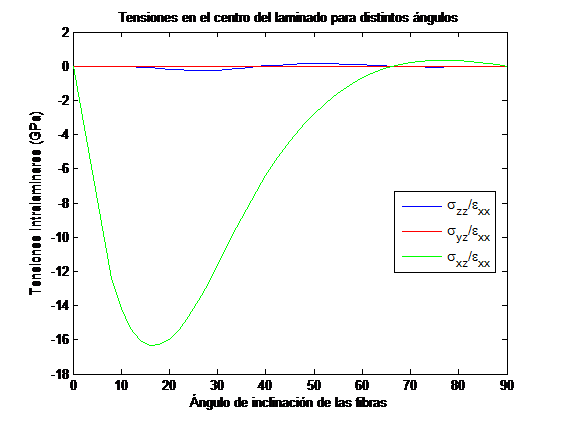
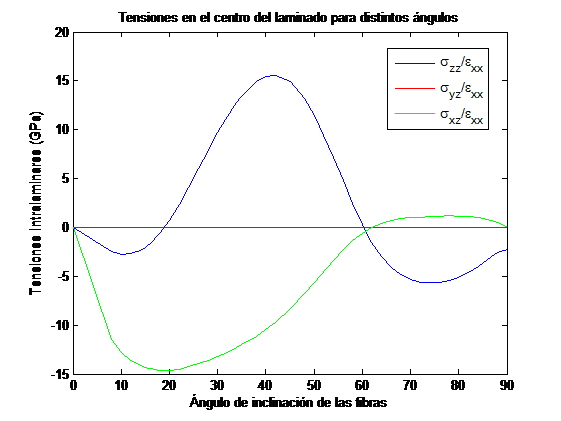
En las Figuras 9 y 10 se muestran los valores de las diferentes componentes de las tensiones interlaminares en puntos cercanos al borde libre a la altura de la interfase, al variar el ángulo θ para los laminados [ð³/−ð³]ð y [2ð³/−ð³]ð , respectivamente. Se observa que en el laminado [ð³/−ð³]ð la componente predominante para todas las orientaciones θ es σ_xz, tomando un valor máximo para θ=15.5º. La componente σ_zz tiene valores un orden de magnitud inferiores, siendo máximo para θ=32º.Dado que esta componente es de compresión en todo el rango de ð³, no contribuye a la aparición de delaminación. Sin embargo, en el laminado [2ð³/−ð³]ð los valores de las componentesσ_zz y σ_xztienen valores similares entre 40º y 90º, siendo los valores de la componente σ_xz mucho mayores para θ entre 0 y 40º. Entre 15º y 60º, la componente σ_zz tiene valores negativos, no contribuyendo por tanto al modo de fallo de delaminación. La componente σ_xzse hace máxima para un ángulo en torno aθ=10.1º, con valores similares a los del laminado [ð³/−ð³]ð .

Figura 9. Tensiones interlaminares en el borde libre a la altura de la interfase para distintas orientaciones de las fibras para un laminado tipo [ð³/−ð³]ð

Figura 10. Tensiones interlaminares en el borde libre a la altura de la interfase para distintas orientaciones de las fibras para un laminado tipo

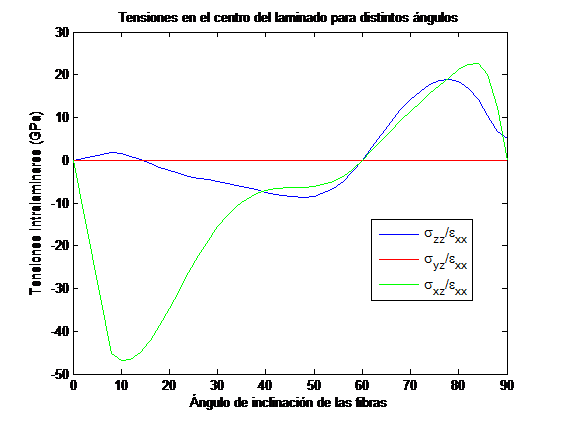
En las Figuras 11 y 12 se muestran los valores de las diferentes componentes de las tensiones interlaminares en el borde libre a la mitad del espesor desde el plano medio, al variar el ángulo θ para los laminados [ð³₂/−ð³]ð y [ð³/2ð³/−ð³]ð , respectivamente. Las tensiones se han obtenido a esa altura para comparar el mismo lugar geométrico en todos los laminados analizados.

En la Figura 11 se observa que en el laminado [ð³₂/−ð³]ð la componenteσ_zzes prácticamentenula para cualquier orientación. La componente σ_xzes máxima para una orientación θ=16º, pero con valores mucho menores de los observados en los láminados de 4 láminas.

En la Figura 12 se observa la variación de las componentes de las tensiones interlaminares para el laminado [ð³/2ð³/−ð³]ð . En este laminado, la componenteσ_zzsolo se anula para orientacionesde 20º y 60º, teniendo valores positivos para ángulos entre 20º y 60º, contribuyendo para estas orientaciones a ladelaminación del laminado. Entre 60º y 90º esta componente es mayor que la componenteσ_xz. La componente σ_xz tiene valores similares a los obtenidos en el laminado [ð³₂/−ð³]ð para los angulos entre 0 y 60, siendo máximo en este caso para 19º.

Figura 11. Tensiones interlaminares en el borde libre a la mitad del espesor desde el plano medio del laminado para distintas orientaciones de las fibras para un laminado tipo

Figura 12. Tensiones intralaminares en el borde libre a la mitad del espesor desde el plano medio para distintas orientaciones de las fibras para un laminado tipo

Observamos como la tensión ${\textstyle {\sigma }_{yz}}$ es nula por condición de contorno en todos los laminados analizados.

4 Conclusiones

Se han analizado las tensiones interlaminares que aparecen debido al efecto de borde libre en laminados simétricos sometidos a cargas uniaxiales en su plano. Se ha puesto de manifiesto que la secuencia de apilamiento no sólo afecta al valor de las tensiones interlaminares sino también a su valor relativo.

En laminados con el mismo número de láminas orientadas a +θ y -θ la tensión predominante es σ_xz para todas las orientaciones. Este comportamiento también se produce cuando se aumenta el número de láminas orientadas a +θ. Sin embargo si la secuencia de apilamiento es del tipo ${\textstyle {[2\theta ,-\theta ]}_{s}}$ o ${\textstyle {[\theta ,2\theta ,-\theta ]}_{s}}$ existe un rango de orientaciones en la que la componenteσ_zz es mayor que σ_xz. Aunque el valor máximo de la componente normal sea inferior a la de cortadura.

Agradecimientos

Los autores agradecen la financiación recibida para el desarrollo de este trabajo del Ministerio de Economía y Finanzas de España en el marco del proyecto DPI2013-42240-R.

Referencias

[1] C.T. Sun, G.D. Chu, Journal of Composite Materials, 25, pág. 142-161 (1991).

[2] S. Sihn, R.Y. Kim, K. Kawabe, S.W. Tsai, Composites Science and Technology, 67, pág. 996–1008 (2007).

[3] L.B. Lessard, A.S. Schmidt, International Journal Solids Structures, 33, 15, pág. 2243-2259 (1996).

[4] V-T. Nguyen, J.F. Caron, Computers and Structures, 84, pág. 1538–1546 (2006).

[5] J. Lindemann, W. Becker, Mechanics of Composite Materials, 36, 3, pág. 208-214 (2000).

[6] R.B. Pipes, N.J. Pagano, Journal of Composite Materials, 4, pág. 538-548 (1970).

[7] T. Kant, K. Swaminathan, Composite Structures, 49, pág. 65–75 (2000).

[8] C. Mittelstedt, W. Becker, Journal of Composite Materials; 38, 12, pág. 1037-1062 (2004).

[9] A.S.D. Wang, F.W. Crossman, Journal of Composite Materials, 11, pág. 92-106 (1977).

@@ Line 75: / Line 75: @@
 ==2 Descripción del modelo==
-Se ha analizado el problema de un laminado simétrico respecto del plano ‘xy’ compuesto por 4 láminas con secuencia de apilamiento ±&theta; sometido a un estado de carga uniaxial en sus bordes, Figura 1. El laminado tiene un ancho <math display="inline">2b</math>, con <math display="inline">b=</math><math>8{h}_{0}</math>, siendo <math display="inline">{h}_{0}</math> el espesor de una lámina.
+Se ha analizado el problema de un laminado simétrico respecto del plano ‘xy’ compuesto por 4 láminas con secuencia de apilamiento ±ð sometido a un estado de carga uniaxial en sus bordes, Figura 1. El laminado tiene un ancho <math display="inline">2b</math>, con <math display="inline">b=</math><math>8{h}_{0}</math>, siendo <math display="inline">{h}_{0}</math> el espesor de una lámina.
 [[Image:Solis_et_al_2018b-image5.png|600px]]
@@ Line 85: / Line 85: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\left( \begin{matrix}\begin{matrix}{\sigma }_{x}\\{\sigma }_{y}\\{\sigma }_{z}\end{matrix}\\\begin{matrix}{\tau }_{yz}\\{\tau }_{xz}\\{\tau }_{xy}\end{matrix}\end{matrix}\right) =</math><math>\left( \begin{matrix}\begin{matrix}\overline{{C}_{11}}&\overline{{C}_{12}}&\overline{{C}_{13}}\\\overline{{C}_{12}}&\overline{{C}_{22}}&\overline{{C}_{23}}\\\overline{{C}_{13}}&\overline{{C}_{23}}&\overline{{C}_{33}}\end{matrix}&\begin{matrix}0&0&\overline{{C}_{16}}\\0&0&\overline{{C}_{26}}\\0&0&\overline{{C}_{36}}\end{matrix}\\\begin{matrix}0&0&0\\0&0&0\\\overline{{C}_{16}}&\overline{{C}_{26}}&\overline{{C}_{36}}\end{matrix}&\begin{matrix}\overline{{C}_{44}}&\overline{{C}_{45}}&0\\\overline{{C}_{45}}&\overline{{C}_{55}}&0\\0&0&\overline{{C}_{66}}\end{matrix}\end{matrix}\right) \left( \begin{matrix}\begin{matrix}{\epsilon }_{x}\\{\epsilon }_{y}\\{\epsilon }_{z}\end{matrix}\\\begin{matrix}{\gamma }_{yz}\\{\gamma }_{xz}\\{\gamma }_{xy}\end{matrix}\end{matrix}\right) \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 1)</math>
+| <math>\left( \begin{matrix}\begin{matrix}{\sigma }_{x}\\{\sigma }_{y}\\{\sigma }_{z}\end{matrix}\\\begin{matrix}{\tau }_{yz}\\{\tau }_{xz}\\{\tau }_{xy}\end{matrix}\end{matrix}\right) =</math><math>\left( \begin{matrix}\begin{matrix}\overline{{C}_{11}}&\overline{{C}_{12}}&\overline{{C}_{13}}\\\overline{{C}_{12}}&\overline{{C}_{22}}&\overline{{C}_{23}}\\\overline{{C}_{13}}&\overline{{C}_{23}}&\overline{{C}_{33}}\end{matrix}&\begin{matrix}0&0&\overline{{C}_{16}}\\0&0&\overline{{C}_{26}}\\0&0&\overline{{C}_{36}}\end{matrix}\\\begin{matrix}0&0&0\\0&0&0\\\overline{{C}_{16}}&\overline{{C}_{26}}&\overline{{C}_{36}}\end{matrix}&\begin{matrix}\overline{{C}_{44}}&\overline{{C}_{45}}&0\\\overline{{C}_{45}}&\overline{{C}_{55}}&0\\0&0&\overline{{C}_{66}}\end{matrix}\end{matrix}\right) \left( \begin{matrix}\begin{matrix}{\epsilon }_{x}\\{\epsilon }_{y}\\{\epsilon }_{z}\end{matrix}\\\begin{matrix}{\gamma }_{yz}\\{\gamma }_{xz}\\{\gamma }_{xy}\end{matrix}\end{matrix}\right) \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 1)</math>
 |}
@@ Line 96: / Line 96: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\begin{matrix}{\epsilon }_{x}={u}_{,x}\\{\epsilon }_{y}={v}_{,y}\\\begin{matrix}{\epsilon }_{y}={v}_{,y}\\{\gamma }_{yz}={w}_{,y}+{v}_{,z}\\\begin{matrix}{\gamma }_{xz}={u}_{,z}+{w}_{,x}\\{\gamma }_{xy}={u}_{,y}+{v}_{,x}\end{matrix}\end{matrix}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 2)</math>
+| <math>\begin{matrix}{\epsilon }_{x}={u}_{,x}\\{\epsilon }_{y}={v}_{,y}\\\begin{matrix}{\epsilon }_{y}={v}_{,y}\\{\gamma }_{yz}={w}_{,y}+{v}_{,z}\\\begin{matrix}{\gamma }_{xz}={u}_{,z}+{w}_{,x}\\{\gamma }_{xy}={u}_{,y}+{v}_{,x}\end{matrix}\end{matrix}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 2)</math>
 |}
@@ Line 102: / Line 102: @@
 Dado que existe simetría de cargas y geométrica en el laminado bajo estudio, el campo de desplazamiento que resulta de la integración de la ecuación (2) deberá tener la siguiente forma funcional:
-<math display="inline">\begin{matrix}u={\epsilon }_{x}x+U(y,z)\\v=V(y,z)\\w=W(y,z)\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 3</math>)
+<math display="inline">\begin{matrix}u={\epsilon }_{x}x+U(y,z)\\v=V(y,z)\\w=W(y,z)\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 3</math>)
 Donde &#x03b5;<sub>x</sub> es la deformación impuesta sobre el laminado bajo estudio. La forma del campo de desplazamientos dada en la ecuación (3) proporciona así un campo de tensiones tal que:
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>{\sigma }_{ij}={\sigma }_{ij}\left( U,V,W\right) ={\sigma }_{ij}\left( y,z\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 4)</math>
+| <math>{\sigma }_{ij}={\sigma }_{ij}\left( U,V,W\right) ={\sigma }_{ij}\left( y,z\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 4)</math>
 |}
@@ Line 114: / Line 114: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\begin{matrix}\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}=0\\\frac{\partial {\sigma }_{y}}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}=0\\\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_{z}}{\partial z}=0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 5)</math>
+| <math>\begin{matrix}\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}=0\\\frac{\partial {\sigma }_{y}}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}=0\\\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_{z}}{\partial z}=0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 5)</math>
 |}
@@ Line 129: / Line 129: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\begin{matrix}{\sigma }_{y}={\tau }_{yz}={\tau }_{xy}=0\, \, en\, \, y=b\\{\sigma }_{z}={\tau }_{yz}={\tau }_{xz}=0\, \, en\, \, z=2{h}_{o}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 6)</math>
+| <math>\begin{matrix}{\sigma }_{y}={\tau }_{yz}={\tau }_{xy}=0\, \, en\, \, y=b\\{\sigma }_{z}={\tau }_{yz}={\tau }_{xz}=0\, \, en\, \, z=2{h}_{o}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 6)</math>
 |}
@@ Line 135: / Line 135: @@
 Para resolver el problema, se ha considerado útil definir las siguientes variables adimensionales:
-<math display="inline">\overline{y}=\frac{y}{b};\quad \overline{z}=\frac{z}{{h}_{o}};\quad \overline{U}=</math><math>\frac{U}{{h}_{o}};\quad \overline{V}=\frac{V}{b};\quad \overline{W}=\frac{W}{{h}_{o}};\quad R=</math><math>\frac{b}{{h}_{o}}\quad \quad \quad \quad (\, \, SEQ\, Eq\, \ast \, MERGEFORMAT\, 7)</math>
+<math display="inline">\overline{y}=\frac{y}{b};\quad \overline{z}=\frac{z}{{h}_{o}};\quad \overline{U}=</math><math>\frac{U}{{h}_{o}};\quad \overline{V}=\frac{V}{b};\quad \overline{W}=\frac{W}{{h}_{o}};\quad R=</math><math>\frac{b}{{h}_{o}}\quad \quad \quad \quad (\, \, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 7)</math>
 Combinando las expresiones anteriores es posible formular las ecuaciones que deben verificar las componentes del campo de desplazamientos en cada punto del dominio, ecuacion 8
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\begin{matrix}R\overline{{C}_{26}}{\overline{V}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{36}}+\overline{{C}_{45}}\right) {\overline{W}}_{,\overline{y}\overline{z}}+\overline{{C}_{66}}{\overline{U}}_{,\overline{y}\overline{y}}+{R}^{3}\overline{{C}_{45}}{\overline{V}}_{,\overline{z}\overline{z}}+{R}^{2}\overline{{C}_{55}}{\overline{U}}_{,\overline{z}\overline{z}}=0\\R\overline{{C}_{22}}{\overline{V}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{23}}+\overline{{C}_{44}}\right) {\overline{W}}_{,\overline{y}\overline{z}}+\overline{{C}_{26}}{\overline{U}}_{,\overline{y}\overline{y}}+{R}^{3}\overline{{C}_{44}}{\overline{V}}_{,\overline{z}\overline{z}}+{R}^{2}\overline{{C}_{45}}{\overline{U}}_{,\overline{z}\overline{z}}=0\\\overline{{C}_{44}}{\overline{W}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{45}}+\overline{{C}_{36}}\right) {\overline{U}}_{,\overline{y}\overline{z}}+{R}^{2}\left( \overline{{C}_{23}}+\overline{{C}_{44}}\right) {\overline{V}}_{,\overline{y}\overline{z}}+{R}^{2}\overline{{C}_{33}}{\overline{W}}_{,\overline{z}\overline{z}}=0\end{matrix}\quad \quad (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 8)\,</math>
+| <math>\begin{matrix}R\overline{{C}_{26}}{\overline{V}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{36}}+\overline{{C}_{45}}\right) {\overline{W}}_{,\overline{y}\overline{z}}+\overline{{C}_{66}}{\overline{U}}_{,\overline{y}\overline{y}}+{R}^{3}\overline{{C}_{45}}{\overline{V}}_{,\overline{z}\overline{z}}+{R}^{2}\overline{{C}_{55}}{\overline{U}}_{,\overline{z}\overline{z}}=0\\R\overline{{C}_{22}}{\overline{V}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{23}}+\overline{{C}_{44}}\right) {\overline{W}}_{,\overline{y}\overline{z}}+\overline{{C}_{26}}{\overline{U}}_{,\overline{y}\overline{y}}+{R}^{3}\overline{{C}_{44}}{\overline{V}}_{,\overline{z}\overline{z}}+{R}^{2}\overline{{C}_{45}}{\overline{U}}_{,\overline{z}\overline{z}}=0\\\overline{{C}_{44}}{\overline{W}}_{,\overline{y}\overline{y}}+R\left( \overline{{C}_{45}}+\overline{{C}_{36}}\right) {\overline{U}}_{,\overline{y}\overline{z}}+{R}^{2}\left( \overline{{C}_{23}}+\overline{{C}_{44}}\right) {\overline{V}}_{,\overline{y}\overline{z}}+{R}^{2}\overline{{C}_{33}}{\overline{W}}_{,\overline{z}\overline{z}}=0\end{matrix}\quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 8)\,</math>
 |}
@@ Line 147: / Line 147: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\begin{matrix}\, \overline{{C}_{22}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{23}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{26}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{12}}{\epsilon }_{x}\\\frac{1}{R}\overline{{C}_{44}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{44}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{45}}{\overline{U}}_{,\overline{z}}=0\\\overline{{C}_{26}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{36}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{66}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{16}}{\epsilon }_{x}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 9)\,</math>
+| <math>\begin{matrix}\, \overline{{C}_{22}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{23}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{26}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{12}}{\epsilon }_{x}\\\frac{1}{R}\overline{{C}_{44}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{44}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{45}}{\overline{U}}_{,\overline{z}}=0\\\overline{{C}_{26}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{36}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{66}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{16}}{\epsilon }_{x}\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 9)\,</math>
 |}
 {|class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\, \begin{matrix}\, \overline{{C}_{23}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{33}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{36}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{13}}{\epsilon }_{x}\\\frac{1}{R}\overline{{C}_{44}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{44}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{45}}{\overline{U}}_{,\overline{z}}=0\\\frac{1}{R}\overline{{C}_{45}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{45}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{55}}{\overline{U}}_{,\overline{z}}=0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 10)\,</math>
+| <math>\, \begin{matrix}\, \overline{{C}_{23}}{\overline{V}}_{,\overline{y}}+\overline{{C}_{33}}{\overline{W}}_{,\overline{z}}+\frac{1}{R}\overline{{C}_{36}}{\overline{U}}_{,\overline{y}}=-\overline{{C}_{13}}{\epsilon }_{x}\\\frac{1}{R}\overline{{C}_{44}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{44}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{45}}{\overline{U}}_{,\overline{z}}=0\\\frac{1}{R}\overline{{C}_{45}}{\overline{W}}_{,\overline{y}}+R\overline{{C}_{45}}{\overline{V}}_{,\overline{z}}+\overline{{C}_{55}}{\overline{U}}_{,\overline{z}}=0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 10)\,</math>
 |}
@@ Line 160: / Line 160: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\begin{matrix}{U}_{,z}\left( y,0\right) =0\\{V}_{,z}\left( y,0\right) =0\\W\left( y,0\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 11)\, \,</math>
+| <math>\begin{matrix}{U}_{,z}\left( y,0\right) =0\\{V}_{,z}\left( y,0\right) =0\\W\left( y,0\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 11)\, \,</math>
 |}
 {|class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\begin{matrix}{U}_{,y}\left( 0,z\right) =0\\V\left( 0,z\right) =0\\{W}_{,y}\left( 0,z\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 12)\, \,</math>
+| <math>\begin{matrix}{U}_{,y}\left( 0,z\right) =0\\V\left( 0,z\right) =0\\{W}_{,y}\left( 0,z\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 12)\, \,</math>
 |}
@@ Line 173: / Line 173: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\begin{matrix}U\left( 0,z\right) =U\left( 0,0\right) =0\\\, V\left( 0,0\right) =0\, \, \\W\left( 0,0\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 13)</math>
+| <math>\begin{matrix}U\left( 0,z\right) =U\left( 0,0\right) =0\\\, V\left( 0,0\right) =0\, \, \\W\left( 0,0\right) =0\end{matrix}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 13)</math>
 |}
 </div>
@@ Line 182: / Line 182: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>x=\left( \begin{matrix}\begin{matrix}{U}_{1}\\{V}_{1}\\{W}_{1}\end{matrix}\\\begin{matrix}\begin{matrix}{U}_{2}\\{V}_{2}\\{W}_{2}\end{matrix}\\\begin{matrix}\ldots \\\begin{matrix}{U}_{N}\\{V}_{N}\\{W}_{N}\end{matrix}\end{matrix}\end{matrix}\end{matrix}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 14)</math>
+| <math>x=\left( \begin{matrix}\begin{matrix}{U}_{1}\\{V}_{1}\\{W}_{1}\end{matrix}\\\begin{matrix}\begin{matrix}{U}_{2}\\{V}_{2}\\{W}_{2}\end{matrix}\\\begin{matrix}\ldots \\\begin{matrix}{U}_{N}\\{V}_{N}\\{W}_{N}\end{matrix}\end{matrix}\end{matrix}\end{matrix}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 14)</math>
 |}
@@ Line 193: / Line 193: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>A\left( \frac{x}{{\epsilon }_{x}}\right) =\left( \frac{b}{{\epsilon }_{x}}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 15)</math>
+| <math>A\left( \frac{x}{{\epsilon }_{x}}\right) =\left( \frac{b}{{\epsilon }_{x}}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \, \, (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 15)</math>
 |}
@@ Line 200: / Line 200: @@
 {| class="formulaSCP" style="width: 100%; text-align: center;"
 |-
-| <math>\frac{b}{{\epsilon }_{x}}\not =f\left( {\epsilon }_{x}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \ast \, MERGEFORMAT\, 16)</math>
+| <math>\frac{b}{{\epsilon }_{x}}\not =f\left( {\epsilon }_{x}\right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\, SEQ\, Eq\, \\ast \, MERGEFORMAT\, 16)</math>
 |}

Revision as of 09:47, 3 May 2022

1 Introducción

2 Descripción del modelo

3 Resultados

4 Conclusiones

Agradecimientos

Referencias

Document information

Document Score

Share this document

Keywords

claim authorship