Revision as of 20:24, 13 April 2021 (view source) Vanderg (talk | contribs) ← Older edit		Revision as of 20:29, 13 April 2021 (view source) Vanderg (talk | contribs) Newer edit →
Line 945:		Line 945:
	<div id="cite-38"></div>		<div id="cite-38"></div>
−	'''[38]'''  J. Zhang, G. Yan, Lattice boltzmann method for one and two-dimensional burgers equation, Physica A (2008).	+	'''[[#citeF-37|[38]]]'''  J. Zhang, G. Yan, Lattice boltzmann method for one and two-dimensional burgers equation, Physica A (2008).
	<div id="cite-39"></div>		<div id="cite-39"></div>
Line 975:		Line 975:
	<div id="cite-48"></div>		<div id="cite-48"></div>
−	'''[48]'''  P. K. Uda, Evapotranspiração real da bacia do rio iguaçu por meio do modelo metric, Ph.D. thesis (2016).	+	'''[[#citeF-37|[48]]]'''  P. K. Uda, Evapotranspiração real da bacia do rio iguaçu por meio do modelo metric, Ph.D. thesis (2016).
	<div id="cite-49"></div>		<div id="cite-49"></div>
Line 1,071:		Line 1,071:
	{|  class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;"		{|  class="floating_tableSCP wikitable" style="text-align: right; margin: 1em auto;min-width:50%;"
−	|+ style="font-size: 75%;" |<span id='table-BC'></span>Tabla. B Caracterização física dos planos das 9 sub-bacias do rio Chopim - pd e pe são, respectivamente, os planos do lado direito e do lado esquerdo no sentido do escoamento.	+	|+ style="font-size: 75%;" |<span id='table-B'></span>Tabla. B Caracterização física dos planos das 9 sub-bacias do rio Chopim - pd e pe são, respectivamente, os planos do lado direito e do lado esquerdo no sentido do escoamento.
	|- style="border-top: 2px solid;"		|- style="border-top: 2px solid;"
	| style="text-align: center;border-right: 2px solid;" |		| style="text-align: center;border-right: 2px solid;" |

---

Revision as of 20:29, 13 April 2021

Simulação Numérica do Escoamento Superficial por meio do Método do Reticulado de Boltzmann utilizando Junção de Sub-bacias

V. Galina J. Cargnelutti E. Kaviski L. M. Gramani A. M. Lobeiro

Resumen

Investigou-se o escoamento superficial em bacia hidrográfica por meio da simulação numérica unidimensional utilizando o método do reticulado de Boltzmann (LBM). Desenvolveu-se um modelo computacional onde a bacia hidrográfica é representada pela junção de nove sub-bacias. Para isto, foram estabelecidas duas funções de distribuição de equilíbrio obtidas por meio da expansão de Chapmann-Enskog e utilizando o reticulado D1Q5, uma adequada para o escoamento na superfície da bacia e outra para o canal principal, obtendo a profundidade da água na superfície da bacia e a área da seção transversal nos canais. Além disso, estabeleceu-se a condição de contorno na passagem de fluxo de uma sub-bacia para outra, levando em consideração a conservação da massa e, para se obter uma simulação mais próxima da realidade, considerou-se uma vazão inicial que ocorre no rio (escoamento de base), em cada trecho de canal. Os resultados numéricos obtidos pelo LBM foram comparados com dados medidos em campo.

Rev. Int. Mét. Num. Cálc. Dis. Ing.

Vanderlei Galina Departamento de Matemática, Universidade Tecnológica Federal do Paraná (UTFPR) Rua Cristo Rei, Vila Becker CEP 85902-490 - Toledo PR, Brasil Telefone Geral +55 (45) 3378-6863 e-mail: vanderleigalina@gmail.com

Jocelaine Cargnelutti Coordenação do Curso de Matemática, Universidade Tecnológica Federal do Paraná (UTFPR) - Toledo PR, Brasil e-mail: jocelainecargnelutti@gmail.com

Eloy Kaviski Departamento de Hidráulica e Saneamento, Universidade Federal do Paraná (UFPR) - Curitiba PR, Brasil e-mail: eloy.dhs@gmail.com

Liliana Madalena Gramani (In memoriam) Departamento de Matemática, Universidade Federal do Paraná (UFPR) - Curitiba PR, Brasil e-mail: l.gramani@gmail.com

Adilandri Mércio Lobeiro Departamento de Matemática Universidade Tecnológica Federal do Paraná (UTFPR) - Campo Mourão PR, Brasil e-mail: adilandri@gmail.com

Palavras-chaves:

Método do reticulado de Boltzmann. Escoamento em bacias hidrográficas. Escoamento superficial. Modelo onda cinemática. Junção de sub-bacias.

NUMERICAL SIMULATION OF SURFACE FLOW THROUGH THE LATTICE BOLTZMANN METHOD USING SUB-BASIN JUNCTION

The watershed surface runoff was investigated through the one-dimensional numerical simulation using the Lattice Boltzmann Method (LBM). A computational model was developed where the watershed is represented by the junction of nine sub-basins. For this, two equilibrium distribution functions were established through the Chapman-Enskog Expansion on a D1Q5 lattice, one suitable for flow on the basin surface and another for the main channel, obtaining the water depth on the basin surface and the channels cross-sectional area. In addition, the boundary condition was established in the flow passage from one sub-basin to another, taking into account the mass conservation and, in order to obtain a simulation closer to reality, it was considered an initial river flow (baseflow) of each channel stretch. The numerical results obtained by the LBM were compared with data measured in field.

Keywords:

Lattice Boltzmann method. Runoff in watersheds. Overland flow. Kinematic wave model. Sub-basin junction.

1 Introdução

O comportamento do escoamento de um fluido pode ser, satisfatoriamente, avaliado por meio de métodos numéricos. Simulações numéricas, análises teóricas, técnicas experimentais e dados coletados, são ferramentais que se complementam na resolução de problemas em hidrodinâmica [1]. Em particular, o LBM se destaca por capturar as características físicas de problemas, até mesmo detalhes microscópicos, e as apresenta de forma macroscópica [2]. A abordagem do LBM é diferenciada quando comparada aos métodos numéricos tradicionais, pois fornece uma maneira indireta para a solução das equações governantes do escoamento. O LBM não utiliza discretização das equações macroscópicas, o método baseia-se em modelos microscópicos e equações que governam a cinética em um nível mesoscópico. No LBM a dinâmica macroscópica de um fluido é resultado do comportamento coletivo de partículas microscópicas e não se altera com os detalhes subjacentes referentes as interações moleculares do fluido [3]. O método tem sido aplicado nas mais diversas áreas de pesquisa e tornou-se de grande potencial no estudo da dinâmica de fluidos computacional. Escoamentos envolvendo águas rasas [2,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], o modelo onda cinemática [6,21,22,23,25,24] e várias outras aplicações como em meios porosos [26,30,27,28,29] foram abrangidos pelo LBM e as simulações apresentaram resultados satisfatórios.

As equações de Saint-Venant governam o escoamento em superfície livre. Porém, para sua resolução, elaboradas técnicas numéricas e uma grande quantidade de informações hidráulicas são necessárias. Na busca em reduzir a quantidade de dados necessários e a dificuldade numérica de resolução das equações diferenciais, são empregadas simplificações das equações de Saint-Venant como o modelo onda cinemática, também denominado modelo hidráulico de propagação de ondas de cheias [31].

O modelo onda cinemática é aplicado para descrever escoamentos superficiais em bacias hidrográficas e cursos de água naturais. Foco de interesse neste estudo, as bacias hidrográficas são um sistema natural que exige monitoramento no sentido de prever seu comportamento em ações como precipitações extremas, cheias, estiagens, entre outros. Com a análise destes eventos, é possível gerenciar os recursos hídricos e evitar a degradação do solo, oferecendo assim planejamento adequado para o espaço rural e urbano [1].

Utilizando o LBM com aperador de colisão BGK, a proposta deste estudo é obter a simulação numérica do escoamento superficial na bacia do rio Chopim, representado pelas equações do modelo onda cinemática. A bacia do rio Chopim abrange uma área de ${\textstyle 7.500}$ km${\textstyle ^{2}}$ e está localizada dentro da bacia do rio Iguaçu, a qual tem grande importância na geração de energia por meio de usinas hidrelétricas e pela grande demanda de recursos hídricos. Considera-se, nesse estudo, um trecho do rio Chopim com comprimento de aproximadamente ${\textstyle 281}$ km com área de drenagem em torno de ${\textstyle 3.205}$ km${\textstyle ^{2}}$ na superfície da bacia.

Lembramos que um artigo, publicado em 2018, dos mesmos autores deste artigo, fornece um estudo menos amplo que o apresentado aqui. No artigo [24] obteve-se a simulação numérica unidimensional do escoamento superficial em uma bacia hidrográfica natural, por meio do LBM. De acordo com as caractrísticas da bacia hidrográfica estudada, foi possivel obter bons resultados na simulação considerando no modelo computacional a superfície da bacia segmentada em apenas dois planos laterais e um canal principal. No novo artigo que estamos apresentando, analizamos outra bacia hidrográfica, que devido as suas características, foi necessário segmentá-la em 9 sub-bacias. Com esta nova configuração, foi necessário estabelecer condições de contorno na passagem de fluxo de uma sub-bacia para outra, levando em consideração a conservação da massa. No artigo [24] determinou-se duas funções de distribuição de equilíbrio obtidas por meio da expansão de Chapmann-Enskog em escalas de tempo e utilizando o reticulado D1Q3. Neste novo artigo, as funções de equilíbrio foram determinadas para o reticulado D1Q5. Além destas novas contribuições, para se obter uma simulação mais próxima da realidade, considerou-se uma vazão inicial que ocorre no rio (escoamento de base), em cada trecho de canal, antes de ocorrer a precipitação.

As quatro principais contribuições deste artigo são: 1) Aplicação do LBM para obter a simulação numérica do escoamento superficial da bacia do rio Chopim representada pela junção de nove sub-bacias formadas por planos laterais e um segmento de canal. Em cada sub-bacia, a água que escoa dos planos entra no canal sob a forma de contribuição lateral. Na saída de cada sub-bacia, obtém-se um hidrograma, que foi utilizado para ajustar as condições de contorno na junção de dois segmentos de canal. A simulação produziu o hidrograma total o qual fornece a variação da vazão em relação ao tempo correspondente a resposta da bacia hidrográfica após a precipitação efetiva do evento simulado; 2) Determinação de duas funções de distribuição de equilíbrio obtidas por meio da expansão de Chapmann-Enskog em escalas de tempo e utilizando o reticulado D1Q5, uma adequada para o escoamento na superfície da bacia e outra para o canal principal, obtendo a profundidade da água na superfície da bacia e área da seção transversal nos canais; 3) Determinação de condição de contorno na passagem de fluxo de uma sub-bacia para outra, levando em consideração a conservação da massa; 4) Para se obter uma simulação mais próxima da realidade, considerou-se uma vazão inicial que ocorre no rio (escoamento de base), em cada trecho de canal, antes de ocorrer a precipitação. Essa vazão entra no modelo computacional como uma condição inicial. Também é considerada como uma condição de contorno ao ser adicionada na contribuição lateral dos planos, em cada passo de tempo.

Este artigo está estruturado da seguinte forma. Na seção 2 tem-se as equações governantes do escoamento. Em seguida, na seção 3, apresenta-se o método numérico que será utilizado e os quatro elementos principais que o caracterizam: Equação do LBM e o operador de colisão BGK, o reticulado D1Q5, a expensão multi-escala e as funções distribuição de equilíbrio. Tem-se, também, nesta seção informações sobre condições de contorno e estabilidade. O estudo de caso é apresentado na seção 4 considerando as características da bacia do rio Chopim, resultados da simulação e discussões. Em seguida, na seção 6, apresentam-se as conclusões deste trabalho.

2 Equações de escoamento

As equações de Saint-Venant unidimensionais formam um sistema de equações não-lineares composto pelas equações da continuidade (1) e da quantidade de movimento (2). Elas governam o escoamento onde há superfície livre, com a suposição de que a componente vertical e transversal da velocidade do escoamento pode ser desprezada em relação aos componentes longitudinais [32],

${\displaystyle {\frac {\partial Q}{\partial x}}+{\frac {\partial A}{\partial t}}={0}}$ (1) ${\displaystyle {\frac {\partial Q}{\partial t}}+{\frac {\partial }{\partial x}}\left({\frac {Q^{2}}{A}}\right)+gA{\frac {\partial h}{\partial x}}=gA({S_{o}}-{S_{f}}),}$ (2)

onde ${\textstyle Q}$ é a vazão, ${\textstyle A}$ é a área da seção transversal, ${\textstyle h}$ é a profundidade do escoamento, ${\textstyle g}$ é a aceleração da gravidade, ${\textstyle t}$ é o tempo, ${\textstyle x}$ é a coordenada espacial, ${\textstyle S_{0}}$ é a declividade do fundo e ${\textstyle S_{f}}$ representa a declividade da linha de energia.

No escoamento em bacias hidrográficas utiliza-se o modelo onda cinemática como simplificação das equações de Saint-Venant. Este modelo, considera a equação da continuidade e a equação da quantidade de movimento, desprezando os termos de pressão e inércia. Dessa forma, a equação da quantidade de movimento resulta [33],

${\displaystyle S_{0}=S_{f}.}$

(3)

O modelo onda cinemática baseia-se, principalmente, na equação da continuidade e faz-se uma aproximação da equação da quantidade de movimento por uma fórmula de fluxo uniforme. Definindo a declividade da linha de energia ${\textstyle S_{f}}$, com uma fórmula de fluxo uniforme, a equação (3) pode ser representada para o escoamento em canal ou em escoamento superficial por uma relação de potência da forma [34],

${\displaystyle Q={\alpha }{A^{\lambda }},}$

(4)

em que ${\textstyle \alpha }$ e ${\textstyle \lambda }$ são coeficientes determinados pelas características do escoamento. Este modelo não-linear considera a variabilidade dos parâmetros de acordo com a vazão. Assim, o escoamento em trechos de canais da bacia é dado pelas equações,

${\displaystyle {\frac {\partial A}{\partial t}}+{\frac {\partial Q}{\partial x}}={q_{l}}}$ ${\displaystyle Q={\beta _{c}}{A^{m_{c}}},}$

(5)

onde ${\textstyle q_{l}}$ é a contribuição lateral, ${\textstyle \beta _{c}}$ e ${\textstyle m_{c}}$ são parâmetros a serem determinados.

As condições iniciais e de contorno nos canais são determinadas por hidrogramas de vazão resultantes do escoamento na superfície e em trechos de canais a montante. A superfície da bacia é aproximada por planos, dessa forma, considerando que a equação da continuidade (1) descreva o escoamento em um canal prismático e retangular, as equações de escoamento para os planos que descrevem a superfície da bacia são as seguintes,

${\displaystyle {\frac {\partial h}{\partial t}}+{\frac {\partial q}{\partial x}}={i_{e}}}$ ${\displaystyle q={\beta _{s}}{h^{m_{s}}},}$

(6)

onde ${\textstyle q}$ é a vazão por unidade de largura, ${\textstyle i_{e}}$ é a precipitação efetiva e ${\textstyle \beta _{s}}$ e ${\textstyle m_{s}}$ são parâmetros a serem determinados.

As condições iniciais e de contorno são representadas por,

${\displaystyle h(0,t)=0,\quad t>0}$ (7) ${\displaystyle h(x,0)=0,\quad 0\leq x\leq L}$ (8)

onde ${\textstyle L}$ é o comprimento de declive.

A aplicação do modelo onda cinemática em escoamento superficial difere da sua aplicação em rios, apenas pelo meio onde ocorre o escoamento. Quanto a rugosidade, utiliza-se a resistência hidráulica de Manning, assim ${\textstyle \beta _{c}=\beta _{s}={\sqrt {S_{0}}}/n_{r}}$ e ${\textstyle m_{c}=m_{s}=5/3}$, onde ${\textstyle n_{r}}$ é o coeficiente de rugosidade de Manning.

3 Método do Reticulado de Boltzmann

De acordo com Chen and Doolen (1998) [3], o LBM é um esquema numérico baseado em equações cinéticas formuladas em uma escala mesoscópica que simula a dinâmica do fluido em uma escala macroscópica. A dinâmica deste método é dada pela equação do reticulado de Boltzmann, a qual mostra como ocorrem as distribuições das micropartículas.

O LBM considera uma dinâmica molecular de partículas fictícias em que o espaço, o tempo e as velocidades são discretas. Essas partículas viajam de um ponto ao outro na malha em tempos discretos, se encontrando nestes pontos ao final de cada passo de tempo e trocam quantidade de movimento e energia. No que se refere aos módulos de velocidades, eles assumem valores contínuos. Por outro lado, o LBM pode ser visto como uma forma simplificada da equação cinética de Boltzmann, em que somente são mantidos os detalhes moleculares essenciais para se recuperar o comportamento macroscópico correto [35].

Quatro elementos principais caracterizam o LBM: a equação governante, o operador de colisão, o reticulado e a função distribuição de equilíbrio [2].

3.1 Equação do LBM e o Operador BGK

Inicialmente apresenta-se em (9), a equação governante do LBM com aperador de colisão BGK, denominada equação do reticulado de Boltzmann. A forma do operador de colisão foi determinada por Bhatnagar, Gross e Krook [36], com o objetivo de simplificar a equação cinética de Boltzmann. A equação do reticulado de Boltzmann, possui as etapas de propagação e colisão. Na etapa de propagação, as partículas se movem de um nó da malha para um dos seus nós vizinhos, com direção dada pela velocidade. Na etapa de colisão, as partículas que chegam no mesmo nó interagem entre si e mudam suas direções conforme as diretrizes do operador de colisão [37].

${\displaystyle {f_{\alpha }}({\vec {x}}+{{\vec {e}}_{\alpha }}\Delta t,t+\Delta t)-{f_{\alpha }}({\vec {x}},t)=\Omega _{\alpha }+{(\Delta t)^{2}}{g_{\alpha }}({\vec {x}},t),}$

(9)

${\displaystyle \Omega _{\alpha }=-{\dfrac {1}{\tau }}\left[{{f_{\alpha }}({\vec {x}},t)-f_{\alpha }^{eq}({\vec {x}},t)}\right],}$

(10)

onde ${\textstyle \Omega _{\alpha }}$ é o operador de colisão, ${\textstyle f_{\alpha }}$ é a função distribuição de partículas e representa a probabilidade de uma partícula seguir determinada direção, ${\textstyle f_{\alpha }^{eq}}$ é a função distribuição de equilíbrio, ${\textstyle {\vec {x}}}$ é o posição do nó na malha, ${\textstyle \Delta t}$ é o incremento no tempo, ${\textstyle {\vec {e_{\alpha }}}}$ são as possíveis direções de movimento na malha, ${\textstyle {(\Delta t)^{2}}{g_{\alpha }}}$ é o termo de força e ${\textstyle \tau }$ é o parâmetro de relaxamento.

3.2 Reticulado D1Q5

No LBM o reticulado tem a função de representar os pontos da malha e determinar as direções de movimento das partículas. As direções finitas e determinadas para o movimento das partículas definem num modelo microscópico para a dinâmica molecular. Na escolha do reticulado a ser utilizado é essencial observar a sua simetria. Ela é necessária para que o reticulado possa representar as equações macroscópicas [2].

Encontra-se em Qian et al. [30], uma família de reticulados denominada ${\textstyle DkQm}$, onde ${\textstyle k}$ indica o espaço ${\textstyle k}$-dimensional e ${\textstyle m}$ as direções de movimento para as distribuições de partículas. O modelo de reticulado D1Q5 é unidimensional com quatro direções de velocidades não nulas e uma para velocidade nula. As partículas do fluido se movimentam para dois nós vizinhos a esquerda e dois nós vizinhos a direita. A Figura 1 mostra o reticulado D1Q5 com velocidades ${\textstyle {\vec {e}}_{0}=0}$, ${\textstyle {\vec {e}}_{1}=-e}$, ${\textstyle {\vec {e}}_{2}=-2e}$, ${\textstyle {\vec {e}}_{3}=e}$ e ${\textstyle {\vec {e}}_{4}=2e}$, sendo ${\textstyle e=\Delta x/\Delta t}$ a velocidade no reticulado, em que ${\textstyle \Delta x}$ é o espaçamento da malha.

Figura 1: Reticulado D1Q5

Fonte: Zhang e Yan (2008) [38].

3.3 Expansão multi-escala

Uma expansão multi-escala deve ser aplicada para fazer a ligação entre a escala mesoscópica, onde se insere o LBM, e a escala macroscópica das equações governantes. A expansão mais utilizada é a expansão de Chapmann-Enskog [39], a qual considera escalas de tempo e espaço para que a partir da equação do reticulado de Boltzmann seja derivada e equação governante do escoamento.

Para que não hajam funções de distribuição negativas associadas a equação de onda cinemática, o que contraria as leis da física, deve-se atribuir a expansão multi-escala apenas a coordenada de tempo [22]. Dessa forma, aplicando-se cinco escalas a coordenada temporal, as formas diferenciais para as coordenadas de espaço e tempo são como seguem,

${\displaystyle {\dfrac {\partial }{\partial t}}={\dfrac {\partial }{\partial {t_{0}}}}+\varepsilon {\dfrac {\partial }{\partial {t_{1}}}}+{\varepsilon ^{2}}{\dfrac {\partial }{\partial {t_{2}}}}+{\varepsilon ^{3}}{\dfrac {\partial }{\partial {t_{3}}}}+{\varepsilon ^{4}}{\dfrac {\partial }{\partial {t_{4}}}}+O({\varepsilon ^{5}}),}$ ${\displaystyle {\dfrac {\partial }{\partial x}}={\dfrac {\partial }{\partial x}}+O(\varepsilon ),}$

(11)

em que ${\textstyle t_{0},\,t_{1},\,t_{2},\,t_{3}}$ e ${\textstyle t_{4}}$ são escalas de tempo e ${\textstyle \varepsilon }$ é o número de Knudsen. O número de Knudsen é uma medida adimensional definido como a razão entre o comprimento do caminho livre médio molecular e uma escala de comprimento fisicamente representativa.

Expandindo ${\textstyle f_{\alpha }}$ em torno da função de distribuição de equilíbrio ${\textstyle f_{\alpha }^{eq}}$ com ${\textstyle \varepsilon }$ pequeno, tem-se,

${\displaystyle {f_{\alpha }}=f_{\alpha }^{(0)}+\varepsilon f_{\alpha }^{(1)}+{\varepsilon ^{2}}f_{\alpha }^{(2)}+{\varepsilon ^{3}}f_{\alpha }^{(3)}+{\varepsilon ^{4}}f_{\alpha }^{(4)}+O({\varepsilon ^{5}}),}$

(12)

em que ${\textstyle f_{\alpha }^{(0)}}$ é função distribuição de equilíbrio,

${\displaystyle f_{\alpha }^{(0)}=f_{\alpha }^{eq},}$

(13)

e, a função distribuição de não equilíbrio é descrita na forma,

${\displaystyle f_{\alpha }^{neq}=\varepsilon f_{\alpha }^{(1)}+{\varepsilon ^{2}}f_{\alpha }^{(2)}+{\varepsilon ^{3}}f_{\alpha }^{(3)}+{\varepsilon ^{4}}f_{\alpha }^{(4)}+O({\varepsilon ^{5}}).}$

(14)

A expansão de ${\textstyle {f_{\alpha }}({\vec {x}}+{{\vec {e}}_{\alpha }}\Delta t,\,t+\Delta t)}$ em série de Taylor de quinta ordem, considerando ${\textstyle \Delta t=\varepsilon }$, comparada com a equação (9) de evolução do LBM, resulta em,

${\displaystyle \varepsilon {\Delta }{f_{\alpha }}+{\frac {\varepsilon ^{2}}{2}}{\Delta ^{2}}{f_{\alpha }}+{\frac {\varepsilon ^{3}}{6}}{\Delta ^{3}}{f_{\alpha }}}$ ${\displaystyle +{\frac {\varepsilon ^{4}}{24}}{\Delta ^{4}}{f_{\alpha }}=-{\frac {1}{\tau }}\left({{f_{\alpha }}-f_{\alpha }^{eq}}\right)+{\varepsilon ^{2}}{g_{\alpha }},}$

(15)

em que,

${\displaystyle \Delta \equiv {\frac {\partial }{\partial {t_{0}}}}+{{\vec {e}}_{\alpha }}{\frac {\partial }{\partial x}}.}$

(16)

Com base nas escalas de tempo e na expansão de ${\textstyle f_{\alpha }}$, equações (11) e (12), respectivamente, e comparando todas as ordens de ${\textstyle \varepsilon }$, determinam-se as equações discretas do reticulado de Boltzmann de diferentes ordens de magnitude,

${\displaystyle O({\varepsilon ^{0}}):f_{\alpha }^{(0)}=f_{\alpha }^{eq},}$ (17) ${\displaystyle O({\varepsilon ^{1}}):\Delta \,f_{\alpha }^{(0)}=-{\frac {1}{\tau }}f_{\alpha }^{(1)},}$ (18) ${\displaystyle O({\varepsilon ^{2}}):{\frac {\partial f_{\alpha }^{(0)}}{\partial {t_{1}}}}+{p}_{2}{\Delta ^{2}}f_{\alpha }^{(0)}=-{\frac {1}{\tau }}f_{\alpha }^{(2)}+{g_{\alpha }},}$ (19) ${\displaystyle O({\varepsilon ^{3}}):{\frac {\partial f_{\alpha }^{(0)}}{\partial {t_{2}}}}+p_{3}{\Delta ^{3}}f_{\alpha }^{(0)}+2p_{2}\Delta {\frac {\partial f_{\alpha }^{(0)}}{\partial {t_{1}}}}=-{\frac {1}{\tau }}f_{\alpha }^{(3)}}$ ${\displaystyle -\tau \Delta {g_{\alpha }},}$ (20) ${\displaystyle O({\varepsilon ^{4}}):{\frac {\partial f_{\alpha }^{(0)}}{\partial {t_{3}}}}+p_{4}{\Delta ^{4}}f_{\alpha }^{(0)}+3p_{3}{\Delta ^{2}}{\frac {\partial f_{\alpha }^{(0)}}{\partial {t_{1}}}}}$ ${\displaystyle +2p_{2}\Delta {\frac {\partial f_{\alpha }^{(0)}}{\partial {t_{2}}}}+p_{2}{\frac {\partial ^{2}f_{\alpha }^{(0)}}{\partial t_{1}^{2}}}=-{\frac {1}{\tau }}f_{\alpha }^{(4)}}$ ${\displaystyle +p_{2}\tau \Delta ^{2}{g_{\alpha }}-\tau {\frac {\partial g_{\alpha }}{\partial {t_{1}}}},}$ (21)

em que ${\textstyle p_{1},\,p_{2},\,p_{3}}$ e ${\textstyle p_{4}}$ são polinômios em relação ao parâmetro de relaxamento ${\textstyle \tau }$, descritos por,

${\displaystyle {p_{1}}(\tau )=\tau ,}$ ${\displaystyle {p_{2}}(\tau )={\frac {1}{2}}-\tau ,}$ ${\displaystyle {p_{3}}(\tau )={\tau ^{2}}-\tau +{\frac {1}{6}},}$ ${\displaystyle {p_{4}}(\tau )=-{\tau ^{3}}+{\frac {3}{2}}{\tau ^{2}}-{\frac {7}{12}}\tau +{\frac {1}{24}}.}$

(22)

Por meio das equações (17), (18), (19), (20) e (21) determinam-se os momentos da função distribuição de equilíbrio, e a partir das equações geradas da expansão dos momentos sobre o reticulado, determinam-se as expressões da função distribuição de equilíbrio nas direções do reticulado.

3.4 Função Distribuição de Equilíbrio

A função distribuição de equilíbrio juntamente com a equação do Reticulado de Boltzmann (9) desempenham um papel essencial que é recuperar a equação macroscópica do fluido. A seguir, recupera-se a equação da onda cinemática unidimensional (5) e determina-se a sua função distribuição de equilíbrio.

A equação da onda cinemática é um caso especial da equação de Burgers. A equação de Burgers é uma equação de convecção-difusão não-linear que representa um modelo simplificado das equações de Navier-Stokes. É utilizada para testar a eficiência de vários esquemas numéricos e para descrever o escoamento por meio de uma onda de choque que viaja em um fluido viscoso [40].

A equação de Burgers unidimensional pode ser escrita da seguinte forma [40,22],

${\displaystyle {\frac {\partial v}{\partial t}}+{\frac {\partial }{\partial x}}\left({\beta {v^{m}}}\right)=\gamma {\frac {{\partial ^{2}}v}{\partial x^{2}}}+F,}$

(23)

onde ${\textstyle v({\vec {x}},t)}$ é uma função que pode representar uma quantidade real como a altura, a vazão ou a área da seção transversal, ${\textstyle \gamma }$ é o coeficiente de difusão, ${\textstyle \beta }$ e ${\textstyle m}$ são parâmetros a serem determinados, e ${\textstyle F}$ representa o efeito externo ou força externa. Assume-se ${\textstyle \gamma }$ nulo para obter a equação da onda cinemática, modelo no qual não é considerada a difusão.

Assumindo que a função distribuição ${\textstyle f_{\alpha }}$ está próxima do equilíbrio localmente, devem ocorrer as seguintes condições de conservação,

${\displaystyle \sum \limits _{\alpha }{{\vec {e}}_{\alpha }^{\,n}}{f_{\alpha }}=\sum \limits _{\alpha }{{\vec {e}}_{\alpha }^{\,n}}f_{\alpha }^{(eq)},\quad n=0,1,2,3,4,}$

(24)

em consequência, as somas sobre a função distribuição de não equilíbrio têm as seguintes restrições,

${\displaystyle \sum \limits _{\alpha }{{\vec {e}}_{\alpha }^{\,n}}f_{\alpha }^{(i)}=0,\,i=1,2,3,4,\,n=0,1,2,3,4.}$

(25)

Combinando as equações (17) a (21), obedecendo as restrições em (24) e (25), em vista das diferentes escalas de tempo e da equação de Burgers, equação (23), determinam-se os momentos da função distribuição de equilíbrio de zero a quarta ordem, descritos na equação (26). Neste artigo, assume-se que a força externa não varia no espaço e no tempo, portanto são nulas as derivadas nos termos que envolvem ${\textstyle g_{\alpha }}$ do lado direito das equações (20) e (21).

${\displaystyle {\begin{array}{lcl}\sum \nolimits _{\alpha }{f_{\alpha }^{(0)}}&=&v,\\\sum \nolimits _{\alpha }{{{\vec {e}}_{\alpha }}f_{\alpha }^{(0)}}&=&\beta {v^{m}},\\\sum \nolimits _{\alpha }{{\vec {e}}_{\alpha }^{\,2}f_{\alpha }^{(0)}}&=&{\dfrac {{\beta ^{2}}{m^{2}}}{2m-1}}{v^{2m-1}},\\\sum \nolimits _{\alpha }{{\vec {e}}_{\alpha }^{\,3}f_{\alpha }^{(0)}}&=&{\dfrac {{\beta ^{3}}{m^{3}}}{3m-2}}{v^{3m-2}},\\\sum \nolimits _{\alpha }{{\vec {e}}_{\alpha }^{\,4}f_{\alpha }^{(0)}}&=&{\dfrac {{\beta ^{4}}{m^{4}}}{4m-3}}{v^{4m-3}}.\end{array}}}$

(26)

Desenvolvendo as equações em (26) nas direções das velocidades do reticulado D1Q5, obtém-se,

${\displaystyle {\begin{bmatrix}1&1&1&1&1\\0&-e&-2e&e&2e\\0&e^{2}&4e^{2}&e^{2}&4e^{2}\\0&-e^{3}&-8e^{3}&e^{3}&8e^{3}\\0&e^{4}&16e^{4}&e^{4}&16e^{4}\end{bmatrix}}{\begin{bmatrix}f_{0}\\f_{1}\\f_{2}\\f_{3}\\f_{4}\end{bmatrix}}={\begin{bmatrix}v\\\beta v^{m}\\{\dfrac {{\beta ^{2}}{m^{2}}}{2m-1}}{v^{2m-1}}\\{\dfrac {{\beta ^{3}}{m^{3}}}{3m-2}}{v^{3m-2}}\\{\dfrac {{\beta ^{4}}{m^{4}}}{4m-3}}{v^{4m-3}}\end{bmatrix}}}$

(27)

A resolução do sistema formado pelas equações em (27) determina a função distribuição de equilíbrio,

${\displaystyle f_{1}^{eq}={\frac {1}{6}}\left({-4{C_{1}}+4{C_{2}}+{C_{3}}-{C_{4}}}\right),}$ ${\displaystyle f_{2}^{eq}={\frac {1}{24}}\left({2{C_{1}}-{C_{2}}-2{C_{3}}+{C_{4}}}\right),}$ ${\displaystyle f_{3}^{eq}={\frac {1}{6}}\left({4{C_{1}}+4{C_{2}}-{C_{3}}-{C_{4}}}\right),}$ ${\displaystyle f_{4}^{eq}={\frac {1}{24}}\left({-2{C_{1}}-{C_{2}}+2{C_{3}}+{C_{4}}}\right),}$ ${\displaystyle f_{0}^{eq}=v-\left({f_{1}^{eq}+f_{2}^{eq}+f_{3}^{eq}+f_{4}^{eq}}\right),}$

(28)

onde,

${\displaystyle {C_{j}}={\left({\frac {\beta m}{e}}\right)^{j}}{\frac {v^{jm-(j-1)}}{jm-(j-1)}},\,\,\,\,\,j=1,2,3,4.}$

(29)

Tomando o valor médio de ${\textstyle F}$ em cada direção de velocidade do reticulado D1Q5, o termo de força é determinado pela expressão,

${\displaystyle g_{\alpha }={\frac {F}{5\varepsilon }},\quad \alpha =0,1,2,3,4,}$

(30)

em que ${\textstyle F}$ pode representar a precipitação quando se trata do escoamento na superfície da bacia, ou representar a contribuição lateral quando se trata do escoamento em canais.

3.5 Condições de Contorno

A representação adequada das características físicas do problema, por meio das condições iniciais e de contorno, é um fator crucial para a estabilidade e precisão das simulações. A Figura 2 ilustra uma malha unidimensional, com as direções de velocidade do reticulado D1Q5, para discretização do domínio que representa o escoamento na superfície e nos canais da bacia hidrográfica.

Figura 2: Malha computacional

As condições de contorno macroscópicas para ambos o escoamento superficial e o escoamento em canal são conhecidas na fronteira esquerda, porém desconhecidas na fronteira direita. O comportamento macroscópico nas fronteiras é alcançado pela correta aplicação das funções de distribuição de partículas. Com esse objetivo, as funções de distribuição de equilíbrio são utilizadas na fronteira esquerda, e para a fronteira direita, as funções de distribuição são determinadas por extrapolação [22].

No reticulado D1Q5 são aplicadas condições de contorno nos dois primeiros e nos dois últimos nós da malha [21]. Na fronteira esquerda, tem-se,

${\displaystyle {\bar {\bar {f_{0}}}}(x_{0})=f_{0}^{eq}(x_{0}),}$ ${\displaystyle {\bar {\bar {f_{1}}}}(x_{0})=f_{1}^{eq}(x_{0}),}$ ${\displaystyle {\bar {\bar {f_{2}}}}(x_{0})=f_{2}^{eq}(x_{0}),}$ ${\displaystyle {\bar {\bar {f_{3}}}}(x_{0})=f_{3}^{eq}(x_{0}),}$ ${\displaystyle {\bar {\bar {f_{4}}}}(x_{0})={v^{*}}}$ ${\displaystyle -({\bar {\bar {f_{0}}}}(x_{0})+{\bar {\bar {f_{1}}}}(x_{0})+{\bar {\bar {f_{2}}}}(x_{0})+{\bar {\bar {f_{3}}}}(x_{0})),}$

${\displaystyle {\bar {\bar {f_{0}}}}(x_{1})={\bar {f_{0}}}(x_{1}),}$ ${\displaystyle {\bar {\bar {f_{1}}}}(x_{1})={\bar {f_{1}}}(x_{2}),}$ ${\displaystyle {\bar {\bar {f_{2}}}}(x_{1})={\bar {f_{2}}}(x_{3}),}$ ${\displaystyle {\bar {\bar {f_{3}}}}(x_{1})={\bar {f_{3}}}(x_{0}),}$ ${\displaystyle {\bar {\bar {f_{4}}}}(x_{1})=2{\bar {\bar {f_{4}}}}(x_{2})-{\bar {\bar {f_{4}}}}(x_{3}).}$

(31)

Na fronteira direita, aplica-se,

${\displaystyle {\bar {\bar {f_{0}}}}(x_{n-1})={\bar {f_{0}}}(x_{n-1}),}$ ${\displaystyle {\bar {\bar {f_{3}}}}(x_{n-1})={\bar {f_{3}}}(x_{n-2}),}$ ${\displaystyle {\bar {\bar {f_{4}}}}(x_{n-1})={\bar {f_{4}}}(x_{n-3}),}$ ${\displaystyle {\bar {\bar {f_{1}}}}(x_{n-1})={\bar {f_{1}}}(x_{n}),}$ ${\displaystyle {\bar {\bar {f_{2}}}}(x_{n-1})=2{\bar {\bar {f_{2}}}}(x_{n-2})-{\bar {\bar {f_{2}}}}(x_{n-3}),}$

${\displaystyle {\bar {\bar {f_{0}}}}(x_{n})={\bar {f_{0}}}(x_{n}),}$ ${\displaystyle {\bar {\bar {f_{3}}}}(x_{n})={\bar {f_{3}}}(x_{n-1}),}$ ${\displaystyle {\bar {\bar {f_{4}}}}(x_{n})={\bar {f_{4}}}(x_{n-2}),}$ ${\displaystyle {\bar {\bar {f_{1}}}}(x_{n})=2{\bar {\bar {f_{1}}}}(x_{n-1})-{\bar {\bar {f_{1}}}}(x_{n-2}),}$ ${\displaystyle {\bar {\bar {f_{2}}}}(x_{n})=2{\bar {\bar {f_{2}}}}(x_{n-1})-{\bar {\bar {f_{2}}}}(x_{n-2}),}$

(32)

em que ${\textstyle {\bar {\bar {f}}}}$ é a função distribuição de velocidade das partículas depois da propagação, ${\textstyle {\bar {f}}}$ é a função distribuição de velocidade das partículas antes da propagação, ${\textstyle v^{*}}$ é a variável macroscópica na fronteira, podendo ser substituída pela profundidade do escoamento ${\textstyle h}$ ou pela área da seção transversal ${\textstyle A}$.

No modelo computacional, as características físicas em cada trecho de canal são mantidas constantes durante a simulação, isto é, não são alterados os valores do comprimento, largura, declividade e coeficiente de Manning do segmento de canal. O que pode implicar em seções transversais diferentes na junção dos canais, levando a necessidade de implementação de condição de contorno. Para que haja a conservação de massa, a vazão de um segmento de canal a montante para um segmento a jusante deve permanecer a mesma. Considerando a Figura 3, e o cálculo da vazão em uma seção transversal dada pela fórmula de Manning, a vazão no início do canal 2 é determinada por,

${\displaystyle {Q_{2}}={\frac {{{S_{0}}_{2}}^{1/2}}{{n_{r}}_{2}P_{2}^{2/3}}}A_{2}^{5/3},}$

(33)

em que ${\textstyle P=b+2h}$ é o perímetro molhado do canal retangular de largura ${\textstyle b}$.

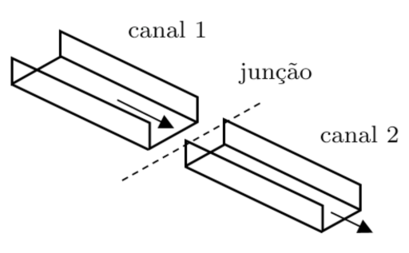
Figura 3: Junção de canais das sub-bacias

Escrevendo o perímetro molhado em termos da área molhada e da largura do canal, e substituindo na equação (33), tem-se,

${\displaystyle {Q_{2}}{\frac {{n_{r}}_{2}}{{{S_{0}}_{2}}^{1/2}}}{\left({{b_{2}}+2{\frac {A_{2}}{b_{2}}}}\right)^{2/3}}-A_{2}^{5/3}=0.}$

(34)

O valor de ${\textstyle A_{2}}$ é calculado pelo método iterativo de Newton-Raphson e considerado no LBM por meio da condição de contorno da equação (31), onde substitui-se ${\textstyle v^{*}}$ por ${\textstyle A_{2}}$. Utiliza-se a variável área ao invés da vazão, pois a função distribuição de equilíbrio é dependente da área, e por meio da área obtém-se a vazão em uma seção transversal. Quanto ao escoamento na superfície da bacia, ${\textstyle v^{*}}$ é sempre nula para cumprir a condição de contorno ${\textstyle h(0,t)=0}$ em todos os passos de tempo.

3.6 Estabilidade

De acordo com Sterling e Chen (1996) [41], não é possível garantir a estabilidade do LBM e isto ocorre devido a grande quantidade de parâmetros que impedem a sua caracterização completa. No entanto, pode-se seguir algumas condições necessárias, que, se forem satisfeitas simultaneamente, obtém-se a estabilidade da simulação [2]. A primeira expressão de (35) relaciona o parâmetro de relaxamento ${\textstyle \tau }$ e a viscosidade cinemática ${\textstyle \nu }$, dessa relação resulta ${\textstyle \tau >1/2}$ [41]. A magnitude da velocidade física ${\textstyle {\vec {v}}}$ resultante do fluido deve ser menor do que a velocidade no reticulado, conforme a segunda expressão. Na terceira expressão tem-se a condição para celeridade e na quarta a restrição para escoamentos subcríticos [2].

${\displaystyle {\frac {\Delta t}{\Delta {x^{2}}}}={\frac {2\tau -1}{6\nu }},\,\,\,{\frac {{\left|{\vec {v}}\right|}^{2}}{e^{2}}}<1,\,\,\,{\frac {gh}{e^{2}}}<1,\,\,\,{\frac {{\left|{\vec {v}}\right|}^{2}}{gh}}<1.}$

(35)

Como o LBM é um método intrinsecamente viscoso [42], utiliza-se com frequência, na simulação numérica, uma viscosidade mais elevada do que a viscosidade cinemática do fluido e os resultados estão em concordância com as simulações disponíveis na literatura [2,5,42,43].

4 Estudo de caso: Escoamento em uma bacia hidrográfica

A bacia hidrográfica consiste em uma área bem definida de captação natural da água de precipitação que faz convergir o escoamento até um curso de água. Na bacia hidrográfica, o escoamento é dividido em superficial e em canal. No escoamento superficial a água desloca-se pela superfície da bacia até encontrar um curso de água. Este deslocamento ocorre como resultado da água precipitada que não foi interceptada pela cobertura vegetal e pela parte que não infiltrou no solo. Devido a grande heterogeneidade espacial, a superfície da bacia é representada por planos onde ocorre o escoamento superficial de pouca profundidade. A contribuição lateral nos canais é dada principalmente pela precipitação que ocorre sobre cada plano [33].

Dependendo do tamanho e das características da bacia hidrográfica, pode-se representá-la por uma forma em “V”, segmentada por dois planos e um segmento de canal, como mostra a Figura 4. Neste estudo, utilizam-se várias destas formas para representar as sub-bacias que compõem a superfície da bacia hidrográfica.

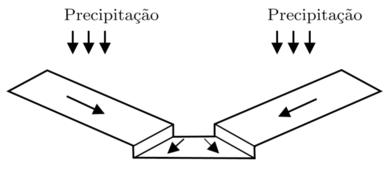
Figura 4: Representação de uma sub-bacia

4.1 Escoamento na bacia hidrográfica do rio Chopim

A bacia do rio Iguaçu (Figura 5), com superfície aproximada de ${\textstyle 70.800}$ km${\textstyle ^{2}}$, tem grande importância na geração de energia por meio de usinas hidrelétricas e pela grande demanda de recursos hídricos no abastecimento público, industrial e agrícola. A região ainda é caracterizada por um grande número de Unidades de Conservação Ambiental, e abriga importantes corredores de biodiversidade [44].

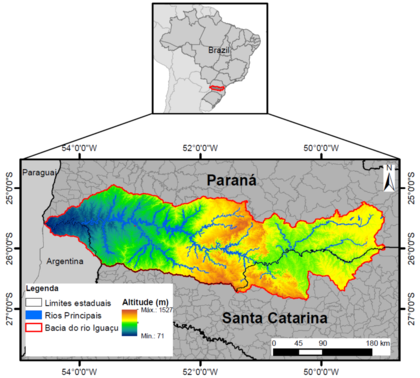
Figura 5: Localização da bacia hidrográfica do rio Iguaçu

Fonte: Franco (2017) [45].

Dentro da bacia do rio Iguaçu está localizada a Bacia do rio Chopim que abrange uma área de ${\textstyle 7.500}$ km${\textstyle ^{2}}$ e desenvolve-se basicamente no sentido sudoeste-noroeste, aproximadamente entre os paralelos ${\textstyle 25\,^{\circ }30'}$ e ${\textstyle 26\,^{\circ }40'}$ de latitude sul e os meridianos ${\textstyle 51\,^{\circ }30'}$ e ${\textstyle 53\,^{\circ }20'}$ de longitude oeste. Seus limites estão entre as bacias do rio Uruguai ao sul e com bacias de afluentes do rio Iguaçu nas outras direções [46].

O rio Chopim é o mais importante afluente da bacia do baixo rio Iguaçu. Suas nascentes estão localizadas em altitudes que superam os 1.200 m. A extensão total do curso principal do rio é da ordem de 450 km. Da nascente do rio até em torno do km 209 a inclinação do leito é de aproximadamente 2,9 m/km, e desde este ponto até a foz, a inclinação é de aproximadamente 1,1 m/km [47].

Considera-se nesse estudo, um trecho do rio Chopim localizado entre suas nascentes no município de Palmas, passando pela estação pluviométrica Salto Claudelino até a estação fluviométrica Porto Palmeirinha. Este trecho do rio tem comprimento de aproximadamente ${\textstyle 281}$ km com área de drenagem na superfície da bacia em torno de ${\textstyle 3.205}$ km${\textstyle ^{2}}$. As características das estações estão listadas na Tabela A.

A Figura 6 ilustra os principais rios da bacia do rio Iguaçu, suas estações pluviométricas, meteorológicas e fluviométricas, e destaca a localizacão da bacia do rio Chopim.

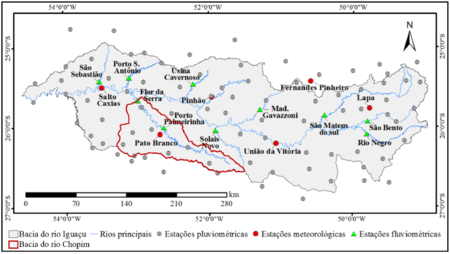
Figura 6: Localização das estações pluviométricas, meteorológicas e fluviométricas da bacia hidrográfica do rio Iguaçu

Fonte: Adaptado de Uda (2016) [48].

A Figura 7 mostra a bacia do rio Chopim com as divisões de sub-bacias conforme Kaviski e Gonçalves (1996) [49] definidas de acordo com as características físicas da bacia.

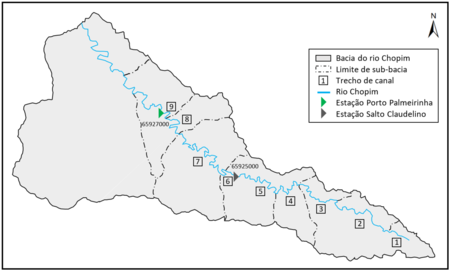
Figura 7: Bacia hidrográfica do rio Chopim

Fonte: Adaptado de Kaviski e Gonçalves (1996) [49].

5 Resultados e Discussões

Levando-se em conta a delimitação das sub-bacias e os trechos de canais apresentados na Figura 7, fez-se a segmentação da bacia do rio Chopim em nove sub-bacias até a estação Porto Palmeirinha. Cada sub-bacia é composta por um trecho de canal e dois planos laterais de escoamento, com exceção da primeira sub-bacia que é representada por apenas um plano lateral. A numeração das sub-bacias foi mantida a mesma que a utilizada na sequência para os trechos de canais. Essa numeração indica o início do escoamento até a estação fluviométrica Porto Palmeirinha. Os dados das características físicas da segmentação da bacia são apresentados na Tabela B para os segmentos planos, e na Tabela C para os segmentos de canais.

Nos trechos de canais não são conhecidos os valores da declividade e do coeficiente de Manning. Para complementar a descrição das características físicas das sub-bacias hidrográficas, listam-se na Tabela C os parâmetros ${\textstyle {\bar {\alpha }}}$ e ${\textstyle {\bar {\beta }}}$, que descrevem as curvas de descarga. De acordo com Kaviski e Gonçalves (1996) [49], a relação entre área da seção transversal e vazão é descrita pela equação,

${\displaystyle A={\bar {\alpha }}Q^{\bar {\beta }},}$

(36)

onde, ${\textstyle {\bar {\alpha }}}$ e ${\textstyle {\bar {\beta }}}$ são estimados pelo método dos mínimos quadrados utilizando valores do nível da água e da descarga, e também da elevação do fundo do canal e a área, medidos em seções transversais.

Ao reescrever a equação (36) como vazão em função da área, tem-se,

${\displaystyle Q={\frac {1}{{\bar {\alpha }}^{1/{\bar {\beta }}}}}{A^{1/{\bar {\beta }}}},}$

(37)

dessa forma, os parâmetros ${\textstyle \beta _{c}}$ e ${\textstyle m_{c}}$ da equação (5) são determinados por,

${\displaystyle {\beta _{c}}={\dfrac {1}{{\bar {\alpha }}^{1/{\bar {\beta }}}}},\,\,\,\,\,{m_{c}}={\dfrac {1}{\bar {\beta }}}.}$

(38)

Na junção de segmentos de canais (Figura 3), a área da seção transversal é encontrada diretamente pela equação (36).

Por não estarem disponíveis os dados de declividade e coeficiente de Manning dos trechos de canais da bacia do rio Chopim, houve a necessidade de adaptar o modelo para utilizar os parâmetros ${\textstyle {\bar {\alpha }}}$ e ${\textstyle {\bar {\beta }}}$. A vantagem em utilizar esses parâmetros é a de aplicar o LBM em um canal com seção transversal estimada pelas características físicas naturais do rio.

Os parâmetros da simulação no LBM para os planos são ${\textstyle \Delta x=10}$ m, ${\textstyle \Delta t=10}$ s e velocidade na malha ${\textstyle e=1}$ m/s. Com relação aos canais, ${\textstyle \Delta x=50}$ m, ${\textstyle \Delta t=10}$ s e velocidade na malha ${\textstyle e=5}$ m/s. Em ambos, o parâmetro de relaxamento utilizado é ${\textstyle \tau =12}$. O número de iterações realizadas foi de ${\textstyle 90.000}$, o que corresponde a um tempo de simulação de ${\textstyle 250}$ horas ou ${\textstyle 10,42}$ dias.

O período de chuva analisado na bacia é dado no mês 07 de 1987 nos dias 07 e 08. Neste mês não houve chuva além dos dias citados. A Tabela D contém a intensidade média de precipitação em cada sub-bacia. Para se obter uma simulação mais próxima da realidade, considerou-se uma vazão inicial que ocorre no rio (escoamento de base), em cada trecho de canal, antes de ocorrer a precipitação. Essa vazão entra no modelo computacional como uma condição inicial. Também é considerada como uma condição de contorno ao ser adicionada na contribuição lateral dos planos, em cada passo de tempo. A Tabela E, lista as vazões iniciais na seção transversal a montante e a jusante em cada trecho de canal. Utilizou-se interpolação linear para determinar os valores de vazões iniciais a cada ${\textstyle \Delta x=50}$ m no comprimento dos canais no instante inicial da simulação. Nos demais passos de tempo, o escoamento de base é incluído pela equação (39),

${\displaystyle {q_{base}}={\frac {{Q_{j}}-{Q_{m}}}{L}},}$

(39)

em que ${\textstyle Q_{j}}$ e ${\textstyle Q_{m}}$ são, respectivamente, a vazão a jusante e a vazão a montante em um segmento de canal de comprimento ${\textstyle L}$. A quantidade ${\textstyle q_{base}}$ é somada a contribuição lateral e uniformemente distribuída no comprimento do canal.

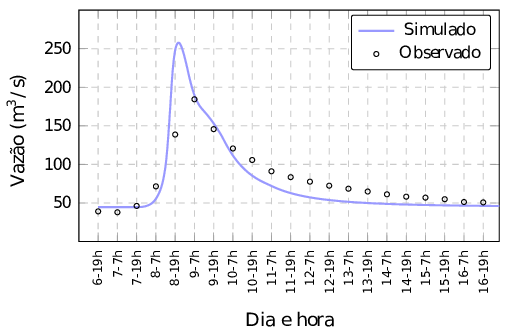
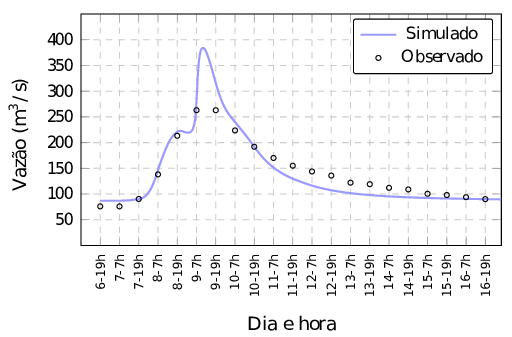
Os resultados obtidos pelo LBM são comparados com dados observados nas duas estações pertencentes ao trecho analisado. Nas Figuras 8 e 9, tem-se os hidrogramas simulado e observado nas estações Salto Claudelino e Porto Palmeirinha referentes a precipitação ocorrida no mês 07/1987.

Figura 8: Hidrograma na sub-bacia 5 - Estação Salto Claudelino

Figura 9: Hidrograma na sub-bacia 9 - Estação Porto Palmeirinha

Os resultados obtidos mostram boa concordância entre a simulação por meio do LBM e os dados observados nas estações, tendo em vista que os dados observados foram coletados a cada 12 horas por leitura feita de forma visual em réguas ou escalas linimétricas fixadas nas margens dos rios para registro das variações no nível da água. Essas leituras são normalmente realizadas por moradores da região. Ainda, assume-se que a precipitação é igualmente distribuída nas últimas 12 horas.

Para quantificar a concordância entre os valores observados e simulados pelo LBM, considerou-se o coeficiente de correlação linear de Pearson ${\textstyle r}$ [50],

${\displaystyle r={\dfrac {n\sum \limits _{i=1}^{n}{{X_{i}}{Y_{i}}-\sum \limits _{i=1}^{n}{X_{i}}\sum \limits _{i=1}^{n}{Y_{i}}}}{\sqrt {\left[{n\sum \limits _{i=1}^{n}{X_{i}^{2}-{{\left({\sum \limits _{i=1}^{n}{X_{i}}}\right)}^{2}}}}\right]\left[{n\sum \limits _{i=1}^{n}{Y_{i}^{2}-{{\left({\sum \limits _{i=1}^{n}{Y_{i}}}\right)}^{2}}}}\right]}}},}$

(40)

onde X e Y são as variáveis em estudo, respectivamente, vazão observada e vazão simulada, ${\textstyle n}$ é o número de pares das observações.

O coeficiente de correlação linear ${\textstyle r}$ é adimensional e tem variação no intervalo ${\textstyle [-1,1]}$. Se ${\textstyle r=-1}$ tem-se a correlação linear negativa perfeita, enquanto que se ${\textstyle r=1}$, tem-se a correlação linear positiva perfeita. Para ${\textstyle r=0}$ não há correlação linear entre as variáveis. Esse coeficiente pode ser avaliado quantitativamente como descrito na Tabela 1.

Tabla. 1 Classificação do coeficiente linear de Pearson

Intervalo	Classificação
${\textstyle 0<|r|<0,3}$	existe fraca correlação linear
${\displaystyle 0,3<|r|<0,6}$	existe moderada correlação linear
${\displaystyle 0,6<|r|<0,9}$	existe forte correlação linear
${\displaystyle 0,9<|r|<1,0}$	existe correlação linear muito forte

Fonte: Marques e Marques (2005) [50].

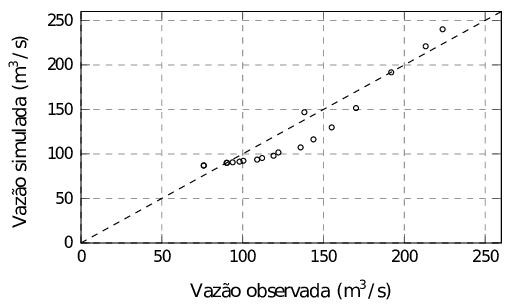
As Figuras 10 e 11 mostram os gráficos de dispersão das vazões observadas pelas vazões simuladas pelo LBM. A reta tracejada, em ambos os gráficos, representa o ajuste perfeito com coeficiente ${\textstyle r=1}$.

Figura 10: Dispersão das vazões observadas e simuladas na sub-bacia 5 - Estação Salto Claudelino

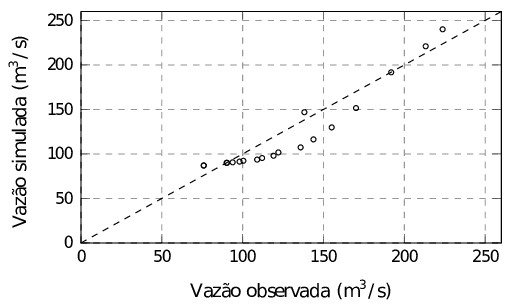
Figura 11: Dispersão das vazões observadas e simuladas na sub-bacia 9 - Estação Porto Palmeirinha

O coeficiente de correlação linear de Pearson calculado na sub-bacia 5 foi de ${\textstyle r=0,88}$ e na sub-bacia 9, de ${\textstyle r=0,97}$. Conforme a Tabela 1, existe forte correlação linear entre as variáveis na sub-bacia 5 e correlação linear muito forte para a sub-bacia 9. Conclui-se que há boa concordância entre as vazões observadas e simuladas. Nota-se na Figura 10 que um ponto está distante da reta, o que faz o coeficiente ${\textstyle r}$ ser um pouco menor.

Para fazer a verificação da significância estatística, foi aplicado o teste de hipóteses com a distribuição t de Student, supondo que os desvios padrões populacionais são desconhecidos e com variâncias equivalentes. A hipótese a ser testada é ${\textstyle H_{0}:\mu _{1}-\mu _{2}=0}$, isto é, não existe diferença significativa entre as médias populacionais das vazões observadas e simuladas. Os resultados obtidos, para as sub-bacias 5 e 9, estão resumidos na Tabela F.

Os testes realizados mostram que a estatística do teste t é menor do que o valor do crítico bi-caudal, portanto aceita-se a hipótese ${\textstyle H_{0}}$, ou seja, não existe diferença significativa, ao nível de significância de ${\textstyle 5\%}$ entre as vazões observadas e vazões simuladas.

6 Conclusão

Esta pesquisa utilizou o LBM com aperador de colisão BGK para obter a simulação numérica do escoamento superficial da bacia do rio Chopim. Computacionalmente a bacia foi representada pela junção de nove sub-bacias dadas por planos laterais e um segmento de canal. A simulação produziu o hidrograma total o qual fornece a variação da vazão em relação ao tempo correspondente a resposta da bacia hidrográfica após a precipitação efetiva do evento simulado. Para que este resultado fosse alcançado, determinou-se duas funções de distribuição de equilíbrio obtidas por meio da expansão de Chapmann-Enskog em escalas de tempo e utilizando o reticulado D1Q5, uma adequada para o escoamento na superfície da bacia e outra para o canal principal, obtendo a profundidade da água na superfície da bacia e área da seção transversal nos canais. Também foi necessário determinar a condição de contorno na passagem de fluxo de um a sub-bacia para outra, levando em consideração a conservação da massa.

Obteve-se uma simulação mais próxima da realidade com a consideração de escoamento de base, em cada trecho de canal, antes que ocorra a precipitação. Essa vazão entra no modelo computacional como uma condição inicial. Também é considerada como uma condição de contorno ao ser adicionada na contribuição lateral dos planos, em cada passo de tempo. Utilizou-se interpolação linear para determinar os valores de vazões iniciais a cada 50 m no comprimento dos canais no instante inicial da simulação. Nos demais passos de tempo, o escoamento de base é incluído como uma condição de contorno. Os resultados obtidos pelo LBM foram comparados com dados observados nas duas estações pertencentes ao trecho analisado e mostram boa concordância, tendo em vista que os dados observados foram coletados a cada 12 horas por leituras feitas de forma visual em réguas fixadas nas margens dos rios para registro das variações no nível da água. Ainda, considera-se que a precipitação é igualmente distribuída nas últimas 12 horas.

Verificou-se que LBM é adequado e preciso na simulação do escoamento em uma bacia hidrográfica representado pelas equações de onda cinemática. Além disso, as condições iniciais e de contorno são de fácil implementação.

BIBLIOGRAFÍA

[1] J. E. Gribbin, Introduction to Hydraulics and Hydrology with Applications for Stormwater Management, 3rd Edition, Cengage Learning, USA, 2008.

[2] J. G. Zhou, Lattice Boltzmann Method for Shallow Water Flows, Springer, New York, 2004.

[3] S. Chen, G. D. Doolen. Lattice Boltzmann Method for fluid flows, Annual Review of Fluid Mechanics, vol. 30, no. 1, pp. 329-364, 1998.

[4] J. G. Zhou, A lattice Boltzmann model for the shallow water equations, Computer Methods in Applied Mechanics and Engineering 191 (2002) 3527-3539.

[5] J. G. Zhou, H. Liu, S. Shafiai, Y. Peng, R. Burrows, Lattice Boltzmann Method for Open-channel Flows, Engineering and Computational Mechanics 163 (2010) 243-249.

[6] P. van Thang, B. Chopard, L. Lefèvre, D. A. Ondo, E. Mendes, Study of the 1D Lattice Boltzmann Shallow Water Equation and Its Coupling to Build a Canal Network, Journal of Computational Physics 229 (19) (2010) 7373-7400.

[7] Y. Peng, J. G. Zhou, R. Burrows, Modelling solute transport in shallow water with the lattice boltzmann method, Computers & Fluids 50 (2011) 181?188.

[8] Y. Peng, J. G. Zhou, J. M. Zhang, R. Burrows, modeling moving boundary in shallow water by lbm, International Journal of Modern Physics C 24 (1).

[9] L. Budinski, Mrt lattice boltzmann method for 2d flows in curvilinear coordinates, Computers & Fluids 94 (2014) 288?301.

[10] Y. Peng, J. G. Zhou, J. M. Zhang, H. Liu, Lattice boltzmann modeling of shallow water flows over discontinuous beds, International Journal for Numerical Methods in Fluids 75 (2014) 608-619.

[11] M. La Rocca, A. Montessori, P. Prestininzi, S. Succi, A multispeed discrete boltzmann model for transcritical 2d shallow water flows, Journal of Computational Physics, 284 (2015) 117-132.

[12] S. Li, P. Huang, Li, A modified lattice boltzmann model for shallow water flows over complex topography, International Journal for Numerical Methods in Fluids 77 (2015) 441-458.

[13] P. Prestininzi, a. Montessori, M. La Rocca, G. Sciortino, Simulation of arrested salt wedges with a multi-layer shallow water lattice boltzmann model, Advances in Water Resources 96 (2016) 282-289.

[14] C.-z. Zhang, C. Y.-G., J.-Y. Wu, W. Diao, Lattice boltzmann simulation of the open channel flow connecting two cascaded hydropower stations, Journal of Hydrodynamics 28 (3) (2016) 400-410.

[15] V. Galina, J. Cargnelutti, E. Kaviski, L. M. Gramani, A. M. Lobeiro, Simulação de onda de maré por meio do método do reticulado de boltzmann, in: I Simpósio de Métodos Numéricos em Engenharia, Universidade Federal do Paraná, Curitiba - Brasil, 2016.

[16] Z.-m. Zhao, P. Huang, S.-t. Li, Lattice boltzmann model for shallow water in curvilinear coordinate grid, Journal of Hydrodynamics 29 (2) (2017) 251-260.

[17] A. De Rosis, A central moments-based lattice boltzmann scheme for shallow water equations, Computer Methods in Applied Mechanics and Engineering 319 (2017) 379-392.

[18] J. Cargnelutti, V. Galina, E. Kaviski, L. M. Gramani, A. M. Lobeiro, Two-dimensional numerical simulation of channel flow with submerged obstacles using the lattice boltzmann method, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 34 (1), 2018.

[19] J. Cargnelutti, V. Galina, E. Kaviski, L. M. Gramani, A. M. Lobeiro, Simulation of the two-dimensional flow of the initiation channel of the itaipu hydroelectric power plant by the lattice boltzmann method, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 34 (1), 2018.

[20] G. Yang, C. Kwok, Y. Sobral, The effects of bed form roughness on total suspended load via the lattice boltzmann method, Applied Mathematical Modelling 63 (2018) 591-610.

[21] X. Zhang, J. Feng, D. Zhang, N. Liu, Comparison of lattice boltzmann method and preissmann implicit difference method in application to overland flow, Nongye Jixie Xuebao/Transactions of the Chinese Society of Agricultural Machinery, 2014

[22] X. Zhang, J. Feng, T. Yang, Lattice Boltzmann Method for Overland Flow Studies and its Experimental Validation, Journal of Hydraulic Research 53 (5) (2015) 561-575.

[23] N. Liu, The numerical simulation of one-dimensional overland flow by Lattice Boltzmann Method, in: 5th International Conference on Advanced Design and Manufacturing Engineeringe, China, 2015.

[24] V. Galina, J. Cargnelutti, E. Kaviski, L. M. Gramani, A. M. Lobeiro, Application of lattice boltzmann method for surface runoff in watershed, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 34 (1), 2018.

[25] H. Liu, H. Wang, S. Liu, C. Hu, Y. Ding, J. Zhang, Lattice Boltzmann Method for the Saint?Venant Equations, Journal of Hydrology 524 (2015) 411-416.

[26] R. Benzi, S. Succi, M. Vergassola, The lattice boltzmann equation: Theory and applications, Physics Reports 222 (3) (1992) 145-197.

[27] B. Nestler, A. Aksi, M. Selzer, Combined lattice boltzmann and phase-field simulations for incompressible fluid flow in porous media, Mathematics and Computers in Simulation 80 (7) (2010) 1458-1468.

[28] W. Sobieski, Numerical investigations of tortuosity in randomly generated pore structures, Mathematics and Computers in Simulation 166 (2019) 1?20.

[29] M. E. Andaluz, V. V. Galarza, A. R. Vera, On hydraulic tortuosity variations due to morphological considerations in 2d porous media by using the lattice boltzmann method, Mathematics and Computers in Simulation 169 (2020) 74?87.

[30] Y. H. Qian, D. D'Humières, P. Lallemand, Lattice bgk models for navier-stokes equation, Europhysics Letters 17 (6) (1992) 479-484.

[31] R. M. Porto, Hidráulica Básica, 4th Edition, EESC-USP, São Carlos, 2006.

[32] M. H. Chaudhry, Open-Channel Flow, Springer, New York, USA, 2008.

[33] C. E. M. Tucci, Modelos Hidrológicos, Editora da Universidade Federal do Rio Grande do Sul, Porto Alegre, RS - Brasil, 1998.

[34] J. E. Miller, Basic Concepts of Kinematic-Wave Models, United States Government Printing office, Washington, 1984.

[35] D. R. Golbert, Método de Lattice Boltzmann em Hemodinâmica Computacional: interações fluido-estrutura e modelos acoplados 1D-3D, Ph.D. thesis, Laboratório Nacional de Computação Científica, Petrópolis, RJ - Brasil.

[36] P. L. Bhatnagar, E. P. Gross, M. Krook, A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems, Physical Review 94 (3) (1954) 511-525.

[37] Z. Guo, C. Zheng, B. Shi, Discrete Lattice Effects on the Forcing Term in the Lattice Boltzmann Method, Physical Review E 65 (2002) 1-6.

[38] J. Zhang, G. Yan, Lattice boltzmann method for one and two-dimensional burgers equation, Physica A (2008).

[39] S. Chapman, T. G. Cowling, The Mathematical Theory of Non-uniform Gases. An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases, 3rd Edition, Cambridge University Press, London, 1970.

[40] J. Zhang, G. Yan, A lattice Boltzmann model for the Burgers-Fisher equation, Chaos: An Interdisciplinary Journal of Nonlinear Science 20 (2010) 023129.

[41] J. D. Sterling, S. Chen, Stability analysis of lattice boltzmann methods, Journal of Computational Physics 123 (1996) 196-206.

[42] M. La Rocca, C. Adduce, G. Sciortino, Development of a Lattice Boltzmann Method for Two-layered Shallow-water Flow, International Journal for Numerical Methods in Fluids 70 (2012) 1048-1072.

[43] J. G. Zhou, H. Liu, Determination of bed elevation in the enhanced lattice Boltzmann method for the shallow-water equations, Physical Review E 88 (2013) 1-6.

[44] S. de Estado do Meio Ambiente e Recursos Hídricos SEMA, Bacias hidrográficas do paraná, Paraná, Brasil (2010).

[45] A. C. L. Franco, Calibração do modelo swat com evapotranspiração proveniente de sensoriamento remoto e vazão observada, Master?s thesis, Florianópolis - SC (2017).

[46] D. I. Chavasse, R. S. Seoane, Assessing and predicting the impact of el nino southern oscillation (enso) events on runoff from the chopim river basin, brazil, Hydrological Processes (23) (2009) 3261-3266.

[47] P. P. Burian, Do estudo de impacto embiental à avaliação ambiental estratégica - ambivalências do processo de licenciamento ambiental do setor elétrico, Ph.D. thesis, Universidade Estadual de Campinas, Campinas, SP - Brasil (Fevereiro 2006).

[48] P. K. Uda, Evapotranspiração real da bacia do rio iguaçu por meio do modelo metric, Ph.D. thesis (2016).

[49] E. Kaviski, L. F. A. Gonçalves, Análise hidrológica e matemática de operação de reservatórios, Tech. rep., Centro de Hidráulica e Hidrologia Professor Parigot de Souza - CEHPAR, Curitiba - PR (1996).

[50] J. M. Marques, M. A. M. Marques, Estatística Básica para os Cursos de Engenharia, Domínio do Saber, 2005.

Apêndice

Tabla. A Estações hidrométricas no rio Chopim

Nome	Código	Município	Lati- tude	Longi- tude	Altitude (m)	Área de contribuição (km${\textstyle ^{2}}$)
Porto Palmeirinha	65927000	Coronel Vivida	-26,03	-52,63	501	3.390
Salto Claudelino	65925000	Clevelândia	-26,28	-52,30	797	1.660

Fonte: Franco (2017) [45].

Tabla. B Caracterização física dos planos das 9 sub-bacias do rio Chopim - pd e pe são, respectivamente, os planos do lado direito e do lado esquerdo no sentido do escoamento.

Sub- Bacia	Plano	Compri- mento ${\displaystyle L}$ (m)	Largura ${\displaystyle b}$ (m)	Declividade ${\displaystyle S_{0}}$ (m/m)	Manning ${\displaystyle n_{r}}$ (m${\displaystyle ^{-1/3}}$s)	Área (km${\displaystyle ^{2}}$)
1	pd	-	-	-	-	-
	pe	6.940	26.830	0,0065	0,1200	186,20
2	pd	3.080	47.500	0,0266	0,0840	146,30
	pe	6.940	47.500	0,0065	0,1200	329,65
3	pd	3.300	30.170	0,0146	0,1044	99,56
	pe	6.940	30.170	0,0065	0,1200	209,38
4	pd	2.800	26.580	0,0102	0,2832	74,42
	pe	9.250	26.580	0,0129	0,2832	245,87
5	pd	2.800	41.670	0,0102	0,2832	116,68
	pe	6.780	41.670	0,0022	0,1020	282,52
6	pd	2.800	13.000	0,0102	0,2832	36,40
	pe	6.780	13.000	0,0022	0,1020	88,14
7	pd	5.180	65.000	0,0170	0,0972	336,70
	pe	9.670	65.000	0,0085	0,0972	628,55
8	pd	10.120	22.000	0,0113	0,0984	222,64
	pe	4.870	22.000	0,0129	0,1020	107,14
9	pd	6.720	8.180	0,0127	0,1032	54,97
	pe	4.870	8.180	0,0129	0,1020	39,84

Fonte: Kaviski e Gonçalves (1996) [49].

Tabla. C Caracterização física dos canais das 9 sub-bacias do rio Chopim

Sub- Bacia	Comprimento do canal ${\displaystyle L}$ (m)	Parâmetro ${\displaystyle {\bar {\alpha }}}$	Parâmetro ${\displaystyle {\bar {\beta }}}$	Área de drenagem (km${\displaystyle ^{2}}$)	Área de dre- nagem acumu- lada (km${\displaystyle ^{2}}$)
1	26.830	0,04113596	1,59495580	186,21	186,21
2	47.500	0,85500771	0,87796837	475,86	662,07
3	30.170	1,01710784	0,86807752	308,94	971,01
4	26.580	1,45162356	0,83154649	320,33	1.291,34
5	41.670	2,55791569	0,76867062	399,15	1.690,49
6	13.000	2,47863913	0,77061510	124,52	1.815,01
7	65.000	2,32144856	0,77466167	965,27	2.780,28
8	22.000	2,14755607	0,77947050	329,82	3.110,10
9	8.180	2,09342670	0,78104723	94,78	3.204,88

Fonte: Kaviski e Gonçalves (1996) [49].

Tabla. D Intensidade média de precipitação no rio Chopim, mês 07/1987 - pd e pe são, respectivamente, os planos do lado direito e do lado esquerdo no sentido do escoamento.

Sub- bacia	Plano	07/07/1987 (m/h) ${\displaystyle \cdot }$ 10${\displaystyle ^{-3}}$		08/07/1987 (m/h) ${\displaystyle \cdot }$ 10${\displaystyle ^{-3}}$
		7h	19h	7h	19h
1	pd	-	-	-	-
	pe	0	0	1,47400098	0,00174585
2	pd	0	0,65031194	2,24260054	0,00242411
	pe	0	0	1,47400098	0,00174585
3	pd	0	0	1,67223974	0
	pe	0	0	1,47400098	0,00174585
4	pd	0	0	0,87767508	0
	pe	0	0	1,15756772	0
5	pd	0	0	0,87767508	0
	pe	0	0	0,99927618	0
6	pd	0	0	0,87767508	0
	pe	0	0	0,99927618	0
7	pd	0	0	0,90541231	0
	pe	0	0	1,15131540	0
8	pd	0	0	1,08201453	0
	pe	0	0	1,26797648	0,00923398
9	pd	0	0,72930031	1,47131551	0,02406490
	pe	0	0	1,26797648	0,00923398

Fonte: Kaviski e Gonçalves (1996) [49].

Tabla. E Vazões iniciais e coeficientes de interpolação da vazão nos trechos de canais do rio Chopim, mês 07/1987

Canal	Vazão inicial na seção tranversal (m${\displaystyle ^{3}}$/s)		Coeficientes da interpolação linear ${\displaystyle Q(x)=ax+b}$		Vazão inicial como contribuição lateral (m${\displaystyle ^{2}}$/s) ${\displaystyle \cdot }$ 10${\displaystyle ^{-4}}$
	Montante	Jusante	${\displaystyle a\,\cdot 10^{-4}}$	${\displaystyle b}$
1	0	4,91134977	1,83054408	0	1,83054408
2	4,91134977	17,46209717	2,64226261	4,91134977	2,64226261
3	17,46209717	25,61030197	2,70076394	17,46209717	2,70076394
4	25,61030197	34,05889511	3,17855272	25,61030197	3,17855272
5	34,05889511	44,58636093	2,52638969	34,05889510	2,52638969
6	44,58636093	48,07283783	2,68190530	44,58636093	2,68190530
7	48,07283783	75,09886169	4,15784983	48,07283783	4,15784983
8	75,09886169	84,33335876	4,19749867	75,09886168	4,19749867
9	84,33335876	86,98714447	3,24423681	84,33335877	3,24423681

Fonte:Kaviski e Gonçalves (1996) [49].

Fonte:Kaviski e Gonçalves (1996) [49].

Tabla. F Teste t de Student para as sub-bacias no rio Chopim

Quantidades estatísticas	Sub-bacia 5 Salto Claudelino		Sub-Bacia 9 Porto Palmeirinha
	Observado	Simulado	Observado	Simulado
Média	80,04	76,58	142,12	139,02
Variância	1.493,98	3.021,13	3.376,02	4.864,39
Número de observações	21		21
Graus de liberdade	40		40
Estatística do teste	0,2361		0,1567
t bi-caudal	2,0211		2,0211
Nível de significância	${\displaystyle 5\%}$		${\displaystyle 5\%}$