Revision as of 14:00, 8 May 2020

Abstract

In science and engineering, mathematical modeling serves as a tool to understand processes and systems acting as a testing bed for several hypotheses. The selection of a specific model, as well as its variables and parameters, depends on the nature of the system under analysis and the acceptable simplifying assumptions. Therefore, it must allow for a good fit between both the hypothesis and the available data. Opposite to other design approaches based on experimental data or/and complex models, this work presents a simpler numerical design method for efficiency maximization of an Hydraulic Jet Pump (HJP) for oil-well extraction process, considering its hydraulic and geometric parameters. The design process consists in setting and solving a constrained non-linear optimization problem by taking into account the hydraulic model of the HJP in terms four design variables: throat area, nozzle area, injection flow, and injection pressure to the oil-well. The objective function of this case aims to maximize the HJP's efficiency avoiding to approach cavitation condition as well fulfilling technical constraints. A numerical technique, Differential Evolution Algorithm (DEA), has been implemented to solve the optimization problem. The proposed methodology leads to a solution set by considering only commercial geometries and feasible operating conditions for the HJP, which facilitates its practical implementation. A set of ten oil-wells with land production data, operating in the southeaster of Mexico, is used to compare and validate several Jet pump designs, i. e., through comparison with actual oil-well's operation condition.

Keywords: Jet pump, optimization, efficiency, differential evolution

1. Nomenclature

This section describes all the nomenclature used in this work.

${\textstyle A_{n}}$= Flow area of nozzle, [in${\textstyle ^{2}}$].

${\textstyle A_{s}}$= Suction area, [in${\textstyle ^{2}}$].

${\textstyle A_{th}}$= Flow area of throat, [in${\textstyle ^{2}}$].

${\textstyle b=A_{n}/A_{th}}$ Nozzle to throat area ratio, [-]

${\textstyle G_{w}}$= Fluid column gradient, [Psi/ft].

${\textstyle h_{1}}$= Pump setting depth, [ft].

${\textstyle H}$=Dimensionless head recovery ratio, [-].

${\textstyle H_{v}}$= Jet velocity, [-].

${\textstyle K_{j}}$= Nozzle loss coefficient,[-].

${\textstyle K_{d}}$= Diffuser loss coefficient, [-].

${\textstyle K_{s}}$= Suction loss coefficient, [-].

${\textstyle K_{t}}$= Throat loss coefficient, [-].

${\textstyle M}$= Dimensionless flow ratio, [-].

${\textstyle M_{c}}$=Cavitation limited flow ratio, [-].

${\textstyle N}$= Index of Losses by Friction, [-].

${\textstyle P_{1}}$= Pressure at the entrance of the nozzle, [Psi].

${\textstyle P_{2}}$=Pressure at the output of the throat, [Psi].

${\textstyle P_{3}}$= Pressure at the intake of the HJP, [Psi].

${\textstyle P_{s}}$= Injection pressure (Surface pressure), [Psi].

${\textstyle P_{f}}$= Average oil-well pressure, [Psi].

${\textstyle PI}$= Productivity index [-].

${\textstyle P_{v}}$=Vapor pressure, [Psi].

${\textstyle P_{wf}}$= Flowing bottom hole pressure, [Psi].

${\textstyle q_{1}}$=Injection flow, [Barrels/Day (BPD)].

${\textstyle q_{3}}$=Production flow, [BPD].

${\textstyle q_{2}}$=Sum of injection and production flows, [BPD].

${\textstyle q_{max}}$= Maximum oil flow from the oil-well, [BPD].

${\textstyle \sigma }$= Cavitation index [-].

${\textstyle \eta }$= HJP efficiency [-].

${\textstyle \gamma }$ = Specific gravity [-].

${\textstyle HP}$ = HJP Horsepower [hp].

${\textstyle F}$ = Mutation factor [-].

${\textstyle CR}$ = Crossover factor [-].

2. Introduction

The challenge of finding new technologies for production and/or improving existing ones in the oil and gas industry, is shaped because of the continuous increase in demand for and rapid depletion of this non-renewable natural resource. Oil has been found naturally in large sedimentary basins at different depths ranging from 15 to 8,000 meters, occupying the empty space of porous and permeable rocks known as oil-well. As time goes by, the natural pressure of an oil-well decreases, until it can not longer produce naturally. This problem gives rise to use Artificial Lift Systems (ALS), as a feasible engineered system to exploit the oil-wells. Indeed, is the fact that more than 95% of the world's oil-wells use some ALS, starting from the oldest and simplest one such as mechanical pumping and pneumatic pumping, to the most technologies such as Electrical Submersible Pumping and hydraulic pumping.

In this work, we focus on the ALS of Hydraulic pumping with an HJP [1]. Hence, HJPs are of vast interest in petroleum engineering because of their design characteristics, and volumetric oil production they can handle. For the Hydraulic ALS, the HJP is introduced into the oil-well via the production pipe and it can be retrieved by simply reversing the working flow sense. In this application, the HJP has some disadvantages such as the cavitation phenomenon and typically low efficiency; nevertheless, both might be mitigated by an optimum design of the HJP and the selection of the best operating conditions for the ALS.

In general, the fundamental parts of this ALS are: a combustion engine that drives a hydraulic piston (or geared) pump; an horizontal three-phase separator containing the mixture (oil, gas and sand) extracted from the oil-well; a control panel that controls the ALS and finally the HJP, installed at the bottom of the oil-well. Note that an HJP includes in a carrier that encloses the nozzle and throat (Figure 1).

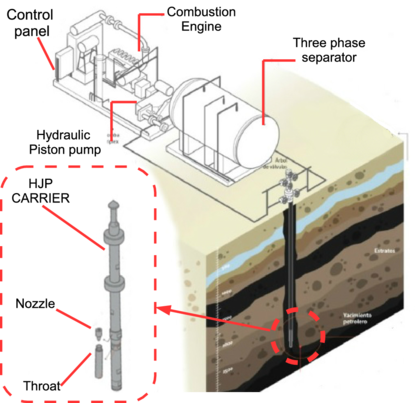
Figure 1. Schematic diagram of an ALS whit an HJP

Early works on HJP design have considered either experimental or numerical approaches or a mix of both. Mallela [2], computed normalized geometries which leads to maximum efficiencies without considering the cavitation phenomenon. S. Mohan [3], reported a numerical analysis and an optimization of an HJP via multi-surrogate model without considering cavitation. In Mohan's study, the area ratio, mixing-tube length to diameter ratio and setback ratio, were varied during an optimization process. In the work of Saker [4], it was pointed out the importance and influence of factors such as cavitation phenomena, which impact the HJP performance. In a more recent paper [5], Xiao presented a numerical and experimental study on the HJP performance and inner flow details of annular Jet pumps under three area ratios. Xiao's results included cavitation phenomenon and indicate that by decreasing outlet pressure, the cavitation generated at the throat inlet renders unstable effects for the HJP. In 2013 [6], the Norwegian University of Science and Technology (NTNU) analyzed oil-wells from the North Sea, by using the principles of the HJP, as those described in [1], to search for an optimal operational conditions of the HJP , i.e. pressures and flows. In a study closer to our approach for the HJP design, J. Fan. [7] developed a design oriented to improve the HJP efficiency by using an analytical approach that considers a computational fluid dynamics (CFD) model. Then, the influence of the pump's geometry on its performance and the CFD simulation results were used to build surrogate models of the pump's behavior. Finally, a global optimization was carried out by means of a genetic algorithm. Works surveyed so far require either extensive experimental data or CFD simulations to provide HJP performance improvement; this can be too costly and time consuming for the oil-well industry needs. For this reason, the creation of a numerical tool to determine the optimal geometric design and operational hydraulic conditions of an HJP is of paramount importance to satisfy industry requirements.

This work introduces a numerical design methodology to maximize the efficiency of an HJP, based on its hydraulic and geometrical models. According to this, the method is based on geometric and hydraulic models transcription into a constrained non-linear optimization problem with four design variables: throat and nozzle areas, the input working fluid flow and the input pressure. The objective function of the optimization problem aims to render the maximum efficiency without reaching the cavitation condition for the HJP and fulfilling technical constraints. Because of the non-linear characteristics and the number of the independent variables, a Differential Evolution Algorithm (DEA) is implemented to solve the optimization problem. As a strategy to calibrate the algorithm, only commercial geometries and real operating conditions for the HJP were used. Evidence on the feasibility of using this algorithm in real applications is demonstrated by comparisons of numerical results with ongoing oil-well production by using HJPs in the southeaster by the Mexican Company, Geolis/Nuvoil. It is important to highlight that feasible HJP geometries and operational conditions are be obtained without extensive simulations or experimentation.

This paper is structured as follows. Section 3 concerns the mathematical models considered, then the problem statement for this work is stated in Section 4. Section 5 of this paper, explains the solution methodology by using the DEA. In Section 6, numerical results are shown and analyzed, and finally Section 7 closes the paper with the conclusions and future work.

3. Mathematical models

The fundamental of operation of an HJP of an ALS is based on the Venturi principle [8]. Basically, this principle consists of applying additional energy to the oil at the bottom of the oil-well, in order to force the fluid to flow to the surface. For this purpose, a driving or working fluid (typically water) is injected through the production pipe to the oil-well. At the return, the mixture between working fluid and oil, is forced to circulate through the annular space between the production and cladding pipes; this working principle is shown in Figure 2.

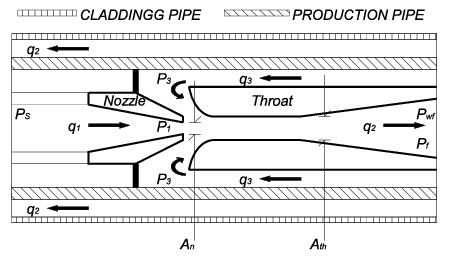
Figure 2. HJP schematic set-up

In order to improve the performance of a HJP, selection of the computational method gives rise to two options. One approach considers the use of pressures and flow ratios [9]. Although it is one of the most used, it is not adequate because in some cases relevant information is insufficient. In a second approach, experimental information such as adimensional coefficients, is used to perform the computations of the HJP efficiency [1].

In this work, we consider the hydraulic model of the HJP described in [1]. The efficiency of a HJP is defined as the ratio of the energy added to the production fluid in relation to the energy lost by the injection fluid. Therefore, we can compute the hydraulic efficiency of the pump as in equation (1), where ${\textstyle M}$ is the input to net production flow ratio as expressed in equation (2), and ${\textstyle H}$ represents the dimensionless head recovery ratio, as in equation (3)

In equation (2), ${\textstyle q_{3}}$ represents the flow from the well in barrels per day (BPD) and ${\textstyle q_{1}}$ represents the flow injected from the surface in BPD. A third flow ${\textstyle q_{2}}$ is the sum of both flows, as shown in Figure 2. Note that the input flow ${\textstyle q_{1}}$ can be controlled via a hydraulic (piston or geared) pump on the surface.

With respect to Equation (3), it presents has a dual definition. On the one hand, in this equation, ${\textstyle H}$ represents the dimensionless head recovery ratio for the pressures ${\textstyle P_{1}}$, ${\textstyle P_{2}}$ and ${\textstyle P_{3}}$ of the HJP. On the other hand, the term ${\textstyle N}$ represents experimental information considering friction loss coefficients ${\textstyle K_{j}}$, ${\textstyle K_{s}}$, ${\textstyle K_{t}}$, ${\textstyle K_{d}}$ and the geometry of the HJP, [1]. Given the values of ${\textstyle M}$, the adimensional coefficients, and once the nozzle area ${\textstyle A_{n}}$ and throat area ${\textstyle A_{th}}$ are selected to compute ${\textstyle b}$, then ${\textstyle N}$ is obtained using equation (4), see [1]

Pressure ${\textstyle P_{1}}$, can be expressed by equation (5), as the sum of the pressure generated by the column of fluid at the production pipe and the surface pressure ${\textstyle P_{s}}$ given by an hydraulic pump

Because of the damage problems associated with cavitation phenomenon (to be considered in the following section), it is also desirable to compute the intake pressure ${\textstyle P_{3}}$ while the pump is operating. This can be accomplished from the input flow ${\textstyle q_{1}}$ at the nozzle, according to equation (6). Note that the intake pressure depends on the input flow, the surface pressure, and the selection of the nozzle area. It is important to remark that, once ${\textstyle M}$ and ${\textstyle N}$ are computed, pressure ${\textstyle P_{2}}$ is obtained from equation (3)

The flow from the oil-well ${\textstyle q_{3}}$ is one of the most challenging data to obtain. When the performance of oil-well is considered, it is often assumed that it can be estimated by the productivity index [9]. This concept is only applicable for oil-wells producing under single-phase flow conditions, i.e. pressures above the oil-well fluid's bubble-point pressure. For oil-well pressures less than the bubble-point pressure, the oil-well fluid presents a two-phase behavior, gas and liquid; then, other techniques must be applied to predict oil-well performance. In this work, we consider the case when the fluid exists as two phases, oil and gas. Thus, to estimate the production rate ${\textstyle q_{3}}$, a Vogel's performance relationship is considered [10]. In Vogel's relationship, to estimate the maximum oil production rate ${\textstyle q_{max}}$ from the oil-well, it is required to measure the real oil production rate ${\textstyle q_{3}}$ and flowing bottom-hole pressure ${\textstyle P_{wf}}$ from a production test. Then, to obtain an measure (or estimate) of the average oil-well pressure ${\textstyle P_{f}}$ at the time of the test, equation (7) is used

The maximum oil production rate ${\textstyle q_{max}}$ can be used to estimate the production rates ${\textstyle q_{3}}$ for other flowing bottom hole pressures ${\textstyle P_{w}f^{*}}$ at the current average oil-well pressure ${\textstyle P_{f}}$ as in equation (8). Moreover, in the following we set ${\textstyle P_{w}f^{*}=P_{3}}$

4. Problem statement

By considering the hydraulic models presented in the last section, the efficiency of the pump depends mainly on four operational variables: the nozzle area ${\textstyle A_{n}}$, throat area ${\textstyle A_{th}}$, the input working flow ratio ${\textstyle q_{1}}$ and the surface pressure ${\textstyle P_{s}}$. System pressures are computed with equations (5)-(6), loss coefficients in equation (4) also affect the HJP efficiency, nevertheless they are considered as constants taken from the literature [1] (Table 3).

The objective function of the optimization problem, represents a mathematical model that allows to quantify the performance of the HJP. In this case, we consider to maximize the HJP efficiency, defined in equation (1). Although hydraulic pumping is an effective and reliable system, it presents some operational risks and disadvantages that are considered by means of the following constraints.

The first constraint is related to the cavitation problem in the HJP [5]. The high speed that is generated between the nozzle and throat, combined with the presence of gas and other solid particles causes cavitation, i.e. the sudden formation of small vapor bubbles into the liquid oil. This is a fundamental phenomenon to be considered because it might cause considerable efficiency decrease and severe damage to the nozzle and throat of the HJP. The mathematical expression of the cavitation is represented by the limit flow ratio ${\textstyle M_{c}}$ [11], as in equation (9)

To compute the Jet velocity ${\textstyle H_{v}}$, equation (10) is used

Substituting (10) into equation (9), then equation (11) is obtained, where ${\textstyle P_{v}}$ has been set to zero because low gas-oil ratio (GOR) relationships for the studied oil-wells are assumed. In the case that ${\textstyle M}$ is less than ${\textstyle M_{c}}$, there is a low risk of cavitation in the HJP and efficiency might be increased

A second set of constraints arise from geometrical characteristics of the HJP performance, specifically related to the commercial availability of nozzle and throat produced by manufacturers. Some technical guidelines are considered as follows. Both, nozzle and throat, use a strict progression of diameter and holes provided by the manufacturer, as depicted in Table 1. The progression establishes areas of ratio between nozzles and throats. In general, high flow volumes renders low lifting and vice versa. Very small area ratios are used in shallow wells, also the injection pressure is very low for these cases. The largest area ratios are installed for high lifting heads, but this is only applicable in specific cases, [12].

The working fluid (water) and the production fluid (oil and gas), must go through the throat area ${\textstyle A_{th}}$. The suction area ${\textstyle (A_{s})}$ is the separation between the nozzle and throat; this area is where the oil-well fluid enters and it also raises a constraint. Moreover, the relationship ${\textstyle b}$ is also constrained by maximum and minimum values due to practical implementations. Considering this, the geometric constrains described above can be mathematically stated as follows:

• The nozzle area ${\textstyle A_{n}}$ must be smaller than the throat area ${\textstyle A_{th}}$. This fact implies the existence of the suction area ${\textstyle A_{s}=A_{th}-A_{n}}$.
• To allow enough fluid production flow, the annular suction area ${\textstyle A_{s}}$, must be bounded as follows: ${\textstyle A_{s_{min}}<A_{s}<A_{s_{max}}}$.
• Commercial nozzle and throat are considered to identify their components by the nozzle to throat ratio ${\textstyle b}$; therefore: ${\textstyle b_{min}<b<b_{max}}$.

In addition, equation (3) and Vogel relationship given by equation (8), renders a set of constraints for the systems pressures in order to get feasible (positive) values for ${\textstyle H}$ and ${\textstyle q_{3}}$, this is:

• System pressures must be computed to satisfy: ${\textstyle P_{3}<P_{2}<P_{1}}$.
• Inlet pressure must satisfy: ${\textstyle 0<P_{3}<P_{f}}$.

After the above considerations, we propose to set the design of a HJP as solving the following constrained non-linear optimization problem:

subject to the hydraulic pump model functions (2)-(8), the cavitation constraints (9)-(11) and the following geometrical and hydraulic constraints:

The solution to this problem offers an optimum configuration of the variables ${\textstyle A_{n}}$, ${\textstyle A_{th}}$, ${\textstyle q_{1}}$ and ${\textstyle P_{s}}$; so that the efficiency is maximized without cavitation problems and considering implementable nozzle and throat areas. This is, it will be possible to extract as much fluid as possible with the least amount of energy possible, thus saving on the pumping equipment to be used.

5. Optimization design process using Differential Evolution

There exist several theoretical and numerical techniques, to solve non-linear constrained optimization problems. In this work, we consider a numerical approach by using a Differential Evolution Algorithm (DEA), [13]. A DEA is a numerical method for the determination of the global minimum or maximum, for highly non-linear problems. It can handle an optimization problem with or without constraints, based on a process of natural selection that imitates biological evolution, [14]. The DEA repeatedly updates a set of ${\textstyle P}$ initial vector designs ${\textstyle [\mathbf {x} _{1,0},\mathbf {x} _{2,0},...,\mathbf {x} _{P,0}]}$ called population, in order to reach a final set of vector designs ${\textstyle [\mathbf {x} _{1,f},\mathbf {x} _{2,f},...,\mathbf {x} _{P,f}]}$, for which an objective function ${\textstyle f(\mathbf {x} _{i,f})}$ is minimized or maximized for ${\textstyle i=1,2,..,P}$, as shown in Figure 3.

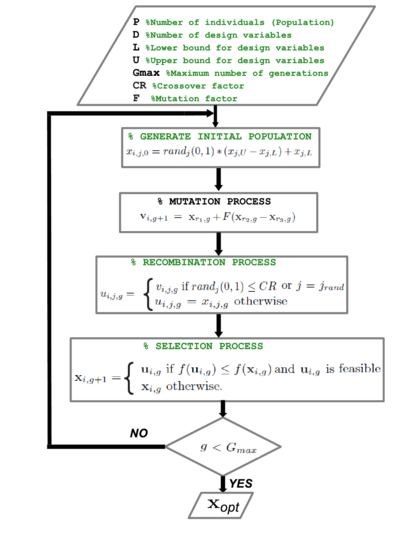
Figure 3. Flow diagram for the DEA

The design vector is defined as ${\textstyle \mathbf {x} =[x_{1},x_{2},...,x_{D}]^{T}}$, where ${\textstyle D}$ is the number of design variables; and the objective function is ${\textstyle f(\mathbf {x} )}$. It is important to mention that the design vector might belong to a set ${\textstyle \Omega =\{\mathbf {x} :\mathbf {x} _{min}\leq \mathbf {x} \leq \mathbf {x} _{max}\}}$. In the following, we assume the search for a minimum of the objective function ${\textstyle f}$, while for searching maximum ${\textstyle -f}$ must be considered. Each population, is a set of vector designs ${\textstyle \mathbf {x} _{i,g}}$, where sub-index ${\textstyle i}$ represents the ${\textstyle i-th}$ vector design for the ${\textstyle g-th}$ generation for ${\textstyle i=1,2,...,P}$.

The initial population for ${\textstyle g=0}$, can be randomly obtained for the ${\textstyle j_{th}}$-component of the vector ${\textstyle \mathbf {x} _{i,0}}$ as: ${\textstyle x_{i,j,0}=rand_{j}(0,1)*(x_{j,U}-x_{j,L})+x_{j,L}}$ where ${\textstyle x_{j,L}}$ and ${\textstyle x_{j,U}}$ represents, respectively, lower and upper bounds for each variable of the vector design and ${\textstyle rand_{j}(0,1)}$ is a random number between 1 and 0.

At each generation ${\textstyle g}$, the DEA algorithm randomly selects individual solutions from the current population and uses them as parents to produce the offspring of the next generation. This is known as mutation and it states that the vector design for the next generation can be computed as ${\textstyle \mathbf {v} _{i,g+1}=\mathbf {x} _{r_{1},g}+F(\mathbf {x} _{r_{2},g}-\mathbf {x} _{r_{3},g})}$, where ${\textstyle r_{1},r_{2}}$ and ${\textstyle r_{3}}$ are integers randomly selected from the set ${\textstyle \{1,2,3,...P\}}$, and ${\textstyle F}$ is a mutation factor. To guarantee that ${\textstyle v_{i,g+1}\in \Omega }$ if ${\textstyle v_{i,j,g+1}\leq x_{j,min}}$ then ${\textstyle v_{i,j,g+1}=2x_{j,min}-v_{i,j,g+1}}$ else if ${\textstyle v_{i,j,g+1}\geq x_{j,max}}$ then ${\textstyle v_{i,j,g+1}=2x_{j,max}-v_{i,j,g+1}}$.

To complement the mutation strategy, in DEA it is defined a recombination process that ensures each design vector copied from two different vectors, crosses with a mutant vector. This is, DEA generates a trial crossed vector ${\textstyle \mathbf {u} _{i,g}}$ with the following definitions for its ${\textstyle j-th}$ component: ${\textstyle u_{i,j,g}=v_{i,j,g}}$ if ${\textstyle rand_{j}(0,1)\leq CR}$ or ${\textstyle j=j_{rand}}$ or ${\textstyle u_{i,j,g}=x_{i,j,g}}$ otherwise, where ${\textstyle CR}$ is a user-defined crossover value that controls the fraction of parameter values that are copied from the mutant and ${\textstyle j_{rand}}$ is a randomly chosen index from the set ${\textstyle \{1,2,...,D\}}$.

Finally, the selection is performed by comparing each trial vector ${\textstyle \mathbf {u} _{i,g}}$ with the target vector ${\textstyle \mathbf {x} _{i,g}}$ as follows: ${\textstyle \mathbf {x} _{i,g+1}=\mathbf {u} _{i,g}}$ if ${\textstyle f(\mathbf {u} _{i,g})\leq f(\mathbf {x} _{i,g})}$ and ${\textstyle \mathbf {u} _{i,g}}$ is feasible, or ${\textstyle \mathbf {x} _{i,g+1}=\mathbf {x} _{i,g}}$ otherwise. The algorithm continues checking feasible individuals using the constraint handling mechanism proposed in [15], for each vector of the ${\textstyle g-th}$ generation, until some criterion is fulfilled, e.g. a maximum number of generations ${\textstyle G_{max}}$ is overcome or other.

After ${\textstyle G_{max}}$ successive generations, the population evolves towards a set of optimal solutions ${\textstyle \mathbf {x} _{i,G_{max}}=\mathbf {x} _{i,opt}}$ for ${\textstyle i=1,2...,N_{P}}$, which in this case render feasible and optimal designs of the HJP and its operational conditions.

5.1 Remarks on the algorithm implementation

Continuing with the solution to the optimization problem, it is necessary to establish the dimensions that will have nozzle and throat according to standard sizes and relationships offered by manufacturers. Figure 4 depicts in red squares commercial nozzle and throat.

Figure 4. Throat and nozzle for an HJP.

There are many manufacturers of HJPs in the world. In Table 1, the nozzle and throat areas (in squared inches) are classified for three different manufacturers: Kobe, National and Guiberson. In this paper we select the last one, since Geolis/Nuvoil company uses Guiberson Jet pumps.

Eddie Smart [16], proposed a throat and nozzle combinations in terms of the parameters ${\textstyle b}$ and ${\textstyle A_{s}}$, that are implementable in practical applications. This represents a set of constraints as explained in Section 4. The feasible relationships between ${\textstyle b}$ and ${\textstyle A_{s}}$ are depicted in Table 2.

6. Results

In this work the vector design is set as ${\textstyle \mathbf {x} =[x_{1},x_{2},x_{3},x_{4}]^{T}=[A_{th},A_{n},P_{s},q_{1}]^{T}}$ and the parameters of the DEA are set to ${\textstyle F=0.7}$ and ${\textstyle CR=0.8}$. The algorithm was implemented in Matlab${\textstyle ^{\mbox{©}}}$.

It is important to remark that in order to implement the considerations presented in Tables 2 and 1, indexed lists are used in the DEA, i.e. any list item can be identified by a sequential integer number that identifies its position. In order to keep operational conditions feasible, as indicated by the technical data-sheet of the surface pumps, the range of values for the input flow and input pressure were set to minimum and maximum values as: ${\textstyle q_{1_{min}}=600[BPD]}$, ${\textstyle q_{1_{max}}=1500[BPD]}$, ${\textstyle P_{s_{min}}=900[Psi]}$ and ${\textstyle P_{s_{max}}=2500[Psi]}$. Table 3 depicts testing parameters experimentally obtained, [9].

In order to validate our design proposal, it has been evaluated a set of ten oil-wells from the asset Aceite Terciario del Golfo (ATG-Mexico), an important oil-well zone in Mexico. The values of the operating oil-well conditions that have been used to perform this analysis have been provided by the Mexican Company Geolis/Nuvoil (Table 4). In this Table, it can be observed low efficiencies and high power consumption for most oil-wells currently operating. It is important to mention that the efficiency and horsepower consumption, were actually computed with models considered in this paper, based in the operational parameters of the Geolis/Nuvoil Company.

6.1 Benchmark oil-well

For the sake of clarity, the sixth oil-well in Table 4 is selected as a benchmark to show our design proposal. Geolis/Nuvoil company disposed of a pressure-temperature sensor of the brand Pioneer Petrotech Services Inc., into the oil-well. The sensor was operating during one month getting the average value of ${\textstyle P_{wf}=1355[PSI]}$, while the predicted with equation (6) is ${\textstyle P_{3}=P_{wf}=1177[Psi]}$ getting a error of 13.14 %

After the application of our approach, the first set of results are depicted in Table 6.1, considering the initial population of 20 individuals and varying the number of maximum generations from 50 to 500. As it can be observed with low generations, convergence is not achieved and the optimal efficiency rounds 9% to 11% In these cases the cavitation indicator ${\textstyle M}$ is quite lower than ${\textstyle M_{c}}$ and power consumption rounds 40 [HP]. Then, with higher number of generations the efficiency is improved up to 16.88 %, with ${\textstyle M}$ closer to ${\textstyle M_{c}}$. Note also that in this case the power consumption is close to 12 [HP] with a clear energy saving.

Table 6 presents numerical results by considering a fixed number of ${\textstyle G_{max}=250}$ generations and varying the number of initial population.

As it can be observed, with low initial population and ${\textstyle G_{max}}$ reasonably high, convergence is achieved and the optimal efficiency rounds 15.8% In this cases the cavitation indicator ${\textstyle M}$ is quite less than ${\textstyle M_{c}}$ and power consumption rounds 11 [HP], thus saving energy. Nevertheless, in this case with higher number of initial population the efficiency is improved up to 17.23 %, with ${\textstyle M}$ equal to ${\textstyle M_{c}}$ and more important, the power consumption is close to 19 [HP]. Here, the geometries selected for ${\textstyle A_{n}}$ and ${\textstyle A_{th}}$ are smaller than the selected for the case when the efficiency rounds 16.8 % Moreover, the input pressure must be increased twice in order to render higher efficiency, which explains the 19 [HP] of power consumption.

6.2 Results for the ten wells from ATG-zone Mexico

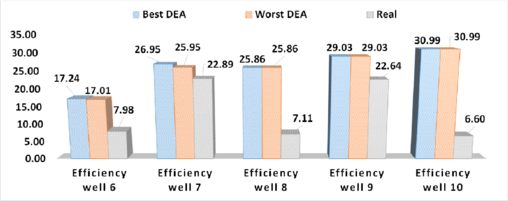
The rest of the wells were analyzed with the proposed DEA by considering ${\textstyle G_{max}=500}$ and ${\textstyle P=100}$. Numerical results are depicted in Table 7. Note that power consumption is between 9 and 19 [HP], remarkably lower than the presented in Table 4. Moreover, the efficiencies are incremented in all cases as shown in Figures 5 and 6. Worst DEA and Best DEA means the worst and best result using the Differential Evolution Algorithm, respectively; while real means the result for the implemented HJP. Note that in most cases ${\textstyle M=M_{c}}$, thus putting in risk of cavitation in the HJP. Nonetheless this result can be improved by considering a safety factor ${\textstyle \beta <1}$ such that ${\textstyle M<\beta M_{c}}$.

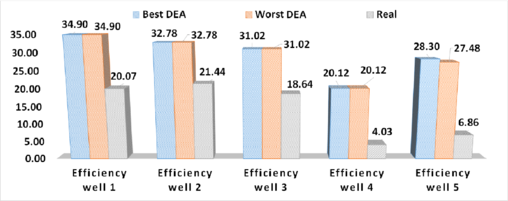
Figure 5. Comparison of implemented and computed efficiency for oil-wells 1 to 5 from ATG-zone Mexico

Figure 6. Comparison of implemented and computed efficiency for oil-wells 6 to 10 from ATG-zone Mexico

7. Conclusion

For each oil-well, although belonging to the same productive zone, has different and unique characteristics; for that reason it should always be performed the analysis for each well. The efficiency of an HJP is linked to the implemented geometry. Nevertheless, the analysis must consider the production capacities of each oil-well, as well as the resources available in the installation of the ALS. The algorithm presented in this work is able to define the optimal geometry and the operational conditions that renders the maximum efficiency of the HJP for a given oil-well, based on its characteristics and its production capacities. By using this design methodology it will be easier for the engineers to select the HJP geometries to install besides knowing the efficiency that it can develop during operation while its conditions remain stable.

From the numerical results it can be concluded that efficiency of the operation of the studied wells can be improved up to 24% for a given implementation of the HJP. In addition, it was observed that similar efficiencies can be achieved with different amount of power required to implement the HJP artificial lift system. This fact encourage us to continue research on the optimization of the HJP in terms of the design of other sections such as the inlet holes for the working fluid and suction for the well fluids.

Acknowledgment

The authors would like to thank the support provided by Geolis/Nuvoil for sponsoring, training and advice provided. Their support served extensively for the development and validation of this research article, driving development within the energetic sector in the country.

References