m (RJPV moved page Draft Portillo Velez 949682510 to Review 115750068379) |
|||
| Line 56: | Line 56: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-avance.png|301px|Escenario de predicción de la coordenada (x(t), y(x)).]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 1:''' | + | | colspan="1" | '''Figura 1:''' Escenario de predicción de la coordenada <math>(x(t), y(x))</math>. |
|} | |} | ||
| Line 92: | Line 92: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-seguimiento1.png|311px|<span style="text-align: center; font-size: 75%;">Identificación de marcador</span>]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-seguimiento3.png|278px|<span style="text-align: center; font-size: 75%;">Búsqueda de máximo y mínimo </span>]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) <span style="text-align: center; font-size: 75%;"> | + | | (a) <span style="text-align: center; font-size: 75%;">Identificación de marcador</span> |
| − | | (b) <span style="text-align: center; font-size: 75%;"> | + | | (b) <span style="text-align: center; font-size: 75%;">Búsqueda de máximo y mínimo </span> |
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-seguimiento2.png|269px|<span style="text-align: center; font-size: 75%;">Cálculo de eje y puntos medios</span>]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-seguimiento4.png|283px|<span style="text-align: center; font-size: 75%;">Compensación de desviación θ</span>]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (c) <span style="text-align: center; font-size: 75%;"> | + | | (c) <span style="text-align: center; font-size: 75%;">Cálculo de eje y puntos medios</span> |
| − | | (d) <span style="text-align: center; font-size: 75%;"> | + | | (d) <span style="text-align: center; font-size: 75%;">Compensación de desviación <math>\theta </math></span> |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="2" | '''Figura 2''' | | colspan="2" | '''Figura 2''' | ||
| Line 110: | Line 110: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-Algoritmo.png|600px|Algoritmo para la estimación de balanceo y predicción de postura de robot. ]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 3:''' Algoritmo para la estimación de balanceo y predicción de postura de robot. | | colspan="1" | '''Figura 3:''' Algoritmo para la estimación de balanceo y predicción de postura de robot. | ||
| Line 128: | Line 128: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-rolle.png|354px|Detección de extremos locales.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 4:''' Detección de extremos locales. | | colspan="1" | '''Figura 4:''' Detección de extremos locales. | ||
| Line 142: | Line 142: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-inicio_trayectoria.png|600px|<span style="text-align: center; font-size: 75%;">Inicio de trayectoria </span>]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-final_trayectoria.png|600px|<span style="text-align: center; font-size: 75%;">Desviación de la trayectoria </span>]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) <span style="text-align: center; font-size: 75%;"> | + | | (a) <span style="text-align: center; font-size: 75%;">Inicio de trayectoria </span> |
| − | | (b) <span style="text-align: center; font-size: 75%;"> | + | | (b) <span style="text-align: center; font-size: 75%;">Desviación de la trayectoria </span> |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="2" | '''Figura 5''' | | colspan="2" | '''Figura 5''' | ||
| Line 227: | Line 227: | ||
|} | |} | ||
| − | donde se requiere la estimación de sus parámetros: amplitud <math display="inline">A</math>, fase <math display="inline">\phi </math> y frecuencia <math display="inline">\omega=2\pi /T</math>, siendo <math display="inline">T</math> el periodo de la función, definido por la distancia horizontal entre dos máximos locales consecutivos. Además, dado que la lista de puntos se conforma de modo que todas las coordenadas sean consecutivas en la horizontal, entonces el periodo también es el número de puntos de la trayectoria que se encuentran entre dos máximos consecutivos. Si los datos describieran una sinusoide ideal, el periodo tendría una longitud constante, sin embargo en la trayectoria real, este valor puede no ser el mismo en cada ciclo. Por lo tanto, para lograr una aproximación más fiel se calcula esta distancia para todos los máximos disponibles en la muestra y el periodo estimado es el promedio de éstos (ver ecuación ([[#eq-2|2]])), por lo que la frecuencia se aproxima a partir del periodo con la ecuación ([[#eq-3|3]]). La amplitud se calcula como la mitad de la distancia entre un máximo y un mínimo consecutivos sobre la perpendicular al eje de la trayectoria y, al igual que el periodo, se aproxima como el promedio de este distancia a lo largo de toda la muestra (ecuación ([[#eq-4|4]])). Por último, el parámetro <math display="inline">\phi </math> se calcula como la distancia horizontal entre el primer punto de la muestra, que coincide con el primer máximo registrado, y el primer punto medio que se puede calcular entre un máximo y un mínimo (ecuación ([[#eq-5|5]])). Así, teniendo la lista de máximos, <math display="inline">M</math>, con pares ordenadas <math display="inline">(Mx_{i}, My_{i})</math> con <math display="inline">i = 0, ..., N</math>, donde N es el número de máximos en la muestra. Y teniendo una lista, <math display="inline">m</math>, de mínimos <math display="inline">(mx_{i}, my_{i}</math> con <math display="inline">i= 0,..., N-1</math>, entonces los parámetros de la función sinusoidal están dados por | + | donde se requiere la estimación de sus parámetros: amplitud <math display="inline">A</math>, fase <math display="inline">\phi </math> y frecuencia <math display="inline">\omega=2\pi /T</math>, siendo <math display="inline">T</math> el periodo de la función, definido por la distancia horizontal entre dos máximos locales consecutivos. Además, dado que la lista de puntos se conforma de modo que todas las coordenadas sean consecutivas en la horizontal, entonces el periodo también es el número de puntos de la trayectoria que se encuentran entre dos máximos consecutivos. Si los datos describieran una sinusoide ideal, el periodo tendría una longitud constante, sin embargo en la trayectoria real, este valor puede no ser el mismo en cada ciclo. Por lo tanto, para lograr una aproximación más fiel se calcula esta distancia para todos los máximos disponibles en la muestra y el periodo estimado es el promedio de éstos (ver ecuación ([[#eq-2|2]])), por lo que la frecuencia se aproxima a partir del periodo con la ecuación ([[#eq-3|3]]). La amplitud se calcula como la mitad de la distancia entre un máximo y un mínimo consecutivos sobre la perpendicular al eje de la trayectoria y, al igual que el periodo, se aproxima como el promedio de este distancia a lo largo de toda la muestra (ecuación ([[#eq-4|4]])). Por último, el parámetro <math display="inline">\phi </math> se calcula como la distancia horizontal entre el primer punto de la muestra, que coincide con el primer máximo registrado, y el primer punto medio que se puede calcular entre un máximo y un mínimo (ecuación ([[#eq-5|5]])). Así, teniendo la lista de máximos, <math display="inline">M</math>, con pares ordenadas <math display="inline">(Mx_{i}, My_{i})</math> con <math display="inline">i = 0, ..., N</math>, donde N es el número de máximos en la muestra. Y teniendo una lista, <math display="inline">m</math>, de mínimos <math display="inline">(mx_{i}, my_{i}</math> con <math display="inline">i= 0,..., N-1</math>, entonces los parámetros de la función sinusoidal están dados por, |
<span id="eq-2"></span> | <span id="eq-2"></span> | ||
| Line 305: | Line 305: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> \begin{array}{lll} n_{1_{y}} & = & x^3y-9\int _0^x{\sigma ^2y(\sigma )d\sigma{+18}}\int _0^x{\int _0^\sigma{\lambda y(\lambda )d\lambda }d\sigma }-6\int _0^x{\int _0^\sigma{\int _0^\lambda{y(\rho )d\rho }d\lambda }d\sigma }\\ d_{1_{y}} & = & -\int _0^x{\int _0^\sigma{\lambda ^3 y(\lambda )d\lambda }d\sigma }+3\int _0^x{\int _0^\sigma{\int _0^\lambda{\rho ^2y(\rho )d\rho }d\lambda }d\sigma }\\ f_1 & = & -\frac{12}{x^4}[-x^3y+11(\int{x^2y})-28(\int ^{(2)}{xy})+12(\int ^3{y})+\\ & & p_1(-2\int ^{(2)}{x^3y}+14(\int ^3{x^2y})-20(\int ^{(4)}xy+4(\int ^{5}{y}))+\\ & & p_1^2(-\int ^{(4)}x^3y+3\int ^{(5)}{x^2y})]\\ f_2 & = & \frac{3}{x^3p_1}[-xy+\int{y}+2p_1(-\int ^{(2)}xy+\int ^{(3)}{y})+\\ & & p_1^2(-\int ^{(4)}xy+\int ^{(5)}{y})-p_1p_3\frac{x^4}{24}+p_3\frac{x^2}{2}] \end{array} </math> | + | | style="text-align: center;" | <math> \begin{array}{lll} n_{1_{y}} & = & x^3y-9\int _0^x{\sigma ^2y(\sigma )d\sigma{+18}}\int _0^x{\int _0^\sigma{\lambda y(\lambda )d\lambda }d\sigma }-6\int _0^x{\int _0^\sigma{\int _0^\lambda{y(\rho )d\rho }d\lambda }d\sigma }\\ d_{1_{y}} & = & -\int _0^x{\int _0^\sigma{\lambda ^3 y(\lambda )d\lambda }d\sigma }+3\int _0^x{\int _0^\sigma{\int _0^\lambda{\rho ^2y(\rho )d\rho }d\lambda }d\sigma }\\ f_1 & = & -\frac{12}{x^4}[-x^3y+11(\int{x^2y})-28(\int ^{(2)}{xy})+12(\int ^3{y})+\\ & & p_1(-2\int ^{(2)}{x^3y}+14(\int ^3{x^2y})-20(\int ^{(4)}xy+4(\int ^{5}{y}))+\\ & & p_1^2(-\int ^{(4)}x^3y+3\int ^{(5)}{x^2y})]\\ f_2 & = & \frac{3}{x^3p_1}[-xy+\int{y}+2p_1(-\int ^{(2)}xy+\int ^{(3)}{y})+\\ & & p_1^2(-\int ^{(4)}xy+\int ^{(5)}{y})-p_1p_3\frac{x^4}{24}+p_3\frac{x^2}{2}], \end{array} </math> |
|} | |} | ||
|} | |} | ||
| + | |||
| + | donde <math display="inline">\sigma </math>, <math display="inline">\rho </math> y <math display="inline">\lambda </math> son variables auxiliares para definir cada integración. | ||
===4.3 Aproximación de parámetros con series de Fourier=== | ===4.3 Aproximación de parámetros con series de Fourier=== | ||
| Line 316: | Line 318: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-trayectoria.png|497px|Caso de trayectoria real del robot con asimetría con respecto a un eje horizontal.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 6:''' | + | | colspan="1" | '''Figura 6:''' Caso de trayectoria real del robot con asimetría con respecto a un eje horizontal. |
|} | |} | ||
| Line 357: | Line 359: | ||
===5.1 Aproximación sinusoidal con mínimos cuadrados=== | ===5.1 Aproximación sinusoidal con mínimos cuadrados=== | ||
| − | La sinusoide es una función con dominio continuo, sin embargo los parámetros calculados mediante [[#eq-2|2]] y [[#eq-4|4]] se calculan a partir de distancias enteras, ya que se obtienen a partir de valores discretos correspondientes a las coordenadas de los pixeles en la imagen. | + | La sinusoide es una función con dominio continuo, sin embargo los parámetros calculados mediante ([[#eq-2|2]]) y ([[#eq-4|4]]) se calculan a partir de distancias enteras, ya que se obtienen a partir de valores discretos correspondientes a las coordenadas de los pixeles en la imagen. |
| + | |||
| + | Debido a esto, como los cálculos de los parámetros son aproximados, cabe preguntarse si se podría lograr un mejor ajuste en el dominio continuo. Para explorar esta idea, se consideran incrementos de <math display="inline">0.05</math> en los intervalos <math display="inline">\Delta _A=\pm 0.5</math>, <math display="inline">\Delta _{T}=\pm 0.5</math> para los parámetros <math display="inline">A</math> y <math display="inline">T</math> respectivamente. En las Figuras [[#img-7|7]]-[[#img-10|10]], la curva amarilla representa la trayectoria real, y la curva magenta, describe su aproximación. | ||
| − | + | En la Figura [[#img-7a|7a]] se muestra la aproximación que se obtiene con el cálculo original de los parámetros, la cual se observa semejante a la curva de la trayectoria. Obsérvese en las Figuras [[#img-7c|7c]], [[#img-7d|7d]] y [[#img-7e|7e]] que al variar los parámetros del modo indicado, la curva sufre un ajuste. La curva que se muestra en la Figura [[#img-7b|7b]] es aquella de todas las variaciones exploradas que presenta el mínimo error de aproximación. Estos casos se evalúan bajo el criterio de minimización del error de aproximación <math display="inline">E_A</math> por mínimos cuadrados de acuerdo a ([[#eq-12|12]]), con respecto a la trayectoria real. | |
<div id='img-7a'></div> | <div id='img-7a'></div> | ||
| Line 369: | Line 373: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-sin_ori.png|219px|Aproximación con A=21.25, T=41 sin minimización del error. E<sub>A</sub>=17.38]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-sin_opt.png|219px|Aproximación con error mínimo. A=20.75, T=41.5. E<sub>A</sub>=11.49 ]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) Aproximación | + | | (a) Aproximación con <math>A=21.25</math>, <math>T=41</math> sin minimización del error. <math>E_A=17.38</math> |
| − | | (b) | + | | (b) Aproximación con error mínimo. <math>A=20.75</math>, <math>T=41.5</math>. <math>E_A=11.49</math> |
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-sin_var1.png|431px|Variación: A=21.5, T=41.25. E<sub>A</sub>=15.17 ]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-sin_var2.png|431px|Variación: A=21.5, T=40.75. E<sub>A</sub>=19.36]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (c) | + | | (c) Variación: <math>A=21.5</math>, <math>T=41.25</math>. <math>E_A=15.17</math> |
| − | | (d) | + | | (d) Variación: <math>A=21.5</math>, <math>T=40.75</math>. <math>E_A=19.36</math> |
|- | |- | ||
| − | | colspan="2"|[[Image: | + | | colspan="2"|[[Image:Review_115750068379-sin_var3.png|431px|Variación: A=21, T=40.75. E<sub>A</sub>= 19.67]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | (e) | + | | colspan="2" | (e) Variación: <math>A=21</math>, <math>T=40.75</math>. <math>E_A= 19.67</math> |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="2" | '''Figura 7''' | | colspan="2" | '''Figura 7''' | ||
| Line 401: | Line 405: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-algebraic_ex1.png|600px|Inicio en x[0]; tamaño de la muestra, 30 pixeles. Parámetros obtenidos A=20.87, ω=0.156]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-algebraic_ex2.png|600px|Inicio en x[5]; tamaño de la muestra, 30 pixeles. Parámetros obtenidos A=19.98, ω=0.160]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| (a) Inicio en <math>x[0]</math>; tamaño de la muestra, 30 pixeles. Parámetros obtenidos <math>A=20.87</math>, <math> \omega =0.156</math> | | (a) Inicio en <math>x[0]</math>; tamaño de la muestra, 30 pixeles. Parámetros obtenidos <math>A=20.87</math>, <math> \omega =0.156</math> | ||
| (b) Inicio en <math>x[5]</math>; tamaño de la muestra, 30 pixeles. Parámetros obtenidos <math>A=19.98</math>, <math> \omega =0.160</math> | | (b) Inicio en <math>x[5]</math>; tamaño de la muestra, 30 pixeles. Parámetros obtenidos <math>A=19.98</math>, <math> \omega =0.160</math> | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-algebraic_ex3.png|600px|Inicio en x[10]; tamaño de la muestra, 30 pixeles. Parámetros obtenidos A=25.33, ω=0.138]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-algebraic_ex4.png|600px|Inicio en x[0]; tamaño de la muestra, 50 pixeles. Parámetros obtenidos A=16.2, ω=0.170]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| (c) Inicio en <math>x[10]</math>; tamaño de la muestra, 30 pixeles. Parámetros obtenidos <math>A=25.33</math>, <math> \omega =0.138</math> | | (c) Inicio en <math>x[10]</math>; tamaño de la muestra, 30 pixeles. Parámetros obtenidos <math>A=25.33</math>, <math> \omega =0.138</math> | ||
| (d) Inicio en <math>x[0]</math>; tamaño de la muestra, 50 pixeles. Parámetros obtenidos <math>A=16.2</math>, <math> \omega =0.170</math> | | (d) Inicio en <math>x[0]</math>; tamaño de la muestra, 50 pixeles. Parámetros obtenidos <math>A=16.2</math>, <math> \omega =0.170</math> | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-algebraic_ex5.png|600px|Inicio en x[5]; tamaño de la muestra, 50 pixeles. Parámetros obtenidos A=19.35, ω=0.150]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-algebraic_ex6.png|600px|Inicio en x[10]; tamaño de la muestra, 50 pixeles. Parámetros obtenidos A=18.83, ω=0.156]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| (e) Inicio en <math>x[5]</math>; tamaño de la muestra, 50 pixeles. Parámetros obtenidos <math>A=19.35</math>, <math> \omega =0.150</math> | | (e) Inicio en <math>x[5]</math>; tamaño de la muestra, 50 pixeles. Parámetros obtenidos <math>A=19.35</math>, <math> \omega =0.150</math> | ||
| Line 426: | Line 430: | ||
===5.3 Aproximación por series de Fourier=== | ===5.3 Aproximación por series de Fourier=== | ||
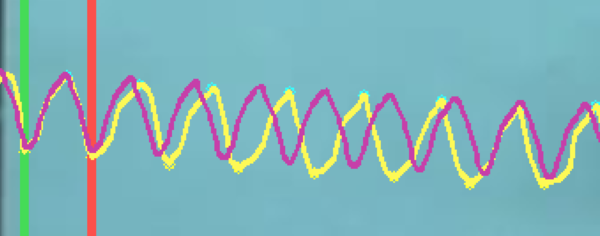
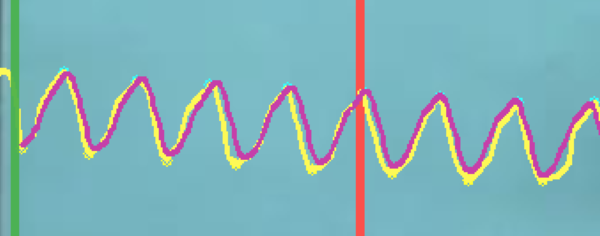
| − | Para una aproximación por series de Fourier es suficiente un único ciclo periódico, sin embargo al extenderse la trayectoria, ésta no necesariamente estará bien aproximada. Para solventar ésto, se propone utilizar una muestra que contenga varios ciclos.En la Figura [[#img-9|9]] se observa una comparación entre estos dos casos. En las Figuras [[#img-9|9]]a y [[#img-9|9]]c, se muestran dos trayectorias desarrolladas por el robot con su correspondiente aproximación de Fourier a través de un sólo ciclo, mientras que en [[#img-9|9]]b y [[#img-9|9]]d, se consideran 5 de ellos. Nótese que las trayectorias se pueden extender y distorsionar por lo que se requieren muestras significativas para poder aproximar de manera eficiente. Para construir la serie de Fourier en el segundo caso, se calculan los coeficientes de la ecuación ([[#eq-11|11]]) para cada uno de los ciclos y después se obtiene el promedio de éstos. | + | Para una aproximación por series de Fourier es suficiente un único ciclo periódico, sin embargo al extenderse la trayectoria, ésta no necesariamente estará bien aproximada. Para solventar ésto, se propone utilizar una muestra que contenga varios ciclos. En la Figura [[#img-9|9]] se observa una comparación entre estos dos casos. Las líneas verticales indican el inicio (verde) y fin (roja) de la muestra. En las Figuras [[#img-9|9]]a y [[#img-9|9]]c, se muestran dos trayectorias desarrolladas por el robot con su correspondiente aproximación de Fourier a través de un sólo ciclo, mientras que en [[#img-9|9]]b y [[#img-9|9]]d, se consideran 5 de ellos. Nótese que las trayectorias se pueden extender y distorsionar por lo que se requieren muestras significativas para poder aproximar de manera eficiente. Para construir la serie de Fourier en el segundo caso, se calculan los coeficientes de la ecuación ([[#eq-11|11]]) para cada uno de los ciclos y después se obtiene el promedio de éstos. |
<div id='img-9a'></div> | <div id='img-9a'></div> | ||
| Line 435: | Line 439: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-fourier_ex1.png|600px|Aproximación de la curva utilizando un único ciclo ]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-fourier_ex3.png|600px|Curva construida con los promedios de los coeficientes de Fourier para 5 ciclos ]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| (a) Aproximación de la curva utilizando un único ciclo | | (a) Aproximación de la curva utilizando un único ciclo | ||
| (b) Curva construida con los promedios de los coeficientes de Fourier para 5 ciclos | | (b) Curva construida con los promedios de los coeficientes de Fourier para 5 ciclos | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-fourier_ex4.png|600px|Aproximación de la curva utilizando un único ciclo]] |
| − | |[[Image: | + | |[[Image:Review_115750068379-fourier_ex6.png|600px|Curva construida con los promedios de los coeficientes de Fourier para 5 ciclos ]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| (c) Aproximación de la curva utilizando un único ciclo | | (c) Aproximación de la curva utilizando un único ciclo | ||
| Line 654: | Line 658: | ||
De la Tabla [[#table-2|2]] se infiere que la técnica que brinda mejores resultados es la de series de Fourier, ya que la desviación estándar DE es menor en ambas métricas de error; esto es, una menor dispersión en los resultados de los experimentos proporciona mayor confianza sobre su capacidad para predecir eficazmente la trayectoria. | De la Tabla [[#table-2|2]] se infiere que la técnica que brinda mejores resultados es la de series de Fourier, ya que la desviación estándar DE es menor en ambas métricas de error; esto es, una menor dispersión en los resultados de los experimentos proporciona mayor confianza sobre su capacidad para predecir eficazmente la trayectoria. | ||
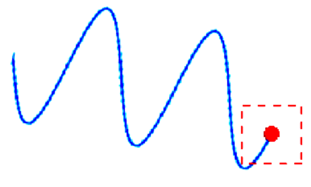
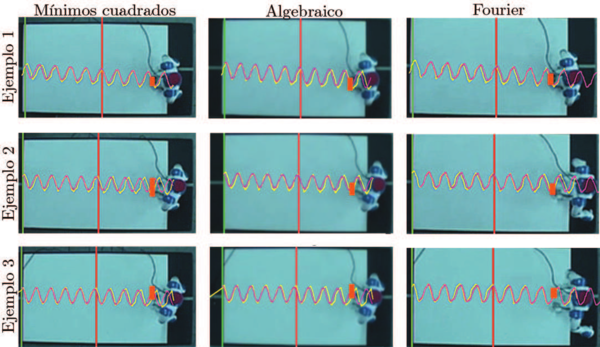
| − | Estos resultados pueden apreciarse en la Figura [[#img-10|10]], donde se muestran tres ejemplos en donde se superponen la trayectoria de seguimiento | + | Estos resultados pueden apreciarse en la Figura [[#img-10|10]], donde se muestran tres ejemplos en donde se superponen la trayectoria de seguimiento y la curva que se obtiene por el método de estimación indicado. El rectángulo colocado a la distancia objetivo resalta la magnitud del error <math display="inline">E_o</math>. |
<div id='img-10'></div> | <div id='img-10'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_115750068379-meth.png|600px|Comparación de tres técnicas de aproximación durante la marcha del robot. ]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 10:''' | + | | colspan="1" | '''Figura 10:''' Comparación de tres técnicas de aproximación durante la marcha del robot. |
|} | |} | ||
| Line 672: | Line 676: | ||
Por su parte, la técnica series de Fourier es la que obtiene mejores resultados ya que los indicadores de error son mínimos comparados con las otras técnicas. Sin embargo, para lograr ésto, ésta técnica requiere un número mayor de periodos. | Por su parte, la técnica series de Fourier es la que obtiene mejores resultados ya que los indicadores de error son mínimos comparados con las otras técnicas. Sin embargo, para lograr ésto, ésta técnica requiere un número mayor de periodos. | ||
| − | Como paso inmediato a la presente investigación, se considera la implementación de estas técnicas de aproximación para realizar tareas complejas de agarre y manipulación por parte del robot en marcha, permitiendo al robot el desarrollo de tareas domésticas de una forma más eficiente. Adicionalmente, se considera la sustitución del sistema sensorial de posición, por un sistema de visión montado en el mismo robot, o bien mediante la implementación de sensores inerciales. | + | Como paso inmediato a la presente investigación, se considera la implementación de estas técnicas de aproximación para realizar tareas complejas de agarre y manipulación por parte del robot en marcha, permitiendo al robot el desarrollo de tareas domésticas de una forma más eficiente. Adicionalmente, se considera la sustitución del sistema sensorial de posición, por un sistema de visión montado en el mismo robot, o bien mediante la implementación de sensores inerciales. Esto permitirá el desarrollo de experimentos fuera de un ambiente de laboratorio. |
==Referencias== | ==Referencias== | ||
Revision as of 20:20, 26 February 2019
Estimación del movimiento de balanceo transversal de un robot bípedo durante la marcha.
Rogelio de J. Portillo-Vélez, Luis Felipe Marín-Urias, J.A. Vazquez-Santacruz, Ana Miguelena-Bada, Antonio Marín-Hernández
| Universidad Veracruzana |
| Facultad de Ingeniería Eléctrica y Electrónica |
| Av. Ruiz Cortines, 415. Boca del Río, Veracruz, México |
| Universidad Veracruzana |
| Centro de Investigación en Inteligencia Artificial |
| Sebastián Camacho, 5. Xalapa, Veracruz, México |
Resumen
Debido al balanceo generado por la dinámica natural y perturbaciones durante la marcha de un robot humanoide, es difícil predecir su postura en determinado instante a lo largo de la misma, complicando así el desarrollo de tareas de manipulación, cooperación, evasión de obstáculos, retroalimentación servo-visual, entre otras. En este documento se describe una metodología para predecir el movimiento de balanceo en el plano transversal del robot, a partir de la trayectoria de un punto fijo en su estructura mecánica. Se considera el estudio de dos modelos matemáticos para aproximar el movimiento de balanceo del humanoide: aproximación mediante una función sinusoidal y aproximación por series de Fourier. En ambos casos, es necesario el conocimiento de los parámetros involucrados del modelo, por lo que se implementan tres técnicas de aproximación paramétrica: mínimos cuadrados e identificación algebraica para el caso de la aproximación sinusoidal, y el cálculo de coeficientes para el caso de las series de Fourier. Para validar la metodología, se lleva a cabo el seguimiento del robot en tiempo real puesto que la trayectoria del punto de interés es afectada por diversos factores como la fricción, inclinación e imperfecciones de la superficie, el estado de conservación del robot, entre otros. A partir de diversos experimentos, se desarrolla una comparación cuantitativa entre las diferentes aproximaciones para verificar aquel que mejor reproduce a la dinámica del balanceo del robot.
keywords
Robot bípedo , Estimación paramétrica, Aproximación de función periódica, Series de Fourier
1 Introducción
Los robots humanoides se han desarrollado para interactuar de manera natural con las personas y su entorno, exhibiendo un aspecto familiar y de confianza. Para que estos robots puedan desplazarse efectivamente en el mismo entorno que los humanos, requieren habilidades motrices similares a las de las personas. Para llevar a cabo tareas en servicio de sus usuarios, es altamente deseable que un robot humanoide tenga la capacidad de realizar una marcha efectiva.
Por ejemplo, el enfoque más común para resolver tareas tales como sujetar un objeto y trasladarlo a otro sitio, consiste en detener la marcha del robot para desempeñar tareas de manipulación; a diferencia de los humanos, capaces de llevar a cabo acciones durante la marcha, como tomar un objeto sin dejar de avanzar. En particular, para asegurar que un robot pueda reproducir esta capacidad, se necesita conocer de qué forma se mueven las extremidades de su arquitectura mecánica mientras camina y así, saber qué movimientos debe realizar para lograr con la extremidad adecuada una postura correcta en el momento preciso.
Convencionalmente, los robots humanoides realizan una marcha poco natural comparada con los humanos, puesto que desarrollan movimientos muy marcados de cadera y rodilla. Esto se debe principalmente a la configuración estructural mecánica del robot, la cual se adapta para evitar posibles caídas o movimientos inesperados; esto a su vez ocasiona que durante la marcha del robot se generen movimientos oscilatorios indeseados tales como el balanceo, principalmente en el plano transversal.
La manera en la que un robot humanoide desarrolla la marcha es comúnmente descrita mediante modelos pasivo-dinámicos como [1], [2], [3], donde se aprovecha el efecto gravitacional en el mismo robot; modelos dinámicos como el descrito en [4], o el de Pendulo Lineal Invertido en 3 Dimensiones (3D-LIPM) [5]. Para la mayoría de los robots humaniodes, se puede conocer la trayectoria del centro de masa (CoM) parametrizada por polinomios y basada en la solución analítica del modelo de 3D-LIPM. Sin embargo, esta solución pocas veces se ajusta a la realidad, ya que el modelo asume condiciones ideales: superficie sin irregularidades o inclinación, funcionamiento perfecto de los actuadores del robot, condiciones ambientales controladas, etc.
Diversos autores proponen utilizar la planeación de la trayectoria del CoM en tiempo real, para responder de manera más flexible a las necesidades de la tarea. Por ejemplo, se tiene a aquellos que utilizan cinemática inversa para determinar el centro de gravedad (CG) y el Punto de Momento Zero (ZMP) en cada instante y por lo tanto dependen de la precisión del modelo [6], [7], [8]. Por otro lado están los enfoques que utilizan control por retroalimentación [9], [10], [11], basado en algún tipo de detección del CoM del robot.
En este documento se describe una metodología para conocer y predecir el movimiento de balanceo en el plano transversal de la trayectoria de un punto fijo en la estructura de un robot bípedo. Esto se realiza usando la información capturada del movimiento de la cabeza y por medio de una cámara ubicada en la parte superior del área de experimentación, con visión plena del plano transversal de la marcha del robot. El objetivo del trabajo consiste en caracterizar un modelo sinusoidal que describa localmente la oscilación desarrollada a través de la identificación de los parámetros asociados a dicho modelo matemático. Se considera el estudio de dos modelos para aproximar el movimiento de balanceo del robot: aproximación mediante una sinusoidal y aproximación por series de Fourier. En ambos casos, es necesario el conocimiento de los parámetros involucrados, por lo que se implementan tres técnicas de aproximación paramétrica: mínimos cuadrados e identificación algebraica para el caso de la aproximación sinusoidal, y el cálculo de los respectivos coeficientes para el caso de las series de Fourier. Para validar la metodología propuesta, se lleva a cabo el seguimiento del robot en tiempo real puesto que la trayectoria del punto de interés es afectada repentinamente por diversos factores como la fricción, inclinación e imperfecciones de la superficie, el estado de conservación del robot, entre otros.
Se utiliza una cámara y técnicas de visión por computadora para hacer el seguimiento del punto de interés, correspondiente a la cabeza del robot. Además, se lleva a cabo una aproximación funcional de la trayectoria del mismo a partir de una serie de muestras obtenidas mediante el seguimiento en tiempo real para la obtención de los parámetros del modelo matemático del balanceo del robot. De esta forma se puede predecir la ubicación del robot en cualquier instante futuro de la marcha con respecto a un sistema de referencia fijo. Se demuestra experimentalmente que esta metodología se adapta a cualquier variación de las condiciones internas y ambientales en las que se opera el robot, puesto que la identificación se puede desarrollar en cualquier instante, tomando en cuenta que la aproximación deberá ser periódicamente actualizada en marchas prolongadas.
El resto de este documento se organiza de la siguiente forma: en la Sección 2 se delimita el problema y el escenario de los experimentos con los que se validan las técnicas aquí propuestas. En la Sección 3 se describe el algoritmo para los métodos utilizados en el seguimiento en tiempo de real de una marca de referencia en la cabeza del robot, así como la definición de las muestras a considerar. En la Sección 4 se explican detalladamente las técnicas de aproximación propuestas, mientras que en la Sección 5 se presenta la implementación experimental con una descripción preliminar de resultados. En la Sección 6 se desarrolla un planteamiento de resultados mediante comparaciones de las técnicas utilizadas, para finalizar con conclusiones del estudio en la Sección 7.
2 Planteamiento del problema
La dificultad de predecir la oscilación producida por el balanceo durante la marcha del robot radica en diversos factores que influyen en la trayectoria desarrollada, por ejemplo: la fricción en la superficie de la marcha, la postura inicial del robot, así como el estado físico de los motores y el desgaste en las extremidades del robot, entre otros. Estos factores pueden tener un efecto diferente en cada experimento, por lo que se busca un modelo matemático que garantice la repetibilidad de la trayectoria de un punto fijo del robot durante la marcha para todos los casos. Esto motiva la búsqueda de una función de predicción de posturas en cualquier instante de tiempo de la marcha para el desarrollo de diversas aplicaciones como tareas de agarre que requieran la compensación de las oscilaciones naturales del movimiento del robot.
La manera en que el robot oscila periódicamente de un lado a otro en el plano transversal, mientras realiza la marcha, sugiere que la trayectoria puede ser aproximada por una sinusoidal o una composición de sinusoidales. Para el análisis, se considera que el eje de la función que describe la trayectoria corresponde a la dirección del desplazamiento del robot , mientras que la amplitud de la misma se describe como , como se muestra en la Figura 1.

|
| Figura 1: Escenario de predicción de la coordenada . |
Para este estudio, el robot siempre es programado para desplazarse en línea recta en dirección del eje ; sin embargo, frecuentemente presenta desviaciones en el eje ocasionadas por los factores ya mencionados. Así, es necesario conocer la dirección real del desplazamiento pues esta define el eje real del dominio del modelo considerado.
Para caracterizar y hacer predicciones sobre la posición y postura del robot en cualquier instante, se busca conocer cual será la ubicación de la cabeza del mismo cuando éste se haya desplazado cierta distancia a lo largo de como se observa en la Figura 1.
3 Preprocesamiento de la trayectoria del robot durante la marcha
La propuesta de solución planteada en este trabajo, consiste en hacer seguimiento de una marca de referencia dispuesta en la cabeza del robot, durante un lapso de tiempo inicial. Así, se obtiene una muestra de la trayectoria durante un intervalo de desplazamiento , como se observa en la Figura 1. Para este efecto, se dispone de una cámara para observar al robot desde una vista superior y realizar un seguimiento visual. Entonces, puesto que se dispone de una secuencia de imágenes, el seguimiento se define mediante coordenadas expresadas en pixeles. Con base en esa muestra, se aplica un método numérico para aproximar la función de dicha trayectoria,
La Figura 1 describe también el escenario experimental de la marcha del robot y el concepto de la oscilación generada por la dinámica natural de la marcha.
Durante el proceso de seguimiento en la marcha, en cada instante de tiempo se captura un fotograma del área dónde se desplaza el robot. Esta imagen es procesada con técnicas de visión por computadora a través de los siguientes pasos:
- Se filtra la imagen capturada para definir los pixeles que corresponden al espectro de color del marcador de la cabeza del robot.
- Se conserva solamente la región que cumpla con las características de tamaño y forma de acuerdo con la marca que se está siguiendo.
- Se determina el centroide de la región de interés
- El centroide se agrega a una lista en donde se van acumulando los puntos obtenidos en cada instante de tiempo.
- Dependiendo de la velocidad de captura, es posible que la trayectoria presente discontinuidades durante el seguimiento. Para evitar esto, se verifica que cada nueva coordenada a agregar sea adyacente al último punto en la lista . Si no lo fuesen, se interpolan en linea recta las coordenadas intermedias necesarias.
Además de este proceso de seguimiento, se necesita detectar el ángulo de desviación de la trayectoria real con respecto al eje para aplicar una transformada de rotación a la curva de la trayectoria con la finalidad de que su eje coincida con el eje . Para esto, se asume que la desviación de la marcha es lineal en el rango de muestreo . Este procedimiento se puede apreciar en la secuencia de imágenes de la Figura 2, en la que a partir de la detección del marcador descrito (2a), se evalúan los puntos necesarios (ver Sección 3.1) para conocer los máximos y mínimos de la función (2b), así como los puntos medios (2c) con el fin de obtener un comportamiento periódico sin desviación (2d) que se someta a una aproximación funcional mediante alguno de los modelos considerados en la Sección 4.
|
|
| (a) Identificación de marcador | (b) Búsqueda de máximo y mínimo |
|
|
| (c) Cálculo de eje y puntos medios | (d) Compensación de desviación |
| Figura 2 | |
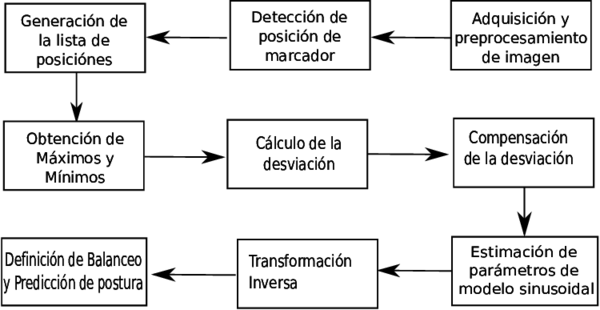
|
| Figura 3: Algoritmo para la estimación de balanceo y predicción de postura de robot. |
3.1 Detección de máximos y mínimos locales
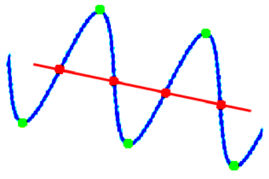
Como se especifica en la Figuras 2 y 3, para identificar el eje de la trayectoria que sigue el robot, se detectan los máximos y mínimos de la curva, asumiendo simetría de los extremos locales con respecto a este eje.
Por el teorema de Rolle se sabe que, si en una función continua se cumple que , entonces existe al menos un extremo local entre y . Nótese que aunque en esta aplicación se dispone de muestras discretas, éstas corresponden a una evolución en el tiempo de la marcha del robot, lo cual claramente describe una función continua. Así, el teorema asegura la existencia de un extremo local en un intervalo donde se verifique la existencia de dos puntos y tales que . Este concepto de detección se muestra en la Figura 4.
Adicionalmente se considera que y deben de ser lo suficientemente cercanos, con , para que exista sólo un extremo local en este intervalo. Para determinar con qué frecuencia se busca un extremo local es necesario tomar en cuenta el periodo de oscilaciones promedio, . Este valor se maneja como un parámetro fijo, ya que depende de la resolución de la cámara, y la cercanía de ésta a el plano del desplazamiento del robot. Se determina haciendo un análisis previo con el que se calcule un promedio de la distancia entre dos máximos locales, identificados manualmente. Así, se puede asumir que dos extremos locales están a, aproximadamente, unidades.
Durante el proceso automático de detección los extremos locales, para cada nueva coordenada,, que se agrega a la lista de la trayectoria, se revisan consecutivamente los puntos anteriores, , con . Si se verifica que la condición del teorema de Rolle se satisface para y algún punto , en el intervalo mencionado, entonces se procede a buscar, entre ambos puntos, un máximo o mínimo, según sea el caso, y este punto se agrega a la lista de extremos locales que se utilizarán para calcular la inclinación del eje de desplazamiento. Una vez que se identifica un extremo local, la búsqueda se suspende por un intervalo de coordenadas, para evitar detectar repetidamente un mismo extremo local.
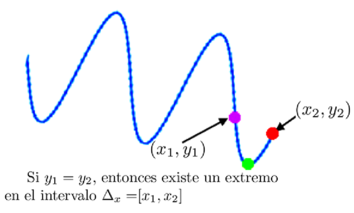
|
| Figura 4: Detección de extremos locales. |
3.2 Transformación para corregir el desvío en la trayectoria
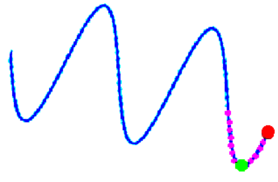
Como se mencionó en la Sección 2, aunque el robot es comandado para seguir una trayectoria recta hacia el frente, éste suele desviarse por razones que no se controlan durante su desplazamiento (vea Fig. 5). Para poder predecir la posición futura, es necesario detectar la desviación de su trayectoria. Ya que se asume que la desviación es lineal a lo largo del intervalo , la compensación de la desviación, se hace mediante la transformación de rotación del vector de datos de la trayectoria real muestreada. De este modo se obtiene una trayectoria como la que se muestra en la Figura 2d, que es objeto del proceso de estimación propuesto, para después ser transformada al contexto real de la trayectoria del robot mediante .

|

|
| (a) Inicio de trayectoria | (b) Desviación de la trayectoria |
| Figura 5 | |
El ángulo de rotación , dados los puntos medios inicial y final de la curva, y respectivamente, se obtiene como,
|
|
De este modo, las coordenadas que se usan para la identificación de parámetros de los modelos sinusoidales, se expresan como,
|
|
|
|
por lo que la estimación real de la posición del robot durante la marcha se calcula con la transformación inversa dada por,
|
|
|
|
3.3 Muestreo
El tamaño de la muestra no está determinado por el número de coordenadas que se ingresan a la trayectoria de seguimiento puesto que éste varia dependiendo de la resolución de la imagen. Por lo tanto la longitud de la muestra se mide en función del número de periodos de oscilación que incluye. La muestra de la trayectoria no puede ser menor a un periodo completo de oscilación, es decir debe contener al menos dos máximos o dos mínimos consecutivos, de lo contrario no podría calcularse el ángulo del eje de desplazamiento.Con una muestra más extensa se pueden obtener dos puntos del eje más alejados entre sí, facilitando un cálculo más acertado del ángulo de desviación del eje de la trayectoria. Se considera como inicio de la muestra el primer máximo que se detecte y la longitud de la muestra se define en función de cuántos máximos contiene. Es importante mencionar que el tamaño de la muestra está relacionado con el intervalo , de tal modo que se debe asegurar que en este intervalo se conserve una desviación lineal de la marcha del robot. El tamaño ideal de la muestra dependerá de las condiciones y objetivos del escenario para el cual se quiere hacer la aproximación del movimiento del robot y/o de predicción de su posición en un instante futuro.
4 Estimación funcional de la trayectoria
Con el preprocesamiento de la información descrita en la Sección 3, se dispone de una señal compensada en relación con la desviación a la marcha del robot. Bajo estas condiciones, se analizan tres técnicas de estimación de parámetros para dos modelos sinusoidales del balanceo durante la marcha del robot, definidos por las ecuaciones (1) y (11).
4.1 Aproximación de parámetros para ajuste sinusoidal
La forma en que el robot se balancea lateralmente en el plano transversal durante la marcha, motiva a un análisis de la trayectoria a través de un ajuste con un modelo sinusoidal de la forma,
|
donde se requiere la estimación de sus parámetros: amplitud , fase y frecuencia , siendo el periodo de la función, definido por la distancia horizontal entre dos máximos locales consecutivos. Además, dado que la lista de puntos se conforma de modo que todas las coordenadas sean consecutivas en la horizontal, entonces el periodo también es el número de puntos de la trayectoria que se encuentran entre dos máximos consecutivos. Si los datos describieran una sinusoide ideal, el periodo tendría una longitud constante, sin embargo en la trayectoria real, este valor puede no ser el mismo en cada ciclo. Por lo tanto, para lograr una aproximación más fiel se calcula esta distancia para todos los máximos disponibles en la muestra y el periodo estimado es el promedio de éstos (ver ecuación (2)), por lo que la frecuencia se aproxima a partir del periodo con la ecuación (3). La amplitud se calcula como la mitad de la distancia entre un máximo y un mínimo consecutivos sobre la perpendicular al eje de la trayectoria y, al igual que el periodo, se aproxima como el promedio de este distancia a lo largo de toda la muestra (ecuación (4)). Por último, el parámetro se calcula como la distancia horizontal entre el primer punto de la muestra, que coincide con el primer máximo registrado, y el primer punto medio que se puede calcular entre un máximo y un mínimo (ecuación (5)). Así, teniendo la lista de máximos, , con pares ordenadas con , donde N es el número de máximos en la muestra. Y teniendo una lista, , de mínimos con , entonces los parámetros de la función sinusoidal están dados por,
|
4.2 Aproximación algebraica de función sinusoidal
Otra técnica que se utiliza en este trabajo es el estimador algebraico de parámetros para la ecuación (1). Esta técnica, presentada por Trapero et al. [12], utiliza la derivada algebraica en el dominio de la frecuencia para obtener una fórmula exacta cuando se convierte al dominio del tiempo. Considerando las definiciones,
|
resultado de la transformada de Laplace de la ecuación (1) para obtener una ecuación algebraica, es posible calcular los parámetros A, y como,
|
|
(9) |
De acuerdo con [12], los parámetros se obtienen en términos de combinaciones lineales de integrales de convolución iteradas sobre los datos de la siguiente forma, donde por simplicidad de notación se define y ,
|
|
(10) |
con,
|
|
donde , y son variables auxiliares para definir cada integración.
4.3 Aproximación de parámetros con series de Fourier
A pesar de que la trayectoria que el robot desarrolla tiene un comportamiento oscilatorio, éste puede ser irregular ya que el balanceo no es totalmente simétrico como puede apreciarse en la Figura 6 para una trayectoria experimental. Esto se debe entre otros factores a variaciones en la superficie sobre la que se desplaza el robot, o bien a un desempeño eficientemente reducido de las articulaciones debido a la fricción o al desgaste de los actuadores. A partir de esta información, se propone utilizar series de Fourier como una técnica de aproximación alterna para describir el balanceo del robot.

|
| Figura 6: Caso de trayectoria real del robot con asimetría con respecto a un eje horizontal. |
Una serie de Fourier [13] es una suma infinita de funciones sinusoidales simples que converge localmente a una función periódica y continua por segmentos. La serie de Fourier tiene la forma,
|
|
(11) |
Donde , y son los coeficientes de Fourier de , definidos como,
|
|
Un aspecto importante a considerar para este enfoque es el tamaño del intervalo de la curva que se quiere aproximar. Por definición, la serie de Fourier aproxima un ciclo de una función periódica, por lo tanto una muestra de mayor longitud podría significar un sobreajuste. Esto sucede porque la trayectoria real del robot no describe un comportamiento necesariamente regular por periodo. En la Sección 5 se describe la forma en que se solventa esta situación.
5 Implementación práctica y resultados
Para el desarrollo de los experimentos, de acuerdo a la Figura 1, se considera una cámara Ethernet Sony Ipela con resolución de 640x480 pixeles a una velocidad de 30fps, colocada a 2m de altura con respecto al marcador en la cabeza del robot en modo estático. El robot, consiste en el humanoide Nao de Aldebaran Robotics. La implementación del método descrito en la Figura 3 se realiza en lenguaje Python en una computadora personal donde se realizan los procesos de cálculo a partir de la información de la cámara obtenida vía ethernet.
5.1 Aproximación sinusoidal con mínimos cuadrados
La sinusoide es una función con dominio continuo, sin embargo los parámetros calculados mediante (2) y (4) se calculan a partir de distancias enteras, ya que se obtienen a partir de valores discretos correspondientes a las coordenadas de los pixeles en la imagen.
Debido a esto, como los cálculos de los parámetros son aproximados, cabe preguntarse si se podría lograr un mejor ajuste en el dominio continuo. Para explorar esta idea, se consideran incrementos de en los intervalos , para los parámetros y respectivamente. En las Figuras 7-10, la curva amarilla representa la trayectoria real, y la curva magenta, describe su aproximación.
En la Figura 7a se muestra la aproximación que se obtiene con el cálculo original de los parámetros, la cual se observa semejante a la curva de la trayectoria. Obsérvese en las Figuras 7c, 7d y 7e que al variar los parámetros del modo indicado, la curva sufre un ajuste. La curva que se muestra en la Figura 7b es aquella de todas las variaciones exploradas que presenta el mínimo error de aproximación. Estos casos se evalúan bajo el criterio de minimización del error de aproximación por mínimos cuadrados de acuerdo a (12), con respecto a la trayectoria real.
|
|
| (a) Aproximación con , sin minimización del error. | (b) Aproximación con error mínimo. , . |

|

|
| (c) Variación: , . | (d) Variación: , . |

| |
| (e) Variación: , . | |
| Figura 7 | |
5.2 Aproximación sinusoidal con estimador algebráico
Los resultados en [12] son reportados muy precisos en intervalos de tiempo cortos, incluso menores a un periodo de la función sinusoidal. Sin embargo el tipo de muestra que utiliza en dicho trabajo es de naturaleza mecánica, diferente a la que se obtiene del seguimiento del robot, que consiste en información visual. Por lo tanto, el proceso de muestreo de la información visual es una aproximación de la marcha continua del robot y su precisión está limitada por la resolución de la imagen, asociada con la localización de la cámara.
Para asegurar que se logre una buena aproximación, se generan sistemáticamente submuestras de la trayectoria. Como se muestra en la Figura 8, el proceso de submuestreo consiste en que, para para una misma trayectoria con diferentes tamaños de muestra (30 y 50 pixeles) e iniciando en diferentes puntos , se obtienen aproximaciones diferentes con sus respectivos parámetros, de los cuales se conservan aquellos de la función con el mínimo error de aproximación .La ventaja de este método es que el cómputo puede hacerse a partir de muestras menores a un periodo de la función. Sin embargo, como se calculan varias integrales numéricas, y suele ser necesario probar con diversas sub-muestras para hallar una estimación que sea una buena aproximación a la curva, el tiempo de computo es mayor comparado con la aproximación de parámetros optimizados por mínimos cuadrados.
5.3 Aproximación por series de Fourier
Para una aproximación por series de Fourier es suficiente un único ciclo periódico, sin embargo al extenderse la trayectoria, ésta no necesariamente estará bien aproximada. Para solventar ésto, se propone utilizar una muestra que contenga varios ciclos. En la Figura 9 se observa una comparación entre estos dos casos. Las líneas verticales indican el inicio (verde) y fin (roja) de la muestra. En las Figuras 9a y 9c, se muestran dos trayectorias desarrolladas por el robot con su correspondiente aproximación de Fourier a través de un sólo ciclo, mientras que en 9b y 9d, se consideran 5 de ellos. Nótese que las trayectorias se pueden extender y distorsionar por lo que se requieren muestras significativas para poder aproximar de manera eficiente. Para construir la serie de Fourier en el segundo caso, se calculan los coeficientes de la ecuación (11) para cada uno de los ciclos y después se obtiene el promedio de éstos.
El periodo de la ecuación (11) se maneja como un parámetro fijo, el cual corresponde a la longitud promedio entre dos máximos locales, calculado experimentalmente.
5.4 Error de aproximación
El error de aproximación mide la exactitud de la función estimada con respecto a la trayectoria real desarrollada por el robot . Si se asume que se caracteriza por coordenadas , entonces el error de aproximación se calcula como:
|
|
(12) |
5.5 Error de predicción al objetivo
Puesto que la aproximación desarrollada está definida localmente en un intervalo , para aplicaciones de predicción de postura o ubicación, es necesario el conocimiento del comportamiento de la aproximación fuera de este intervalo. Para evaluar la efectividad de la aproximación en un punto objetivo fuera del intervalo se quiere predecir cuál será la posición exacta del robot y compararla con la posición real , por lo que se define el error de predicción al objetivo , como,
|
|
(13) |
6 Discusión de resultados
En esta sección se comparan los resultados obtenidos por las técnicas de aproximación descritas. Para medir la eficacia en el ajuste de la estimación a la curva original y para medir la eficiencia de la función estimada para predecir posiciones futuras, se utilizan las definiciones de error de las ecuaciones (12) y (13), respectivamente.
Para evaluar la efectividad de las técnicas de ajuste se han realizado 13 experimentos de marcha del robot bajo las mismas condiciones. Se ha desarrollado el seguimiento de las trayectorias y la aproximación de la curva mediante la estimación de parámetros de una función sinusoidal, de forma algebráica y con mínimos cuadrados, así como mediante la técnica de series de Fourier.
El punto objetivo se ha seleccionado como , medido a partir de la posición inicial del robot. La muestra utilizada para desarrollar la aproximación se ha definido para contener 5 periodos completos en cada experimento.
| Estimador sinusoidal | Estimador algebráico | Series de Fourier | ||||
| 1 | 13.149 | 3.078 | 17.01 | 5.24 | 6.66 | 0.96 |
| 2 | 13.77 | 4.81 | 19.2 | 11.96 | 13.8 | 5.33 |
| 3 | 11.49 | 27 | 10.13 | 22.2 | 7.29 | 6.4 |
| 4 | 16.76 | 21.28 | 8.81 | 17.89 | 8.49 | 12.25 |
| 5 | 19.62 | 39.3 | 17.7 | 36.7 | 8.17 | 0.25 |
| 6 | 20.09 | 29.19 | 20.75 | 43.1 | 7.09 | 3.95 |
| 7 | 7.49 | 10.9 | 14.49 | 29.76 | 5.9 | 2.9 |
| 8 | 6.05 | 1.8 | 8.54 | 10.27 | 7.91 | 10.59 |
| 9 | 14.37 | 27.9 | 6.97 | 10.59 | 8.36 | 5.92 |
| 10 | 9.95 | 13.4 | 9.92 | 18.31 | 5.94 | 1.5 |
| 11 | 16.27 | 2.04 | 2.34 | 8.7 | 7.59 | 1.04 |
| 12 | 16.94 | 8.86 | 14.42 | 6.07 | 8.8 | 8.14 |
| 13 | 5.93 | 2.46 | 8.3 | 12.12 | 10.76 | 0.52 |
A partir de la información obtenida por cada experimento con las tres técnicas de aproximación, se han calculado los errores definidos en las ecuaciones (12) y (13). Estos resultados se muestran en la Tabla 1.
Para cuantificar estadísticamente los resultados de la Tabla 1, se han calculado la media y la desviación estándar para ambos errores en las tres técnicas de aproximación. Estos resultados describen una métrica para verificar la efectividad de cada una y se muestran en la Tabla 2.
| Estimador sinusoidal | Estimador algebráico | Series de Fourier | ||||
| Media | 13.77 | 14.77 | 13.61 | 17.92 | 8.28 | 4.6 |
| D. E. | 4.32 | 12.73 | 4.31 | 11.95 | 1.99 | 3.95 |
De la Tabla 2 se infiere que la técnica que brinda mejores resultados es la de series de Fourier, ya que la desviación estándar DE es menor en ambas métricas de error; esto es, una menor dispersión en los resultados de los experimentos proporciona mayor confianza sobre su capacidad para predecir eficazmente la trayectoria.
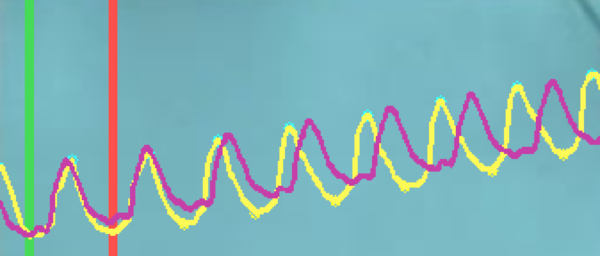
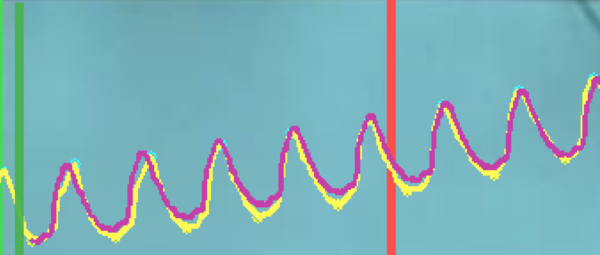
Estos resultados pueden apreciarse en la Figura 10, donde se muestran tres ejemplos en donde se superponen la trayectoria de seguimiento y la curva que se obtiene por el método de estimación indicado. El rectángulo colocado a la distancia objetivo resalta la magnitud del error .
|
| Figura 10: Comparación de tres técnicas de aproximación durante la marcha del robot. |
7 Conclusiones
Este trabajo se ha enfocado en la aproximación de la trayectoria de un robot humanoide mediante la estimación de parámetros de una señal sinusoidal por mínimos cuadrados y algebraicamente; así como la aproximación por series de Fourier. Los resultados obtenidos con cada una de las técnicas son eficaces ya que logran aproximar la trayectoria de marcha del robot, sin embargo cada una requiere de ciertas consideraciones que se exponen enseguida.
El estimador sinusoidal por mínimos cuadrados es la mejor opción sólo si se tiene certeza de que el movimiento oscilatorio del robot durante la marcha describe estrictamente una función sinusoidal. El estimador algebraico sólo se recomienda si se tiene un seguimiento de la trayectoria con una resolución muy alta, de manera que se disponga de una gran cantidad de puntos de muestra para intervalos cortos de una trayectoria de marcha sinusoidal.
Por su parte, la técnica series de Fourier es la que obtiene mejores resultados ya que los indicadores de error son mínimos comparados con las otras técnicas. Sin embargo, para lograr ésto, ésta técnica requiere un número mayor de periodos.
Como paso inmediato a la presente investigación, se considera la implementación de estas técnicas de aproximación para realizar tareas complejas de agarre y manipulación por parte del robot en marcha, permitiendo al robot el desarrollo de tareas domésticas de una forma más eficiente. Adicionalmente, se considera la sustitución del sistema sensorial de posición, por un sistema de visión montado en el mismo robot, o bien mediante la implementación de sensores inerciales. Esto permitirá el desarrollo de experimentos fuera de un ambiente de laboratorio.
Referencias
BIBLIOGRAFÍA
[1] Garcia, Mariano and Chatterjee, Anindya and Ruina, Andy and Coleman, Michael and others. (1998) "The simplest walking model: stability, complexity, and scaling", Volume 120. J Biomech Eng Trans ASME 2 281–288
[2] McGeer, Tad and others. (1990) "Passive dynamic walking", Volume 9. I. J. Robotic Res. 2 62–82
[3] Collins, Steven H and Wisse, Martijn and Ruina, Andy. (2001) "A three-dimensional passive-dynamic walking robot with two legs and knees", Volume 20. SAGE Publications. The International Journal of Robotics Research 7 607–615
[4] Kuo, Arthur D. (2007) "The six determinants of gait and the inverted pendulum analogy: A dynamic walking perspective", Volume 26. Elsevier. Human movement science 4 617–656
[5] Kajita, Shuuji and Kanehiro, Fumio and Kaneko, Kenji and Fujiwara, Kiyoshi and Harada, Kensuke and Yokoi, Kazuhito and Hirukawa, Hirohisa. (2003) "Biped walking pattern generation by using preview control of zero-moment point", Volume 2. IEEE. Robotics and Automation, 2003. Proceedings. ICRA'03. IEEE International Conference on 1620–1626
[6] Huang, Qiang and Yokoi, Kazuhito and Kajita, Shuuji and Kaneko, Kenji and Arai, Hirohiko and Koyachi, Noriho and Tanie, Kazuo. (2001) "Planning walking patterns for a biped robot", Volume 17. IEEE. IEEE Transactions on robotics and automation 3 280–289
[7] Buschmann, Thomas and Lohmeier, Sebastian and Bachmayer, Mathias and Ulbrich, Heinz and Pfeiffer, Friedrich. (2007) "A collocation method for real-time walking pattern generation". IEEE. Humanoid Robots, 2007 7th IEEE-RAS International Conference on 1–6
[8] Harada, Kensuke and Kajita, Shuuji and Kaneko, Kenji and Hirukawa, Hirohisa. (2006) "An analytical method for real-time gait planning for humanoid robots", Volume 3. World Scientific. International Journal of Humanoid Robotics 01 1–19
[9] Kagami, Satoshi and Kitagawa, Tomonobu and Nishiwaki, Koichi and Sugihara, Tomomichi and Inaba, Masayuki and Inoue, Hirochika. (2002) "A fast dynamically equilibrated walking trajectory generation method of humanoid robot", Volume 12. Springer. Autonomous Robots 1 71–82
[10] Dune, Claire and Herdt, Andrei and Stasse, Olivier and Wieber, P-B and Yokoi, Kazuhito and Yoshida, Eiichi. (2010) "Cancelling the sway motion of dynamic walking in visual servoing". IEEE. Intelligent Robots and Systems (IROS), 2010 IEEE/RSJ International Conference on 3175–3180
[11] Graf, Colin and Röfer, Thomas. (2011) "A center of mass observing 3D-LIPM gait for the RoboCup Standard Platform League humanoid". Springer. Robot Soccer World Cup 102–113
[12] Trapero, Juan R and Sira-Ramirez, Hebertt and Batlle, Vicente Feliu. (2007) "An algebraic frequency estimator for a biased and noisy sinusoidal signal", Volume 87. Elsevier. Signal Processing 6 1188–1201
[13] Dym, H McKean and others. (1972) "Fourier series and integrals"
Document information
Published on 18/03/19
Accepted on 10/03/19
Submitted on 01/08/18
Volume 35, Issue 1, 2019
DOI: 10.23967/j.rimni.2019.03.002
Licence: CC BY-NC-SA license
![Inicio en x[0]; tamaño de la muestra, 30 pixeles. Parámetros obtenidos A=20.87, ω=0.156](/wd/images/thumb/1/10/Review_115750068379-algebraic_ex1.png/600px-Review_115750068379-algebraic_ex1.png)
![Inicio en x[5]; tamaño de la muestra, 30 pixeles. Parámetros obtenidos A=19.98, ω=0.160](/wd/images/thumb/6/6b/Review_115750068379-algebraic_ex2.png/600px-Review_115750068379-algebraic_ex2.png)
![Inicio en x[10]; tamaño de la muestra, 30 pixeles. Parámetros obtenidos A=25.33, ω=0.138](/wd/images/thumb/a/ab/Review_115750068379-algebraic_ex3.png/600px-Review_115750068379-algebraic_ex3.png)
![Inicio en x[0]; tamaño de la muestra, 50 pixeles. Parámetros obtenidos A=16.2, ω=0.170](/wd/images/thumb/d/de/Review_115750068379-algebraic_ex4.png/600px-Review_115750068379-algebraic_ex4.png)
![Inicio en x[5]; tamaño de la muestra, 50 pixeles. Parámetros obtenidos A=19.35, ω=0.150](/wd/images/thumb/5/58/Review_115750068379-algebraic_ex5.png/600px-Review_115750068379-algebraic_ex5.png)
![Inicio en x[10]; tamaño de la muestra, 50 pixeles. Parámetros obtenidos A=18.83, ω=0.156](/wd/images/thumb/1/11/Review_115750068379-algebraic_ex6.png/600px-Review_115750068379-algebraic_ex6.png)