m (Cmillan moved page Draft Millan 345648887 to Review Millan 2018a) |
|||
| Line 140: | Line 140: | ||
Generar solución inicial ( <math display="inline">S</math>) elegida en la etapa de exploración preliminar ec. (2) | Generar solución inicial ( <math display="inline">S</math>) elegida en la etapa de exploración preliminar ec. (2) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <math>{T=T}_{initial}</math> | ||
Mientras ( <math display="inline">{T>T}_{final}</math>) //Ciclo de temperatura | Mientras ( <math display="inline">{T>T}_{final}</math>) //Ciclo de temperatura | ||
| − | Para <math display="inline">np=1</math> a <math display="inline">{np}_{max}</math> | + | : Para <math display="inline">np=1</math> a <math display="inline">{np}_{max}</math> |
| − | Generar <math display="inline">S'</math> por paso de búsqueda ec. (3) | + | :: Generar <math display="inline">S'</math> por paso de búsqueda ec. (3) |
| − | Obtener la diferencia <math display="inline">\left( \Delta f\right)</math> entre funciones objetivos evaluadas en <math display="inline">S'</math> y <math display="inline">S</math> | + | ::Obtener la diferencia <math display="inline">\left( \Delta f\right)</math> entre funciones objetivos evaluadas en <math display="inline">S'</math> y <math display="inline">S</math> |
| − | Si ( <math display="inline">\left( \Delta f\right)</math> ≤ 0) luego | + | ::Si ( <math display="inline">\left( \Delta f\right)</math> ≤ 0) luego |
| − | Aceptar <math display="inline">S'</math> | + | :::Aceptar <math display="inline">S'</math> |
| − | Si no | + | ::Si no |
| − | <math display="inline">P=1/(1+e((\Delta | + | :::<math display="inline">P=1/(1+e((\Delta f/T)\, )\, )</math> ec. (4) |
| − | Si (rand(0, 1)<P) entonces | + | :::Si (rand(0, 1)<math display="inline"><</math>P) entonces |
| − | Aceptar <math display="inline">S'</math> | + | ::::Aceptar <math display="inline">S'</math> |
| − | Fin Si | + | :::Fin Si |
| − | Fin Si | + | ::Fin Si |
| − | Fin Para | + | :Fin Para |
| − | Disminuir <math display="inline">T</math> mediante función de enfriamiento <math display="inline">{T}_{k+1}=</math><math>{T}_{k}\cdot \alpha</math> | + | :Disminuir <math display="inline">T</math> mediante función de enfriamiento <math display="inline">{T}_{k+1}=</math><math>{T}_{k}\cdot \alpha</math> |
Fin Mientras | Fin Mientras | ||
Revision as of 08:47, 3 April 2018
Abstract
Structural optimization aims to design structures under certain constraints to achieve better behavior and have a proper manufacturing cost. This type of optimization corresponds to highly non-linear and non-convex problems including several local optima. Therefore, to solve such problems effectively, designers need to use adequate optimization methods which can make a good balance between the computational cost and the quality of solutions. In this paper the modified simulated annealing algorithm (MSAA) is employed to solve optimal design of steel structures. MSSA is a newly improved version of the simulated annealing (SA) algorithm with three modifications: preliminary exploration, search step and a new probability of acceptance. The performance, robustness and applicability of the MSAA are demonstrated through six structural optimization problems. Obtained results in all considered examples indicate that the MSAA is superior to several other methods in existing literature in terms of the quality of solution and convergence speed.
Keywords: Modified simulated annealing algorithm (MSAA); structural optimization; optimal design; steel structures.
1. Introducción
La optimización estructural se ha convertido en una de las ramas más activas de la ingeniería estructural en la última década. En este tipo de optimización, el número de variables de diseño, el tamaño del área de búsqueda y el número de restricciones son factores que influyen en el tiempo que los diseñadores necesitan para encontrar diseños optimizados. Además, es un problema no convexo, debido a la naturaleza no convexa de la función objetivo y a la geometría compleja del dominio factible conformado por las restricciones de diseño [1]. Debido a esto, los algoritmos metaheurísticos se han convertido en una herramienta poderosa para resolver estos problemas de optimización complejos. Estos métodos no requieren información de gradiente de la función objetivo y son independientes del punto de partida. Gracias a sus capacidades de búsqueda global, estos algoritmos son adecuados para espacios de búsqueda complejos, no lineales y no convexos, especialmente cuando se buscan soluciones óptimas casi globales después de usar un esfuerzo computacional limitado.
El principal inconveniente de los algoritmos más antiguos, como los algoritmos genéticos simples (GA) [2] o el recocido simulado básico (SA) [3] es la tasa de convergencia lenta y el alto costo computacional. Algoritmos más recientes como: optimización del enjambre de partículas (PSO) [4], optimización de colonias de hormigas (ACO) [5], búsqueda de tabu (TS) [6], búsqueda de armonía (HS) [7] y big bang-big crunch (BB-BC) [8] son generalmente más rápidos, pero aún sufren la posibilidad de quedar atrapados en algún optima local. En general, se necesitan algoritmos metaheurísticos más potentes para resolver problemas complicados de optimización. En los últimos años, se han dedicado muchos esfuerzos para aumentar la velocidad y robustez del proceso de optimización. Con este fin, algunos investigadores han trabajado para mejorar los algoritmos existentes superando algunos de sus inconvenientes, otros han obtenido algoritmos más potentes hibridando dos o más de los algoritmos existentes combinando sus características fuertes y complementarias y algunos investigadores han trabajado en el desarrollo de nuevos algoritmos metaheurísticos basados en otros fenómenos naturales o físicos. Una revisión del estado del arte sobre nuevos enfoques de optimización metaheurísticos se encuentra disponible en las referencias [9,10].
Diferentes algoritmos diferentes se han utilizado para el diseño óptimo de estructuras de acero. Por ejemplo, para optimizar armaduras de acero Lamberti [11] utilizó CMLPSA (Corrected Multi-Level & Multi-Point Simulated Annealing); Hasançebi et al. [12] emplearon PSO (particle swarm optimization); Degertekin [13] usó EHS (efficient harmony search) y SAHS (self adaptive harmony search algorithm); Sadollah. et al. [14] utilizaron MBA (mine blast algorithm); Kaveh et al. [15,16] aplicaron CBO (colliding bodies optimization) y IMCSS (improved magnetic charged system search); Ho-Huu et al. [17,18] emplearon D-ICDE (improved constrained differential evolution using discrete variables) y aeDE (adaptive elitist differential evolution); y Do y Lee [19] utilizaron mSOS (modified symbiotic organisms search). En cuanto a la optimización de pórticos metálicos, Kaveh and Talatahari [20,21] empleraon ICA (imperialist competitive algorithm) y CSS (charged system search); Kazemzadeh et al. [22] utilizaron BB-BC (big bang–big crunch); Maheri y Narimani [23] aplicaron EHS (enhanced harmony search); Gholizadeh y Poorhoseini [24] usaron DEA (Dolphin Echolocation Algorithm); Kaveh and Bakhshpoori [25,26] usaron CSA (Cuckoo Search Algorithm) and AWEO (accelerated water evaporation optimization); y Maheri y Talezadeh [27] aplicaron EICA (enhanced imperialist competitive algorithm). En todos estos trabajos, el peso de estas estructuras debe minimizarse sujeto a restricciones de esfuerzos, estabilidad y desplazamiento. Esta tarea de optimización es, en general, difícil de resolver debido a la no linealidad de las restricciones y a las regiones factibles no convexas.
En este estudio, el algoritmo de optimización recientemente desarrollado llamado Algoritmo Simulated Annealing Modificado (ASAM) introducido por Millán et al. [28,29], es empleado en el diseño óptimo de estructuras de acero. El desempeño de ASAM es evaluado mediante seis problemas numéricos de referencia (4 armaduras y 2 pórticos metálicos) y los resultados obtenidos son comparados con los resultados reportados por otros algoritmos de la literatura. El resto del documento está organizado de la siguiente manera. La descripción del problema de optimización estructural se presenta en la Sección 2. La Sección 3 describe la ASAM en detalle. La Sección 4 presenta los seis ejemplos numéricos de referencia para ilustrar la efectividad y la robustez de ASAM. Finalmente, la Sección 5 termina con las conclusiones.
2. Descripción del problema de optimización
En este estudio, el objetivo es minimizar el peso de la estructura a la vez que se satisfacen algunas limitaciones de resistencia y desplazamiento. La formulación matemática de estos problemas se puede expresar de la siguiente manera:
|
|
(1) |
Donde es el vector que contiene las variables de diseño; es el número de variables de diseño; es el peso de la estructura; el numero de elementos de la estructura; , y denotan la densidad del material, el área de la sección transversal y la longitud del elemento i, respectivamente. y son los limites inferior y superior de la variable de diseño , respectivamente. denota las restricciones de diseño y el numer de restricciones.
3. Algoritmo simulated annealing modificado (ASAM)
Antes de resumir las características del ASAM, se describe brevemente el funcionamiento del simulated annealing básico (SA). SA [3] se ha desarrollado a partir de la termodinámica estadística para simular el comportamiento de los arreglos atómicos en materiales líquidos o sólidos durante el proceso de enfriamiento. El material alcanza el nivel de energía más bajo (condición globalmente estable) a medida que la temperatura disminuye. SA incluye una estrategia de optimización bastante simple. Un punto de prueba se genera aleatoriamente y la función objetivo del problema se evalúan en ese punto. Si el punto no es factible, se rechaza y se evalúa un nuevo punto de prueba . Si el punto de prueba es factible y la función objetivo es menor que el mejor registro actual, entonces se acepta el punto y se actualiza el mejor registro [11]. Si el punto de prueba es factible pero la función objetivo es más alta que el mejor valor, entonces el punto es aceptado o rechazado según un criterio probabilístico que estima si el diseño puede mejorar en las siguientes evaluaciones de funciones. La probabilidad depende de la diferencia de las funciones objetivos y de un parámetro llamado temperatura . Inicialmente, con valores grandes de , frecuentemente se aceptan soluciones con un mayor valor de función objetivo; a medida que el valor de disminuye, tal tipo de soluciones raramente se aceptan, y cuando se acerca a cero, solo se aceptan aquellas soluciones que mejoran la anterior.
Cuando se tienen funciones altamente modales y no convexas, la generación de los puntos de pruebas (aleatoriamente) generan al algoritmo mayores tiempos de búsqueda y un alto costo computacional. Además, la probabilidad de aceptación de una solución peor se encuentra en un intervalo de entre 0 y 1, lo cual causa que a temperaturas iniciales el algoritmo acepte un gran número de soluciones de peor calidad, aumentando el riesgo de quedar atrapado en un óptimo local y que el algoritmo tenga una tasa lenta de convergencia.
EL ASAM propuesto por Millán et al. [28] tiene tres modificaciones que permiten al algoritmo tener un equilibrio entre la intensificación y la diversificación.. En primer lugar, se realiza una exploración preliminar para generar el punto de inicio de la búsqueda. Luego, la transición desde el punto de inicio al nuevo punto se realiza por un paso de búsqueda. Por último, se reduce el rango de probabilidad de aceptar una peor solución.
3.1. Exploración preliminar
En esta etapa el algoritmo realiza una exploración en todo el espacio de búsqueda que viene dada por la siguiente matriz:
|
|
(2) |
donde es el número de puntos (estados) que se desean en el espacio de búsqueda; es el número de dimensiones del problema; es una matriz identidad de tamaño ; es el límite inferior del problema; es el límite superior del problema y es una matriz de números aleatorios (aleatoriedad pura) entre 0 y 1. Para comenzar el proceso de optimización con ASAM se evalúan todos los puntos generados con la ec. (2) mediante la función objetivo del problema y se escoge el que tenga menor valor (en el caso de estar buscando el valor mínimo de la función) como punto inicial de la búsqueda.
3.2. Paso de búsqueda
Desde el punto de partida determinado en el paso de exploración preliminar, se genera un paso de búsqueda para determinar el estado vecino. Este paso depende de un radio (R) de acción que disminuye gradualmente a medida que disminuye la temperatura del sistema. La transición desde el punto de inicio al nuevo punto (paso de búsqueda) se realiza mediante la adición de números aleatorios que están entre [-R, R]. Esto permite que el algoritmo ejecute una exploración global a altas temperaturas y una exploración local a bajas temperaturas, proporcionando un equilibrio entre la exploración y la explotación del algoritmo. El radio se actualiza de la siguiente manera:
|
|
(3) |
donde, es el radio inicial ciclo y el coeficiente de reducción del radio.
3.3. Probabilidad de aceptación
En el ASAM, la probabilidad de aceptar una peor solución está dada por:
|
|
(4) |
donde es la probabilidad de aceptar el nuevo estado; la diferencia de las evaluaciones de la función para cada estado; temperatura del sistema y número de Euler. Esta probabilidad se encuentra en un intervalo entre 0 y ½, lo que permite al algoritmo tener un rango menor de aceptación de peores soluciones.
En resumen, las 3 modificaciones permiten al algoritmo mejorar la exploración inicial, permitir un balance entre exploración inicial y final y controlar la convergencia en la etapa final de búsqueda. El pseudocódigo de ASAM es el siguiente:
Establecer temperatura inicial ( )
Establecer temperatura final ( )
Establecer número máximo de perturbaciones para cada ciclo de temperatura
Generar solución inicial ( ) elegida en la etapa de exploración preliminar ec. (2)
Mientras ( ) //Ciclo de temperatura
- Para a
- Generar por paso de búsqueda ec. (3)
- Obtener la diferencia entre funciones objetivos evaluadas en y
- Si ( ≤ 0) luego
- Aceptar
- Si no
- ec. (4)
- Si (rand(0, 1)P) entonces
- Aceptar
- Fin Si
- Fin Si
- Fin Para
- Disminuir mediante función de enfriamiento
Fin Mientras
Mostrar mejor solución ( )
4. Problemas numéricos
En esta sección, seis ejemplos de referencias de optimización estructural son empleados para investigar el rendimiento de ASAM. Cuatro ejemplos son sobre optimización de armaduras y los otros sobre optimización pórticos. Las propiedades del material, los límites de las variables de diseño y las restricciones estructurales cada problema se presentan en cada descripción del problema. Cada problema de referencia se ejecutó de forma independiente 100 veces. El algoritmo fue codificado en Matlab y las estructuras fueron analizadas usando el método de la rigidez directa.
Los resultados numéricos indicaron que una población de 100 (exploración preliminar); temperatura inicial Tinicial=1; temperatura final Tfinal=1x10-3; número máximo de perturbaciones npmax=125 (para el quinto problema npmax=280); función de enfriamiento Tk+1=Tk·α; coeficiente de reducción de temperatura α=0.8; and paso de búsqueda R=8; son adecuados para proporcionar buenos resultados. ASAM finaliza su proceso de búsqueda cuando la temperatura (T) es menor que la temperatura final (Tfinal). Es importante tener en cuenta que todos los diseños obtenidos por ASAM son factibles.
4.1. Estructura plana de 52 barras
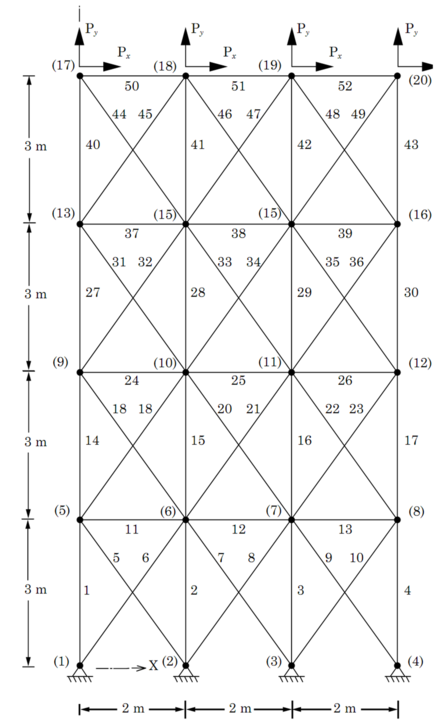
La geometría de la armadura plana de 52 barras se muestra en la Fig. 1. Los elementos de la armadura son divididos en 12 grupos de la siguiente manera: (1) A1-A4, (2) A5-A10, (3) A11-A13, (4) A14-A17, (5) A18-A23, (6) A24-A26, (7) A27-A30, (8) A31-A36, (9) A37-A39, (10) A40-A43, (11) A44-A49, y (12) A50-A52. La densidad del material es 7860.0 kg/m3 y el módulo de elasticidad es 207 GPa. Los máximos esfuerzo permisible para todos los miembros en términos de tensión y compresión es de 180 MPa. Los nodos superiores (17, 18, 19 y 20) de la estructura están cargados en ambas direcciones con PX=100 kN y PY=200 kN. Los valores discretos de las secciones transversales son seleccionados del código de diseño AISC (American Institute of Steel Construction) como se muestra en la Tabla 1.
Figura 1. Armadura plana de 52 barras
Tabla 1. Áreas transversales disponibles del código de diseño AISC
La Tabla 2 presenta los resultados de ASAM comparados con otros diseños publicados tales como HHS [30], MBA [14], aeDE [18] y IMCSS [16]. Se puede observar que todos los métodos obtienen el mismo peso óptimo de 1902.61 kg, pero el ASAM requiere menos números de iteraciones que HHS, MBA y IMCSS (5000 análisis para el HHS, y 5450 análisis para el MBA) para converger a la solución óptima. También se aprecia que la velocidad de convergencia del aeDE es más rápida que la del ASAM (3720 análisis para aeDE), pero el ASAM es más estable que el aeDE con un mejor valor de desviación estándar (0.52 lb para ASAM y 6.68 lb para aeDE). La Fig. 2 muestra la curva de convergencia del mejor resultado obtenido por ASAM para la armadura plana de 52 barras.
Tabla 2. Comparación de diseños óptimos para la armadura plana de 52 barras.
Figura 2. Curva de convergencia del mejor resultado para la armadura plana de 52 barras.
4.2. Armadura plana de 200 barras
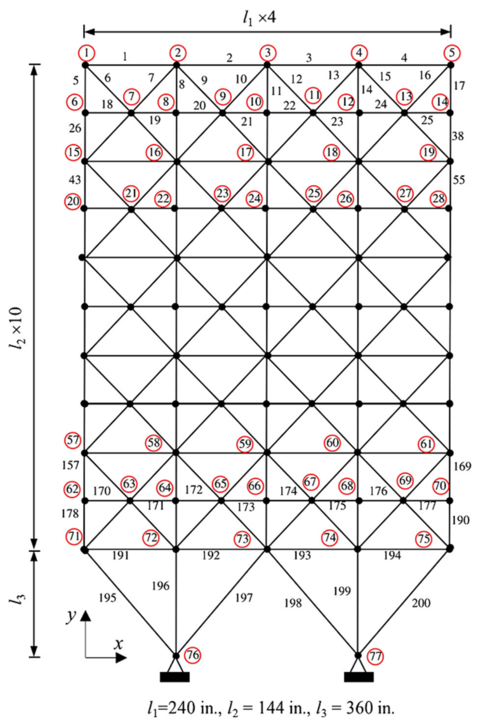
El segundo problema se refiere a la estructura plana de 200 barras que se muestra en la Fig. 3. El módulo de elasticidad y la densidad del material son 30 psi y 0.238 lb7in3, respectivamente. Los esfuerzos a tensión y a compresión no pueden exceder los 10 ksi. La estructura está sujeta a 3 condiciones de cargas de la siguiente manera: (1) 1 kip actuando en la dirección positiva del eje x en los nodos 1, 6, 15, 20, 29, 34, 43, 48, 57, 62 y 71; (1) 10 kips actuando en la dirección negativa del eje y en los nodos 1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 15, 16, 17, 18, 19, 20, 22, 24, 26, 28, 29, 30, 31, 32, 33, 34, 36, 38, 40, 42, 43, 44, 45, 46, 47, 48, 50, 52, 54, 56, 58, 59, 60, 61, 62, 64, 66, 68, 70, 71, 72, 73, 74 y 75; (3) condiciones 1 y 2 actuando al mismo tiempo. Esta estructura incluye 29 variables de diseño correspondientes a 29 grupos de elementos cuyos valores se eligen de la siguiente lista disponible: S={0.1, 0.347, 0.44, 0.539, 0.954, 1.081, 1.174, 1.333, 1.488, 1.764, 2.142, 2.697, 2.8, 3.131, 3.565, 3.813, 4.805, 5.952, 6.572, 7.192, 8.525, 9.3, 10.85, 3.131, 3.565, 4.805, 5.952, 6.572, 7.192, 8.525, 9.3, 10.85, 13.33, 14.29, 17.17, 19.18, 23.68, 28.08, 33.7} (in2).
Figura 3. Armadura plana de 200 barras
La Tabla 3 muestra las soluciones óptimas obtenidas por el ASAM y otros enfoques de la literatura, tales como el HACOHS-T [31], ESASS [32], HHS [30] y aeDE [18]. En este caso, el mejor diseño adquirido por ASAM (27190.49 lb) es mejor que otros métodos (28030.2 lb para el HACOHS-T, 28075.49 lb para el ESASS y 27858.50 lb para el aeDE). Además, ASAM requiere menos análisis que HACOHS-T, ESASS, HHS y aeDE (20000 análisis para HACOHS-T, 11156 análisis para ESASS, 5000 análisis para HHS y 12325 para aeDE). Finalmente, el ASAM es más estable que el aeDE y el HHS con la desviación estándar más pequeña (481.59 lb para el aeDE, 1149.91 lb para el HHS y 198.35 lb para el ASAM). La Fig. 4 muestra la curva de convergencia del mejor resultado obtenido por ASAM para la armadura plana de 200 barras.
Tabla 3. Comparación de diseños óptimos para la armadura plana de 200 barras
Figura 4. Curva de convergencia del mejor resultado para la armadura plana de 200 barras.
4.3. Armadura espacial de 72 barras
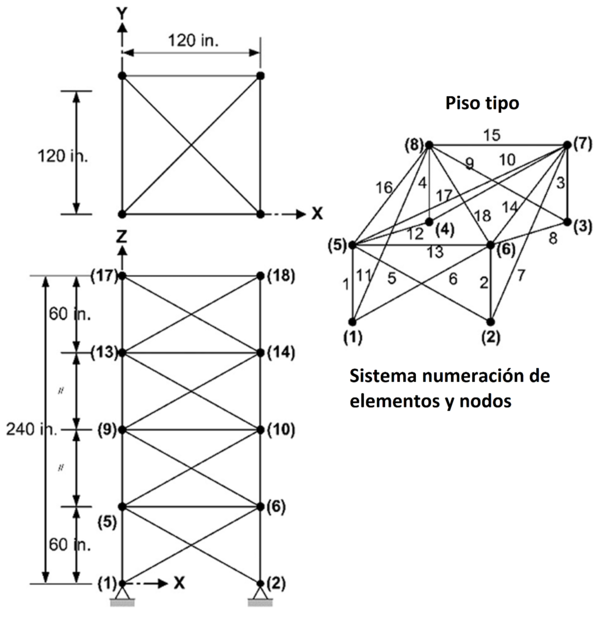
La Fig. 5 muestra la armadura espacial de 72 barras. Las propiedades del material son los siguientes: la densidad del material es 1.1 lb/in3 y módulo de elasticidad de 10Msi. Los esfuerzos en los elementos no pueden exceder los 25000 psi tanto a tensión como a compresión. Los desplazamientos nodales deben ser menores a ±0.25 in. La estructura fue diseñada para la condición de carga según Kaveh y Ghazaan [33]. Los 72 elementos de la armadura están categorizados simétricamente en 16 grupos: A1–A4, (2) A5–A12, (3) A13–A16, (4) A17–A18, (5) A19–A22, (6) A23–A30, (7) A31–A34, (8) A35–A36, (9) A37–A40, (10) A41–A48, (11) A49–A52, (12) A53–A54, (13) A55–A58, (14) A59–A66 (15), A67–A70, and (16) A71–A72. Las variables de diseño son seleccionadas de la Tabla 1.
Figura 5. Armadura espacial de 72 barras
La Tabla 4 compara los resultados obtenidos con ASAM y otros métodos de optimización como el MBA [14], aeDE [18], CBO [34] y ECBO [33]. El peso óptimo logrado por el ASAM (389.33 lb) concuerda con los dados por el ECBO y el aeDE, pero mejor que los reportados por el MBA y el CBO (390.73 lb para el MBA y 391.07 lb para el CBO). Por otro lado, ASAM solo requiere 4290 análisis para converger la solución óptima, mientras que el ECBO necesita 17010 análisis. Aunque la velocidad de convergencia del aeDE (4160 análisis) es más rápida que la de ASAM, este es más estable que el aeDE ya que consigue una desviación estándar más pequeña (0.76 lb para ASAM y 1.16 lb para aeDE). La Fig. 6 muestra la curva de convergencia del mejor resultado obtenido por ASAM para la armadura espacial de 72 barras.
Tabla 4. Comparación de diseños óptimos para la armadura espacial de 72 barras.
Figura 6. Curva de convergencia del mejor resultado para la armadura espacial de 72 barras.
4.4. Torre espacial de 582 barras
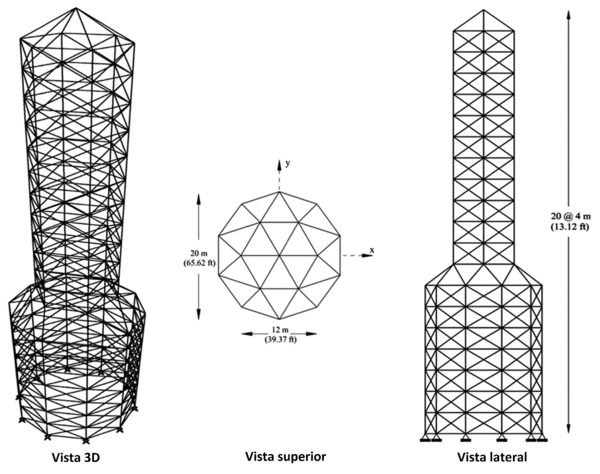
La torre de 582 barras mostrada en la Fig. 7 es optimizada para minimizar su volumen. Los 582 miembros son divididos en 32 grupos debido a la simetría estructural. Las áreas de los elementos son seleccionadas de la lista estándar de perfiles W en función del área y radio de giro. Dichas áreas pueden variar entre 6.16 y 215 in2. La torre está cargada en todos los nodos de la siguiente manera: una carga lateral en las direcciones x y y de 1.12 kips y una carga vertical en la dirección z de -6.74 kips. Las limitaciones de esfuerzo y estabilidad de los elementos de la armadura se imponen de acuerdo a la ASD-AISC [35] de la siguiente manera:
Figura 7. Torre espacial de 582 barras.
Los esfuerzos admisibles para los miembros sometidos a tensión se calculan mediante
|
|
(5) |
donde es el límite de fluencia.
Los límites de esfuerzo admisible para miembros de compresión se calculan en función de dos posibles modos de fallo conocidos como pandeo elástico e inelástico. Así
|
|
(6) |
donde es el modulo de elasticidad; es la relación de esbeltez ; denota la relación de esbeltez que divide las regiones de pandeo elástico e inelástico ; es el factor de longitud efectiva ( se estableció valor de 1 para todos los elementos); es la longitud del elemento; es el radio de giro mínimo. En el código de diseño ASD-AISC [35], la relación de esbeltez máxima está limitada a 300 para miembros de tensión, y se recomienda que sea 200 para miembros de compresión. Los desplazamientos nodales en todas las direcciones no deben exceder ±3.15 in.
La Tabla 5 presenta los resultados obtenidos por ASAM, DHPSACO [36], HBB-BC [37], CBO [38] y ECBO [38]. Se puede ver el peso encontrados por ASAM (1302038 in3) es mejor que los reportados por otros métodos (1346227 in3 para DHPSACO, 1365143 in3 para HBB-BC y 1334994 in3 para CBO). Aunque el volumen obtenido por el ECBO (1296776 in3) es más ligero que el de ASAM, ASAM es más estable con una desviación estándar más pequeña (6581 in3 para el ASAM y 7536 in3 para el ECBO) y con una velocidad de convergencia más rápida (9240 análisis para ASAM y 19700 análisis para ECBO). Está claro que ASAM es efectiva y robusto en el tratamiento de problemas con un gran número de variables de diseño, logrando soluciones de alta calidad con una reducción significativa del costo computacional. La Fig. 8 muestra la curva de convergencia del mejor resultado obtenido por ASAM para la torre espacial de 582 barras
Tabla 5. Comparación de diseños óptimos para la torre espacial de 582 barras.
Figura 8. Curva de convergencia del mejor resultado para la torre espacial de 582 barras.
4.5. Pórtico de 3 vanos y 15 pisos
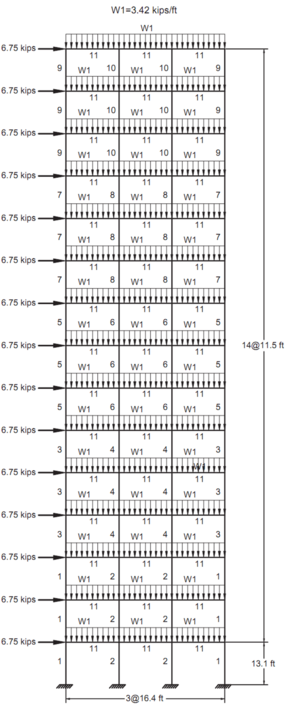
La Fig. 9 muestra la configuración del pórtico, las cargas aplicadas y la numeración de los grupos de diseño. El módulo de elasticidad del material E es 29 Msi y un límite de fluencia de 36 ksi. Los factores de longitud efectiva de los miembros se evaluaron con ≥0 y =1.0. Cada columna se considera como no arriostrada a lo largo de su altura. Además, la longitud no arriostrada para cada miembro de viga se especifica como una quinta parte de la longitud del vano. La deriva del piso superior no puede exceder los 9.25 in.
Figura 9. Pórtico de 3 vanos y 15 pisos.
Las limitaciones de desplazamiento y resistencia se imponen de acuerdo con las disposiciones del AISC [39] de la siguiente manera:
(a) Máximo desplazamiento lateral
|
|
(7) |
donde es el máximo desplazamiento lateral; es la altura del pórtico; es el índice de deriva máxima que es igual a 1/300.
(b) Desplazamiento entre pisos
|
|
(8) |
Donde es la deriva entre pisos; es la altura entre piso del piso i; es el número total de pisos; es el índice de deriva entre pisos (1/300).
(c) Restricciones de resistencia
|
|
(9) |
Donde es la resistencia requerida (tensión o compresión); es la resistencia nominal axial (tensión o compresión); es el factor de resistencia ( = 0.9 para tensión, = 0.85 para compresión); es la resistencia requerida a flexión; es la resistencia nominal a flexión; es el factor de resistencia a flexión ( = 0.90). La resistencia nominal a tensión en la sección bruta se calcula mediante
|
|
(10) |
La resistencia nominal a compresión de un elemento se calcula por
|
|
(11) |
|
|
(12) |
donde es el area de la sección transversal del elemento y es el factor de longitud efectiva que se calcula mediante
|
|
(13) |
donde y son las relaciones de rigidez de columnas y vigas en las uniones, A y B, de la sección de columna que se considera.
Los resultados obtenidos por HBB-BC [37], ICA [20], CSS [21], CBO [33], EICA [27] y ASAM son comparados en la Tabla 6. En este caso, ASAM obtuvo el peso más bajo, 88651 lb. Además, requirió de menos número de análisis que HBB-BC, ICA, CSS y CBO (9900 análisis para el HBB-BC, 6000 análisis para el ICA, 5000 análisis para el CSS and 9520 análisis para el CBO) para converger al óptimo. Pese a que el EICA converge más rápido (3300 análisis) que ASAM, ASAM es más estable presentando una desviación estándar más pequeña (852 lb para ASAM y 899 lb para EICA). La Fig. 10 muestra la curva de convergencia del mejor resultado obtenido por ASAM para el pórtico de 3 vanos y 15 pisos.
Tabla 6. Comparación de diseños óptimos para el pórtico de 3 vanos y 15 pisos.
Figura 10. Curva de convergencia del mejor resultado para el pórtico de 3 vanos y 15 pisos.
4.6. Pórtico de 3 vanos y 24 pisos
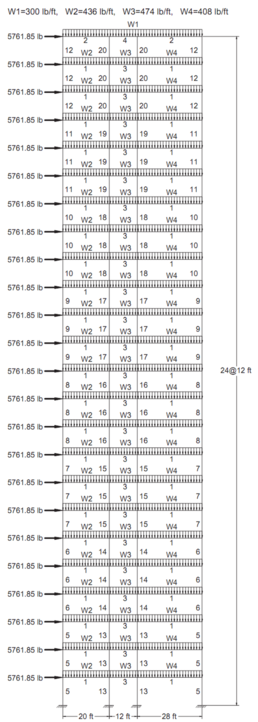
La Fig. 11 muestra el esquema del pórtico de 3 vanos y 24 pisos. Los elementos del pórtico están categorizados en 20 grupos (16 grupos de columna y 4 grupos de vigas). Las áreas de los grupos compuesto por vigas son escogidas de la lista estándar de perfiles W, mientras que los de las columnas están limitados a las secciones W14. Similar al ejemplo anterior, la estructura fue diseñada en base a las especificaciones AISC-LRFD [39] y una restricción de deriva de entre pisos de 1/300 de la altura del piso. El material tiene un módulo de elasticidad (E) de 29.732 Msi y límite de fluencia ( ) de 33.4 ksi. Los factores de longitud efectiva de los miembros se evaluaron con ≥0 y =1.0. Todas las columnas y vigas se consideran no arriostradas a lo largo de sus longitudes.
Figura 11. Pórtico de 3 vanos y 24 pisos.
Los resultados óptimos obtenidos con ASAM y el ICA [20], CSS [21], CBO [33] y EICA [27] están resumidos en la Tabla 7. Se observa que el peso logrado con ASAM es mejor que el de los alcanzados por otros métodos (212640 lb para el ICA, 212364 lb para el CSS and 215874 lb para el CBO). Por otro lado, ASAM requiere solo 4290 análisis para obtener la solución óptima, mientras que ICA, CSS y CBO requieren 7500, 5500 y 8280 análisis, respectivamente. ASAM solo fue superado por los resultados del algoritmo EICA. A partir de los valores de peso promedio y desviación estándar obtenidos con ASAM, se puede concluir que el algoritmo es estable y eficiente. La Fig. 12 muestra la curva de convergencia del mejor resultado obtenido por ASAM para el pórtico de 3 vanos y 24 pisos.
Tabla 7. Comparación de diseños óptimos para el pórtico de 3 vanos y 24 pisos.
Figura 12. Curva de convergencia del mejor resultado para el pórtico de 3 vanos y 24 pisos.
5. Conclusiones
En este trabajo, el algoritmo de simulated annealing modificado (ASM) es aplicado al problema de minimización de peso de estructuras de acero. El rendimiento de ASAM se investigó comparando los diseños óptimos de ASAM en seis problemas de optimización estructural con los mejores diseños obtenidos por otros algoritmos metaheurísticos. Los resultados numéricos demuestran que las soluciones óptimas obtenidas por ASAM son mejores o iguales que las de muchos algoritmos disponibles en la literatura. Esto indica que el ASAM es robusto en la búsqueda de la solución óptima global, incluso en problemas con un gran número de variables de diseño.
Con respecto a la capacidad de convergencia, ASAM en casi todos los problemas de optimización se desempeñó mejor que otras soluciones metaheurísticas, requiriendo una cantidad mucho menor de análisis para lograr la solución óptima global. Esto indica que el ASAM es muy efectivo para escapar rápidamente de óptimos locales. Finalmente, el ASAM es un algoritmo simple y robusto, lo que permite su extensión para tratar problemas complejos de optimización de ingeniería, como la optimización de placas compuestas, estructuras laminares y de diseños basados en confiabilidad.
Agradecimientos
Los autores agradecen a la Universidad Tecnológica Federal de Paraná y al apoyo financiero brindado por CAPES-Brasil.
Referencias
[1] H.-S. Li, Y.-Z. Ma, Discrete Optimum Design for Truss Structures by Subset Simulation Algorithm, J. Aerosp. Eng. 28 (2015) 4014091. doi:10.1061/(ASCE)AS.1943-5525.0000411.
[2] D.E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning, 1989. doi:10.1007/s10589-009-9261-6.
[3] S. Kirkpatrick, C.D. Gelatt, M.P. Vecchi, Optimization by Simulated Annealing, Science (80-. ). 220 (1983) 671–680. doi:10.1126/science.220.4598.671.
[4] J. Kennedy, R. Eberhart, Particle swarm optimization, 1995 IEEE Int. Conf. Neural Networks (ICNN 95). 4 (1995) 1942–1948. doi:10.1109/ICNN.1995.488968.
[5] M. Dorigo, V. Maniezzo, A. Colorni, Ant system: optimization by a colony of cooperating agents, IEEE Trans. Syst. Man Cybern. Part B. 26 (1996) 29–41. doi:10.1109/3477.484436.
[6] F. Glover, Heuristics for integer programming using surrogate constraints, Decis. Sci. 8 (1977) 156–166. doi:10.1111/j.1540-5915.1977.tb01074.x.
[7] Zong Woo Geem, Joong Hoon Kim, G.V. Loganathan, A New Heuristic Optimization Algorithm: Harmony Search, Simulation. 76 (2001) 60–68. doi:10.1177/003754970107600201.
[8] O.K. Erol, I. Eksin, A new optimization method: Big Bang–Big Crunch, Adv. Eng. Softw. 37 (2006) 106–111. doi:10.1016/j.advengsoft.2005.04.005.
[9] L. Lamberti, C. Pappalettere, Metaheuristic Design Optimization of Skeletal Structures: A Review, Comput. Technol. Rev. 4 (2010) 1–32. doi:10.4203/ctr.4.1.
[10] M.P. Saka, E. Dogan, Recent Developments in Metaheuristic Algorithms: A Review, Comput. Technol. Rev. 5 (2012) 31–78. doi:10.4203/ctr.5.2.
[11] L. Lamberti, An efficient simulated annealing algorithm for design optimization of truss structures, Comput. Struct. 86 (2008) 1936–1953. doi:10.1016/j.compstruc.2008.02.004.
[12] O. Hasançebi, S. Çarbaş, E. Doğan, F. Erdal, M.P. Saka, Performance evaluation of metaheuristic search techniques in the optimum design of real size pin jointed structures, Comput. Struct. 87 (2009) 284–302. doi:10.1016/j.compstruc.2009.01.002.
[13] S.O. Degertekin, Improved harmony search algorithms for sizing optimization of truss structures, Comput. Struct. 92–93 (2012) 229–241. doi:10.1016/j.compstruc.2011.10.022.
[14] A. Sadollah, A. Bahreininejad, H. Eskandar, M. Hamdi, Mine blast algorithm for optimization of truss structures with discrete variables, Comput. Struct. 102–103 (2012) 49–63. doi:10.1016/j.compstruc.2012.03.013.
[15] A. Kaveh, V.R. Mahdavi, Colliding Bodies Optimization method for optimum discrete design of truss structures, Comput. Struct. 139 (2014) 43–53. doi:10.1016/j.compstruc.2014.04.006.
[16] A. Kaveh, B. Mirzaei, A. Jafarvand, An improved magnetic charged system search for optimization of truss structures with continuous and discrete variables, Appl. Soft Comput. J. 28 (2015) 400–410. doi:10.1016/j.asoc.2014.11.056.
[17] V. Ho-Huu, T. Nguyen-Thoi, M.H. Nguyen-Thoi, L. Le-Anh, An improved constrained differential evolution using discrete variables (D-ICDE) for layout optimization of truss structures, Expert Syst. Appl. 42 (2015) 7057–7069. doi:10.1016/j.eswa.2015.04.072.
[18] V. Ho-Huu, T. Nguyen-Thoi, T. Vo-Duy, T. Nguyen-Trang, An adaptive elitist differential evolution for optimization of truss structures with discrete design variables, Comput. Struct. 165 (2016) 59–75. doi:10.1016/j.compstruc.2015.11.014.
[19] D.T.T. Do, J. Lee, A modified symbiotic organisms search (mSOS) algorithm for optimization of pin-jointed structures, Appl. Soft Comput. 61 (2017) 683–699. doi:10.1016/j.asoc.2017.08.002.
[20] A. Kaveh, S. Talatahari, Optimum design of skeletal structures using imperialist competitive algorithm, Comput. Struct. 88 (2010) 1220–1229. doi:10.1016/j.compstruc.2010.06.011.
[21] A. Kaveh, S. Talatahari, Charged system search for optimal design of frame structures, Appl. Soft Comput. 12 (2012) 382–393. doi:10.1016/j.asoc.2011.08.034.
[22] S. Kazemzadeh Azad, O. Hasançebi, S. Kazemzadeh Azad, Upper bound strategy for metaheuristic based design optimization of steel frames, Adv. Eng. Softw. 57 (2013) 19–32. doi:10.1016/j.advengsoft.2012.11.016.
[23] M.R. Maheri, M.M. Narimani, An enhanced harmony search algorithm for optimum design of side sway steel frames, Comput. Struct. 136 (2014) 78–89. doi:10.1016/j.compstruc.2014.02.001.
[24] S. Gholizadeh, H. Poorhoseini, Optimum design of steel frame structures by a modified dolphin echolocation algorithm, Struct. Eng. Mech. 55 (2015) 535–554. doi:10.12989/sem.2015.55.3.535.
[25] A. Kaveh, T. Bakhshpoori, Optimum design of steel frames using Cuckoo Search algorithm with Lévy flights, Struct. Des. Tall Spec. Build. 22 (2013) 1023–1036. doi:10.1002/tal.754.
[26] A. Kaveh, T. Bakhshpoori, An accelerated water evaporation optimization formulation for discrete optimization of skeletal structures, Comput. Struct. 177 (2016) 218–228. doi:10.1016/j.compstruc.2016.08.006.
[27] M.R. Maheri, M. Talezadeh, An Enhanced Imperialist Competitive Algorithm for optimum design of skeletal structures, Swarm Evol. Comput. (2017). doi:10.1016/j.swevo.2017.12.001.
[28] C. Millán Páramo, O. Begambre Carrillo, E. Millán Romero, Propuesta y validación de un algoritmo Simulated annealing modificado para la solución de problemas de optimización, Rev. Int. Métodos Numéricos Para Cálculo Y Diseño En Ing. 30 (2014) 264–270. doi:10.1016/j.rimni.2013.10.003.
[29] C. Millán Páramo, O. Begambre Carrillo, Solución de problemas de optimización topológica empleando el Algoritmo Simulated Annealing Modificado, Rev. Int. Métodos Numéricos Para Cálculo Y Diseño En Ing. 32 (2016) 65–69. doi:10.1016/j.rimni.2014.11.005.
[30] M.-Y. Cheng, D. Prayogo, Y.-W. Wu, M.M. Lukito, A Hybrid Harmony Search algorithm for discrete sizing optimization of truss structure, Autom. Constr. 69 (2016) 21–33. doi:10.1016/j.autcon.2016.05.023.
[31] M.H. Talebpour, A. Kaveh, V.R. Kalatjari, Optimization of skeletal structures using a hybridized ant colony-harmony search-genetic algorithm, Iran. J. Sci. Technol. - Trans. Civ. Eng. 38 (2014) 1–20.
[32] S.K. Azad, O. Hasançebi, An elitist self-adaptive step-size search for structural design optimization, Appl. Soft Comput. 19 (2014) 226–235. doi:10.1016/j.asoc.2014.02.017.
[33] A. Kaveh, M. Ilchi Ghazaan, A comparative study of CBO and ECBO for optimal design of skeletal structures, Comput. Struct. 153 (2015) 137–147. doi:10.1016/j.compstruc.2015.02.028.
[34] A. Kaveh, V.R. Mahdavi, Colliding Bodies Optimization method for optimum design of truss structures with continuous variables, Adv. Eng. Softw. 70 (2014) 1–12. doi:10.1016/j.advengsoft.2014.01.002.
[35] American Institute of Steel Construction (AISC), Manual of steel construction–allowable stress design, 9th ed. Ch, 1989.
[36] A. Kaveh, S. Talatahari, A particle swarm ant colony optimization for truss structures with discrete variables, J. Constr. Steel Res. 65 (2009) 1558–1568. doi:10.1016/j.jcsr.2009.04.021.
[37] A. Kaveh, S. Talatahari, A discrete Big Bang - Big Crunch algorithm for optimal design of skeletal structures, Asian J. Civ. Eng. 11 (2010) 103–122.
[38] A. Kaveh, M. Ilchi Ghazaan, Enhanced colliding bodies optimization for design problems with continuous and discrete variables, Adv. Eng. Softw. 77 (2014) 66–75. doi:10.1016/j.advengsoft.2014.08.003.
[39] American Institute of Steel Construction (AISC), Load and resistance factor design, American Institute of Steel Construction, 2001.
Tablas
Tabla 1. Áreas transversales disponibles del código de diseño AISC
| No | in² | mm² | No | in² | mm² |
| 1 | 0.111 | 71.613 | 33 | 3.840 | 2477.414 |
| 2 | 0.141 | 90.968 | 34 | 3.870 | 2496.769 |
| 3 | 0.196 | 126.451 | 35 | 3.880 | 2503.221 |
| 4 | 0.250 | 161.29 | 36 | 4.180 | 2696.769 |
| 5 | 0.307 | 198.064 | 37 | 4.220 | 2722.575 |
| 6 | 0.391 | 252.258 | 38 | 4.490 | 2896.768 |
| 7 | 0.442 | 285.161 | 39 | 4.590 | 2961.284 |
| 8 | 0.563 | 363.225 | 40 | 4.800 | 3096.768 |
| 9 | 0.602 | 388.386 | 41 | 4.970 | 3206.445 |
| 10 | 0.766 | 494.193 | 42 | 5.120 | 3303.219 |
| 11 | 0.785 | 506.451 | 43 | 5.740 | 3703.218 |
| 12 | 0.994 | 641.289 | 44 | 7.220 | 4658.055 |
| 13 | 1.000 | 645.16 | 45 | 7.970 | 5141.925 |
| 14 | 1.228 | 792.256 | 46 | 8.530 | 5503.215 |
| 15 | 1.266 | 816.773 | 47 | 9.300 | 5999.988 |
| 16 | 1.457 | 939.998 | 48 | 10.850 | 6999.986 |
| 17 | 1.563 | 1008.385 | 49 | 11.500 | 7419.34 |
| 18 | 1.620 | 1045.159 | 50 | 13.500 | 8709.66 |
| 19 | 1.800 | 1161.288 | 51 | 13.900 | 8967.724 |
| 20 | 1.990 | 1283.868 | 52 | 14.200 | 9161.272 |
| 21 | 2.130 | 1374.191 | 53 | 15.500 | 9999.98 |
| 22 | 2.380 | 1535.481 | 54 | 16.000 | 10322.56 |
| 23 | 2.620 | 1690.319 | 55 | 16.900 | 10903.204 |
| 24 | 2.630 | 1696.771 | 56 | 18.800 | 12129.008 |
| 25 | 2.880 | 1858.061 | 57 | 19.900 | 12838.684 |
| 26 | 2.930 | 1890.319 | 58 | 22.000 | 14193.52 |
| 27 | 3.090 | 1993.544 | 59 | 22.900 | 14774.164 |
| 28 | 3.130 | 2019.351 | 60 | 24.500 | 15806.42 |
| 29 | 3.380 | 2180.641 | 61 | 26.500 | 17096.74 |
| 30 | 3.470 | 2,238,705 | 62 | 28.000 | 18064.48 |
| 31 | 3.550 | 2290.318 | 63 | 30.000 | 19354.8 |
| 32 | 3.630 | 2341.931 | 64 | 33.500 | 21612.86 |
Tabla 2. Comparación de diseños óptimos para la armadura plana de 52 barras
| Grupo (mm2) | HHS [30] | MBA [14] | aeDE [18] | IMCSS [16] | ASAM | |
| 1 | A1-A4 | 4658.06 | 4658.06 | 4658.06 | 4658.06 | 4658.06 |
| 2 | A5–A10 | 1161.29 | 1161.29 | 1161.29 | 1161.29 | 1161.29 |
| 3 | A11–A13 | 494.19 | 494.19 | 494.19 | 494.19 | 494.19 |
| 4 | A14–A17 | 3303.22 | 3303.22 | 3303.22 | 3303.22 | 3303.22 |
| 5 | A18–A23 | 940.00 | 940.00 | 940.00 | 940.00 | 940.00 |
| 6 | A24–A26 | 494.19 | 494.19 | 494.19 | 494.19 | 494.19 |
| 7 | A27–A30 | 2238.71 | 2283.71 | 2283.71 | 2238.71 | 2238.71 |
| 8 | A31–A36 | 1008.39 | 1008.39 | 1008.39 | 1008.39 | 1008.39 |
| 9 | A37–A39 | 494.19 | 494.19 | 494.19 | 494.19 | 494.19 |
| 10 | A40–A43 | 1283.87 | 1283.87 | 1283.87 | 1283.87 | 1283.87 |
| 11 | A44–A49 | 1161.29 | 1161.29 | 1161.29 | 1161.29 | 1161.29 |
| 12 | A50–A52 | 494.19 | 494.19 | 494.19 | 494.19 | 494.19 |
| Peso (kg) | 1902.61 | 1902.61 | 1902.61 | 1902.61 | 1902.61 | |
| Peso promedio (kg) | 1904.59 | 1906.08 | 1906.74 | - | 1903.12 | |
| Desv. Estándar (kg) | 1.31 | 4.09 | 6.68 | - | 0.52 | |
| Numero de análisis | 5000 | 5450 | 3720 | 4075 | 4290 | |
Tabla 3. Comparación de diseños óptimos para la armadura plana de 200 barras
| Grupo (in2) | HACOHS-T [31] | ESASS [32] | HHS [30] | aeDE [18] | ASAM |
| 1 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 |
| 2 | 1.08 | 0.95 | 0.95 | 0.95 | 0.95 |
| 3 | 0.35 | 0.10 | 0.10 | 0.35 | 0.35 |
| 4 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 |
| 5 | 2.14 | 2.14 | 2.14 | 2.14 | 2.14 |
| 6 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 |
| 7 | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 |
| 8 | 3.13 | 3.13 | 3.13 | 3.13 | 3.13 |
| 9 | 0.10 | 0.10 | 0.10 | 0.35 | 0.10 |
| 10 | 4.81 | 4.81 | 4.81 | 4.81 | 4.81 |
| 11 | 0.44 | 0.35 | 0.44 | 0.54 | 0.44 |
| 12 | 0.10 | 0.10 | 0.35 | 0.35 | 0.10 |
| 13 | 5.95 | 5.95 | 5.95 | 5.95 | 5.95 |
| 14 | 0.10 | 0.10 | 0.35 | 0.10 | 0.10 |
| 15 | 6.57 | 6.57 | 6.57 | 6.57 | 6.57 |
| 16 | 0.54 | 0.44 | 0.95 | 0.95 | 0.54 |
| 17 | 1.17 | 0.54 | 0.35 | 0.44 | 0.10 |
| 18 | 8.53 | 7.19 | 8.53 | 8.53 | 8.53 |
| 19 | 0.10 | 0.44 | 0.10 | 0.10 | 0.54 |
| 20 | 9.30 | 8.53 | 9.30 | 9.30 | 9.30 |
| 21 | 1.33 | 0.95 | 1.08 | 0.95 | 0.95 |
| 22 | 0.54 | 1.17 | 0.35 | 1.08 | 0.10 |
| 23 | 13.33 | 10.85 | 13.33 | 13.33 | 10.85 |
| 24 | 1.17 | 0.44 | 0.95 | 0.54 | 0.95 |
| 25 | 13.33 | 10.85 | 13.33 | 14.29 | 13.33 |
| 26 | 2.70 | 1.76 | 1.76 | 2.14 | 1.33 |
| 27 | 3.57 | 8.53 | 3.81 | 3.81 | 7.19 |
| 28 | 8.53 | 13.33 | 8.53 | 8.53 | 10.85 |
| 29 | 17.17 | 13.33 | 17.17 | 17.17 | 14.29 |
| Peso (lb) | 28030.20 | 28075.49 | 27163.59 | 27858.50 | 27190.49 |
| Peso promedio (lb) | - | - | 28159.59 | 28425.87 | 27653.83 |
| Desv. Estándar (lb) | - | - | 1149.91 | 481.59 | 198.35 |
| Numero de análisis | 20000 | 11156 | 5000 | 12325 | 4290 |
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N
Tabla 4. Comparación de diseños óptimos para la armadura espacial de 72 barras
| Grupo (in2) | MBA [14] | CBO [34] | ECBO [33]. | aeDE [18] | ASAM | |
| 1 | A1–A4 | 0.20 | 1.62 | 1.99 | 1.99 | 1.99 |
| 2 | A5–A12 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 |
| 3 | A13–A16 | 0.44 | 0.11 | 0.11 | 0.11 | 0.11 |
| 4 | A17–A18 | 0.60 | 0.11 | 0.11 | 0.11 | 0.11 |
| 5 | A19–A22 | 0.44 | 1.46 | 1.23 | 1.23 | 1.23 |
| 6 | A23–A30 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 |
| 7 | A31–A34 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 |
| 8 | A35–A36 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 |
| 9 | A37–A40 | 1.27 | 0.60 | 0.56 | 0.56 | 0.56 |
| 10 | A41–A48 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 |
| 11 | A49–A52 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 |
| 12 | A53–A54 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 |
| 13 | A55–A58 | 1.80 | 0.20 | 0.20 | 0.20 | 0.20 |
| 14 | A59–A66 | 0.60 | 0.60 | 0.56 | 0.56 | 0.56 |
| 15 | A67–A70 | 0.11 | 0.39 | 0.39 | 0.39 | 0.39 |
| 16 | A71–A72 | 0.11 | 0.56 | 0.56 | 0.56 | 0.56 |
| Peso (lb) | 390.73 | 391.07 | 389.33 | 389.33 | 389.33 | |
| Peso promedio (lb) | 395.43 | 403.71 | 391.59 | 390.91 | 389.87 | |
| Desv. Estándar (lb) | 3.04 | 24.80 | - | 1.16 | 0.76 | |
| Numero de análisis | 11600 | 4500 | 17010 | 4160 | 4290 | |
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N
Tabla 5. Comparación de diseños óptimos para la torre espacial de 582 barras
| Grupo | DHPSACO [36] | HBB-BC [37] | CBO [38] | ECBO [38] | ASAM |
| 1 | W8 X 24 | W8 X 24 | W8 X 21 | W8 X 21 | W8 X 21 |
| 2 | W12 X 72 | W24 X 68 | W14 X 8 | W14 X 90 | W14 X 90 |
| 3 | W8 X 28 | W8 X 28 | W8v28 | W8 X 24 | W8 X 24 |
| 4 | W12 X 58 | W18 X 60 | W12 X 5 | W14 X 61 | W14 X 61 |
| 5 | W8 X 24 | W8 X 24 | W8 X 24 | W8 X 24 | W8 X 24 |
| 6 | W8 X 24 | W8 X 24 | W8 X 21 | W8 X 21 | W8 X 21 |
| 7 | W10 X 49 | W21 X 48 | W12 X 5 | W10 X 49 | W10 X 49 |
| 8 | W8 X 24 | W8 X 24 | W12 X 2 | W8 X 24 | W8 X 24 |
| 9 | W8 X 24 | W10 X 26 | W8 X 21 | W8 X 21 | W8 X 21 |
| 10 | W12 X 40 | W14 X 38 | W14 X 4 | W14 X 43 | W10 X 39 |
| 11 | W12 X 30 | W12 X 30 | W8 X 24 | W8 X 24 | W8 X 24 |
| 12 | W12 X 72 | W12 X 72 | W14 X 6 | W12 X 72 | W12 X 72 |
| 13 | W18 X 76 | W21 X 73 | W14 X 8 | W12 X 72 | W14 X 74 |
| 14 | W10 X 49 | W14 X 53 | W12 X 5 | W10 X 54 | W12 X 50 |
| 15 | W14 X 82 | W18 X 86 | W14 X 7 | W12 X 65 | W10 X 77 |
| 16 | W8 X 31 | W8 X 31 | W8 X 40 | W8 X 31 | W8 X 31 |
| 17 | W14 X 61 | W18 X 60 | W12 X 5 | W10 X 60 | W10 X 49 |
| 18 | W8 X 24 | W8 X 24 | W6 X 25 | W8 X 24 | W8 X 24 |
| 19 | W8 X 21 | W16 X 36 | W8 X 21 | W8 X 21 | W8 X 21 |
| 20 | W12 X 40 | W10 X 39 | W8 X 40 | W14 X 43 | W14 X 48 |
| 21 | W8 X 24 | W8 X 24 | W8 X 24 | W8 X 24 | W6 X 25 |
| 22 | W14 X 22 | W8 X 24 | W8 X 21 | W8 X 21 | W10 X 22 |
| 23 | W8 X 31 | W8 X 31 | W12 X 2 | W8 X 21 | W8 X 21 |
| 24 | W8 X 28 | W8 X 28 | W12 X 2 | W8 X 24 | W8 X 24 |
| 25 | W8 X 21 | W8 X 21 | W10 X 2 | W8 X 21 | W8 X 21 |
| 26 | W8 X 21 | W8 X 24 | W10 X 2 | W8 X 21 | W10 X 2 |
| 27 | W8 X 24 | W8 X 28 | W6 X 25 | W8 X 24 | W8 X 24 |
| 28 | W8 X 28 | W14 X 22 | W8 X 21 | W8 X 21 | W8 X 21 |
| 29 | W16 X 36 | W8 X 24 | W8 X 21 | W8 X 21 | W8 X 21 |
| 30 | W8 X 24 | W8 X 24 | W8 X 24 | W8 X 24 | W8 X 24 |
| 31 | W8 X 21 | W14 X 22 | W8 X 21 | W8 X 21 | W8 X 21 |
| 32 | W8 X 24 | W8 X 24 | W6 X 25 | W8 X 24 | W8 X 28 |
| Volumen (in3) | 1346227 | 1365143 | 1334994 | 1296776 | 1302038 |
| Volumen promedio (in3) | - | - | 1345429 | 1306728 | 1311290 |
| Desv. Estándar (in3) | - | - | 9116 | 7536 | 6581 |
| Número de análisis | 8500 | 12500 | 17700 | 19700 | 9240 |
Nota: 1 in3 = 16.3871 cm3;
Tabla 6. Comparación de diseños óptimos para el pórtico de 3 vanos y 15 pisos
| Grupo | HBB-BC [37] | ICA [20] | CSS [21] | CBO [33] | EICA [27] | ASAM |
| 1 | W24 X 117 | W24 X 117 | W21 X 147 | W24 X 104 | W18 X 71 | W14 X 90 |
| 2 | W21 X 132 | W21 X 147 | W18 X 143 | W40 X 167 | W30 X 235 | W30 X 173 |
| 3 | W12 X 95 | W27 X 84 | W12 X 87 | W27 X 84 | W18 X 46 | W12 X 79 |
| 4 | W18 X 119 | W27 X 114 | W30 X 108 | W27 X 114 | W30 X 132 | W27 X 114 |
| 5 | W21 X 93 | W14 X 74 | W18 X 7 | W21 X 68 | W12 X 40 | W14 X 68 |
| 6 | W18 X 97 | W18 X 86 | W24 X 103 | W30 X 90 | W14 X 120 | W30 X 90 |
| 7 | W18 X 76 | W12 X 96 | W21 X 68 | W8 X 48 | W10 X 22 | W21 X 48 |
| 8 | W18 X 65 | W24 X 68 | W14 X 61 | W21 X 68 | W12 X 53 | W14 X 68 |
| 9 | W18 X 60 | W10 X 39 | W18 X 35 | W14 X 34 | W8 X 28 | W8 X 24 |
| 10 | W10 X 39 | W12 X 40 | W10 X 33 | W8 X 35 | W12 X 50 | W14 X 48 |
| 11 | W21 X 48 | W21 X 44 | W21 X 44 | W21 X 50 | W21 X 44 | W21 X 44 |
| Peso (lb) | 97689 | 93846 | 92723 | 93795 | 91560 | 88651 |
| Peso promedio (lb) | - | - | - | 98738 | 91910 | 90534 |
| Desv. Estándar (lb) | - | - | - | 899 | 852 | |
| Numero de análisis | 9900 | 6000 | 5000 | 9520 | 3300 | 4290 |
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N
Tabla 7. Comparación de diseños óptimos para el pórtico de 3 vanos y 24 pisos
| Grupo | ICA [20] | CSS [21] | CBO [33] | EICA [27] | ASAM |
| 1 | W30 X 90 | W30 X 90 | W27 X 102 | W16 X 31 | W30 X 90 |
| 2 | W21 X 50 | W21 X 50 | W8 X 18 | W12 X 210 | W10 X 30 |
| 3 | W24 X 55 | W21 X 48 | W24 X 55 | W21 X 44 | W24 X 55 |
| 4 | W8 X 28 | W12 X 19 | W6 X 8.5 | W10 X 12 | W6 X 8.5 |
| 5 | W14 X 109 | W14 X 176 | W14 X 132 | W14 X 426 | W14 X 159 |
| 6 | W14 X 159 | W14 X 145 | W14 X 120 | W14 X 22 | W14 X 99 |
| 7 | W14 X 120 | W14 X 10 | W14 X 145 | W14 X 132 | W14 X 120 |
| 8 | W14 X 90 | W14 X 90 | W14 X 82 | W14 X 22 | W14 X 74 |
| 9 | W14 X 74 | W14 X 74 | W14 X 61 | W14 X 26 | W14 X 74 |
| 10 | W14 X 68 | W14 X 61 | W14 X 43 | W14 X 82 | W14 X 43 |
| 11 | W14 X 30 | W14 X 34 | W14 X 38 | W14 X 370 | W14 X 30 |
| 12 | W14 X 38 | W14 X 34 | W14 X 22 | W14 X 26 | W14 X 22 |
| 13 | W14 X 159 | W14 X 145 | W14 X 99 | W14 X 455 | W14 X 90 |
| 14 | W14 X 132 | W14 X 132 | W14 X 109 | W14 X 22 | W14 X 120 |
| 15 | W14 X 99 | W14 X 109 | W14 X 82 | W14 X 132 | W14 X 90 |
| 16 | W14 X 82 | W14 X 82 | W14 X 90 | W14 X 30 | W14 X 99 |
| 17 | W14 X 68 | W14 X 68 | W14 X 74 | W14 X 22 | W14 X 68 |
| 18 | W14 X 48 | W14 X 43 | W14 X 61 | W14 X 22 | W14 X 61 |
| 19 | W14 X 34 | W14 X 34 | W14 X 30 | W14 X 38 | W14 X 43 |
| 20 | W14 X 22 | W14 X 22 | W14 X 22 | W14 X 22 | W14 X 22 |
| Peso (lb) | 212640 | 212364 | 215874 | 189720 | 203490 |
| Peso promedio (lb) | - | 215226 | 225071 | 190422 | 206846 |
| Desv. Estándar (lb) | - | - | 1714 | 2546 | |
| Numero de análisis | 7500 | 5500 | 8280 | 3640 | 4290 |
Nota: 1 in2 = 6.452 cm2; 1lb = 4.45N
Figuras
Figura 1. Armadura plana de 52 barras
Figura 2. Curva de convergencia del mejor resultado para la armadura plana de 52 barras.
Figura 3. Armadura plana de 200 barras
Figura 4. Curva de convergencia del mejor resultado para la armadura plana de 200 barras.
Figura 5. Armadura espacial de 72 barras
Figura 6. Curva de convergencia del mejor resultado para la armadura espacial de 72 barras.
Figura 7. Torre espacial de 582 barras.
Figura 8. Curva de convergencia del mejor resultado para la torre espacial de 582 barras.
Figura 9. Pórtico de 3 vanos y 15 pisos.
Figura 10. Curva de convergencia del mejor resultado para el pórtico de 3 vanos y 15 pisos.
Figura 11. Pórtico de 3 vanos y 24 pisos.
Figura 12. Curva de convergencia del mejor resultado para el pórtico de 3 vanos y 24 pisos.
Document information
Published on 19/03/19
Accepted on 18/03/19
Submitted on 31/03/18
Volume 35, Issue 1, 2019
DOI: 10.23967/j.rimni.2019.03.003
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?