Revision as of 13:37, 22 March 2018 (view source) Cinmemj (talk | contribs) ← Older edit		Revision as of 13:38, 22 March 2018 (view source) Cinmemj (talk | contribs) Newer edit →
Line 40:		Line 40:
	{| style="text-align: left; margin:auto;"		{| style="text-align: left; margin:auto;"
	|-		|-
−	| style="text-align: center;" | <math>\rho(\textbf{X},t) \frac{ \partial \textbf{v}(\textbf{X},t)}{\partial t}-\frac{\partial\bm{\sigma}(\textbf{X},t)}{\partial\textbf{x}}-\textbf{b}(\textbf{X},t)=0  \quad \quad \hbox{in } \ \Omega \times (0,T)  </math>	+	| style="text-align: center;" | <math>\rho(\textbf{X},t) \frac{ \partial \textbf{v}(\textbf{X},t)}{\partial t}-\frac{\partial\mathboth{\sigma}(\textbf{X},t)}{\partial\textbf{x}}-\textbf{b}(\textbf{X},t)=0  \quad \quad \hbox{in } \ \Omega \times (0,T)  </math>
	|}		|}
	| style="width: 5px;text-align: right;" | (1)		| style="width: 5px;text-align: right;" | (1)

---

Revision as of 13:38, 22 March 2018

Abstract

In this work, a unified updated Lagrangian formulation for solving fluid-structure interaction (FSI) problems is derived. The mixed velocity-pressure formulation for hypoelastic solids and quasi and fully incompressible Newtonian fluids is obtained as an extension of the velocity formulation derived for a general continuum. The space discretization for the fluid domain is performed via the Particle Finite Element Method (PFEM), where for the solid domain a standard FEM is used. Linear interpolation is used for both the velocity and the pressure fields. The global FSI problem is solved using a Gauss-Seidel iterative scheme. The required stabilization for dealing with incompressible situations is given by an enhanced formulation of the Finite Calculus (FIC) technique [22]. The efficiency of the proposed strategy is tested by solving benchmark FSI problems.

keywords Unified Updated Lagrangian Formulation, Quasi and Fully Incompressible, Partitioned Scheme, Particle Finite Element Method

1 Introduction

The great interest of the computational mechanics community in solving fluid-structure interaction (FSI) problems is due to two main reasons. On the one hand the analytical solution of these problems is generally impossible to obtain and experimental tests can not be performed, or they have an excessive cost. On the other hand, FSI problems are very attractive for their multidisciplinarity: they occur in many fields, such as civil, aerospace and nuclear engineering, or biology.

In the last decades, many numerical methods have been proposed for solving FSI problems. The most common classification distinguishes the monolithic and the staggered (or partitioned) approaches. The first group includes those strategies in which the fluid and the structure are solved within the same global linear system ([13], [20] and [26], among others). Instead, staggered methods solve the FSI problem via an iterative loop where the fluid solver and solid solvers are activated alternatively. The fluid and the solid domains interact tranfering the Dirichlet and Neumann conditions through the interface ([11], [28] and [9]).

In this paper, a unified updated Lagrangian finite element formulation for solving FSI problems is derived and discussed. The present method belongs to the monolithic category of FSI strategies. The aim of the work is to give a general procedure for dealing with solid and fluid mechanics problems indifferently and for modeling their interaction in a natural way. With this purpose, the derivation of the formulation is developed so that the changes required by a specific material are minimized and introduced only at the end of the derivation. The materials considered in this work are hypoelastic solids and Newtonian fluids. However, it will be shown that the formulation can be easily extended to other types of materials, such as incompressible or elasto-plastic solids among others. The mixed velocity pressure formulation emanates from the velocity formulation and both cases are derived first for a general continuum. Only later the formulations are adapted to specific materials. The finite element approximation is performed by interpolating both the velocity and the pressure fields using linear shape functions.

Concerning the mixed formulation, the global system of algebraic equations is solved via an iterative partitioned Gauss-Seidel scheme. This means that first the momentum equations are solved in terms of the unknown velocity increments using the pressures computed at the previous iteration and then the unknown pressures are computed using the updated velocities. This procedure is the key point of the unified formulation. In fact, it allows to treat hypoelastic solids and quasi-incompressible fluids in a similar way. In particular, in the momentum equations, the structure of the tangent matrix and the terms of the right hand side are the same for both materials.

The main differences in the treatment of fluids and solids are in the incompressibility of the fluid and in the distortion of its mesh. In order to overcome the latter difficulty, the Particle Finite Element Method has been adopted for the analysis of the fluid domain. The PFEM is a Lagrangian formulation based on an Alpha-Shape [10] remeshing procedure that allows one to deal with a fine and regular mesh all over the duration of the analysis. Many scientific publications have shown the efficiency of the PFEM in the simulation of free-surface fluids ([16] and [17] among others) and FSI problems ([18] and [23] among others).

In regard to the fluid incompressibility (or quasi-incompressibility) a specific stabilization is required because the linear interpolations chosen for the velocity and the pressure fields do not fulfil the so-called ${\textstyle {LBBinf-supcondition}}$ [4]. In this work, the mass balance equation in the fluid is stabilized using the updated formulation of Finite Increment Calculus (FIC) technique [22]. This choice is motivated by the small intrusively of this method (its stabilization terms affect the continuity equation only) and by its mass preservation features [22].

The FSI solver is based on the mixed velocity-pressure formulations for hypoelastic solids and Newtonian fluids. Fluids and solids are computed by using the same unknown variables (velocities and pressure), the same framework (Lagrangian) and the same solving scheme (Gauss-Seidel). All this simplifies the coupling for solving FSI problems allowing the use of a monolithic scheme; ${\textstyle {}}$ fluids and solids can be easily solved using a similar system of equations ensuring a strong coupling automatically. The FSI coupling is performed in a natural way and it essentially consists in realizing two tasks: to detect the interface creating the coupling elements (elements that share at least one interface node) and to assembly properly the global system.

The outline of paper is the following. First the velocity formulation in the updated Lagrangian framework is derived for a general continuum. Then the unknown pressures are introduced and the mixed velocity-pressure formulation is presented. In the third section, the formulations are adapted to specific materials. First, both the velocity and the mixed formulations are specified for the case of hypoelastic solids. Then the mixed formulation is adapted for the analysis of quasi-incompressible free surface fluids. Some reminders remarks about the stabilization procedure and the Particle Finite Element Method are also given. In the fifth section, the coupling algorithm for solving FSI problems is explained. Particular attention is devoted to the detection of the interface and the assembly of the global system. In the next section, some representative problems are solved and discussed in order to test the efficiency of the proposed FSI solution strategy. In particular, the collapse of a water column on a deformable membrane and the water entry of a nylon sphere are analyzed. Finally, the main conclusions are given.

2 Velocity formulation

In this section, the velocity formulation for solving transient problems for a general continuum is derived. The governing equations are the linear momentum equations and they are derived in the updated Lagrangian (UL) framework. The essential feature of a Lagrangian description is that the independent variables are the Lagrangian coordinates [3]. For this reason, a typical Eulerian measure, as the Cauchy stress tensor, can be used in a Lagrangian framework if it is expressed in function of the Lagrangian coordinates. In the UL formulation used in this work the governing equations are integrated over the unknown configuration ${\textstyle {\Omega }}$ (the so-called updated configuration). As a consequence, the space derivatives for the UL description are computed with respect to the spatial coordinates.

2.1 From local form to the spatial semi-discretization

In this section the spatial semi-discretization of the linear momentum equations is derived.

For a general continuum, the local form of the linear momentum equations using the updated Lagrangian description reads:

Failed to parse (unknown function "\mathboth"): \rho(\textbf{X},t) \frac{ \partial \textbf{v}(\textbf{X},t)}{\partial t}-\frac{\partial\mathboth{\sigma}(\textbf{X},t)}{\partial\textbf{x}}-\textbf{b}(\textbf{X},t)=0 \quad \quad \hbox{in } \ \Omega \times (0,T)

(1)

where ${\textstyle \rho }$ is the density of the material, ${\textstyle v}$ are the velocities, ${\textstyle \sigma }$ is the Cauchy stress tensor and ${\textstyle b}$ is the body force. The variables within the brackets are the independent variables. In particular, X are the Lagrangian or material coordinates, x the Eulerian or spatial coordinates and ${\textstyle t}$ is the time. For simplicity, in the following the independent variables will be not specified.

The set of governing equations is completed by the following conditions at the Dirichlet (${\textstyle \Gamma _{v}}$) and Neumann (${\textstyle \Gamma _{t}}$) boundaries:

${\displaystyle v_{i}-v_{i}^{p}=0\qquad {\hbox{on }}\Gamma _{v}}$

(2)

${\displaystyle \sigma _{ij}n_{j}-t_{i}^{p}=0\qquad {\hbox{on }}\Gamma _{t}}$

(3)

where ${\textstyle v_{i}^{p}}$ and ${\textstyle t_{i}^{p}}$, ${\textstyle i=1,...,n_{s}}$ are the prescribed velocities and the prescribed tractions, respectively.

The spaces for the trial and test functions are defined, respectively, as:

${\displaystyle v_{i}\in {U},\quad \quad {U}=\{v_{i}|v_{i}\in C^{0},v_{i}=v_{i}^{p}on\Gamma _{v}\}}$

(4)

${\displaystyle w_{i}\in {U_{0}},\quad \quad {U_{0}}=\{w_{i}|w_{i}\in C^{0},w_{i}=0on\Gamma _{v}\}}$

(5)

Multiplying Eqs.(1) by the test functions and integrating over the updated configuration domain, the following global integral form is obtained:

${\displaystyle \int _{\Omega }w_{i}\left(\rho {\frac {\partial v_{i}}{\partial t}}-{\partial \sigma _{ij} \over \partial x_{j}}-b_{i}\right)d\Omega =0}$

(6)

Integrating by parts the term involving ${\textstyle \sigma _{ij}}$ in Eq.(6) and using the Neumann boundary conditions (3) yields the weak variational form of the momentum equations as:

${\displaystyle \int _{\Omega }w_{i}\rho {\frac {\partial v_{i}}{\partial t}}d\Omega +\int _{\Omega }{\frac {\partial w_{i}}{\partial x_{j}}}\sigma _{ij}d\Omega -\int _{\Omega }w_{i}b_{i}d\Omega -\int _{\Gamma _{t}}w_{i}t_{i}^{p}d\Gamma =0}$

(7)

Eq.(7) is the standard form of the principle of virtual power [3].

The spatial discretization is introduced using the classical FEM-Galerkin prodedure. Hence both the trial and the test functions are interpolated in the space by means of the same shape functions ${\textstyle {N}}$.

${\displaystyle v_{i}=\sum \limits _{I=1}^{n}N_{I}{\bar {v}}_{iI}\quad ,\quad w_{i}=\sum \limits _{I=1}^{n}N_{I}{\bar {w}}_{iI}}$

(8)

where ${\textstyle n=3/4}$ for 2D/3D problems is the number of the nodes of the finite element, ${\textstyle {\bar {(\cdot )}}}$ denotes a nodal value, the capital subscript specifies the node and the lower case subscript represents the cartesian direction. In this work, the velocities have been interpolated using linear shape functions.

Using the arbitrariness of the test functions and introducing the spatial discretization (8) into Eq.(7), the spatial semi-discretized form of the momentum equations in the UL framework reads:

${\displaystyle \underbrace {\int _{\Omega }N_{I}\rho d\Omega {\dot {v_{i}}}} _{{W}_{Ii}^{k}}+\underbrace {\int _{\Omega }{\frac {\partial N_{I}}{\partial x_{j}}}\sigma _{ij}d\Omega } _{{W}_{Ii}^{int}}=\underbrace {\int _{\Omega }N_{I}b_{i}d\Omega +\int _{\Gamma _{t}}N_{I}t_{i}^{p}d\Gamma } _{{W}_{Ii}^{ext}}}$

(9)

For convenience, the semi-discretized form of the momentum equations in the total Lagrangian (TL) framework is also presented here. This is written as [3]:

${\displaystyle \underbrace {\int _{\Omega _{0}}N_{I}\rho _{0}d\Omega {\dot {v_{i}}}} _{^{TL}{W}_{Ii}^{k}}+\underbrace {\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}P_{ij}d\Omega } _{^{TL}{W}_{Ii}^{int}}=\underbrace {\int _{\Omega _{0}}N_{I}b_{i}d\Omega +\int _{\Gamma _{t}^{0}}N_{I}t_{i}^{0p}d\Gamma } _{^{TL}{W}_{Ii}^{ext}}}$

(10)

where ${\textstyle {P}}$ is the first Piola-Kirchhoff stress tensor, or the nominal stress tensor, and all the variables with the subscript ${\textstyle {(\cdot )}_{0}}$ refer to the last known configuration. Note that Eq.(10) can be obtained from Eq.(9) by properly performing pull back transformations on all its terms [3].

For the sake of clarity in the notation, the terms referred to the TL description are denoted with the exponent ${\textstyle {^{TL}(\cdot )}}$. If not specified, the variables belong to the UL description.

2.2 Time integration

In this work, the kinematic variables have been integrated in time using a second order scheme. In particular, the implicit Newmark's integration rule has been adopted. For the general case, the Newmark's integration rule states that accelerations and displacements are computed as:

${\displaystyle {\dot {v}}_{n+1}}$ ${\displaystyle ={\frac {1}{\gamma \Delta t}}\left(v_{n+1}-v_{n}\right)-{\frac {1-\gamma }{\gamma }}{\dot {v}}_{n}}$ ${\displaystyle u_{n+1}}$ ${\displaystyle =u_{n}+{\Delta t}{\frac {\gamma -\beta }{\gamma }}v_{n}+\Delta t{\frac {\beta }{\gamma }}v_{n+1}+{\Delta t^{2}}{\frac {\gamma {-}2\beta }{2\gamma }}{\dot {v}}_{n}}$

(11)

Where ${\textstyle {\beta }}$ and ${\textstyle {\gamma }}$ are the so-called Newmark's parameters [3]. A time integration scheme is unconditionally stable if the following relation holds:

${\displaystyle \gamma \geq 2\beta \geq {\frac {1}{2}}}$

(12)

In the present work, the time integration scheme is implicit and the Newmark's parameters chosen are ${\textstyle {\beta ={\frac {1}{4}}}}$ and ${\textstyle {\gamma ={\frac {1}{2}}}}$ in order to fulfill relation (12).

Replacing the numerical values of the constants in Eq.(11) yields:

${\displaystyle {\dot {v}}_{n+1}={\frac {2}{\Delta t}}\left(v_{n+1}-v_{n}\right)-{\dot {v}}_{n}}$

(13)

${\displaystyle u_{n+1}=u_{n}+{\frac {\Delta t}{2}}\left(v_{n+1}+v_{n}\right)}$

(14)

2.3 Linearization

Although the problem is setted out in the UL framework, the linearization of the momentum equations is performed first on the TL semi-discretized form (10). The updated Lagrangian linearized form is subsequently obtained by performing a push-forward transformation on the total Lagrangian form. The reason for this is that the derivation of the tangent matrix in the total Lagrangian framework is easier. In fact, in Eq.(10) the only variable that depends on time is the nominal stress ${\textstyle {P}}$, while in the updated Lagrangian form (9) the time-dependent variables are the updated domain ${\textstyle {\Omega }}$, the Cauchy stress tensor ${\textstyle {\sigma }}$ and the spatial derivatives ${\textstyle {\partial N/\partial x}}$. For the sake of clarity, the linearization of the internal and kinematic work terms will be performed separately. Thus, in the following section First the internal components of the tangent matrix are derived.

2.3.1 Internal components of the tangent matrix

From Eq.(10) the internal work in the TL description is defined as:

${\displaystyle ^{TL}W_{Ii}^{int}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}P_{ij}d\Omega }$

(15)

In order to obtain the tangent matrix, the material time derivative of (15) is computed as:

${\displaystyle ^{TL}{\dot {W}}_{Ii}^{int}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}{\dot {P}}_{ij}d\Omega }$

(16)

The material time derivative of the material part of the internal work is now discretized to obtain its increment in a time interval ${\textstyle {\Delta t}}$:

${\displaystyle {\frac {\Delta ^{TL}W_{Ii}^{int}}{\Delta t}}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}{\dot {P}}_{ij}d\Omega }$

(17)

From Eq.(17) we deduce:

${\displaystyle \Delta ^{TL}W_{Ii}^{int}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}\Delta t{\dot {P}}_{ij}d\Omega }$

(18)

The first Piola-Kirchhoff stress tensor ${\textstyle {P}}$ is not typically used because it is not symmetric and its rate is a non-objective measure. For these reasons, the second Piola-Kirchhoff stress tensor ${\textstyle {S}}$ and its rate are preferred quantities in the TL framework. The mentioned stress rate measures are related each other through the following relation:

${\displaystyle {\dot {P}}_{ij}={\dot {S}}_{ir}F_{rj}^{T}+S_{ir}{\dot {F}}_{rj}^{T}}$

(19)

where ${\textstyle {F}}$ is the so-called deformation gradient defined as:

${\displaystyle {F}_{ij}={\frac {\partial x_{i}}{\partial X_{j}}}}$

(20)

Substituting Eq.(19) into (18) yields:

${\displaystyle \Delta ^{TL}{W}_{Ii}^{int}=\underbrace {\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}F_{ir}\Delta t{\dot {S}}_{jr}d\Omega } _{^{TL}{\dot {W}}_{Ii}^{m}}+\underbrace {\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}S_{ir}\Delta t{\dot {F}}_{rj}^{T}d\Omega } _{^{TL}{\dot {W}}_{Ii}^{g}}}$

(21)

Eq.(17) shows that the internal power can be split into the material and the geometric parts, ${\textstyle {{\dot {W}}^{m}}}$ and ${\textstyle {{\dot {W}}^{g}}}$, respectively. The former accounts for the material response through the rate of the second Piola-Kirchhoff stress tensor, the second term is the initial stress term that contains the information of the updated stress field. It is to be noted that, up to now, no constitutive relations have been introduced and the present derivation holds for a general continuum.

Material tangent matrix

For the derivation of the material tangent matrix, the constitutive relation between the stress and the strain measures needs to be defined. In order to maintain the formulation as general as possible, the stress rate measure is related to the deformation rate through a tangent modulus tensor, such that

${\displaystyle {\dot {S}}_{ij}=C_{ijkl}{\dot {E}}_{kl}=C_{ijkl}{\frac {\partial N_{J}}{\partial X_{s}}}F_{kl}{\bar {v}}_{sJ}}$

(22)

where ${\textstyle {C}}$ is a fourth-order tangent moduli tensor and ${\textstyle {E}}$ is the Green-Lagrange strain tensor and the following substitution has been made:

${\displaystyle {\dot {E}}_{kl}={\frac {\partial N_{J}}{\partial X_{s}}}F_{kl}{\bar {v}}_{sJ}}$

(23)

One may note that in literature ([3],[2]), often the term ${\textstyle {{\frac {\partial N_{I}}{\partial X}}F}}$ is grouped in the matrix ${\textstyle {B_{0}^{I}}}$ defined in two dimension as:

${\displaystyle {\begin{array}{l}\\{B_{0}^{I}}=\left[{\begin{array}{cccccc}{\frac {\partial N_{I}}{\partial {X}}}{\frac {\partial x}{\partial {X}}}&{\frac {\partial N_{I}}{\partial {X}}}{\frac {\partial y}{\partial {X}}}\\{\frac {\partial N_{I}}{\partial {Y}}}{\frac {\partial x}{\partial {Y}}}&{\frac {\partial N_{I}}{\partial {Y}}}{\frac {\partial y}{\partial {Y}}}\\{\frac {\partial N_{I}}{\partial {X}}}{\frac {\partial x}{\partial {Y}}}+{\frac {\partial N_{I}}{\partial {Y}}}{\frac {\partial x}{\partial {X}}}&{\frac {\partial N_{I}}{\partial {X}}}{\frac {\partial y}{\partial {Y}}}+{\frac {\partial N_{I}}{\partial {Y}}}{\frac {\partial y}{\partial {X}}}\\\end{array}}\right]\\\\\end{array}}}$

In this work, for convenience, the matrix ${\textstyle {B_{0}^{I}}}$ is not used. As it will be shown in the following sections, Eq.(22) can represent both a Kirchhoff solid material and a quasi-incompressible fluid. If different constitutive laws are used, Eq.(22) should be modified accordingly in order to derive the material part of the tangent matrix.

Substituting Eq.(22) into ${\textstyle {{\dot {W}}^{m}}}$ of Eq.(17) yields

${\displaystyle \Delta ^{TL}{W}_{Ii}^{m}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}F_{rj}\Delta tC_{ijkl}{\frac {\partial N_{J}}{\partial X_{s}}}F_{kl}d\Omega {\bar {v}}_{sJ}}$

(24)

where ${\textstyle {v_{sJ}}}$ is the ${\textstyle {s}}$-component of the velocity of node ${\textstyle {J}}$.

From Eq.(24), the material tangent matrix in the TL description can be computed as

${\displaystyle ^{TL}{K}_{IJis}^{m}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}F_{rj}\Delta tC_{ijkl}{\frac {\partial N_{J}}{\partial X_{s}}}F_{kl}d\Omega }$

(25)

The material tangent matrix for the UL framework can be derived by applying a push-forward transformation on each term of Eq.(25). The following relations hold

${\displaystyle {\Omega _{0}}={\frac {\Omega }{J}}andd{\Omega _{0}}={\frac {d\Omega }{J}}}$

(26)

${\displaystyle {\frac {\partial N_{I}}{\partial X_{j}}}={\frac {\partial N_{I}}{\partial x_{k}}}F_{kj}}$

(27)

${\displaystyle C_{ijkl}=F_{mi}^{-1}F_{nj}^{-1}F_{ok}^{-1}F_{pl}^{-1}c_{mnop}^{\tau }=F_{mi}^{-1}F_{nj}^{-1}F_{ok}^{-1}F_{pl}^{-1}c_{mnop}^{\sigma }J}$

(28)

where ${\textstyle {c^{\tau }}}$ is the tangent moduli corresponding to the material time derivative of the Kirchhoff stress tensor and ${\textstyle {c^{\sigma }}}$ is the tangent moduli for the rate of the Cauchy stress. The rate of the Cauchy stress tensor is related to the rate of deformation ${\textstyle {D}}$ through the fourth-order tensor ${\textstyle {C}}$ in the following way

${\displaystyle \sigma ^{\bigtriangledown }=c^{\sigma }:D}$

(29)

Substituting Eqs.(26-28) into (25), the material tangent matrix for the UL description is obtained as

${\displaystyle K_{IJis}^{m}=\int _{\Omega }{\frac {\partial N_{I}}{\partial x_{j}}}\Delta tc_{ijkl}^{\sigma }{\frac {\partial N_{J}}{\partial x_{s}}}d\Omega }$

(30)

Geometric tangent matrix

The geometric tangent matrix for the UL framework is here derived by using the same procedure adopted for the material components. Hence, first the linearization is performed on the TL form and then the UL tangent matrix is obtained by performing the required transformation over the TL terms.

From Eq.(17)

${\displaystyle \Delta ^{TL}{W}_{Ii}^{g}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}\Delta tS_{ir}{\dot {F}}_{rj}^{T}d\Omega }$

(31)

where the rate of the deformation gradient is defined as

${\displaystyle {\dot {F}}_{ij}={\frac {\partial N_{J}}{\partial X_{i}}}{\bar {v}}_{Jj}}$

(32)

Substituting Eq.(32) into (31), the geometric components of the internal power in the TL description can be written as

${\displaystyle \Delta ^{TL}{W}_{Ii}^{g}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}\Delta tS_{ir}{\frac {\partial N_{J}}{\partial X_{r}}}d\Omega {\bar {v}}_{Jj}}$

(33)

The geometric tangent matrix reads:

${\displaystyle ^{TL}K_{IJij}^{g}=\int _{\Omega _{0}}{\frac {\partial N_{I}}{\partial X_{j}}}\Delta tS_{ir}{\frac {\partial N_{J}}{\partial X_{r}}}d\Omega }$

(34)

In order to recover the UL form, the Piola identity has to be recalled, ${\textstyle {}}$

${\displaystyle {S}={F}^{-1}{\sigma }{F}^{-T}J}$

(35)

The geometric tangent matrix in the UL framework is obtained by substituting Eqs.(26), (27) and (35) into (34). This leads to

${\displaystyle K_{IJij}^{g}=\int _{\Omega }{\frac {\partial N_{I}}{\partial x_{j}}}\Delta t{\sigma }_{ir}{\frac {\partial N_{J}}{\partial x_{r}}}d\Omega }$

(36)

2.3.2 Kinematic components of the tangent matrix

The kinematic components of the tangent matrix in the UL description can be derived directly from the UL kinematic term ${\textstyle {{W}_{Ii}^{k}}}$ of Eq.(9).

${\displaystyle W_{Ii}^{k}=\int _{\Omega }N_{I}\rho d\Omega {\dot {v}}_{i}}$

(37)

Eq.(37) has to be discretized on time with the purpose of replacing the accelerations with the velocities using the time integration described in Eq.(13).

Introducing Eq.(13) into (37) and differentiating with respect of the unknown velocities ${\textstyle {v_{n+1}}}$, the kinematic components of the tangent matrix are obtained as:

${\displaystyle K_{IJ}^{k}=\int _{\Omega }N_{I}{\frac {2\rho }{\Delta t}}N_{J}d\Omega }$

(38)

The tangent matrix is computed as the sum of the internal and the kinematic components (30), (36) and (38) as

${\displaystyle K=K^{m}+K^{g}+K^{k}}$

(39)

2.4 Residual form and incremental solution scheme

With the aim of deriving the incremental solution scheme, Eq.(9) has to be rewritten in a residual form. Using Eq.(13) and shifting all the terms to the left hand side, yields:

${\displaystyle R_{Ii}^{n+1}=\int _{\Omega }N_{I}\rho N_{J}d\Omega {\bar {\dot {v}}}_{Ji}^{n+1}+\int _{\Omega }{\frac {\partial N_{I}}{\partial x_{j}}}\sigma _{ij}^{n+1}d\Omega -\int _{\Omega }N_{I}b_{i}^{n+1}d\Omega }$ ${\displaystyle -\int _{\Gamma _{t}}N_{I}t_{i}^{p,n+1}d\Gamma =0}$

(40)

where ${\textstyle {R_{Ii}^{n+1}}}$ is the residual of the momentum equations referred to node ${\textstyle {I}}$ and the cartesian direction ${\textstyle {i}}$. One can note that in Eq.(40), as for Eq.(36), the Cauchy stress tensor still appears. This tensor will be expressed as a function of the nodal unknowns of the problem in the following sections dedicated to the constitutive laws.

In Box 1 the iterative solution incremental scheme of the velocity formulation for a generic time increment ${\textstyle [n,n+1]}$ of duration ${\textstyle {\Delta t}}$ is described.

3 Mixed velocity-pressure formulation

In solid and fluid mechanics, there are problems where a mixed formulation is recommendable, or even necessary. In fluid dynamics, the mixed formulation is required to apply properly the incompressibility constraint and to guarantee the stability of the problem. In solid mechanics, the mixed formulation represents the most reasonable choice to circumvent the locking problem in rubber-type materials, or in cases where plasticity or fracture is induced ([4],[6],[7],[24]). Also, for modelling FSI problems with standard compressible solids involved, the mixed formulation may represent an useful choice [14]. In fact using the same variables for the analysis of the fluid and the solid represents both an important facility and a computational advantage: fluid and solid can be solved through an unified code and the risk of ill-conditioning the global problem is significally reduced. For all these reasons, the velocity formulation is here extended to the mixed velocity-pressure problems, considering the pressure as an additional unknown. Furthermore, in order to obtain a well-posed problem, the continuity equation is introduced in the solution scheme.

The whole problem is solved using a Gauss-Seidel partitioned iterative scheme. Hence, first the momentum equations are solved in terms of increments of the velocities and including the (known) pressures of the previous iteration in the residual, then the continuity equation is solved for the pressure using the updated velocities computed from the momentum equations. It will be shown that using this not intrusive scheme, it is possible to take advantage of most of the velocity-formulation derived so far. In particular, the incremental velocity scheme for the momentum equations (Box 1) and the structure of the tangent matrix (39) are still applicable. In this work, the same linear interpolation has been used for the velocity and the pressure fields. It is well known that, for incompressible (or quasi-incompressible) problems, this combination does not fulfill the ${\textstyle {inf-sup}}$ condition [4] and a stabilization method is required.

3.1 Splitting of the stress measures

The Cauchy stress tensor is rewritten as the sum of its deviatoric and hydrostatic parts as

${\displaystyle \sigma =\sigma '-pI}$

(41)

where ${\textstyle {\sigma '}}$ is the deviatoric part of the Cauchy stress, ${\textstyle {p}}$ is the pressure and ${\textstyle {I}}$ is the identity tensor.

In terms of stress rate, that would be:

${\displaystyle \sigma ^{\bigtriangledown }=\sigma '^{\bigtriangledown }-p^{\bigtriangledown }I}$

(42)

where

${\displaystyle \sigma '^{\bigtriangledown }=c^{\sigma '}:D^{dev}}$

(43)

where ${\textstyle {{\sigma }'^{\bigtriangledown }}}$ is the deviatoric part of the Cauchy stress rate tensor, ${\textstyle {p^{\bigtriangledown }}}$ is the rate of the pressure, ${\textstyle {c^{\sigma '}}}$ is the tangent moduli for ${\textstyle {{\sigma }'^{\bigtriangledown }}}$ and ${\textstyle {D^{dev}}}$ is the deviatoric part of the deformation rate tensor. The pressure is related to the volumetric part of the rate of deformation by the following relation:

${\displaystyle {\frac {1}{\kappa }}{\frac {\partial p}{\partial t}}={D}^{v}}$

(44)

where ${\textstyle {\kappa }}$ is the bulk modulus of the material and ${\textstyle {{D}^{v}=trace(D)}}$ is the volumetric strain rate. Eq.(44) is the closure equation for the mixed velocity-pressure formulation.

3.2 Time integration

As regards the variation on time of the pressure, a linear scheme has been adopted. That is because in fluid dynamics the lagrangian mesh suffers large displacements and the nodal pressure information of the previous time steps has to be recovered by means of an adequate interpolation. This operation introduces approximation errors in the scheme that increase beyond the current time step. This also has a huge computational cost because the information of the previous steps has to be stored. With the procedure here presented only the current time step is needed and only the first variation in time of pressure has to be saved. Hence, the first and the second variations in time of the pressure are respectively:

${\displaystyle {^{n+1}{\dot {p}}}={\frac {^{n+1}{p}-{^{n}p}}{\Delta t}}}$

(45)

${\displaystyle {^{n+1}{\ddot {p}}}={\frac {^{n+1}{p}-{^{n}p}}{{\Delta t}^{2}}}-{\frac {^{n}{\dot {p}}}{\Delta t}}}$

(46)

Using Eq.(45), the time discretization of Eq.(44) within the time interval ${\textstyle {[n,n+1]}}$ of duration ${\textstyle {\Delta t}}$ leads to:

${\displaystyle ^{n+1}p=^{n}p+\Delta t\kappa ^{n+1}{D}^{v}}$

(47)

3.3 Fully discretized form and incremental solution scheme

As already mentioned, the pressure field is interpolated with the same linear shape functions used for the velocity field (Eqs.(8)). So:

${\displaystyle p=\sum \limits _{I=1}^{n}N_{I}{\bar {p}}_{I}}$

(48)

The Galerking-FEM approximation of the global form of Eq.(47) leads to the following matrix form:

${\displaystyle -{\bf {Q}}^{T}{^{n+1}{\bar {\bf {v}}}}+{\frac {1}{\Delta t}}{\bf {M}}_{1}{^{n+1}{\bar {\bf {p}}}}}$ ${\displaystyle ={^{n}g}}$

(49)

where:

${\displaystyle {M}_{1_{IJ}}=\int _{\Omega ^{e}}N_{I}{\frac {1}{\kappa }}N_{J}d\Omega }$

(50)

${\displaystyle {\bf {Q}}_{IJ}=\int _{\Omega ^{e}}{\bf {B}}_{I}^{T}{\bf {m}}N_{J}d\Omega }$

(51)

${\displaystyle ^{n}g_{I}=\int _{\Omega ^{n}}N_{I}{\frac {1}{\kappa \Delta t}}N_{J}d{\Omega }{^{n}{\bar {p}}}_{J}}$

(52)

with

Finally, for ensuring the coupling of the linear momentum equations with Eq.(49), the pressure must be expressed explicitly in the residual of the momentum equations (Eqs.(40)). For this reason, in Eq.(40) the Cauchy stress tensor is split into its deviatoric and pressure parts via Eq.(41). The resulting residual form is

${\displaystyle R_{Ii}^{n+1}=\int _{\Omega }N_{I}\rho N_{J}d\Omega {\bar {\dot {v}}}_{Ji}^{n+1}+\int _{\Omega }{\frac {\partial N_{I}}{\partial x_{j}}}\sigma _{ij}^{n+1}d\Omega -\int _{\Omega }{\frac {\partial N_{I}}{\partial x_{j}}}\delta _{ij}N_{J}d\Omega {\bar {p}}_{J}^{n+1}+}$ ${\displaystyle -\int _{\Omega }N_{I}b_{i}^{n+1}d\Omega -\int _{\Gamma _{t}}N_{I}t_{i}^{p,n+1}d\Gamma =0}$

(53)

In Box 2, the iterative solution incremental solution scheme for a generic continuum using the mixed velocity-pressure formulation is shown for a time increment ${\textstyle {}}$.

4 Constitutive laws

In the formulation derived so far the constitutive model has not been specified. The only requirement stated so far is that the relation between the rate of the Cauchy stress and the rate of deformation is linear (Eq.(29)). This means that the constitutive relation must be rate-independent, incrementally linear and reversible [25].For small increments the relation between the stress and strain increments is linear and they are recovered upon unloading. However, for large deformations, the energy is not necessarily conserved and the work done in a closed deformation path is not necessarily zero [3].

As it has already been pointed out, the Cauchy stress tensor, or its deviatoric part, still appear explicitly (36, 40) in the formulation. In the present section, the formulation will be adapted to specific constitutive laws and the stress tensor will be defined in terms of the nodal velocities.

First, it will be shown that both the velocity and the mixed velocity-pressure formulations hold for hypoelastic materials. Then, the case of quasi-incompressible Newtonian fluids will be studied. Due to the (quasi) incompressibility constraint, the fluid problem can be solved only using the mixed velocity-pressure formulation. Furthermore, because linear shape functions have been used for the interpolation of both the velocity and pressure fields, the ${\textstyle {inf-sup}}$ condition [4] is not satisfied and the solution needs to be stabilized.

For both constitutive relations, the complete form of the tangent matrix will be derived and the incremental solution scheme will be explained in detail.

4.1 Hypoelastic material

The direct relation between the rate of stress and the rate of deformation is the main feature of hypoelastic material laws. In a large class of these, this relation is linear. The fundamental requirement for the stress rate measures is that they must be objective, or, equally, frame-invariant. If not, many inconveniences can appear; for instance, rigid rotations can originate undesiderable states of stress. Many objective measures for the stress rates are available; the most common ones are the Truesdell and Jaumann measures of the Cauchy stress rate.

In this section, both the velocity and the mixed formulations are adapted for hypoelastic solids.

Velocity formulation

The Truesdell and Jaumann measures of the Cauchy stress rate are defined, respectively, as

${\displaystyle \sigma ^{\bigtriangledown \tau }=C^{\sigma \tau }:D}$

(54)

${\displaystyle \sigma ^{\bigtriangledown J}=C^{\sigma J}:D}$

(55)

where ${\textstyle {C^{\sigma \tau }}}$ and ${\textstyle {C^{\sigma J}}}$ are the Truesdell and Jaumann tangent moduli and the relation between the two tensors is

${\displaystyle C^{\sigma \tau }=C^{\sigma J}-C^{*}}$

(56)

where:

${\displaystyle C_{ijkl}^{\sigma J}=\lambda \delta _{ij}\delta _{kl}+\mu \left(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{kj}\right)}$

(57)

${\displaystyle C_{ijkl}^{*}={\frac {1}{2}}\left(\delta _{ik}\sigma _{jl}+\delta _{il}\sigma _{jk}+\delta _{jk}\sigma _{il}+\delta _{jl}\sigma _{ik}\right)-\delta _{kl}\sigma _{ij}}$

(58)

where ${\textstyle {\lambda }}$ and ${\textstyle {\mu }}$ are the Lamé constants.

Eqs.(54-58) show that, contrary to the Truesdell measure, the Jaumann tangent moduli tensor ${\textstyle {C^{\sigma J}}}$ is symmetric. This feature represents the main advantage of the Jaumann measure and it explains why it is the largest used measure of the Cauchy stress rate. However, the Jaumann stress rate represents an approximation of the Truesdell's one. The solution given by the latter is more accurate especially for shear-dominant problems [3].

The material rate for the Cauchy stress tensor can be computed as:

${\displaystyle {\dot {\sigma }}=\sigma ^{\bigtriangledown \tau }+\Omega ^{\bigtriangledown \tau }}$

(59)

${\displaystyle {\dot {\sigma }}=\sigma ^{\bigtriangledown J}+\Omega ^{\bigtriangledown J}}$

(60)

where ${\textstyle {\Omega ^{\bigtriangledown \tau }}}$ and ${\textstyle {\Omega ^{\bigtriangledown J}}}$ are the part of the material rate of the Cauchy stress due to the rotations for the Truesdell and the Jaumann measures, respectively. They are defined as follows:

${\displaystyle \Omega ^{\bigtriangledown \tau }=-W\cdot \sigma -\sigma \cdot W^{T}}$

(61)

${\displaystyle \Omega ^{\bigtriangledown J}=W\cdot \sigma +\sigma \cdot W^{T}}$

(62)

where ${\textstyle {W}}$ is the spin tensor defined as

${\displaystyle W_{ij}={\frac {1}{2}}\left(L_{ij}-L_{ji}\right)={\frac {1}{2}}\left({\frac {\partial v_{i}}{\partial x_{j}}}-{\frac {\partial v_{j}}{\partial x_{i}}}\right)}$

(63)

Discretizing in time and introducing the constitutive laws into Eqs.(59 and 60), for the time step increment ${\textstyle {}}$ the following relations hold

${\displaystyle {\frac {{^{n+1}\sigma }-{^{n}\sigma }}{\Delta t}}={^{n+1}C}^{\sigma \tau }:{^{n+1}D}-{^{n+1}W}\cdot {^{n+1}\sigma }-{^{n+1}\sigma }\cdot {^{n+1}W^{T}}}$

(64)

${\displaystyle {\frac {{^{n+1}\sigma }-{^{n}\sigma }}{\Delta t}}=C^{\sigma J}:{^{n+1}D}+{^{n+1}W}\cdot {^{n+1}\sigma }+{^{n+1}\sigma }\cdot {^{n+1}W}^{T}}$

(65)

Relations (64) and (65) are not linear and the Cauchy stress tensor can not be computed explicitly. Hence, the stress tensor has to computed iteratively within the loop of the incremental solution scheme described in Box 1. Once the Cauchy stress tensor has been computed, it has to be introduced into the geometric part of the tangent matrix (36) and into the residual term (40). Concerning the material part (30), the tangent moduli tensor has to be replaced at each iteration only if the Truesdell stress measure is used. In fact, the Jaumann tangent moduli tensor does not change with time and it can be computed only once at the beginning of the analysis.

In Box 3, the iterative solution incremental solution scheme for hypoelastic solids using the velocity formulation is described for a generic time increment ${\textstyle [n,n+1]}$.

Mixed velocity - pressure formulation

In order to solve an hypoelastic solid with the mixed velocity-pressure formulation, the modifications over the velocity scheme described in Section 3 have to be introduced.

The deviatoric part of the Truesdell and Jaumann stress rate measure are:

${\displaystyle \sigma '^{\bigtriangledown \tau }=C^{\sigma '\tau }:D^{dev}}$

(66)

${\displaystyle \sigma '^{\bigtriangledown J}=C^{\sigma 'J}:D^{dev}}$

(67)

where ${\textstyle {C^{\sigma '\tau }}}$ and ${\textstyle {C^{\sigma 'J}}}$ are defined as

${\displaystyle C^{\sigma '\tau }=C^{\sigma 'J}-C'^{*}}$

(68)

with:

${\displaystyle C_{ijkl}^{\sigma 'J}=\mu \left(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{kj}\right)}$

(69)

${\displaystyle {C'}_{ijkl}^{*}={\frac {1}{2}}\left(\delta _{ik}\sigma '_{jl}+\delta _{il}\sigma '_{jk}+\delta _{jk}\sigma '_{il}+\delta _{jl}\sigma '_{ik}\right)-\delta _{kl}\sigma '_{ij}}$

(70)

Using the time discretization described in Eqs.(59-65) the material rate for the Cauchy stress tensor can be computed as:

${\displaystyle {\frac {{^{n+1}\sigma '}-{^{n}\sigma '}}{\Delta t}}={^{n+1}C}^{\sigma '\tau }:{^{n+1}D^{dev}}+\Omega '^{\bigtriangledown \tau }}$

(71)

${\displaystyle {\frac {{^{n+1}\sigma '}-{^{n}\sigma '}}{\Delta t}}=C^{\sigma 'J}:{^{n+1}D^{dev}}+\Omega '^{\bigtriangledown J}}$

(72)

with:

${\displaystyle \Omega '^{\bigtriangledown \tau }=-{^{n+1}W}\cdot {^{n+1}\sigma '}-{^{n+1}\sigma '}\cdot {^{n+1}W^{T}}}$

(73)

${\displaystyle \Omega '^{\bigtriangledown J}={^{n+1}W}\cdot {^{n+1}\sigma '}+{^{n+1}\sigma '}\cdot {^{n+1}W}^{T}}$

(74)

As for Eqs. (64) and (65), the computation of the deviatoric part of the Cauchy stress tensor (Eqs. (71) and (72)) is performed iteratively within the global solution scheme.

In Box 4, the iterative solution incremental scheme for hypoelastic solids using the mixed velocity-pressure formulation is described for a generic time increment ${\textstyle [n,n+1]}$.

Note that the linear momentum and the continuity equations can be easily decoupled. For this purpose, the residual of the linear momentum equations is written in terms of the Cauchy stress and this tensor is computed using the velocity only and not as the sum of its deviatoric part and the pressure. In this case, a velocity formulation is recovered because the continuity equation is used to compute the pressures only.

4.2 Quasi-incompressible Newtonian fluid

The formulation is here adapted to the case of quasi-incompressible Newtonian fluids. Considering a quasi-incompressible fluid is equivalent to solving a Navier-Stokes problem where the divergence of the velocity is not required to vanish in the continuity equation. At the same time, this compressibility is such small that the variation with time of the density is considered null as for a fully incompressible material. As already mentioned, in order to avoid the numerical instabilities, for this type of material only the mixed velocity-pressure formulation can be used with confidence. In this work, the fluid is discretized using the Particle Finite Element Method (PFEM) (www.cimne.com/pfem) [5,17,19]. The essential features of the PFEM will be given in Section 4.2.3. The same linear interpolation has been used for the velocity and pressure fields. It is well known that this combination does not fulfill the ${\textstyle {inf-sup}}$ condition [4] and the solution needs to be stabilized. In this work, the required stabilization is provided by the Finite Calculus (FIC) technique presented in [22]. The stabilization terms only affect the continuity equation. In conclusion, the momentum equation is modified only by introducing the Newtonian constitutive law into the internal component of the tangent matrix.

First of all the constitutive law for a Newtonian fluid is recalled as

${\displaystyle \sigma =\sigma '-pI=2\mu D^{dev}-pI}$

(75)

where ${\textstyle {\mu }}$ is the fluid viscosity.

For Newtonian fluids the governing equations are Eqs.(1) and (44). Note that, if a fully-incompressible material is considered, ${\textstyle {\kappa \rightarrow \infty }}$ and the standard form of the incompressibility equation is recovered from Eq.(44) (${\textstyle {{D}^{v}}=0}$).

Considering a time interval ${\textstyle {[n,n+1]}}$ and substituting Eq.(47) into Eq.(41) yields:

${\displaystyle ^{n+1}\sigma =\left(2\mu I^{dev}-\Delta t\kappa I\otimes I\right):D-^{n}pI}$

(76)

where:

${\displaystyle I^{dev}=I-{\frac {1}{3}}I\otimes I}$

(77)

For convenience, Eq.(76) is rewritten in the following form:

${\displaystyle ^{n+1}\Delta \sigma =^{n+1}\sigma -^{n}\sigma =\left(C^{d}+C^{\kappa }\right):D}$

(78)

where the following substitutions have been done:

${\displaystyle ^{n}\sigma _{ij}=-^{n}pI}$

(79)

${\displaystyle C^{d}=2\mu I^{dev}}$

(80)

${\displaystyle C^{\kappa }=-\Delta t\kappa I\otimes I}$

(81)

The goal is to obtain a relation between the measure of rate of stress and the rate of deformation similar to the one introduced in the material part of the tangent matrix (Eq.(29)). As shown in Eq.(78), in fluids the rate of deformation is related through the constitutive parameter to Cauchy stress and not to rate of the Cauchy stress, as for Eq.(29). For this reason, in fluids the concept of objectivity of the stress rate measures is not as important as for solids. Rigid rotations do not cause any state of stress, because the Cauchy stress is expressed in term of the rate of deformation. For these reasons, the rate of Cauchy stress can be simply defined using Eq.(78) as:

${\displaystyle {\dot {\sigma }}={\frac {\Delta \sigma }{\Delta t}}=\left({\frac {C^{d}}{\Delta t}}+{\frac {C^{\kappa }}{\Delta t}}\right):D}$

(82)

Note that Eq.(82) has the same structure as Eq.(29). For convenience, the constitutive matrix has been split in the deviatoric and volumetric part. As a consequence, for a quasi incompressible Newtonian fluid, the material part of the tangent matrix is written as the sum of two submatrices defined as follows:

${\displaystyle K_{NF}^{m}=K^{\mu }+K^{\kappa }}$

(83)

where ${\textstyle {K^{\mu }}}$ and ${\textstyle {K^{\kappa }}}$ are defined for a generic finite element ${\textstyle {e}}$ and the pair of nodes ${\textstyle {I,J}}$ as:

${\displaystyle K_{IJ}^{\mu }=\int _{\Omega ^{e}}B_{I}^{eT}C^{\mu }B_{J}^{e}d\Omega }$

(84)

${\displaystyle K_{IJ}^{\kappa }=\int _{\Omega ^{e}}B_{I}^{eT}m\kappa m^{T}B_{J}^{e}d\Omega }$

(85)

${\textstyle {\begin{array}{l}\\{\hbox{with}}{C^{\mu }}=\mu \left[{\begin{array}{cccccc}2/3&-1/3&-1/3&0&0&0\\&2/3&-1/3&0&0&0\\&&2/3&0&0&0\\&&&1&0&0\\{Sym.}&&&&1&0\\&&&&&1\\\end{array}}\right]\\\\\end{array}}}$

The volumetric part of the tangent matrix can compromise the conditioning of the linear system because its terms are orders of magnitude larger than the viscous part. In order to prevent the numerical instabilities originated by the ill-conditioning of the tangent matrix, a reduced pseudo-bulk modulus can be used in the expression of ${\textstyle {K^{\kappa }}}$ without altering the numerical results [12].

Concerning the material part of the tangent matrix, the form of Eq.(36) holds also for quasi-incompressible Newtonian fluids. Now the Cauchy stress tensor should be simply replaced with the expression obtained using Eq.(76).

4.2.1 Stabilization procedure using FIC

The interpolation orders of the velocity and pressure fields do not fullfil the so-called ${\textstyle {LBBinf-supcondition}}$ [4]. Consequently the numerical scheme needs to be stabilized. The required stabilization is introduced via the Finite Calculus (FIC) technique presented in [22]. In the mentioned work, a FIC-based stabilized finite element formulation for quasi-incompressible Lagrangian fluids is presented and successfully applied to the analysis of several free-surface flow problems. The formulation has excellent mass preservation features. The details of this stabilized formulation lie outside the objectives of this work and can be found in [22]. As already mentioned, this stabilization technique only affects the continuity equation (Eq.(44)) and not the linear momentum equations (Eq.(9)).

The fully-discretized form of the stabilized mass conservation equation reads

${\displaystyle \left({\frac {1}{\Delta t}}{\hbox{M}}_{1}+{\frac {1}{{\Delta t}^{2}}}{\hbox{M}}_{2}+{L}+{M}_{b}\right){^{n+1}{\bar {p}}}={Q}^{T}{^{n+1}{\bar {v}}}+{^{n}g}^{S}}$

(86)

where:

${\displaystyle ^{n}{g}^{S}={f}_{p}+{\frac {1}{\Delta t}}{\hbox{M}}_{1}{^{n}{\bar {p}}}+{\frac {1}{\Delta t}}{\hbox{M}}_{2}\left({\frac {^{n}{\bar {p}}}{\Delta t}}+{^{n}{\dot {\bar {p}}}}\right)}$

(87)

with:

${\displaystyle {\begin{array}{l}\displaystyle \displaystyle {M}_{2_{IJ}}=\int _{\Omega ^{e}}{\frac {\tau }{\kappa }}N_{I}N_{J}d\Omega ~{where}\displaystyle ~\tau =\left({\frac {8\mu }{h^{2}}}+{\frac {2\rho }{\delta }}\right)^{-1}\\[.4cm]\displaystyle {M}_{b_{IJ}}=\int _{\Gamma _{t}}{\frac {2\tau }{h_{N}}}N_{I}N_{J}d\Gamma ~;~L_{IJ}=\int _{\Omega ^{e}}\tau \left(\bigtriangledown ^{T}N_{I}\right)\bigtriangledown N_{J}d\Omega ;\\[.4cm]\displaystyle f_{p_{I}}=\int _{\Gamma _{t}}q\tau N_{I}\left[{\frac {Dv_{N}}{Dt}}-{\frac {2}{h_{N}}}(2\mu D_{N}-t_{N})\right]d\Gamma -\int _{\Omega ^{e}}\tau {\bigtriangledown ^{T}N_{I}{b}}d\Omega \end{array}}}$

where ${\textstyle {\tau }}$ is the stabilization parameters and ${\textstyle {h}}$ and ${\textstyle {\delta }}$ are characteristic distances in space and time, respectively. In practice, ${\textstyle {h}}$ and ${\textstyle {\delta }}$ have the order of magnitude of the element size and the time step increment, respectively. The subscripts ${\textstyle {(\cdot )_{N}}}$ denote the normal component of the variable.

4.2.2 Incremental solution scheme

For treating Newtonian quasi-incompresible fluids, the iterative scheme for the mixed formulation described in Box 2 has to be modified slightly for taking into account the features of the material described at the beginning of this section. In particular, the material part tangent matrix in the momentum equations has two contributions (Eqs.(84) and (85)), the continuity equation must be considered in its stabilized form (Eq.(86)) and, obviously, the stress measures are computed using the Newtonian constitutive law (Eq.(41)).

The incremental iterative solution scheme for a quasi incompressible Newtonian fluid is described for a generic time increment ${\textstyle [n,n+1]}$ in Box 5.

4.2.3 About the Particle Finite Element Method (PFEM)

The Particle Finite Element Method is a particular class of Lagrangian finite element formulation. Its efficacy has been proved in many scientific publications, as [17], [21] and many others. PFEM treats the mesh nodes in the fluid and solid domains as particles which can freely move and even separate from the main fluid domain representing, for instance, the effect of water drops. A mesh connects the nodes discretizing the domain where the governing equations are solved using a stabilized FEM. These characteristic features makes this method the ideal instrument to model and simulate free surface flows.

Consider a global domain containing a fluid and a solid subdomains. In the PFEM both subdomains are modelled using an updated Lagrangian formulation. The finite element method (FEM) is used to solve the equations of continuum mechanics for each of the subdomains. Hence a mesh discretizing these domains is generated in order to solve the governing equations for each subdomain in the standard FEM fashion.

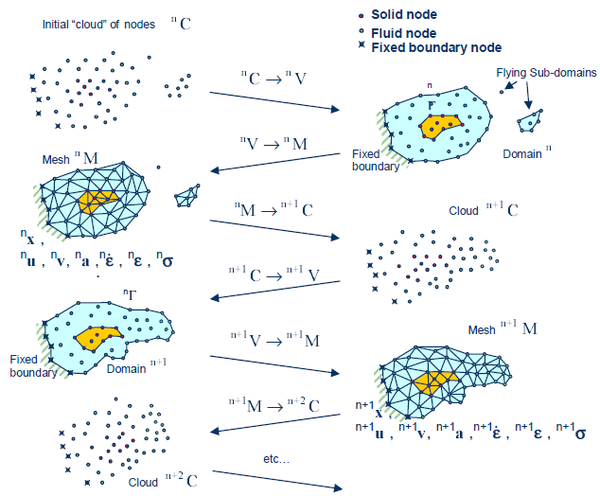
For clarity purposes, the collection or cloud of nodes pertaining to the fluid and solid domains is defined C, the volume defining the analysis domain for the fluid and the solid is termedVand the mesh discretizing both domains is called M.

The solution steps within a time step are as follows:

Figure 1: Sequence of steps to update a “cloud” of nodes representing a domain containing a fluid and a solid part from time ${\displaystyle n}$ (${\displaystyle t=^{n}t}$) to time ${\displaystyle n+2}$ (${\displaystyle t=^{n}t+2\Delta t}$)

1. The starting point at each time step is the cloud of points in the fluid and solid domains. For instance ${\textstyle ^{n}C}$ denotes the cloud at time ${\textstyle t=^{n}t}$ Fig.(1).
2. Identify the boundaries of both the fluid and solid domains defining the analysis domain ${\textstyle ^{n}V}$ in the fluid and the solid. This is an essential step as some boundaries (such as the free surface in fluids) may be severely distorted during the solution, including separation and re-entering of nodes. The Alpha Shape method [10] is used for the boundary definition.
3. Discretize the fluid and solid domains with a finite element mesh${\textstyle ^{n}M.}$ In this work, an efficient mesh generation scheme based on the extended Delaunay tesselation [15] is used.
4. Solve the Lagrangian equations of motion for the overall continuum. Compute the state variables in at the next (updated) configuration for ${\textstyle t+\Delta t}$: velocities, pressure and viscous stresses in the fluid and displacements, stresses and strains in the solid.
5. Move the mesh nodes to a new position ${\textstyle ^{n+1}C}$ where n+1 denotes the time ${\textstyle t^{n}+\Delta t}$, in terms of the time increment size. This step is typically a consequence of the solution process of step 4.
6. Go back to step 1 and repeat the solution for the next time step to obtain${\textstyle ^{n+2}C}$

It is to note that the key differences between the PFEM and the classical FEM are the remeshing technique and the identification of the domain boundary at each time step.

The quality of the numerical solution depends on the discretization chosen as in the standard FEM. Adaptive mesh refinement techniques can be used to improve the solution.

5 Coupling strategy for fluid-structure interaction (FSI) analysis

In this section the coupling strategy for solving FSI problems using the unified formulation is described and tested. The algorithm uses the same mixed velocity-pressure formulations for hypoelastic solids and Newtonian fluids. As explained in the previous sections, in the unified formulation solids and fluids are treated practically in the same way. Apart from the material parameters, the analysis of newtonian fluids and hypoelastic solids with the PFEM formulation here presented differs only for the stabilization and the remeshing step that are implemented for the fluid only. Solids and fluids have many common points: they use the same set of the same unknown variables (velocities and pressure), the same framework (Lagrangian) and the same solution scheme (Gauss-Seidel). All these common features simplify the solution of the FSI problems with a monolithic scheme. In summary fluids and solids can be easily solved within a unique system of equations.

The main advantage of the monolithic scheme versus the staggered approach, is that it ensures a strong coupling automatically. In fact in the staggered schemes, a few iterations may be necessary in order to obtain a similar degree of coupling as for a monolithic scheme.

On the other hand, a monolithic scheme can lead to ill-conditioned linear systems because the order of magnitude of the terms corresponding to the fluid and the solid parts of the domain may be very different. In this work, this drawback is overcome via the segregated scheme and the unified formulation. In fact, the partitioning of the governing equations separates the velocity and pressure unknowns and the matrices referred to them. In this way the size of the matrices is reduced and its conditioning is improved as the risk of mixing in the same matrix terms with different order of magnitude is prevented. Moreover, in the unified formulation the solid and the fluid use the same nodal unknowns. As consequence, the fluid and solid matrices terms differ only in the material constants and in for the variable transformation.

By using the unified formulation and the PFEM, FSI problems can be solved in a natural way. It essentially consists in performing two tasks: to detect the interface for creating the coupling elements (elements that share at least one interface node) and to assembly properly the global system.

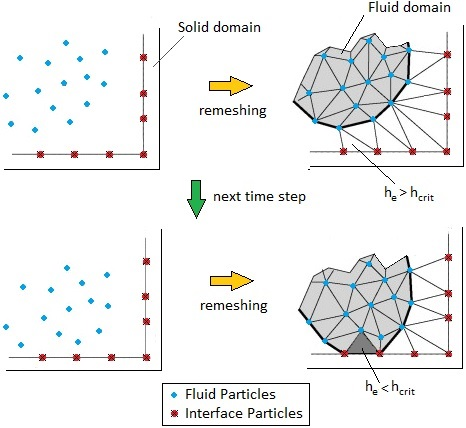
As explained in the previous sections, the classical FEM is used for the solid while the PFEM is adopted for the fluid. Hence, the solid domain keeps the same grid during all over the analysis, whereas a remeshing of the fluid domain is performed whenever its discretization becomes excessively distorted as it is typically done in the PFEM. The nodes over the boundaries of the solid are the interface nodes, and they may be part of the fluid domain too. The solid boundaries are detected by exploiting the capability of the PFEM to match contours. In practise, the fluid domain detect the solid interface in the same way it recognizes its fixed contours. This represents one of the key features of the PFEM. The technique uses an extended Delaunay partition for recognizing boundary nodes [15]. For all the nodes a characteristic length h, typically the minimum distance between two nodes, is assigned. All the nodes on an empty sphere with a radius greater than a critical value are considered as boundary nodes. The critical value is defined as ${\textstyle {h_{crit}=\alpha h}}$, where ${\textstyle \alpha }$ is a parameter close to one (typically, values of ${\textstyle \alpha }$ ranging between 1.3 and 1.5 are chosen). This criterion is coincident with the Alpha Shape concept [10]. In this way, the fluid boundaries are recognized exactly. In the case of FSI problems, this test is realized also on the solid interface particles. If the fluid domain is sufficiently close to the interface, at least, one interface node will have the variable h smaller than ${\textstyle {h_{crit}}}$. If this occurs, an element joining the fluid domain and the solid interface will be built, whereas the two domains keep separated. Fig. 2 shows a graphic representation of this technique. In order to avoid that particles of fluid pass through the solid boundary, the solid discretization in the region close to the interface should have a size similar to that used for the fluid mesh.

Figure 2: Detection of the interface using PFEM

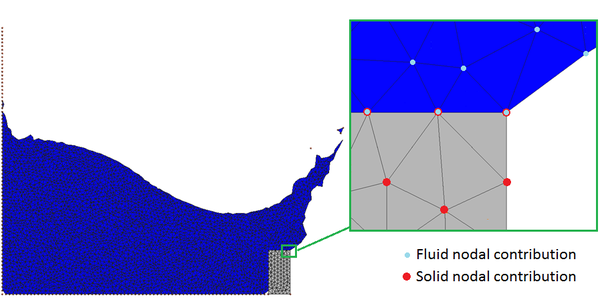
When at least one coupling element is created, there will be some nodes on the interface that belong to both the solid and the fluid domains. In regard to the DOFs of these nodes, the velocities are the same as for the fluid and the solid (in this way the Dirichlet condition is prescribed strongly) while the pressure DOFs must be duplicated. In fact, along the interface the Neumann transmission condition has to be imposed (in weak form) on the normal component of the Cauchy stress and not on the pressure. Hence only for the momentum equations, the interface nodes contribute to the global linear system the sum of the contributions of the solid and the fluid elements they are sharing, as represented in Fig.3.

Figure 3: Graphic representation of domain contributions to the momentum equations global system

6 Numerical examples

6.1 Collapse of a water column on a deformable elastic membrane

The problem is illustrated in Fig.(4) and it was introduced by Walhorn ${\textstyle {etal.}}$ in [27]. The water column collapses by instantaneously removing the vertical wall retaining the water. This originates the flow of water within the tank, the formation of a jet after the water stream hits the rigid step and the subsequent sloshing of the fluid as it impacts a highly deformable elastic membrane. The membrane bends and starts oscillating under the effect of its inertial forces and the impact with the water stream.

Figure 4: Collapse of a water column on a deformable membrane: starting geometry and problem data.

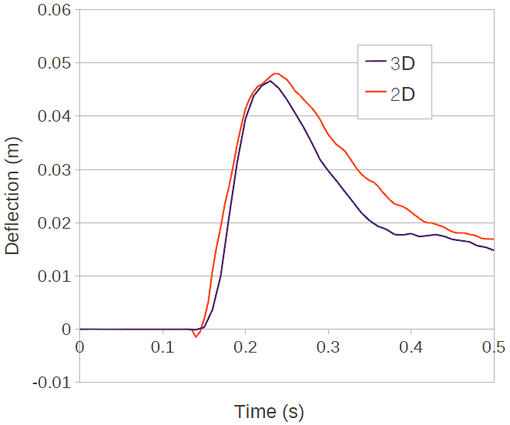
In Figs.(5,6) some representative snapshots of 2D and 3D numerical simulation results are illustrated. The results obtained with the present formulation have been compared with the ones computed by other formulations presented in scientific publications [13], [14] and [8]. In the graph of Fig.(7) the time evolution of the horizontal deflection of the right top corner is illustrated. The diagram shows that the present formulation agrees well with the results found in the literature. In the graph of Fig.(8) the numerical results obtained with the 2D and 3D simulations are compared.

(a) t = 0.235 s	(b) t = 0.515 s
(c) t = 0.595s
Figure 5: Collapse of a water column on a deformable membrane: snapshots at different instants of the 2D simulation.

t = 0.23 s	t = 0.49 s
t = 0.89 s
Figure 6: Collapse of a water column on a deformable membrane: snapshots of different instants of the 3D simulation.

Figure 7: Collapse of a water column on a deformable membrane: horizontal deflection of the right top corner on time. Comparison with numerical results obtained by other formulations. Curves '1', '2', '3' correspond to [27], [14] and [8] respectively

Figure 8: Collapse of a water column on a deformable membrane: horizontal deflection of the right top corner on time. Comparison between 2D and 3D analyses.

6.2 Water entry of a nylon sphere

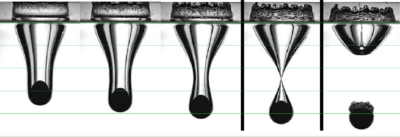
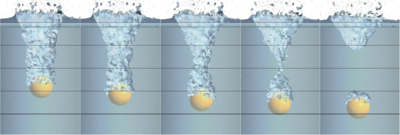
The problem was presented by Aristoff ${\textstyle {etal.}}$ in [1]. In the mentioned work the experimental results of the water entry of spheres of different materials are studied. In this section, the case of a nylon sphere is analyzed. The numerical results given by the unified formulation are compared with the results of the laboratory test. The sphere has a diameter of 2.54 cm and impacts the water in the tank with a vertical velocity of 2.17 ${\textstyle {m/s}}$. The density of nylon is 1140 ${\textstyle {kg/m^{3}}}$ and its Young modulus and Poisson coefficient are 3 ${\textstyle {GPa}}$ and 0.2, respectively. Water has been simulated considering a density of 1000 ${\textstyle {kg/m^{3}}}$, a dynamic viscosity 0.00089 ${\textstyle {Pa\cdot s}}$ and bulk modulus 2.15 ${\textstyle {GPa}}$. In order to simulate this problem correctly, a very fine mesh was necessary. For this reason the whole domain has been discretized using 1059924 tetrahedra. The time step used for the analysis is ${\textstyle {\Delta t=10^{-4}s}}$.

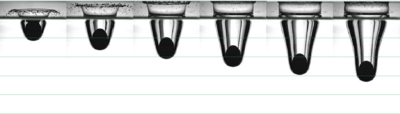
In Fig.(9) the numerical results are compared with the experimental ones published in [1]. The comparison shows the good agreement of the results obtained with the present formulation with the laboratory experience.

Figure 9: Water entry of a nylon sphere: comparison between experimental and numerical results.

7 Conclusions

A unified updated Lagrangian finite element formulation for solving FSI problems has been derived, discussed and tested. The method belongs to the monolithic strategies for FSI problems because both the solid and the fluid domains are solved with a general system of equations. First a velocity formulation for a general continuum has been derived. After that, the mixed velocity-pressure formulation has been obtained. After, both formulations have been adapted for specific materials. In this paper only hypoelastic solids and quasi incompressible fluids have been studied. However the formulation holds for other type of material, such as incompressible and elasto-plastic solids, among others.

It has been shown that the essential differences in the treatise of the fluid and the solid domain are the different meshing techniques and the inclusion of the stabilization terms in the mass balance equation of the fluid. In this work, the stabilized formulation emanates from the Finite Calculus (FIC) technique presented in [22]. Concerning the meshing, the Particle Finite Element Method is adopted for the fluid analysis, while for the discretization of the solid domain the classical FEM is used.

With the unified mixed formulation, both fluid and solid domains are solved in a Lagrangian framework via a Gauss-Seidel solution scheme using the velocities and the pressure as the unknown variables. All these common points facilitate the coupling for solving FSI problems. In fact, it has been shown that the coupling essentially consists in detecting the interface between the fluid and the solid domains and assembling the global system. It has been shown the importance of the PFEM for the former task.

Finally, the unified formulation has been tested solving different benchmark problems. In particular, the collapse of a water column on a deformable membrane and the water entry of a nylon sphere have been numerically studied in 2D and 3D. The comparison of the numerical results with the ones published in the literature and with scientific tests is fully satisfactory and evidences the efficiency and the accuracy of the proposed method.

BIBLIOGRAPHY

[1] J. Aristoff, T.T. Truscott, A.H. Techet, and J.W.M Bush. The water entry of decelerating spheres. Physics of Fluids, 22:032102, 2010.

[2] K.J. Bathe. Finite Element Procedures. Prentice-Hall, New Jersey, 1996.

[3] T. Belytschko, W.K. Liu, and B. Moran. Nonlinear Finite Elements For Continua And Structures. John Wiley & Sons, New York, 2000.

[4] F. Brezzi. On the existence, uniqueness and approximation of saddle-point problems arising from lagrange multipliers. Revue francaise d'automatique, informatique, recherche opérationnelle. Série rouge. Analyse numérique, 8(R-2):129–151, November 1974.

[5] J.M. Carbonell, E. Oñate, and B. Suarez. Modeling of ground excavation with the particle finite-element method. Journal of Engineering Mechanics, 136:455–463, 2010.

[6] M. Cervera, M. Chiumenti, and R. Codina. Mixed stabilized finite element methods in nonlinear solid mechanics: Part i: Formulation. Computer Methods In Applied Mechanics And Engineering, 199:2559–2570, 2010.

[7] M. Chiumenti, Q. Valverde, C. Agelet De Saracibar, and M.Cervera. A stabilized formulation for incompressible elasticity using linear displacement and pressure interpolations. Computer Methods In Applied Mechanics And Engineering, 191:5253–5264, 2002.

[8] M. Cremonesi. Doctoral thesis: A Lagrangian Finite Element Method for the Interaction Between Flexible Structures and Free Surfaces Fluid Flows. 2010.

[9] M. Cremonesi, A. Frangi, and U. Perego. A lagrangian finite element approach for the analysis of fluid–structure interaction problems. International Journal of Numerical Methods in Engineering, 84:610–630, 2010.

[10] H. Edelsbrunner and E.P. Mucke. Three dimensional alpha shapes. ACM Trans Graphics, 13:43–72, 1999.

[11] C.A. Felippa and K.C. Park. Staggered transient analysis procedures for coupled mechanical systems: Formulation. Computer Methods in Applied Mechanics and Engineering, 24:61–111, 1980.

[12] A. Franci, E. Oñate, and J.M. Carbonell. On the effect of the tangent bulk stiffness matrix in the analysis of free surface lagrangian flows using pfem. Researh Report CIMNE PI402Computational Mechanics, Submitted to International Journal for Numerical Methods in Engineering.

[13] B. Hubner, E. Walhorn, and D.Dinkler. A monolithic approach to fluid-structure interaction using space-time finite elements. Computer Methods in Applied Mechanics and Engineering, 193:2087–2104, 2004.

[14] S.R. Idelshon, J. Marti, A. Limache, and E. Oñate. Unified lagrangian formulation for elastic solids and incompressible fluids: Applications to fluid-structure interaction problems via the pfem. Computer Methods In Applied Mechanics And Engineering, 197:1762–1776, February 2008.

[15] S. Idelsohn, N. Calvo, and E. Oñate. Polyhedrization of an arbitrary point set. Computer Methods in Applied Mechanics and Engineering, 92(22–24):2649–2668, 2003.

[16] S.R. Idelsohn, M.Mier-Torrecilla, and E. Oñate. Multi-fluid flows with the particle finite element method. Computer methods in applied mechanics and engineering, 198:2750–2767, 2007.

[17] S.R. Idelsohn, E. Oñate, and F. Del Pin. The particle finite element method: a powerful tool to solve incompressible flows with free-surfaces and breaking waves. International Journal for Numerical Methods in Engineering, 61:964–989, 2004.

[18] S.R. Idelsohn, E. Oñate, F. Del Pin, and N. Calvo. Fluid-structure interaction using the particle finite element method. Computer methods in applied mechanics and engineering, 195:2100–2113, 2006.

[19] A. Larese, R. Rossi, E. Oñate, and S.R. Idelsohn. Validation of the particle finite element method (pfem) for simulation of free surface flows. International Journal for Computer-Aided Engineering and Software, 25:385–425, 2008.

[20] C. Michler, S.J. Hulshoff, and E.H. Van Brummelenand R. De Borst. A monolithic approach to fluid-structure interaction. Computers and Fluids, 33:839–848, 2004.

[21] E. Oñate, M.A. Celigueta, S.R. Idelsohn, F. Salazar, and B. Suarez. Possibilities of the particle finite element method for fluid–soil–structure interaction problems. Computation mechanics, 48:307–318, 2011.

[22] E. Oñate, A. Franci, and J.M. Carbonell. Lagrangian formulation for finite element analysis of quasi-incompressible fluids with reduced mass losses. International Journal for Numerical Methods in Fluids, 74.

[23] E. Oñate, A. Franci, and J.M. Carbonell. A particle finite element method for analysis of industrial forming processes. Computational Mechanics, DOI: 10.1007/s00466-014-1016-2.

[24] E. Oñate, J. Rojek, R.L. Taylor, and O.C. Zienkiewicz. Finite calculus formulation for incompressble solids using linear triangles and tetrahedra. International Journal For Numerical Methods In Engineering, 59:1473–1500, November 2004.

[25] W. Prager. Introduction to Mechanics of Continua. Ginn and Company, Boston, 1961.

[26] P.B. Ryzhakov, R. Rossi, S.R. Idelsohn, and E. Oñate. A monolithic lagrangian approach for fluid-structure interaction problems. Computational Mechanics, 46:883–899, 2010.

[27] E. Walhorn, A. Kolke B. Hubner, and D.Dinkler. Fluid-structure coupling within a monolithic model involving free surface flows. Computer Failed to parse (syntax error): {&}

Structures Methods in Applied Mechanics and   Engineering, 83 (25-26):2100–2111, 2005.

[28] C. Wood, A.J. Gil, O.Hassan, and J.Bonet. Partitioned block gauss-seidel coupling for dynamic fluid-strucure interaction. Computers and Structures, 88:1367–1382, 2010.