| Line 1: | Line 1: | ||
| + | A. Rodrigues<sup>1,2</sup>, L.M. Gramania<sup>1</sup>, E. Kaviskia<sup>1</sup> | ||
| + | |||
| + | <sup>1</sup> Programa de Pós-Graduação em Métodos Numéricos em Engenharia, UFPR,<br /> | ||
| + | Centro Politécnico, Curitiba, Paraná, Brasil<br /> | ||
| + | <sup>2</sup> Instituto Federal de Educação<br /> | ||
| + | Ciência e Tecnologia Catarinense, Araquari, Santa Catarina, Brasil | ||
| + | |||
| + | Submitted: 25/11/2016 | ||
| + | Accepted: 08/05/2017 | ||
| + | |||
| + | |||
==Resumo== | ==Resumo== | ||
Revision as of 13:41, 18 July 2017
A. Rodrigues1,2, L.M. Gramania1, E. Kaviskia1
1 Programa de Pós-Graduação em Métodos Numéricos em Engenharia, UFPR,
Centro Politécnico, Curitiba, Paraná, Brasil
2 Instituto Federal de Educação
Ciência e Tecnologia Catarinense, Araquari, Santa Catarina, Brasil
Submitted: 25/11/2016 Accepted: 08/05/2017
Resumo
Este artigo apresenta um novo esquema explícito para a solução das equações de águas rasas em uma e duas dimensões, desenvolvido a partir do método dos elementos de conservação e elementos de solução espaço-tempo, aqui abreviado por método CE/SE. As funções de base utilizadas são expansões de Taylor de segunda ordem no tempo e no espaço. Esse aumento na ordem das funções de aproximação produz o aumento no número de variáveis de marcha no tempo, por isso, além das variáveis fluxo e suas inclinações, também são incógnitas no presente esquema suas derivadas espaciais de segunda ordem. Um processo iterativo para o cálculo das derivadas de primeira e segunda ordem é formulado para problemas com choques e descontinuidades. Experimentos computacionais demonstram acurácia de terceira ordem. Os problemas de ruptura de barragem unidimensional e bidimensional considerados validam a acurácia e robustez do esquema.
Palavras-Chave: Leis de conservação, Equações de águas rasas, Volume de controle espaço-tempo, Alta ordem de acurácia.
Abstract
This paper presents a new explicit scheme for the solution of shallow water equations in one and two space dimensions, developed from the space-time conservation element and solution element (CE/SE) method. The basis functions used are second-order Taylor expansions in time and space. This increase in the order of the approximation functions produces an increase in the number of unknowns in the scheme, therefore, besides the flow variables and their slopes, their second-order partial derivatives are also unknown in the present scheme. An iterative process for the calculation of the first and second order derivatives is formulated for problems with shocks and discontinuities. Computational experiments demonstrate third-order accuracy. The one-dimensional and two-dimensional dam-break problems presented validate the accuracy and robustness of this scheme.
1 Introdução
As equações de águas rasas constituem um dos modelos mais comumente usados na análise de fluxo de água em rios ou áreas costais [1], sobretudo no que tange à simulações de fluxo de ruptura de barragem [2,3,4,5], parte essencial do projeto e avaliação da segurança de barragens, controle de inundação de rios, mitigação de desastres de bacias hidrográficas, etc [6]. Além da importância prática em hidráulica e engenharia costal, fornecem um ótimo modelo matemático para equações diferenciais hiperbólicas não lineares que podem ter soluções como ondas de choque [7] e, por isso, também são frequentemente utilizadas como problema de referência para novos esquemas de previsão numérica [8,9].
Extensivos estudos numéricos foram feitos no sentido de analisar os fenômenos governados por essas equações e diversos métodos foram desenvolvidos, como de volumes finitos [10,11,12], elementos finitos [13,14,15,16], diferenças finitas [17,18] e outros [19,20].
Recentemente, um novo método baseado em volumes de controle, denominado método dos elementos de conservação e elementos de solução espaço-tempo, do inglês, space-time conservation element and solution element method (CE/SE), foi proposto por Chang e To (1991) [21] e aplicações do mesmo em problemas de ruptura de barragem logo foram feitas [22,23,24]. Este método foi desenvolvido com o objetivo de obter soluções numéricas de leis de conservação e possui características importantes [25,26,27,28]: sua construção combina informações de ambas as formas diferencial e integral das leis de conservação; o conjunto de variáveis de marcha é formado pelas variáveis fluxo e suas derivadas espaciais; não são utilizadas técnicas de interpolação ou extrapolação nos valores da malha; não são utilizadas técnicas baseadas nas características, o que torna o método de fácil extensão à várias dimensões, bem como aplicável à equações não hiperbólicas, como as equações de Navier-Stokes, por exemplo; possui uma simples notação estêncil, o que facilita a programação. É caracterizado, também, por sua versatilidade, tendo em vista que pode ser adaptado à malhas não uniformes e não estruturadas [29,30], bem como pode ser estendido à altas ordens [31,32], razão pela qual possui aplicações nas mais diversas áreas [33,34,35,36].
O objetivo deste trabalho é apresentar a construção de um novo esquema CE/SE explícito de alta ordem para as equações de águas rasas e verificar sua eficiência em problemas de ruptura de barragem. Para isso, este artigo está organizado da seguinte maneira: na seção 2 é apresentado o modelo matemático a ser estudado (subseção 2.1), bem como é desenvolvido o esquema numérico discreto (subseção 2.2); na seção 3, experimentos numéricos unidimensionais e bidimensionais são considerados com a finalidade de validar o método; as conclusões são tecidas junto à seção 4 e, ao final, na seção 5, dispõe-se a lista de referências.
2 Equações Governantes e Método CE/SE
2.1 Equações de Águas Rasas
As equações de águas rasas, também conhecidas como equações de Saint Venant, possuem a seguinte forma vetorial conservativa
|
|
(1) |
em que
|
|
(2) |
|
|
(3) |
sendo a profundidade do fluxo (m); e são as velocidades médias do escoamento (m/s) nas direções e , respectivamente; é a aceleração da gravidade (m/s); e são as inclinações do fundo do canal cuja topografia é dada por ; e são os termos de resistência ao escoamento, nas direções e , respectivamente, definidos por
|
|
(4) |
em que (s/m) é o coeficiente de fricção de Manning.
2.2 Esquema CE/SE
Considere, por simplicidade, a Eq. (1) como
|
|
(5) |
então, pelo teorema da divergência no espaço , tem-se que a Eq. (5) representa a forma diferencial da lei integral de conservação
|
|
(6) |
em que , e representa o contorno de uma região espaço-tempo .
No método CE/SE, um elemento de conservação (CE) é uma região espaço-tempo em que a conservação do fluxo, Eq. (6), é forçada, enquanto que um elemento de solução (SE) é uma região espaço-tempo, normalmente distinta, em que as variáveis fluxo são supostamente suaves e a Eq. (5) é válida. Para definir estes dois importante objetos, considere primeiramente uma malha no plano -, conforme Fig. 1a. Existem dois grupos de pontos, marcados por círculos e cruzes, que representam nós da malha em dois níveis de tempo diferentes. A cada ponto da malha associa-se um CE e um SE. O CE é definido como o quadrilátero e o SE é a união do quadrilátero e o polígono (veja Fig. 1b).
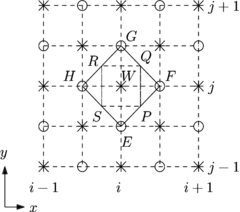
|
![a) Pontos da malha representativa no plano x-y e (b) as definições dos elementos de solução SE(i,j,k) e elementos de conservação CE(i,j,k) no ponto (i,j,k) da malha [2012_Zhang, 1999_Zhang].](/wd/images/thumb/3/39/Draft_Aparicio_Nogu%C3%A9_501194349-CE_2D.png/300px-Draft_Aparicio_Nogu%C3%A9_501194349-CE_2D.png)
|
| (a) | (b) |
| Figura 1: (a) Pontos da malha representativa no plano - e (b) as definições dos elementos de solução SE e elementos de conservação CE no ponto da malha [23,37]. | |
Para todo , aproxima-se por um polinômio de Taylor de segunda ordem
|
|
(7) |
Aproximações análogas são feitas sobre as funções e , . O termo fonte, por outro lado, é aproximado por uma ordem a menos:
|
|
(8) |
Dessa forma, a Eq. (5) pode ser aproximada no SE por div , em que , , ao mesmo tempo em que a Eq. (6) é aproximada no CE por
|
|
(9) |
2.2.1 Avaliação de 2.2.1 Avaliação de
(
q
m
)
i
,
j
k
{\displaystyle (q {m}) {i,j}^{k}}
Substituindo as funções e em (9), após diversas simplificações, obtém-se o esquema de avanço no tempo para a variável :
|
|
(10) |
em que
|
|
(11) |
É importante notar que as Equações (10) e (11) dependem apenas das incógnitas e do tempo , para pois, pelas Equações (1)-(4), , e também dependem destas últimas. Por outro lado, é preciso conhecer e previamente à obtenção de no tempo , conforme Eq. (10). A seção a seguir descreve a obtenção dessas derivadas espaciais duplas.
2.2.2 Avaliação de , e 2.2.2 Avaliação de
[
(
q
m
)
x
x
]
i
,
j
k
{\displaystyle [(q {m}) {xx}] {i,j}^{k}}
,
[
(
q
m
)
x
y
]
i
,
j
k
{\displaystyle [(q {m}) {xy}] {i,j}^{k}}
e
[
(
q
m
)
y
y
]
i
,
j
k
{\displaystyle [(q {m}) {yy}] {i,j}^{k}}
Para prosseguir com o cálculo de , constrói-se primeiramente uma equação auxiliar a partir da Eq. (5), derivando-a duas vezes em relação a , obtendo as seguintes formas diferencial e integral
|
|
(12) |
As Equações em (12) possuem, conforme Equações (7) e (8), para todo SE, os seguintes análogos numéricos:
|
|
(13) |
O campo vetorial aproximado é constante, de modo que a avaliação da Eq. (13) sobre o elemento de conservação descrito pela Fig. 1a retorna, para :
|
|
(14) |
Para computar as variáveis de marcha e procede-se de modo análogo, obtendo-se após todos os cálculos e simplificações:
|
Aborda-se na seção a seguir o cálculo das derivadas de primeira ordem das variáveis dinâmicas , .
2.2.3 Avaliação de e 2.2.3 Avaliação de
[
(
q
m
)
x
]
i
,
j
k
{\displaystyle [(q {m}) {x}] {i,j}^{k}}
e
[
(
q
m
)
y
]
i
,
j
k
{\displaystyle [(q {m}) {y}] {i,j}^{k}}
As variáveis e podem ser determinadas por meio de uma estratégia análoga àquela apresentada na seção [[#2.2.2 Avaliação de , e |2.2.2]] anterior, bastando, para isso, construir leis diferenciais de conservação (já nas formas aproximadas)
|
|
(17) |
e integrais
|
|
(18) |
As avaliações das equações em (18) fornecem as inclinações equacionadas por
|
|
(19) |
para e , em que
|
O esquema formado pelo conjunto de Equações (10), (14)-(16) e (19) é interessante apenas em problemas com soluções de comportamento suave. Para problemas com descontinuidades ou formação de choque, é necessário modificar o cálculo das variáveis em (14)-(16) e (19). A proposta apresentada neste artigo é uma variação do procedimento adotado por [38,39] e consiste num processo iterativo.
Para prosseguir, considere as seguintes formas regressivas e progressivas:
|
|
(22) |
tal que o operador seja definido como
|
|
(23) |
As aproximações para as derivadas serão definidas como
|
e a função [26,24]:
|
|
(26) |
Observe que neste caso, as Equações (24) e (25) representam médias ponderadas das diferenças progressivas e regressivas descritas em (22) e (23). No caso de , (24) e (25) tornam-se diferenças finitas centrais [23]. Adota-se neste trabalho .
Importante notar, no entanto, que as Equações (24) e (25) dependem da variável que, por sua vez, depende de e , conforme Eq. (10). Dito de outra forma, para obter é necessário obter antes e , e vice-versa. Para sanar esta dificuldade, construímos o processo iterativo descrito no Algoritmo 1.
A estabilidade do esquema CE/SE satisfaz a condição de Courant-Friedrichs-Lewy (CFL) que, para as equações de Saint Venant unidimensional e bidimensional são as restrições [23]
|
|
(27) |
respectivamente, onde o número de Courant satisfaz . Maiores detalhes sobre estabilidade do método CE/SE pode ser encontrado em [40].
3 Exemplos Numéricos
Esta seção tem por objetivo avaliar e validar o esquema numérico desenvolvido. Para isso, alguns problemas teste são avaliados, como testes de acurácia em uma e duas dimensões, bem como problemas clássicos de ruptura de barragem unidimensionais (subseção 3.1) e bidimensionais (subseção 3.2).
3.1 Exemplos Unidimensionais
Exemplo 3.1.1: O objetivo deste exemplo teste é verificar experimentalmente a ordem de acurácia do esquema CE/SE. Considere o sistema hiperbólico linear unidimensional
|
|
(28) |
e é uma constante dada. Impondo as condições inicias e , é possível obter a seguinte solução exata [41,42]:
|
|
(29) |
As soluções são computadas com as Equações (10), (14)-(16) e (19). A Tabela 1 apresenta os erros calculados nas normas e , nas simulações realizadas sobre o domínio computacional , , até atingir o tempo s, sendo o número de células no espaço. O experimento verifica a terceira ordem de acurácia do esquema para ambas as variáveis e .
| Norma | Norma | ||||||||
| n | Erro () | Ordem | Erro () | Ordem | Erro () | Ordem | Erro () | Ordem | |
| 20 | 8.322 | – | 1.662 | – | 7.157 | – | 1.347 | – | |
| 40 | 1.849 | 2.170 | 2.524 | 2.719 | 1.488 | 2.266 | 2.042 | 2.722 | |
| 80 | 3.067 | 2.592 | 3.401 | 2.892 | 2.443 | 2.607 | 2.715 | 2.911 | |
| 160 | 4.369 | 2.811 | 4.386 | 2.955 | 3.493 | 2.806 | 3.465 | 2.970 | |
| 320 | 5.813 | 2.910 | 5.566 | 2.978 | 4.665 | 2.904 | 4.369 | 2.987 | |
| 640 | 7.490 | 2.956 | 7.010 | 2.989 | 6.030 | 2.952 | 5.490 | 2.992 | |
Exemplo 3.1.2: Considera-se agora um problema ideal de ruptura de barragem sobre um domínio molhado, isto é, a quebra de barragem é instantânea, o fundo é plano e não existe resistência ao escoamento. As condições iniciais para esta configuração seguem o clássico problema de Riemann
|
|
(30) |
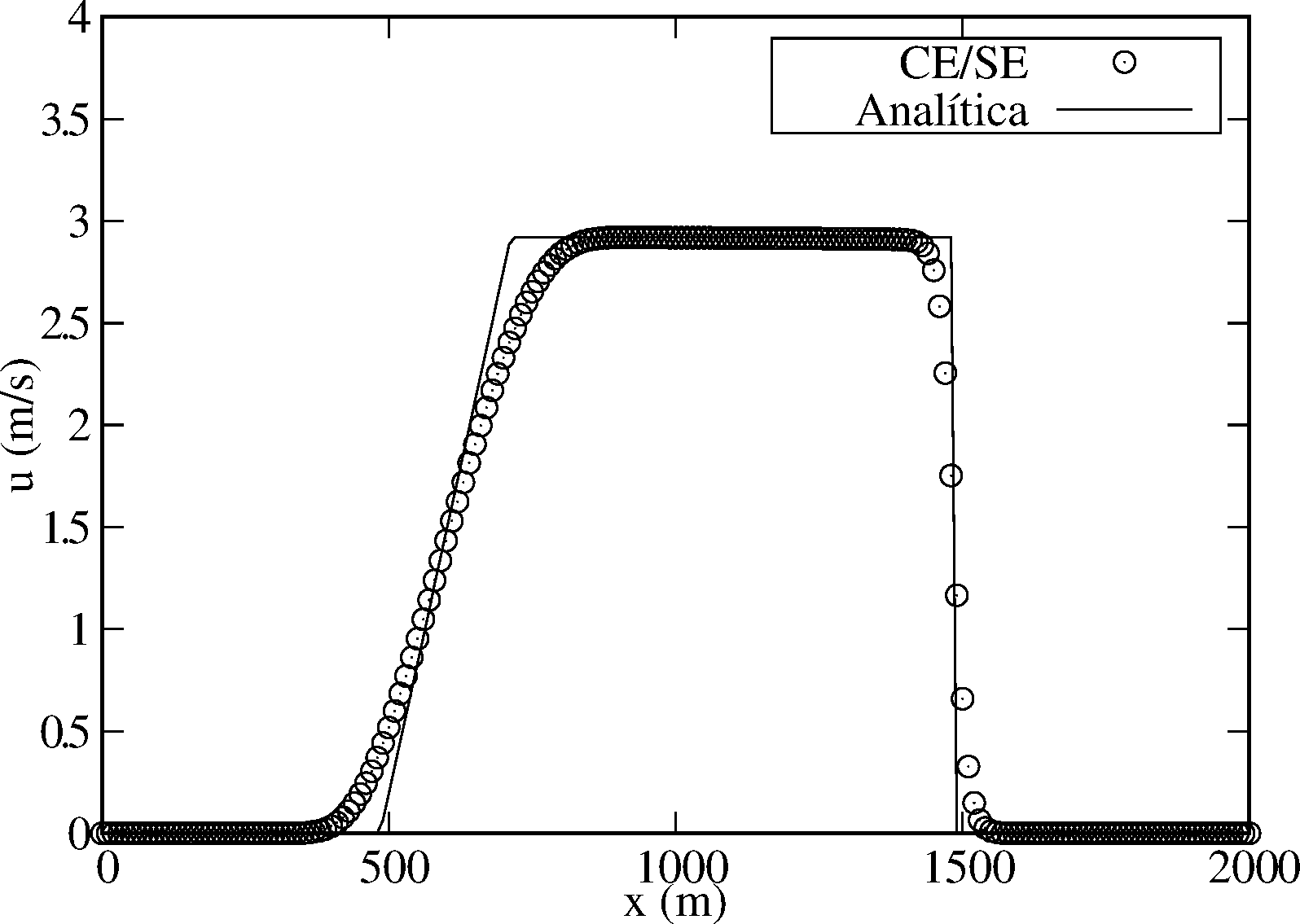
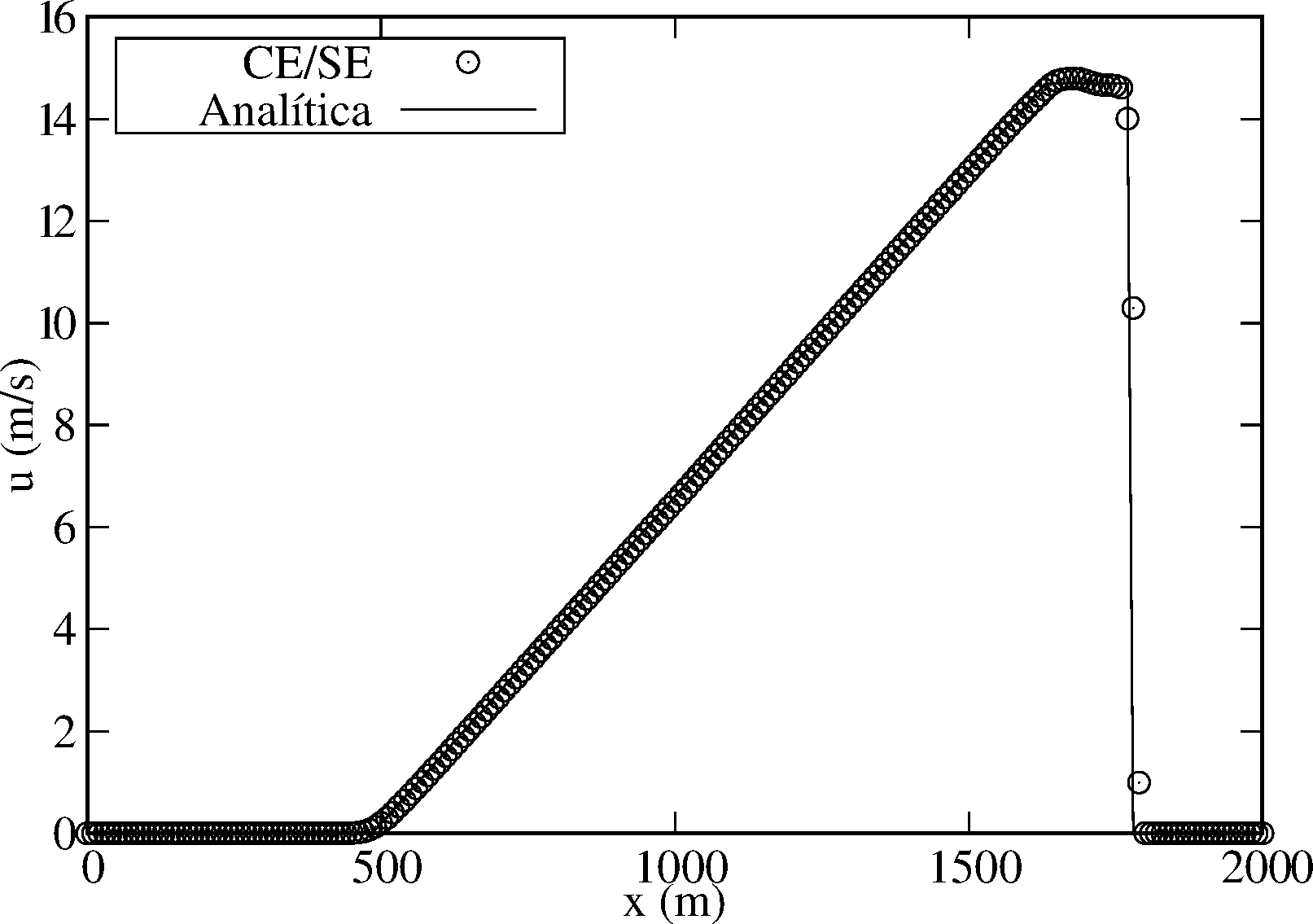
O domínio considerado é , e a solução analítica pode ser encontrada em [43] ou [44]. Utiliza-se, para fins de análise de comportamento, a mesma relação de equações do Ex. 3.1.1 anterior, isto é, Equações (10), (14)-(16) e (19). As Fig. 2a e Fig. 2b demonstram o comportamento da solução numérica em relação à analítica, calculadas no tempo , com pontos, incremento espacial , e profundidades iniciais a montante e a jusante e , respectivamente. Note que a resposta numérica é coerente com a analítica, embora apresente suavidade que a distancie nas regiões com mudanças abruptas.
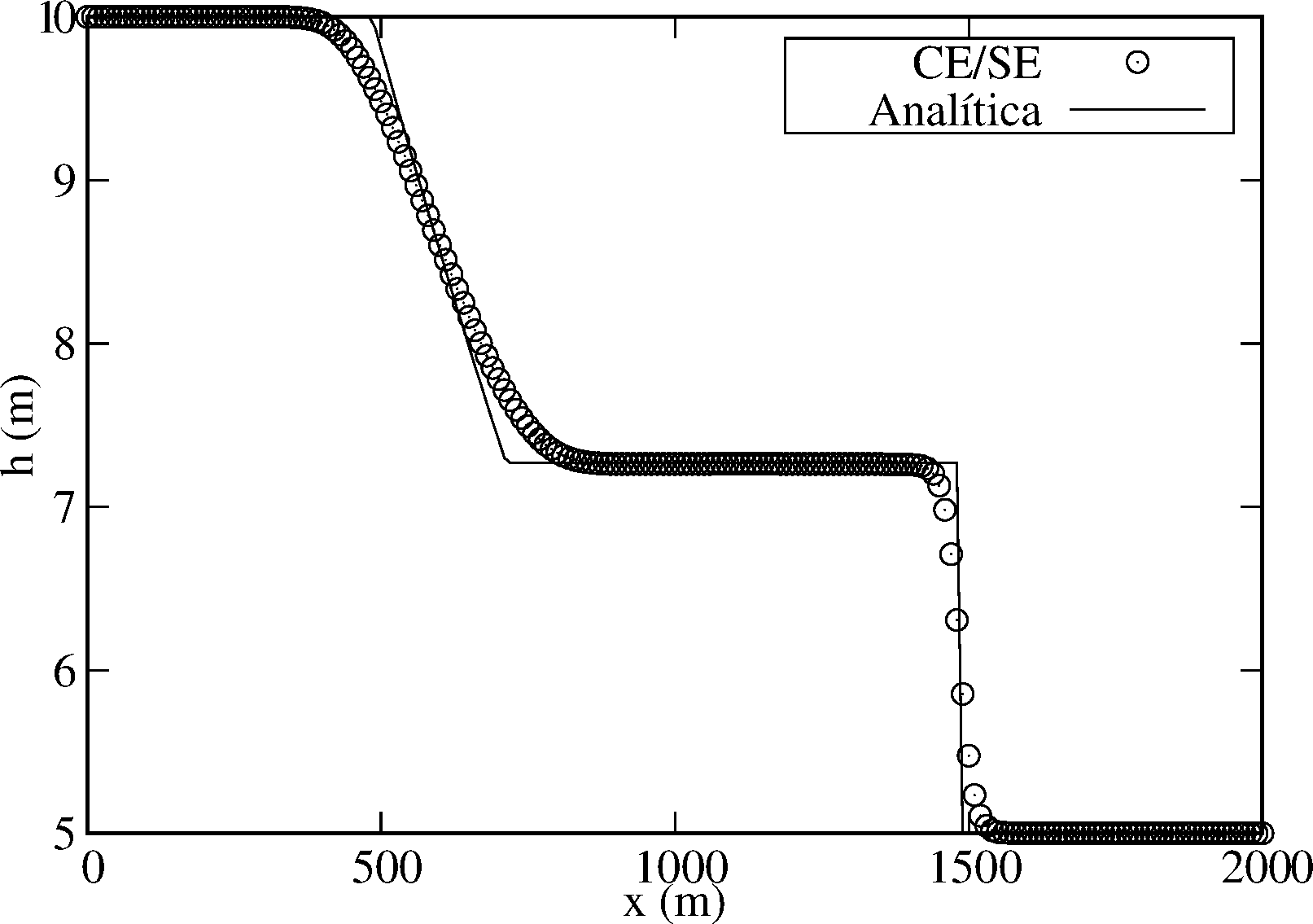
|
|
| (a) | (b) |
| Figura 2. Elevação da superfície da água e velocidade para o problema de ruptura de barragem, computada no tempo , utilizando uma malha uniforme com pontos, incremento espacial e . | |
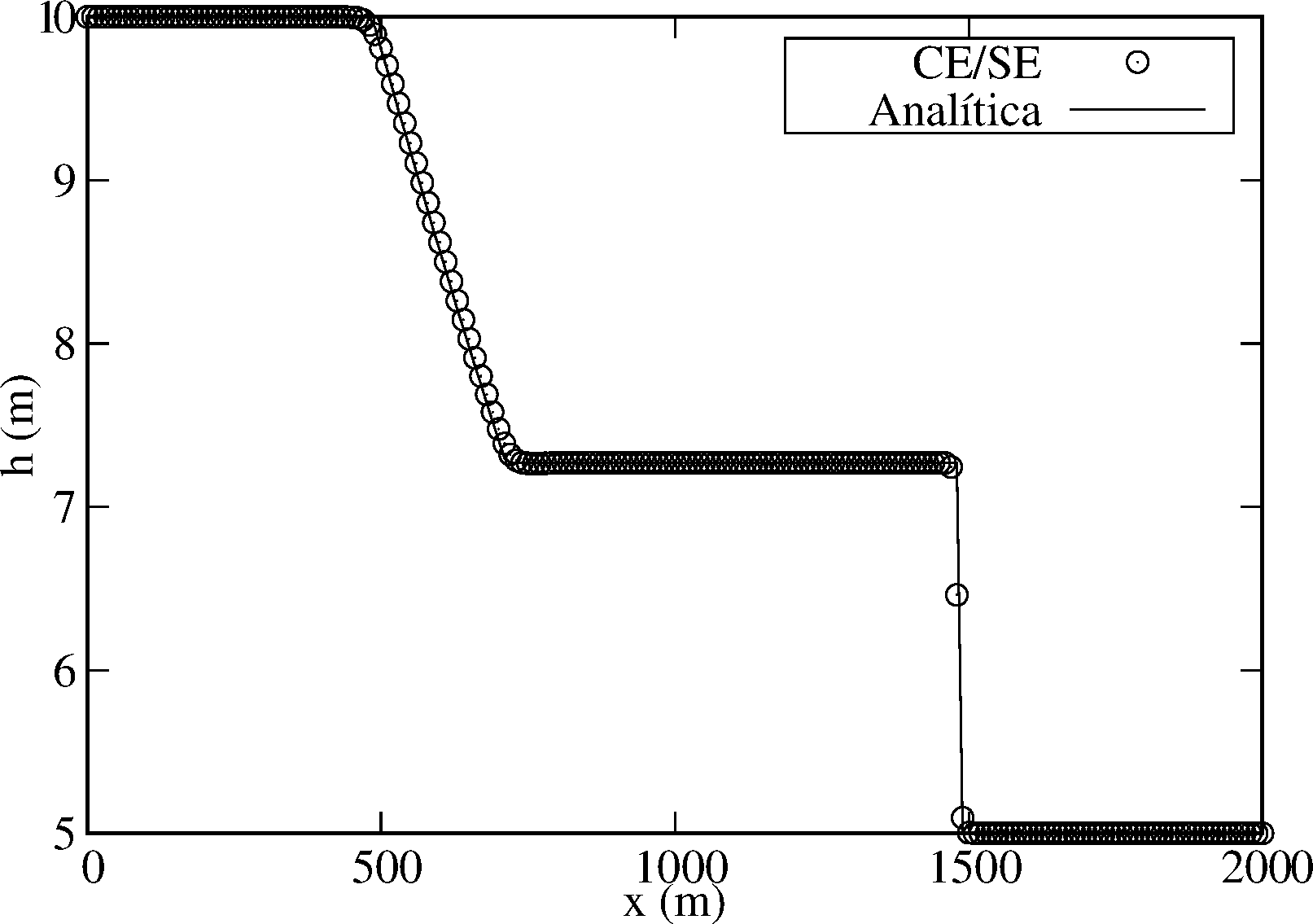
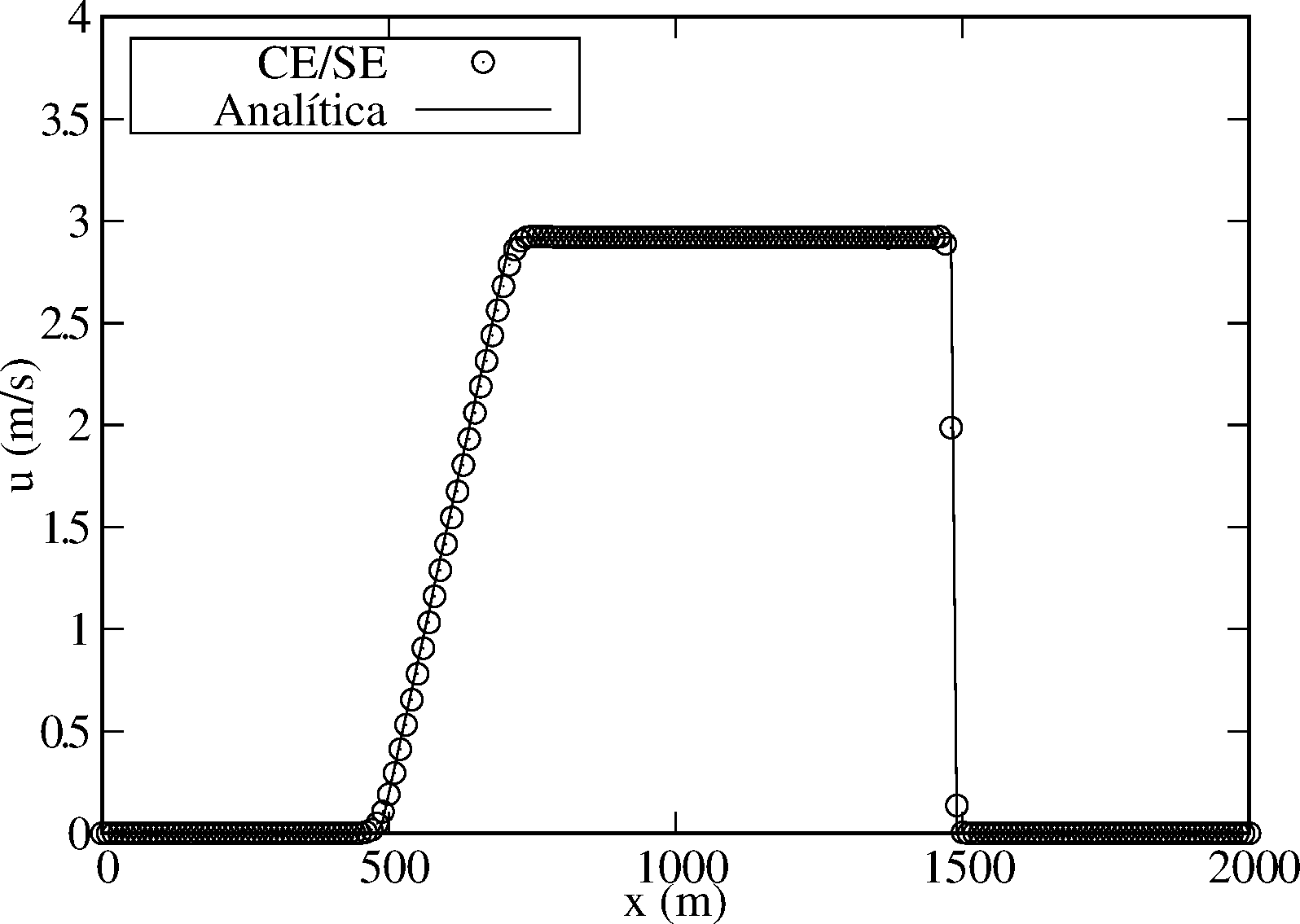
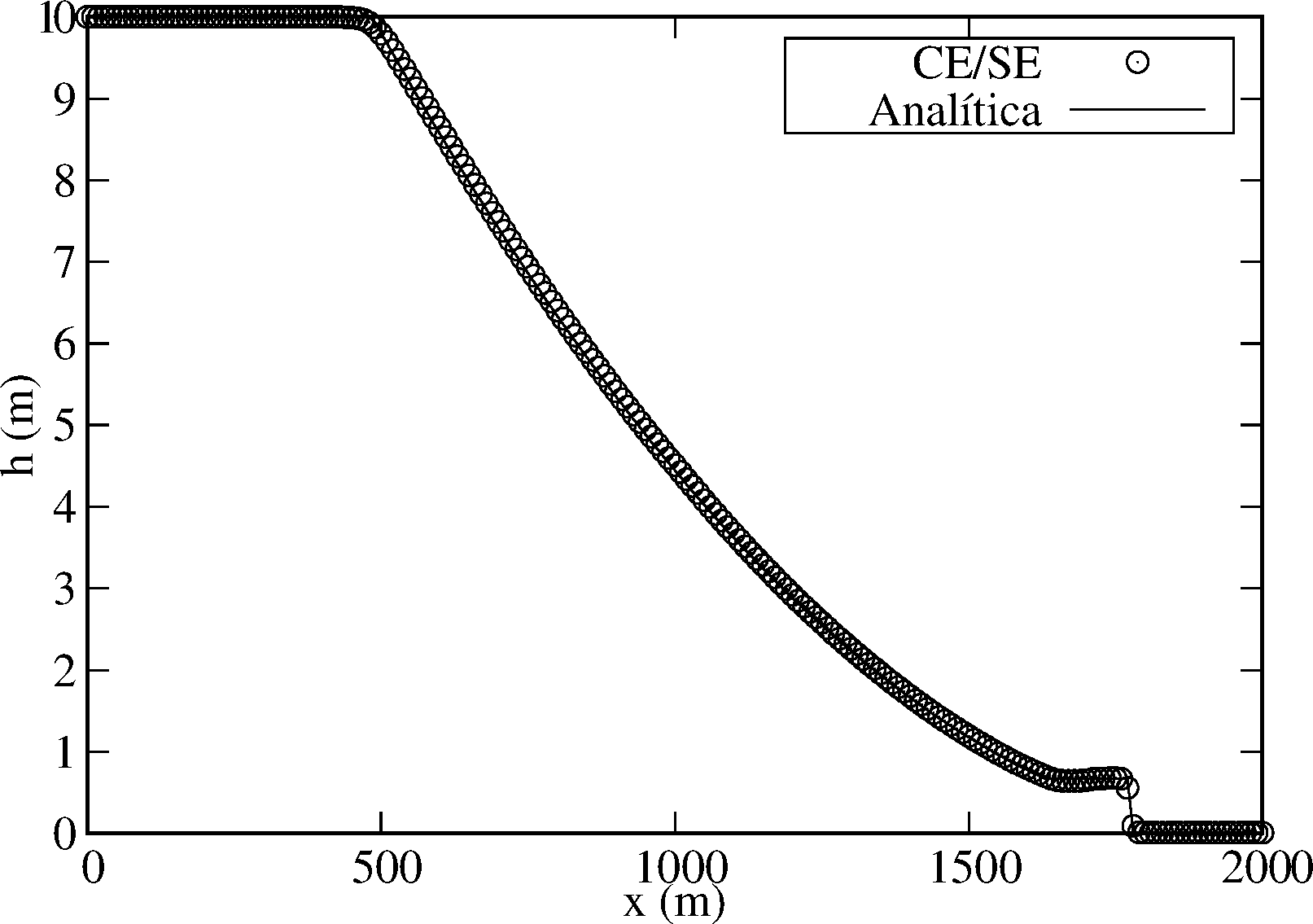
Utilizando o Algoritmo 1, sob as mesmas condições e com os mesmos parâmetros, obtém-se os gráficos constantes na Fig. 3. Observa-se que esta solução numérica é superior à anterior, sobretudo no que tange às regiões de rápidas mudanças. Conforme Zhang et al. (2012) [23], a razão é um importante índice para julgar a aplicabilidade e a acurácia de esquemas numéricos no modelo 1D de ruptura de barragem. Segundo os mesmos autores, os regimes de escoamentos subcrítico e supercrítico existem simultaneamente num canal sem fricção, horizontal e retangular, quando . Altera-se, neste sentido, estes parâmetros para uma razão . Os resultados simulados são mostrados nas Figs. 3c e 3d.
| (a) | (b) |
| (c) | (d) |
| Figura 3. Elevação da superfície da água e velocidade para o problema de ruptura de barragem, no tempo , numa malha uniforme com pontos e respectivo incremento espacial , calculados com o Algoritmo 1, sendo: (a)-(b) e , (c)-(d) e . | |
3.2 Exemplos Bidimensionais
Exemplo 3.2.1: Considere agora o sistema hiperbólico linear bidimensional
|
|
(31) |
e é uma constante dada. Para os dados iniciais e , este problema admite a seguinte solução exata [41,42]:
|
|
(32) |
A Tabela 2 apresenta os erros numéricos calculados nas normas e , no tempo s, com parâmetros especificados em , e domínio computacional definido em , sendo o número de células utilizadas na discretização. O experimento confirma novamente a acurácia de terceira ordem do esquema CE/SE.
| Norma | Norma | ||||||||
| Erro () | Ordem | Erro () | Ordem | Erro () | Ordem | Erro () | Ordem | ||
| 2.595 | – | 1.283 | – | 1.797 | – | 7.478 | – | ||
| 4.231 | 2.617 | 2.032 | 2.658 | 3.377 | 2.412 | 1.169 | 2.678 | ||
| 7.519 | 2.492 | 2.924 | 2.797 | 6.111 | 2.466 | 1.653 | 2.822 | ||
| 1.197 | 2.651 | 3.938 | 2.892 | 9.602 | 2.670 | 2.217 | 2.898 | ||
| 1.735 | 2.786 | 5.128 | 2.941 | 1.397 | 2.781 | 2.895 | 2.937 | ||
| 2.364 | 2.876 | 6.554 | 2.968 | 1.939 | 2.849 | 3.723 | 2.959 | ||
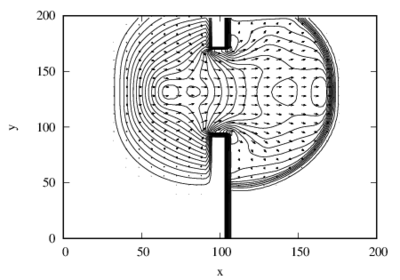
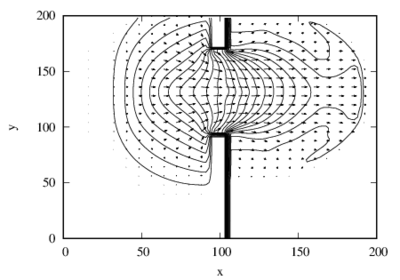
Exemplo 3.2.2: Este problema hipotético bidimensional é um exemplo utilizado por [23,45,46]. Neste problema as velocidades iniciais são todas nulas, a profundidade a montante é de m, enquanto que a profundidade a jusante é assumida ser m ou m. O domínio computacional consiste de uma região de , com uma parede que se estende paralelamente ao eixo , tendo m de largura e está centrada em m. A falha é suposta ser instantânea, possui m de extensão a partir de m. O canal é horizontal e desconsidera-se resistência ao escoamento. Espera-se a formação de uma frente de choque após o rompimento. Os resultados em s são computados a partir de uma malha uniforme composta por células e . Constam nas Figuras 4a e 4b gráficos da profundidade, vetores velocidade e curvas de nível para o problema com profundidade inicial a jusante de m, enquanto que as Figuras 4c e 4d referem-se ao problema com profundidade inicial a jusante de m. Os resultados são consistentes com aqueles presentes na literatura [23,45,46].
Exemplo 3.2.3: Este problema teste visa avaliar a habilidade do esquema em preservar simetria. Considera-se um domínio de com condições iniciais:
|
|
(33) |
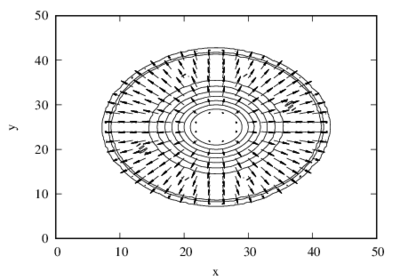
No instante da falha da barragem, supõe-se que a parede circular seja removida completamente e, subsequentemente, formam-se ondas que se espalham radialmente. A solução numérica é computada numa malha retangular uniforme com células e o passo de tempo é tal que . A Fig. 5a apresenta o perfil da superfície da água s após a hipotética falha na barragem circular. Vetores velocidade e curvas nível relativas à superfície estão dispostos na Fig. 5b. A simetria da solução numérica é bem preservada e está de acordo com a literatura [7,47].
4. Conclusões
Este artigo apresentou o desenvolvimento de um novo esquema CE/SE explícito para a solução das equações de águas rasas em uma e duas dimensões. Na formulação construída, as variáveis dinâmicas e, consequentemente, as leis diferencial e integral de conservação, foram aproximadas localmente por expansões de Taylor de segunda ordem. O conjunto de variáveis de marcha tornou-se constituído pelas variáveis fluxo e suas derivadas espaciais de primeira , e segunda ordem e . Os experimentos computacionais realizados indicaram acurácia de terceira ordem sobre os problemas hiperbólicos lineares testados. As soluções numéricas dos problemas teste de ruptura de barragem unidimensional e bidimensional, caracterizados pela formação de choque, descontinuidade ou simetria, apresentaram concordância com as soluções analíticas e/ou com a literatura. Conclui-se, com isso, que o esquema proposto possui considerável habilidade em capturar choques e descontinuidades fazendo com que seja uma boa ferramenta para análise de fluxo de ruptura de barragem.
Agradecimentos
Os autores agradecem à CAPES pelo apoio financeiro, ao Programa de Pós-Graduação em Métodos Numéricos em Engenharia (PPGMNE - UFPR) e ao Instituto Federal de Educação, Ciência e Tecnologia Catarinense, Campus Araquari, pelo apoio à pesquisa.
Referências
[1] S. Yang, A. Kurganov, Y. Liu, Well-balanced central schemes on overlapping cells with constant subtraction techniques for the Saint-Venant shallow water system. Journal of Scientific Computing 63 (3) (2015) 678–698.
[2] J. Singh, M. S. Altinakar, Y. Ding, Two-dimensional numerical modeling of dam-break flows over natural terrain using a central explicit scheme. Advances in Water Resources 34 (10) (2011) 1366–1375.
[3] J. Soler, E. Bladé, M. Sánchez-Juny, Ensayo comparativo entre modelos unidimensionales y bidimensionales en la modelización de la rotura de una balsa de materiales sueltos erosionables. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 28 (2) (2012) 103–111.
[4] H. Ozmen-Cagatay, S. Kocaman, H. Guzel, Investigation of dam-break flood waves in a dry channel with a hump. Journal of Hydroenvironment Research 8 (3) (2014) 304–315.
[5] S. Kocaman, H. Ozmen-Cagatay, Investigation of dam-break induced shock waves impact on a vertical wall, Journal of Hydrology 525 (2015) 1–12.
[6] T.-J. Chang, H.-M. Kao, K.-H. Chang, M.-H. Hsu, Numerical simulation of shallow-water dam break flows in open channels using smoothed particle hydrodynamics. Journal of Hydrology 408 (1-2) (2011) 78–90.
[7] R. Akoh, S. Li, F. Xiao, A CIP/multi-moment finite volume method for shallow water equations with source terms. Int. J. Numer. Meth. Fluids 56 (2008) 2245–2270.
[8] K. Toda, Y. Ogata, T. Yabe, Multi-dimensional conservative semi-Lagrangian method of characteristics CIP for the shallow water equations. Journal of Computational Physics 228 (13) (2009) 4917–4944.
[9] R. Borsche, A well-balanced solver for the Saint Venant equations with variable cross-section. Journal of Numerical Mathematics 23 (2) (2015) 99–115.
[10] J.-W.Wang, R.-X. Liu, Combined finite volume-finite element method for shallow water equations. Computers & Fluids 34 (10) (2005) 1199–1222.
[11] M. C. Díaz, J. López-García, C. Parés, High order exactly well-balanced numerical methods for shallow water systems. Journal of Computational Physics 246 (2013) 242–264.
[12] F. Benkhaldoun, S. Sari, M. Seaid, Projection finite volume method for shallow water flows. Mathematics and Computers in Simulation 118 (2015) 87 – 101, MAMERN V-2013: 5th International Conference on Approximation Methods and Numerical Modeling in Environment and Natural Resources.
[13] S.-J. Liang, T.-W. Hsu, Least-squares finite-element method for shallow-water equations with source terms. Acta Mechanica Sinica 25 (5) (2009) 597–610.
[14] C. Dawson, J. H. Videman, A streamline diffusion finite element method for the viscous shallow water equations. Journal of Computational and Applied Mathematics 251 (2013) 1–7.
[15] G. Kesserwani, D. Caviedes-Voullième, N. Gerhard, S. M Multiwavelet discontinuous Galerkin h-adaptive shallow water model. Computer Methods in Applied Mechanics and Engineering 294 (2015) 56–71.
[16] D. Wirasaet, S. Brus, C. Michoski, E. Kubatko, J. Westerink, C. Dawson, Artificial boundary layers in discontinuous Galerkin solutions to shallow water equations in channels. Journal of Computational Physics 299 (2015) 597–612.
[17] M. Rasulov, Z. Aslan, O. Pakdil, Finite differences method for shallow water equations in a class of discontinuous functions. Applied Mathematics and Computation 160 (2) (2005) 343–353.
[18] X. Zhengfu, S. Chi-Wang, Anti-diffusive finite difference weno methods for shallow water with transport of pollutant. Journal of Computational Mathematics 24 (3) (2006) 239–251.
[19] Y.-H. Hwang, A characteristic particle method for the Saint Venant equations. Computers & Fluids 76 (2013) 58–72.
[20] H. Liu, H. Wang, S. Liu, C. Hu, Y. Ding, J. Zhang, Lattice Boltzmann method for the Saint-Venant equations. Journal of Hydrology 524 (2015) 411–416.
[21] S.-C. Chang, W.-W. To, A new numerical framework for solving conservation laws - the method of space-time conservation element and solution element. Technical Memo TM 104495, NASA, Lewis Research Center, NASA (August 1991).
[22] T. Molls, F. Molls, Space-time conservation method applied to Saint Venant equations. Journal of Hydraulic Engineering 124 (5) (1998) 501–508.
[23] Y. Zhang, Z. Zeng, J. Chen, The improved space-time conservation element and solution element scheme for two-dimensional dam-break flow simulation. International Journal for Numerical Methods in Fluids 68 (5) (2012) 605–624.
[24] S. Qamar, S. Zia, W. Ashraf, The space-time CE/SE method for solving single and two-phase shallow flow models. Computers & Fluids 96 (2014) 136–151.
[25] S.-C. Chang, New developments in the method of space-time conservation element and solution element - aplications to the Euler and Navier-Stokes equations. Technical Memo TM 106226, NASA, Lewis Research Center, NASA (August 1993).
[26] S.-C. Chang, The method of space-time conservation element and solution elemen - a new approach for solving the Navier-Stokes and Euler equations. Journal of Computational Physics 119 (2) (1995) 295–324.
[27] S.-C. Chang, X.-Y. Wang, C.-Y. Chow, The space-time conservation element and solution element method: A new high-resolution and genuinely multidimensional paradigm for solving conservation laws. Journal of Computational Physics 156 (1) (1999) 89–136.
[28] S.-C. Chang, X.-Y. Wang, W.-M. To, Application of the space-time conservation element and solution element method to one-dimensional convection-diffusion problems. Journal of Computational Physics 165 (1) (2000) 189–215.
[29] Z.-C. Zhang, S. T. John Yu, X.-Y.Wang, S.-C. Chang, A. Himansu, P. C. E. Jorgenson, The CE/SE method for Navier-Stokes equations using unstructured meshes for flows at all speeds. AIAA 2000-0393 (2000) 7.
[30] Z.-C. Zhang, S. T. J. Yu, S.-C. Chang, A space-time conservation element and solution element method for solving the two- and threedimensional unsteady Euler equations using quadrilateral and hexahedral meshes. J. Comput. Phys. 175 (1) (2002) 168–199.
[31] S.-C. Chang, A new approach for constructing highly stable high order CESE schemes. Technical Memo TM 2010-216766, NASA, Lewis Research Center, NASA (August 2010).
[32] D. L. Bilyeu, S.-T. J. Yu, Y. Y. Chen, J. L. Cambier, A two-dimensional fourth-order unstrutured-meshed Euler solver based on the CESE method. J. Comput. Phys. 257 (1) (2014) 981–999.
[33] S. Jerez, J. Romero, M. Roselló, F. Arnau, A semi-implicit space-time CE-SE method to improve mass conservation through tapered ducts in internal combustion engines. Mathematical and Computer Modelling 40 (9-10) (2004) 941–951.
[34] S. Qamar, G. Warnecke, Application of space-time CE/SE method to shallow water magnetohydrodynamic equations. Journal of Computational and Applied Mathematics 196 (1) (2006) 132–149.
[35] X. Luo, M. Wang, J. Yang, G. Wang, The space-time CESE method applied to phase transition of water vapor in compressible flows. Computers & Fluids 36 (7) (2007) 1247–1258.
[36] Y. Chou, R.-J. Yang, Application of CESE method to simulate non-Fourier heat conduction in finite medium with pulse surface heating. International Journal of Heat and Mass Transfer 51 (13-14) (2008) 3525–3534.
[37] Z.-C. Zhang, S. T. John Yu, S.-C. Chang, A. Himansu, P. C. E. Jorgenson, A modified space-time conservation element and solution element method for Euler and Navier-Stokes equations. AIAA 99-3277 (1999) 10.
[38] Y.-I. Lim, S.-C. Chang, S. B. Jørgensen, A novel partial differential algebraic equation (PDAE) solver: iterative space-time conservation element/solution element (CE/SE) method. Computers & Chemical Engineering 28 (8) (2004) 1309–1324.
[39] S.-T. J. Yu, L. Yang, R. L. Lowe, S. E. Bechtel, Numerical simulation of linear and nonlinear waves in hypoelastic solids by the CESE method. Wave Motion 47 (3) (2010) 168–182.
[40] S.-C. Chang, X.-Y. Wang, C.-Y. Chow, The space-time conservation element and solution element method - a new high-resolution and genuinely multidimensional paradigm for solving conservaton laws. Technical Memo TM 1998-208843, NASA, Lewis Research Center, NASA (August 1998).
[41] M. Lukácová, K. W. Morton, G. Warnecke, Evolution Galerkin methods for hyperbolic systems in two space dimensions, Mathematics of Computation 69 (232) (2000) 1355–1384.
[42] Qurrat-Ul-Ain, S. Qamar, G. Warnecke, A high-resolution space-time conservative method for non-linear hyperbolic conservation laws. International Journal of Computational Methods 4 (2) (2007) 223–247.
[43] J. J. Stoker, Water Waves: The Mathematical Theory with Applications, Interscience Publishers, New York, 1957.
[44] O. Delestre, C. Lucas, P.-A. Ksinant, F. Darboux, C. Laguerre, T.-N.-T. Vo, F. James, S. Cordier, SWASHES: a compilation of shallow water analytic solutions for hydraulic and environmental studies. International Journal for Numerical Methods in Fluids 72 (3) (2013) 269–300.
[45] R. J. Fennema, M. H. Chaudhry, Implicit methods for two-dimensional unsteady free-surface flows. Journal of Hydraulic Research 27 (3) (1989) 321–332.
[46] C. Zoppou, S. Roberts, Numerical solution of the two-dimensional unsteady dam break. Applied Mathematical Modelling 24 (7) (2000) 457–475.
[47] F. Alcrudo, P. Garcia-Navarro, A high-resolution Godunov-type scheme in finite volumes for 2D shallow-water equations. International Journal for Numerical Methods in Fluids 16 (1993) 489–505.
Document information
Published on 03/01/18
Accepted on 07/05/17
Submitted on 24/11/16
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.7.007
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?