Revision as of 15:02, 6 July 2017

Subm:31/01/2017

Accep.: 06/06/2017

Resumo

Os elementos estruturais, em muitas situações, estão apoiados em outros corpos, tais como o solo, que podem oferecer restrições de movimentos em algumas direções. Por isso, a análise estática e dinâmica desses elementos considerando sua interação com o solo torna-se importante na concepção de um projeto estrutural. Este artigo apresenta a análise dinâmica não linear de sistemas estruturais considerando tal interação através do Método dos Elementos Finitos. Um elemento de viga-coluna geometricamente não linear é usado para modelar a estrutura, enquanto o solo é idealizado como uma fundação contínua, através dos modelos de Winkler e Pasternak. Admite-se que a fundação reage aos esforços de tração e compressão, de modo que durante o processo de deformação os elementos estruturais são sujeitos a restrições de contato bilaterais. O método de integração de Newmark e a estratégia incremental-iterativa de Newton-Raphson são usados no processo de resolução das equações dinâmicas não lineares no domínio do tempo. Durante o estudo foram avaliadas situações práticas envolvendo a interação entre solo e estrutura, destacando a influência do contato nas frequências naturais de vibração e na resposta transiente dessas estruturas.

Palavras-Chave: Análise Dinâmica, Fundação Elástica, Contato Bilateral, Não Linearidade Geométrica.

Abstract

Structural elements, in many situations, are supported by other surfaces, such as soil, which may offer movement constraints in some directions. Therefore, the static and dynamic analysis of these elements considering their interaction with the soil becomes important in the design of a structural design. This paper presents the nonlinear dynamic analysis of structural systems considering such interaction through the Finite Element Method. A geometrically nonlinear beam-column element is used to model the structure, while the soil can be idealized as a continuum foundation, through the Winkler and Pasternak models. It is assumed that the foundation reacts to tension and compression stresses, so during the deformation process the structural elements are subjected to bilateral contact constraints. The analysis is based on the modeling of the structural system using the finite element method, where the Newmark integration method and Newton-Raphson iterative strategy are used in the process of solving the nonlinear dynamic equations in the time domain. Practical situations involving the interaction between soil and structure were evaluated during the study, showing the influence of contact in the natural vibration frequency and transient response of these structures.

1. Introdução

Com o intuito de otimizar sistemas de fundação de estruturas, inúmeros esforços têm sido feitos para avançar na modelagem de solos, bem como na simulação da interação entre esse meio e a estrutura. O estudo dessa interação é muito importante e dificuldades são encontradas na representação tanto o comportamento da estrutura quanto o do solo. O contato entre esses dois corpos é bastante comum na engenharia civil. Estruturas de fundações, trilhos de trem, tubulações enterradas, muros de contenção, túneis são algumas situações onde tal interação acontece. Esse tipo de problema é denominado problema de contato, podendo ser caracterizado como unilateral ou bilateral. O contato bilateral considera que o meio de contato reage tanto às solicitações de tração quanto às de compressão. Entretanto, uma modelagem mais realística do comportamento do solo pode ser obtida considerando na sua formulação a sua reação apenas às solicitações de compressão, o que caracteriza o contato como unilateral.

Por outro lado, uma análise elástica linear não é capaz de reproduzir o comportamento de estruturas em situações de carregamento limite ou em condições não usuais, pois essas estruturas, em geral, comportam-se de forma não linear antes de atingirem seus limites de resistência. Dessa forma, o comportamento não linear das estruturas passa a ser relevante, e deve ser considerado nas análises estruturais. Com o avanço da tecnologia e da construção civil, torna-se possível projetar estruturas mais esbeltas e com a possibilidade de vencer vãos cada vez maiores. Como consequência, as estruturas mais esbeltas tornam-se mais susceptíveis a problemas excessivos de vibrações, e nesse contexto, a análise estrutural dinâmica, além da estática, passa também a ser importante na concepção de um projeto estrutural.

O comportamento real do solo tem difícil descrição e diferentes modelos matemáticos foram desenvolvidos para representá-lo. Dutta e Roy [1] reuniram em seu trabalho uma revisão dos modelos mais comuns de fundações elásticas de um, dois e três parâmetros que definem as propriedades do solo. Em Silva [2] encontram-se os fundamentos da solução numérica, via Método dos Elementos Finitos (MEF), para problemas de equilíbrio estático de placas com restrições bilaterais e unilaterais de contato, considerando pequenos deslocamentos e deformações, e material elástico linear. Uma metodologia de solução numérica não linear para resolver problemas de instabilidade de elementos estruturais esbeltos com restrições unilaterais de contato foi desenvolvida por Silveira [3]. Mais recentemente, em Maciel [4] e Silveira et al. [5] é estudado o equilíbrio e estabilidade de barras em contato bilateral, via MEF, considerando os efeitos da não linearidade geométrica da estrutura.

Tratando o comportamento estrutural dinâmico, um estudo de vibração livre de vigas sobre base elástica, modelada através de molas discretas, foi realizado por Lai et al. [6] utilizando o MEF e considerando o contato com comportamento bilateral. Uma análise semelhante foi feita por Thambiratnam e Zughe [7]. Uma análise dinâmica não linear de vigas-coluna em fundação elástica de Winkler foi realizada por Sapountzakis e Kampitsis [8]. O contato foi considerado unilateral e bilateral, e utilizou-se o Método dos Elementos de Contorno (MEC). Bhattiprolu et al. [9] desenvolveram uma metodologia de solução para uma viga biapoiada em contato com uma fundação viscoelástica não linear, considerando contato bilateral e unilateral, sob carregamentos estáticos e dinâmicos. Muñoz [10] desenvolveu uma metodologia de análise dinâmica não linear de sistemas estruturais reticulados sob excitações de base, considerando a não linearidade geométrica da estrutura e apoios, representados por molas unidimensionais com comportamento elastoplástico. Mais recentemente, Rosas [11] realizou a análise dinâmica de sistemas estruturais reticulados em contato com o solo. Em seu trabalho, considerou os efeitos geométricos de segunda ordem e o comportamento não linear da fundação elástica.

Nesse contexto, este artigo trata da análise estrutural dinâmica não linear considerando a interação entre o solo e a estrutura. Na análise de vibração forçada, a estratégia iterativa de NewtonRaphson é utilizada para solução do problema estático não linear, e o problema de autovalor para determinação das frequências naturais de vibração é resolvido pelo método de Jacobi [12]. O problema transiente não linear é resolvido através do método de integração de Newmark, em combinação com a estratégia iterativa de Newton-Raphson. Cabe mencionar que as formulações numéricas usadas nas análises foram implementadas e adaptadas em linguagem Fortran 95 [13], no sistema computacional, CS-ASA [14]. Esse programa realiza a análise numérica avançada, estática e dinâmica, de estruturas baseado no MEF.

Situações práticas envolvendo a interação entre o solo e a estrutura são avaliadas neste estudo, procurando evidenciar a influência do contato nas frequências naturais de vibração e na resposta transiente não linear dessas estruturas.

2. O problema de contato

Como já mencionado, a interação entre o solo e a estrutura pode ter tratada como bilateral ou unilateral. O contato bilateral considera que o solo reage tanto às solicitações de tração quanto às de compressão. Admite-se, nesse caso, que o solo trabalha integralmente conectado à estrutura, e que a região de contato entre os corpos é conhecida à priori, uma vez que não é considerada a perda de contato. No entanto, uma modelagem mais realística do solo pode ser obtida considerando na sua formulação a reação apenas às solicitações de compressão, o que caracteriza o contato como unilateral. Nesse caso, a definição da região de contato entre os corpos vai depender da configuração deformada da estrutura, para uma determinada solicitação. Sendo assim, mesmo considerando a hipótese de pequenos deslocamentos e material elástico, o problema será não linear no caso unilateral.

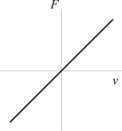
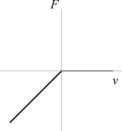
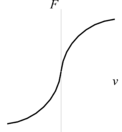
A diferença entre os dois casos pode ser compreendida através da Figura 1. Na Figura 1a, nota-se que a fundação oferece reação às solicitações de tração e compressão e, ainda, a relação constitutiva força F versus deslocamento v é linear, indicando que a rigidez do solo permanece constante. Já na Figura 1c, tem-se o caso bilateral onde o solo tem comportamento não linear. Nas Figuras 1b e 1d está caracterizado o contato unilateral ─ reação do meio apenas aos esforços de compressão ─ e o comportamento linear e não linear para o solo, respectivamente.


(a) Fundação bilateral linear	(b) Fundação linear unilateral

(c) Fundação bilateral não linear	(d) Fundação unilateral não linear
Figura 1. Relação força-deslocamento da fundação

Modelos matemáticos foram desenvolvidos para representar o comportamento do solo. Os modelos considerados mais simples são os que apresentam apenas um parâmetro definindo a sua propriedade. Dentre esses modelos, destaca-se o modelo de Winkler [15], que representa a região de contato através de um sistema de molas estreitamente espaçadas e independentes entre si, como mostra a Figura 2.

Esse modelo não considera a interação entre as molas, o que significa que, se uma fundação é submetida a uma carga distribuída em sua superfície, as molas localizadas fora da região carregada não serão afetadas. Por esse motivo, os modelos definidos por apenas um parâmetro ─ representado na Figura 2 pelo termo k₁ ─ não representam precisamente as características de alguns tipos de fundações, pois o solo é, na realidade, um corpo contínuo.

Figura 2. Viga sobre uma fundação de Winkler.

Os modelos com dois parâmetros definindo o comportamento do solo, como os de Pasternak e Filonenko-Borodich, já consideram as interações entre as molas, o que melhora o modelo anterior, proposto por Winkler. O modelo de Pasternak [16] considera que as molas são conectadas por uma camada incompressível que se deforma apenas sob tensões de cisalhamento.

Para os modelos representativos do solo apresentados, a equação que expressa a reação da fundação elástica é dada por:

(1)

em que r_b e v_b são, respectivamente, a reação da base e o deslocamento, k₁ é o parâmetro de rigidez de Winkler e k₂ representa o parâmetro de rigidez cisalhante da camada do modelo de Pasternak.

Considerando a Equação (1), pode-se escrever a energia interna de deformação armazenada pela fundação da seguinte forma:

(2)

Aplicando o MEF, o deslocamento, u_b, pode ser relacionado com os valores nodais do elemento, û_b, onde B_b é a matriz que contém as funções de interpolação de Hermite, como segue:

(3)

Ao substituir (3) em (2), obtém-se:

(4)

sendo:

(5)

(6)

Para se obter a matriz de rigidez global da fundação elástica devese então considerar a contribuição de todos os m elementos na região de contato, chegando a:

(7)

3. Equilíbrio estático não linear do sistema solo-estrutura

Adotase neste trabalho a formulação geométrica não linear para a estrutura proposta por Yang e Kuo [17], que utiliza um referencial Lagrangiano atualizado (todas as variáveis do problema são conhecias na configuração de equilíbrio t e deseja-se obtê-las em t+Δt) e a teoria de barra de Euler-Bernoulli. Assim, ao se considerar o sistema solo-estrutura, escreve-se o seu funcional de energia:

(8)

sendo U_L e U_σ definidas por:

(9)

{\begin{array}{ll}U_{\mbox{σ}}=&\displaystyle {\frac {1}{2}}\int _{0}^{L}{}^{t}P\left[{\left({\frac {d{\mbox{Δ}}u}{dx}}\right)}^{2}+{\left({\frac {d{\mbox{Δ}}v}{dx}}\right)}^{2}+{\frac {I}{A}}{\left({\frac {d^{2}{\mbox{Δ}}v}{dx^{2}}}\right)}^{2}\right]{\mbox{ }}{\mbox{ }}dx\\&\displaystyle +{\frac {1}{2}}\int _{0}^{L}\left[{}^{t}M{\frac {d{\mbox{Δ}}u}{dx}}{\frac {d^{2}{\mbox{Δ}}v}{dx^{2}}}\right]{\mbox{ }}{\mbox{ }}dx+{\frac {1}{2}}\int _{0}^{L}\left[{}^{t}Q{\frac {d{\mbox{Δ}}u}{dx}}{\frac {d{\mbox{Δ}}v}{dx}}\right]{\mbox{ }}{\mbox{ }}dx\end{array}}

(10)

e U_b dada pela Equação (2). Nas equações anteriores, P corresponde ao esforço axial, Q ao esforço cortante e M ao momento fletor. O módulo de elasticidade é representado por E, enquanto inércia e área da seção transversal são designados por I e A, respectivamente. Os esforços iniciais resultantes na configuração de equilíbrio t (^tP, ^tM, e ^tQ) são calculados através da integração das tensões de Cauchy. Aproximando-se os deslocamentos incrementais Δu (função de Lagrange) e Δv (função de Hermite) através dos deslocamentos nodais do elemento finito, pode-se reescrever o funcional ΔΠ na forma discreta, chegando-se a:

(11)

Na equação anterior, K_L é a matriz elástica linear convencional, K_σ é a matriz de tensões iniciais, ou matriz de rigidez geométrica, cujos termos dependem das forças nodais iniciais, e K_b é a matriz de rigidez da fundação (solo). O termo ∆urepresenta o vetor de deslocamentos incrementais e f_i é o vetor de forças internas nodais; ⁽^t+∆t⁾λf_r caracteriza o vetor das forças externas que atuam no elemento. As componentes das matrizes K_L e K_σ podem ser obtidas diretamente da energia interna de deformação, através da diferenciação dos termos das Equações (9) e (10) [14].

Através da primeira variação da energia potencial total chega-se na equação de equilíbrio não linear do elemento finito considerado. Uma vez obtida a contribuição de todos os elementos que compõem o sistema solo-estrutura, escreve-se:

(12)

com:

(13)

em que ${\textstyle {\mbox{Δ}}{\boldsymbol {F}}_{\mbox{is}}}$ é o vetor de forças internas incremental e ${\textstyle {\bf {K}}_{s}}$ é a matriz de rigidez do sistema composto pela fundação elástica (solo) e estrutura.

4. Equilíbrio dinâmico não linear do sistema solo-estrutura

A equação de equilíbrio que governa a resposta dinâmica de um sistema estrutural pode ser obtida através do Princípio dos Trabalhos Virtuais (PTV). São consideradas as tensões provocadas pela deformação da estrutura e as forças externas, além das forças inerciais e dissipativas (amortecimento). Como já comentado, utiliza-se o referencial Lagrangiano atualizado para determinar a configuração de equilíbrio do sistema estrutural em t+Δt, com a configuração t usada como referência.

Ao empregar os procedimentos usuais do MEF, obtém-se o campo de deformações e os deslocamentos dos elementos em função dos deslocamentos nodais. Sendo assim, a equação matricial que governa a resposta transiente não linear do sistema solo-estrutura pode ser escrita como:

(14)

ou ainda,

(15)

Nas Equações (14) e (15), M é a matriz de massa, C a matriz de amortecimento e ${\textstyle {\bf {K}}_{s}}$ corresponde à matriz de rigidez do sistema, somando-se a contribuição da fundação elástica e da estrutura. Os vetores U, ${\textstyle {\boldsymbol {\dot {U}}}}$ e Ü correspondem a deslocamento, velocidade e aceleração, respectivamente. Por fim, ${\textstyle {\bf {F}}_{ext}}$ representa o vetor de forças externas, ${\textstyle {\bf {F}}_{is}}$ é o vetor de forças internas do sistema, ${\textstyle {\bf {F}}_{r}}$ é o vetor de forças externas de referência (apenas sua direção é importante), e ${\textstyle \lambda }$ é o parâmetro de carga que estabelece a intensidade e sentido desse vetor no instante considerado.

O problema transiente não linear é solucionado através de um procedimento que combina o método de integração implícito de Newmark e a técnica iterativa de Newton-Raphson. Esse processo está indicado, resumidamente, na Tabela 1.

Além do problema transiente, é estudada a resposta do sistema estrutural em vibração livre, assim como a vibração do sistema pré-carregado. A vibração livre ocorre exclusivamente pelas energias potencial e cinemática existentes na estrutura na ausência da ação de forças externas, depois de ter sido excitada em curta duração. Desprezando o efeito do amortecimento, a equação de movimento do sistema estrutural em vibração livre é definida como:

(16)

Pode-se chegar à equação característica do problema, na forma de um problema de autovalor generalizado, ou seja:

(17)

em que foi assumindo para o vetor U:

(18)

Nas Equações (17) e (18), ω² é o autovalor que representa o quadrado das frequências naturais de vibração em rad/s, e ϕ é o autovetor que representa o modo de vibração, contendo as amplitudes dos movimentos associadas aos graus de liberdade nodais da estrutura.

Para a análise de vibração do sistema pré-carregado, é necessário, antes de se determinar as frequências naturais, conhecer a sua configuração de equilíbrio estático para um determinado nível de carregamento. A solução do problema estático não linear é realizada através de uma estratégia incremental que incorpora procedimentos iterativos de Newton-Raphson. De forma resumida, em cada passo de carga pode-se definir duas fases, ou seja: a fase predita, que envolve a solução dos deslocamentos incrementais a partir de um determinado acréscimo de carregamento; e a fase corretiva, que busca a correção das forças internas incrementais obtidas dos acréscimos de deslocamentos, que são comparadas com o carregamento externo, obtendo-se a quantificação do desequilíbrio existente entre as forças internas e externas. O processo corretivo é refeito até que o sistema solo-estrutura esteja em equilíbrio. A correção nos deslocamentos nodais é governada pela seguinte equação de equilíbrio [14]:

(19)

na qual δU denota a correção dos deslocamentos nodais, h se refere ao contador do número de iterações, g é o vetor gradiente, e λ é o parâmetro de carga responsável pelo escalonamento de F_r. Procura-se anular o vetor gradiente ao longo do ciclo iterativo, indicando que foi atingido um ponto de equilíbrio do sistema solo-estrutura.

Logo após esse processo, deve-se avaliar as matrizes de rigidez e de massa, e através do emprego do método de Jacobi [12] consegue-se obter as frequências naturais e modos de vibração. O procedimento de solução numérica adotado aqui para a solução problema de vibração livre do sistema carregado está detalhado Tabela 2.

Tabela 1. Metodologia de solução numérica para análise transiente não linear do sistema solo-estrutura

1. Dados gerais: geometria do sistema e parâmetros dos materiais, malha, rigidez da fundação elástica, entre outros

2. Define-se: vetor de cargas nodais de referência, F_r

3. Consideram-se os deslocamentos, ${\textstyle {\mbox{ }}^{t}{\boldsymbol {U}},}$ velocidades, ${\textstyle {\mbox{ }}^{t}{\boldsymbol {\dot {U}}},}$ e acelerações, ${\textstyle {\mbox{ }}^{t}{\boldsymbol {\ddot {U}}},}$ no instante t

4. Para cada instante t+Δt

4.1 Calculam-se as matrizes: rigidez do sistema, K_s, a matriz de massa, M, e amortecimento, C

4.2 Através dos parâmetros do método, γ e β, determinam-se as constantes:

$a_{0}={\frac {1}{\beta {\mbox{Δ}}t^{2}}};{\mbox{ }}a_{1}={\frac {\mbox{γ}}{\beta {\mbox{Δ}}t}};{\mbox{ }}a_{2}=$ ${\frac {1}{{\mbox{βΔ}}t}};{\mbox{ }}a_{3}=\left({\frac {1}{2{\mbox{β}}}}-\right.$ $\left.1\right);{\mbox{ }}a_{4}={\frac {\mbox{γ}}{\mbox{β}}}-$ $1;{\mbox{ }}a_{5}={\frac {{\mbox{Δ}}t}{2}}\left({\frac {\mbox{γ}}{\mbox{β}}}-\right.$ $\left.2\right)$ ;

_{$a_{6}=a_{0};{\mbox{ }}a_{7}=-a_{2};{\mbox{ }}a_{8}=-a_{3};{\mbox{ }}a_{9}=$ ${\mbox{Δ}}t(1-{\mbox{γ}});{\mbox{ }}a_{10}={\mbox{αΔ}}t$}

4.3 Monta-se a matriz de rigidez efetiva: ${\boldsymbol {\overset {\mbox{ˆ}}{K}}}={\boldsymbol {K}}+$ $a_{0}{\boldsymbol {M}}+a_{1}{\boldsymbol {C}}$

4.4 Determina-se o vetor de cargas efetivo: ${\boldsymbol {\overset {\mbox{ˆ}}{F}}}={\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\mbox{λ}}{\boldsymbol {F}}_{\mbox{r}}+$ ${\boldsymbol {M}}(a_{2}{\mbox{ }}^{t}{\boldsymbol {\dot {U}}}+$ $a_{3}{\mbox{ }}^{t}{\boldsymbol {\ddot {U}}})+{\boldsymbol {C}}(a_{4}{\mbox{ }}^{t}{\boldsymbol {\dot {U}}}+$ $a_{5}{}^{t}{\boldsymbol {\ddot {U}}})-{\mbox{ }}^{t}{\boldsymbol {F}}_{\mbox{i}}$

4.5 Obtem-se o vetor de deslocamentos nodais incrementais: ${\boldsymbol {\overset {\mbox{ˆ}}{K}}}{\mbox{Δ}}{\boldsymbol {U}}=$ ${\boldsymbol {\overset {\mbox{ˆ}}{F}}}$

5. Processo iterativo de Newton-Raphson: h=1, 2, 3, ...

5.1 Avaliam-se os deslocamentos, velocidades e acelerações:

${}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {U}}^{h}={\mbox{ }}^{t}{\boldsymbol {U}}+$ ${\mbox{Δ}}{\boldsymbol {U}}^{h}{\mbox{ }};{\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {\dot {U}}}^{h}=$ $a_{1}{\mbox{Δ}}{\boldsymbol {U}}^{h}-a_{4}{\mbox{ }}^{t}{\boldsymbol {\dot {U}}}-$ $a_{5}{\mbox{ }}^{t}{\boldsymbol {\ddot {U}}}{\mbox{ }};{\mbox{ }}{\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {\ddot {U}}}^{h}=$ $a_{0}{\mbox{Δ}}{\boldsymbol {U}}^{h}-a_{2}{\mbox{ }}^{t}{\boldsymbol {\dot {U}}}-$ $a_{3}{\mbox{ }}^{t}{\boldsymbol {\ddot {U}}}{\mbox{ }}$

5.2 Atualizam-se as coordenadas nodais

5.3 Calcula-se o vetor de forças internas: ${}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {F}}_{\mbox{i}}{}^{h}=$ $\left({}^{t}{\boldsymbol {F}}_{\mbox{ie}}+{\mbox{ }}^{t}{\boldsymbol {F}}_{\mbox{ib}}\right)+$ ${\boldsymbol {K}}_{\mbox{e}}{\mbox{Δ}}{\boldsymbol {U}}^{h}+{\boldsymbol {K}}_{\mbox{b}}{\mbox{Δ}}{\boldsymbol {U}}^{h}$

5.4 Calcula-se o vetor de forças residuais: ${}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {R}}^{\left(h+1\right)}=$ ${\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\mbox{λ}}{\boldsymbol {F}}_{\mbox{r}}-$ $\left({\boldsymbol {M}}{\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {\ddot {U}}}^{h}+\right.$ $\left.{\boldsymbol {C}}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {\dot {U}}}^{h}+\right.$ $\left.{\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {F}}_{\mbox{i}}{}^{h}\right)$

5.5 Corrige-se os deslocamentos nodais: ${\boldsymbol {\overset {\mbox{ˆ}}{K}}}{\mbox{δ}}{\boldsymbol {U}}^{\left(h+1\right)}=$ ${\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {R}}^{\left(h+1\right)}$

5.6 Atualiza-se o vetor de deslocamentos incrementais: ${\mbox{Δ}}{\boldsymbol {U}}^{\left(h+1\right)}={\mbox{Δ}}{\boldsymbol {U}}_{}^{h}+$ ${\mbox{δ}}{\boldsymbol {U}}_{}^{\left(h+1\right)}$

5.7 Verifica-se a convergência do processo iterativo: ${\frac {\vert \Delta {\boldsymbol {U}}^{\mbox{(h+1)}}\vert }{\vert {}^{t}{\boldsymbol {U}}+\Delta {\boldsymbol {U}}^{\mbox{(h+1)}}\vert }}\leq \xi ,$ sendo ξ um fator de tolerância

NÃO: Retorna-se ao item 5

5.8 Obtém-se os vetores de deslocamentos, velocidades e acelerações no tempo t+Δt

${\begin{array}{c}{}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {U}}^{\left(h+1\right)}={\mbox{ }}^{t}{\boldsymbol {U}}+{\mbox{Δ}}{\boldsymbol {U}}^{\left(h+1\right)}{\mbox{ }};{\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {\dot {U}}}^{\left(h+1\right)}=a_{1}{\mbox{Δ}}{\boldsymbol {U}}^{\left(h+1\right)}-a_{4}{\mbox{ }}^{t}{\boldsymbol {\dot {U}}}-a_{5}{\mbox{ }}^{t}{\boldsymbol {\ddot {U}}}{\mbox{ }};{\mbox{ }}\\{}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {\ddot {U}}}^{\left(h+1\right)}=a_{0}{\mbox{Δ}}{\boldsymbol {U}}^{\left(h+1\right)}-a_{2}{\mbox{ }}^{t}{\boldsymbol {\dot {U}}}-a_{3}{\mbox{ }}^{t}{\boldsymbol {\ddot {U}}}{\mbox{ }}\end{array}}$

6. Para o próximo instante:

6.1 Avalia-se o vetor de forças internas: ${}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {F}}_{\mbox{i}}{}^{\left(h+1\right)}=$ $\left({}^{t}{\boldsymbol {F}}_{\mbox{ie}}+{\mbox{ }}^{t}{\boldsymbol {F}}_{\mbox{ib}}\right)+$ ${\boldsymbol {K}}{\mbox{Δ}}{\boldsymbol {U}}^{\left(h+1\right)}$

6.2 Retorna-se ao item 4

Tabela 2. Metodologia de solução numérica para análise de vibração livre do sistema solo-estrutura carregado

1. Dados gerais: geometria do sistema e parâmetros dos materiais, malha, rigidez da fundação elástica, entre outros

2. Define-se o vetor de cargas nodais de referência, F_r

3. Consideram-se os deslocamentos e o parâmetro de carga da última configuração de equilíbrio, t: ^tU e ^tλ

4. Solução predita: Δλ⁰ e ΔU⁰

4.1 Calcula-se a matriz de rigidez tangente do sistema: K_s

4.2 Resolve-se: δU_r = K^-1F_r

4.3 Define-se: Δλ⁰

4.4 Calcula-se: ΔU⁰ = Δλ⁰δU_r

4.5 Atualizam-se as variáveis na configuração t+Δt: ${}^{{\mbox{(t+}}{\mbox{Δ}}{\mbox{t)}}}\lambda ={\mbox{ }}^{\mbox{t}}\lambda +$ $\Delta {\lambda }^{0}$ e ${}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {U}}={\mbox{ }}^{t}{\boldsymbol {U}}+$ ${\mbox{Δ}}{\boldsymbol {U}}^{0}$

5. Processo iterativo de Newton-Raphson: h=1, 2, 3, ...

5.1 Calcula-se o vetor de forças internas:

${}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {F}}_{\mbox{i}}{}^{\left(h-1\right)}=$ $\left({}^{t}{\boldsymbol {F}}_{\mbox{ie}}+{\mbox{ }}^{t}{\boldsymbol {F}}_{\mbox{ib}}\right)+$ ${\boldsymbol {K}}_{\mbox{e}}{\mbox{Δ}}{\boldsymbol {U}}^{\left(h-1\right)}+$ ${\boldsymbol {K}}_{\mbox{b}}{\mbox{Δ}}{\boldsymbol {U}}^{\left(h-1\right)}$

5.2 Calcula-se o vetor de forças desequilibradas:

${\boldsymbol {g}}^{\left(h-1\right)}={\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {F}}_{\mbox{ie}}{}^{\left(h-1\right)}+$ ${\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {F}}_{\mbox{ib}}{}^{\left(h-1\right)}{\mbox{ }}-$ ${\mbox{ }}^{\left(t+{\mbox{Δ}}t\right)}{\mbox{λ}}{\boldsymbol {F}}_{\mbox{r}}$

5.3 Verifica-se a convergência (critério baseado em forças e deslocamentos conjuntamente)

5.4 Atualiza-se a matriz de rigidez tangente do sistema, K_s

5.5 Corrige-se o parâmetro de carga, δλ^h

5.6 Determina-se o vetor correção dos deslocamentos nodais ${\mbox{δ}}{\boldsymbol {U}}^{h}={\mbox{δ}}{\boldsymbol {U}}_{g}^{h}+$ ${\mbox{δλ}}^{h}{\mbox{δ}}{\boldsymbol {U}}_{r}^{h}$ , com:

${\mbox{δ}}{\boldsymbol {U}}_{g}^{h}=-{\boldsymbol {K}}^{-(h-1)}{\mbox{ }}{\boldsymbol {g}}^{\left(h-1\right)}$ e ${\mbox{δ}}{\boldsymbol {U}}_{r}^{h}={\boldsymbol {K}}^{-(h-1)}{\boldsymbol {F}}_{\mbox{r}}$

5.7 Verifica-se a convergência (critério baseado em forças e deslocamentos conjuntamente)

SIM: Pare o processo iterativo e siga para o item 5.10, apenas se houve convergência no item 5.3

5.8 Atualizam-se o parâmetro de carga, λ, e o vetor de deslocamentos nodais, U:

a) Incremental: ${\mbox{Δλ}}^{h}={\mbox{Δλ}}^{\left(h-1\right)}+{\mbox{δλ}}^{h}$ e ${\mbox{Δ}}{\boldsymbol {U}}^{h}={\mbox{Δ}}{\boldsymbol {U}}^{\left(h-1\right)}+$ ${\mbox{δ}}{\boldsymbol {U}}_{}^{h}$

b) Total: ${}^{\left(t+{\mbox{Δ}}t\right)}{\mbox{λ}}^{h}={\mbox{ }}^{t}{\mbox{λ}}+$ ${\mbox{Δλ}}^{h}$ e ${}^{\left(t+{\mbox{Δ}}t\right)}{\boldsymbol {U}}^{h}={\mbox{ }}^{t}{\boldsymbol {U}}+$ ${\mbox{Δ}}{\boldsymbol {U}}^{h}$

5.9 Retorna-se ao passo 5

5.10 Determinam-se as frequências naturais e os correspondentes modos de vibração através do método de Jacobi [12]

6. Realiza-se um novo incremento de carga e retorna ao item 4

5. Exemplos numéricos

São apresentadas nesta sessão duas aplicações envolvendo interação solo-estrutura, onde as metodologias de solução descritas na seção anterior foram usadas. O contato foi considerado como bilateral, e o solo foi modelado através dos modelos de Winkler e Pasternak. Em todos os exemplos admitiu-se o material com comportamento elástico linear e a não linearidade geométrica da estrutura. Um critério de convergência baseado em cargas e deslocamentos, com tolerância de 10^-4, foi adotado nas análises.

5.1 Viga sobre fundação elástica

Considere a viga biapoiada ilustrada na Figura 2. As propriedades geométricas e físicas dessa estrutura são: comprimento de 6.096 m, área da seção transversal 185.81 x 10^-3 m², momento de inércia 1.44 x 10^-3 m⁴, módulo de elasticidade 2.483 x 10¹⁰ N/m², e densidade 446.08 kg/m. A viga está apoiada em uma fundação elástica com rigidez k₁ = 16.554 MN/m². Esse problema foi estudado também por Timoshenko e Young [18], Lai et al. [6], Thambiratnam e Zhuge [7], e por Sapountzakis e Kampitsis [8]. O solo foi representado pelo modelo de Winkler.

Foi realizada uma análise de vibração livre dessa estrutura e as três primeiras frequências de vibração foram comparadas com os resultados disponíveis na literatura. Nessa análise, a discretização utilizada foi de 10 elementos finitos. Observa-se que a metodologia utilizada neste trabalho conduziu a resultados satisfatórios, conforme apresentado na Tabela 3.

Tabela 3. Três primeiras frequências de vibração da viga

Frequência (Hz)	Timoshenko e Young [18]	Lai et al. [6]	Thambiratnam e Zhuge [7]	Sapountzakis e Kampitsis [8]	Presente estudo
f₁	32.9032	32.9049	32.9033	32.7946	32.9123
f₂	56.8135	56.8220	56.8193	56.5476	56.8499
f₃	112.908	111.9730	111.9610	110.7220	112.0392

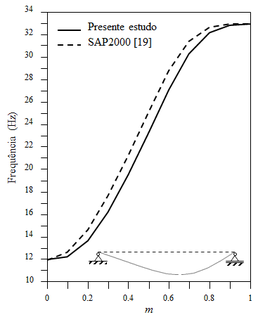
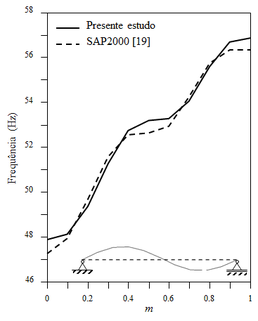
Considerando agora a mesma viga, mas sobre uma fundação de comprimento variável, foram analisadas as duas primeiras frequências de vibração do sistema. Nesse estudo, o parâmetro m (ilustrado na Figura 3) variou de zero (sem a presença do meio elástico) a um (toda a estrutura apoiada sobre a fundação).

Figura 3. Viga em fundação elástica de comprimento variável

Os resultados são expostos na Figura 4, onde se mostram também os modos de vibração para a condição m = 0.5, ou seja, metade da viga em contato com o solo. O mesmo exemplo foi modelado no software SAP2000 [19] para comparação dos resultados. Nesse caso, percebe-se que com o aumento de m, ou seja, aumento da área de contato, maiores são as frequências de vibração, pois o sistema se torna mais rígido.


(1) Primeira frequência natural	(2) Segunda frequência natural

Figura 4. Frequências de vibração em função da variação do comprimento da fundação elástica (valor de m)

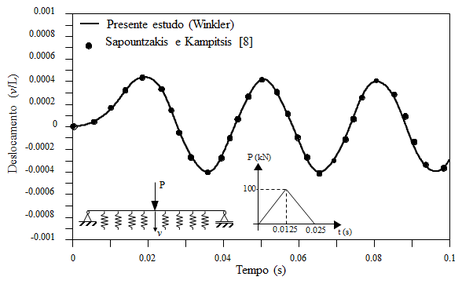
A Figura 5 exibe o histórico de deslocamento vertical obtido no centro do vão da viga (L/2), submetida a uma carga de impacto, conforme ilustrado nessa mesma figura. O incremento de tempo utilizado foi de 10^-4. Essa figura exibe também a resposta obtida por Sapountzakis e Kampitsis [8], onde verifica-se a boa concordância com os resultados obtidos neste trabalho.

Figura 5. Resposta transiente

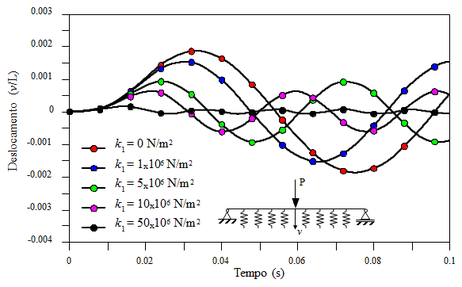
Para verificar a influência da rigidez da fundação elástica na resposta transiente da viga, a mesma análise foi realizada utilizando diferentes fundações, avaliadas pelo parâmetro k₁. O histórico de deslocamento no centro da viga foi avaliado e ilustrado na Figura 6. Notase, como esperado, que as fundações mais rígidas (maiores valores de k₁) ocasionaram menores deslocamentos e menores períodos de vibração.

Figura 6. Resposta transiente para diferentes valores de k₁

5.2 Pórtico de aço suportado por colunas de concreto em contato com o solo

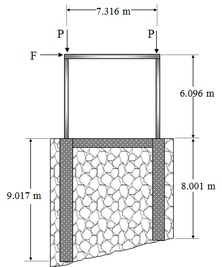
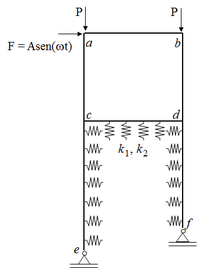
Considere o pórtico mostrado na Figura 7a. A estrutura é composta de seis membros: dois pilares de concreto (ec e fd) conectados por uma viga também de concreto (cd); e os membros ab, ca e db feitos de aço estrutural W14 x 26. Os pilares de concreto têm módulo de elasticidade 25998.75 MPa, densidade 1886.88 kg/m, e seção transversal circular de área 0.7854 m². A viga de concreto possui módulo de elasticidade 25998.75 MPa, densidade 600 kg/m, e seção transversal quadrada de área 0.25 m². Os membros em aço estrutural apresentam área da seção transversal 4.961x10^-3 m², momento de inércia 101.9767x10^-6 m⁴, módulo de elasticidade 206842.72 MPa, e densidade 38.86 kg/m. O solo foi representado através dos modelos de Winkler e Pasternak, com parâmetros de rigidez k₁ = 2.0684 MN/m² e k₂ = 3200 kN. A Figura 7b ilustra o modelo estrutural utilizado.


(1) Dimensões e cargas aplicadas	(2) Modelo matemático estrutural

Figura 7. Pórtico plano em contato com o solo

Realizou-se a análise de vibração livre dessa estrutura, adotando os modelos de Winkler (k₂= 0) e Pasternak (k₂= 3200 kN) para modelagem do solo. Os resultados para os cinco primeiros modos são apresentados nas Tabela 4. Para o modelo de Winkler, as respostas foram comparadas com aquelas obtidas através da modelagem no software SAP2000 [19], e também com aquelas encontradas por Arboleda-Monsalve et al. [20]. Vale ressaltar que, para o modelo de Pasternak, esses autores consideraram a existência de ligações semirrígidas nos nós c e d, com fatores fixos de rigidez (γ) de 0.2 e 0.9 respectivamente. No CS-ASA, programa utilizado como base computacional deste trabalho, existe a possibilidade de considerar ligações semirrígidas, permitindo realizar essa análise para comparação. Maiores detalhes sobre a formulação dessas ligações são encontrados em Silva [14]. Foram obtidos resultados com boa concordância, conforme exposto na Tabela 4.

Tabela 4. Frequências naturais (Hz) do pórtico plano

Modos	k₂ = 0			k₂ = 3200 kN
Modos	ArboledaMonsalve et al. [20]	SAP2000 [19]	Presente estudo	Arboleda-Monsalve et al. [20]	Presente estudo
1	4.587	4.766	4.654	4.519	4.678
2	5.516	5.756	5.574	5.526	5.717
3	5.890	6.285	6.122	5.703	6.226
4	8.754	9.458	9.900	7.257	8.071
5	24.866	25.049	29.201	25.213	29.469

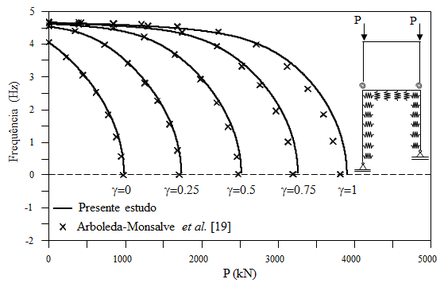
A Figura 8 apresenta a variação da frequência de vibração da estrutura com a magnitude do carregamento aplicado, para cinco diferentes valores de rigidez das ligações nos nós c e d. Essa análise foi realizada supondo o solo representado através do modelo de Winkler (k₁= 2.068 MN/m² e k₂= 0). Ressalta-se que a carga crítica é encontrada quando a frequência de vibração se anula (ω = 0). Dessa forma, para uma ligação com rigidez γ = 0, obteve-se a carga crítica de 980.561 kN. Conforme a rigidez da ligação aumenta, o sistema torna-se evidentemente mais rígido, e a frequência natural também sofre um pequeno acréscimo de 4.061 Hz para 4.657 Hz. Como esperado, as cargas críticas para ligações mais rígidas são mais elevadas. O valor da carga crítica obtido para uma ligação perfeitamente rígida (γ = 1) foi de 3886.142 kN. Nota-se boa concordância das respostas obtidas neste trabalho com os resultados encontrados na literatura.

Figura 8. Variação da frequência com a magnitude do carregamento aplicado

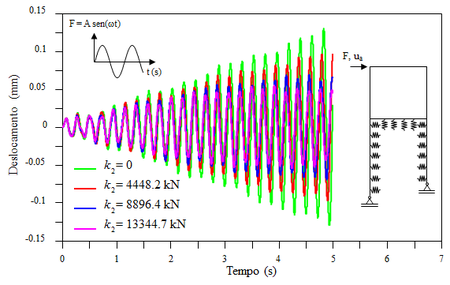
Realizou-se também a análise transiente do pórtico considerando um carregamento harmônico F = A sen(ωt), onde A corresponde a aceleração da gravidade (9.807 m/s²) e ω representa a primeira frequência natural do sistema (4.654 Hz). A Figura 9 apresenta a resposta transiente, considerando os deslocamentos no nó a. O incremento de tempo utilizado foi de 10^-3. É possível observar como o segundo parâmetro da fundação elástica (k₂) influencia na resposta. Quanto maior o valor de k₂, o sistema torna-se mais rígido e causa menores amplitudes de deslocamentos, sem alterar significativamente os períodos de vibração.

Figura 9. Resposta transiente não linear para diferentes valores de k₂

6. Conclusões

Este trabalho traz análises dinâmicas não lineares considerando os efeitos da interação solo-estrutura. O problema de contato foi considerado como bilateral, e o solo foi modelado através dos modelos de Winkler e Pasternak. A metodologia de solução do problema estático não linear fundamentou-se no emprego do Método dos Elementos Finitos (MEF) e do método de Newton-Raphson; já o problema de autovalor para determinação das frequências naturais do sistema solo-estrutura carregado foi resolvido pelo método de Jacobi. O problema dinâmico foi resolvido no domínio do tempo, onde a análise transiente não linear foi realizada através do método de integração de Newmark, em combinação com a estratégia iterativa de Newton-Raphson. Houve boa concordância entre as respostas obtidas aqui com os resultados disponíveis na literatura, o que permite afirmar que a metodologia utilizada é eficiente. Outras aplicações podem ser encontradas em Rosas [11].

Através das análises de vibração livre foi possível concluir que a interação solo-estrutura torna o sistema mais rígido, aumentando as frequências naturais. Quanto mais rígida é a fundação, maiores são as frequências naturais do sistema. Nas análises de vibração da estrutura pré-carregada, nota-se que o critério dinâmico de estabilidade pode ser diretamente empregado, ou seja, as frequências tendem a zero quando aproxima-se da carga crítica do sistema. Como também esperado, na análise transiente verificou-se que os deslocamentos no tempo foram menores quanto maior a rigidez da fundação, tanto para o modelo de Winkler quanto para o de Pasternak.

Por fim, como extensão natural deste trabalho, tem-se a consideração do contato unilateral entre os corpos, com emprego de modelos não lineares para a representação da fundação, e a introdução da inelasticidade material que compõe a estrutura.

Agradecimentos

Os autores agradecem ao CNPq e CAPES (agências federais), FAPEMIG (agência estadual) e PROPEC/PROPP/UFOP, pelo apoio recebido para a realização deste trabalho.

Referências

[1] S.C. Dutta, R. Roy. A critical review on idealization and modeling for interaction among soil-foundation-structure system. Computer and Structures 80 (2002) 1579-1584.

[2] A.R.D. Silva. Análise de placas com restrições de contato. Dissertação, Universidade Federal de Ouro Preto, Brasil (1998).

[3] R.A.M. Silveira. Análise de Elementos Estruturais Esbeltos com Restrições Unilaterais de Contato. Tese, PUC-Rio, Brasil (1995).

[4] F.P. Maciel. Equilíbrio e estabilidade de elementos estruturais com restrições bilaterais impostas por bases elásticas. Dissertação, Universidade Federal de Ouro Preto, Brasil (2012).

[5] R.A.M. Silveira, F.V. Maciel, A.R.D. Silva, F.C.S. Machado, C.L. Nogueira. Nonlinear Equilibrium and Stability Analysis of Axially Loaded Piles Under Bilateral Contact Constraints. Latin American Journal of Solids and Structures 12 (2015). 250-270.

[6] Y.C. Lai, B.Y. Ting, W. Lee, B.R. Becker. Dynamic response of beams on elastic foundation. J. Struct. Eng 118 (1992) 853-858.

[7] D. Thambiratnam, Y. Zhuge. Free vibration analysis of beams on elastic foundation. Computers and Structures 60 (1996) 971-980.

[8] E.J. Sapountzakis, A.E. Kampitsis. Nonlinear dynamic analysis of Timoshenko beam-columns partially supported on tensionless Winkler foundation. Computer and Structures 88 (2010) 1206-1219.

[9] U. Bhattiprolu, A.K. Bajaj, P. Davies. An efficient solution methodology to study the response of a beam on viscoelastic and nonlinear unilateral foundation: Static response. International Journal of Solids and Structures 50 (2013) 2328-2339.

[10] L.F.P. Muñoz. Análise dinâmica não linear de pórticos sob excitação de base considerando interação solo-estrutura. Tese, PUC-Rio, Brasil (2015).

[11] L.R.B. Rosas. Análise dinâmica de sistemas estruturais reticulados com restrições de contato. Dissertação, Universidade Federal de Ouro Preto, Brasil (2016).

[12] J.W. Tedesco, W.G. Mcdougal, C.A. Ross. Structural dynamics: Theory and applications. Addison-Wesley, Menlo Park, CA (1999).

[13] S.J. Chapman. Fortran 90/95 for Scientists and Engineers. McGraw-Hill, 2nd ed. (2003).

[14] A.R.D. Silva. Sistema computacional para a análise avançada estática e dinâmica de estruturas metálicas. Tese, Universidade Federal de Ouro Preto, Brasil (2009).

[15] E. Winkler. Die Lehre Von der Elasticitaet und Festigkeit. Prag, Dominucus (1867).

[16] P. L. Pasternak. On a New Method Analysis of an Elastic Foundation by Means of Two Foundation Constants. Gousuedarstvennoe Izadatesvo Literaturi po Stroitelstvuri Arkhitekture (1954).

[17] Y.B. Yang, S.B. Kuo. Theory & analysis of nonlinear framed structures. Prentice Hall (1994).

[18] S. Timoshenko, D.H. Young. Vibration problems in engineering. Wiley, New York (1974).

[19] Computers and Structures, Inc. SAP2000 14.1. Structural Analysis Program, 2009.

[20] L.G. Arboleda-Monsalve, D.G. Zapata-Medina, J.D. Aristizabal-Ochoa. Timoshenko beam-column with generalized end conditions on elastic foundation: Dynamic-stiffness matrix and load vector. Journal of Sound and Vibration 310 (2008) 1057-1079.

@@ Line 229: / Line 229: @@
 Ao empregar os procedimentos usuais do MEF, obtém-se o campo de deformações e os deslocamentos dos elementos em função dos deslocamentos nodais. Sendo assim, a equação matricial que governa a resposta transiente não linear do sistema solo-estrutura pode ser escrita como:
-{| style="width: 100%;"
+{| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
-|  <math>\boldsymbol{M\ddot{U}}\mbox{ }\mbox{+}\mbox{ }\boldsymbol{C\dot{U}}\mbox{ }\mbox{+}\mbox{ }\boldsymbol{K}_\mbox{s}\boldsymbol{U}\mbox{ }\mbox{ }\mbox{=}\mbox{ }\mbox{ }\boldsymbol{F}_{\mbox{ext}}</math>
+|
-| (14)
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\boldsymbol{M\ddot{U}}\mbox{ }\mbox{+}\mbox{ }\boldsymbol{C\dot{U}}\mbox{ }\mbox{+}\mbox{ }\boldsymbol{K}_\mbox{s}\boldsymbol{U}\mbox{ }\mbox{ }\mbox{=}\mbox{ }\mbox{ }\boldsymbol{F}_{\mbox{ext}} </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (14)
 |}
 ou ainda,
-{| style="width: 100%;"
+{| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
-|  <math>\boldsymbol{M\ddot{U}}\mbox{ }\mbox{+}\mbox{ }\boldsymbol{C\dot{U}}\mbox{ }\mbox{+}\mbox{ }\boldsymbol{F}_{\mbox{is}}\mbox{ }\mbox{=}\mbox{ }\mbox{ }\mbox{λ}(t)\boldsymbol{F}_\mbox{r}</math>
+|
-| (15)
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" | <math>\boldsymbol{M\ddot{U}}\mbox{ }\mbox{+}\mbox{ }\boldsymbol{C\dot{U}}\mbox{ }\mbox{+}\mbox{ }\boldsymbol{F}_{\mbox{is}}\mbox{ }\mbox{=}\mbox{ }\mbox{ }\mbox{λ}(t)\boldsymbol{F}_\mbox{r} </math>
+|}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (15)
 |}
-Nas Equações (14) e (15), '''M''' é a matriz de massa, '''C''' a matriz de amortecimento e '''K'''<sub>s</sub> corresponde à matriz de rigidez do sistema, somando-se a contribuição da fundação elástica e da estrutura. Os vetores '''U''',  <math display="inline">\boldsymbol{\dot{U}}</math> e''' Ü''' correspondem a deslocamento, velocidade e aceleração, respectivamente. Por fim, '''F'''<sub>ext</sub> representa o vetor de forças externas, '''F'''<sub>is</sub> é o vetor de forças internas do sistema, '''F'''<sub>r</sub> é o vetor de forças externas de referência (apenas sua direção é importante), e &#x03bb; é o parâmetro de carga que estabelece a intensidade e sentido desse vetor no instante considerado.
+Nas Equações (14) e (15), '''M''' é a matriz de massa, '''C''' a matriz de amortecimento e <math display="inline">{\bf K}_s</math> corresponde à matriz de rigidez do sistema, somando-se a contribuição da fundação elástica e da estrutura. Os vetores '''U''',  <math display="inline">\boldsymbol{\dot{U}}</math> e''' Ü''' correspondem a deslocamento, velocidade e aceleração, respectivamente. Por fim, <math display="inline">{\bf F}_{ext}</math> representa o vetor de forças externas, <math display="inline">{\bf F}_{is}</math> é o vetor de forças internas do sistema, <math display="inline">{\bf F}_{r}</math> é o vetor de forças externas de referência (apenas sua direção é importante), e <math display="inline">\lambda</math> é o parâmetro de carga que estabelece a intensidade e sentido desse vetor no instante considerado.
 O problema transiente não linear é solucionado através de um procedimento que combina o método de integração implícito de Newmark e a técnica iterativa de Newton-Raphson. Esse processo está indicado, resumidamente, na Tabela 1.
@@ Line 249: / Line 257: @@
 Além do problema transiente, é estudada a resposta do sistema estrutural em vibração livre, assim como a vibração do sistema pré-carregado. A vibração livre ocorre exclusivamente pelas energias potencial e cinemática existentes na estrutura na ausência da ação de forças externas, depois de ter sido excitada em curta duração. Desprezando o efeito do amortecimento, a equação de movimento do sistema estrutural em vibração livre é definida como:
-{| style="width: 100%;"
+{| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
-|  <math>\boldsymbol{M\ddot{U}+}\boldsymbol{K}_\mbox{s}\boldsymbol{U=</math><math>0}</math>
+|
-| (16)
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" |<math> \boldsymbol{M\ddot{U}+}\boldsymbol{K}_\mbox{s}\boldsymbol{U}={\bf 0} </math>
 |}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (16)
+|}
 Pode-se chegar à equação característica do problema, na forma de um problema de autovalor generalizado, ou seja:
-{| style="width: 100%;"
+{| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
-|  <math>(\boldsymbol{K}_\mbox{s}-\mbox{ω}{^2}\boldsymbol{M})\mbox{ }\phi =</math><math>\boldsymbol{0}</math>
+|
-| (17)
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" |<math> (\boldsymbol{K}_\mbox{s}-\mbox{ω}{^2}\boldsymbol{M})\mbox{ }\phi =\boldsymbol{0} </math>
 |}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (17)
+|}
 em que foi assumindo para o vetor '''U''':
-{| style="width: 100%;"
+{| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
-|  <math>\boldsymbol{U}=\phi \mbox{ }\mbox{sen}(\mbox{ω}\mbox{t})</math>
+|
-| (18)
+{| style="text-align: left; margin:auto;width: 100%;"
+|-
+| style="text-align: center;" |<math> \boldsymbol{U}=\phi \mbox{ }\mbox{sen}(\mbox{ω}\mbox{t}) </math>
 |}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (18)
+|}
 Nas Equações (17) e (18), ω² é o autovalor que representa o quadrado das frequências naturais de vibração em rad/s, e '''ϕ '''é o autovetor que representa o modo de vibração, contendo as amplitudes dos movimentos associadas aos graus de liberdade nodais da estrutura.
@@ Line 275: / Line 295: @@
 Para a análise de vibração do sistema pré-carregado, é necessário, antes de se determinar as frequências naturais, conhecer a sua configuração de equilíbrio estático para um determinado nível de carregamento. A solução do problema estático não linear é realizada através de uma estratégia incremental que incorpora procedimentos iterativos de Newton-Raphson. De forma resumida, em cada passo de carga pode-se definir duas fases, ou seja: a fase predita, que envolve a solução dos deslocamentos incrementais a partir de um determinado acréscimo de carregamento; e a fase corretiva, que busca a correção das forças internas incrementais obtidas dos acréscimos de deslocamentos, que são comparadas com o carregamento externo, obtendo-se a quantificação do desequilíbrio existente entre as forças internas e externas. O processo corretivo é refeito até que o sistema solo-estrutura esteja em equilíbrio. A correção nos deslocamentos nodais é governada pela seguinte equação de equilíbrio [14]:
-{| style="width: 100%;"
+{| class="formulaSCP" style="width: 100%; text-align: left;"
+|-
+|
+{| style="text-align: left; margin:auto;width: 100%;"
 |-
-|  <math>\boldsymbol{K}_\mbox{s}{}^{\left(h-1\right)}\mbox{δ}\boldsymbol{U}^h=</math><math>-\mbox{ }\boldsymbol{g}^{\left(h-1\right)}+\mbox{δλ}{\mbox{ }}^h\boldsymbol{F}_\mbox{r}</math>
+| style="text-align: center;" |<math> \boldsymbol{K}_\mbox{s}{}^{\left(h-1\right)}\mbox{δ}\boldsymbol{U}^h=-\mbox{ }\boldsymbol{g}^{\left(h-1\right)}+\mbox{δλ}{\mbox{ }}^h\boldsymbol{F}_\mbox{r} </math>
-| (19)
 |}
+| style="width: 5px;text-align: right;white-space: nowrap;" | (19)
+|}
 na qual &#x03b4;'''U '''denota a correção dos deslocamentos nodais, ''h'' se refere ao contador do número de iterações, '''g''' é o vetor gradiente, e λ é o parâmetro de carga responsável pelo escalonamento de '''F'''<sub>r</sub>. Procura-se anular o vetor gradiente ao longo do ciclo iterativo, indicando que foi atingido um ponto de equilíbrio do sistema solo-estrutura.

Revision as of 15:02, 6 July 2017

Resumo

Abstract

1. Introdução

2. O problema de contato

3. Equilíbrio estático não linear do sistema solo-estrutura

4. Equilíbrio dinâmico não linear do sistema solo-estrutura

5. Exemplos numéricos

6. Conclusões

Agradecimentos

Referências

Document information

Document Score

Share this document

Keywords

claim authorship