| Line 422: | Line 422: | ||
|} | |} | ||
| − | {| class="floating_imageSCP" style="text-align: center | + | {| class="floating_imageSCP" style="text-align: center; margin: 1em auto; width: 100%;max-width: 100%;" |
|- | |- | ||
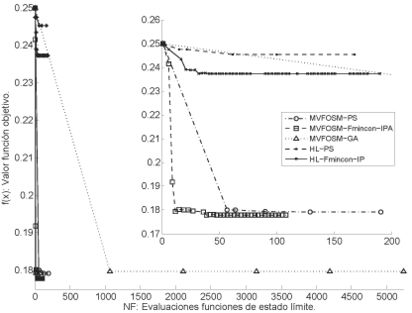
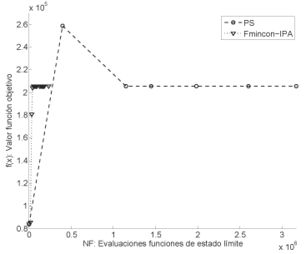
| − | |[[Image:draft_Samper_628401738-image3.jpeg|center| | + | |[[Image:draft_Samper_628401738-image3.jpeg|center|412px|thumb|'''Figure 2.''' Convergencia de los algoritmos ''PS, Fmincon-IP ''y ''GA'' para el problema de diseño de una columna con covarianza de 0.10.]] |
|} | |} | ||
Revision as of 15:21, 20 June 2017
Resumen
El diseño de estructuras confiables requiere de herramientas robustas que permitan analizar el comportamiento del sistema sometido a variabilidad en su resistencia y cargas aplicadas. Para esto, se disponen de diversas formulaciones y algoritmos computacionales que permiten modelar el comportamiento estructural bajo incertidumbres. Bajo estos requerimientos, la metodología de diseño óptimo más popular y confiable es la optimización basada en confiabilidad (RBO, reliability based optimization), que puede implementarse a través de la combinación de modelos matemáticos o computacionales de alta fidelidad, e.g. modelos de elementos finitos, métodos eficientes y precisos de estimación de la confiabilidad, y algoritmos eficientes y eficaces de optimización en ingeniería. La mayoría de aplicaciones de RBO para optimización estructural cuenta con los últimos desarrollos de técnicas computacionales eficientes para simulación y cálculo de confiabilidad, sin embargo, a pesar de que existe una gran variedad de métodos de optimización, generalmente no realizan una selección del algoritmo de optimización más apropiado para cada aplicación. En este contexto, la contribución principal de este artículo es la realización de un estudio comparativo del desempeño computacional de algoritmos de optimización aplicados en optimización estructural por RBO. El estudio realizado comparó el desempeño numérico de algoritmos de optimización en tres problemas. Los algoritmos comparados corresponden a algoritmos basados en derivadas, algoritmos de búsqueda directa, y algoritmos bioinspirados; incluyendo los algoritmos más representativos de cada categoría. Los resultados del estudio comparativo señalan ventajas y desventajas del uso de los diferentes tipos de algoritmos y permiten concluir sobre los criterios que deben considerarse para la selección de un algoritmo que favorezca el rendimiento computacional.
Palabras clave: optimización estructural; confiabilidad; métodos de optimización; índice de confiabilidad; eficiencia numérica
Abstract
The design of reliable structures requires robust tools that allow the analysis of the behavior of the system subject to variability in its resistance and applied loads. For this, there are several formulations and computational algorithms that enable to model the structural behavior under uncertainties. Under these requirements, the most popular and reliable optimum design methodology is the reliability based optimization (RBO), which should be implemented through the combination of high fidelity mathematical or computational models, e.g. finite element models, efficient and accurate reliability estimation methods, and efficient and effective engineering optimization algorithms. Most RBO applications for structural optimization has the latest developments in efficient computational techniques for simulation and reliability calculations, however, although a variety of optimization methods exist, they generally do not perform a selection of the optimization algorithm more appropriate for each application. In this context, the main contribution of this article is the performing of a comparative study of the computational performance of optimization algorithms applied in structural optimization by RBO. The study compared the numerical performance of optimization algorithms in three problems. Compared algorithms correspond to derivative based algorithms, direct search algorithms, and bioinspired algorithms; including the most representative algorithms of each category. The results of the comparative study point out advantages and disadvantages of the use of the different types of algorithms and allow to conclude on the criteria that must be considered for the choice of an algorithm that favors the computational performance.
1. Introducción
La optimización basada en confiabilidad (RBO, reliability-based optimization) es una metodología que hace posible resolver problemas de optimización que requieren el modelamiento explícito de los efectos de las incertidumbres. En aplicaciones de optimización estructural, la metodología de RBO es más apropiada que los procedimientos de diseño determinísticos, debido a que en estas aplicaciones se debe tener en cuenta de forma precisa la inherente incertidumbre presente en el sistema. Los códigos de diseño y la optimización estructural determinística modelan la incertidumbre a través de factores de seguridad que no están vinculados directamente a la incertidumbre existente en las variables de diseño y en los demás parámetros del sistema estructural. Esto último lleva generalmente a estructuras sobrediseñadas e inclusive en algunos casos a diseños inviables.
Si bien la metodología RBO presenta ventajas sobre los métodos determinísticos en aplicaciones de diseño en ingeniería, también presenta retos debido al alto costo numérico involucrado en su solución. Tanto la estimación de la confiabilidad estructural como el proceso iterativo de optimización requieren muchas evaluaciones de modelos numéricos para simulación computacional.
La cuantificación de la incertidumbre en optimización estructural se realiza generalmente a través de restricciones de confiabilidad, definidas en términos de probabilidades de falla o índices de confiabilidad. Cualquiera de estos dos conceptos probabilísticos requiere algoritmos apropiados y eficientes de simulación estocástica, e.g. Monte Carlo Simulation [1]; de estimación aproximada de la confiabilidad, e.g. método de confiabilidad de primer orden (FORM, first order reliability method) [2] y el método de confiabilidad de segundo orden (SORM, second order reliability method) [3] que destacan por su simplicidad y eficiencia desde el punto de vista de implementación y costo computacional. Sin embargo, existen métodos de estimación de confiabilidad más avanzados que involucran metamodelos, que permiten reemplazar los modelos computacionales intensivos por unos más eficientes, pero su implementación es más compleja y su eficiencia está siendo evaluada en la actualidad con resultados prometedores [4]. Entre los métodos basados en metamodelos se destacan los modelos substitutos de kriging (kriging surrogates) [5], y caos polinomial (polynomial chaos) [6].
Hay un interés creciente en la investigación de metodologías RBO, sin embargo, hay pocos trabajos de revisión que ofrezcan una comparación completa del desempeño de implementaciones de RBO. Los pocos estudios existentes se centran en métodos específicos de estimación de confiabilidad o en la implementación de esquemas generales de RBO, dejando sin comparar las diferentes posibilidades que pueden brindar las diferentes familias de algoritmos de optimización [7,8]. No obstante, para la selección de un esquema eficiente de RBO en aplicaciones de optimización estructural es fundamental conocer las diferencias en el desempeño de las diferentes familias de algoritmos de optimización.
Ante el escenario descrito, el objetivo de este trabajo es contribuir con una visión general de los diferentes tipos de algoritmos que se pueden emplear para optimización estructural dentro de la metodología de RBO. Los algoritmos implementados y presentados representan a cada una de las tres principales familias de algoritmos de optimización: algoritmos basados en derivadas (e.g. interior point algorithms), algoritmos de búsqueda directa (e.g. PS, pattern search) y algoritmos bioinspirados (e.g. GA, genetic algorithms). El desempeño numérico de los algoritmos de optimización evaluados se prueba a través de varios problemas de prueba de optimización estructural basada en confiabilidad que involucran desde modelos matemáticos a modelos numéricos de elementos finitos. Finalmente, se concluye con la discusión de los resultados sobre el desempeño numérico de los algoritmos estudiados para dar un panorama de sus capacidades y limitaciones.
2. Optimización basada en confiabilidad (RBO)
La optimización basada en confiabilidad tiene como objetivo buscar el mejor compromiso entre costo y seguridad por medio del control de las incertidumbres presentes en el proceso de diseño. Dentro de los diferentes métodos de RBO, la estimación de la confiabilidad puede ser calculada por medio de la probabilidad de falla del sistema o a través del índice de confiabilidad.
Los métodos de cálculo de confiabilidad tienen como objetivo principal la evaluación de la probabilidad de falla estructural al determinar si se superan los límites representados por las funciones de estado límite [9]. Se conoce como estado límite a la condición específica a partir de la cual la estructura o parte de esta es incapaz de desempeñarse como se requiere. Generalmente, en RBO para el caso de estructuras la función de estado límite se puede definir como el margen de seguridad que hay entre la resistencia y la carga de una estructura. De esta manera la función de estado límite y la probabilidad de falla se pueden definir como [10]:
| (1) | ||
| (2) | ||
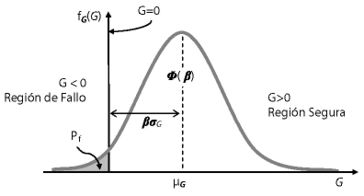
donde es la resistencia y es la carga a la que está sometido el sistema. Tanto la resistencia como la solicitación son funciones de las variables aleatorias X, por lo que la notación denota la región de falla, indica la superficie de falla (estado límite) y representa la región segura, como se muestra en la Figura 1.
|
| Figure 1: Densidad de Probabilidad para la función de estado límite , para un caso unidimensional. |
Para el caso especial con G(X) lineal, variables aleatorias independientes y normalmente distribuidas, el índice de confiabilidad (β) puede ser calculado como:
| (3) |
donde representa la media y la desviación estándar de la función de estado límite G(X). Es decir, que entre mayor sea mayor será la distancia entre el valor medio y la superficie de fallo de G(X), lo que representa una menor probabilidad de fallo y por lo tanto una mayor confiabilidad.
Para el caso en que G(X) es no lineal, y se obtienen a través de la linealización de la función G(X) a través de la expansión en serie de Taylor de primer orden. Este método se conoce como el método de valor medio (MVFOSM, mean value first-order second moment), por lo que y se calculan como [2,11]:
| (4) | |
| (5) |
2.1. Formulación básica de RBO
La formulación general para un problema de RBO consiste en minimizar la función objetivo sujeta a restricciones probabilísticas. En esta formulación hay dos tipos de variables: variables de diseño y variables aleatorias X. Un problema de optimización estructural basada en confiabilidad se representa matemáticamente como:
| (6) |
donde d es el vector de variables de diseño, X es el vector de variables aleatorias, C es la función objetivo, es la i-ésima función de estado límite, son las restricciones determinísticas, P[⋅] es el operador de probabilidad, es la probabilidad de falla admisible, m es el número de funciones de estado límite y M es el número total de restricciones. Las restricciones determinísticas generalmente son límites inferiores y superiores de las variables de diseño. Las restricciones probabilísticas definen la región factible al restringir la probabilidad de violar el estado límite para la probabilidad de falla admisible , donde la probabilidad de falla puede ser calculada por la siguiente integral múltiple:
| (7) |
donde es la función de densidad de probabilidad conjunta de las variables aleatorias X. Calcular de forma exacta la integral es poco práctico. En la práctica se utilizan métodos numéricos que aproximan el cálculo de probabilidad de falla, a través de simulación numérica, e.g. métodos avanzados de simulación; métodos de aproximación de la función de estado límite por expansión en series de Taylor, e.g. FORM y SORM; y métodos de aproximación de la función de estado límite por modelos substitutos.
2.2. Implementación de una técnica RBO
La aproximación del índice de confiabilidad (RIA, reliability index approach) [12] usa el método FORM a través del algoritmo Hasofer y Lind (HL) [13] para el análisis de confiabilidad. Dentro de las formulaciones RBO, RIA es uno de las aproximaciones clásicas del índice de confiabilidad y se define matemáticamente como:
donde y son el índice de confiabilidad calculado y el índice de confiabilidad objetivo respectivamente para la i-ésima función de estado límite. Para transformar las variables aleatorias en variables normalizadas no correlacionadas [6], el índice de confiabilidad se calcula resolviendo el problema de optimización restringida:
| (8) |
La solución es el punto más probable de falla (MPFP, most probable failure point), y el índice de confiabilidad está dado por . De acuerdo a la aproximación de FORM, la probabilidad de falla está dada por: donde es la distribución Gaussiana estándar.
3. Algoritmos de optimización
3.1. Algoritmo de punto interior (IPA, interior point algorithm)
Es un algoritmo basado en gradientes para minimizar funciones objetivo no lineales sujetas a restricciones no lineales de igualdad y desigualdad. En este trabajo se usa la versión del algoritmo que está implementada en el toolbox de optimización de Matlab©, presentada por R.H. Byrd et. al. [14], el cual aplica técnicas de programación cuadrática secuencial (SQP, sequential quadratic programming), y usa la metodología de la región de confianza (TR, trust región), para asegurar la robustez y permitir el uso directo de derivadas de segundo orden.
3.2. Algoritmo de búsqueda en patrón (PS, pattern search)
Es un algoritmo de optimización creado en 1961 [15], para resolver problemas de optimización que no requiere información sobre el gradiente de la función objetivo. A diferencia de los métodos de optimización más tradicionales que usan información sobre el gradiente o derivadas superiores para buscar un punto óptimo, un algoritmo de búsqueda directa explora alrededor del punto actual, buscando un punto donde el valor de la función objetivo sea inferior al valor en el punto actual. El método es aplicable también en problemas de optimización para funciones no diferenciables o discontinuas. En este trabajo se usa la versión del algoritmo que esta implementada en el toolbox de optimización de Matlab©, presentada por T. Kolda et. al. [16].
3.3 Algoritmo genético (GA, genetic algorithm)
Es un método basado en la selección natural de la evolución, teoría que fue propuesta por Charles Darwin. El algoritmo genético modifica repetidamente una población de individuos (soluciones). En cada paso, el algoritmo genético selecciona individuos aleatoriamente a partir de la población actual, para ser parientes y usarlos para producir a los descendientes de la siguiente generación. A través de generaciones sucesivas, la población "evoluciona" hacia una solución óptima [17]. El algoritmo genético es aplicable también a problemas en los cuales la función objetivo es discontinua, no diferenciable, estocástica, o altamente no lineal. Los algoritmos genéticos pueden también manejar problemas de optimización con variables discretas, enteras o mixtas. El GA al ser un algoritmo basado en una población de individuos, en la práctica llega generalmente a un óptimo global. Al tener un mecanismo aleatorio de selección y combinación de individuos, los resultados obtenidos por el GA tienen una variabilidad inherente, y requieren por lo general un elevado número de evaluaciones de la función objetivo. El GA al no ser un algoritmo de punto interior intenta llevar al cumplimiento de las restricciones a través de una función de penalidad, motivo por el cual puede tener dificultades en encontrar una solución viable. Debido a su simplicidad, los algoritmos genéticos son fáciles de implementar y usar, siendo usados por lo general en aplicaciones de optimización multiobjetivo y de RBO [18].
4. Comparación Numérica
Para este estudio se implementó en Matlab© el método RIA como método de RBO por su simplicidad y eficiencia. Para el cálculo de confiabilidad se usó el método FORM, a través del código de Kostandyan E.E. [19].
El desempeño numérico de los algoritmos de optimización que se evalúan en este trabajo para aplicaciones estructurales de RBO, se estudia a través de tres ejemplos: 1) diseño óptimo de una columna corta, 2) optimización de un bastidor, y 3) optimización de una armadura de 10 barras. Para este estudio comparativo se usan las versiones de los tres algoritmos de optimización mencionados en la sección 3, que hacen parte del toolbox de optimización de Matlab©. Para el ejemplo 3 las funciones de estado límite representan restricciones que fueron implementadas usando el toolbox de elementos finitos CALFEM [20].
Los criterios de convergencia de los algoritmos de optimización comprenden: el cambio relativo en la función objetivo, a través del parámetro TolFun; el cambio absoluto en las variables de optimización, a través del parámetro TolX; y la verificación de las restricciones, a través del parámetro TolCon. Para el caso específico del algoritmo GA, el tamaño de la población (PopulationSize) se fijó en 20 individuos y la fracción de cruzamiento (CrossFraction) se fijó en el valor por defecto, correspondiente a 0.8 (lo que implica una fracción de mutación de 0.2). Para el algoritmo IPA en el cálculo de las derivadas se usaron diferencias finitas (forward finite differences). Para el algoritmo PS y Fmincon-IPA se asignaron los siguientes valores para los parámetros de convergencia: TolFun=10-8, TolCon=10-8 y TolX=10-12. Para el algoritmo GA se asignaron los siguientes valores para los parámetros de convergencia: TolFun=10-6 y TolCon=10-6.
4.1. Diseño de una columna corta
Este problema fue propuesto en el 2009 por Y. Aoues y A. Chateauneuf [7], usando el algoritmo de optimización SQP y diferentes estrategias de RBO como RIA, PMA (performance measure approach) y SORA (sequential optimization and reliability assessment). Para este problema, con los algoritmos de optimización evaluados en este trabajo la confiabilidad se estimó por el método MVFOSM y HL.
Este problema consiste en minimizar el área de la sección transversal de una columna corta. La columna tiene una sección transversal rectangular de dimensiones y , está sometida a una fuerza aleatoria y a momentos de flexión biaxial y . De acuerdo a la ley constitutiva elástico-plástica, la función de estado límite está dada por:
| (9) |
El índice de confiabilidad objetivo es de ; las variables de diseño son los valores medios de la base y la altura de la sección transversal, el punto inicial de diseño es: = [0.5, 0.5]. Las variables aleatorias son el límite elástico del material , los momentos flexionantes aplicados y , la fuerza normal aplicada , la base y la altura de la sección transversal. Todas las variables aleatorias de este problema tienen distribución normal como se muestra en la Tabla 1. Se aplican diferentes coeficientes de variación para h y b: 0.00, 0.05, 0.10 y 0.15 (un coeficiente de variación 0.0 indica que la variable es determinística).
| Variable | Distribución | Media | COV | |
| Normal | ||||
| Normal | ||||
| ( | Normal | |||
| Normal | ||||
| Normal | ||||
| Normal | ||||
Entonces, el problema de RBO se define como:
| (10) |
En la Tabla 2, están consignados los resultados obtenidos con el β calculado por MVFOSM y FORM a través de HL. En los dos casos se observa que Fmincon-IPA tuvo la mejor eficiencia, al tener el menor número de evaluaciones de las funciones de estado límite (G-eval), seguido de PS y GA. La eficiencia de los tres algoritmos de optimización usando los dos esquemas del cálculo de β también se corrobora en la Figura 2. En el caso del β calculado por MVFOSM, para una covarianza de 0.10 los tres algoritmos convergieron a d*= [0.3, 0.6]T correspondiendo a un área de aproximadamente 0.18 m2, sin embargo, para el caso del β calculado por HL, los algoritmos convergieron a d*= [0.34, 0.69]T con un área aproximada de 0.24 m2, con la particularidad de que PS convergió a un valor ligeramente mayor, y el GA no logró convergencia (nc). El resultado más estable y ligeramente mejor del MVFOSM frente al HL se debe a que en la implementación de MVFOSM se usaron las derivadas analíticas de la función de estado límite. Al comparar los resultados de los tres algoritmos estudiados con los resultados de la literatura [6]se observa que la eficiencia de los tres primeros algoritmos es mayor, seguido de cerca por el algoritmo SORA-SQP y con una eficiencia mucho menor PMA-SQP y RIA-SQP. Teniendo en cuenta que el valor inicial de la función objetivo es de A(x0) =0.25 m, para el caso de covarianza de 0.1, los porcentajes de reducción de área para los algoritmos con el método MVFOSM fue de 27%, mientras que para los algoritmos con el método FORM fue de 5%.
- Tabla 2. Resultados para diseño de una columna corta. por RBO
| Método | A(m) | COV | |||
| 0 | 0.05 | 0.1 | 0.15 | ||
| β-MVFOSM | |||||
| Fmincon-IPA | h*b* | 0.129 | 0.154 | 0.1778 | 0.1993 |
| β* | 3 | 3 | 3 | 3 | |
| G-eval(iter) | 196(39) | 103(31) | 108(32) | 96(30) | |
| PS | h*b* | 0.128 | 0.155 | 0.179 | 0.2022 |
| β* | 3 | 3 | 3 | 3 | |
| G-eval(iter) | 224(5) | 196(5) | 191(5) | 175(5) | |
| GA | h*b* | 0.1343 | 0.1596 | 0.1811 | 0.2088 |
| β* | 3.083 | 3.124 | 3.01 | 3.105 | |
| G-eval(iter) | 3150(3) | 5436(5) | 5236(5) | 5236(5) | |
| β-FORM | |||||
| Fmincon-IPA-HL | h*b* | 0.191 | 0.202 | 0.237 | 0.303 |
| β* | 3 | 3 | 3 | 3 | |
| G-eval(iter) | 145(38) | 192(53) | 190(46) | 407(41) | |
| PS-HL | h*b* | 0.194 | 0.205 | 0.245 | 0.306 |
| β* | 3 | 3 | 3 | 3 | |
| G-eval(iter) | 189(5) | 182(5) | 168(5) | 147(5) | |
| GA-HL | h*b* | nc | nc | nc | nc |
| β* | nc | nc | nc | nc | |
| G-eval(iter) | nc | nc | nc | nc | |
| RIA-SQP-HL1 | h*b* | 0.192 | 0.202 | 0.237 | 0.302 |
| β* | 3 | 2.999 | 3 | 3 | |
| G-eval(iter) | 600(4) | 525(5) | 630(5) | 945(5) | |
| PMA-SQP-HL1 | h*b* | 0.191 | 0.202 | 0.237 | 0.302 |
| β* | 2.996 | 2.997 | 2.999 | 2.999 | |
| G-eval(iter) | 450(5) | 651(5) | 570(4) | 684(5) | |
| SORA-SQP1 | h*b* | 0.192 | 0.202 | 0.237 | 0.301 |
| β* | 2.999 | 2.999 | 2.997 | 2.998 | |
| G-eval(iter) | 119(11 | 196(14 | 252(15) | 346(19) | |
| 1 Resultados obtenidos por Younes Aoues · Alaa Chateauneuf [6] | |||||
Cabe mencionar que el MVFOSM-GA mostró una alta confiabilidad en los resultados estadísticos como se puede observar en la Tabla 3.
- Tabla 3. Resultados estadísticos para el problema de diseño de una columna corta por RBO, con 10 ejecuciones independientes del GA
| Función Objetivo | # G-eval | ||||
| COV | Media | Desviación Estándar | Media | Desviación Estándar | |
| 0.00 | 0.1355 | 0.0072 | 3150.0 | 312.9 | |
| 0.05 | 0.1625 | 0.0030 | 5236.0 | 0.0 | |
| 0.10 | 0.1877 | 0.0064 | 5236.0 | 0.0 | |
| 0.15 | 0.2116 | 0.0082 | 5236.0 | 0.0 | |
| Nota: Se usaron los parámetros por defecto del GA con un tamaño de población 20. | |||||
4.2. Optimización de un bastidor
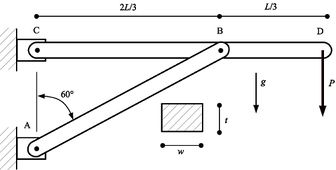
Este problema fue presentado por Y. Tsompanakis, et. al. [21] y V. Dubourg, et. al. [5] empelando SORA, RIA y Kriging. Como se muestra en la Figura 3, el bastidor soporta la carga de su propio peso debido a la gravedad y una carga adicional en su extremo derecho. Los elementos tienen sección transversal rectangular y
- Figura 3. Bastidor
El problema RBO consiste en minimizar la masa total de la estructura, sujeto a dos restricciones estocásticas en los esfuerzos permisibles y a dos restricciones determinísticas sobre las variables de optimización , que corresponden a las dimensiones de las secciones transversales de los elementos. La formulación matemática del problema es:
| (9) |
y representan los índices de confiabilidad definidos para las funciones de estado límite y respectivamente, que están definidas por las ecuaciones (12) y (13). El modelo probabilístico para este ejemplo comprende variables aleatorias independientes cuyos datos están consignados en la Tabla 4.
- Tabla 4. Datos estadísticos de las variables aleatorias para el bastidor.
| Variable | Distribución | Media | COV | |
| Normal | ||||
| Normal | ||||
| Normal | ||||
| Gumbel | ||||
| Gumbel | ||||
| Log-normal | ||||
| Weibull | ||||
| Normal | ||||
restringe el esfuerzo máximo debido a flexión en la viga horizontal (CD, en el punto B), el cual no debe exceder el límite de elasticidad del material de manera que la primera función de estado límite es la siguiente:
| (10) |
con:
restringe la máxima carga axial permisible en el elemento AB, la cual no debe exceder la carga critica por pandeo de Euler (despreciando su propio peso).
| (11) |
con:
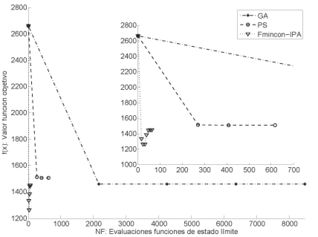
En la Tabla 5 están consignados los resultados óptimos obtenidos a través de diferentes métodos de RBO y algoritmos de optimización. RIA-Fmincon-IPA muestra la mejor eficiencia con el menor número de evaluaciones de las funciones de estado límite (G-eval=64), seguido de Kriging (G-eval=150), RIA-PS(G-eval=618), SORA-SQP(G-eval=1340), RIA-SQP(G-eval=2340) y finalmente RIA-GA (G-eval=8470). La eficiencia de los tres algoritmos de optimización evaluados en este trabajo se corrobora en el gráfico de convergencia ilustrado en la Figura 4. Adicionalmente con esos tres algoritmos se obtuvo un mejor valor de la función objetivo, lo que indica que los demás algoritmos posiblemente llegaron a un óptimo local. Teniendo en cuenta que el valor inicial de la función objetivo es de W(x0) =2660.68 kg, los porcentajes de reducción de masa para cada algoritmo son los siguientes: RIA-Fmincon-IPA (46%), Kriging, (39%), RIA-PS(43%), SORA-SQP(42%), RIA-SQP(37%) y por ultimo RIA-GA (45%).
- Tabla 5. Resultados para el bastidor por RBO
| Método | Variables de diseño. | W* función objetivo | G-eval(iter) | β | |
| (mm) | (kg) | ||||
| RIA-Fmincon-IPA | wab* | 61.16 | |||
| wcd* | 75.9 | 1449.98 | 64(7) | β 1=2.00 | |
| t* | 299.93 | β 2=2.00 | |||
| RIA-PS | wab* | 63.21 | |||
| wcd* | 92.15 | 1507.60 | 618(3) | β 1=2.00 | |
| t* | 272.41 | β 2=2.00 | |||
| RIA-GA | wab* | 61.51 | |||
| wcd* | 78.52 | 1459.35 | 8470(4) | β 1=2.00 | |
| t* | 294.98 | β 2=2.00 | |||
| RIA-SQP2 | wab* | 61 | |||
| wcd* | 157 | 1675 | 2340(5) | β 1=1.96 | |
| t* | 209 | β 2=2.01 | |||
| SORA-SQP2' | wab* | 61 | |||
| wcd* | 157 | 1550 | 1340(22) | β 1=1.96 | |
| t* | 209 | β 2=2.01 | |||
| Kriging-SQP 1 | wab* | 59 | |||
| wcd* | 135 | 1610 | 150(10) | β 1=2.01 | |
| t* | 226 | β 2=2.03 | |||
| 1 Resultados obtenidos por [5],2 Resultados Obtenidos por [21] | |||||
- Figura 4. Convergencia de los algoritmos PS, Fmincon-IPA y GA para el diseño del bastidor
Los resultados del GA para este problema muestran una confiabilidad razonable en relación al valor de la función objetivo, y una variabilidad alta del número de evaluaciones las funciones de estado límite (G-eval). Ver Tabla 6.
:Tabla 6. Resultados estadísticos para el problema del bastidor, con 10 ejecuciones independientes del Algoritmo Genético (GA)
| Función Objetivo | # G-eval | |||
| Media | Desviación Estándar | Media | Desviación Estándar | |
| 1497.14 | 41.796 | 10345.0 | 3784.5 | |
| Nota: Fueron usados los parámetros por defecto del AG con un tamaño de población 20. | ||||
4.3. Optimización de una armadura de 10 barras por RBO
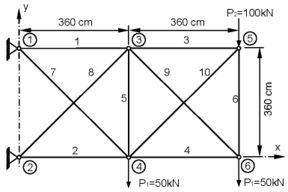
Este ejemplo consiste en la optimización basada en confiabilidad de una estructura plana articulada de 10 barras, mostrada en la Figura 5, sometida a restricciones de desplazamientos y de tensiones [22].
- Figura 5. Estructura plana articulada de 10 barras
Este ejemplo sirve para analizar el comportamiento de métodos RBO con un problema estructural en el que las funciones de estado límite dependen de forma implícita de las variables de diseño. El problema RBO para la estructura articulada de 10 barras consiste minimizar el volumen de la estructura sujeto a restricciones de confiabilidad sobre las tensiones, desplazamientos y pandeo. La estructura está soportando las siguientes cargas aleatorias: P1=100 kN aplicada en al nodo 5 y P2=50 kN aplicada en los nodos 4 y 6. Las barras son de acero y sección trasversal rectangular maciza. Se considera que las barras de la estructura están agrupadas por motivos de fabricación en 3 grupos correspondientes a las barras horizontales (A1), verticales (A2) y diagonales (A3). El problema RBO considera estos tres grupos como las variables de diseño , que corresponden a las áreas de las secciones trasversales de las barras de cada grupo. El módulo de elasticidad E y la tensión admisible σa son variables aleatorias, definidas en la Tabla 7.
- Tabla 7. Datos estadísticos de las variables aleatorias del problema de la estructura de 10 barras.
| Variable | Distribución | Media. | COV | |
| Log-Normal | 20 | 0.05 | ||
| Log-Normal | 20 | 0.05 | ||
| Log-Normal | 20 | 0.05 | ||
| Log-Normal | 21000 | 0.05 | ||
| Log-Normal | 21 | 0.05 | ||
| Log-Normal | 100 | 0.20 | ||
| Log-Normal | 50 | 0.05 | ||
La formulación matemática del problema es:
| (12) |
La restricción del desplazamiento vertical en el nodo 6 ) está definida por la ecuación (15) para desplazamientos positivos y por la ecuación (16) para desplazamientos negativos, limitado por un desplazamiento máximo admisible de
| (13) | |
| (14) |
Las restricciones de tensión en los elementos de la estructura están dadas por la ecuación (17), limitadas por la tensión admisible que puede soportar cada elemento y está dada por:
| (15) |
donde es la tensión calculada en cada elemento.
Las restricciones de compresión en los elementos de la estructura están dadas por la ecuación (18), limitadas por la tensión crítica de pandeo de Euler .
| (16) |
con
donde Ik es el momento de inercia mínimo de la sección transversal, Lk la longitud del elemento y Ak es el área de sección trasversal de la k-ésima barra.
En la Tabla 8 están consignados los resultados óptimos obtenidos a través de diferentes métodos de RBO y algoritmos de optimización. RIA-Fmincon-IPA muestra la mejor eficiencia con el menor número de evaluaciones de las funciones de estado límite (G-eval) seguido de RIA-PS. La eficiencia de estos dos algoritmos de optimización se corrobora en el gráfico de convergencia ilustrado en la Figura 6. No se puede concluir sobre la eficiencia de los demás algoritmos registrados en la Tabla 8 debido a que en la literatura no registran el número de evaluaciones de las funciones de estado límite realizadas (G-eval) y el algoritmo genético no logró convergencia. Como se evidencia en la Tabla 8 todos los algoritmos llegaron a un óptimo cercano, sin embargo, se diferencian dos grupos de resultados. Teniendo en cuenta que el valor inicial de la función es V(x0) = 83929.4 cm3, los dos primeros algoritmos logran una estructura con un volumen 16% menor respecto al volumen de la estructura obtenida por los últimos seis algoritmos de la tabla. Cerrolio L.[22] usa algoritmos de optimización basados en derivadas, obtenidas por: derivación directa (DDM) y por diferencias finitas (FFD, forward finite differences).
- Tabla 8. Resultados para el problema de la estructura de 10 barras por RBO
| Método RBDO | Volumen (cm3) | Variables de diseño (cm2) | G-eval(iter) | ||
| RIA-Fmincon-IPA | 205723.9 | 54.892 | 21.150 | 54.727 | 233940(15) |
| RIA-PS | 205723.91 | 54.892 | 21.150 | 54.727 | 3173610(6) |
| RIA-GA | nc | nc | nc | nc | nc |
| RIA-DDM1 | 218918.69 | 55.789 | 22.695 | 60.026 | - (10) |
| PMA-DDM 1 | 218925.81 | 55.791 | 22.694 | 60.029 | - (13) |
| SORA-DDM1 | 218926.87 | 55.791 | 22.695 | 60.029 | - (10) |
| RBDO-FFD1 | 219326.19 | 55.886 | 22.810 | 60.118 | - (8) |
| PMA-FFD1 | 219330.28 | 55.886 | 22.810 | 60.120 | - (8) |
| SORA-FFD1 | 219330.28 | 55.886 | 22.810 | 60.120 | - (8) |
| 1 Resultados de Cerrolio L.[22]. Nota: nc significa que el algoritmo no converge. | |||||
- Figura 6. Convergencia de los algoritmos PS y Fmincon-IPA para para el problema de las 10 barras
5. Resultados y discusiones
Los resultados obtenidos en los problemas de prueba implementados en este estudio se presentan en la sección 4, a través de tablas de resultados, gráficos de convergencia y un breve análisis de estos.
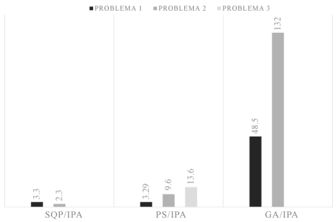
La comparación directa entre los tres algoritmos que se implementaron para los tres problemas de optimización estructural por RBO muestra que el algoritmo de optimización Fmincon-IPA (como IPA) fue el más eficiente al tener un menor costo computacional por requerir menos evaluaciones de las funciones de estado límite (G-eval), seguido por el algoritmo PS y finalmente el algoritmo GA. Al comparar estos resultados con los obtenidos por otros algoritmos disponibles en la literatura se ratifica que el algoritmo más eficiente sigue siendo Fmincon-IPA, seguido de SQP, PS y GA. Estos resultados comparativos de eficiencia computacional se observan claramente en el diagrama de barras de la Figura 7, que compara el cociente del G-eval de cada uno de los algoritmos de optimización y el G-eval del algoritmo más eficiente (el de menor G-eval).
- Figura 7. Eficiencia comparativa a través de G-eval para los algoritmos de optimización.
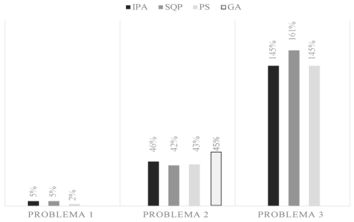
La eficacia, definida como la capacidad de llegar al óptimo con precisión, puede cuantificarse al comparar los porcentajes de reducción de la función objetivo, obtenidos por cada algoritmo de optimización. Como se puede observar en la Figura 8, para los dos primeros problemas de prueba IPA fue el más eficaz, seguido de cerca por SQP y PS, al tener los mayores porcentajes. Para el tercer problema de prueba IPA y PS fueron los más eficaces al lograr el menor porcentaje de aumento de la función objetivo, seguido de cerca por SQP.
- Figura 8. Eficacia comparativa a través del porcentaje de reducción de la función objetivo.
6. Conclusiones
En este trabajo se presenta un estudio comparativo del desempeño numérico de algoritmos de optimización representativos de las principales familias de algoritmos de optimización en la solución computacional de problemas de optimización estructural por RBO. Esta comparación ofrece la información suficiente para la selección de un algoritmo de optimización apropiado para aplicaciones de optimización estructural computacionalmente intensivas típicas de la RBO, teniendo en cuenta características como la eficiencia, eficacia y facilidad de implementación. Para problemas de optimización estructural por RBO de estructuras de pequeño porte, la familia de algoritmos de optimización basados en derivadas presentó la mayor eficiencia y eficacia computacional, seguido por la familia de algoritmos de optimización de búsqueda directa y por la familia de algoritmos de optimización bioinspirados basado en poblaciones de individuos. En relación a la facilidad de implementación, los algoritmos de optimización más fáciles de implementar son los de búsqueda directa y los bioinspirados; sin embargo, en relación a la facilidad de uso, todas las familias de algoritmos de optimización poseen parámetros particulares y criterios de convergencia que hacen que en general todos sean relativamente fáciles de usar.
Los algoritmos bioinspirados poblacionales presentan una característica particular que, si bien les puede permitir obtener óptimos globales, también los hace menos estables al involucrar mecanismos aleatorios en su funcionamiento y al no garantizar el cumplimiento de las restricciones en todo el proceso de optimización.
Dentro de las estrategias del cálculo de confiabilidad, los métodos aproximados de primer orden muestran resultados eficientes y precisos. Sin embargo, para potenciar su eficiencia y precisión se aconseja que, en caso de ser posible, se implementen en su versión analítica o semianalítica, disponiendo de las derivadas analíticas de las funciones de estado límite para cuantificar los índices de confiabilidad.
Las aplicaciones de optimización estructural por RBO para problemas en estructuras de grande porte es aún una tarea desafiante debido al alto costo computacional demandado. En esta área aún se esperan grandes progresos que permitan incrementar drásticamente la eficiencia computacional para poder abordar problemas de optimización estructural de mayor complejidad.
Agradecimientos
Los autores agradecen el apoyo económico que han recibido para la realización de este trabajo por parte de la Universidad Santo Tomás, a través de los proyectos del fondo de investigación FODEIN con códigos 003 del 2013 y 051 del 2014. También agradecen el apoyo recibido por la Universidad Nacional de Colombia.
Referencias
[1] R. Reuven Y., Simulation and the Monte Carlo method, 1st ed., John Wiley & Sons., New York, 1981.
[2] A.M. Hasofer, N.C. Lind, An Exact and Invariant First-order Reliability Format, J. Eng. Mech. Div. (1973) 111–121.
[3] A. Der Kiureghian, H.-Z. Lin, S.-J. Hwang, Second-Order Reliability Approximations, J. Eng. Mech. 113 (1987) 1208–1225. doi:10.1061/(ASCE)0733-9399(1987)113:8(1208).
[4] V. Keshavarzzadeh, H. Meidani, D.A. Tortorelli, Gradient based design optimization under uncertainty via stochastic expansion methods, Comput. Methods Appl. Mech. Eng. 306 (2016) 47–76. doi:10.1016/j.cma.2016.03.046.
[5] V. Dubourg, B. Sudret, J.M. Bourinet, Reliability-based design optimization using kriging surrogates and subset simulation, Struct. Multidiscip. Optim. 44 (2011) 673–690. doi:10.1007/s00158-011-0653-8.
[6] B. Sudret, Meta-models for structural reliability and uncertainty quantification, Fifth Asian-Pacific Symp. Struct. Reliab. Its Appl. (2012) 53–76.
[7] Y. Aoues, A. Chateauneuf, Benchmark study of numerical methods for reliability-based design optimization, Struct. Multidiscip. Optim. 41 (2009) 277–294. doi:10.1007/s00158-009-0412-2.
[8] M.A. Valdebenito, G.I. Schuëller, A survey on approaches for reliability-based optimization, Struct. Multidiscip. Optim. 42 (2010) 645–663. doi:10.1007/s00158-010-0518-6.
[9] O. Ditlevsen, P. Bjerager, Methods of Structural Systems Reliability, Struct. Saf. 3 (1986) 195–229. doi:10.1016/0167-4730(86)90004-4.
[10] S.-K. Choi, R.V.. Grandhi, R.A. Canfield, Reliability-based Structural Design, Springer, London, 2007.
[11] C.A. Cornell, A probability-based structural code, J. Proc. 66 (1969) 974–985.
[12] E. Nikolaidis, R. Burdisso, Reliability based optimization: A safety index approach, Comput. Struct. 28 (1988) 781–788. doi:10.1016/0045-7949(88)90418-X.
[13] A.M. Hasofer, N.C. Lind, Exact and Invariant Second-Moment Code Format, J. Eng. Mech. Div. 100 (1974) 111–121.
[14] R.H. Byrd, J.C. Gilbert, J. Nocedal, A Trust Region Method Based on Interior Point Techniques for Nonlinear Programming, Math. Program. Ser. B. 89 (2000) 149–185. doi:10.1007/PL00011391.
[15] R. Hooke, T.A. Jeeves, Direct Search Solution of Numerical and Statistical Problems, J. ACM. 8 (1961) 212–229. doi:10.1145/321062.321069.
[16] T.G. Kolda, R.M. Lewis, V. Torczon, A generating set direct search augmented Lagrangian algorithm for optimization with a combination of general and linear constraints, Tech. Rep. SAND2006-5315, Sandia Natl. Lab. (2006) 44.
[17] D.E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed., Addison-Wesley Publishing Company, New York, 1989.
[18] L.L. Corso, H.M. Gomes, G.P. Mezzomo, A. Molter, Otimização baseada em confiabilidade para uma célula de carga multiaxial utilizando algoritmos genéticos, Rev. int. métodos numér. cálc. diseño ing. 32 (2016) 221–229. doi:10.1016/j.rimni.2015.07.002.
[19] E.E. Kostandyan, J.D. Sorensen, Reliability assessment of IGBT modules modeled as systems with correlated components, Proc. - Annu. Reliab. Maintainab. Symp. (2013) 1–6. doi:10.1109/RAMS.2013.6517663.
[20] P.-E. AUSTRELL, O. DAHLBLOM, J. LINDEMANN, A. OLSSON, CALFEM-a finite element toolbox, version 3.4, Lund University, Sweden, 2004.
[21] Y. Tsompanakis, N.D. Lagaros, M. Papadrakakis, Structural design optimization considering uncertainties (Structures and Infrastructures 1), Taylor & Francis, London, 2008.
[22] L. Cerrolio, Metodología eficiente de optimización de diseño basada en fiabilidad aplicada a estructuras, Ph.D. Thesis, Universidad de la Rioja, Logroño, España, 2013.
Document information
Published on 03/01/18
Accepted on 06/06/17
Submitted on 18/01/17
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.7.003
Licence: CC BY-NC-SA license