| Line 1: | Line 1: | ||
| + | Submitted: 20/12/2016 | ||
| + | |||
| + | Accepted: 06/06/2017 | ||
| + | |||
==Abstract== | ==Abstract== | ||
Revision as of 15:06, 21 June 2017
Submitted: 20/12/2016
Accepted: 06/06/2017
Abstract
This work shows the variability of the friction angle based on the geological history, over the bearing capacity of shallow foundations. This study was developed through the generation of random fields of friction angle using the matrix decomposition technique for a self-correlated lognormal distribution. In addition, to recreate the geological history, the anisotropic random fields were created using the rotation matrix with angles of 0, 45 and 90 degrees. Subsequently, these random fields were implemented in a finite element model of a continuous footing. A linear elastoplastic constitutive model was selected to represent stress-strain soil behavior together with the Mohr-Coulomb failure criteria. This last work was done in order to understand the influence of geological history and the variability of the friction angle in the bearing capacity of shallow foundations. Results include the weight of the variability of the friction angle in the bearing capacity and the influence of the dip over the friction angle and the bearing capacity.
Resumen
Este trabajo muestra el estudio de la variabilidad del ángulo de fricción con el análisis de la historia geológica y su influencia en la capacidad de carga de cimentaciones superficiales. Esto se realizó con la generación de campos aleatorios del ángulo de fricción por medio de la técnica de matriz de descomposición para una distribución lognormal autocorrelacionada. Adicionalmente, para recrear la historia geológica se crearon los campos aleatorios de forma anisotrópica por medio de la matriz de giro con ángulos de 0, 45 y 90 grados. Posteriormente estos campos aleatorios fueron implementados en un modelo de elementos finitos de una zapata continua. El modelo constitutivo usado fue un modelo lineal elástico con criterio de falla de Mohr Coulomb. Lo anterior, para el entender la influencia de la historia geológica y la variabilidad del ángulo de fricción en la capacidad de carga de cimentaciones superficiales. Como resultados se muestran los pesos de la variabilidad del ángulo de fricción en la capacidad de carga y la influencia del buzamiento de este ángulo fricción en la capacidad de carga.
Palabras claves: Campos aleatorios, ángulo de fricción con buzamiento, elementos finitos con aleatoriedad, cimentaciones superficiales, modelo elastoplástico.
1. Introducción
En el proceso de formación de los suelos transportados se tiene una deposición de partículas de diferentes orígenes que cuentan con diferentes características geotécnicas, esto ya crea una variabilidad de las propiedades geotécnicas. Posteriormente a la formación del suelo y durante su historia geológica ocurren diferentes procesos geológicos, uno de estos procesos son los plegamientos que generan buzamiento de los estratos. En la actualidad estas características no son tomadas en cuenta en el proceso de diseño. Por lo anterior, el presente trabajo estudia la influencia de la historia geológica y la variabilidad del ángulo de fricción en la capacidad de carga de cimentaciones superficiales
En la actualidad varios autores han tratado el tema de la variabilidad de los parámetros geotécnicos en la capacidad de carga de fundaciones, con parámetros aleatorios y campos aleatorios de parámetros [1-7]. Sin embargo, los resultados obtenidos no llegan a ser implementados en la geotecnia práctica y obtener un consenso general con las diferentes técnicas utilizadas. Aunque se sabe que la variabilidad espacial existe y puede tener cambios importantes de valores de los parámetros geotécnicos de un punto a otro. Sin embargo, los cambios generados en la capacidad de carga por el efecto de la variabilidad generalmente son cubiertos por el factor de seguridad.
Las anteriores características crean la necesidad de comprender mejor la influencia buzamiento de la distribución de la variabilidad del ángulo de fricción y su influencia en la capacidad portante de cimentaciones superficiales. Para abordar este problema, inicialmente se crean campos aleatorios con la variabilidad del ángulo de fricción por la técnica de matriz de descomposición, posteriormente se gira el campo aleatorio por medio de la matriz de giro. Esto fue realizado para observar la influencia de la variabilidad espacial del ángulo de fricción en la capacidad de carga de cimentaciones superficiales. El paso siguiente fue implementar los campos aleatorios en un modelo del método de elementos finitos MEF, por el programa Abaqus. Estas simulaciones fueron de una cimentación superficial. Además, el modelo constitutivo usado fue un modelo elástico con criterio de ruptura de Mohr Coulomb que cuenta con gran popularidad entre la geotecnia práctica [8]. Con todo lo anterior se encontró la importancia de la variabilidad espacial del ángulo de fricción en el valor de capacidad de carga y como este valor cambia según la rotación del campo aleatorio.
El trabajo se divide en siete secciones. La primera es la introducción del trabajo realizado. La segunda sección corresponde a la presentación del modelo constitutivo usado en las simulaciones. La tercera sección presenta la generación de los campos aleatorios del ángulo de fricción, su funcionamiento, implementación y automatización. La cuarta sección muestra la realización del modelo de elementos finitos de la cimentación superficial en cuanto a su geometría, condiciones de borde, tipo de elementos usados, pasos de análisis. La quinta sección es integración del modelo de elementos finitos con los campos aleatorios generados. La sexta sección muestra los resultados obtenidos de las simulaciones y su análisis en cuanto a la influencia de la variabilidad del ángulo de fricción en la capacidad de carga de la cimentación superficial estudiada. Por último, se resaltan los resultados más importantes del trabajo desarrollado en las conclusiones.
2. Modelo constitutivo
El modelo más usado en geotecnia es el modelo elástico con criterio de falla de Mohr Coulomb M-C [8], este modelo es una extensión de los modelos elasto-plásticos para metales que fueron los primeros modelos constitutivos usados en suelos [9]. Este modelo constitutivo cuenta con gran popularidad porque solo cuenta con 4 parámetros y todos ellos tienen explicación física. Además, los parámetros pueden ser obtenidos de un ensayo triaxial [10]. Por otra parte, el modelo constitutivo seleccionado para el comportamiento del suelo en esfuerzos y deformaciones ya está implementado en varios programas de elementos finitos (uno de estos es el programa Abaqus) y ha mostrado una gran capacidad para reproducir el comportamiento del suelo en problemas geotécnicos [7-12].
El modelo en el rango elástico trabaja con dos parámetros el Módulo de Young E y la relación de Poisson para relacionar esfuerzos y deformaciones. Esta relación de esfuerzos y deformaciones es validad hasta que se alcanza la envolvente de fluencia, en este punto comienzan a presentarse deformaciones elastoplásticas. Para describir la envolvente de fluencia se usan dos parámetros el ángulo de fricción y la cohesión c [10, 13].
3. Generación de campos aleatorios
Como un objetivo del presente trabajo es el entendimiento de la variación espacial del ángulo de fricción, se describe abajo la técnica de descomposición de Cholesky para la distribución espacial de valores del ángulo de fricción.
La variabilidad de parámetros o variables geotécnicas ya ha sido usada en varios trabajos [1, 3, 6, 7, 15-18]. Estos trabajos son realizados por medio de distribuciones normales, log-normales y usando análisis de Montecarlo, campos aleatorios, entre otras técnicas. En este estudio se quiere estudiar la variabilidad espacial del ángulo de fricción por tal razón se utiliza la técnica de matriz de descomposición, la cual ha tenido gran éxito en los últimos años [17]. Los valores de la variable de salida Y son generados por medio de la ecuación 1. Esta ecuación está compuesta por el valor medio μ, ε que es un vector que tiene valores aleatorios con una distribución normal y L es una matriz definida en la ecuación 2. La ecuación 2 muestra la matriz de covarianza A del campo, esta matriz es la parte positiva de la descomposición de una matriz triangular inferior con entradas diagonales estrictamente positivas L por la matriz transpuesta. El anterior concepto es llamado factorización o descomposición de Cholesky. Por otra parte, la Matriz A (ecuación 3) tiene la distancia de autocorrelación en x y y, por medio de los parámetros Lx y Ly para tomar anisotropía vertical y horizontal. Adicionalmente, esta matriz es afectada por el giro con la matriz de giro presentada en la ecuación 4
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
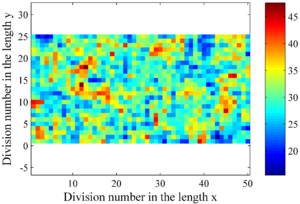
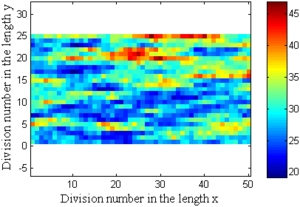
Para generar el campo de distribución espacial del ángulo de fricción se necesitan dos parámetros estadísticos de la variable; éstos son el valor medio con un valor de μ=29 y la desviación estándar con valor de σ=5. Además del valor del ángulo de giro de este campo donde se usaron tres valores de giro 0, 45 y 90 grados. Sin embargo, con los mismos parámetros se pueden generar distintos campos aleatorios, para tratar esto se generaron 100 campos aleatorios para cada valor de giro. Las distancias de autocorrelación en cada dirección son Lx=5.0 y Ly=1.0. La Figura 1 muestra tres campos aleatorios generados para un Angulo de giro de 0, 45, 90 grados. Por otra parte, la longitud en x fue dividida en 50 partes y la longitud en y fue dividida en 25 partes, la multiplicación de estas divisiones en x y y dan el número total de valores generados en la variable de salida. Posteriormente, los valores generados de la variable de salida son introducidos en el modelo de elementos finitos como se muestra mas adelante.
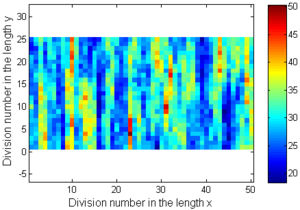
|
|
| (a) | (b) |
4. Modelo de elementos finitos
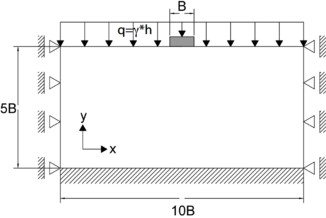
Se realizó un modelo de elementos finitos de una zapata continúa usando el programa ABAQUS. El modelo de elementos finitos tiene como objetivo simular la prueba de carga de una zapata de 1m de ancho a un metro de profundidad. La parametrización de la geometría del modelo se realizó en función del ancho de la zapata. Se colocó en el modelo una profundidad de cinco veces el ancho de la zapata (B=1 m), con un ancho del modelo de 10 veces el ancho de la zapata [9]. La parametrización del modelo se ilustra en la Figura 2.
Los elementos seleccionados para el enmallado son del tipo CPE4 (Cuadriláteros de deformación plana, dos dimensiones, 4 nodos), los tamaños promedios de los elementos del modelo son de 0.1 m × 0.1 m. Se considera el suelo en una condición seca. Las condiciones de borde son tres: en la base del modelo con una condición fija que no permite los desplazamientos en la dirección x y y; la segunda condición es en los bordes laterales del modelo con una condición que no permite desplazamientos en la dirección x (ver Figura 2). La última condición es una carga en la superficie del modelo para simular la profundidad de la zapata por medio del peso unitario del suelo (17kN/m3) por el metro de profundidad.
Una vez creada la geometría del modelo de zapata se aplicaron dos pasos de análisis: El pasó geo-estático que induce los esfuerzos a los que está sometido el suelo, generando una distribución lineal contra la profundidad. Posteriormente se crea el paso de carga, con una condición de desplazamiento en el tiempo para simular una prueba de carga a velocidad de desplazamiento constante.
5. Integración del modelo de elementos finitos con los campos aleatorios generados
Para capturar el efecto de la variabilidad espacial del parámetro escogido en el modelo constitutivo, se usó el método descomposición de Cholesky, como ya fue descrito. Esto con el fin de entender el comportamiento de la capacidad de carga en cimentaciones superficiales incorporando el efecto de la heterogeneidad del ángulo de fricción espacialmente y el giro de este campo aleatorio. Lo anterior fue desarrollado con simulaciones en elementos finitos y un modelo constitutivo elasto-plástico.
Las simulaciones de elementos finitos tomando en cuenta la variabilidad espacial del ángulo de fricción y el giro se realizaron de la siguiente manera:
• Por medio de un loop se generaron 100 campos aleatorios para un ángulo de giro de 0°, 45° y 90°, con una función de densidad de probabilidad mostrada en la ecuación 5. Esta distribución fue usada dado que la variable seleccionada no puede tomar valores negativos, además, se usó un condicional para que la variable no tome valores menores de 10. Por otra parte, la alternativa más usada para mapear variables del tipo geomecánico es la distribución tipo log-normal [19-21]. Sin embargo, los campos aleatorios generados pueden ser descritos con una distribución normal, como se muestra en la ecuación 6 de la función de distribución acumulada , una alternativa comúnmente usada es cambiar los parámetros estadísticos con parámetros log-normales, como se muestra en las ecuaciones 7 y 8. El valor medio de ángulo de fricción es 39° [22] y una desviación estándar es de 5° [7]
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
• Se carga cada la matriz del campo aleatorio generada en el modelo de elementos finitos mediante el uso de una subrutina en lenguaje Python y que procesa de forma automática los datos por medio de algunos loops.
• Se guardan en un archivo externo las variables de salida importantes del problema (deformaciones y esfuerzos), de cada una de las 300 simulaciones realizadas.
• Por último, se analizan las curvas carga deformación de las simulaciones realizadas. Lo anterior, se realiza obteniendo la carga de ruptura por medio de dos criterios de ruptura por asentamiento límite absoluto a 5 centímetros y 10 centímetros.
Los parámetros usados en las simulaciones son parámetros típicos de un suelo arenoso, como se muestran en la Tabla 1 [23]. Sin embargo, se reconoce el hecho que todas las propiedades geomecánicas del terreno tienen una variabilidad espacial, y esa variabilidad afecta los resultados de las pruebas de carga, pero en este trabajo solo se toma en cuenta el ángulo de fricción. Por otra parte, de los resultados de las simulaciones se puede estimar la distribución de probabilidades de las variable respuestas [5,24,25].
| E | c | Φ | μ |
| (kPa) | (kPa) | (°) | (-) |
| 30000 | 20 | 29 | 0.3 |
6. Resultados y análisis de resultados
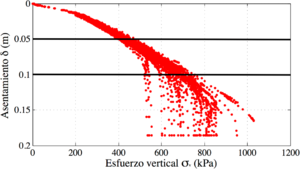
Para una mejor compresión de la influencia de la variabilidad espacial ángulo de fricción en la capacidad de carga de cimentaciones superficiales se grafica las curvas esfuerzo vertical y asentamiento, como se muestra en la Figura 3. Además, en estas curvas se obtiene la carga de ruptura de la cimentación por el método de asentamiento límite absoluto [26, 27], este método toma un valor límite del asentamiento para obtener la carga de ruptura. En el presente trabajo se tomaron dos asentamientos límites a 5 centímetros y 10 centímetros, el primero es donde la estructura puede comenzar a presentar grietas y el segundo donde se pueden comienzan a presentar daños en la estructura [28, 29].
De la Figura 3, se observa que a mayor asentamiento mayor influencia de la variabilidad del ángulo de fricción. Este resultado se puede explicar porque el ángulo de fricción solo trabaja cuando las trayectorias de esfuerzos tocan el criterio de Falla de M-C, este criterio es función de la cohesión del suelo y el ángulo de fricción. Antes que las trayectorias de esfuerzos lleguen al criterio de Falla de M-C el material se comporta de forma elástica. El comportamiento elástico del material es función del módulo de elasticidad y la relación de Poisson. Lo anterior se puede observar en la Figura 3 hasta un asentamiento cercano a los 0.02 metros, sin embargo, se sabe que no todas las trayectorias de esfuerzos de los puntos de gauss de los elementos finitos llegan al mismo tiempo al criterio de falla de M-C.

|
|
| (a) | (b) |
La Figura 4 muestra la carga de ruptura para cada simulación, con los dos criterios de falla descritos. La Figura 4b muestra un número menor de 100 puntos esto debido a que no todas las simulaciones llegaron hasta 10 centímetros de asentamiento. Por otra parte, la Figura 4 muestra de nuevo la influencia que toma el ángulo de fricción a mayor asentamiento. Esto se puede corroborar con el aumento del coeficiente de variabilidad CV (desviación estándar sobre la media), como se muestra en la Tabla 2. Un aspecto importante que se observa del coeficiente de variabilidad CV de las simulaciones es un valor no constante, esto partiendo que los campos aleatorios del ángulo de fricción se generaron con un valor constante del coeficiente de variación de CV=12.82%. Además, para los asentamientos limites escogidos se obtienen coeficientes de variabilidad menores al coeficiente de variabilidad con que se generó el campo aleatorio. Otro aspecto es que a mayor asentamiento se calcula el coeficiente de variación aumenta el valor. De esto, se puede inferir que a mayor asentamiento mayor importancia tiene el ángulo de fricción en el valor de la carga de ruptura. Un dato interesante es que el menor coeficiente de variación se presenta a una inclinación de 45 grados para los dos criterios de ruptura estudiados.
| (a) | (b) |
| Criterio 5 cm | Criterio 10 cm | |||||
| Giro | Media | Desviación estándar | Coeficiente de variación | Media | Desviación estándar | Coeficiente de variación |
| ° | kPa | kPa | % | kPa | kPa | % |
| 0° | 433.21 | 17.24 | 3.97 | 669.40 | 53.73 | 8.02 |
| 45° | 438.91 | 16.17 | 3.68 | 679.32 | 28.14 | 4.14 |
| 90° | 437.31 | 23.90 | 5.46 | 673.95 | 38.51 | 5.71 |
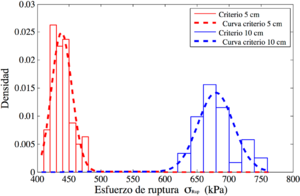
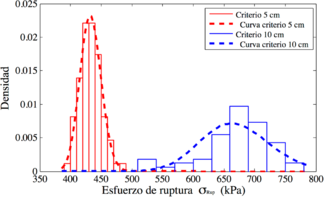
La Figura 5 muestra el histograma y la curva de densidad log-normal de la carga de ruptura para las simulaciones realizadas, esto tomando en cuenta el giro del campo aleatorio y los criterios de ruptura seleccionados. De esta figura se observa que a mayor asentamiento mayor valor medio de la carga de ruptura, esto es lógico, como ya fue mencionado. Sin embargo, lo interesante es que el mayor valor medio se obtiene a una inclinación del campo aleatorio de 45 grados sin importar el valor del asentamiento (en este caso a 5 y 10 centímetros), esto también se puede observar en la Tabla 2. Otro aspecto importante a resaltar es que ocurre lo contrario con la desviación estándar y el coeficiente de variación porqué los valores más bajos están con una inclinación de 45 grados. Esto es importante porque muestra la importancia del buzamiento de los estratos. Además, la Figura 5 muestra que el valor medio, la desviación estándar y el coeficiente de variación sube con el aumento del asentamiento, en este caso fue el criterio de ruptura de 10 centímetros, los mismos resultados se muestran en la Tabla 2.
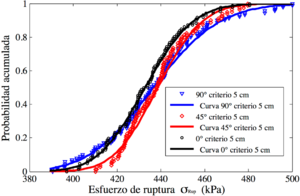
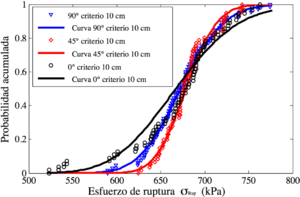
De los datos obtenidos de la Figura 5 se obtiene la curva de probabilidad acumulada respecto a las cargas de ruptura, como se muestra en la Figura 6. Las curvas de probabilidad acumuladas fueron generadas con una distribución log-normal, sin embargo, esta distribución no se ajustó bien para el giro de cero grados y criterio de ruptura de 10 centímetros, como se puede observar en la Figura 5c y la Figura 6b.
La Tabla 3 muestra la carga de ruptura para el 50% de probabilidad acumulada (Figura 6) con las inclinaciones estudiadas. La inclinación que presento menor carga de ruptura fue la inclinación de ángulo de fricción con cero grados, seguida por la inclinación de noventa grados y la inclinación con mayor resistencia es la de cuarenta y cinco grados. Otro aspecto importante de la Tabla 3 es que el aumento de carga de ruptura para para los tres ángulos estudiados aumenta un 54% al tomar un criterio de falla de 10 centímetros en comparación con el criterio inicial de 5 centímetros.
Tabla 3. Carga de ruptura para el 50% de probabilidad obtenida de las curvas de probabilidad acumulada.
| Giro | Unidad | Criterio de ruptura 5 cm | Criterio de ruptura 10 cm |
| 0° | kPa | 433 | 668 |
| 45° | kPa | 439 | 679 |
| 90° | kPa | 437 | 674 |
La ecuación 9 muestra la ecuación de capacidad portante de Terzaghi, donde esta ecuación es función de la cohesión c, el esfuerzo al nivel de cimentación q, el peso unitario del suelo , el ancho de la zapara B y los factores de carga Nc, Nq y N, esto factores de carga a su vez son función del ángulo de fricción [23, 28]. Se realizó una comparación de las cargas de ruptura obtenidas y la ecuación de capacidad portante clásica de Tezaghi. El valor de la capacidad portante es de 1162 kPa (datos de Tabla 1 y sección 4), la cual es mayor a todas las cargas de rupturas obtenidas en las 300 simulaciones, como se puede observar en las Figuras 3 y 4. Sin embargo la carga de trabajo que es la capacidad portante dividido un factor de seguridad de 3 [28] es 387.33 kPa que es menor a la carga de ruptura obtenida en todas las simulaciones. Esto muestra que el efecto de la variabilidad está cubierto por el factor de seguridad. Ahora bien, realizando un ejercicio académico de suponer que las cargas de ruptura de las simulaciones es la resistencia real del suelo y la carga de trabajo calculada es la solicitación el factor de seguridad cambia de con los menores valores de carga de ruptura obtenidos de las simulaciones son: F.S.=1.008 para una inclinación de 90 grados; F.S.=1.059 para una inclinación de 45 grados; F.S.=1.024 para una inclinación de 0 grados, estos valores son obtenidos con un criterio de ruptura de 5 centímetros. Para el criterio de ruptura de 10 centímetros los factores de seguridad son: F.S.=1.521 para una inclinación de 90 grados; F.S.=1.612 para una inclinación de 45 grados; F.S.=1.350 para una inclinación de 0 grados. Estos resultados muestran un menor factor de seguridad cercano a uno tomando los menores valores obtenidos de las simulaciones, otro aspecto importante es que el mayor factor de seguridad se da con una inclinación de 45 grados. También se observa que al tomar un criterio de ruptura de 10 centímetros se aumenta el factor de seguridad en un porcentaje mayor al 50% para una inclinación de 90 grados; 52% para una inclinación de 45 grados y 32% para una inclinación de 0 grados
|
|
(9) |
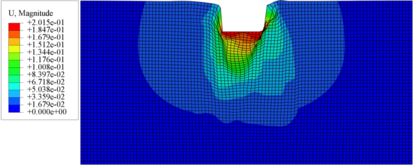
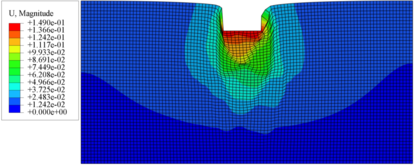
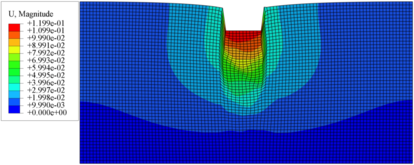
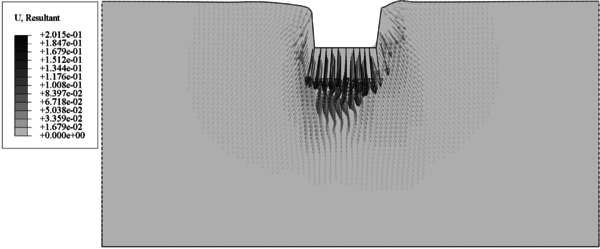
La Figura 7 muestra la malla deformada para tres diferentes ángulos de giro de los campos aleatorios generados del ángulo de fricción, para esta figura se escogieron las simulaciones donde obtuvieron las mayores resistencias. De la anterior figura se observa la variación espacial de la resistencia del suelo, al presentar bulbos de deformación bastante no uniformes. La Figura 7a presenta los bulbos de deformaciones con mayor no simetría, en comparación con los bulbos mostrados en la Figura 7c. De la Figura 7a se obtiene los vectores de desplazamiento, como se muestran en la Figura 8. De esta figura se observa que las magnitudes de los vectores de desplazamiento no son simétricas, además se enfatiza mecanismos de falla no simétrico en las deformaciones. La no simetría de las deformaciones y de los mecanismos de falla ya fue mostrado en el trabajo de Griffiths and Fenton [3]. Lo anterior significar que los cálculos para obtener deformaciones y esfuerzos a diferentes profundidades cuando se construyen estructuras geotécnicas no están bien calculados en la actualidad al considerar los estratos como homogéneos, una consecuencia es cuando se calculan las deformaciones generadas en tuberías enteradas al construir una obra geotécnicas porque estas resisten pocos milímetros de deformación antes de romper.
7. Conclusiones
El presente estudio presenta un procedimiento innovador para obtener la capacidad de carga de cimentaciones superficiales tomando en cuenta la variabilidad natural (intrínseca) del suelo, en este caso se estudió la variabilidad del ángulo de fricción. Además de los anterior se tomó en cuenta los procesos geológicos que pueden generar que la distribución espacial de la variabilidad del ángulo de fricción pueda estar con diferentes ángulos. Del trabajo se obtuvieron las siguientes conclusiones:
- 1. Se muestra que la capacidad portante está relacionada con el buzamiento del ángulo de fricción en el campo aleatorio al tener que el estrato con giro de 45 grados presentó mayor que el valor medio de la capacidad de carga, menor la desviación estándar y por ende menor coeficiente de variación.
- 2. La resistencia de las cimentaciones superficiales está influencia por la variabilidad del ángulo de fricción. Esta influencia aumenta a mayor asentamiento de la zapata, esto se puede observar al obtener un mayor coeficiente de variabilidad CV mayor con el aumento del asentamiento.
- 3. Otro aspecto importante observado en el coeficiente de variabilidad de las simulaciones realizadas es que para un ángulo de 45 grados se presenta el menor valor. Además, los coeficientes de variabilidad no son constantes para los tres diferentes ángulos medidos y son función del ángulo de giro y de la profundidad donde se obtenga la carga de ruptura. Esto es interesante partiendo que todos los campos aleatorios del ángulo de fricción fueron generados con el mismo coeficiente de variación.
- 4. Se muestra que para todas las simulaciones realizadas se tiene un aumento de carga de ruptura para para los tres ángulos estudiados del 54% al tomar un criterio de falla de 10 centímetros en comparación con el criterio inicial de 5 centímetros.
- 5. Se muestra la influencia de la variación del ángulo de fricción en los campos de deformación generados en la profundidad del estrato de suelo. Esto causa que en la actualidad los cálculos de deformaciones generadas por la construcción de obras geotécnicas no estén bien obtenidos y se puede incurrir en errores cuando se chequea deformaciones generadas en tuberías enteradas porque estas resisten pocos milímetros de deformación antes de romper.
Referencias
[1] Lump P. (1970). The Safety factors and the probability distributions of soil strength. Canadian Geotechnical Journal. 7(3), p. 225–242.
[2] Schultze E. Frequency distributions and correlations of soil properties. In: Lumb P, editor. Proceedings of the 1st International Conference on Applications of Statistics and Probability in Soil and Structural Engineering (ICASP), Hong-Kong, University Press, Hong-Kong; 1972. p. 372–87.
[3] Griffiths D. V. and G. A. Fenton (2001). Bearing capacity of spatially random soil: the undrained clay Prandtl problem revisited. Géotechnique, 51:4, 351-359.
[4] Suchomel R and Masín D. (2011). Probabilistic analysis of a strip footing on horizontally stratified sandy deposit using advanced constitutive model. Computers and Geotechnics; 38:363-374.
[5] Mendoza, Cristhian, Ramos, Alfonso M, Cunha, Renato, & Lizcano, Arcesio. (2012). Análisis del proceso constructivo y variabilidad de parámetros geotécnicos en la capacidad de carga de micropilotes usando elementos finitos aleatorios. Obras y proyectos, (11), 61-70.
[6] Pieczyńska-Kozłowska J.M., W. Puła, D.V. Griffiths, G.A. Fenton, Influence of embedment, self-weight and anisotropy on bearing capacity reliability using the random finite element method, Computers and Geotechnics, Volume 67, June 2015, Pages 229-238.
[7] Mendoza, C., Caicedo, B., and Cunha, R. (2016). "Determination of Vertical Bearing Capacity of Pile Foundation Systems in Tropical Soils with Uncertain and Highly Variable Properties." J. Perform. Constr. Facil. 10.1061/(ASCE)CF.1943-5509.0000918, 04016068.
[8] Johnson, K., Lemcke, P., Karunasena, W., and Sivakugan, N. (2006). “Modeling the load deformation response of deep foundations under oblique loading.” Environ. Model. Software, 21(9), 1375–1380.
[9] Helwany, S. (2007). Applied soil mechanics with ABAQUS applications, 1st Ed., Wiley.
[10] Desai CS, Siriwardane HJ. (1984). Constitutive laws for engineering materials with emphasis on geologic materials. 1 ed. Englewood Cliffs, New Jersey, USA: Prentice-Hall, Inc. ISBN 0-13-167940-6.
[11] Potts David and Lidija Zdravković (2001). Finite Element Analysis in Geotechnical Engineering: Volume two – Application, 1st Ed., Thomas Telford Publishing.
[12] Janda, T., Cunha, R. P., Kuklík, P., and Anjos, G. M. (2009). Three dimensional finite element analysis and back-analysis of cfa standard pile groups and piled rafts founded on tropical soil. Soils and Rocks, 32(1), 3-18.
[13] Gasparre, A. (2005). “Advanced laboratory characterisation of London clay.” Ph.D. thesis, Imperial College, London.
[14] Lua YJ, Sues RH. Probabilistic finite-element analysis of airfield pavements. Transp Res Rec 1996;1540: 29–38.
[15] El-Kadi, A. I. and Williams, S. A. (2000), Generating Two-Dimensional Fields of Autocorrelated, Normally Distributed Parameters by the Matrix Decomposition Technique. Ground Water, 38: 530–532.
[16] Caro S, Masad E, Sánchez-Silva M, Little D. Stochastic micromechanical model of the deterioration of asphalt mixtures subject to moisture diffusion processes. Int J Numer Anal Methods Geomech 2011;35: 1079–97.
[17] Castillo Daniel, Silvia Caro, Probabilistic modeling of air void variability of asphalt mixtures in flexible pavements, Construction and Building Materials, Volume 61, 30 June 2014, Pages 138-146.
[18] Cai Jing-Sen, E-Chuan Yan, Tian-Chyi Jim Yeh, Yuan-Yuan Zha, Yue Liang, Shao-Yang Huang, Wen-Ke Wang, Jet-Chau Wen (2017). Effect of spatial variability of shear strength on reliability of infinite slopes using analytical approach, Computers and Geotechnics, Volume 81, Pages 77-86.
[19] Griffiths, D. V., Fenton, G. A., and Tveten, D. E. (2005). “Probabilistic earth pressure analysis by the random finite element method.” Proc., 11th Int. Conf. on Computer Methods and Advances in Geomechanics (IACMAG 05), Vol. 4, G. Barla and M. Barla, eds., Pátron Editore, Bologna, 235–249.
[20] Papaioannou, I., and Straub, D. (2012). “Reliability updating in geotechnical engineering including spatial variability of soil.” Comput. Geotech., 42, 44–51.
[21] Huang, J., Griffiths, D. and Fenton, G. (2010). Probabilistic analysis of coupled soil consolidation. Journal of Geotechnical and Geoenvironmental Engineering 136 (3), 417-430.
[22] Ching, J., Chen, J., Yeh, J., and Phoon, K. (2012). "Updating Uncertainties in Friction Angles of Clean Sands." J. Geotech. Geoenviron. Eng., 10.1061/(ASCE)GT.1943-5606.0000573, 217-229.
[23] Lambe TW, Whitman RV (1979). Soil Mechanics, SI Version. John Wiley & Sons, New York.
[24] Zevgolis, I. and Bourdeau, P. (2010). Probabilistic analysis of retaining walls. Computers and Geotechnics 37, 359-373.
[25] Prada, L.F., Ramos, A., Solaque, D. y Caicedo, B. (2011). Confiabilidad aplicada al diseño geotécnico de un mutro de contención. Obrasy Proyectos 9, 49-58.
[26] Velloso D. A. and Lopes F. (2010). Fundações profundas, Vol. 2. Brasil: Oficina de textos, 1 ed.
[27] Mendoza, C. C. (2013). “Experimental and numerical behaviour of deep fundations made up by anker alluvial type piles founded in a porous soil of federal district.” Ph.D. thesis, Univ. of Brasilia, Brasilia, DF, Brazil.
[28] Sowers, G., and Sowers, G. (1970). Introductory soil mechanics and foundations, 3rd Ed., Macmillan, New York.
[29] Asociación Colombiana de Ingeniería Sísmica-AIS (2010) Reglamento Colombiano de Construcción Sismo Resistente, NSR-10. Comité AIS-100.
Document information
Published on 03/01/18
Accepted on 06/06/17
Submitted on 20/12/16
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.8.003
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?