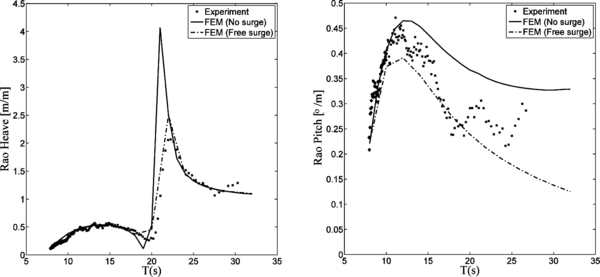Revision as of 20:19, 11 May 2017 (view source) Julio (talk | contribs) ← Older edit		Revision as of 20:33, 11 May 2017 (view source) Julio (talk | contribs) Newer edit →
Line 1,144:		Line 1,144:
	|  style="border: 1pt solid black;text-align: center;"|0.05		|  style="border: 1pt solid black;text-align: center;"|0.05
	|}		|}
		+
	<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">		<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
−	[[Image:draft_García-Espinosa_946341310-image152.png|270px]] </div>	+	[[Image:Draft_García-Espinosa_946341310_1645_mesh.png|600px]] </div>
	<div id="_Ref329162537" class="center" style="width: auto; margin-left: auto; margin-right: auto;">		<div id="_Ref329162537" class="center" style="width: auto; margin-left: auto; margin-right: auto;">
	<span style="text-align: center; font-size: 75%;">'''Figure 10: '''Multi-body simulation. (a), case 1 mesh; (v) case 2 mesh; (c) case 3 mesh.</span></div>		<span style="text-align: center; font-size: 75%;">'''Figure 10: '''Multi-body simulation. (a), case 1 mesh; (v) case 2 mesh; (c) case 3 mesh.</span></div>
		+
	<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">		<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
Line 1,156:		Line 1,158:
	<div id="_Ref330459397" class="center" style="width: auto; margin-left: auto; margin-right: auto;">		<div id="_Ref330459397" class="center" style="width: auto; margin-left: auto; margin-right: auto;">
	<span style="text-align: center; font-size: 75%;">'''Figure 11: '''Multi-body simulation: Free surface elevation at time=49.8 seconds.</span></div>		<span style="text-align: center; font-size: 75%;">'''Figure 11: '''Multi-body simulation: Free surface elevation at time=49.8 seconds.</span></div>
		+
	<div id="_Ref330459481" class="center" style="width: auto; margin-left: auto; margin-right: auto;">		<div id="_Ref330459481" class="center" style="width: auto; margin-left: auto; margin-right: auto;">

---

Revision as of 20:33, 11 May 2017

Abstract

Being capable of predicting seakeeping capabilities in the time domain is of great interest for the marine and offshore industry. However, most computer programs used in the industry work in the frequency domain, with the subsequent limitation in the accuracy of their model predictions. The main objective of this work is the development of a time domain solver based on the finite element method capable of solving multi-body seakeeping problems on unstructured meshes. In order to achieve such an objective, several techniques are combined: the use of an efficient algorithm for the free surface boundary conditions, the use of deflated conjugate gradients, and the use of a graphic processing unit for speeding up the linear solver. The results obtained results by the developed model showed good agreement with analytical solutions, experimental data for an actual offshore structure model, as well as numerical solutions obtained by other numerical method. Also, a simulation with sixteen floating bodies was carried out in a affordable CPU time, showing the potential of this approach for multi-body simulation.

1. Introduction

Seakeeping is a topic of great interest in naval and offshore engineering. This interest is growing in the last years due to the boost given by the development of marine renewable energies. In this context, the development of time-domain seakeeping programs is a main request from the industry. Moreover, the simulation of multi-body systems is a key point in the development of more efficient marine renewable technologies such as wave energy converters, floating wind turbines, etc.

Up to date the numerical simulation of seakeeping has been mostly carried out using the frequency domain solvers. The reason might be that the computational cost of time domain simulations were too high and computational time was too long. Moreover, assumptions like linear waves and the harmonic nature of water waves made the frequency domain to be the right choice. However, nowadays computing capabilities make possible to carry out numerical simulations in the time domain in a reasonable time, with the advantage of making easier bringing into the algorithm non-linearities when coupling with other phenomena. Furthermore, in the frequency domain, the simulation of multi-body systems requires calculating the interaction among the bodies, which increases quickly the computational effort as the number of bodies increase. On the other hand, if simulating in the time, domain, the interaction among bodies is solved in a natural way without leading to a big increase of computational effort.

Regarding the numerical method usually adopted, the boundary element method (BEM) has dominated over others like finite element method (FEM). The main advantage of BEM over FEM resides in the fact that only boundary meshes are required, while FEM demands meshing the whole three dimensional volume, with the corresponding increase in the number of variables of the discrete problem. However, despite of the higher number of variables required by FEM, it is not clear that BEM has to be more efficient. Mostly due to the sparse pattern in FEM and the large availability of iterative solvers as well as preconditioner that can improve the resolution of the corresponding linear system of equations. In [1] Cai et al. a heuristic comparison between both methods is given and demonstrate that a solution to the boundary value problem can be obtained more efficiently by the FEM for large problems.

In the last decade, there have been extensive applications of the finite element method (FEM) to free surface problems. For example, Oñate and García [2] presented a stabilized FEM for fluid structure interaction in the presence of free surface where the latter was modelled by solving a fictitious elastic problem on the moving mesh. In [3,4] Löhner et al. developed a FEM capable of tracking violent free surface flows interacting with objects. Also García et al. [5] developed a new technique to track complex free surface shapes. However, many works like the previous ones are based on solving the Navier-Stokes equations, too expensive computationally speaking when it comes to simulating real problems regarding ocean waves interacting with floating structures. These sorts of problems can be more cheaply simulated using potential flow theory along with Stokes perturbation approximation

With regards to wave–body interaction problems, there has been extensive work as well in the last decade. In [6], Wu et al. used both the FEM and the mixed FEM to analyze the two-dimensional (2-D) nonlinear transient water wave problems. Later Wu and Taylor [7] made a detailed comparison between FEM and the boundary element method (BEM) for the nonlinear free surface flow problem and found that the former was more efficient in terms of both CPU and memory requirement. Greaves et al. [8] employed quad-tree-based unstructured meshes to model fully nonlinear waves in 2D, using an ALE formulation in structured meshes. In [9] an hp-element technique was adopted to simulate the 2-D free surface flow problem. Application of FEM schemes to simulated interactions between waves and 3-D fixed structures in numerical tanks used moving meshes along with an explicit time marching scheme for the free surface boundary condition were presented in [10] and [11]. However, in those cases, remeshing and interpolation were needed, which leads to a high CPU cost. Westhuis [12] in his PhD dissertation developed a FEM code for nonlinear waves and focussed in the development of groups of waves. The code relied in some specific structured mesh configurations and no body interaction was studied. Hu et al. [13] applied FEM to study the case of a vertical under forced motions based on the works [5] and [6]. Turnbull et al. [14] coupled structured and unstructured meshes to simulate 2-D wave–body interactions. The vertical velocity at nodes belonging to the free surface required a prescribed number of nodes to be aligned vertically. Wu et al. [15] solved a 3D problem using a semistructured mesh in the vertical direction. This way the nodes will be aligned vertically and the vertical derivative at the free surface can be easily estimated by finite difference. Wang et al. [16] used FEM to study the effect of second order wave sloshing within a tank in 2D. The 4^th order Runge Kutta method was used as a time marching scheme for the free surface boundary condition. A FEM solver for a second order wave diffraction by an array of vertical cylinder using semistructured mesh has been presented in [17]. Again, in order to estimates vertical velocity at the free surface nodes it is required a prescribed number of nodes to be aligned vertically. An explicit fourth-order Adams–Bashforth scheme was used for the free surface boundary condition to march in time. Later on the same authors in [18] used a structured mesh based on rectangular elements to study second-order resonance effects. Yan et al. [19] applied the fully non-linear potential for modelling overturning waves. To achieve that, a moving mesh technique was adopted to track down the free surface. Consequently, computational times are large. Recently, Song et al. developed a new scaled boundary finite element method (SBFEM) for linear waves and structure interaction [20]. The SBFEM works in the frequency domain, and base functions for boundary elements based on Hankel functions were used for unbounded sub-domains were waves are to disappear, decreasing the number of elements needed for the simulation which improves the numerical efficiency of the method.

Despite of the great effort invested in the last years to the development of FEM algorithms, to the authors’ knowledge, yet there has not been developed a fast FEM (by fast we mean in the order of minutes for practical problems) for solving first order wave structure interaction in the time domain using unstructured meshes. The use of structure or semi-structures meshes is a big limitation since it limits the complexity of the geometry to be used. In this study we present a FEM for wave-structure interaction that can be used with unstructured meshes. Besides, since it is based on Stokes wave theory, no re-meshing or moving mesh technique are needed, which keeps computational costs and computational times low. The algorithm has been adapted to include non-linear external forces, like those used to define mooring systems.

The outline of this paper is as follows. In section two, the statement of the governing equations of the first order diffraction-radiation problem of a set of floating bodies is presented. In section three the FEM formulation is presented, the free surface and radiation boundary condition are applied to the problem, and the boundary condition on the bodies and the body dynamics solution are explained in detailed. The accuracy of the new formulation for analysis of waves and floating structures interaction is verified in different validation cases in section four, comparing against analytical, experimental and BEM solutions. Finally, section 5 contains the conclusions of this work.

2. Problem statement

2.1 Governing equations

We consider the first order diffraction-radiation problem of a set of floating bodies.

${\displaystyle {\nabla }^{2}\varphi =0}$ in ${\displaystyle \Omega }$

(1)

${\displaystyle {\partial }_{t}\varphi +g\eta =-P_{a}/\rho +C}$ on ${\displaystyle z=0}$ (dynamic free surface boundary condition)

(2)

${\displaystyle {\partial }_{t}\eta -{\partial }_{z}\varphi =0}$ on ${\displaystyle z=0}$ (kinematic free surface boundary condition)

(3)

${\displaystyle {\partial }_{z}\varphi =0}$ on ${\displaystyle z=-H}$

(4)

${\displaystyle \nabla \varphi \cdot {\boldsymbol {n}}_{B}={\boldsymbol {v}}_{B}\cdot {\boldsymbol {n}}_{B}}$ on ${\displaystyle {\Gamma }_{B}}$

(5)

where ${\displaystyle \varphi }$ and ${\displaystyle \eta }$ are the first order potential and free surface elevation respectively; ${\displaystyle \Omega }$ is the fluid domain bounded by ${\displaystyle z=0}$ ; ${\displaystyle P_{a}}$ is the atmospheric pressure; ${\displaystyle \rho }$ is the water density; C is a constant value; ${\displaystyle {\Gamma }_{B}}$ represents the wetted surface of the present bodies; ${\displaystyle {\boldsymbol {v}}_{B}}$ represent the local body velocity on the body surface; and ${\displaystyle H}$ is the water depth. The domain is assumed to be infinite in the horizontal directions.

2.2 Velocity potential decomposition

The aim of this work is to simulate the dynamics of a set of floating bodies subjected to the action of waves. To do so, we will first model the environment as the sum of a number of airy waves. This can be expressed in terms of a velocity potential given by:

${\displaystyle \psi =\sum _{m}{\frac {A_{m}g}{{\omega }_{m}}}{\frac {cosh\left(\vert {\boldsymbol {k}}_{m}\vert (H+z)\right)}{cosh\left(\vert {\boldsymbol {k}}_{m}\vert H\right)}}cos\left(\vert {\boldsymbol {k}}_{m}\vert (xcos{\alpha }_{m}+\right.}$${\displaystyle \left.ysin{\alpha }_{m}-{\omega }_{m}t+{\delta }_{m}\right)}$

(6)

where ${\displaystyle A_{m}}$ are the wave amplitudes; ${\displaystyle {\omega }_{m}}$ are the wave frequencies; ${\displaystyle {\boldsymbol {k}}_{m}}$ are the wave numbers; ${\displaystyle {\alpha }_{m}}$ are the wave directions; and ${\displaystyle {\delta }_{m}}$ are wave phases. From this point on, we will refer to ${\displaystyle \psi }$ as the incident potential. This potential, along with the dispersion relation ${\displaystyle {\omega }_{m}^{2}=g\vert {\boldsymbol {k}}_{m}\vert tanh\left(\vert {\boldsymbol {k}}_{m}\vert H\right)}$ , fulfils Eqs. (1)-(4), and therefore is solution of the mathematical model in the absence of bodies.

In order to obtain the solution to the governing equations, we will use a velocity potential decomposition. Let ${\displaystyle \varphi }$ be the solution to the governing equations. Then ${\displaystyle \varphi }$ can be decomposed as ${\displaystyle \varphi =\psi +\phi }$ , where ${\displaystyle \phi }$ represents the velocity potential of waves diffracted and radiated by the bodies.

Introducing the velocity potential decomposition into the governing equations we obtained the equation to be fulfilled by ${\displaystyle \phi }$ :

${\displaystyle {\nabla }^{2}\phi =0}$ in ${\displaystyle \Omega }$

(7)

${\displaystyle {\partial }_{t}\phi +g\eta =-P_{a}/\rho +C{}'}$ on ${\displaystyle z=0}$ (dynamic free surface boundary condition)

(8)

${\displaystyle {\partial }_{t}\eta -{\partial }_{z}\phi =0}$ on ${\displaystyle z=0}$ (kinematic free surface boundary condition)

(9)

${\displaystyle {\partial }_{z}\phi =0}$ on ${\displaystyle z=-H}$

(10)

${\displaystyle \nabla \phi \cdot {\boldsymbol {n}}_{B}=\left({\boldsymbol {v}}_{B}-\right.}$${\displaystyle \left.\nabla \psi \right)\cdot {\boldsymbol {n}}_{B}}$ on ${\displaystyle {\Gamma }_{B}}$

(11)

Our purpose is to find ${\displaystyle \phi }$ for a given incident potential and given ${\displaystyle {\boldsymbol {v}}_{B}}$ . To do so, we will solve Eqs. (7)-(11) in a finite domain by means of the finite element method.

2.3 Radiation condition and wave dissipation

Waves represented by ${\displaystyle \phi }$ are born at the bodies and propagate in all directions away from the bodies. These waves have to either be dissipated or to be let go out the domain so they will not come back and interact with the bodies. Then, we will make use of a Sommerfeld radiation condition at the edge of the computational domain:

${\displaystyle {\partial }_{t}\phi +c\nabla \phi \cdot {\boldsymbol {n}}_{R}=}$${\displaystyle 0}$ on ${\displaystyle {\Gamma }_{R}}$

(12)

where ${\displaystyle {\Gamma }_{R}}$ is the surface limiting of the domain in the horizontal directions, and ${\displaystyle c}$ is a prescribed wave velocity. Eq. (12) will let waves moving at velocity ${\displaystyle c}$ to escape out the domain. However, waves with very different velocities will not be leaving the domain. Then, wave dissipation is inserted into the dynamic free surface boundary condition by varying the pressure such that:

${\displaystyle P_{a}/\rho =\kappa ({\boldsymbol {x)}}{\partial }_{z}\phi }$

(13)

where ${\displaystyle \kappa ({\boldsymbol {x)}}}$ is a damping coefficient. Eq. (13) increases pressure when the free surface is moving upwards, while decreases the pressure when the free surface is moving downwards. By doing this, energy is transfer from the waves to the atmosphere and waves are damped. However, the coefficient ${\displaystyle \kappa ({\boldsymbol {x)}}}$ will be set to zero in the area nearby the bodies so damping will no affect to the wave structure interaction.

Combining the dynamic and kinematic boundary condition, introducing Eq.(13), and adding Eq.(12), and choosing ${\displaystyle C{}'=0}$ , the governing equations for ${\displaystyle \phi }$ becomes:

${\displaystyle {\nabla }^{2}\phi =0}$ in ${\displaystyle \Omega }$

(14)

${\displaystyle {\partial }_{tt}\phi =-g{\partial }_{z}\phi -\kappa ({\boldsymbol {x)}}{\partial }_{t}{\partial }_{z}\phi }$ on ${\displaystyle z=0}$

(15)

${\displaystyle {\partial }_{z}\phi =0}$ on ${\displaystyle z=-H}$

(16)

${\displaystyle \nabla \phi \cdot {\boldsymbol {n}}_{B}=\left({\boldsymbol {v}}_{B}-\right.}$${\displaystyle \left.\nabla \psi \right)\cdot {\boldsymbol {n}}_{B}}$ on ${\displaystyle {\Gamma }_{B}}$

(17)

${\displaystyle {\partial }_{t}\phi +c\nabla \phi \cdot {\boldsymbol {n}}_{R}=}$${\displaystyle 0}$ on ${\displaystyle {\Gamma }_{R}}$

(18)

${\displaystyle \eta =-{\frac {1}{g}}{\partial }_{t}\phi -{\frac {P_{a}}{\rho g}}}$ on ${\displaystyle z=0}$ (kinematic free surface boundary condition)

(19)

where the free surface elevation has been decoupled from the problem of obtaining the velocity potential.

3. Finite element formulation

This section presents the FEM formulation to solve the above equations. This formulation has been developed to be used in conjunction with unstructured meshes. The use of unstructured meshes enhances geometry flexibility and speed ups the initial modelling time. An automatic unstructured grid generator based on the advancing front method is used to generate triangular surface grids and tetrahedral volume meshes.

Let ${\displaystyle Q_{h}^{\ast }}$ be the finite element space to interpolate functions, constructed in the usual manner. From this space, we can construct the subspace ${\displaystyle Q_{h,\phi }}$ , that incorporates the Dirichlet conditions for the potential ${\textstyle \phi }$ . The space of test functions, denoted by ${\displaystyle Q_{h}}$ , is constructed as ${\displaystyle Q_{h,\phi }}$ , but with functions vanishing on the Dirichlet boundary. The weak form of the problem can be written as follows:

Find ${\displaystyle \left[{\phi }_{h}\right]\in Q_{h,\phi }}$ , by solving the discrete variational problem:

${\displaystyle \int _{\Omega }\nabla v_{h}\cdot \nabla {\phi }_{h}d\Omega =}$${\displaystyle \int _{{\Gamma }^{B}}v_{h}\cdot {\overset {\frown }{\phi }}_{n}^{B}d\Gamma +}$${\displaystyle \int _{{\Gamma }^{R}}v_{h}\cdot {\overset {\frown }{\phi }}_{n}^{R}d\Gamma +}$${\displaystyle \int _{{\Gamma }^{Z_{0}}}v_{h}\cdot {\overset {\frown }{\phi }}_{n}^{Z_{0}}d\Gamma +}$${\displaystyle \int _{{\Gamma }^{Z_{-H}}}v_{h}\cdot {\overset {\frown }{\phi }}_{n}^{Z_{-H}}d\Gamma {\mbox{ }}\forall v_{h}\in Q_{h}}$

(20)

where ${\displaystyle {\overset {\frown }{\phi }}_{n}^{B}}$ , ${\displaystyle {\overset {\frown }{\phi }}_{n}^{R}}$ , ${\displaystyle {\overset {\frown }{\phi }}_{n}^{Z_{0}}}$ and ${\displaystyle {\overset {\frown }{\phi }}_{n}^{Z_{-H}}}$ are the potential normal gradients corresponding to the Neumann boundary conditions on bodies, radiation boundary, free surface and bottom, respectively.

At this point, it is useful to introduce the associated matrix form

${\displaystyle {\overline {\overline {\boldsymbol {L}}}}\phi ={\boldsymbol {b}}^{B}+}$${\displaystyle {\boldsymbol {b}}^{R}+{\boldsymbol {b}}^{Z_{0}}+{\boldsymbol {b}}^{Z_{-H}}}$

(21)

where ${\displaystyle {\overline {\overline {\boldsymbol {L}}}}}$ is the standard laplacian matrix, and ${\displaystyle {\boldsymbol {b}}^{B}}$ , ${\displaystyle {\boldsymbol {b}}^{R}}$ , ${\displaystyle {\boldsymbol {b}}^{Z_{0}}}$ and ${\displaystyle {\boldsymbol {b}}^{Z_{-H}}}$ are the vector resulting of integrating the corresponding boundary condition term. Regarding the bottom boundary for the refracted and radiated potential, it is imposed naturally in FEM by ${\displaystyle {\boldsymbol {b}}^{Z_{-H}}=0}$ .

3.1 Free surface boundary condition

Solving the velocity potential free surface boundary condition efficiently is the most important point of the problem stated since this is the where a difference is made when solving the mathematical model in Eqs. (14)-(19) using FEM.

The free surface boundary condition represents the temporal evolution of the velocity potential. Therefore, it is commonly used time marching schemes such as the fourth order Runge-Kutta (RK4) and fourth order Adams-Bashforth (AB4). The RK4 is a explicit four steps methods that required estimation of intermediate point to advance from time ${\textstyle t}$ to time ${\textstyle t+\Delta t}$ . Then, the Laplace equation has to be solved four times and ${\displaystyle {\partial }_{z}\phi }$ has to be estimated each time. On the other hand, the AB4 is an explicit scheme that only requires solving the Laplace equation and estimate ${\displaystyle {\partial }_{z}\phi }$ once per time step. However the AB4 requires storing information at the free surface of the previous 4 time steps. For both algorithms, RK4 and AB4, the values of ${\displaystyle {\partial }_{z}\phi }$ at the free surface are to be estimated so that the scheme can keep marching in time. Following this reasoning, an implicit scheme looks like an expensive option since convergence of the Laplace solution and the free surface numerical scheme would need to be achieved through an iterating procedure. Moreover, based on a literature review, the estimation of ${\displaystyle {\partial }_{z}\phi }$ is usually carried out by finite difference schemes requiring the first layer of nodes to be vertically aligned. From our point of view this is a big restriction since not completely unstructured meshes can be used near the free surface. In order to overcome the above mentioned limitations, we use a forth order compact Padé scheme [21]. This scheme is implicit with symmetric stencils, which provides good stability properties and requires solving the linear system in Eq. (21) once per time step.

Although the free surface boundary condition is usually implemented as a Dirichlet boundary condition [12,17,18] by imposing the value of the velocity potential at the time step to be calculated, in this work is implemented as a Neumann boundary condition that fulfils the flux boundary integral:

${\displaystyle {\boldsymbol {b}}^{Z_{0}}={\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}{\phi }_{z}^{Z_{0}}}$

(22)

Where ${\displaystyle {\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}}$ is the corresponding boundary mass matrix. Rather than obtaining the vector ${\displaystyle {\phi }_{z}^{Z_{0}}}$ and calculating the values of ${\displaystyle {\boldsymbol {b}}^{Z_{0}}}$ , we will proceed in a different manner. Let’s consider the free surface boundary condition outside the absorbing zone (where the absorbing factor equals zero, which is inside the analysis area). The forth order compact Padé scheme reads, for Eq.(15), as:

${\displaystyle {\frac {{\phi }^{n+1}-2{\phi }^{n}+{\phi }^{n-1}}{\Delta t^{2}}}=}$${\displaystyle -g{\partial }_{z}{\phi }^{n}-{\frac {1}{12}}g\left({\partial }_{z}{\phi }^{n+1}-\right.}$${\displaystyle \left.2{\partial }_{z}{\phi }^{n}+{\partial }_{z}{\phi }^{n-1}\right)}$

(23)

Introducing Taylor series expansion around time t in Eq. (23), and using Eq. (15) , we recover the free surface boundary condition with ${\textstyle O(\Delta t^{4})}$ . Eq. (23) is an implicit scheme which has to be solved along with the linear system given in Eq (21). At first sight seems like an iterating procedure should be used requiring solving the linear system several times per time steps. However, this can be avoided by decoupling ${\displaystyle {\phi }^{n+1}}$ and. ${\displaystyle {\partial }_{z}{\phi }^{n+1}}$ .The decoupling is carried out as follows: from Eq. (23) we can write ${\displaystyle {\phi }_{z}^{n+1}}$ as a function of ${\displaystyle {\phi }^{n+1}}$ :

${\displaystyle {\partial }_{z}{\phi }^{n+1}=-10{\partial }_{z}{\phi }^{n}-}$${\displaystyle {\partial }_{z}{\phi }^{n-1}-{\frac {12}{g\Delta t^{2}}}\left({\phi }^{n+1}-\right.}$${\displaystyle \left.2{\phi }^{n}+{\phi }^{n-1}\right)}$

(24)

This approximation is used to evaluate ${\displaystyle {\overset {\frown }{\phi }}_{z}^{Z_{0}}}$ in ${\displaystyle t^{n+1}}$ , and therefore, the integral of ${\displaystyle {\boldsymbol {b}}^{Z_{0}}}$ in ${\displaystyle t^{n+1}}$ can be calculated as follows:

${\displaystyle {\left({\boldsymbol {b}}^{Z_{0}}\right)}^{n+1}={\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}{\left({\phi }_{z}^{Z_{0}}\right)}^{n+1}=}$${\displaystyle {\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}\left[-\right.}$${\displaystyle \left.10{\left({\phi }_{z}^{Z_{0}}\right)}^{n}-{\left({\phi }_{z}^{Z_{0}}\right)}^{n-1}-\right.}$${\displaystyle \left.{\frac {12}{g\Delta t^{2}}}\left({\phi }^{n+1}-2{\phi }^{n}+\right.\right.}$${\displaystyle \left.\left.{\phi }^{n-1}\right)\right]}$

(25)

Introducing Eq. (25) into Eq. (21) we obtain:

${\displaystyle \left({\overline {\overline {\boldsymbol {L}}}}+{\frac {12}{g\Delta t^{2}}}{\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}\right){\phi }^{n+1}=}$${\displaystyle {\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}\left({\frac {12}{g\Delta t^{2}}}\left(2{\phi }^{n}-\right.\right.}$${\displaystyle \left.\left.{\phi }^{n-1}\right)-10{\left({\phi }_{z}^{Z_{0}}\right)}^{n}-\right.}$${\displaystyle \left.{\left({\phi }_{z}^{Z_{0}}\right)}^{n-1}\right)+}$${\displaystyle {\left({\boldsymbol {b}}^{B}\right)}^{n+1}+{\left({\boldsymbol {b}}^{R}\right)}^{n+1}}$

(26)

Eq. (26) imposes a strong coupling between the free surface boundary condition and the Laplace equation. This is carried out by modifying the system matrix ${\displaystyle {\overline {\overline {\boldsymbol {L}}}}}$ . Once the system is solved, ${\displaystyle {\partial }_{z}{\phi }^{n+1}}$ at the free surface is obtained using Eq. (24).

Then, whenever the velocity potential is solved at the present time step, the free surface elevation is computed by means of ${\displaystyle \eta =-(1/g){\partial }_{t}\varphi }$ using the following fourth order finite difference scheme:

${\displaystyle {\eta }^{n+1}=-{\frac {1}{g\Delta t}}\left({\frac {25}{12}}{\varphi }^{n+1}-\right.}$${\displaystyle \left.4{\varphi }^{n}+3{\varphi }^{n-1}-{\frac {4}{3}}{\varphi }^{n-2}+\right.}$${\displaystyle \left.{\frac {1}{4}}{\varphi }^{n-3}\right)}$

(27)

3.2 Implementing the free surface boundary condition with absorption

In order to include the wave damping effect, we discretize Eq. (15) as follows:

${\displaystyle {\frac {{\phi }^{n+1}-2{\phi }^{n}+{\phi }^{n-1}}{\Delta t^{2}}}=}$${\displaystyle -g{\partial }_{z}{\phi }^{n}-{\frac {1}{12}}g\left({\partial }_{z}{\phi }^{n+1}-\right.}$${\displaystyle \left.2{\partial }_{z}{\phi }^{n}+{\partial }_{z}{\phi }^{n-1}\right)-}$${\displaystyle \kappa ({\boldsymbol {x)}}{\frac {{\partial }_{z}{\phi }^{n+1}-{\partial }_{z}{\phi }^{n-1}}{2\Delta t}}}$

(28)

Eq. (28) is simply Eq. (24) plus a second order finite difference in time for the absorbing term. Then ${\displaystyle {\partial }_{z}{\phi }^{n+1}}$ can be obtained as:

${\displaystyle {\partial }_{z}{\phi }^{n+1}=-{\frac {10g\Delta t}{g\Delta t+6\kappa ({\boldsymbol {x)}}}}{\partial }_{z}{\phi }^{n}-}$${\displaystyle \left({\frac {g\Delta t-6\kappa ({\boldsymbol {x)}}}{g\Delta t+6\kappa ({\boldsymbol {x)}}}}\right){\partial }_{z}{\phi }^{n-1}-}$${\displaystyle {\frac {12}{g\Delta t^{2}+6\kappa ({\boldsymbol {x)}}\Delta t}}\left({\phi }^{n+1}-\right.}$${\displaystyle \left.2{\phi }^{n}+{\phi }^{n-1}\right)}$

(29)

Proceeding like in the previous section, we obtain:

${\displaystyle \left({\overline {\overline {\boldsymbol {L}}}}+{\frac {12}{g\Delta t^{2}+6\kappa ({\boldsymbol {x)}}\Delta t}}{\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}\right){\phi }^{n+1}=}$${\displaystyle {\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}\left({\frac {12}{g\Delta t^{2}+6\kappa ({\boldsymbol {x)}}\Delta t}}\left(2{\phi }^{n}-\right.\right.}$${\displaystyle \left.\left.{\phi }^{n-1}\right)\right)-{\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}\left({\frac {10g\Delta t}{g\Delta t+6\kappa ({\boldsymbol {x)}}}}{\left({\phi }_{z}^{Z_{0}}\right)}^{n}+\right.}$${\displaystyle \left.\left({\frac {g\Delta t-6\kappa ({\boldsymbol {x)}}}{g\Delta t+6\kappa ({\boldsymbol {x)}}}}\right){\left({\phi }_{z}^{Z_{0}}\right)}^{n-1}\right)+}$${\displaystyle {\left({\boldsymbol {b}}^{B}\right)}^{n+1}+{\left({\boldsymbol {b}}^{R}\right)}^{n+1}}$

(30)

his implementation has several advantages over traditional implementations such as RK4 and AB4. The linear system has to be solved only once per time step (RK4 requires four times); the free surface numerical scheme is implicit (AB4 and RK4 are explicit); only information from two previous times at the free surface is required (AB4 requires information from four previous times); there is no restriction about the grid structure, hence unstructured meshes can be used with no restriction; and the vertical fluid velocity at the free surface is easily computed using Eq.(29).

Regarding the wave absorption algorithm used in this work, we recognize that more sophisticated absorption mechanism can be found in the literature. However, despite of its simplicity, our experience tell us that the performance of this mechanism is good enough for the purpose of this work. The increase of the number of elements needed for absorbing the waves is not that big compared with the number of elements required for the analysis area, where no wave absorption exists. The element size is usually much smaller in the analysis area, and increases gradually in the absorption area as it gets farther form the analysis area where smaller waves have been already absorbed.

3.3 Radiation boundary condition

When the fluid domain is unbounded, an implementation of a radiation boundary condition is recommended to avoid artificial wave reflexions at the edges of the computational domain, where waves are supposed to go through without reflection. We make use of the Sommerfeld radiation condition given in Eq. (12). We assume that the waves scattered by the bodies hit the outlet boundary in perpendicular. Then we approximate the radiation condition by:

${\displaystyle {\left({\overset {\frown }{\phi }}_{n}^{R}\right)}^{n+1}=}$${\displaystyle -{\frac {{\phi }^{n+1}-{\phi }^{n}}{c\Delta t}}}$

(31)

Then the term ${\displaystyle {\boldsymbol {b}}_{{}^{}}^{R}}$ can be calculated through:

${\displaystyle {\left({\boldsymbol {b}}^{R}\right)}^{n+1}={\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{R}}{\left({\phi }_{n}^{R}\right)}^{n+1}=}$${\displaystyle {\frac {1}{\Delta t}}{\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{R}}\left({\phi }^{n}-\right.}$${\displaystyle \left.{\phi }^{n-1}\right)}$

(32)

and ${\displaystyle {\Gamma }^{R}}$ represent the outlet Boundary condition and has been assume to be vertical. Introducing Eq. (32) into Eq. (30) we get:

${\displaystyle \left({\overline {\overline {\boldsymbol {L}}}}+{\frac {12}{g\Delta t^{2}+6\kappa ({\boldsymbol {x)}}\Delta t}}{\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}+\right.}$${\displaystyle \left.{\frac {c}{\Delta t}}{\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{R}}\right){\phi }^{n+1}=}$${\displaystyle {\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}\left({\frac {12}{g\Delta t^{2}+6\kappa ({\boldsymbol {x)}}\Delta t}}\left(2{\phi }^{n}-\right.\right.}$${\displaystyle \left.\left.{\phi }^{n-1}\right)\right)-{\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{Z_{0}}}\left({\frac {10g\Delta t}{g\Delta t+6\kappa ({\boldsymbol {x)}}}}{\left({\phi }_{z}^{Z_{0}}\right)}^{n}+\right.}$${\displaystyle \left.\left({\frac {g\Delta t-6\kappa ({\boldsymbol {x)}}}{g\Delta t+6\kappa ({\boldsymbol {x)}}}}\right){\left({\phi }_{z}^{Z_{0}}\right)}^{n-1}\right)+}$${\displaystyle {\frac {c}{\Delta t}}{\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{R}}{\phi }^{n}+}$${\displaystyle {\left({\boldsymbol {b}}^{B}\right)}^{n+1}}$

(33)

A strong coupling between the Sommerfeld radiation condition and the Laplace equation has been defined, as we did with the free surface in the previously. Then the boundary condition is integrated within the system matrix, avoiding iterating among the equations.

Despite of the simplicity of the radiation condition used, we found that its performance of good enough for the purpose of this work, and there is no need of using more sophisticated radiation conditions.

3.4 Body boundary condition

The boundary condition to be imposed over the surface of the bodies is given by Eq. (11). The movements of the bodies are assumed to be small enough so the computational domain can remind steady, as well as the normals to be bodies’ surface. Then the term ${\displaystyle {\boldsymbol {b}}_{}^{B}}$ will be calculated by:

${\displaystyle {\left({\boldsymbol {b}}^{B}\right)}^{n+1}={\overline {\overline {\boldsymbol {M}}}}_{{\Gamma }^{B}}{\left({\phi }_{n}^{B}\right)}^{n+1}}$

(34)

3.5 Multi-body dynamics

Once the velocity potential has been obtained, the pressure at any point can be calculated from:

${\displaystyle P=-\rho gz-\rho {\partial }_{t}\varphi }$

(35)

Eq. (35) requires estimating the value of ${\displaystyle {\partial }_{t}\varphi }$ . The same fourth order finite difference scheme that has been used for the free surface elevation is used here:

${\displaystyle P^{n+1}=-\rho gz-{\frac {\rho }{\Delta t}}\left({\frac {25}{12}}{\varphi }^{n+1}-\right.}$${\displaystyle \left.4{\varphi }^{n}+3{\varphi }^{n-1}-{\frac {4}{3}}{\varphi }^{n-2}+\right.}$${\displaystyle \left.{\frac {1}{4}}{\varphi }^{n-3}\right)}$

(36)

Integrating the pressure over the bodies’ surface, the resulting forces and moments are obtained. On the other hand, the bodies dynamics is given by the equation of motion:

${\displaystyle {\overline {\overline {M}}}{\boldsymbol {X}}_{tt}+{\overline {\overline {K}}}{\boldsymbol {X}}=}$${\displaystyle {\boldsymbol {F}}}$

(37)

where ${\displaystyle {\overline {\overline {M}}}}$ is the mass matrix of te multi-body system; ${\displaystyle {\overline {\overline {K}}}}$ is the hydrostatic restoring coefficient matrix of the multi-body system; ${\displaystyle {\boldsymbol {F}}}$ is the hydrodynamic forces induced over the bodies plus any other external forces; and ${\displaystyle {\boldsymbol {X}}}$ represent the movements of the six degrees of freedom of each body.

In the specific case where the bodies are fixed, only refracted waves are calculated and the linear system given in Eq. (33) is to be solved just once per time step. However, when solving the body dynamics along with the wave problem requires an iterative procedure since interaction between the waves and the movements of the structure exist, giving birth to waves radiated by the bodies.

In order to solve Eq.(37), we use a implicit Newmark´s average acceleration method:

${\displaystyle {\boldsymbol {X}}_{tt}^{n+1}={\overline {\overline {M}}}^{-1}({\boldsymbol {F}}^{n+1}-}$${\displaystyle {\overline {\overline {K}}}{\boldsymbol {X}}^{n+1})}$

(38)

${\displaystyle {\boldsymbol {X}}_{t}^{n+1}={\boldsymbol {X}}_{t}^{n}+\Delta t({\frac {1}{2}}{\boldsymbol {X}}_{tt}^{n}+}$${\displaystyle {\frac {1}{2}}{\boldsymbol {X}}_{tt}^{n+1})}$

(39)

${\displaystyle {\boldsymbol {X}}_{}^{n+1}={\boldsymbol {X}}_{}^{n}+\Delta t{\boldsymbol {X}}_{t}^{n}+}$${\displaystyle {\frac {\Delta t^{2}}{2}}({\frac {1}{2}}{\boldsymbol {X}}_{tt}^{n}+}$${\displaystyle {\frac {1}{2}}{\boldsymbol {X}}_{tt}^{n+1})}$

(40)

Within each time step the systems of Eqs.(38)-(40) are solved iteratively along with Eq.(33). This requires predicting the body velocities by solving Eq.(39), introducing this velocities into Eq.(34), solving the linear system in Eq. (33), introducing the pressure forces into eq.(37), and repeating the process until convergence is reached. In order to accelerate convergence, we used the secant method for predicting the bodies’ velocities and positions.

The algorithm implemented also allows considering non-linear external forces acting on the bodies such as mooring forces. In this implementation they are evaluated for every iteration of the solver and added to the right hand side of Eq. (37).

4. Solver acceleration

Most of the computational effort of the proposed numerical algorithm is spent in solving the linear system given in Eq. (33). Therefore, our main focused to reduce the computational time is speeding up the linear solver resolution. In order to do so, two techniques, that can be used combined, have been undertaken: the use of deflated solver, and the use of parallel computing in graphic processing units.

4.1 Deflated conjugate gradient

Deflation works by considering constant approximations on coarse sub-domains. This piecewise constant approximations are associated to the low frequencies eigenmodes of the solution, which are also the slow convergence modes [22,23]. Then, these slow modes can be quickly approximated by solving a small linear system of equations, which can be incorporated to the traditional preconditioned iterative solvers in order to accelerate the convergence of the solution.

The first step is to divide the domain into a set of coarse sub-domains that will be capable of capturing the slow modes. Several techniques have been developed for this purpose [22,23]. The most commonly techniques are the using seed-points and the advancing front technique. The former use prescribed seed-points and then sub-domains are built by associating points to seeds based on a distance criterion. The latter uses the advancing from method, where points are associated to a central point based of neighbouring preference, and once a number of points is reached, the sub-domain will be considered filled, and the next point will be used as the following central point.

The seed-points technique requires prescribing the seeds beforehand, and the advancing front requires a number of refinements to achieve a level of reliability. In this work, the technique used is slightly different to the advancing front. Our technique is also based on neighbouring criteria, but instead of prescribing a number of nodes within each sub-domain, we prescribed the maximum level of neighbouring “L”. The procedure goes as follows:

Step 0: Assigned level L+1 to all nodes (nodes will accept only lower levels when they are offered)

Step 1: Start building sub-domain 0: offer level 0 to the first node of the mesh. It will become node (sub-domain, level)=(0,0)

Step 2: Identify neighbours of node (0,0) and offer them level 1: (0,1)

Step 3: Identify neighbours of nodes (0,1), and offer them level 2: (0,2).

Step 4: The procedure is repeated until the prescribed level “L” is reached.

Step 5: The next node in the mesh with level L+1 is used to start building zone 1, and it is offered level 0, becoming a node (1,0).

Step 6: Identify neighbours of node (1,0) and offer them level 1: (1,1) (Notice that some (0,L) nodes might become (1,1)).

Step 7: Identify neighbours of nodes (1,1), and offer them level 2: (1,2). (Notice that some (0,L) or (0,L-1) nodes might become (1,2)).

Step 8: The procedure is repeated until the prescribed level “L” is reached (1,L).

Step 9: Repeat Steps 5-8 until there is no node with level L+1.

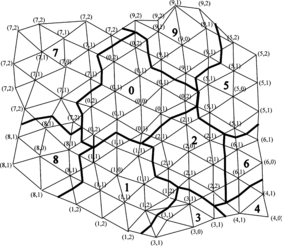
At the end of the previous procedure, all nodes will be denoted with the coordinate (R,L), representing the sub-domain and level within its sub-domain. It is guaranteed that any node cannot have a lower level in a different sub-domain. Moreover, the higher the prescribed level, the lower the number of sub-domains created. Figure 1 shows a domain decomposition obtained using the aforementioned algorithm. Notice that the level at the sub-domain boundaries is the minimum possible.

Although the previous algorithm provides good results, it can be improved by using it twice. Let’s say that in a first round, instead of using the prescribed level L, it is used the prescribed level 2L. A first decomposition is found with a lower number of sub-domains and twice the number of levels. Then, in a second round, the procedure is repeated using level L as the highest possible and starting with those nodes of level 2L to start building new sub-domains, without deleting the previous ones. Figure 2 shows the sub-domain decomposition obtained using the two rounds technique. The first one shows the decomposition at level 2L, and the second shows the decomposition at level L starting of the first decomposition at level 2L. Notice that the level at the sub-domains boundaries is lower or equal than the prescribed level L, and always minimum respect to any central node (node of level zero).

The recommended number of sub-domains might depend on the specific case under study. Usually in the order of hundred is a recommended value. However, in our specific case, the matrix of the linear system to be solved remains the same during the calculation, so that the sub-domain decompositions have to be carried out just once.

The deflated system has to be solved every iteration of the solver. Therefore, and since in our case the deflated matrix will remain the same, the inverse of the deflated matrix is calculated once, so that the resolution of the deflated system in each iteration is substituted by a matrix vector multiplication.

4.2 GPU acceleration

Pushed by the videogame industry, graphic processing units are achieving higher and higher computational performance. Therefore, their use for heavy computations is more extended every day (see [24] for instance).

The implementation done for this work is based on the well-known CUDA, a parallel computing platform and programming model invented by NVIDIA, for speeding up all the operations carried out by the iterative solver. The linear algebra library provided by Nvidia (cublas) is used to performed dot product operations. The sparse matrix vector multiplication is carried out using the kernel proposed in [25]. Regarding the matrix vector operation to be carried out in the deflated conjugate gradient, a regular kernel has been implemented.

For the purpose of this work, a deflated and non-deflated preconditioned conjugate gradient (CG) algorithm has been implemented in CUDA using cublas and cusparse libraries. A sparse approximate inverse (SPAI) preconditioner will be used. An incomplete LU decomposition (ILU) preconditioner was also tested using the sparse lower and upper triangular solvers provided in the cusparse library. However, in our specific case, the performance was poor even when compared to a diagonal preconditioner. Therefore we will omit the use of the ILU preconditioner when computing in GPU.

Let’s remind that either preconditioner is calculated just once at the beginning of the simulation since the matrix system remains the same at all times. Then, computational time invested in calculating the preconditioner can be vanished when compared to the total time spent in the linear solver along the whole simulation.

5. Numerical results

5.1 Waves refracted by a vertical circular cylinder

In order to prove the efficiency of the proposed numerical schemes, we will solve the problem of a monochromatic wave interacting with a fix bottom mounted circular cylinder. We have chosen this case study because exist an analytical solution to this problem. This analytical solution was found by McCamy and Fuchs in 1954 [26]. The potential for a monochromatic wave travelling along the OX axis in cylindrical coordinates is given by:

${\displaystyle {\phi }^{I}=Re\left\{{\frac {iAg}{\omega }}{\frac {cosh\left(k(H+z)\right)}{cosh\left(kH\right)}}\left[\sum _{m\geq 0}{\epsilon }_{m}J_{m}(kr)cos(m\theta )\right]exp(i\omega t)\right\}}$

(41)

where ${\textstyle \left(r,\theta ,z\right)}$ are the cylindrical coordinates; ${\displaystyle A}$ is the amplitude of the wave; ${\displaystyle \omega }$ is the wave frequency; ${\textstyle H}$ is the water depth; ${\displaystyle J_{m}}$ are the Bessel functions of the first kind; and ${\displaystyle {\epsilon }_{m}=1}$ if ${\displaystyle m=0}$ , and ${\displaystyle {\epsilon }_{m}=2{\left(-i\right)}^{m}}$ if ${\displaystyle m>0}$ . The scattered waves potential is given by:

${\displaystyle {\phi }^{S}=Re\left\{{\frac {iAg}{\omega }}{\frac {cosh\left(k(H+z)\right)}{cosh\left(kH\right)}}\left[\sum _{m\geq 0}-\right.\right.}$${\displaystyle \left.\left.{\epsilon }_{m}{\frac {J_{m}^{'}(kR)}{H_{m}^{\left(2\right)}{}^{'}(kR)}}H_{m}^{\left(2\right)}(kr)cos(m\theta )\right]exp(i\omega t)\right\}}$

(42)

where ${\textstyle \left({}'\right)}$ denotes derivatives respect to the argument; ${\displaystyle R}$ is the radius of the cylinder; and ${\displaystyle H_{m}^{\left(2\right)}}$ are the Hankel function of the second kind. Summing up Eqs. (41) and (42), we obtain the analytical solution to the wave scattering by vertical circular cylinder problem.

${\displaystyle \phi =Re\left\{{\frac {iAg}{\omega }}{\frac {cosh\left(k(H+z)\right)}{cosh\left(kH\right)}}\left[\sum _{m\geq 0}{\epsilon }_{m}\left(J_{m}(kr)-\right.\right.\right.}$${\displaystyle \left.\left.\left.{\frac {J_{m}^{'}(kR)}{H_{m}^{\left(2\right)}{}^{'}(kR)}}H_{m}^{\left(2\right)}(kr)\right)cos(m\theta )\right]exp(i\omega t)\right\}}$

(43)

The pressure value at any point is obtained by Eq.(35). We can further decompose the pressure into the hydrostatic pressure and the pressure induced by the velocity potential ${\textstyle P^{\phi }=-\rho {\partial }_{t}{\phi }^{1}}$ , which is given by:

${\displaystyle P^{\phi }=Re\left\{A\rho g{\frac {cosh\left(k(H+z)\right)}{cosh\left(kH\right)}}\left[\sum _{m\geq 0}{\epsilon }_{m}\left(J_{m}(kr)-\right.\right.\right.}$${\displaystyle \left.\left.\left.{\frac {J_{m}{}'(kR)}{H_{m}^{\left(2\right)}{}'(kR)}}H_{m}^{\left(2\right)}(kr)\right)cos(m\theta )\right]exp(i\omega t)\right\}}$

(44)

The horizontal force induced over the cylinder is obtained by integration of ${\displaystyle P^{\phi }}$ over the cylinder. This force is given by the following equation:

${\displaystyle F_{x}=Re\left\{2iAR\rho g\pi {\frac {tanh\left(kH\right)}{k}}\left(J_{1}(kR)-\right.\right.}$${\displaystyle \left.\left.{\frac {J_{1}{}'(kR)}{H_{1}^{\left(2\right)}{}'(kR)}}H_{1}^{\left(2\right)}(kR)\right)exp(i\omega t)\right\}}$

(45)

Next we compare numerical results obtained by the analytical solution with numerical results obtained by our FEM schemes for the specific case of ${\displaystyle R=1{\mbox{ }}m}$ , ${\displaystyle H=1{\mbox{ }}m}$ , ${\displaystyle A=0.1{\mbox{ }}m}$ , ${\displaystyle L=2{\mbox{ }}m}$ . Using ${\textstyle \rho =1025{\mbox{ }}kg/m^{3}}$ , ${\textstyle g=9.81{\mbox{ }}m/s^{2}}$ and by mean of the dispersion relation for first order waves, we obtain the frequency value ${\displaystyle \omega ={\sqrt {g\pi tanh(\pi )}}={\mbox{5}}{\mbox{.5411}}}$ rad/s, and the wave period T = 1.1339s.

The simulation is carried out using a circular domain with a radius of 6 meters. The mesh size is set to 0.1 m in an inner volume within a radius of 2 meters. In the outer volume, the mesh size grows smoothly up to 0.5meters.

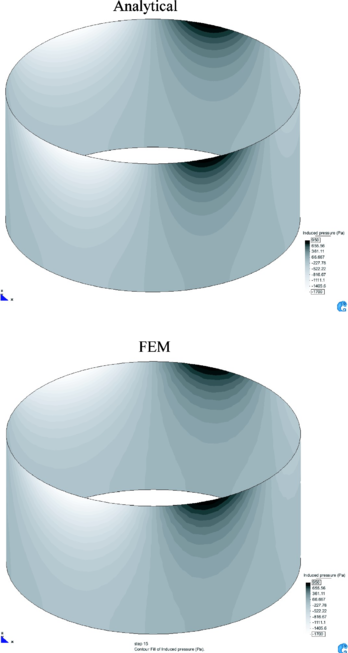
Figure 3 compares the contour lines of the free surface elevation at any time ${\displaystyle t=nT}$ . Notice that the FEM solution mostly lie over the analytical solution.

Figure 4 compares the pressure distribution over the cylinder obtained by the analytical solution and the FEM solution. Both pressure distributions are obtained using the same colour scale, with a maximum value of 950Pa and a minimum of -1700Pa.

Integration of the x component of ${\displaystyle P^{\phi }}$ over the cylinder provides the Horizontal force induced over the cylinder. This force is given by the following equation:

${\displaystyle F_{x}=Re\left\{2iAR\rho g\pi {\frac {tanh\left(kH\right)}{k}}\left(J_{1}(kR)-\right.\right.}$${\displaystyle \left.\left.{\frac {J_{1}{}'(kR)}{H_{1}^{\left(2\right)}{}'(kR)}}H_{1}^{\left(2\right)}(kR)\right)exp(i\omega t)\right\}}$

(46)

Figure 5 compares the force induced over the cylinder obtained by the analytical solution and FEM. It can be seen that the forces obtained in both ways are quite close to each other.

5.2 Freely floating tension leg platform (TLP)

In this section we analyze the seakeeping behaviour of a freely floating tension leg platform (TLP). The platform used is the ISSC TLP [27]. The mass is obtained internally to equal the displacement of the platform. The gravity centre position and radii of inertia are provided in Table 1. Figure 6 shows the mesh used for the present case study.

XG (m)	0
YG (m)	0
ZG (m)	3
Ixx/Mass (m2)	38.876
Iyy/Mass (m2)	38.876
Izz/Mass (m2)	42.420

The gravity used is ${\displaystyle {\mbox{g=9}}{\mbox{.80665}}{\mbox{ }}{\mbox{m/s}}^{\mbox{2}}}$ , the water density used is ${\displaystyle \rho {\mbox{=1025}}{\mbox{ }}{\mbox{kg/m}}^{\mbox{3}}}$ , and water depth is assume to be infinite. The Hydrostatic tensor ${\textstyle {\overline {\overline {\boldsymbol {K}}}}}$ is calculated by the corresponding boundary integrals.

We are interested in how the body moves when excited by a regular wave. In this specific case where the only excitation is the wave, the TLP is expected to respond harmonically with the same frequency that the frequency of the incident wave. However, since the method developed solves the problem in the time domain, initial conditions will be important.

Simulations were carried out for periods ranging between eight and fifteen seconds for three different wave heading. Figure 7 compares the response amplitude operators (RAOs) obtained by the present FEM model and RAOs obtained by the well known program WAMIT [28], which is based on the BEM and solves in the frequency domain. The obtained results show very good agreement between both solvers.

5.3 Seakeeping of a GVA 4000 Semisubmersible platform

Next we carry out comparison, between experimental data [29] and numerical results obtained via the method presented in this work, regarding the seakeeping behaviour of the GVA 4000 semisubmersible platform. The results to be compared are the heave and pitch response amplitude operators of the GVA 400 in heading seas, with a range of wave periods between 6 and 32 seconds.

The platform displacement is 25940 tonnes. The center of gravity is located 21.35 m above the keel, and the horizontal position corresponds to the geometric center of the platform. The radii of inertia are rxx=30.40 m, ryy=31.06 m, and rzz=37.54 m. The geometry of the GVA 4000 can be found in [29].

Based on [29], the model tests were carried out with the surge movement constraint by the action of a pre-stressed spring whose mission is to keep in place the structure during the testing. Besides, this spring creates also a pitching moment. Therefore, the pitch movement will be influenced not just by the waves, but also by the surge movement and the spring.

Since we have no data regarding the mechanism used by the model basin to keep in place the platform during the tests, we cannot include it in the simulation. Instead, simulations have been carried out in two cases: no surge and free surge. Figure 8 compares the experimental results and numerical FEM results. The experimental results lay within the numerical results obtained for free surge and no surge cases as expected.

5.4 Deflated solver

Solver deflation is gaining popularity as a way to improve convergence in linear solvers, and therefore in order to reduce solver iteration and CPU time. Deflation acts by solving in a fast and coarse manner eigenmodes associated with the lowest eigenvalues [22]. Therefore, it will improve convergence better in those problems with a larger range of eigenmodes, such as flows in pipes.

In order to check the performance of deflated solver in our problems, simulations using the ISSC TLP platform have been carried out using five different meshes. For each case, different levels of deflation have been used, and they have been compared to a non-deflated case. Table 2 provides the particulars of each case.

	Case 1	Case 2	Case 3	Case 4	Case 5
Number of Nodes	17804	51333	153758	459538	913149
Number of Elements	101572	292705	792372	2335374	4640638
h (m)	4	2	0.5	0.35	0.25
Δt (s)	0.75	0.5	0.1	0.075	0.05

Comparisons are made using the conjugate gradient along with an incomplete LU preconditioner. In the case of deflated solver, different levels of neighbouring have been used, resulting in different number of subdomains in each case. Once the deflation space is built, the resulting deflated matrix is inverted. This inversion is carried out just once since the system matrix remains unchanged during the simulation. In all cases, the same CPU has been used.

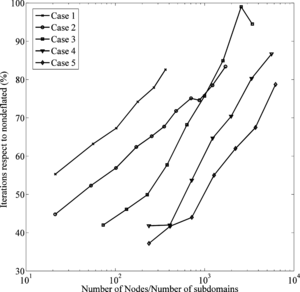
Figure 9 shows the reduction in iterations for each case as the number of subdomains changes. Table 3, Table 4,Table 5, Table 6 and Table 7 shows the average number of iterations and speed up respect to the non-deflated case. It can be observed that the number of iterations decreases as the dimension of the deflated subspace increases. This reduction in the number of iteration when using an ILU preconditioner indicates that the proposed technique for building subdomains is performing well.

However, when using deflated solver, a few operations are added to each solver iteration. Hence reducing iterations is not a synonym of reducing CPU time. Based on the results obtained, it can be said that the larger the system, the larger the speed up that can be obtained, and also the larger the number of subdomains must be. However, care must be taken because a dimension of the deflated subspace might end up in increasing the CPU time. Moreover, for smaller cases, deflation might even not be capable of speeding up at all.

Case 1: Number of nodes = 17804
Neighbouring level	Number of Sub-domains	Average Number Iterations	Speed up
2	836	15.89	0.556
3	316	18.18	0.963
4	174	19.36	0.989
5	100	21.34	0.894
6	66	22.39	0.871
7	49	23.74	0.829
Non-deflated		28.75	1

Case 2: Number of nodes = 51333
Neighbouring level	Number of Sub-domains	Average Number Iterations	Speed up
2	2419	17.34	0.310
3	963	20.23	0.908
4	506	22.00	1.081
5	299	24.15	1.055
6	201	25.20	1.023
7	146	26.17	0.943
8	107	27.77	0.907
9	73	29.04	0.889
10	59	28.84	0.912
11	42	30.36	0.863
12	30	32.27	0.789
Non-deflated		38.68	1

Case 3: Number of nodes = 153758
Neighbouring level	Number of Sub-domains	Average Number Iterations	Speed up
4	2101	20.82	0.77
5	1153	22.82	1.20
6	675	24.71	1.30
7	405	28.59	1.17
8	243	33.8	1.00
9	154	37.5	0.91
10	96	42.06	0.82
11	60	49.03	0.71
12	45	46.83	0.72
Non-deflated		49.53	1

Case 4: Number of nodes = 459538
Neighbouring level	Number of Sub-domains	Average Number Iterations	Speed up
6	1936	25.46	1.01
7	1128	25.58	1.39
8	641	32.66	1.22
9	374	39.38	1.03
10	232	42.86	0.94
11	137	48.90	0.84
12	82	52.76	0.76
Non-deflated		60.86	1

Case 5: Number of nodes = 913149
Neighbouring level	Number of Sub-domains	Average Number Iterations	Speed up
6	3837	26.70	0.54
7	2229	29.95	1.10
8	1271	31.60	1.40
9	717	39.55	1.20
10	413	44.55	1.07
11	246	48.50	0.99
12	147	56.55	0.83
Non-deflated		71.85	1

5.5 Multi-body simulation.

In this section we will simulate an array of sixteen freely floating bodies in the presence of a regular wave. The purpose of this simulation is to show that our approach can handle multi-body simulations in a reasonable time. Let’s recall that when solving in the frequency domain, it is required to compute how each body affects all the others. Therefore, the number of interactions will grow with the number of bodies squared, making the computational effort to grow very quickly as the number of bodies increases.

The case study consists of simulating the dynamics of an array of sixteen freely floating cylinders in the presence of a regular wave. Each cylinder has a radius of one meter, and a draft of half meter. The six degrees of freedom are free to move for each single body. Then, since they are freely floating, the mass of each equals the mass of the displaced water. Radii of gyration respect to their own centre of gravity are equal to one. Regarding the incident wave, it has a wave period of two seconds, amplitude of ten centimetres, and the incident direction is 22.5º. The cylinders are placed on a regular pattern and the distance between the centres of adjacent cylinders is three meters. A fifty second simulations is carried out, where the first twenty-five second correspond to an initialization period where the amplitude of the incident wave increases smoothly up to ten centimetres. Absorption starts at a distance of 12 meters from the origin of coordinates.

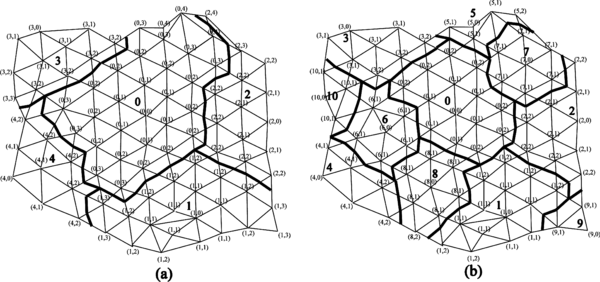
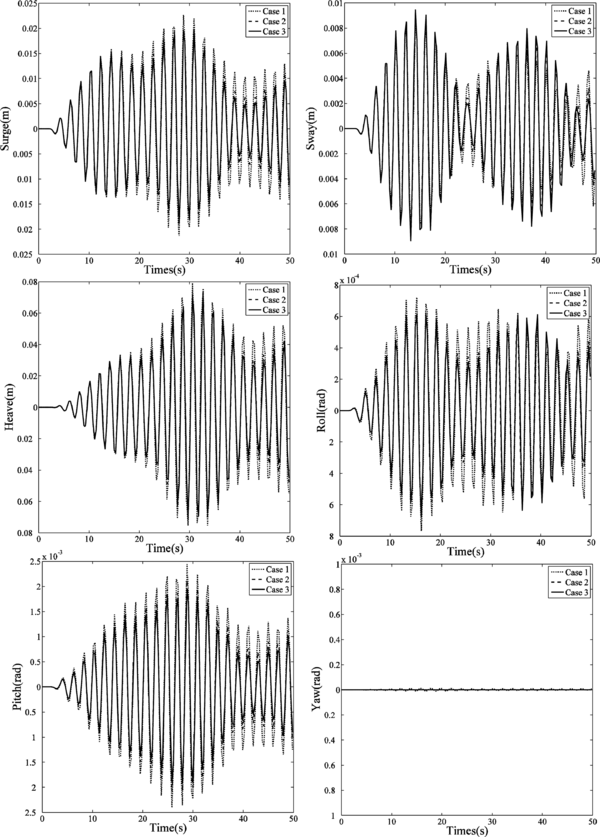
The case study is simulated with three levels of grid refinement. Computational time spent to solve the linear system of equation in every time step during the simulations were measured and are reported in the next section. Table 8 provides the particulars of the meshes and numerical parameters used, and Figure 10 shows the three different meshes used in this study. Figure 11 shows the free surface elevation at the end of the simulation.

Figure 12 compares the movements of the cylinder located in the upper right corner for the three meshes used. While some difference is found for the coarser mesh, results are very close to cases 2 and 3.

	Number of nodes	Number of elements	Characteristic element size (m)	Time step (s)
Case 1	137556	799665	0.2	0.1
Case 2	369410	2152774	0.1	0.07
Case 3	1181302	6878083	0.05	0.05

5.5 GPU solver acceleration.

We use the previous case study to carry out some speed-ups analyses when using different types of GPU/CPU architecture, as well as using different types of preconditioner. When computing in parallel in the GPU, the sparse approximate inverse (SPAI) preconditioner will be used. When carrying out serial computation in the CPU, the SPAI and incomplete LU decomposition preconditioner will be used. Let’s remind that the matrix system does not change along the simulation. Therefore, preconditioner and deflated matrices are only requested to be computed once. Also, let’s point out that the use of the ILU preconditioner in GPU architectures is not recommended due to its poor parallelization across thousands of threads as required by GPUs to hide memory latency.

In order to compare computational performance, we carried out simulation in four different platforms: two GPU platforms, and two CPU platforms. Table 9 provides the particulars of each platform used.

Platform	Description
GPU1	NVIDIA GTX 280
CPU1	Intel(R ) Core(TM )2 CPU Q9400 @ 2.66GHz 2.67GHz
GPU2	NVIDIA TESLA C2075
CPU2	Intel(R ) Core(TM ) i7-3930K CPU @ 3.20GHz 3.20GHz

Since hardware evolve quite fast, it is necessary to take into account whether comparison are made with same generation hardware or not. We have named GPU1 and CPU1 to the older platforms, belonging more or less to the same generation, and named CPU2 and GPU2 to the newer platforms, also belonging to the same generation. Therefore, when comparing computational time, it must be taken into account that the newer platforms are about three years younger than the older ones.

Table 10 shows the computational time required for simulating fifty seconds with the coarser mesh and under different solver strategies. The first thing we should point out is that more than eighty percent of the computational time is spent in the linear solver. Therefore, speeding up this part of the code is the key point for acceleration.

	PLATFORM	PRECONDITIONER	Solver time (s)	GPU-CPU Speed-up	Total time (s)	Solver(%)
Case 1	GPU1	SPAI	564	1	695	81.2
	CPU1		3256	5.77	3325	97.9
		ILU	2868	5.09	2938	97.6
	GPU2	SPAI	282	1	314	89.7
	CPU2		1217	4.32	1249	97.5
		ILU	1123	3.98	1154	97.3
Case 2	GPU1	SPAI	2012	1	2284	88.1
	CPU1		15051	7.48	15312	98.3
		ILU	13549	6.73	13812	98.1
	GPU2	SPAI	1060	1	1178	90.0
	CPU2		6052	5.71	6165	98.2
		ILU	5198	4.90	5311	97.9
Case 3	GPU1	SPAI	8519	1	9854	86.4
	CPU1		85605	10.04	86740	98.7
		ILU	75223	8.83	76307	98.6
	GPU2	SPAI	4743	1	5302	89.4
	CPU2		37479	7.90	37941	98.8
		ILU	30110	6.35	30588	98.4

The linear solver is the only part of the code also implemented in GPU. Therefore, and since this is the most time consuming part, we will compare computational time spent in solving the linear system.

When comparing GPU1 versus CPU1, the speed up obtained in the linear solver are x5,09, x6.73, and x8.83 for case 1, 2 and 3 respectively. On the other hand, when comparing GPU2 versus CPU2, the speed up obtained in the linear solver are x3.98, x4.90, and x6.35 for case 1, 2 and 3 respectively. It seems like the speed up increases as the size of the case study increases.

When comparing GPU1 versus GPU2, it can be observed that the speed up obtained using the newer generation is in the order of 2. We should also point out that the price of the newer is in the order of ten times more expensive.

Comparing the performance of GPU1 respect to CPU2, we observe that GPU1 performs better, getting speed-ups of x2, x2.58, and x3.53.

The fifty second simulation can be carried out with enough accuracy in some 20 minutes using the platform GPU2. Since the length scale of the model is one meter, those fifty seconds are equivalent to 500 seconds if the radius of each cylinder was one hundred meters. This leads to a ratio between computational time and real time around 2 for offshore engineering problems.

6. Conclusions

A FEM solver for wave structure interaction in the time domain has been presented. The wave modelling is based on Stokes perturbation theory, which allows keeping the same computational domain along the simulation. The FEM has been developed so unstructured meshes can be used, no matter the complexity of the structure.

Both, the free surface and outlet boundary conditions are based on implicit schemes. They have been introduced within the system matrix so that no iterations are required within the time step to reach convergence among the Laplace and boundary conditions.

FEM results have been compared to analytical results available for a circular vertical cylinder. The agreement between both solutions shows that the algorithms develop in this work perform well. Response amplitude operators for a freely floating TLP structure obtained by the present FEM and BEM also compare well. Moreover, comparison of response amplitude operators for a semisubmersible platform obtained experimentally shows that the present FEM code is capable of providing practically accurate results.

Deflated solvers have been put to the test for the problem stated in this work. While deflation might be useful for accelerating convergence and reducing CPU time achieving up to x1.4 speed up. However, care must be taken since the acceleration depends on the size of the problem and the dimension of the deflated space. A wrong used of deflated solver might end up in increasing CPU time.

GPUs have been used for solver acceleration. Results indicates that GPUs can perform faster than CPUs, and the speed-ups obtained in this work are in the range of 2-7, depend on the size of the problem, and the generation of GPU/CPU used.

A multi-body simulation has been carried out using sixteen freely floating bodies. It has been shown that the computational time can be reduced so that multi-body ocean engineering problems might be simulated closed to real time. Therefore, this sort of approach could be used for operational purposes in the near future.

Acknowledgements

This study was partially supported by the Ministry for Science and Innovation of Spain in the AIDMAR project CTM2008-06565-C03-01, and the Office of Naval Research Global (USA) by the Navy Grant N62909-10-1-7053.

The authors also want to acknowledge Prof. Clauss and Dr. Schmittner, for providing the main characteristics of the GVA4000 model used in the experimental tests.

References

[1] Cai, X., Langtangen, H. P., Nielsen, B. F. & Tveito, A., A finite element method for fully nonlinear water waves. J. Comput. Phys. 1998; 143: 544–568.

[2 ] Oñate E. & García, J., A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation, Comp. Methods Appl. Mech. and Eng. 2001; 191: 635-660.

[3 ] Löhner, R., Yang, C. & Oñate, E., On the simulation of flows with violent free surface motion, Comp. Methods Appl. Mech. Eng. 2006; 195: 5597-5620.

[4] Löhner, R., Yang, C. & Oñate, E., On the simulation of flows with violent free surface motion and moving objects using unstructured meshes, Comp. Methods Appl. Mech. Engng. 2007; 53: 1315-1338.

[5 ] García, J., Valls A., & Oñate, E., ODDLS: A new unstructured mesh finite element method for the analysis of free

surface flow problems, Int. J. Numer.  Meth.  Fluids 2008; 76 (9): 1297-1327.

[6] Wu, G.X. & Eatock Taylor, R., Finite element analysis of two dimensional non-linear transient water

waves, Appl. Ocean Res. 1994 ; 16: 363-372.

[7] Wu, G.X. & Eatock Taylor, R., Time stepping solution of the two dimensional non-linear wave

radiation problem, Ocean Eng. 1995; 22: 785-798.

[8] Greaves, D.M., Borthwick, A.G.L., Wu, G.X. and Eatock Taylor, R., A moving boundary finite

element method for fully nonlinear wave simulation, J. Ship Res. 1997; 41: 181-194.

[9] Robertson, I. & Sherwin, S., Free-surface flow simulation using hp/spectral elements, J. Comp. Phys. 1999; 155: 26-53.

[10] Ma, Q.W., Wu, G.X. and Eatock Taylor, R., Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves--part 1 methodology and numerical procedure, Int. J. Numer.  Meth.  Fluids 2001; 36: 265-285.

[11] Ma, Q.W., Wu, G.X. and Eatock Taylor, R., Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves--part 2 numerical results and validation, Int. J. Numer. Meth.  Fluids 2001; 36: 265-285.

[12] Westhuis, J.H., The numerical simulation of nonlinear waves in the hydrodynamic model test basin, Ph.D. Thesis 2001, Universiteit Twente, The Netherlands.

[13] P.X. Hu, G.X. Wu and Q.W. Ma, Numerical simulation of nonlinear wave radiation by a moving vertical cylinder, Ocean Engn . 2002; 29: 1733–1750.

[14] M.S. Turnbull, A.G.L. Borthwick and R. Eatock Taylor, Wave-structure intersection using coupled structured-unstructured finite element meshes, Applied Ocean Research 2003; 25: 63–77.

[15] G.X. Wu and Z.Z. Hu, Simulation of nonlinear interactions between waves and floating bodies through a finite element based numerical tank”, Proceedings of the Royal Society of London A 2004; 460: 2797–2817.

[16] C.Z. Wang and B.C. Khoo, Finite element analysis of two-dimensional nonlinear sloshing problems in random excitations, Ocean Engineering 2005; 32: 107–133.

[17] C.Z. Wang and G.X. Wu, Time domain analysis of second order wave diffraction by an array of vertical cylinders, Journal of Fluids and Structures 2007; 23 (4): 605–631.

[18] C.Z. Wang and G.X. Wu, Analysis of second-order resonance in wave interactions with floating bodies through a finite-element method, Ocean Engineering 2008; 35: 717–726.

[19] S. Yan, Q.W. Ma, QALE-FEM for modelling 3D overturning waves, Int. J. Numer. Meth. Fluids 2009 ; doi:10.1002/fld.2100.

[20] Song, H. Tao, L., and Chakrabarti, S., Modelling of water wave interaction with multiple cylinders of arbitrary shape, J. Comp. Phys. 2010; 229: 1498-1513.

[21] Lele, S. K., Compact Finite Difference Schemes with Spectral-like Resolution, J. Comp. Phys. 1992; 103: 16-42.

[22] Aubry, R., Mut, F., Löhner, R., and Juan R. Cebral, Deflated preconditioned conjugate gradient solvers for the Pressure–Poisson equation, J. Comp. Phys. 2008; 227: 10196-10208.

[23] Mut, F., Aubry, R., Houzeaux, G., Cebral, J., and Löhner, R., Deflated preconditioned conjugate gradient solvers: extensions and improvements, 48th Aerospace Sciences Meeting and Exhibit, Orlando, FL, January, 2010.

[24] F. Mossaiby, R. Rossi, P. Dadvand, and S. Idelsohn, OpenCL-based implementation of an unstructured edge-based finite element convection-diffusion solver on graphics hardware. Int. J. Numer.  Meth.  Engng. 2011; 89, 13:  1635–1651.

[25] Bell, N. and Garland, M., Effcient Sparse Matrix-Vector Multiplication on CUDA, NVIDIA Technical Report NVR-2008-004, Dec. 2008.

[26] R. McCamy and R. Fuchs, Wave forces on piles: a diffraction theory, Tech. Memo No. 69, U.S. Army Corps of Engrs. 1954.

[27] Eatock Taylor, R. and Jefferys, ER., Variability of Hydrodynamic Load Predictions for a Tension Leg Platform, Ocean Eng. 1986, Vol 13; 5, 449-490.

[28] WAMIT User Manual. http://www.wamit.com/manual.htm.

[29] Clauss, G. F. , Schmittner, C., and Stutz, K., Time-domain investigation of a semisubmersible in rouge waves, 21st International Conference on Offshore Mechanics and Arctic Engineering June 23-28, 2002, Oslo, Norway. OMAE2002-28450.