m (Scipediacontent moved page Draft Content 885907969 to Castilla Ordonez 2013a) |
|||
| Line 53: | Line 53: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{a}\cdot \boldsymbol{b}=\ | + | | <math>\boldsymbol{a}\cdot \boldsymbol{b}=\;\frac{1}{2}(\boldsymbol{ab}+</math><math>\boldsymbol{ba})</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | ( 1) | | style="width: 5px;text-align: right;white-space: nowrap;" | ( 1) | ||
| Line 86: | Line 86: | ||
La ecuación [[#eq0020|(3)]] es la suma de un escalar <math display="inline">\alpha =\boldsymbol{a}\cdot \boldsymbol{b}\in \mathbb{R}</math> y un bivector <math display="inline">\boldsymbol{B}=\boldsymbol{a}\wedge \boldsymbol{b}\subset {\mathbb{R}}^3</math> , donde <math display="inline">\tilde{\boldsymbol{m}}</math> es un multivector. | La ecuación [[#eq0020|(3)]] es la suma de un escalar <math display="inline">\alpha =\boldsymbol{a}\cdot \boldsymbol{b}\in \mathbb{R}</math> y un bivector <math display="inline">\boldsymbol{B}=\boldsymbol{a}\wedge \boldsymbol{b}\subset {\mathbb{R}}^3</math> , donde <math display="inline">\tilde{\boldsymbol{m}}</math> es un multivector. | ||
| − | Las ecuaciones [[#eq0010|(1)]] y [[#eq0015|(2)]] pueden ser utilizadas para obtener el ''reverso ( ''<math display="inline">{\tilde{\boldsymbol{m}}}^{\ | + | Las ecuaciones [[#eq0010|(1)]] y [[#eq0015|(2)]] pueden ser utilizadas para obtener el ''reverso ( ''<math display="inline">{\tilde{\boldsymbol{m}}}^{\dagger }</math>'') '' del multivector <math display="inline">\tilde{\boldsymbol{m}}</math> , |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 93: | Line 93: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{\tilde{\boldsymbol{m}}}^{\ | + | | <math>{\tilde{\boldsymbol{m}}}^{\dagger }=\boldsymbol{ba}=\boldsymbol{a}\cdot \boldsymbol{b}-</math><math>\boldsymbol{a}\wedge \boldsymbol{b}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | ( 4) | | style="width: 5px;text-align: right;white-space: nowrap;" | ( 4) | ||
| Line 120: | Line 120: | ||
|} | |} | ||
| − | En el entorno del AG, los subespacios orientados de alta dimensión se llaman ''blades'' . Consecuentemente, un término ''k-blade'' es utilizado para un subespacio homogéneo ''k-dimensional.'' Así, un ''vector'' es ''1-blade'' y el grado ''k-ésimo'' de un multivector, '''''B'''''<sub>''k''</sub> (''k-blade '' ),viene dado por el producto: <math display="inline">\boldsymbol{B}_k=\boldsymbol{x}_1\wedge \boldsymbol{x}_2\wedge \boldsymbol{x}_3...\wedge \boldsymbol{x}_k=</math><math>\left\langle \boldsymbol{x}_1,\boldsymbol{x}_2,\boldsymbol{x}_3...\boldsymbol{x}_k\right\rangle</math> , donde '''''x'''''<sub>'''''1'''''</sub>''''',''''' '''''x'''''<sub>'''''2'''''</sub> , '''''x'''''<sub>'''''3'''''</sub> … son vectores. | + | En el entorno del AG, los subespacios orientados de alta dimensión se llaman ''blades'' . Consecuentemente, un término ''k-blade'' es utilizado para un subespacio homogéneo ''k-dimensional.'' Así, un ''vector'' es ''1-blade'' y el grado ''k-ésimo'' de un multivector, '''''B'''''<sub>''k''</sub> (''k-blade '' ),viene dado por el producto: <math display="inline">\boldsymbol{B}_k=\boldsymbol{x}_1\wedge \boldsymbol{x}_2\wedge \boldsymbol{x}_3...\wedge \boldsymbol{x}_k=</math><math>\left\langle \boldsymbol{x}_1,\boldsymbol{x}_2,\boldsymbol{x}_3...\boldsymbol{x}_k\right\rangle</math> , donde '''''x'''''<sub>'''''1'''''</sub>''''',''''' '''''x'''''<sub>'''''2'''''</sub> , '''''x'''''<sub>'''''3'''''</sub> … son vectores. |
==3. Algoritmo Ray Tracing== | ==3. Algoritmo Ray Tracing== | ||
Latest revision as of 10:13, 18 April 2017
Resumen
El objetivo de este artículo es explorar la implementación de una reconstrucción real de imágenes en 3D utilizando el álgebra geométrica (AG). Con ello queremos mostrar la utilidad del AG para la representación de estructuras y el desarrollo de algoritmos para las aplicaciones de computer graphics , y especialmente para otras aplicaciones de ingeniería, como el modelado de imágenes en 3D. Una primera consecuencia es la obtención de un eficiente entorno de modelado para su implementación en un hardware programable. Los resultados obtenidos muestran que utilizando AG, los cálculos son menos complejos y se materializan como simples operaciones geométricas. El modelo obtenido para el hardware puede ser implementado como un paso siguiente en la reconstrucción de imágenes en 3D. Este artículo pone de manifiesto el potencial del AG para optimizaciones e implementaciones altamente eficientes.
Abstract
The objective of this paper is exploring implementation of a realistic images reconstruction 3D using geometric algebra (GA). We illustrate the suitability of GA for representing structures and developing algorithms in computer graphics, especially for engineering applications as 3D images modeling. A first consequence is to propose an efficient framework model to be implemented in hardware programmable. The obtained results showed that using GA, the computations are less complex and shows as simple computations geometrical operations. The obtained model to hardware can be implemented as a next step in 3D image reconstruction. We also include the potential of GA for optimizations and highly efficient implementations.
Palabras clave
Objetos geométricos ; Procesamiento eficiente ; Gable software ; Cálculos numéricos y geométricos ; Ray tracing ; Diseño gráfico
Keywords
Geometrical objects ; Efficient processing ; Gable software ; Numerical and geometrical computing ; Ray tracing ; Graphic design
1. Introducción
1.1. Motivación
En la actualidad, el espacio tridimensional en aplicaciones de diseño asistido por ordenador se interpreta a partir de la geometría euclídea 3D. Para desarrollar algunas aplicaciones, los programadores utilizan coordenadas homogéneas, las cuales usan un álgebra lineal (AL) 4D para interpretar algunas de las geometrías euclídeas 3D. Generalmente, en el desarrollo de estas aplicaciones la elección del método es confusa, debido precisamente a la utilización del AL compleja para manipular espacios poco familiares como 4D, 5D y 6D. En este artículo proponemos la utilización del álgebra geométrica (AG) para resolver estos problemas en las aplicaciones de modelado de imágenes en 3D, ya que permite que los «objetos geométricos» como vectores, bivectores, trivectores, y en general multivectores, sean elementos básicos de cálculo, y tanto las operaciones como las transformaciones con dichos «objetos» puedan ser ejecutadas directa y organizadamente.
1.2. Estado actual de la investigación
El AG es un entorno matemático desarrollado en los últimos 50 años basado en los espacios de Clifford, que describe fácilmente «objetos geométricos» y operaciones, y ha sido estudiada para analizar sistemas mediante un cálculo geométrico universal [1] . Las posibilidades de esta herramienta son enormes, ya que integra varios sistemas algebraicos, como vectores, matrices, spinors, cuaterniones y álgebra compleja, dentro de un leguaje unificado y coherente, permitiendo la representación de conceptos geométricos mediante términos simbólicos. En este sentido, la representación de «objetos geométricos» y sus transformaciones en el espacio tridimensional 3D, tal como traslaciones, rotaciones, reflexiones, etc., son 2 aspectos clave en las aplicaciones del diseño asistido por ordenador. En consecuencia, estas operaciones no están sometidas a ningún tipo de coordenadas y son fácilmente generalizables a todas las dimensiones, teniendo además la ventaja de proporcionar un alto grado de optimización y muy eficiente implementación [2] .
Existe un gran número de publicaciones dirigidas a los distintos campos de la ingeniería. Entre los trabajos pioneros debemos citar los desarrollados por D. Hestenes, que aplicó el AG a distintos problemas de física [3] . Motivados por esta línea de investigación, los trabajos de Lasenby et al. [4] y de Perwass [5] desarrollaron una línea en aplicaciones de visión computarizada, y Wareham et al. [6] y Fontjne y Dors [7] dirigieron sus investigaciones hacia el diseño asistido por ordenador. En particular, son dignos de mención los trabajos de Dors [8] and [9] . Últimamente, el AG se utiliza en aplicaciones de ingeniería eléctrica dirigidas al análisis de la teoría de potencia [10] and [11] . El propósito de este artículo es usar el AG para obtener un modelo de cálculo para la reconstrucción de imágenes en 3D y que además pueda servir para otras aplicaciones de la ingeniería.
2. Fundamentos matemáticos
El AG está basado en los conceptos de «objetos» con diferente dimensión geométrica, caracterizados exclusivamente por las propiedades de magnitud, dirección y sentido. En este entorno, un vector está representado por un segmento dirigido.
De forma general, un AG puede ser definido simplemente mediante un conjunto de reglas apropiadas para multiplicar vectores.
Sea σ1 σ2 σ3 … σn una base ortonormal de νn , espacio lineal n- dimensional sobre los números reales. Los elementos en AG se llaman multivectores , y en forma expandida se representan por:
|
|
El producto geométrico de vectores a ⊗ b o ab si a ,b ∈ νn puede ser descompuesto en un producto simétrico interno:
|
|
( 1) |
y un producto antisimétrico externo :
|
|
( 2) |
teniendo en cuenta que ab tiene una descomposición canónica de la forma:
|
|
( 3) |
La ecuación (3) es la suma de un escalar y un bivector , donde es un multivector.
Las ecuaciones (1) y (2) pueden ser utilizadas para obtener el reverso ( ) del multivector ,
|
|
( 4) |
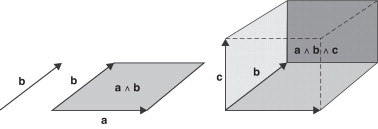
El producto interno a ·b es un escalar y el producto externo a ∧ b es un bivector o (2-vector). Geométricamente, un bivector se representa por un plano dirigido, así como un vector se representa por un segmento dirigido. Podemos equiparar el bivector a ∧ b , con un área dirigida con magnitud |a ∧ b |. Por último, un trivector (3-vector) representa un volumen (esfera). Vectores, bivectores, trivectores y en general multivectores , son llamados simplemente «objetos geométricos» ( fig. 1 ).
|
|
|
Figura 1. Objetos geométricos. |
En el entorno del AG, los subespacios orientados de alta dimensión se llaman blades . Consecuentemente, un término k-blade es utilizado para un subespacio homogéneo k-dimensional. Así, un vector es 1-blade y el grado k-ésimo de un multivector, Bk (k-blade ),viene dado por el producto: , donde x1, x2 , x3 … son vectores.
3. Algoritmo Ray Tracing
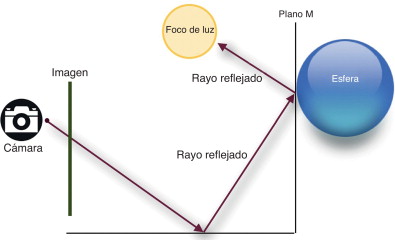
El método Ray Tracing (fig. 2 ) es un avanzado algoritmo de generación de imágenes reales por ordenador con 2 etapas. La primera de ellas está relacionada con la determinación de una superficie visible. Durante esta etapa, se trazan varios rayos desde un punto de visión hasta el plano de proyección e interseccionan con los objetos de la escena. La intersección más cercana, que está frente al punto de visión, determina el objeto visible a lo largo de este rayo. La segunda etapa consiste en el cálculo de la iluminación en el punto de intersección del rayo con el objeto de la escena. Esta incluye la cámara, iluminación y el modelo poligonal de información, que contiene a su vez la posición, las propiedades de los materiales, etc.
|
|
|
Figura 2. Diagrama básico del método Ray Tracing. |
El método requiere representaciones de vectores, puntos, líneas, planos y esferas, así como sus posibles transformaciones. La ejecución del Ray Tracing con AG en una CPU de propósito general ha sido estudiada en Deul et al. [12] , pero sin considerar las implementaciones presentadas en Fender [13] .
4. Metodología: cálculos geométricos y transformaciones
El algoritmo que proponemos para el modelado de imágenes e implementaciones de imágenes tridimensionales es el Ray Tracing, realizando los cálculos geométricos y transformaciones mediante el AG.
Así el AG de un espacio de alta dimensión es útil para el tratamiento de objetos geométricos, tales como puntos, líneas, círculos, planos y esferas. En los subapartados siguientes explicamos los cálculos y las operaciones a implementar en nuestro modelo para construir el algoritmo Ray Tracing.
4.1. Rotación y traslación de primitivas arbitrarias (puntos, líneas y planos)
La rotación de un vector v respecto a un eje que pasa por el origen viene dada por un vector v’ :
|
|
( 5) |
El rotor R puede ser calculado como R = e(−θ /2b ) = cos(θ /2) − b sin(θ /2), donde b es un bivector unitario que representa al plano de rotación y θ es el ángulo de rotación. Un plano puede ser caracterizado ahora por su bivector unitario b y su distancia al origen δ , pudiendo ser girado o trasladado como sigue:
|
|
( 6) |
donde t representa al vector translación.
4.2. Intersección de línea y plano
El punto de intersección Qi entre una línea y un plano puede ser calculado como:
|
|
( 7) |
donde Ql es un punto cualquiera de la línea, b es el bivector que representa el plano, u es el vector director de la recta, * es la operación conjugación y δ es la distancia al origen del plano.
4.3. Intersección de línea y esfera
Sean Q1 y Q2 los puntos posibles de intersección de una línea con una esfera de centro Qc y radio ρ . El punto de la línea más cercano al centro de la esfera viene dado por:
|
|
( 8) |
donde Qs es un punto de la superficie de la esfera, y u el vector normal en Qs. La distancia euclídea normalizada desde Qc a Qs determina si la línea intersecta o no a la esfera.
|
|
( 9) |
Si , la línea no corta a la esfera. Si , el único punto de intersección es Qr , y si obtenemos 2 puntos de intersección:
|
|
( 10) |
4.4. Reflexión
La dirección reflejada u ′ de una línea en un plano puede calcularse:
|
|
( 11) |
La línea reflejada vendrá dada por Qi y u ’. El punto de intersección entre la línea y el plano Qi debe ser calculado antes para obtener la representación de la línea reflejada.
4.5. Proyecciones ortogonales de un vector respecto a un plano
Dado un vector ν y un plano caracterizado por su bivector b , la proyección paralela y ortogonal de este vector respecto del plano vienen dadas por:
|
|
( 12) |
4.6. Ley de Snell
Un rayo que se dirige de un medio a otro, se refracta de acuerdo con la ley de Snell:
|
|
( 13) |
donde φ1 es el ángulo de incidencia (entrada), φ2 es el ángulo de refracción (salida) y η1 y η2 son los índices de refracción del medio correspondiente. La ley de Snell se construye en AG de igual forma que en AL, teniendo en cuenta que el vector n , normal a la superficie refractante, debe ser sustituido por el bivector b , representante de esa superficie plana. Si , la dirección del rayo refractado u ′ puede calcularse a partir de:
|
|
( 14) |
donde u es el vector del rayo incidente y n es el vector normal a la superficie, definido en el párrafo anterior.
5. Resultados de la evaluación experimental
El resultado de la implementación en Matlab de distintas transformaciones con AG viene dado en las siguientes figuras:
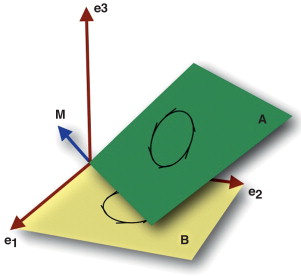
La figura 3 muestra la línea de intersección definida por 2 bivectores A y B .
|
|
|
Figura 3. Línea de intersección. |
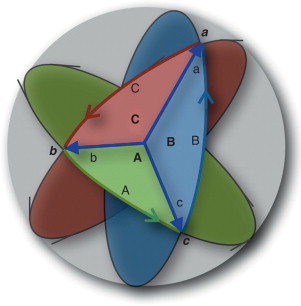
La figura 4 muestra el modelo de espacio vectorial y la más directa visualización de la estructura del AG.
|
|
|
Figura 4. Modelo del espacio vectorial. |
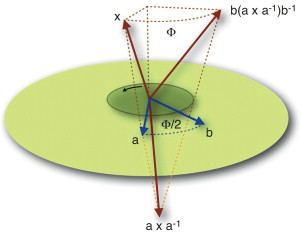
La figura 5 muestra la transformación ortogonal de un objeto X mediante un versor y su inverso. El versor más básico es el vector x (1-blade) , y la transformación asociada es una reflexión en el plano perpendicular a x .
|
|
|
Figura 5. Transformación ortogonal. |
6. Arquitectura de cálculo para implementación en hardware programable: programación del álgebra geométrica usando Gable
El AG de un m -dimensional espacio vectorial contiene objetos lineales (blades) , y puede ser representada en una base que contiene 2m elementos (necesitamos mk elementos por cada k-blade ). Los productos entre blades son todos lineales, y, por lo tanto, pueden implementarse como un producto de (2m)2 matrices. Esta operación puede hacerse de forma directa, pero es ineficiente cuando unimos espacio y tiempo, aunque sí es eficiente si utilizamos el modelo homogéneo. Teniendo en cuenta además que los elementos importantes son blades y sus productos, permite una implementación más eficiente. La ventaja de multiplicar k-blades es el conocimiento que tenemos de los k grados resultantes, y esto permite programar mediante un sencillo código. Por otro lado, la división requiere inversión , operación relacionada con la reversión con solo intercambiar los signos de ciertos grados. Para un elemento genérico del álgebra, la única diferencia a la hora de codificarlo es tener en cuenta sus distintos grados de homogeneidad (k-blades).
Desde los cálculos efectuados en la sección 4, la implementación de productos geométricos 3D sobre 2 multivectores puede generar un gran número de multiplicaciones entre los coeficientes de cada blade y una acumulación de productos parciales, precisamente los coeficientes de los nuevos k-blades.
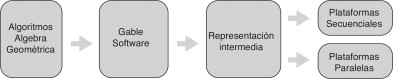
Para multiplicar 2 multivectores necesitamos 22n productos y 2n (2n – 1) sumas, siendo n la dimensión del espacio. Así, para un espacio 3D existen 23 = 8 blades, (23 )2 = 64 productos y 23 (23 –1) = 56 sumas. Para un espacio 5D, por ejemplo, se necesitan 1.024 productos y 960 sumas. Pero muchas de las aplicaciones del AG dependen a su vez de una apropiada arquitectura de cálculo. Por ello, una de las principales aportaciones de este trabajo es la arquitectura de cálculo en AG que proponemos en la figura 6 . En ella, Gable software es especialmente útil para implementar el AG en 3D y representa seguras ventajas respecto de algunas librerías convencionales desde el punto de vista de la programación, como:
- La programación en Gable es vectorizada.
- Los métodos de cálculo en AG son implementados como simples comandos de forma muy eficiente.
- La estructura de datos es muy simple y clara.
|
|
|
Figura 6. Arquitectura de cálculo. |
Así mismo, Gable utiliza 2 pasos para la optimización de algoritmos. Primero los optimiza con la ayuda del cálculo simbólico. En una segunda etapa estos algoritmos pueden ser usados para la optimización del hardware, ya que Gable es un toolbox de Matlab.
En el sistema de la figura 6 , la entrada es un algoritmo en AG (algoritmo Ray Tracing) que, vía simplificación simbólica, es transformado en etapa intermedia de representación. Esta a su vez puede ser utilizada para la creación de diferentes plataformas de salida. Por ejemplo, una de la plataformas paralelas de salida puede ser un PC de propósito general en el que las operaciones se ejecutan en AG, mediante un multiplicador AG, sumador AG, rotor AG, etc., reconstruyéndose una imagen en 3D con un coste operacional y tiempo de procesamiento muy bajos. Desde las plataformas paralelas, una Field Programmable Gate Array (FPGA) [13] , basada en un coprocesador de cálculo gráfico, puede ofrecer un soporte de hardware apropiado para la ejecución de operaciones en AG.
7. Análisis comparativo para el modelado en 3D
7.1. Implementación del algoritmo Ray Tracing en álgebra geométrica
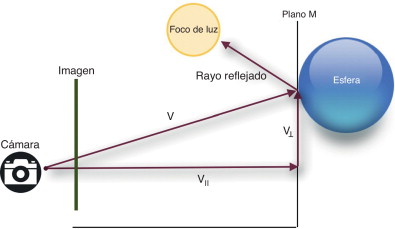
Sea el vector y el subespacio M = a ∧ b (plano tangente a la esfera), siendo a = σ2 + σ3 y b = 2σ1 (fig. 7 ). Estos son datos correspondientes al algoritmo Ray Tracing en AG, en el caso del subespacio M , contenidos en la primera etapa de la arquitectura de cálculo de la figura 6 . A continuación se ejecutan los siguientes cálculos y transformaciones en AG, a partir de los datos de entrada:
|
|
( 15) |
|
|
|
Figura 7. Vector en un punto de un plano tangente a la esfera y sus componentes. |
En la figura 7 se representa el vector v y sus componentes en la base {σ1 , σ2 , σ3 }.
En la ecuación (15) , ν|| y ν⊥ son las componentes del vector ν = ν|| + ν⊥ . Terminado este proceso, vía simbólica representación, se transforma en etapa de representación intermedia y pueden ser usados en distintas plataformas de salida. En consecuencia, las operaciones que realiza Gable Software son: cálculo de M–1 (un producto); cálculo de ν · M (3 sumas y 4 productos); cálculo de ν ∧ M (3 sumas y 4 productos), que hacen un total de 6 sumas y 9 productos. Refiriendo estos cálculos a la representación de una esfera sabemos que necesitamos solo 4 puntos no coplanarios para calcularla. Luego nos bastaría determinar en cada punto las componentes paralela y ortogonal respecto del plano imagen, para poder reconstruir la sombra paralela y perpendicular de la esfera, vía Ray Tracing. Esto equivaldría a un total de 4(6 + 9) = 60 operaciones.
En general, y si tenemos m puntos y trabajamos en un espacio de dimensión n , el número total de operaciones sería: m (2n + 3n −1 ).
7.2. Implementación del algoritmo Ray Tracing en álgebra lineal
En este caso, M es el plano de ecuación, , y las componentes del vector v son ν = (1; 0,5; 1,5). Para hallar la proyección ortogonal sobre M, debemos hallar primeramente una base ortonormal de M, , y calcular las componentes del vector: .
Observamos en este caso que para calcular la componente paralela de un vector necesitamos 3 + 3 + 3 = 9 sumas y 18 productos. Un total de 27 operaciones. Para la componente perpendicular, además, añadimos 3 sumas. Luego para 4 puntos (caso de la esfera), necesitamos 4(27 + 3) = 120 operaciones. Generalizando a m puntos, necesitaríamos m (3n + n ) operaciones. Así, el número de operaciones en AG es la mitad que en AL. Esta proporción se va a cumplir en cada una de las operaciones detalladas en la implementación del algoritmo Ray Tracing, con lo que el coste operacional en 3D AG es sustancialmente menor que en 3D AL, y, consecuentemente, también es menor el volumen de datos a procesar y los tiempos de procesamiento.
8. Conclusiones
La finalidad de este artículo es utilizar el AG como una herramienta muy eficiente para el desarrollo de un modelo de cálculo para la reconstrucción de imágenes en 3D, obtenida con solo ecuaciones de planos y representación de volúmenes. Se profundiza además en las propiedades del AG para el procesamiento de imágenes y aplicaciones de ingeniería gráfica. Estas propiedades son básicas para implementaciones altamente eficientes en 3D, utilizando software Gable. Ofrece además un camino natural para modelar objetos, independientemente de sus coordenadas, mediante simplificación simbólica, con tiempos de procesamiento muy inferiores a los empleados con otras metodologías [7] . Por otro lado, la potencialidad de Gable se basa en su propia estrategia de optimización, ya que, mediante una etapa previa de procesamiento, Gable reconoce los grados iniciales de las distintas entradas y simplifica el cálculo a partir de este dato.
Para conseguir estos objetivos, proponemos una original arquitectura de cálculo, cuya finalidad es la implementación de algoritmos para la reconstrucción de imágenes y la utilización de un posible hardware programable. Este hardware puede facilitar los cálculos, porque pueden ser ejecutados en una Arithmetic Logic Unit (ALU) específica, que utiliza datos y operaciones propias del AG.
Bibliografía
- [1] C. Doran; Introduction to Geometric Algebra; Cambridge University, Geometric Algebra (2008)
- [2] S. Franchini, G. Vassallo, F. Sorbello. A brief introduction to Clifford algebra. Universitá degli Studi di Palermo. Technical Report, 2010.
- [3] D. Hestenes, G. Sobcyk; Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics; Kluwer Academic Publishers, Dordrecht (1987)
- [4] J. Lasenby, W.J. Fitzgerald, A. Lasenby, C. Doran; New geometric methods for computer vision: An application to structure and motion estimation; IJCV, 3 (26) (1998), pp. 191–213
- [5] C. Perwass. Application of Geometric Algebra in Computer vision [Ph.D. Thesis]. Cambridge University, 2000.
- [6] R. Wareham, R. Cameron, J. Lasenby; Applications of conformal geometric algebra in computer vision and graphics; LNCS, 3519 (2005), pp. 329–349
- [7] D. Fontjne, L. Dors; Modeling 3D Euclidean geometry; IEEE CGA, 23 (2) (2003), pp. 68–78
- [8] L. Dors, S. Mann; Geometric Algebra: A computational framework for geometrical applications (Parts 1 and 2); IEEE CGA (2002) May/June and July/August
- [9] L. Dors, D. Fontijne, S. Mann; Geometric Algebra for Computer Science; An Object-Oriented Approach to Geometry, Morgan Kaufman (2007)
- [10] M. Castilla, J.C. Bravo, M. Ordoñez, J.C. Montaño; Clifford Theory: A Geometrical Interpretation of Multivectorial Apparent Power; IEEE TCAS-I-Regular Papers, 55 (10) (2008), p. 2008
- [11] M. Castilla, J.C. Bravo, M. Ordoñez, J.C. Montaño; The geometric algebra as a power theory analysis tool; PE, 2009 (1) (2009), pp. 202–208
- [12] C. Deul, P. Burger, D. Hildenbrand, A. Koch; Ray Tracing clouds using geometric algebra; GraVisMa (2009), pp. 32–39
- [13] J. Fender; A high-speed raytracing engine built on a field-programmable system; ICFPT. IEEE (2003), pp. 188–195
Document information
Published on 01/03/14
Accepted on 04/10/12
Submitted on 25/12/11
Volume 30, Issue 1, 2014
DOI: 10.1016/j.rimni.2012.10.003
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?