Revision as of 02:31, 12 December 2024 (view source) OmarMtzRosas (talk | contribs) (Tag: Visual edit) ← Older edit		Revision as of 03:05, 12 December 2024 (view source) OmarMtzRosas (talk | contribs) (Tag: Visual edit) Newer edit →
Line 227:		Line 227:
	===2.2 Fracción crítica de nodos eliminados y densidad de una red===		===2.2 Fracción crítica de nodos eliminados y densidad de una red===
−		+	La fracción crítica de nodos eliminados (denotada como ( q^* )) es el punto en el que, al eliminar nodos de una red, la reducción en el tamaño de la CG deja de ser lineal y constante o pierde su comportamiento robusto, y se produce una disminución abrupta y significativa. Este comportamiento se observa en una gráfica donde el eje de la abscisa representa la proporción de nodos eliminados q y el eje de la ordenada muestra el tamaño de la CG s(q). La fracción crítica ( q^* ) indica el umbral a partir del cual la red pierde su funcionalidad o conectividad principal de manera drástica. Identificar ( q^* ) es esencial para evaluar la robustez de la red frente a ataques. Esta fracción se determina aplicando el residual de un ajuste lineal o una regresión lineal <span id='citeF-16'></span>[19]:<span id="eq-9"></span>
−	Al analizar la reducción en el tamaño de la CG de una red tras un ataque, ya sea aleatorio u objetivo, se observan variaciones significativas. Sin embargo, estas variaciones por sí solas no proporcionan suficiente información para determinar con claridad la robustez de la red. En este escenario, buscamos identificar la fracción crítica de nodos eliminados, denotada como <math display="inline">q^{*}</math>. Esta fracción se determina aplicando el residual de un ajuste lineal o una regresión lineal <span id='citeF-16'></span>[19]:	+
−		+
−	<span id="eq-9"></span>	+
	{| class="formulaSCP" style="width: 100%; text-align: left;"		{| class="formulaSCP" style="width: 100%; text-align: left;"
	|-		|-

---

Revision as of 03:05, 12 December 2024

1 Introducción y relevancia

La robustez es una cualidad deseada en cualquier sistema conectado en el cual las unidades interactúen entre sí y su funcionamiento global depende de esta comunicación. En un universo interconectado y en constante cambio, la capacidad de resistir perturbaciones, adaptarse a desafíos inesperados y mantener su funcionalidad esencial se convierte en un criterio fundamental para evaluar la eficacia y la viabilidad de diversos sistemas interconectados [1-2].

Algunas de las áreas donde la robustez se constituye como una piedra angular para evaluar la estabilidad y la capacidad de respuesta incluyen la redes eléctricas y de transporte de energía [3], los ecosistemas naturales (desde bosques hasta arrecifes de coral) [4] así como las redes de transporte urbano [5], por mencionar solo algunas. La evaluación de la robustez en estos contextos proporcionan un marco invaluable para comprender cómo estos sistemas pueden enfrentar y sobrellevar situaciones de estrés, identificando sus vulnerabilidades y fortalezas ante diferentes escenarios. En particular, el estudio de la robustez en las redes de transporte es fundamental para garantizar la eficiencia y la continuidad del servicio en caso de perturbaciones. Diversos trabajos han abordado este tema desde distintas perspectivas y en diferentes tipos de redes de transporte, proporcionando una base sólida para comprender cómo la estructura y las características topológicas influyen en su capacidad para resistir fallos y ataques [6-8].

En uno de estos trabajos, los autores examinan la robustez del sistema de metro de Madrid [9], destacando la importancia de la teoría de redes para entender cómo la infraestructura responde a fallos y ataques . Su investigación revela que la robustez de la red puede variar significativamente dependiendo de la topología y las características específicas del sistema.

Por otro lado, en [10] se ofrece un análisis completo sobre la red del metro de Nueva York, aportando una visión detallada sobre cómo el sistema mantiene su conectividad frente a diversas perturbaciones. Este estudio subraya la capacidad de la red para adaptarse y recuperarse de fallos, y proporciona una base para comparar con otros sistemas de transporte. La vulnerabilidad de las redes de transporte público que se estudia en [11] realiza un análisis de comparación entre la robustez de las redes de metro y de autobuses, demostrando que cada tipo de red tiene características distintas que influyen en su resiliencia. Este enfoque comparativo es fundamental para comprender las ventajas y limitaciones de cada sistema de transporte en situaciones de crisis.

En el ámbito del transporte aéreo, como se menciona en [12], es posible analizar la estabilidad de la red aeroportuaria global cuando enfrenta ataques a los aeropuertos de forma aleatorios y objetiva. Su investigación revela cómo la red global de aeropuertos puede verse afectada por perturbaciones en nodos clave, y proporciona una perspectiva importante sobre la gestión de redes complejas a nivel internacional. Finalmente, como se ha demostrado en [13], se utiliza la teoría de grafos (graph-theory) y simulaciones para identificar las debilidades estructurales de la red ferroviaria de la ciudad de Londres y proponer mejoras para un funcionamiento más robusto y equilibrado de dicha red. Este enfoque es crucial para garantizar la continuidad del servicio ferroviario y minimizar los impactos de los fallos.

Inspirado por los estudios anteriores, este artículo se centra en analizar la robustez de la Red Aeroportuaria de la República Mexicana a través de grafos y redes complejas. Se utilizará el concepto de componente gigante, que es el subconjunto mayor de nodos que están conectados a través de enlaces o aristas, para estimar la reducción en el tamaño de la componente conectada principal de la red para entender la estructura topológica, vulnerabilidad y funcionalidad de la red y así evaluar estrategias para mejorar su capacidad de resistir perturbaciones, contribuyendo así a un sistema de transporte aéreo más eficiente y seguro.

2 Metodología: Componente gigante y robustez ${\textstyle {\mathcal {R}}}$ de un grafo2 Metodología: Componente gigante y robustez R {\textstyle {\mathcal {R}}} de un grafo

Una red o grafo, denotado como ${\textstyle G}$, consiste en un conjunto de nodos ${\textstyle N}$, los cuales están interconectados mediante un conjunto de enlaces ${\textstyle E}$. La cantidad de enlaces que conectan a un nodo ${\textstyle n_{i}}$ se denota como ${\textstyle k_{i}}$, lo cual representa el grado ${\textstyle k_{i}}$ del nodo ${\textstyle n_{i}}$ (con ${\textstyle i=1,2,3,\ldots ,N}$). Cada conexión entre nodos representa una relación o interacción específica. Una red se puede representar formalmente mediante la notación ${\textstyle G=G(N,E)}$. Asimismo vamos a considerar únicamente y exclusivamente redes no dirigidas (que todos sus enlaces son bidireccionales y no tienen orientación específica) y simples (que no formen conexiones directas desde un nodo hacia sí mismo).

La distribución de probabilidad de grado o distribución de grado, que la denotamos de la forma ${\textstyle p_{k}}$, nos proporciona la probabilidad de que un nodo ${\textstyle n_{i}}$ seleccionado de forma aleatoria tenga grado ${\textstyle k_{i}}$ [14]. Dado que ${\textstyle p_{k}}$ es una probabilidad, debe normalizarse, es decir

${\displaystyle \sum _{k=1}^{N-1}p_{k}=1}$

La distribución de probabilidad de grado ${\textstyle p_{k}}$ se expresa como la proporción de nodos con grado ${\textstyle k}$ en relación con el total de nodos ${\textstyle N}$ en la red. Por lo tanto:

${\displaystyle p_{k}={\frac {N_{k}}{N}}}$

(2)

indica la probabilidad de que un nodo seleccionado al azar tenga exactamente ${\textstyle k}$ conexiones. La distribución ${\textstyle p_{k}}$ nos ayuda a comprender la topología, estructura y conectividad de una red, lo cual nos permite identificar nodos de mayor relevancia.

Una forma de representar un grafo es a través de un arreglo matricial. La matriz asociada ${\textstyle A}$ de una red dada ${\textstyle G(N,E)}$ es de tamaño ${\textstyle N\times N}$ e indica si dos nodos ${\textstyle n_{i}}$ y ${\textstyle n_{j}}$ (con ${\textstyle i,j=1,2,3,\ldots ,N}$) están conectados o no. Esto es, los elementos ${\textstyle a_{ij}}$ de la matriz de adyacencia

• ${\textstyle a_{ij}=1}$ si hay conexión simple entre los nodos ${\textstyle n_{i}}$ y ${\textstyle n_{j}}$;
• ${\textstyle a_{ij}=0}$ en caso contrario.

Por consiguiente, ${\textstyle G(N,E)}$ lo podemos representar de la forma:

${\displaystyle A={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1N}\\a_{21}&a_{22}&\cdots &a_{2N}\\\vdots &\vdots &\ddots &\vdots \\a_{N1}&a_{N2}&\cdots &a_{NN}\end{pmatrix}}}$

Tal como se mencionó previamente este arreglo matricial es conocida como la matriz de adyacencia [15]. En el caso de grafos no dirigidos, la matriz de adyacencia es simétrica, es decir, ${\textstyle A=A^{T}}$ (por ser una red no dirigida).

Es posible calcular el grado ${\textstyle k_{i}}$ de cada nodo mediante la matriz de adyacencia sumando los elementos de la fila o columna de ${\textstyle A}$ de la forma:

${\displaystyle k_{i}=\sum _{j=1}^{N}A_{ij}=\sum _{j=1}^{N}A_{ji}}$

(3)

El número de enlaces que posee la red lo podemos calcular utilizando ${\textstyle A}$ mediante:

${\displaystyle E={\frac {1}{2}}\sum _{i,j=1}^{N}A_{ij}}$

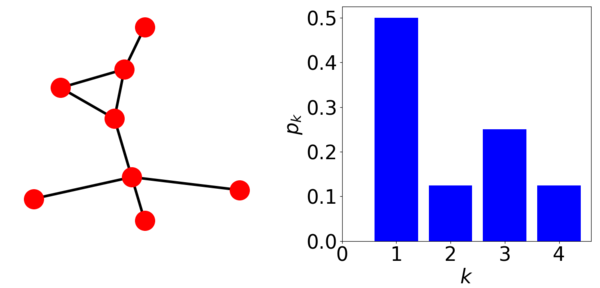
Teniendo presente los conceptos anteriores, en la Figura 1 podemos observar un ejemplo de una red ${\textstyle G(N,E)}$ con su respectiva distribución de probabilidad de grado ${\textstyle p_{k}}$ graficado de la forma ${\textstyle p_{k}}$ versus ${\textstyle k}$

Figura 1: Red ${\displaystyle G(8,8)}$ con sus respectiva ${\displaystyle p_{k}}$

La Figura 1 provee la proporción de nodos cuyo grado es ${\textstyle k}$.

La matriz de adyacencia ${\textstyle A}$ asociada al grafo ${\textstyle G}$ anterior es de la forma:

${\displaystyle A={\begin{pmatrix}0&1&1&1&1&0&0&0\\1&0&0&0&0&1&1&0\\1&0&0&0&0&0&0&0\\1&0&0&0&0&0&0&0\\1&0&0&0&0&0&0&0\\0&1&0&0&0&0&1&1\\0&1&0&0&0&1&0&0\\0&0&0&0&0&1&0&0\end{pmatrix}}}$

Al calcular el grado del nodo ${\textstyle n_{2}}$ utilizando la ecuación (3) obtenemos:

${\displaystyle k_{2}=\sum _{j=1}^{8}A_{2j}=3}$

(4)

Asimismo, es evidente notar que la red de la Figura 1 es no dirigida (${\textstyle A=A^{T}}$ ) y es simple (${\textstyle a_{ii}=0\forall i=1,2,\ldots ,8}$ ).

La distribución de probabilidad de grado la retomaremos más adelante para definir la existencia de la componente gigante en una red que es la parte esencial para analizar la vulnerabilidad o resistencia de una red cuando enfrenta ataques a sus ${\textstyle N}$ nodos.

2.1 Componente gigante y robustez de la red

La componente gigante (que la denotamos como CG) de una red la podemos definir como el subconjunto mayor de nodos que se encuentran conectados por los enlaces, dicho de otra forma, es la componente conectada que contiene la mayor proporción o la mayor cantidad de nodos.

Denotemos con ${\textstyle u=1-{\frac {N_{C}}{N}}}$ la fracción de nodos que no están en la Componente Gigante, cuyo tamaño es ${\textstyle N_{C}}$; y sea ${\textstyle p}$ la probabilidad de que un par de nodos estén conectados por un enlace. Si un nodo ${\textstyle n_{i}}$ forma parte de la CG, debe unirse a otro nodo ${\textstyle n_{j}}$, que también debe de formar parte de la CG. Por ende, si ${\textstyle n_{i}}$ no es parte de la CG, podría suceder dos casos:

• No existe una conexión entre ${\textstyle n_{i}}$ y ${\textstyle n_{j}}$ (la probabilidad para esto es ${\textstyle 1-p}$).
• Existe una conexión entre ${\textstyle n_{i}}$ y ${\textstyle n_{j}}$, pero ${\textstyle n_{j}}$ no es parte de CG (la probabilidad para esto es ${\textstyle pu}$).

Por lo tanto, la probabilidad total de que ${\textstyle n_{i}}$ no sea parte de la CG a través del nodo ${\textstyle n_{j}}$ es ${\textstyle 1-p+pu}$. La probabilidad de que ${\textstyle n_{i}}$ no esté conectado a la CG a través de ningún otro nodo es ${\textstyle (1-p+pu)^{N-1}}$, ya que hay ${\textstyle N-1}$ nodos que podrían servir como conexiones a la CG para el nodo ${\textstyle N-{i}}$. Como ${\textstyle u}$ es la fracción de nodos que no pertenecen a la CG, para cualquier ${\textstyle N}$ y un valor ${\textstyle p}$ con ${\textstyle 0<p\leq 1}$ el modelo matemático

${\displaystyle u=(1-p+pu)^{N-1}}$

(5)

proporciona el tamaño de la CG mediante ${\textstyle N_{C}=N(1-u)}$.

También podemos representar el tamaño de la CG de la siguiente forma. Denotemos con ${\textstyle {\tilde {N}}}$ el número de nodos que forman parte de la CG; y ${\textstyle Q=qN}$ representa el número de nodos a eliminar o quitar de la red, cuya forma normalizada lo tomamos como ${\textstyle q={\frac {Q}{N}}}$ (Más adelante explicamos las formas de eliminar ${\textstyle Q}$ nodos). En consecuencia, para cualquier ${\textstyle N}$ y ${\textstyle Q}$ (con ${\textstyle Q\leq N}$) el modelo matemático:

${\displaystyle s(Q)={\frac {\tilde {N}}{N}}}$

(6)

proporciona el tamaño de la componente gigante a través de la cantidad de nodos a eliminar de una red.

El criterio de Molloy-Reed nos garantiza la existencia de la CG dentro de una red [16]. Sea:

${\displaystyle \langle k\rangle ={\frac {1}{N}}\sum _{i=1}^{N}k_{i}=\sum _{k_{min}}^{k_{max}}kp_{k}}$

el promedio de los grados de todos los nodos en una red, también conocido como el grado promedio; y

${\displaystyle \langle k^{2}\rangle ={\frac {1}{N}}\sum _{i=1}^{N}k_{i}^{2}=\sum _{k_{min}}^{k_{max}}k^{2}p_{k}}$

el promedio del cuadrado de los grados de los nodos. Este último proporciona la dispersión o variabilidad de los grados en la red, mejor conocido como la varianza.

Por lo tanto, podemos determinar la existencia de la CG de la siguiente manera:

${\displaystyle \kappa ={\frac {\langle k^{2}\rangle }{\langle k\rangle }}}$

(7)

Si ${\textstyle \kappa {>2}}$, entonces existe una CG. En caso contrario, la red carece de una CG.

Para entender mejor este concepto, mostraremos unos ejemplos de la CG. En la figura 2 (a) podemos observar una red conexa y en la figura 2 (b) visualizamos una red disconexa con varias componentes conectadas. Para ambos casos, aplicando la ecuación (7) tenemos como resultado que ${\textstyle \kappa \approx 2.75>2}$ para la red del inciso (a) y ${\textstyle \kappa \approx 2.64>2}$ para la red del inciso (b), es decir, existe una CG en ambas redes. De forma visual podemos identificar que en la red del inciso (a) la CG es toda la red y en la red del inciso (b) la CG es la componente conectada con el mayor número de nodos (ubicada en la parte izquierda).

(a) Red conexa	(b) Red disconexa
Figura 2: Ejemplos de redes con existencia de la CG

La CG será de interés para medir la robustez de la red debido a su importancia de conectividad y, en ocasiones, por su facilidad para romper dicha componente en componentes diminutas.

La robustez de la red se refiere a la capacidad de dicha red para resistir y mantener su estructura y funcionalidad frente a la pérdida de nodos [17-18]. Llamaremos ${\textstyle {\mathcal {R}}}$ a la medición de la robustez de la red, el cual se puede estimar mediante:

${\displaystyle {\mathcal {R}}={\frac {1}{N}}\sum _{Q=0}^{N}s(Q)}$

(8)

Tengamos en cuenta que el posible rango de ${\textstyle {\mathcal {R}}}$ estará entre ${\textstyle 1/N}$ y ${\textstyle 0.5}$, ${\textstyle 0\leq s(Q)\leq 1}$ y ${\textstyle q=Q/N}$ es la forma normalizada de ${\textstyle Q}$ .

La eliminación de nodos de una red lo realizaremos uno por uno a través de dos tipos: fallas aleatorias y ataques objetivo.

a) Fallas aleatorias

En este caso, eliminaremos de manera aleatoria y secuencial los nodos ${\textstyle Q}$ (con ${\textstyle Q\leq N}$ ) de una red. El nodo seleccionado para remover podría ser un nodo de grado bajo o de conectividad alta que forma parte de la CG, un nodo sin conectividad (nodo aislado) o incluso un nodo con conectividad que no forma parte de la CG.

b) Ataques objetivo

En este tipo de eliminación, nos enfocaremos en atacar selectivamente los nodos de mayor a menor conectividad en la red, es decir, comenzaremos eliminando los nodos ${\textstyle n_{1},n_{2},n_{3},\ldots }$ donde ${\textstyle k_{n_{1}}\geq k_{n_{2}}\geq k_{n_{3}}\geq \ldots }$. Los nodos con mayor conectividad son ideales para eliminar debido a su importancia en la red, ya que están altamente conectados con otros nodos. En esta ocasión, la eliminación de nodos se llevará a cabo de manera específica y selectiva.

Nuestro objetivo es analizar, a través de una gráfica q contra s(q), cómo se reduce el tamaño de la CG, que concentra la funcionalidad principal de la red. Si la reducción es lineal y constante, la red se considera robusta. En cambio, si la reducción es agresiva, es decir, si el tamaño de la CG tiende a cero o se acerca a s(q)=0 al atacar pocos nodos, la red se considera no robusta. No obstante, también es posible que la reducción no se ajuste completamente a ninguno de estos dos casos. En la siguiente sección examinaremos este comportamiento utilizando el residual de un ajuste lineal para argumentar sobre la posible robustez de la red.

2.2 Fracción crítica de nodos eliminados y densidad de una red

La fracción crítica de nodos eliminados (denotada como ( q^* )) es el punto en el que, al eliminar nodos de una red, la reducción en el tamaño de la CG deja de ser lineal y constante o pierde su comportamiento robusto, y se produce una disminución abrupta y significativa. Este comportamiento se observa en una gráfica donde el eje de la abscisa representa la proporción de nodos eliminados q y el eje de la ordenada muestra el tamaño de la CG s(q). La fracción crítica ( q^* ) indica el umbral a partir del cual la red pierde su funcionalidad o conectividad principal de manera drástica. Identificar ( q^* ) es esencial para evaluar la robustez de la red frente a ataques. Esta fracción se determina aplicando el residual de un ajuste lineal o una regresión lineal [19]:

${\displaystyle re=|s(q_{i})-{\tilde {s}}(q_{i})|>15\%\forall i=1,2,\ldots ,N}$

(9)

donde ${\textstyle s(q_{i})}$ corresponde al valor de la función de reducción en el tamaño de la CG de una red y ${\textstyle {\tilde {s}}(q_{i})}$ corresponde al valor de la función de reducción (${\textstyle s(q)=1-q}$) en el tamaño de la CG de una red robusta. Con un error del ${\textstyle 15\%}$ en ${\textstyle re}$ encontraremos ${\textstyle q^{*}}$, en caso contrario, ${\textstyle q^{*}=1}$.

Para comprender el significado de ${\textstyle q^{*}}$, en la figura 3 podemos observar dos reducciones en el tamaño de la CG de una red ${\textstyle G(100,175)}$ y de una red robusta bajo ataques aleatorios. Asimismo, observamos ${\textstyle q^{*}}$ que se obtuvo aplicando la ecuación (9).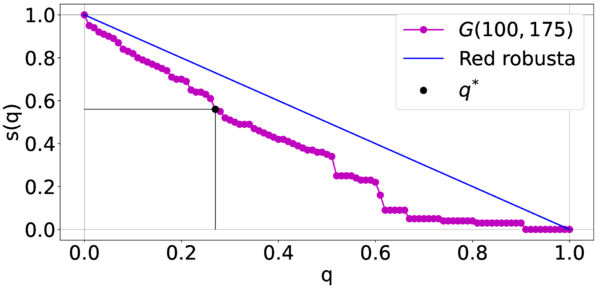

Figura 3: Identificación de ${\displaystyle q^{*}}$ en el análisis de la reducción en el tamaño de la CG de una red ${\displaystyle G(100,175)}$

En caso de que ${\textstyle re\leq 15\forall i=1,2,\ldots ,N}$, es decir, no se identifica ${\textstyle q^{*}}$ en la reducción en el tamaño de la CG de una red similar a la de la figura 3, entonces se le asigna a esa red ${\textstyle q^{*}=1}$.

Por otro lado, la densidad ${\textstyle \rho }$ de una red cuantifica la proporción de conexiones entre los nodos con respecto al máximo número posible de conexiones en la red. Una red es densa si el número de enlaces alcanza el máximo de enlaces posibles. En este caso, tenemos una red completa con ${\textstyle \rho =1}$. En caso contrario, una red es vacía si no cuenta con enlaces, es decir, ${\textstyle \rho =0}$ [20]. La densidad de una red se define formalmente como:

${\displaystyle \rho ={\frac {E}{\begin{pmatrix}N\\2\end{pmatrix}}}={\frac {2L}{N(N-1)}}}$

(10)

donde ${\textstyle 0\leq \rho \leq 1}$. Para redes completas podemos calcular el número máximo de enlaces posibles de la forma:

${\displaystyle E_{max}={\frac {N(N-1)}{2}}}$

Dicho lo anterior, la robustez de la red se determina a través de la fracción crítica ${\textstyle q^{*}}$ y la densidad ${\textstyle \rho }$, especialmente cuando la reducción en el tamaño de la componente gigante no sea de tipo decaimiento exponencial o de tipo reducción lineal similar a la red robusta de la figura 3.

3 Aplicaciones a la red aeroportuaria de la República Mexicana

En este trabajo analizaremos la conectividad aeroportuaria de la República Mexicana utilizando el formalismo anterior. Para ello utilizaremos una base de datos pública de siete aerolíneas mexicanas que corresponden al transporte aéreo local de pasajeros, es decir, vuelos comerciales y vuelos privados de pasajeros nacionales [21].

3.1 Red de tráfico aéreo de la República Mexicana

Definamos ${\textstyle G}$ como a la red aeroportuaria de la República Mexicana (RARM), Los aeropuertos o terminales aéreas los denotaremos como los nodos ${\textstyle N}$ y los enlaces ${\textstyle E}$ corresponden a los vuelos directos comerciales y privados nacionales que brindan las siete aerolíneas mexicanas que están consideradas en la tabla 1.

Tabla. 1 Aerolíneas mexicanas que ofrecen transporte aéreo de pasajeros

	Aerolineas mexicanas
1	Aeromar
2	Calafia Airlines
3	Grupo Aeroméxico
4	Magnicharters
5	Transportes Aéreos Terrestres
6	Viva Aerobus
7	Volaris

La base de datos de los vuelos directos comerciales y privados lo podemos encontrar en las páginas web de cada una de las siete aerolíneas mexicanas de la forma: vuelos de ciudad a ciudad o vuelos directos entre dos ciudades y la vamos a guardar o almacenar en un programa o un sistema de gestión de bases de datos. Posteriormente con la programación de Python y NetworkX podemos estructurar esa base de datos para darle forma de red.

Como resultado de este análisis, en la figura 4 visualizamos el tráfico aéreo de la RARM correspondiente a enero de 2023.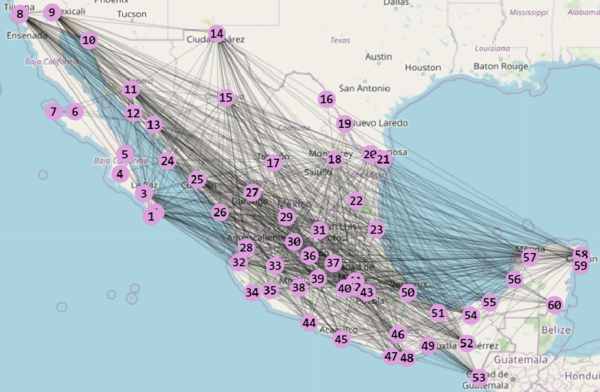

Figura 4: Red de tráfico aéreo de la República Mexicana. Los nodos indican los aeropuertos y los enlaces indican los vuelos directos

La red consta de ${\textstyle N=60}$ aeropuertos que ofrecen ${\textstyle E=723}$ vuelos directos comerciales y privados nacionales. Como podemos observar, la RARM es no dirigida, es decir, cada vuelo es de ida y vuelta; y es simple, es decir, solamente contemplamos un vuelo entre cada par de aeropuertos.

3.2 Robustez de la red aeroportuaria

En esta sección nos dedicaremos a analizar la reducción en el tamaño de la CG y la robustez de la RARM cuando enfrenta ataques aleatorios y ataques objetivo a sus 60 aeropuertos.

Es importante considerar que al simular el ataque a un aeropuerto ya sea de forma aleatoria u objetiva, estamos representando situaciones en las que un aeropuerto interrumpe totalmente sus operaciones debido a diversos eventos, como desastres naturales, condiciones climatológicas adversas, mantenimiento, modernización de la terminal u otros escenarios que puedan suspender completamente su funcionamiento. Dicho lo anterior, en la figura 5 se muestran las gráficas de interés correspondientes a la reducción en el tamaño de la CG ${\textstyle s(q)}$ y la robustez de la red ${\textstyle {\mathcal {R}}}$, donde se simularon fallas aleatorias.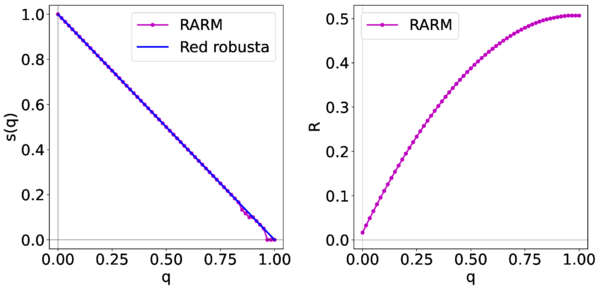

Figura 5: Reducción en el tamaño de la CG y robustez de la RARM bajo fallas aleatorias

Podemos analizar en la gráfica de la figura 5 que la reducción en el tamaño de la CG de la RARM no es significativa, es decir, reduce de forma lineal y casi se parece a la reducción de una red robusta a dicho ataque que es la función continua ${\textstyle s(q)=1-q}$. En en caso de la robustez, vemos que la función discreta converge a la cota superior de la estimación de la robustez, es decir, al rango superior con valor cercano al 1/2. Esto quiere decir que la red es robusta. Por lo tanto, las dos gráficas de la figura 5 indican una robustez en la RARM bajo fallas aleatorias.

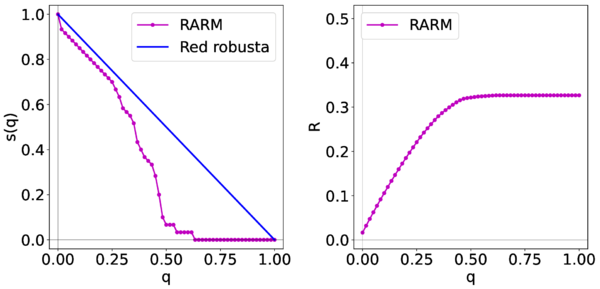
Ahora analizaremos el comportamiento de la reducción en el tamaño de la CG y la robustez de la RARM bajo ataques objetivo contra sus aeropuertos de mayor conectividad a menor conectividad destacando al Aeropuerto Internacional de la Ciudad de México, Benito Juárez; Aeropuerto Internacional de Tijuana, Gral. Abelardo Rodríguez y el Aeropuerto Internacional de Hermosillo, Gral. Ignacio Pesqueira García como los primeros para atacarlos. Por lo que, en la figura 6 analizaremos lo dicho en este párrafo.

Figura 6: Robustez de la red aeroportuaria de la República Mexicana bajo ataques objetivo

En la gráfica 6 vemos que su reducción en el tamaño de la CG tiene variaciones y pierde su parecido a la función de reducción de una red robusta. En la gráfica de la robustez, la función discreta no converge a la cota superior como en el caso de fallas aleatorias. Si la robustez de la RARM hubiese tenido una convergencia a la cota inferior, es decir, al valor 1/N que es cercano al valor 0, entonces la RARM hubiese sido no robusta. Sin embargo, no sucede eso y las dos gráficas de la figura 6 no nos dice nada sobre la robustez de la red. Por lo que, debemos de identificar la fracción crítica de nodos eliminados para decidir si la RARM es o no robusta bajo ataques objetivo.

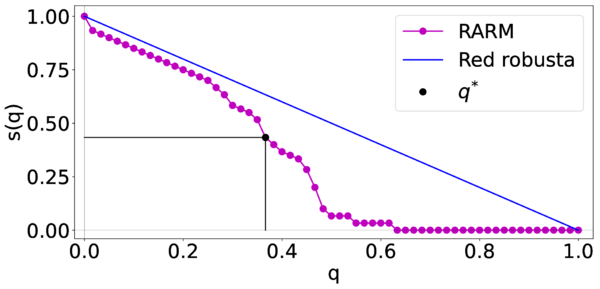
Con base a la reducción en el tamaño de la CG de la RARM bajo ataques objetivo. En la figura 7 observamos la identificación de la fracción crítica de nodos eliminados ${\textstyle q^{*}}$. Teniendo en cuenta esa fracción crítica cuyo valor en el eje ${\textstyle q}$ es de 0.37 y calculando la densidad ${\textstyle \rho }$ de la red aeroportuaria es de 0.408 podemos analizar la robustez de la RARM.

Figura 7: Identificación de ${\displaystyle q^{*}}$ en la reducción en el tamaño de la CG de la RARM bajo ataques objetivo

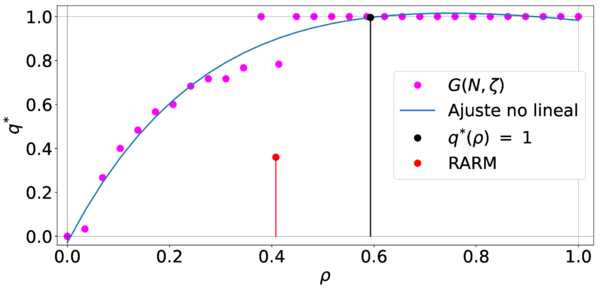
Para analizar la robustez de la RARM a través de su ${\textstyle q^{*}}$ y ${\textstyle \rho }$, graficaremos ${\textstyle q^{*}}$ y ${\textstyle \rho }$ de diferentes redes aleatorias empleando el modelo de Gilbert ${\textstyle G(N,\zeta )}$ donde ${\textstyle 0<\zeta \leq 1}$ es la probabilidad de que un par de nodos entre conectados por un enlace [22]. La ventajas del modelo de Gilbert para crear diferentes redes aleatorias es por la coincidencia de ${\textstyle \zeta }$ y la densidad ${\textstyle \rho }$, es decir, con una densidad ${\textstyle 0<\rho \leq 1}$ podemos crear una red aleatoria ${\textstyle G(N,\zeta )}$ con ${\textstyle \zeta =\rho }$. Dicho lo anterior, en la figura 8 podemos observar la gráfica ${\textstyle \rho }$ contra ${\textstyle q^{*}}$

Figura 8: Análisis de la vulnerabilidad de la RARM bajo ataques objetivo empleando ${\displaystyle q^{*}}$

Notemos que se empleó un ajuste no lineal en la figura 8 a la nube de puntos ${\textstyle G(N,\zeta )}$ con la finalidad de encontrar el punto ${\textstyle q^{*}(\rho )=1}$ que está unidos con una línea vertical y esta línea nos permita separar a las redes que están ubicados en el lado izquierdo y a las redes que están ubicados en el lado derecho de dicha línea. Las redes de lado izquierdo y las redes de lado derecho son considerados redes no robustas y redes robustas a ataques objetivo, respectivamente. Como podemos observar, la RARM que es el punto de color rojo se ubica en la parte izquierda. Esto quiere decir, que es no robusta cuando enfrenta ataques objetivo.

4 Conclusiones

Al analizar la robustez en RARM, hemos obtenido resultados interesantes que nos permiten comprender mejor su conectividad, estructura y características.

Se ha demostrado que la RARM exhibe un alto nivel de robustez cuando enfrenta fallas o ataques de forma aleatoria a sus 60 aeropuertos. En estas condiciones, la red demuestra una capacidad notable para mantener su estructura y funcionamiento fundamental, como se refleja en la preservación de su CG incluso en presencia de fallas aleatorias.

Sin embargo, se ha observado que la RARM es no robusta cuando se somete a ataques de forma objetiva. Específicamente, cuando se atacan selectivamente los aeropuertos de mayor conectividad a menor conectividad. La red muestra diferentes variaciones en la disminución con el tamaño de su CG, lo que indica una mayor susceptibilidad y una mayor posibilidad de experimentar interrupciones significativas en la conectividad entre los aeropuertos, generando retrasos masivos y afectaciones en la operación regular de los vuelos, o inclusive, el sistema puede colapsar o deje de funcionar de forma inesperada ante este tipo de ataques focalizados.

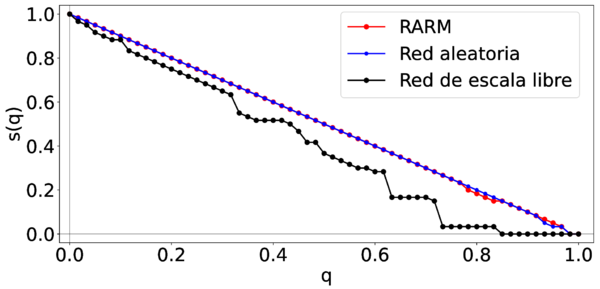
A continuación, se presentan dos gráficas que refuerzan las conclusiones obtenidas en la robustez. En la gráfica de la figura 9, se comparó la reducción en el tamaño de la CG de la RARM, una red aleatoria y una red de escala libre [23] cuando se atacaron a sus aeropuertos de forma aleatoria. Los resultados indican que tanto la red aleatoria como la RARM demostraron robustez, manteniendo la conectividad de su CG, mientras que la red de escala libre presentó variaciones a considerar en la reducción en el tamaño de su CG.

Figura 9: Comparaciones ${\displaystyle s(q)}$ de una red aleatoria, una red de escala libre y de la RARM bajo fallas aleatorias

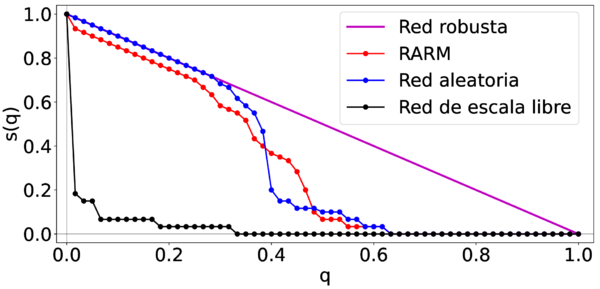
En la segunda gráfica de la figura 10, se analizó la reducción en el tamaño de la CG de las tres redes cuando se atacaron de manera objetiva, enfocándose en los nodos de mayor conectividad y los comparamos con una red robusta a dicho ataque. En este caso, la red de escala libre mostró una reducción significativa en el tamaño de su CG, lo que la hace especialmente no robusta. Por otro lado, tanto la RARM como la red aleatoria exhibieron cierta variabilidad cuando se ataca más del 20% de los nodos, demostrando que son más robusta que la red de escala libre, pero aún así no completamente robustas.

Figura 10: Comparaciones ${\displaystyle s(q)}$ de una red aleatoria, una red de escala libre y de la RARM bajo ataques objetivo

En consecuencia, estos hallazgos resaltan la importancia de la distribución de la conectividad del sistema aeroportuario mexicano. Si bien la red muestra robustez ante eventos aleatorios, se hace evidente la necesidad de implementar estrategias específicas para proteger y fortalecer los aeropuertos de mayor importancia y conectividad en la red. Estos resultados tienen implicaciones prácticas para el diseño y la gestión de la RARM, ya que podríamos comprender la importancia de la conectividad y la distribución de los aeropuertos y pueden ayudar a diseñar estrategias más efectivas para garantizar su funcionamiento óptimo y su resiliencia en situaciones adversas.

Agradecimientos

Omar Martínez Rosas agradece a la Universidad Autónoma de la Ciudad de México UACM-SLT por las oportunidades para realizar este trabajo y a los organizadores del Premio Mixbaal 2024 y a la Sociedad Mexicana de Computación Científica y sus Aplicaciones (SMCCA) por la invitación a escribir este artículo. Luis Agustín Olivares Quiroz desea expresar su agradecimiento al Colegio de Ciencia y Tecnología (CCyT) de la Universidad Autónoma de la Ciudad de México (UACM) y al Sistema Nacional de Investigadores SNII-CONAHCyT por el apoyo para la realización de este Proyecto.

BIBLIOGRAFÍA

[1] Albert-László Barabási. Network science. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 371(1987):20120375, 2013.

[2] Hiroki Sayama. Introduction to the modeling and analysis of complex systems. Open SUNY Textbooks, 2015.

[3] Ian Dobson, Benjamin A Carreras, Vickie E Lynch, and David E Newman. Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos: An Interdisciplinary Journal of Nonlinear Science, 17(2), 2007.

[4] Brian Walker and David Salt. Resilience thinking: sustaining ecosystems and people in a changing world. Island Press, 2012.

[5] Rémi Louf, Camille Roth, and Marc Barthelemy. Scaling in transportation networks. PLoS One, 9(7):e102007, 2014.

[9] Elisa Frutos Bernal and Angel Martín del Rey. Study of the structural and robustness characteristics of Madrid metro network. Sustainability, 11(12):3486, 2019.

[10] Xiaolong Ren, Zhenyu Zhang, and Zixvan Yu. Analysis of the complex characteristics of the New York City subway network. Highlights in Science, Engineering and Technology, 64:99–106, 2023.

[11] Gengxin Sun. Robustness analysis of an urban public traffic network based on a multi-subnet compo site complex network model. Entropy, 25(10):1377, 2023.

[12] Xiaoqian Sun, Volker Gollnick, and Sebastian Wandelt. Robustness analysis metrics for worldwide airport network: A comprehensive study. Chinese Journal of Aeronautics, 30(2):500–512, 2017.

[13] Alessio Pagani, Guillem Mosquera, Aseel Alturki, Samuel Johnson, Stephen Jarvis, Alan Wilson, Weisi Guo, and Liz Varga. Resilience or robustness: identifying topological vulnerabilities in rail networks. Royal Society Open Science, 6(2):181301, 2019.

[14] Sergey N Dorogovtsev, Jos FF Mendes, and Alexander N Samukhin. Size-dependent degree distribution of a scale-free growing network. Physical Review E, 63(6):062101, 2001.

[15] Ravindra B Bapat. Graphs and matrices, volume 27. Springer, 2010.

[16] Michael Molloy and Bruce Reed. A critical point for random graphs with a given degree sequence. Random structures & algorithms, 6(2-3):161–180, 1995.

[17] Christian M Schneider, André A Moreira, José S Andrade Jr, Shlomo Havlin, and Hans J Herrmann. Mitigation of malicious attacks on networks. Proceedings of the National Academy of Sciences, 108(10):3838–3841, 2011.

[18] Shangjia Dong, Haizhong Wang, Ali Mostafavi, and Jianxi Gao. Robust component: a robustness measure that incorporates access to critical facilities under disruptions. Journal of the Royal Society Interface, 16(157):20190149, 2019.

[19] SC Chapra and RP Canale. Regresión por mínimos cuadrados. Métodos numéricos para ingenieros, L. Campa, Mexico DF, Mc Graw Hill, pages 466–474, 2006.

[20] Thomas F Coleman and Jorge J Moré. Estimation of sparse Jacobian matrices and graph coloring problems. SIAM Journal on Numerical Analysis, 20(1):187–209, 1983.

[21] Agencia Federal de Aviación Civil. Boletín de estadística operacional, 2022.

[22] Edgar N Gilbert. Random graphs. The Annals of Mathematical Statistics, 30(4):1141–1144, 1959.

[23] Réka Albert and Albert-László Barabási. Statistical mechanics of complex networks. Reviews of modern physics, 74(1):47, 2002.