Revision as of 12:24, 18 June 2024

Abstract

Momentum shift is an important sign of nonadiabatic tunnelling ionization process. To investigate the mechanism of momentum shift, we use the strong-field approximation theory to track the formation of ionization momentum spectra of hydrogen atom under the action of different laser pulses in the time domain. By observing the ionization momentum spectra of different structures over time, we find that the momentum shift is formed by the continuous interference and evolution of ionization signals. Meanwhile, we further analyze how subcycle and intercycle interference influence the formation of momentum shift. Before the duration is long enough for intercycle interference to emerge, momentum shift grows smoothly. Our findings reveal different intrinsic mechanisms for the formation of momentum shift in many-cycle and few-cycle laser pulses, showing that subcycle interference plays a dominant role in the former while intercycle interference is critical in the latter. This work lays the foundation for a deeper understanding of the nonadiabatic tunnelling process and makes the regulation of momentum shift possible.

Keywords: Momentum shift, nonadiabatic tunnelling ionization, time-resolved interference, subcycle and intercycle interference

1. Introdution

Nonadiabatic tunneling ionization is one of the most fundamental and common dynamic processes in ultrafast ionization, and has always been a hot topic of concern in the study of ultrafast laser physics. Instead of adiabatic tunneling ionization, the barrier formed by the Coulomb field and the laser field can’t be regarded as static any more. We often use the Keldysh parameter to distinguish these two ionization processes [1,2]. The physical meaning of the Keldysh parameter ${\textstyle \gamma ={\frac {w_{laser}}{w_{tunnel}}}={\sqrt {\frac {I_{p}}{2U_{p}}}}}$ is the ratio of the time an electron in ground state takes to tunnel through the entire potential barrier to the time of a single cycle of the external laser field, where ${\textstyle I_{p}}$ is the ionization energy, ${\textstyle U_{p}={\frac {E_{0}^{2}}{4{\omega }^{2}}}}$ is the pondermotive energy with ${\textstyle E_{0}}$ being the amplitude of the laser field and ${\textstyle \omega }$ being the angular frequency of the laser field. If ${\textstyle \gamma \ll 1}$, the ground state electron crossing the potential barrier time is much smaller than the laser field period, and the tunneling ionization process can be regarded as an adiabatic process. When the parameter is higher ${\textstyle \gamma \approx 1}$, the laser field is no longer quasi-static during electron tunneling, in this condition the nonadiabatic properties of tunneling ionization begin to emerge [3-6].

Recently, many interesting works have revolved around the nonadiabatic properties of tunneling ionization, such as the non-zero ionization initial momentum [7-8], distorted tunneling exit positions [9-10]，and the tunneling delay time phenomenon [11-15]. The existence of the above nonadiabatic properties leads to a fact that the photoelectrons will not be distributed near the negative vector potential of the laser field as the adiabatic tunneling photoelectrons. There is a difference between the maximum of the photoelectron momentum distributions (PMDs) and the negative vector potentials corresponding to the laser electric-field peaks, leading to the phenomenon of nonadiabatic momentum shift [16-22].

Numerous studies on the formation mechanism of ionization momentum spectra have shown that the formation of ionization momentum spectra is not instantaneous, but evolves over time. During the ionization process, subsequent ionized electrons continuously interfere with previously ionized electrons, ultimately preserving the signal that satisfies the Feynman path integral to form the momentum spectrum [23-24]. During the formation of ionization momentum spectra, subcycle interference (SCI) [25-28] and intercycle interference (ICI) [29,30] are two important types of interferences. They ultimately determined the interference structure of the PMDs. In order to further explore the internal mechanism of momentum shift formation and whether the formation of momentum shift also follows the law of time evolution, it is necessary to analyze the phenomenon in time domain.

In this paper, we numerically simulate the formation of the PMDs of a hydrogen atom ionized by few-cycle laser pulses with the strong-field approximation (SFA) theory [31,32] in the time domain. The SFA is a widely used theoretical framework in strong-field physics, which simplifies the problem by neglecting the Coulomb potential after ionization and treating the electron as a free particle in the laser field. This approximation allows us to efficiently model the ionization process and capture the key dynamics of electron motion under the influence of intense laser fields. By tracking the relative positions of the maximum of the PMDs and the negative vector potential corresponding to the circularly polarized laser electric-field peak, we find that the momentum shift is formed by the continuous interference of ionization signals over time. It's worth noting that a drastic change occurs in the evolution, which we analyze further to understand its cause. To find the reason for this change, we examine the momentum shift induced by orthogonal two-color laser fields with different durations. In such laser fields, interference types are distinguishable. Ultimately, we conclude that subcycle and intercycle interferences significantly influence the formation of momentum shift, as reflected in the irregular changes of momentum shift over time. These in-depth studies of the momentum shift phenomenon contribute to a deeper understanding of the nonadiabatic tunneling process.

We use the SFA to simulate the direct ionization process of a hydrogen atom exposed to ultrafast laser field. In the SFA, the Coulomb potential is neglected and the final continuum wave function is described as a plane wave. The probability amplitude of a photoelectron with momentum ${\textstyle {\boldsymbol {p}}}$ can be written formally as [atomic units (a.u.) are used throughout the paper unless indicated otherwise]:

in which, the ground state wave function ${\textstyle {\psi }_{0}\left({\boldsymbol {r}},t\right)=e^{iI_{p}t}{\psi }_{0}\left({\boldsymbol {r}}\right)}$, for hydrogen atom ${\textstyle {\psi }_{0}\left({\boldsymbol {r}}\right)={\frac {1}{\sqrt {\pi }}}e^{-r}}$. ${\textstyle W\left(t\right)={\boldsymbol {r}}\cdot {\boldsymbol {E}}\left(t\right)}$ is electron-laser interaction operator under dipole approximation (length gauge), with ${\textstyle {\boldsymbol {r}}}$ the electronic coordinate, and ${\textstyle {\boldsymbol {E}}\left({\boldsymbol {t}}\right)}$ the electric field. ${\textstyle t_{i}}$ is the moment the laser pulse starts to play.

For the scattering state ${\textstyle \vert {\psi }_{p}^{\left(V\right)}\left({\boldsymbol {r}},t\right)\rangle }$ with canonical momentum ${\textstyle {\boldsymbol {p}}}$ can be written as a Gordon–Volkov state

with the Volkov phase

where ${\textstyle A\left(t\right)}$ is the vector potential, from which the laser field can be derived ${\textstyle E\left(t\right)=-{\frac {d}{dt}}A\left(t\right)}$.

Finally, Eq. (1) can be rewritten in detail as

where ${\textstyle I_{p}{\mbox{=0}}{\mbox{.5 }}a.u.}$ is the ionization potential, ${\textstyle {\boldsymbol {q}}={\boldsymbol {p}}+{\boldsymbol {A}}\left(t\right)}$ is the mechanical momentum.

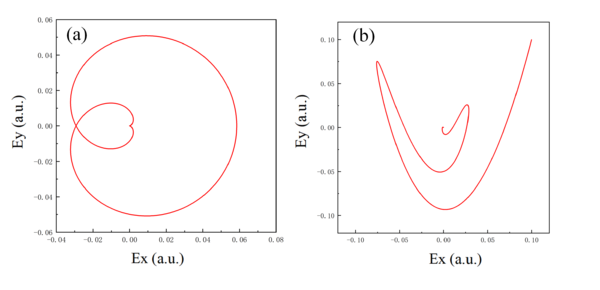
In our simulation two types of lasers are used to interact with hydrogen atom, they can be written as: ${\textstyle {\boldsymbol {E}}_{\boldsymbol {cp}}\left(t\right)=E_{0}f\left(t\right)\left[{\overset {\rightarrow }{e}}_{x}\cos \left(\omega t\right)+\right.}$${\displaystyle \left.{\overset {\rightarrow }{e}}_{y}\sin \left(\omega t\right)\right]}$ is the electric-field strength of the circularly polarized(CP) laser field as shown in Figure 1(a), ${\textstyle E_{OTC}\left(t\right)=E_{0}f\left(t\right)\left[{\overset {\rightarrow }{e}}_{x}\cos \left(\omega t\right)+{\overset {\rightarrow }{e}}_{y}\sin \left(2\omega t+{\frac {\pi }{2}}\right)\right]}$ is the electric-field strength of the orthogonal two-color laser field(OTC) in Figure 1(b). The intensities of CP and OTC pulses are ${\textstyle I{\mbox{=}}1.2\times {10}^{14}W/{\mbox{cm}}^{2}}$ and ${\textstyle I{\mbox{=}}3.5\times {10}^{14}W/{\mbox{cm}}^{2}}$ where ${\displaystyle \left(I{\mbox{ in }}{\mbox{ W/cm}}^{2})=3.51\times {10}^{16}\times (E_{0}^{2}{\mbox{ in }}a.u.\right)}$. We point out that the laser pulses used here are strong enough to contribute significant ionization, the SFA will give a quite accurate simulation for the parameters we used [33]. Meanwhile, the frequency ${\textstyle \omega =0.057a.u.}$ makes the ponderomotive energy ${\textstyle U_{p}}$ close to the ionization potential, hence ${\textstyle \gamma \approx 1}$. Under this condition, ionization process will exhibit significant nonadiabatic effects. In additional, all the pulses have the same envelop function ${\textstyle f\left(t\right)={\cos }^{2}({\frac {\pi t}{\tau }})}$, the duration ${\textstyle \tau }$ changes from ${\textstyle 2T}$ to ${\textstyle 3T}$. Because of the influence of the pulse envelope, the few-cycle CP and OTC laser plulses will show us more pronounced interference structures in the momentum spectrum, including subcycle and intercycle interferences.

Figure 1. (Color online) (a) Electric field of a 2-cycle (full width) circularly polarized laser pulse with the photon energy ${\textstyle \omega =0.057a.u.}$ and the intensity ${\textstyle I=1.2\times {10}^{14}{\mbox{ W/cm}}^{2}}$. (b) The red solid line represents the electric field of OTC field comprising three 800-nm cycles, the peak intensity ${\textstyle I=3.5\times {10}^{14}{\mbox{ W/cm}}^{2}}$ and the relative phase is ${\textstyle {\frac {\pi }{2}}}$. Both pulses have the ${\textstyle {\cos }^{2}}$ envelope

3. Results and discussion

Firstly，we use a simple CP laser pulse to interact with a hydrogen atom as shown in Figure 1(a), of which the pulse duration is ${\textstyle N=2}$. The formation of the PMDs corresponding to different instantaneous moments are tracked by the SFA theory in time domain ${\textstyle -T\leq t\leq T}$. These time-resolved PMDs showcased the details of the ionization processes, which helps us investigate the nonadiabatic effect in the tunneling ionization.

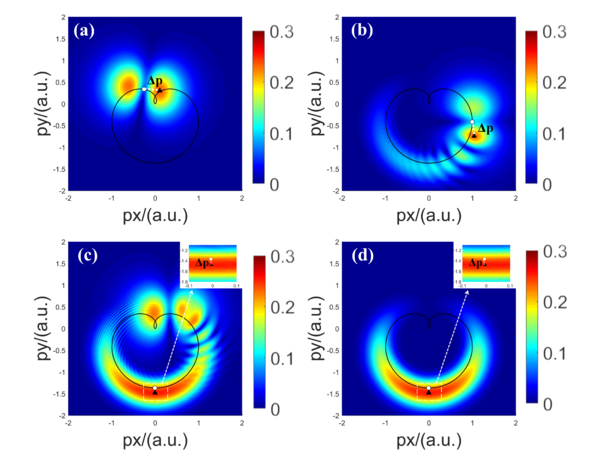
Figure 2 shows four chosen PMDs at the moments: (a) ${\textstyle t=-{\frac {1}{2}}T}$, (b) ${\textstyle t={\frac {1}{4}}T}$, (c) ${\textstyle t={\frac {1}{2}}T}$, and (d) ${\textstyle t=T}$. More details in Figure 2(a)-(d), the black closed curve is the negative vector potential of the CP laser pulse, the white dots denote the negative vector potential corresponding to the electric-field peak intensity, the black triangles denote the maximum ionization rate of the PMDs. Among them, ${\textstyle \Delta p}$ is the offset difference between the white dots and the black triangles, as known as the momentum shift in nonadiabatic tunneling ionization [34].

Figure 2. (Color online) Instantaneous PMD of hydrogen atom exposed to a 2-cycle circularly polarized laser field at the moment (a) ${\textstyle t=-{\frac {1}{2}}T}$. (b) ${\textstyle t={\frac {1}{4}}T}$. (c) ${\textstyle t={\frac {1}{2}}T}$. (d) ${\textstyle t=T}$ with ${\textstyle T={\frac {2\pi }{\omega }}}$, ${\textstyle \omega =0.057a.u.}$ and the intensity ${\textstyle I=1.2\times {10}^{14}{\mbox{ W/cm}}^{2}}$. The black closed curves are negative vector potentials. White dots mark the most probable momentum corresponding to the peak electric field and black triangles mark the most probable momentum corresponding to the maximum ionization rate. The white dotted lines indicate the magnitude of the momentum shift ${\textstyle \Delta p}$. The small image in the upper right corner of (c) and (d) shows an enlargement of the marked area with a white dashed box

We can see that, at the beginning of the interaction, there is no complex interference between electron wave packets, as shown in Figure 2(a). As time evolves, the instantaneous ionization events add coherently, making the ionization momentum spectrum becoming increasingly complex as shown in Figure 2(b)-(c). Finally, at the end of the interaction ${\textstyle t=T}$, the electron wave packets has already obtained all informations of the laser field, the ionization momentum spectrum gradually forms in Figure 2(d) [23]. At the same time, one can see that the momentum shift ${\textstyle \Delta p}$ also varies with time as the interference structure.

Due to the theoretical derivation with imag-time theory [35,36], we know that, circularly polarized laser pulse does not cause a non-zero initial transverse momentum ${\textstyle p_{z}}$, but rather a non-zero initial longitudinal momentum ${\textstyle p_{\perp }}$. Therefore, the nonadiabatic momentum shift ${\textstyle \Delta p}$ will only have the longitudinal momentum component ${\textstyle p_{\perp }}$. However, with time evolves, the momentum shift ${\textstyle \Delta p}$ is composed of lateral momentum ${\textstyle p_{z}}$ and longitudinal momentum ${\textstyle p_{\perp }}$ in Figure 2(a)-(c). Until the last moment, only ${\textstyle p_{\perp }}$ is preserved in Figure 2(d). Which indicates that, the nonadiabatic term ${\textstyle \Delta p}$ is time-resolved, ${\textstyle p_{z}}$ is disappeared through interference during the evolution.

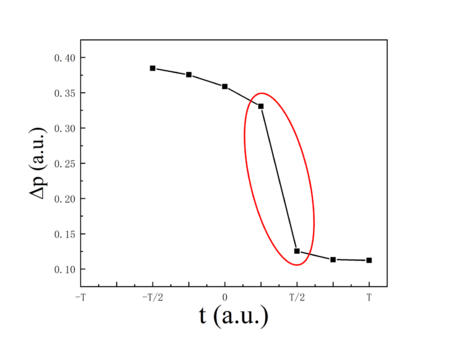
To understand the law of ${\textstyle \Delta p}$ varing over time more deeply, we record the magnitude of ${\textstyle \Delta p}$ at different times. In Figure 3, seven black squares guided by a solid line from left to right represent the momentum shift ${\textstyle \Delta p}$ corresponding to seven moments from ${\textstyle t=-T}$ to ${\textstyle t=T}$. Unsurprisingly, the magnitude of ${\textstyle \Delta p}$ changs with time as expected. However, something unusual has happened here. We can see that, in Figure 3, ${\textstyle \Delta p}$ changes smoothly overall except the area indicated with a red circle, where ${\textstyle \Delta p}$ sharply decreases from ${\textstyle t={\frac {1}{4}}T}$ to ${\textstyle t={\frac {1}{2}}T}$. This notable phenomenon interests us and the evolution of the interference structure in Figure 2 prompts us.

Correspondingly, the PMDs at these two moments are presented in Figure 2(b) and (c). In Figure 2(b), we can see many crescent interference structures, which is corresponding to subcycle interference (SCI) with electron wave packets (EWPs) from different half cycle within one optical cycle. Differently, for the situation ${\textstyle t={\frac {1}{2}}T}$ (Figure 2(c)), many ATI (above-threshold ionization)-like structures emerge, this indicates that intercycle interference (ICI) with EWPs released from different laser optical cycles starts to dominate [37]. So far we can say that, the time-resolved changing of the interference type from only SCI to SCI+ICI for a 2-cycle CP laser pulse results in the drastic decrease of ${\textstyle \Delta p}$ in Figure 3.

Figure 3. (Color online) Momentum shift ${\textstyle \Delta P}$ with respect to the moment as mentioned in Figure 2. The red circle indicates a rapidly changing of ${\textstyle \Delta p}$ corresponding to the interference type changes from SCI to SCI+ICI

To further validate our conclusion, we will use more complex few-cycle OTC laser pulses as shown in Figure 1(b) with different durations to repeat the simulations discussed above. When interacting with hydrogen atom, the few-cycle OTC laser pulse will give more details of the interference type in the PMD.

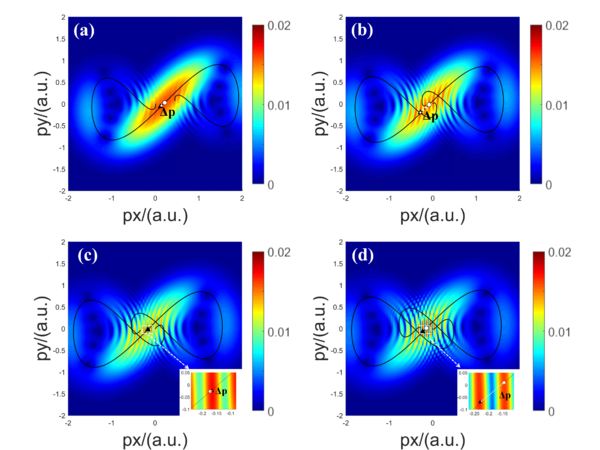
In Figure 4, final PMDs of hydrogen atom exposed to OTC laser pulses are presented, when the pulse durations are (a) ${\textstyle \tau =1.8T}$, (b) ${\textstyle \tau =2.1T}$, (c) ${\textstyle \tau =2.3T}$, and (d) ${\textstyle \tau =2.6T}$, respectively. The photon energy ${\textstyle \omega =0.057a.u.}$, the intensity ${\textstyle I=3.5\times {10}^{14}W/{\mbox{cm}}^{2}}$ and the keldysh parameter ${\textstyle \gamma \approx 1}$, hence, nonadiabatic tunneling ionization occurs. Meanwhile, the momentum shift ${\textstyle \Delta p}$ is marked as the same way as in Figure 2.

Figure 4. (Color online) Final PMD of hydrogen atom exposed to OTC laser pulse when the pulse duration is: (a) ${\textstyle \tau =1.8}$T. (b) ${\textstyle \tau =2.1}$T. (c) ${\textstyle \tau =2.3}$T. (d) ${\textstyle \tau =2.6}$T with ${\textstyle T={\frac {2\pi }{\omega }}}$, ${\textstyle \omega =0.057a.u.}$ and the intensity ${\textstyle I=3.5\times {10}^{14}{\mbox{ W/cm}}^{2}}$. The white dots mark the most probable momentum corresponding to the peak electric field and black triangles mark the most probable momentum corresponding to the maximum ionization rate. The white dotted lines indicate the magnitude of the momentum shift ${\textstyle \Delta P}$. The small image in the lower right corner of (c) and (d) shows an enlargement of the marked area with a white dashed box

Obviously, the interference fringes depend strongly on the duration of an OTC laser pulse. When the duration is short enough, the momentum spectrum only involves simple crescent structures as shown in Figure 4(a) and (b), telling us that subcycle interference is in effect. As the number of cycles increases, the structures of the PMDs become more and more complex. In Figure 4(c), we can slightly find the ATI-like cyclic structures upon the crescent structures. While in Figure 4(d), ATI-like cyclic structures are already very obvious. This evolution can be attributed to the gradual emerging of intercycle interference. At the same time, it can be observed that, the momentum shift ${\textstyle \Delta p}$ also evolves with the duration.

In order to unfold the trend of ${\textstyle \Delta p}$ more accurately, we present the momentum shift ${\textstyle \Delta p}$ with respect to the laser pulse duration in Figure 5. The momentum shift depends sensitively on the pulse duration. We can find that, the trends are the same when the duration varies from ${\textstyle \tau =1.7}$T to ${\textstyle \tau =2.1}$T and from ${\textstyle \tau =2.3}$T to ${\textstyle \tau =2.7}$T. However, an obvious difference appears between ${\textstyle \tau =2.1}$T and ${\textstyle \tau =2.3}$T (red circle), where ${\textstyle \Delta p}$ decreases sharply as had happened in Figure 3. What is more important, when the duration ranges from ${\textstyle \tau =2.1}$T to ${\textstyle \tau =2.3}$T, the interference type ICI is emerging significantly as shown in Figure 4. This correspondence further illustrates that the interference type is influencing the momentum shift synchronously.

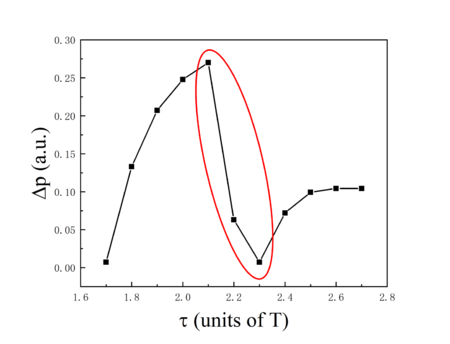
Figure 5. (Color line) Momentum shift ${\textstyle \Delta P}$ with respect to the laser pulse duration ${\textstyle \tau }$, as mentioned in Figure 4 with units of ${\textstyle T={\frac {2\pi }{\omega }}}$, ${\textstyle \omega =0.057a.u.}$. The red circle indicates a rapidly changing of ${\textstyle \Delta P}$ corresponding to the emerging of ICI

4. Conclusion

In conclusion, the time-resolved nonadiabatic tunnelling ionization PMDs of a hydrogen atom exposed to strong laser fields are studied with the strong-field approximation. Our simulations show that the nonadiabatic momentum shift ${\textstyle \Delta p}$ evolves with time, meanwhile, it will be influenced by the interference type. When the electric wave of a laser pulse oscillates over time periodically, the interference type ICI gradually becomes important. This makes ${\textstyle \Delta p}$ drastic change from the situation that only SCI dominates. Momentum shift is an important nonadiabatic phenomenon, to look into it in time domain provide us a new perspective, more interesting details are presented.

Acknowledgments

This work gratefully acknowledges the financial support of China Postdoctoral Fund (No. 2020M671352) and the National Natural Science Foundation of China (No. 1601190097).

References