m (Arias moved page Draft Arias 206842899 to Arias 2023a) |
|||
| Line 1: | Line 1: | ||
| − | == | + | ==Parametrización del álabe de una turbina Francis 99 usando polinomios de Bernstein== |
| − | ''' | + | '''Heriberto Arias-Rojasheriberto.arias@umich.mx<sup>a,b</sup>, Francisco J. Dominguez-Mota<sup>a,b</sup>, Juan I. López-Pérez<sup>b</sup>, Miguel A. Rodríguez-Velázquez<sup>b</sup>''' |
| − | ==2 | + | ==2 Introducción== |
| − | + | En la teoría de variable compleja existen técnicas que nos permiten diseñar secciones de álabes con formas relativamente complicadas empleando mapeos conformes <span id='citeF-1'></span>[[#cite-1|[1]]], pero estos tienen un costo computacional elevado por lo que en la práctica es necesario recurrir a metodologías mas simples como la parametrización empleando polinomios. Los métodos de parametrización de álabes pueden clasificarse en dos principales grupos: aproximación por secciones y parches sobre superficies. Para ambas metodologías, la clave de su implementación eficiente consiste en reducir el número de parametros para representar geometrías complejas con el menor costo computacional, lo cual ha llevado al desarrollo y uso de un gran número de técnicas en busca de la parametrización más optima <span id='citeF-1'></span><span id='citeF-2'></span><span id='citeF-3'></span><span id='citeF-4'></span><span id='citeF-5'></span>[[#cite-1|[1,2,3,4,5]]]. Por su parte, los álabes de turbinas Francis son formas complejas que difícilmente pueden ser reconstruidas geométricamente a partir de una sola función. Una opción versátil e intuitiva para realizar el ajuste numérico es la implementación de los Polinomios de Bernstein <span id='citeF-6'></span>[[#cite-6|[6]]]. Estos pueden utilizarse con la idea de realizar ajustes suficientemente precisos de curvas continuas que representan líneas de corriente en un intervalo cerrado. Originalmente fueron propuestos por Bernstein en 1912, y fueron empleados en relativamente pocas aplicaciones debido a limitaciones de las capacidades de cómputo en ese momento <span id='citeF-7'></span><span id='citeF-8'></span>[[#cite-7|[7,8]]]. Actualmente, su versatilidad ha permitido aplicarlos en áreas como el cálculo, análisis de elementos fínitos, control de sistemas dinámicos, modelado y optimización de geometrías complejas, etc. <span id='citeF-9'></span><span id='citeF-6'></span><span id='citeF-7'></span><span id='citeF-10'></span><span id='citeF-11'></span><span id='citeF-12'></span>[[#cite-9|[9,6,7,10,11,12]]]. El presente trabajo muestra una implementación de los polinomios de Bernstein para realizar un ajuste numérico de un álabe de una turbina Francis 99. A continuación, se describe el proceso de parametrización implementado y los resultados obtenidos. | |
| − | + | ==3 Descripción de la turbina== | |
| − | + | Las turbinas hidráulicas son turbomáquinas motoras que absorben energia del fluido y la convierte en energía mecánica. Estas se pueden clasificar en función de su grado de reacción (<math display="inline">\varepsilon _T </math>) como turbinas de acción y reacción <span id='citeF-13'></span>[[#cite-13|[13]]]. Las turbinas Francis son turbinas de reacción que trabajan con flujo radio-axial y son utilizadas para la producción de energia eléctrica. El caso de estudio se basa en la parametrización del álabe de una turbina hidráulica Francis 99 (Figura [[#img-1a|1a]]), cuyo rotor esta compuesto por 15 álabes principales (Figura [[#img-1b|1b]]) y 15 divisores, y tiene un diámetro de <math display="inline">0.63 \, m</math>. El rotor puede alcanzar una velocidad de <math display="inline">335.4 \, rpm</math> y una eficiencia hidráulica de <math display="inline">92.61 % </math>. | |
| − | + | <div id='img-1a'></div> | |
| + | <div id='img-1b'></div> | ||
| + | <div id='img-1'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[Image:Arias_2023a-turb1.png|522px|Rotor.]] | ||
| + | |[[Image:Arias_2023a-turb3.png|342px|Álabe principal.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | (a) Rotor. | ||
| + | | (b) Álabe principal. | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="2" | '''Figura 1:''' Turbina Francis 99. | ||
| + | |} | ||
| − | + | ==4 Metodología de parametrización== | |
| − | + | El proceso de parametrización puede realizarse en tres etapas: extracción de datos, reconstrucción del álabe y evaluación numérica (Figura [[#img-2|2]]). | |
| − | + | <div id='img-2'></div> | |
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[Image:Arias_2023a-diagrama.png|480px|Etapas del proceso de parametrización.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" | '''Figura 2:''' Etapas del proceso de parametrización. | ||
| + | |} | ||
| − | === | + | ===4.1 Extracción de datos=== |
| − | + | El primer paso consiste en la obtención de las coordenadas <math display="inline">(x_i, y_i, z_i)</math> a partir de un escaneo del álabe real de una turbina Francis 99. El perfil se divide en <math display="inline">n</math> secciones (para este caso en particular <math display="inline">n=10</math>) las cuales definen los planos de corte en los que la sección es escaneada (Figura [[#img-3a|3a]]). Para definir cada plano se obtienen las coordenadas de <math display="inline">m</math> puntos en cada una de las caras de succión y presión (<math display="inline">m=128</math> para este caso en particular) (Figura [[#img-3b|3b]]). Los datos del escaneo usados en este trabajo fueron proporcionados por ''the Norwegian Hydropower Centre'' <span id='citeF-14'></span>[[#cite-14|[14]]]. | |
| − | < | + | <div id='img-3b'></div> |
| − | + | <div id='img-3'></div> | |
| − | </ | + | <div id='img-3a'></div> |
| − | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | |
| − | </ | + | |
| − | + | ||
| − | < | + | |
| − | + | ||
| − | </ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {| class=" | + | |
|- | |- | ||
| − | | | + | |[[Image:Arias_2023a-planos2.png|378px|Datos del escaneo.Definición de los planos de corte.]] |
| − | + | |[[Image:Arias_2023a-planos.png|486px|Planos de corte.]] | |
| − | | | + | |- style="text-align: center; font-size: 75%;" |
| − | | style="text-align: center;" | | + | | (b) Datos del escaneo. |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="2" | '''Figura a:''' Planos de corte. | ||
|} | |} | ||
| − | |||
| − | |||
| − | + | ===4.2 Reconstrucción de la geometría del álabe=== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | En la etapa de reconstrucción se realiza el ajuste de las caras de presión y succión de la sección transversal del álabe para cada uno de los planos previamente definidos. Para esto se realiza un proceso de interpolación empleando un polinomio <math display="inline">P(t)</math> definido por 8 curvas de Bernstein <math display="inline">P^{(k)}(t)</math> de de cuarto orden ([[#eq-1|1]]). | |
<span id="eq-1"></span> | <span id="eq-1"></span> | ||
| Line 72: | Line 64: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>P^{(k)}(t) = \sum _{i=0}^{n=4} C_i^{(k)}B_i^4 (t), \quad , k=1,...8 </math> |
| − | + | ||
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (1) | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
|} | |} | ||
| − | </ | + | donde <math display="inline"> t </math> representa la longitud de arco de cada una de las 8 piezas de la sección de la cara correspondiente (presión o succión) <math display="inline"> 0\leq t \leq 1 </math>, <math display="inline">C_i^{(k)}</math> son 5 puntos de control que definen la forma del ajuste en cada curva, y <math display="inline">k</math> representa la curva correspondiente a cada uno de las piezas de la parametrización (figura [[#img-5|5]]). Como sabemos, los polinomios <math display="inline">B_i^4 (t)</math> pueden escribirse como |
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | |
| − | \ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | + | ||
| − | + | ||
<span id="eq-2"></span> | <span id="eq-2"></span> | ||
| − | |||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 99: | Line 77: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>B_i^n (t)= \left(\begin{array}{lclc}n \\ i \end{array}\right)t^{i} \,(1-t)^{n- i} </math> |
| + | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (2) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | donde, | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | <span id="eq-3"></span> | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 123: | Line 90: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>\left(\begin{array}{lclc}n \\ i \end{array}\right)= \dfrac{n!}{(n-i)! \, i!}. </math> |
| − | + | ||
| − | + | ||
|} | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
|} | |} | ||
| − | + | <div id='img-4'></div> | |
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[Image:Arias_2023a-Bernstein4.png|600px|Polinomio de Bernstein de cuarto orden.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" | '''Figura 4:''' Polinomio de Bernstein de cuarto orden. | ||
| + | |} | ||
| − | < | + | Algunas de las propiedades más importantes de los polinomios de Bernstein son la simetría, la positividad y la partición de la unidad <span id='citeF-15'></span>[[#cite-15|[15]]], entre otras, que los convierten en herramientas útiles para el diseño asistido por computadora. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | de | + | Proponiendo un problema de mínimos cuadrados a través de la evaluación de <math display="inline">P(t)</math> simultáneamente para todas las coordenadas considerando restricciones para continuidad para los diferentes <math display="inline">P^{(k)}</math>, se determinan los puntos de control <math display="inline">C_{i}^{(k)};k=1,...,8;i=0,...,4</math>. Cada cara es definida usando <math display="inline">4</math> polinomios (Figura [[#img-5|5]]) generando así <math display="inline">20</math> puntos de control. La condición de continuidad viene dada por |
| − | |||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 174: | Line 112: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>P^{(k)}(\tau _k)=P^{(k+1)}(\tau _k),</math> |
|} | |} | ||
| − | |||
|} | |} | ||
| − | + | donde los valores <math display="inline">\tau _k</math> se eligen de tal manera que el error cuadrático medio entre <math display="inline">P(t)</math> y los puntos escaneados sea un mínimo. Una vez definidos los coeficientes se puede generar la sección transversal del álabe usando <math display="inline">N</math> puntos. Es importante mencionar que la precisión del ajuste está directamente relacionada con el valor de <math display="inline">N</math>; a mayor número de puntos, menor error, lo cual se puede observar a simple vista en la Figura ([[#img-6|6]]) en donde se muestra los resultados del ajuste para <math display="inline">N=10</math> y <math display="inline">N=100</math> (La línea punteada representa el ajuste y la línea continua la geometría real). | |
| − | + | ||
| − | </math> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | <div id='img-5'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[Image:Arias_2023a-seccion_polinomios.png|600px|Puntos de control.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" | '''Figura 5:''' Puntos de control. | ||
|} | |} | ||
| − | + | <div id='img-6a'></div> | |
| − | + | <div id='img-6b'></div> | |
| − | + | <div id='img-6'></div> | |
| − | {| | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" |
| − | + | ||
|- | |- | ||
| − | | | + | |[[Image:Arias_2023a-N10.png|600px|N=10.]] |
| − | + | |[[Image:Arias_2023a-N100.png|600px|N=100.]] | |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | + | | (a) N=10. | |
| − | + | | (b) N=100. | |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | + | | colspan="2" | '''Figura 6:''' Ajuste numérico usando N puntos. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | | | + | |
| − | + | ||
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | + | ||
| − | | | + | |
| − | + | ||
| − | | | + | |
| − | | | + | |
| − | + | ||
| − | + | ||
| − | | | + | |
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | + | Después de generar una sección el proceso se repite para generar cada uno de los planos (Figura [[#img-3|3]]) y posteriormente construir la superficie del álabe (Figura [[#img-7|7]]). | |
| − | + | <div id='img-7'></div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <div id='img- | + | |
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Arias_2023a-superficie.png|540px|Superficie del álabe.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura | + | | colspan="1" | '''Figura 7:''' Superficie del álabe. |
|} | |} | ||
| − | + | ===4.3 Evaluación del error=== | |
| − | + | La etapa final del proceso de parametrización es la evaluación del error para determinar la precisión del ajuste sobre toda la superficie del álabe y los datos escaneados. Empleamos para el efecto el error medio cuadrático dado por ([[#eq-4|4]]): | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | <span id="eq-4"></span> |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | ||
| − | + | ||
| − | {| class=" | + | |
|- | |- | ||
| − | | | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
| − | | | + | |- |
| − | | | + | | style="text-align: center;" | <math>SME = \sqrt{\frac{\sum _{i=1}^{n}D_{i}^{2}}{n}} </math> |
| − | | | + | |} |
| − | | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) |
| − | | | + | |
| − | + | ||
| − | | | + | |
|} | |} | ||
| − | + | donde <math display="inline">D_{i}</math>, es la distancia euclidiana entre el punto <math display="inline">(x_i</math>, <math display="inline">y_i</math>, <math display="inline">z_i)</math> y la tangente a la superficie definida por el correspondiente vector unitario normal a la superficie generada del álabe <span id='citeF-3'></span>[[#cite-3|[3]]]. | |
| − | ===3. | + | Al evaluar la ecuación ([[#eq-4|4]]) tomando <math display="inline">N=128</math>, el error medio cuadrático obtenido entre los datos del escaneo y el ajuste es de <math display="inline">1.5496 \times 10^{-3} %</math> en la cara de presión y <math display="inline">9.685 \times 10^{-5} %</math> para la cara de succión <span id='citeF-6'></span>[[#cite-6|[6]]], ambos valores dentro de la tolerancia sugerida por expertos en la materia <span id='citeF-9'></span>[[#cite-9|[9]]]. |
| − | + | ==5 Conclusiones== | |
| − | + | El presente trabajo se enfocó en mostrar la implementación de la metodología de aproximación por secciones usando polinomios de Bernstein para la parametrización de formas geometricas complejas, y en particular de álabes de turbinas. Los polinomios de Bernstein muestran ser una opción viable y adecuada, relativamente fácil de implementar. Los resultados obtenidos son muy satisfactorios, y la versatilidad con la que los polinomios se adaptan a la geometría compleja sugiere que esta metodología puede ser implementada para parametrizar álabes de muchos tipo de turbina, hélices o cualquier otro tipo de geometría compleja. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ===BIBLIOGRAFÍA=== | |
| − | = | + | <div id="cite-1"></div> |
| + | '''[[#citeF-1|[1]]]''' Abbott, Ira H and Von Doenhoff, Albert E. (2012) "Theory of wing sections: including a summary of airfoil data". Courier Corporation 53–63, 1 Edition | ||
| − | + | <div id="cite-2"></div> | |
| + | '''[[#citeF-2|[2]]]''' Cerriteño, A and Delgado, G and Galván, S and Dominguez, F and Ramírez, R. (2021) "Reconstruction of the Francis 99 main runner blade using a hybrid parametric approach.", Volume 774. IOP Publishing. IOP Conference Series: Earth and Environmental Science 1 012074 | ||
| − | < | + | <div id="cite-3"></div> |
| − | + | '''[[#citeF-3|[3]]]''' Delgado, Giovanni and Galván, Sergio and Dominguez-Mota, Francisco and García, JC and Valencia, Esteban. (2020) "Reconstruction methodology of a Francis runner blade using numerical tools", Volume 34. Springer. Journal of Mechanical Science and Technology 1237–1247 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <div id="cite-4"></div> | |
| − | + | '''[[#citeF-4|[4]]]''' Farin, Gerald. (2014) "Curves and surfaces for computer-aided geometric design: a practical guide". Elsevier 41–62, 3 Edition | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <div id="cite-5"></div> | |
| + | '''[[#citeF-5|[5]]]''' Ferrando, Lluis and Kueny, Jean-Louis and Avellan, Francois and Pedretti, Camille and Tomas, Laurent. (2004) "Surface parameterization of a Francis runner turbine for optimum design". 22nd IAHR Symposium on hydraulic machinery and systems | ||
| − | = | + | <div id="cite-6"></div> |
| + | '''[[#citeF-6|[6]]]''' Pérez Rubio, Luis David and Galván González, Sergio Ricardo and Domínguez Mota, Francisco Javier and Cerriteño Sánchez, Angel and Tamayo Soto, Miguel Angel and Delgado Sánchez, Giovanni. (2021) "Reconstruction of a Steam Turbine Blade Using Piecewise Bernstein Polynomials and Transfinite Interpolation", Volume 85017. American Society of Mechanical Engineers. Turbo Expo: Power for Land, Sea, and Air V008T22A005 | ||
| − | + | <div id="cite-7"></div> | |
| + | '''[[#citeF-7|[7]]]''' Farouki, Rida T. (2012) "The Bernstein polynomial basis: A centennial retrospective", Volume 29. Elsevier. Computer Aided Geometric Design 6 379–419 | ||
| − | + | <div id="cite-8"></div> | |
| + | '''[[#citeF-8|[8]]]''' Steffens, Karl-Georg. (2006) "The history of approximation theory: from Euler to Bernstein". Springer | ||
| − | < | + | <div id="cite-9"></div> |
| + | '''[[#citeF-9|[9]]]''' Dubé, Jean-Francois and Guibault, Francois and Vallet, Marie-Gabrielle and Trépanier, Jean-Yves. (2006) "Turbine blade reconstruction and optimization using subdivision surfaces". 44th AIAA Aerospace Sciences Meeting and Exhibit 1327 | ||
| − | < | + | <div id="cite-10"></div> |
| − | + | '''[[#citeF-10|[10]]]''' Yousefi, Sohrab Ali and Behroozifar, Mahmoud. (2010) "Operational matrices of Bernstein polynomials and their applications", Volume 41. Taylor & Francis. International Journal of Systems Science 6 709–716 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <div id="cite-11"></div> | |
| − | + | '''[[#citeF-11|[11]]]''' Joy, Kenneth I. (2000) "Bernstein polynomials", Volume 13. On-Line Geometric Modeling Notes 5 | |
| − | </ | + | <div id="cite-12"></div> |
| + | '''[[#citeF-12|[12]]]''' Arias-Rojas, Heriberto and Rodríguez-Velázquez, Miguel A and Cerriteño-Sánchez, Ángel and Domínguez-Mota, Francisco J and Galván-González, Sergio R. (2023) "A FEM Structural Analysis of a Francis Turbine Blade Parametrized Using Piecewise Bernstein Polynomials", Volume 11. MDPI. Computation 7 123 | ||
| − | <div id | + | <div id="cite-13"></div> |
| − | + | '''[[#citeF-13|[13]]]''' Mataix, Claudio. (1986) "Mecánica de fluidos y máquinas hidráulicas" 460–517, 2 Edition | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | = | + | <div id="cite-14"></div> |
| + | '''[[#citeF-14|[14]]]''' . () "''Norwegian Hydropower Centre'', 2016" Avialable online: https://www.ntnu.edu/nvks/norwegian-hydropower-center | ||
| − | <div id="cite- | + | <div id="cite-15"></div> |
| − | '''[[#citeF- | + | '''[[#citeF-15|[15]]]''' Kelisky, Richard and Rivlin, Theodore. (1967) "Iterates of Bernstein polynomials", Volume 21. Mathematical Sciences Publishers. Pacific Journal of Mathematics 3 511–520 |
| − | + | ||
| − | + | ||
| − | + | ||
Revision as of 20:29, 23 November 2023
Parametrización del álabe de una turbina Francis 99 usando polinomios de Bernstein
Heriberto Arias-Rojasheriberto.arias@umich.mxa,b, Francisco J. Dominguez-Motaa,b, Juan I. López-Pérezb, Miguel A. Rodríguez-Velázquezb
2 Introducción
En la teoría de variable compleja existen técnicas que nos permiten diseñar secciones de álabes con formas relativamente complicadas empleando mapeos conformes [1], pero estos tienen un costo computacional elevado por lo que en la práctica es necesario recurrir a metodologías mas simples como la parametrización empleando polinomios. Los métodos de parametrización de álabes pueden clasificarse en dos principales grupos: aproximación por secciones y parches sobre superficies. Para ambas metodologías, la clave de su implementación eficiente consiste en reducir el número de parametros para representar geometrías complejas con el menor costo computacional, lo cual ha llevado al desarrollo y uso de un gran número de técnicas en busca de la parametrización más optima [1,2,3,4,5]. Por su parte, los álabes de turbinas Francis son formas complejas que difícilmente pueden ser reconstruidas geométricamente a partir de una sola función. Una opción versátil e intuitiva para realizar el ajuste numérico es la implementación de los Polinomios de Bernstein [6]. Estos pueden utilizarse con la idea de realizar ajustes suficientemente precisos de curvas continuas que representan líneas de corriente en un intervalo cerrado. Originalmente fueron propuestos por Bernstein en 1912, y fueron empleados en relativamente pocas aplicaciones debido a limitaciones de las capacidades de cómputo en ese momento [7,8]. Actualmente, su versatilidad ha permitido aplicarlos en áreas como el cálculo, análisis de elementos fínitos, control de sistemas dinámicos, modelado y optimización de geometrías complejas, etc. [9,6,7,10,11,12]. El presente trabajo muestra una implementación de los polinomios de Bernstein para realizar un ajuste numérico de un álabe de una turbina Francis 99. A continuación, se describe el proceso de parametrización implementado y los resultados obtenidos.
3 Descripción de la turbina
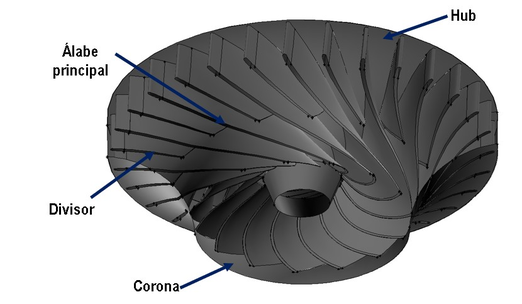
Las turbinas hidráulicas son turbomáquinas motoras que absorben energia del fluido y la convierte en energía mecánica. Estas se pueden clasificar en función de su grado de reacción () como turbinas de acción y reacción [13]. Las turbinas Francis son turbinas de reacción que trabajan con flujo radio-axial y son utilizadas para la producción de energia eléctrica. El caso de estudio se basa en la parametrización del álabe de una turbina hidráulica Francis 99 (Figura 1a), cuyo rotor esta compuesto por 15 álabes principales (Figura 1b) y 15 divisores, y tiene un diámetro de . El rotor puede alcanzar una velocidad de y una eficiencia hidráulica de .
|
|
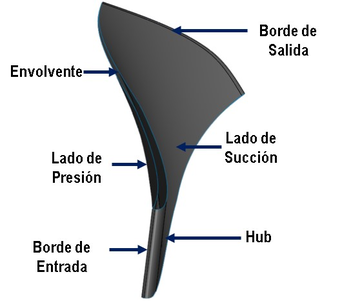
| (a) Rotor. | (b) Álabe principal. |
| Figura 1: Turbina Francis 99. | |
4 Metodología de parametrización
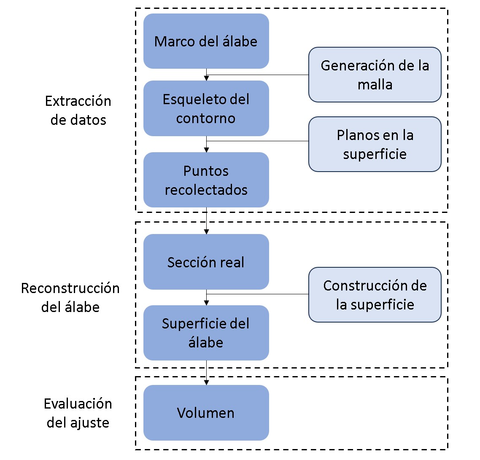
El proceso de parametrización puede realizarse en tres etapas: extracción de datos, reconstrucción del álabe y evaluación numérica (Figura 2).
|
| Figura 2: Etapas del proceso de parametrización. |
4.1 Extracción de datos
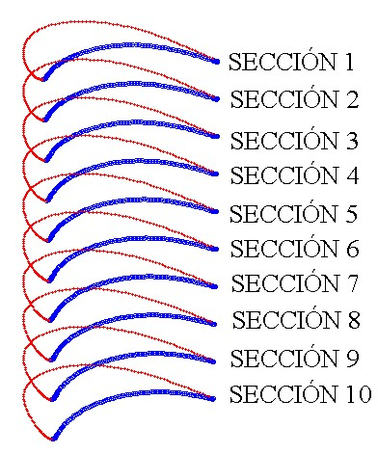
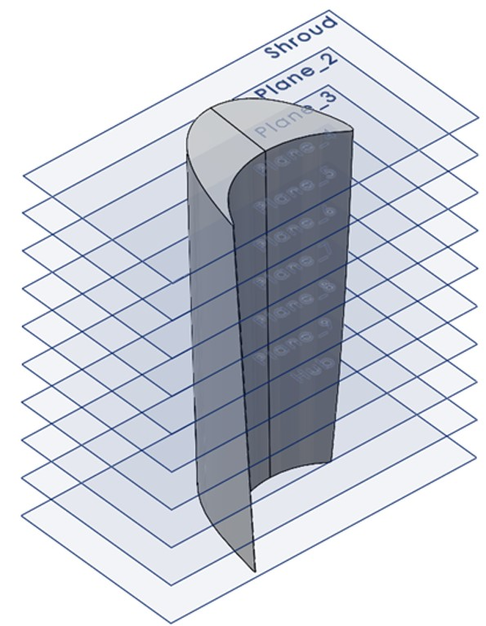
El primer paso consiste en la obtención de las coordenadas a partir de un escaneo del álabe real de una turbina Francis 99. El perfil se divide en secciones (para este caso en particular ) las cuales definen los planos de corte en los que la sección es escaneada (Figura 3a). Para definir cada plano se obtienen las coordenadas de puntos en cada una de las caras de succión y presión ( para este caso en particular) (Figura 3b). Los datos del escaneo usados en este trabajo fueron proporcionados por the Norwegian Hydropower Centre [14].
|
|
| (b) Datos del escaneo. | |
| Figura a: Planos de corte. | |
4.2 Reconstrucción de la geometría del álabe
En la etapa de reconstrucción se realiza el ajuste de las caras de presión y succión de la sección transversal del álabe para cada uno de los planos previamente definidos. Para esto se realiza un proceso de interpolación empleando un polinomio definido por 8 curvas de Bernstein de de cuarto orden (1).
|
|
(1) |
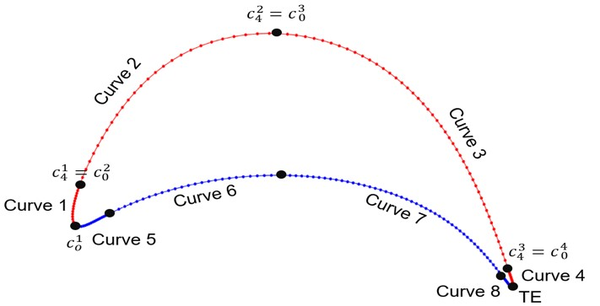
donde representa la longitud de arco de cada una de las 8 piezas de la sección de la cara correspondiente (presión o succión) , son 5 puntos de control que definen la forma del ajuste en cada curva, y representa la curva correspondiente a cada uno de las piezas de la parametrización (figura 5). Como sabemos, los polinomios pueden escribirse como
|
|
(2) |
donde,
|
|
(3) |
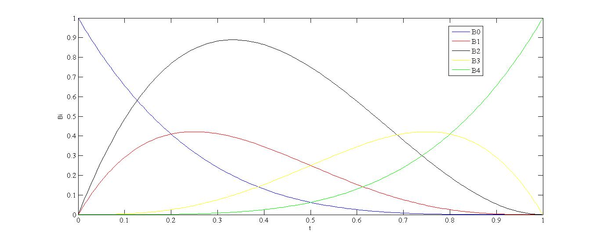
|
| Figura 4: Polinomio de Bernstein de cuarto orden. |
Algunas de las propiedades más importantes de los polinomios de Bernstein son la simetría, la positividad y la partición de la unidad [15], entre otras, que los convierten en herramientas útiles para el diseño asistido por computadora.
Proponiendo un problema de mínimos cuadrados a través de la evaluación de simultáneamente para todas las coordenadas considerando restricciones para continuidad para los diferentes , se determinan los puntos de control . Cada cara es definida usando polinomios (Figura 5) generando así puntos de control. La condición de continuidad viene dada por
|
|
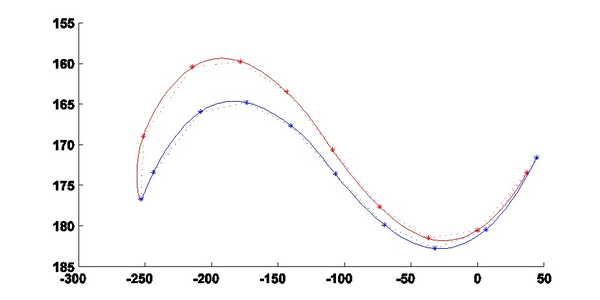
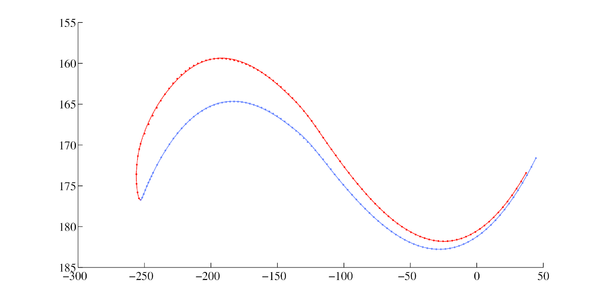
donde los valores se eligen de tal manera que el error cuadrático medio entre y los puntos escaneados sea un mínimo. Una vez definidos los coeficientes se puede generar la sección transversal del álabe usando puntos. Es importante mencionar que la precisión del ajuste está directamente relacionada con el valor de ; a mayor número de puntos, menor error, lo cual se puede observar a simple vista en la Figura (6) en donde se muestra los resultados del ajuste para y (La línea punteada representa el ajuste y la línea continua la geometría real).
|
| Figura 5: Puntos de control. |
|
|
| (a) N=10. | (b) N=100. |
| Figura 6: Ajuste numérico usando N puntos. | |
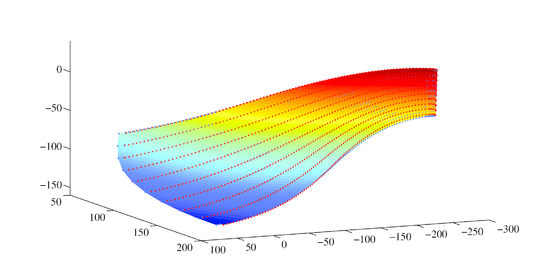
Después de generar una sección el proceso se repite para generar cada uno de los planos (Figura 3) y posteriormente construir la superficie del álabe (Figura 7).
|
| Figura 7: Superficie del álabe. |
4.3 Evaluación del error
La etapa final del proceso de parametrización es la evaluación del error para determinar la precisión del ajuste sobre toda la superficie del álabe y los datos escaneados. Empleamos para el efecto el error medio cuadrático dado por (4):
|
|
(4) |
donde , es la distancia euclidiana entre el punto , , y la tangente a la superficie definida por el correspondiente vector unitario normal a la superficie generada del álabe [3].
Al evaluar la ecuación (4) tomando , el error medio cuadrático obtenido entre los datos del escaneo y el ajuste es de en la cara de presión y para la cara de succión [6], ambos valores dentro de la tolerancia sugerida por expertos en la materia [9].
5 Conclusiones
El presente trabajo se enfocó en mostrar la implementación de la metodología de aproximación por secciones usando polinomios de Bernstein para la parametrización de formas geometricas complejas, y en particular de álabes de turbinas. Los polinomios de Bernstein muestran ser una opción viable y adecuada, relativamente fácil de implementar. Los resultados obtenidos son muy satisfactorios, y la versatilidad con la que los polinomios se adaptan a la geometría compleja sugiere que esta metodología puede ser implementada para parametrizar álabes de muchos tipo de turbina, hélices o cualquier otro tipo de geometría compleja.
BIBLIOGRAFÍA
[1] Abbott, Ira H and Von Doenhoff, Albert E. (2012) "Theory of wing sections: including a summary of airfoil data". Courier Corporation 53–63, 1 Edition
[2] Cerriteño, A and Delgado, G and Galván, S and Dominguez, F and Ramírez, R. (2021) "Reconstruction of the Francis 99 main runner blade using a hybrid parametric approach.", Volume 774. IOP Publishing. IOP Conference Series: Earth and Environmental Science 1 012074
[3] Delgado, Giovanni and Galván, Sergio and Dominguez-Mota, Francisco and García, JC and Valencia, Esteban. (2020) "Reconstruction methodology of a Francis runner blade using numerical tools", Volume 34. Springer. Journal of Mechanical Science and Technology 1237–1247
[4] Farin, Gerald. (2014) "Curves and surfaces for computer-aided geometric design: a practical guide". Elsevier 41–62, 3 Edition
[5] Ferrando, Lluis and Kueny, Jean-Louis and Avellan, Francois and Pedretti, Camille and Tomas, Laurent. (2004) "Surface parameterization of a Francis runner turbine for optimum design". 22nd IAHR Symposium on hydraulic machinery and systems
[6] Pérez Rubio, Luis David and Galván González, Sergio Ricardo and Domínguez Mota, Francisco Javier and Cerriteño Sánchez, Angel and Tamayo Soto, Miguel Angel and Delgado Sánchez, Giovanni. (2021) "Reconstruction of a Steam Turbine Blade Using Piecewise Bernstein Polynomials and Transfinite Interpolation", Volume 85017. American Society of Mechanical Engineers. Turbo Expo: Power for Land, Sea, and Air V008T22A005
[7] Farouki, Rida T. (2012) "The Bernstein polynomial basis: A centennial retrospective", Volume 29. Elsevier. Computer Aided Geometric Design 6 379–419
[8] Steffens, Karl-Georg. (2006) "The history of approximation theory: from Euler to Bernstein". Springer
[9] Dubé, Jean-Francois and Guibault, Francois and Vallet, Marie-Gabrielle and Trépanier, Jean-Yves. (2006) "Turbine blade reconstruction and optimization using subdivision surfaces". 44th AIAA Aerospace Sciences Meeting and Exhibit 1327
[10] Yousefi, Sohrab Ali and Behroozifar, Mahmoud. (2010) "Operational matrices of Bernstein polynomials and their applications", Volume 41. Taylor & Francis. International Journal of Systems Science 6 709–716
[11] Joy, Kenneth I. (2000) "Bernstein polynomials", Volume 13. On-Line Geometric Modeling Notes 5
[12] Arias-Rojas, Heriberto and Rodríguez-Velázquez, Miguel A and Cerriteño-Sánchez, Ángel and Domínguez-Mota, Francisco J and Galván-González, Sergio R. (2023) "A FEM Structural Analysis of a Francis Turbine Blade Parametrized Using Piecewise Bernstein Polynomials", Volume 11. MDPI. Computation 7 123
[13] Mataix, Claudio. (1986) "Mecánica de fluidos y máquinas hidráulicas" 460–517, 2 Edition
[14] . () "Norwegian Hydropower Centre, 2016" Avialable online: https://www.ntnu.edu/nvks/norwegian-hydropower-center
[15] Kelisky, Richard and Rivlin, Theodore. (1967) "Iterates of Bernstein polynomials", Volume 21. Mathematical Sciences Publishers. Pacific Journal of Mathematics 3 511–520
Document information
Published on 18/09/24
Submitted on 23/11/23
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?