(→3.4. Parámetros de amortiguamiento y comparación de parámetros de rigidez) |
|||
| Line 519: | Line 519: | ||
|} | |} | ||
| − | ===3.4 | + | ===3.4 Parámetros de amortiguamiento y comparación de parámetros de rigidez=== |
En esta etapa se realiza una calibración de los parámetros involucrados en el sistema, los cuales son aplicados a nuestro modelo numérico por MED, dentro de las fuerzas del sistema, de contacto y de amortiguamiento. De esta manera los parámetros como la rigidez y amortiguamiento se establecen a través de pruebas básicas que involucran comparaciones entre gráficas histeréticas del experimento y el modelo numérico. | En esta etapa se realiza una calibración de los parámetros involucrados en el sistema, los cuales son aplicados a nuestro modelo numérico por MED, dentro de las fuerzas del sistema, de contacto y de amortiguamiento. De esta manera los parámetros como la rigidez y amortiguamiento se establecen a través de pruebas básicas que involucran comparaciones entre gráficas histeréticas del experimento y el modelo numérico. | ||
Revision as of 11:17, 21 June 2023
Resumen
El sistema de conexión viga-columna mediante una conexión postensada auto-centrante es una alternativa en la actualidad para mejorar el comportamiento sísmico en edificios de hormigón armado; al permitir que sus elementos tengan un comportamiento lineal (sin daño) ante los desplazamientos producidos por acciones sísmica. En el presente trabajo se presenta la simulación numérica del comportamiento sísmico para una conexión auto-centrante con base en el Método de Elementos Discretos (MED), con el objetivo de validar la respuesta histerética del modelo numérico con una prueba experimental de la literatura. Los resultados demuestran las distorsiones horizontales en la columna, las cuales son producto de la simulación numérica del modelo sujeto a una carga que se incrementa con el paso del tiempo con 4 coeficientes de rigidez diferentes. Se presenta la gráfica histerética como resultado de la simulación numérica del modelo, con un coeficiente de rigidez y amortiguamiento normal adecuado, sujeto a una carga cíclica que se invierte en función al tiempo. El movimiento de la conexión es controlado por las distorsiones horizontales de la columna, logrando reproducir de forma aproximada el comportamiento histérico esperado en este tipo de conexiones. Con los resultados mostrados se propone una sencilla ley de histéresis bilineal, que permita su uso simplificado para su aplicación en el modelado de edificios de hormigón armado con conexiones auto-centrantes.
Palabras clave: Método de Elementos Discretos, sistemas de auto-centrado, postensado, simulación, elementos tipo cable, grafica histerética
Abstract
At present, the beam-column connection system through a self-centering post-tensioned connection is currently an alternative to improve the seismic behavior in reinforced concrete buildings; by allowing its elements to have a linear behavior (no damage) in the face of displacements produced by seismic actions. This paper deals with the numerical modeling of the seismic behavior for a self-centering connection based on the Discrete Element Method (MED) is presented, with the aim of validating the hysterical response of the numerical model with an experimental test of the literature. The results demonstrated the horizontal distortions in the column, which are the product of the numerical simulation of the model subjected to a load that increases over time with 4 different stiffness coefficients. In addition, the hysteretic graph is presented as a result of the numerical simulation of the model, with an adequate stiffness coefficient and normal damping, subject to a cyclic load that is reversed as a function of time. The movement of the connection is controlled by the horizontal distortions of the column, achieving an approximate reproduction of the hysterical behavior expected in this type of connection. With the results shown, a simple bilinear hysteresis law is proposed, which allows its simplified use for its application in the modeling of reinforced concrete buildings with self-centering connections.
Keywords: Discrete Element Method, self-centering, post-tensioning, numerical simulation, cable elements, hysteretic graph
1. Introducción
La formulación de los elementos discretos fue introducida por Cundall [1-3] utilizando elementos esféricos para modelar materiales granulares. Desde su implementación, se ha desarrollado una gran cantidad de aplicaciones en distintas áreas, así como metodologías que permiten una gran precisión y rapidez en el procesamiento de los datos.
Las aplicaciones del MED en problemas de ingeniería que involucran comportamiento dinámico son muy variadas, estos van desde la simulación tradicional de flujo de partículas hasta la representación de estructuras sólidas interactuando [4].
Una de las mayores ventajas que ofrece el MED en el estudio de estructuras sólidas, es que permite el libre movimiento de partículas como cuerpos rígidos para simular fenómenos que con los métodos analíticos tradiciones resulta complejo su estudio. Además, es utilizado para estudiar la estabilidad de sistemas estructurales, en donde los elementos son sometidos a cargas dinámicas y monitoreados en función del tiempo.
Las estructuras auto-centrantes son sistemas especiales que al ser sometidos a desplazamientos laterales presentan muy poca distorsión residual, por lo que el sistema regresa a su posición inicial una vez terminado el ciclo de movimientos.
La pieza principal de estos sistemas auto-centrantes se encuentra en la unión entre la columna y viga, la cual debe mantenerse siempre sin daño con un comportamiento elástico.
En los últimos años, la idea del auto-centrado ha adquirido gran atención. Se ha revisado y aplicado este concepto en conexiones viga-columna [5-9], además se ha extendido a las conexiones a momentos en estructuras de acero [10-12]; muros de hormigón prefabricado [13-17] así como en columnas de puentes [18-23].
La carga dinámica más critica que se analiza para un sistema auto-centrante es la sísmica, debido a las fuerzas dinámicas que se presentan en las uniones de los elementos. Para reducir los daños ocasionados por sismos y disipar la energía durante el evento, se desarrollan estos sistemas que devuelven la estructura a una posición vertical (auto-centrado), después de haber ocurrido el fenómeno [24].
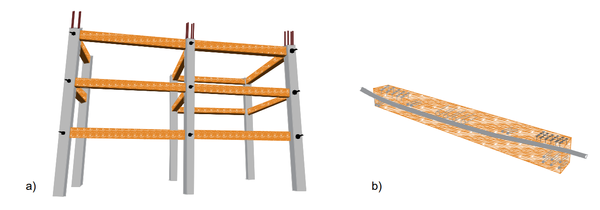
Después de los eventos sísmicos ocurridos en la región de Christchurch en 2010, se reconstruyeron una serie de edificios basados en sistemas estructurales postensado en combinación de materiales mixtos (madera, hormigón y acero), con el objetivo de reducir los efectos de las cargas laterales por sismo [25]. En la Figura 1 se ilustra uno de los edificios que se reconstruyeron en la zona con columnas de hormigón y vigas postensadas de madera. Este ejemplo nos da una introducción a las estructuras reales que utilizan sistemas continuos postensados por viga-columna que resisten cargas laterales.
El objetivo de este artículo es demostrar una formulación con elementos discretos que permita predecir el comportamiento que adquieren los sistemas auto-centrantes sometidos a movimientos en su base, así como la obtención de resultados sobre relaciones mecánicas de cada material. La modelación numérica es realizada con el programa de cómputo Scilab 5.5.2. [26] con la implementación del MED a un nivel macroscópico permitiendo el modelado de partículas que representen sistemas estructurales auto-centrantes.
2. Cuestiones clave de simulación con MED
La metodología para lograr la simulación de un sistema auto-centrante, mediante el Método de Elementos Discretos, consta de la implementación de las ecuaciones de movimiento considerando las condiciones y fuerzas de contacto entre partículas. La integración del tiempo se realizará por medio del método de la segunda diferencia central, partiendo de las variables de posición hasta llegar a la aceleración con expresiones recursivas, obteniendo así los parámetros de posición, velocidad y aceleración.
2.1 Ecuaciones de movimiento
El movimiento de las partículas en el espacio está dado por un sistema de ecuaciones dinámico lineal para cuerpos rígidos, como se muestra a continuación:
|
|
(1) |
donde es la masa, es la aceleración, es el coeficiente de amortiguamiento, es la velocidad, es el coeficiente de rigidez, es el desplazamiento y es la fuerza externa en el sistema. El subíndice indica el paso en el tiempo.
Para obtener las fuerzas que actúan en el sistema podemos dividir la ec. (1) en los siguientes términos:
|
|
(2) | |
|
|
(3) |
Considerando la simplificación, la fuerza resultante queda establecida de la siguiente manera:
|
|
(4) |
La fuerza externa es obtenida de las acciones externas sobre el cuerpo y de la interacción con las otras partículas:
|
|
(5) |
Las fuerzas de interacción normal y tangencial entre partículas están dadas por la siguiente ecuación:
|
|
(6) |
Las fuerzas de cuerpo consideran el peso del elemento:
|
|
(7) |
Las ecuaciones de movimiento traslacional para cada partícula quedan expresadas como:
|
|
(8) |
Y para el movimiento rotacional queda:
|
|
(9) |
donde es la aceleración angular, es la velocidad angular, son las componentes del momento resultante aplicada a la partícula y es el momento de inercia principal de la partícula.
2.2. Condiciones de contacto
La forma en que interactúan las partículas se relaciona con las magnitudes y direcciones de las fuerzas de contacto entre ellas. Al momento en que dos partículas entran en contacto, se genera un par de fuerzas en direcciones opuestas, tal como lo establece la Tercera Ley de Newton. La magnitud de la fuerza depende directamente de la penetración de una partícula sobre otra y de la rigidez de los materiales. Mientras que la dirección de la fuerza depende de la ubicación del contacto generado entre las partículas [27].
El criterio empleado para simular los efectos de interacción entre las partículas es a partir de la suposición de resortes, definidos por la rigidez de los materiales, y de coeficientes de amortiguamiento, tanto en la dirección vertical como en la dirección horizontal de las superficies. En la Figura 2 se puede observar la configuración de los resortes y amortiguadores durante el choque, generando fuerzas normales y tangenciales al entrar en contacto.
2.3. Fuerzas de contacto
En cada uno de los contactos presentes, se producen fuerzas en la dirección perpendicular a la superficie de contacto llamadas “fuerzas normales”, además de fuerzas paralelas a la superficie llamadas “fuerzas tangenciales”. Su magnitud depende del ángulo de inclinación y de la rotación de las partículas en ese paso de tiempo.
Para generar las fuerzas de contacto se emplea el criterio llamado método de castigo “penalty method” en donde la fuerza queda definida por la magnitud de la penetración de una partícula sobre otra y un valor de la rigidez establecido dependiendo de los materiales.
La Figura 3 muestra los parámetros utilizados para calcular las fuerzas normales y tangenciales en la interacción de partículas circulares y cuadrilaterales.
Las fuerzas normales quedan establecidas asumiendo una ley lineal de fuerza-desplazamiento:
|
|
(17) |
donde es la penetración normal y es la rigidez normal del material.
Las fuerzas tangenciales se calculan incrementalmente y consisten en la sumatoria de los desplazamientos horizontales para cada intervalo.
|
|
(18) | |
|
|
(19) |
donde es la penetración horizontal en el paso de tiempo y es la rigidez tangencial del material.
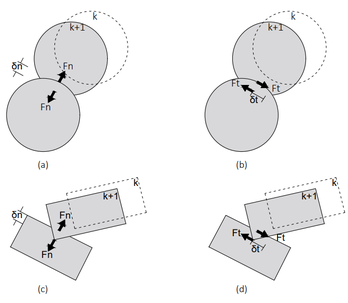
|
| Figura 3. Partículas circulares: (a) Fuerzas normales. (b) Fuerzas tangenciales. Partículas rectangulares: (c) Fuerzas normales. (d) Fuerzas tangenciales |
2.4. Fuerza de fricción
El valor de la fricción queda limitado con respecto a la fuerza normal. En el modelo se establece que sí, en cualquier momento del análisis, el valor de la fuerza tangencial excede el parámetro , en donde es el ángulo de fricción, se presenta un deslizamiento del objeto, y la fuerza tangencial asume ese valor límite:
|
|
(20) |
La Figura 4 muestra el comportamiento de la fuerza tangencial cuando se tiene un cuerpo al que se le aplica una fuerza instantánea. Se puede ver como la fuerza llega a un valor máximo y después permanece constante hasta que se reduce gradualmente a un valor de cero cuando el objeto se ha detenido.
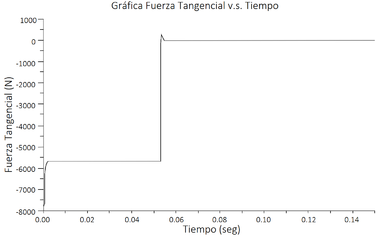
|
| Figura 4. Gráfica que muestra el comportamiento de la fuerza tangencial al deslizarse un cuerpo |
2.5. Fuerzas de amortiguamiento
Para el efecto del amortiguamiento normal y tangencial se emplea un modelo resorte-amortiguador [28] que involucra un factor de amortiguamiento viscoso , el valor de la rigidez normal y tangencial , y la velocidad normal y tangencial en ese instante.
Por lo tanto, el valor de la fuerza normal y tangencial es calculado de la siguiente manera:
|
|
(21) |
|
|
(22) |
3. Validación y aplicación de MED a sistemas auto-centrantes
La pieza más importante en un sistema estructural auto-centrante se encuentra en la conexión entra la viga y la columna, la cual al ser sometida a cargas laterales debe conservar un nivel muy bajo o nulo de distorsiones residuales en el sistema.
Varios comportamientos histeréticos de auto-centrado han sido observados en estudios experimentales. Todos esos modelos tienen el propósito de que la estructura presente el menor daño posible debido a grandes distorsiones laterales. Algunos ejemplos de modelos histeréticos para sistemas de auto-centrado se pueden observar en estudios experimentales previos, como en el caso de las referencias de Christopoulos et al. [29] y Watkins et al. [30].
El problema es que el conocimiento actual de las demandas sísmicas que tienen los sistemas estructurales auto-centrantes sigue siendo muy limitado. Particularmente es necesario una mejor comprensión y caracterización de varios tipos de demanda sísmica, así como nuevos sistemas de auto-centrado que resistan estas demandas sin tener distorsiones residuales considerables.
Dentro del sistema auto-centrante existen una gran cantidad de variables generadas por los comportamientos dinámicos de la conexión que no son tomadas en cuenta mediante los métodos numéricos tradicionales. Debido a lo anterior, es de vital importancia desarrollar una metodología que permita su estudio involucrando los parámetros dinámicos que se describirán en las subsecciones posteriores.
En consecuencia, en este trabajo se propone una metodología basada en los elementos discretos, que trata de predecir el comportamiento que tienen los sistemas auto-centrantes cuando se encuentran sometidos a diferentes condiciones de cargas dinámicas en su base.
3.1 Comportamiento de la conexión en sistemas de auto-centrado
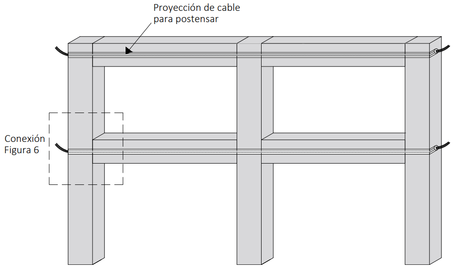
El sistema consta de marcos prefabricados de hormigón (vigas y columnas) montadas en campo mediante un cable que permite postensar los elementos estructurales, como se muestra en la Figura 5.
|
| Figura 5. Sistema estructural con columnas y vigas prefabricadas con conexiones postensadas |
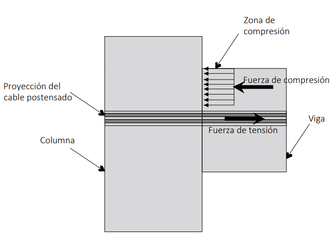
La función del cable postensado es la de darle capacidad a corte a la conexión (fricción), aumentar la capacidad a flexión (a momento) de la conexión, así como introducir una función de “auto-centrado” que disminuya las deformaciones laterales permanentes, haciendo que la estructura vuelva a su lugar de origen, tras los desplazamientos producidos por la carga dinámica. Algunas pruebas experimentales y estudios analíticos han mostrado que la conexión tiene un excelente comportamiento ante cargas laterales [6-8]. En la Figura 6 se aprecia a detalle la conexión viga-columna, unida por el cable postensado y las fuerzas que se ejercen dentro de la estructura, en donde el cable postensado genera una fuerza de tensión recibiendo como respuesta una fuerza en compresión por parte de la viga hacia la columna.
|
| Figura 6. Detalle de una conexión exterior postensada propuesta con viga de un solo lado |
La principal condición consiste en que la deformación del acero postensado siempre permanezca en un rango elástico. Al cumplir con esta condición, se asegurará un comportamiento auto-centrante sin desplazamientos residuales después de la acción dinámica. Otra condición que se busca cumplir es que el hormigón debe permanecer sin daño durante y después del movimiento.
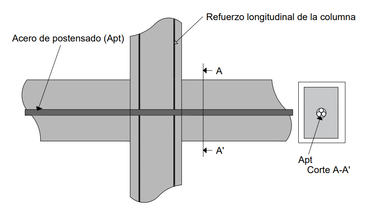
La geometría típica del sistema auto-centrante, así como su conexión postensada en el sistema viga-columna se muestra en la Figura 7. Los procedimientos para determinar la resistencia de las conexiones para este tipo de sistemas consisten en parámetros geométricos que toman en cuenta los niveles de desplazamientos laterales (distorsiones), además de algunas suposiciones para simplificar el proceso de análisis. Algunas de estas suposiciones son las siguientes:
- Las rotaciones en las uniones son obtenidas por medio de la distorsión en los entrepisos usando la geometría del sistema.
- Las vigas son de sección transversal constante.
- Todo el acero postensado se encuentra a lo largo de la viga.
- El acero postensado está desadherido a través de las columnas.
- El acero postensado está anclado en la cara exterior de la primera y última columna.
- El centroide del acero de postensado está localizado a la mitad de la sección transversal de la viga.
|
| Figura 7. Configuración típica de una conexión |
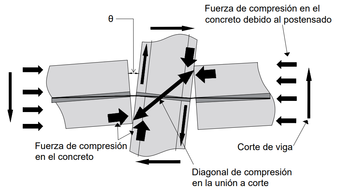
La Figura 8 muestra una visualización de las fuerzas actuantes ante una carga lateral. Al recibir las cargas dinámicas, dentro de la conexión se empiezan a desplazar las piezas del sistema generando fuerzas de acción y reacción entre sí. La columna tiende a realizar movimientos desde su base y las vigas empiezan a separarse formando un ángulo de apertura (), en donde la conexión empieza a hacer contacto entre los vértices de la viga y la columna, generando en estos puntos fuerzas por compresión debido a la tensión que ejerce el cable de postensado para devolver a la estructura a su forma original.
|
| Figura 8. Fuerzas en la conexión en el desplazamiento |
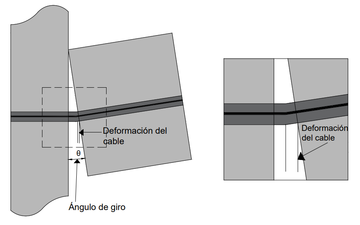
El ángulo de giro es fundamental dentro del movimiento rotacional que el sistema realiza al aplicarle una carga dinámica, ocasionando momentos al hacer contacto la conexión viga-columna, esto debido al desplazamiento del cable postensado por la distorsión de la columna, formando un ángulo en la unión, hasta llegar a un máximo en donde la viga solo hace contacto con la columna a través de sus vértices, este proceso se ilustra en la Figura 9.
|
| Figura 9. Desplazamientos |
Para la apertura del ángulo, es necesario aplicar una fuerza significativa (fuerza inicial provocada por una carga lateral) que ocasione, primeramente, una deformación del cable, esto a su vez inicia un desplazamiento en el sistema, de manera que la viga empieza a desplazarse junto con el cable, en un proceso de colisión contra el movimiento en diagonal de la columna, hasta el punto en donde el ángulo, una vez ya realizada su apertura, incrementa con más facilidad, ocasionando una mayor distorsión entre la conexión.
3.2 Fuerzas en el cable
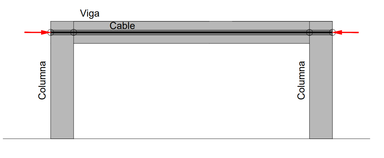
La finalidad del cable es generar una fuerza de unión entre los elementos de la conexión. Dicha fuerza proporciona una restricción al movimiento vertical debido a la fricción generada tanto en la columna como en la viga. Para el modelo numérico, la fuerza está ubicada en la cara externa de las columnas (Figura 10).
|
| Figura 10. Geometría de marco (viga-columna) con cable postensado |
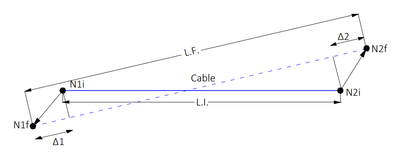
Para simular el efecto del cable se considera que éste se encuentra en una etapa elástica. Por lo tanto, se utilizan los criterios de linealidad del material como se muestra en las siguientes ecuaciones, primeramente, calculando el estiramiento del cable (Figura 11)
|
|
(23) |
donde es la deformación del cable que puede ser negativa (en tal caso se optará por una fuerza de presfuerzo igual a la aplicada inicialmente), es la longitud al final del paso del cable y es la longitud en el paso cero del cable de presfuerzo.
La deformación unitaria del módulo de Young, , se calcula:
|
|
(24) |
El esfuerzo en el cable es:
|
|
(25) |
donde el esfuerzo en el cable, es la deformación unitaria y es el módulo de elasticidad del cable postensado.
La fuerza del cable en el paso que se trate se calcula como:
|
|
(26) |
donde es la fuerza de tensión en el cable y el área transversal del cable postensado.
|
| Figura 11. Diagrama que representa el comportamiento del cable |
Los desplazamientos que se generan en el marco debido a los movimientos laterales ocasionan que el cable se extienda y se contraiga, por lo que se tendrá una fuerza de tensión variable a lo largo de la prueba. Estos desplazamientos se ilustran dentro del sistema auto-centrante en la Figura 12, en donde la columna se distorsiona, debido a las cargas dinámicas, provocando las deformaciones en el cable en cada una de las uniones de la viga y columna.

|
| Figura 12. Marco sometido a una carga dinámica |
3.3. Modelo experimental
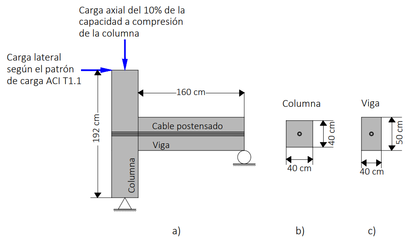
Para conocer el comportamiento que tiene una conexión auto-centrante se realiza una validación sobre el modelo experimental de Ozden y Ertas [31] que permita realizar una simulación del mismo para formar la gráfica histerética y comparar los resultados. El espécimen consiste en una viga y columna con conexión auto-centrante como se observa en la Figura 13. Esta permite el libre movimiento de la conexión. El espécimen fue modelado como juntas exteriores de un edificio de varios niveles, siendo éstos escalados a aproximadamente la mitad de la geometría original. La viga se compone de 6 tendones postensados de 13 mm de diámetros, colocados al centro de la sección transversal de la viga y 4 varillas de refuerzo de 20 mm de diámetro; mientras que la columna cuenta con 10 varillas de refuerzo del mismo diámetro. Ambas diseñadas de acuerdo con los requisitos para zonas de alta sismicidad. La columna se diseña con una conexión articulada en su base, mientras que la viga, en su extremo derecho, se diseña con un rodillo como apoyo. Las propiedades y parámetros de los materiales del modelo se indican en la Tabla 1.
|
| Figura 13. Detalle de conexión auto-centrante. (a) Esquema de conexión viga-columna y ubicación de apoyos y cargas. (b) Sección transversal de columna. (c) Sección transversal de viga |
| Acero de presfuerzo | |
|---|---|
| Cantidad de tendones | 6 |
| Diámetro (mm) | 13 |
| Fuerza efectiva de post-tensado (MPa) | 3 |
| Resistencia ultima (MPa) | 1860 |
| Elementos de hormigón prefabricado | |
| Resistencia a la compresión (MPa) | 60 |
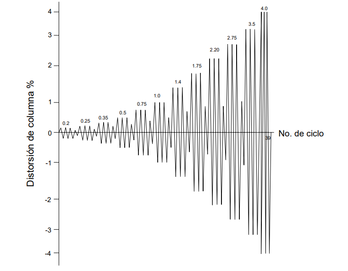
Dentro del modelo experimental de Ozden y Ertas [31] se aplica una carga lateral variable que se invierte en la parte superior de la columna según el patrón de carga de la Figura 14, siguiendo lo recomendado en ACI T1.1 [32]. De esta manera por cada nivel de desplazamiento se aplican 3 ciclos de desplazamiento completos, siendo un total de 39 ciclos de carga; teniendo así desde el nivel de desplazamiento de 0.15% hasta 4%. Se aplica simultáneamente una carga vertical constante en la columna equivalente al 10% de su capacidad a compresión con un ariete hidráulico y un marco cerrado. Para medir el desplazamiento del entrepiso, la rotación de la unión, abertura entre viga y columna, curvatura y desplazamiento de la viga se usaron transductores de desplazamiento lineal variable (LVDTs).
|
| Figura 14. Historia de carga, de acuerdo con lo recomendado por el ACI T1.1.[31] |
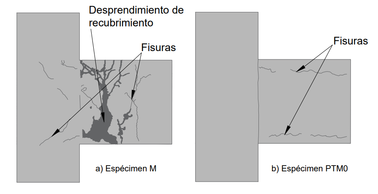
Los resultados experimentales se basaron en el comportamiento de especímenes de prueba, los cuales fueron considerados como juntas exteriores de un edificio de varios pisos. Las muestras de prueba fueron comparadas con una conexión tradicional monolítica viga-columna de hormigón armado (M), en donde visualmente se observa la diferencia de daño (Figura 15), comparada con el sistema que uso una conexión viga-columna con hormigón armado con cable postensado (PTM0) [30].
3.4 Parámetros de amortiguamiento y comparación de parámetros de rigidez
En esta etapa se realiza una calibración de los parámetros involucrados en el sistema, los cuales son aplicados a nuestro modelo numérico por MED, dentro de las fuerzas del sistema, de contacto y de amortiguamiento. De esta manera los parámetros como la rigidez y amortiguamiento se establecen a través de pruebas básicas que involucran comparaciones entre gráficas histeréticas del experimento y el modelo numérico.
Previamente a la simulación del experimento de Ozden y Ertas [31], con la misma estructura y conexión, se plantearon diferentes parámetros de rigidez normal para observar el comportamiento de la simulación. El coeficiente de amortiguamiento normal utilizado en todas las pruebas es de 0.4, mientras que la carga se incrementa con una razón de 100 kN/s, con la diferencia de que no se detiene tal incremento en la dirección horizontal.
Las curvas de fuerza contra desplazamiento resultantes se observan en la Figura 16. Las cinco curvas tienen en común que empiezan con una pendiente alta y continua, posterior a ello se observa una desestabilización de la curva correspondiente al periodo en que la cara de la viga se separa de la columna para solo mantener contacto con sus dos vértices superiores. Tras la desestabilización, la curva se estabiliza de nuevo con una pendiente inferior a la inicial.
| Figura 16. Gráfica de Fuerza vs. Desplazamiento en la parte superior de la columna. Se muestran la simulación del modelo con cuatro coeficientes de rigidez distintos. La rigidez de 15 kN fue elegida con base a la fuerza obtenida por una distorsión de 4%, en donde es similar a los 92 kN de fuerza obtenido en el experimento de Ozden y Ertas [31] |
Para llegar a la distorsión de 4% en la columna, se requieren fuerzas de 80, 90, 120, 140 y 165 kN respectivamente para las simulaciones con coeficientes de rigidez normal de 10, 15, 20, 30 y 40 kN/mm, de modo que se muestra que una conexión genera más rigidez conforme se incrementa el coeficiente de rigidez. De este modo se prevé que con una rigidez normal de 15 kN/mm se pueda obtener una gráfica histerética (con la historia de carga aplicada en el modelo) tal que sea más aproximada a la del modelo experimental propuesto por Ozden y Ertas [31], en donde el espécimen de prueba a comparar “descrito anteriormente” requirió una fuerza de 92 kN para llegar a una distorsión del 4%, comparada con los 90 kN con el coeficiente de rigidez de 15 kN/mm al llegar a la distorsión del 4% en de rigidez simuladas.
3.5. Simulación del modelo experimental
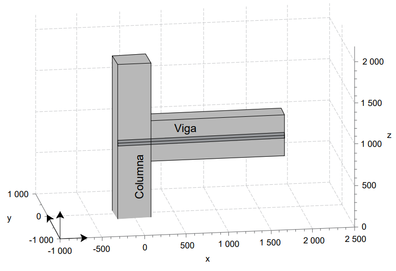
El modelo matemático tridimensional (Figura 17) fue generado a través de Scilab 5.5.2 [26]. para verificar finalmente la relación de los resultados entre el experimento y la simulación. Para la simulación del apoyo tipo articulación (localizado en la parte inferior de la columna) se realiza una restricción traslacional (X, Y y Z) y rotacional (X y Z). Para el apoyo tipo rodillo, el movimiento traslacional (Y y Z) y rotacional (X, Y y Z) es restringido. Se aplicarán cargas externas en la parte superior de la columna, de manera lateral, de acuerdo con la historia de carga presentada previamente.
|
| Figura 17. Modelo 3D para la simulación, generado con Scilab 5.5.2 [26] |
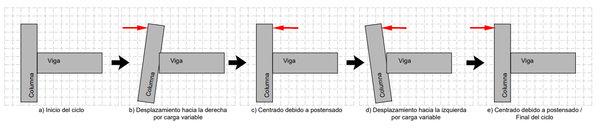
Para la simulación se pueden emplear parámetros distintos de interacción entre los vértices de las partículas, siendo la rigidez y amortiguamiento los utilizados en la simulación con un coeficiente de rigidez normal de 15 kN/mm y un coeficiente de amortiguamiento normal de 0.4. El incremento de la carga lateral es constante en el tiempo, siendo de 100 kN/s. En la Figura 18 se muestra el movimiento que sigue la columna debido a la aplicación de la historia de carga.
|
| Figura 18. Esquema de comportamiento de conexión con sistema auto-centrante, se muestra un ciclo de aplicación de la historia de carga |
4. Resultados
Tras la simulación numérica se obtiene un trazado histerético de carga vs distorsión de la columna, el cual se compara con el obtenido en el experimento (Figura 19). Inicialmente se puede observar un comportamiento de la simulación similar al típico en una conexión real, con forma de “S”, teniendo en la parte más central un comportamiento en donde los cuatro vértices de la cara unidos a la columna aún se mantienen unidos. Tras llegar a distorsiones mayores, se disminuye la pendiente en la gráfica, lo cual sucede cuando solamente 2 vértices de la cara de la viga (superior o inferior) se encuentran en contacto con la columna, generando así mayor fuerza en el cable postensado debido al incremento en su longitud.
La gráfica describe un diagrama de histéresis bilineal utilizando el modelo de Takeda [33], en donde se involucran fuerzas aplicadas a la simulación durante los 39 ciclos de carga hasta un nivel de desplazamiento del 4%, en cada uno de los ciclos existe una rigidez inicial, conforme incrementa la carga, el sistema empieza a desplazarse formando una pendiente de carga, sin embargo esta llega a un punto donde los desplazamientos aumentan exponencialmente, este punto es un factor de descarga que permite dentro de la simulación desplazamientos más altos, con menos nivel de carga, llegando a un rigidez de descarga a fuerzas negativas con desplazamientos pequeños, para que posteriormente de manera exponencial disminuya en un punto donde un factor de recarga incremente las fuerzas completando el ciclo. Según las observaciones experimentales realizadas por Otani [34], lo factores recomendados para obtener un comportamiento similar a los resultados experimentales de Ozden y Ertas [31] en la simulación con MED, para un factor de descarga es 0.1 y un factor de recarga de 0.1.
Como se observa en la Figura 19, hay una diferencia entre los resultados experimentales y analíticos, la carga lateral máxima de avance en la simulación fue de aproximadamente 80 kN, mientras que en el experimento fue de 92 kN (15% de diferencia), además, la carga lateral de retroceso para la simulación fue de -75 kN y en el experimento fue de -89 kN (18% de diferencia). Se muestran diferencias bajas y un comportamiento similar de forma general entre ambas gráficas, al comparar los resultados simulados con el modelo experimental, se obtuvo un error cuadrático medio del 11.60%, en donde el mayor error se encuentra en los cambios de pendiente de carga y descarga durante los 39 ciclos.
Dentro de simulación se utilizaron todos los parámetros que intervienen en el sistema auto-centrante ante una carga dinámica en la base. Los parámetros deben ser analizados dentro de la simulación para mejorar los resultados, como los son el coeficiente de rigidez, el coeficiente de amortiguamiento y las condiciones de contacto y fricción. La cantidad de ciclos fue simulada de manera que se representen los ciclos dentro de la gráfica por cada curva histerética.
5. Conclusiones
En este artículo, se realizó la simulación de un prototipo con conexión auto-centrante con un cable postensado en la viga por medio del Método de Elementos Discretos (MED). Este método se comprueba al comparar la historia en el tiempo de la fuerza vs distorsión de la columna, cuya comparación se trató en la sección 3.5. Las conclusiones obtenidas a través de los resultados se pueden resumir en lo siguiente:
- Los resultados de la simulación con MED muestran un buen nivel de consistencia con los resultados del experimento de la conexión auto-centrante al que se sometió el espécimen, lo que indica el potencial y la utilidad de este método para la modelación de estructuras con características auto-centrantes.
- Se encontró una relación entre el modelo experimental y la simulación en los parámetros para una ley de histerisis bilineal, con pendientes de carga y descarga dentro de cada ciclo, formando pendientes en relación con la rigidez y obteniendo resultados de distorsión y fuerzas aplicadas similares entre ambas gráficas.
- Las diferencias observadas entre las gráficas de la modelación numérica y la experimental se deben principalmente al efecto de estabilidad que las partículas muestran cuando se les aplica fuerzas externas, tales como los parámetros de rigidez y de amortiguamiento para los vértices, utilizados para calibrar el sistema. Además, otro parámetro que interviene son las magnitudes de los parámetros que conforman las ecuaciones de interacción y movimiento.
- Es de vital importancia llevar a cabo la etapa de calibración de los parámetros de rigidez y amortiguamiento para así obtener un comportamiento adecuado y que no se presenten problemas de estabilidad en el sistema. Se recomienda que esta calibración se base en los resultados de las gráficas histeréticas experimentales para mayor precisión.
Con base en los resultados, podemos resaltar que se requiere de una gran cantidad de fuerza para que la conexión alcance la máxima distorsión dentro de la simulación, por lo que este tipo de estructuras cumplen con el objetivo de resistir fuerzas dinámicas ocasionadas por un sismo, presentando el menor daño posible.
Considerando los buenos resultados obtenidos en este artículo, se alienta a futuras investigaciones en este rubro para la modelación con técnicas perfeccionadas que puedan incluirse con ayuda del Método de Elementos Discretos y diferentes herramientas informáticas.
Es esencial llevar a cabo estudios detallados de los rangos numéricos ideales de los parámetros que forman el sistema, llevando a cabo pruebas experimentales para que se comparen con los resultados numéricos. Con lo anterior se busca tener parámetros de rigidez y amortiguamiento ideales para cada tipo de prueba a realizar, y tras esto, el modelado de conexiones más avanzadas, tales como aquellas que usan elementos de acero reforzado reemplazables para amortiguamiento, elementos amortiguadores por medio de fricción, la simulación con cables pretensados dispuestos a alturas variables de la sección transversal, entre otras variantes para el empleo de estructuras auto-centrantes.
Agradecimientos
Los autores agradecen al Consejo Nacional de Ciencia y Tecnología (CONACYT) del gobierno de México por el apoyo financiero provisto, al Tecnológico de Monterrey y al Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE) por el apoyo recibido.
Referencias
[1] Cundall P.A. A computer model for simulating progressive, large-scale movements in blocky rock systems. Proc. Symp. Int. Soc. Rock Mech., 1(2):2, 1971.
[2] Cundall P.A., Strack O.D.L. A discrete numerical model for granular assemblies. Géotechnique, 29(1):47-65, 1979.
[3] Cundall P.A. Formulation of a three dimensional distinct element model - Part 1. A scheme to detect and represent contacts in a system of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr., 25(3):107-116, 1988.
[4] Kremmer M., Favier J.F. A method for representing boundaries in discrete element modelling – Part II: Kinematics. Journal for Numerical Methods in Engineering, 51:1423-1436, 2001.
[5] Priestley M.J.N., Tao J.R. Seismic response of precast prestressed concrete frames with partially debonded tendons. PCI Journal, Precast/Prestressed Concrete Institute, 38(1):58-69, 1993.
[6] Davey M.J., Abdouka K., Al-Mahaidi R. Exterior post-tensioned band beam to column connections under earthquake loading. Australian Journal of Structural Engineering, 17(1):14-27, 2016.
[7] Oudah F., El-Hacha R. Innovative self-centering concrete beam-column connection reinforced using shape memory alloy. ACI Structural Journal, 115(3):607–620, 2018.
[8] Kim H.J., Choi S., Hwang J., Jeong H., Han S., Kim K.S. Experimental study on lateral behavior of post-tensioned precast beam-column joints. Structures, 31:841-854, 2021.
[9] Husain M., Yu. H., Osman B.H., Jian J. Progressive collapse resistance of post-tensioned concrete beam-column assemblies under a middle column removal scenario. Journal of Building Engineering, 34:101945, 2021.
[10] Christopoulos C., Filiatrault A., Floz B. Seismic response of self-centering hysteretic SDOF systems. Earthquake Engineering and Structural Dynamics, 31(5):1131-1150, 2002.
[11] Torabipour A., Mahmoudreza S. Post-tensioned steel connections self-centering behavior using the finite element method. Journal of Structural Engineering and Geotechnics, 7(1):15-22, 2017.
[12] Zhu L., Zhao C. Self-centering steel frame systems for seismic-resistant structures. Advances in Civil Engineering, 2020:1-20, 2020.
[13] Perez F.J., Pessiki S., Sauce R. Seismic design of unboned post-tensioned precast walls with vertical joint connectins. PCI Journal, Precast/Prestressed Concrete Institute, 49(1):58-79, 2004.
[14] Perez F.J., Pessiki S., Sause R. Lateral load behavior of unbonded post-tensioned precast walls with vertical joint connections. PCI Journal, Precast/Prestressed Concrete Institute, 49(2):88-101, 2004.
[15] Lu X., Wu H., Zhou Y. Seismic collapse assessment of self-centering hybrid precast walls and conventional reinforced concrete walls. Struct. Concrete, 18:938–949, 2017.
[16] Wu H., Zhou Y., Liu W. Collapse fragility analysis of self-centering precast concrete walls with different post-tensioning and energy dissipation designs. Bull Earthquake Eng., 17:3593–3613, 2019.
[17] Zhou Y., Zhu X., Wu H., Djerrad A., Ke X. Seismic demands of structural and non-structural components in self-centering precast concrete wall buildings. Soil Dynamics and Earthquake Engineering, 152:107052, 2022.
[18] Kwan W.P., Billington S.L. Unbonded postensioned concrete bridge piers. I: Monotonic and cyclic analysis. Journal of Bridge Engineering (ASCE), 8(2):92-101, 2003a.
[19] Kwan W.P., Billington S.L. Unbonded postensioned concrete bridge piers. II: Seismic Analyses. Journal of Bridge Engineering (ASCE), 8(2):102-111, 2003b.
[20] Kwan W.P., Billington. S.L. Influence of hysteretic behavior on equivalent period and damping of structural systems. Journal of Bridge Engineering (ASCE), 129(5):576-585, 2003c.
[21] Lee W.K., Billington S.L. Performance-based earthquake engineering assessment of a self-centering, post-tensioned concrete bridge system. Earthquake Engineering Structural Dynamics, 40:887-902, 2010.
[22] Guerrini G., Restrepo J.I., Schoettler M.J. Self-centering, low-damage, precast post-tensioned columns for accelerated bridge construction in seismic regions. World Conference on Earthquake Engineering, 16:1921, 2017.
[23] Wang Z., Wang J., Zhao G., Zhang J. Design criterion for the self-centering capacity of precast segmental UHPC bridge columns with unbonded post-tensioning tendons. Engineering Structures, 200:109706, 2019.
[24] Chancellor N.B., Eatherton M.R., Roke D.A., Akbaş T. Self-centering seismic lateral force resisting systems: High performance structures for the city of tomorrow. Buildings, 4:520-548, 2014.
[25] Pampanin S. Towards the “Ultimate Earthquake-Proof” building: development of an integrated low-damage system. Perspectives on European Earthquake Engineering and Seismology, 2:321-358, 2015.
[26] Copyright © 1989-2005. INRIA ENPC. and Scilab is a trademark of INRIA, Scilab (Versión 5.5.2) [Software de computador], INRIA. www.scilab.org.
[27] Barbosa RE. Discrete element models for granular materials and rock masses. PhD Thesis, Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, 1990.
[28] Zhao D., Erfan G., Youssef M.A., Ghaboussi J. Three-dimensional discrete element simulation for granular materials. Engineering Computations, 23(7):749-770, 2006.
[29] Christopoulos C., Filiatrault A., Uang C., Folz B. Posttensioning energy dissipating connections for moment-resisting steel frames. Journal of Structural Engineering, 128:1118, 2002.
[30] Watkins J., Henry R., Sirtharan S. Computational modelling of self-centering precast concrete walls. Computational Methods in Structural Dynamics and Earthquake Engineering, 1:2880-2891, 2013.
[31] Ozden S., Ertas O. Behavior of unbonded, post-tensioned, precast concrete connections with different percentages of mild steel reinforcement. PCI Journal, Precast/Prestressed Concrete Institute, 52(2):34-39, 2007.
[32] ACI Innovation Task Group 1. Acceptance criteria for moment frames based on structural testing and commentary T1.1-01. American Concrete Institute, Farmington Hills, Mich., 2001.
[33] Takeda T., Sozen M., Nielsen N. Reinforced concrete response to simulated earthquakes. Journal of Structural Division, 96(12):2557-2573, 1970.
[34] Otani S., Sozen M. Behavior of multistory reinforced concrete frames during earthquakes. Structural Research Series-392, University of Illinois-Urbana Champaign, Illinois, 1972.Document information
Published on 21/06/23
Accepted on 15/06/23
Submitted on 28/08/22
Volume 39, Issue 2, 2023
DOI: 10.23967/j.rimni.2023.06.005
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?