(Tag: Visual edit) |
(Tag: Visual edit) |
||
| Line 135: | Line 135: | ||
<div id="_Ref481741711" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Ref481741711" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | ''Figura | + | ''Figura 3-1. Fuerza distribuida sobre la viga.''</div> |
La <span id='cite-_Ref481741711'></span>[[#_Ref481741711|''Figura '' '''3''' '''1''']] muestra un modelo simplificado de las fuerzas distribuidas en la mitad inferior de la probeta DCB, basado en los resultados obtenidos por otros autores. | La <span id='cite-_Ref481741711'></span>[[#_Ref481741711|''Figura '' '''3''' '''1''']] muestra un modelo simplificado de las fuerzas distribuidas en la mitad inferior de la probeta DCB, basado en los resultados obtenidos por otros autores. | ||
| Line 158: | Line 158: | ||
Las tensiones residuales provocan una rotación en cada una de las partes agrietadas de la probeta. Como se observa en la <span id='cite-_Ref481743076'></span>[[#_Ref481743076|''Figura '' '''3''' '''2''']], mientras que en el caso de los laminados anti-simétricos ambos brazos rotan en el mismo sentido, en los laminados simétricos la rotación es opuesta. En este último caso, teniendo en cuenta que la rotación en el punto de carga está impedido, la propias bisagras están aplicando un momento torsor. De hecho las bisagras aplican una carga no uniforme cuya resultante es la fuerza aplicada <math display="inline">P</math> y el momento resultante es el momento torsor. | Las tensiones residuales provocan una rotación en cada una de las partes agrietadas de la probeta. Como se observa en la <span id='cite-_Ref481743076'></span>[[#_Ref481743076|''Figura '' '''3''' '''2''']], mientras que en el caso de los laminados anti-simétricos ambos brazos rotan en el mismo sentido, en los laminados simétricos la rotación es opuesta. En este último caso, teniendo en cuenta que la rotación en el punto de carga está impedido, la propias bisagras están aplicando un momento torsor. De hecho las bisagras aplican una carga no uniforme cuya resultante es la fuerza aplicada <math display="inline">P</math> y el momento resultante es el momento torsor. | ||
| − | + | [[File:Captura de pantalla 2022-09-20 153617.png|centre|589x589px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | ||
<div id="_Ref481743076" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Ref481743076" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | ''Figura | + | ''Figura 3-2. Deformación debida a efectos higrotérmicos. a) Laminado simétrico. b) Laminado anti-simétrico.''</div> |
La <span id='cite-_Ref481743478'></span>[[#_Ref481743478|''Figura '' '''3''' '''3''']] muestra el momento torsor en el punto de aplicación de carga y la reacción en el frente de grieta, relacionada con la distribución no uniforme en la anchura de las fuerzas de la <span id='cite-_Ref481741711'></span>[[#_Ref481741711|''Figura '' '''3''' '''1''']]. Se ha supuesto dicho momento concentrado en el frente de grieta. | La <span id='cite-_Ref481743478'></span>[[#_Ref481743478|''Figura '' '''3''' '''3''']] muestra el momento torsor en el punto de aplicación de carga y la reacción en el frente de grieta, relacionada con la distribución no uniforme en la anchura de las fuerzas de la <span id='cite-_Ref481741711'></span>[[#_Ref481741711|''Figura '' '''3''' '''1''']]. Se ha supuesto dicho momento concentrado en el frente de grieta. | ||
| Line 176: | Line 169: | ||
<div id="_Ref481743478" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Ref481743478" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | ''Figura | + | ''Figura 3-3. Momento Torsor.''</div> |
Por tanto, las fuerzas y momentos resultantes son: | Por tanto, las fuerzas y momentos resultantes son: | ||
| Line 189: | Line 182: | ||
N_y^{HT}\\ | N_y^{HT}\\ | ||
0 | 0 | ||
| − | \end{array}\right\}</math> | + | \end{array}\right\}</math> <math>\left\{\overline{M}\right\}=\left\{\begin{array}{c} |
M_x\\ | M_x\\ | ||
0\\ | 0\\ | ||
M_s+M_s^{HT} | M_s+M_s^{HT} | ||
| − | \end{array}\right\}</math> | + | \end{array}\right\}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (6) | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
| Line 202: | Line 195: | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
|- | |- | ||
| − | | <math>\, \frac{1}{2}{\int }_{L_x}{\int }_{L_y}\left(\left(4b_{xs}N_x^{HT}+\right. \right. | + | | <math>\, \frac{1}{2}{\int }_{L_x}{\int }_{L_y}\left(\left(4b_{xs}N_x^{HT}+\right. \right.\left. \left. 2d_{ss}M_s^{HT}\right)M_{s_{,X}}+2d_{ss}M_sM_{s_{,X}}\right)dxdy=0 </math> |
|} | |} | ||
| Line 239: | Line 232: | ||
<div id="_Ref481745465" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_Ref481745465" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | ''Figura | + | ''Figura 3-4. Componentes de P en el frente de grieta.''</div> |
Las fuerzas y momentos resultantes en este caso son: | Las fuerzas y momentos resultantes en este caso son: | ||
| Line 302: | Line 295: | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
|- | |- | ||
| − | | <math>\, G=\frac{d_{xx}P^2}{b^2}\left({\alpha }_0+{\alpha }_1a+\right. | + | | <math>\, G=\frac{d_{xx}P^2}{b^2}\left({\alpha }_0+{\alpha }_1a+\right.\left. a^2\right)+\frac{{\kappa }_s^{HT}P^2a^2}{b^2}\left(\frac{a_{ss}{\kappa }_s^{HT}}{4}+\right.\left. (b_{xs}\right) \biggr) </math> |
|} | |} | ||
| Line 332: | Line 325: | ||
Teniendo en cuenta el coportamiento durante la propagación y de acuerdo con otros autores, únicamente se considerarán datos de iniciación para calcular la resistencia interlaminar. Con el objetivo de comparar resultados, la tasa de relajación de energía se calculará también mediante el método MBT propuesto por Williams [11] y mediante el método de las áreas. Con respecto a este último, aunque los valores obtenidos no se pueden asociar a una longitud de grieta determinada, ya que corresponde a un valor medio durante un incremento de grieta, se va a usar un incremento mínimo de 1mm para su cálculo. De esta manera, además de evitar valores de propagación aor a 1mm, el valor obtenido se puede asociar a la longitud de grieta inicial. | Teniendo en cuenta el coportamiento durante la propagación y de acuerdo con otros autores, únicamente se considerarán datos de iniciación para calcular la resistencia interlaminar. Con el objetivo de comparar resultados, la tasa de relajación de energía se calculará también mediante el método MBT propuesto por Williams [11] y mediante el método de las áreas. Con respecto a este último, aunque los valores obtenidos no se pueden asociar a una longitud de grieta determinada, ya que corresponde a un valor medio durante un incremento de grieta, se va a usar un incremento mínimo de 1mm para su cálculo. De esta manera, además de evitar valores de propagación aor a 1mm, el valor obtenido se puede asociar a la longitud de grieta inicial. | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:Captura de pantalla 2022-09-20 154402.png|centre|600x600px]]''' '''.</div>''Figura 51. Tasa crítica de relajación de energía. Laminado simétrico'' <div id="_Ref481740274" class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:Captura de pantalla 2022-09-20 154446.png|centre|600x600px]]''Figura 52. Tasa crítica de relajación de energía. Laminado antisimétrico''</div> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | ''Figura 51. Tasa crítica de relajación de energía. Laminado simétrico'' | + | |
| − | + | ||
| − | <div id=" | + | |
| − | ''Figura 52. Tasa crítica de relajación de energía. Laminado antisimétrico''</div> | + | |
Las figuras<span id='cite-_Ref481740274'></span>[[#_Ref481740274|Figura '''51''']] y <span id='cite-_Ref481740283'></span>[[#_Ref481740283|Figura'' '' '''52''']] muestran la media para cinco probetas en cada caso de la <math display="inline">{G}_{c}</math> obtenida mediante los tres métodos descritos anteriormente. | Las figuras<span id='cite-_Ref481740274'></span>[[#_Ref481740274|Figura '''51''']] y <span id='cite-_Ref481740283'></span>[[#_Ref481740283|Figura'' '' '''52''']] muestran la media para cinco probetas en cada caso de la <math display="inline">{G}_{c}</math> obtenida mediante los tres métodos descritos anteriormente. | ||
Revision as of 14:50, 20 September 2022
1 Introducción
El ensayo DCB es el método más utilizado para medir la fractura en modo I y ha sido estandarizado para el caso de polímeros reforzados con fibra [1].
A pesar de que el estándar ha sido descrito para laminados unidireccionales, a menudo se utilizan para medir la tasa crítica de liberación de energía de laminados multidireccionales. Sin embargo, algunos factores que pueden tener poca importancia en el ensayo de laminados unidireccionales, pueden afectar seriamente en el caso de multidireccionales [2], como es el caso del apilamiento del laminado, la simetría, la curvatura del frente de grieta, la mezcla de modos, las tensiones residuales o las diversas formas de daño que se producen durante el crecimiento de grieta. Nicholls et al. [3] estudiaron el valor de en laminados multidireccionales observando que la grieta puede avanzar por diferentes intercaras e identificando cuatro formas diferentes de propagación de la grieta. Además, el ensayo la medición de la grieta se realiza de forma visual, lo que no siempre resulta fácil y puede inducir a error.
Teniendo en cuenta lo anterior, además de que el valor inicial es el más conservador, la resistencia a deslaminación de laminados multidireccionales mediante el test DCB debería limitarse solo a los valores de iniciación.
La mayoría de los estudios para calcular la resistencia de laminados multidireccionales no tienen en cuenta las tensiones residuales debidas a efectos higrotérmicos y se aplican a secuencias de apilamiento que evitan acoplamientos de flexión-torsión. Nairn [4] estudió la energía de relajación mediante DCB de adhesivos y laminados teniendo en cuenta las tensiones residuales concluyendo que en el caso de que cada uno de los brazos de deslaminación sea un laminado anti-simétrico el error de no considerarlas puede ser importante.
El objetivo de este trabajo es estimar la tasa de energía de relajación de laminados carbón/epoxi cruzados, simétricos y anti-simétricos mediante el ensayo DCB. Para ello se extenderá el modelo desarrollado en [5] para laminados unidireccionales incluyendo además los efectos de las tensiones residuales.
2 Laminados anti-simétricos
2.1 Relaciones carga-deformación
Se van a considerar laminados anti-simétricos y laminados simétricos . En ambos casos, cada uno de los brazos de la parte agrietada es anti-simétrico. Teniendo en cuenta las secuencias estudiadas, las relaciones constitutivas para un laminado anti-simétrico vienen dadas por [6]:
Además, el hecho de que el ángulo de las láminas sea de 45º, resulta en las siguientes relaciones:
En cuanto a los efectos higrotérmicos, aunque los ensayos se realizan a temperatura ambiente, se deben tener en cuenta las cargas higrotérmicas equivalentes debidas al proceso de enfriamiento del material. En las secuencias estudiadas las cargas higrotérmicas no nulas son las fuerzas (que son igualesen este caso) y el momento torsor .
2.2 Energía complementaria de deformación y sus derivadas
La energía complementaria de deformación de un laminado multidireccional debida a un estado de tensión plana se puede expresar como [7]:
|
|
(1) |
Donde es la distancia desde el plano medio a la superficie más baja de la lámina . y indican la dirección longitudinal y transversal respectivamente. es la longitud total de la probeta; y son las matrices suma de fuerzas y momentos mecánicos e higrotérmicos.
Se considera un sistema equilibrado sujeto a una fuerza generalizada . Aplicando el primer principio de la termodinámica en términos energía complementaria y asumiendo que un avance de grieta infinitesimal es un proceso reversible y por consiguiente la energía complementaria es una diferencial exacta [8]:
|
|
(2) |
|
|
(3) |
La ecuación (2) es el teorema de Engesser-Castigliano, siendo el desplazamiento generalizado en la dirección de La ecuación (3) relaciona la energía de relajación con la energía complementaria, siendo la anchura de la grieta.
Derivando (1) con respecto a y a y teniendo en cuenta que los términos higrotérmicos no dependen de estas variables, las ecuaciones anteriores quedan:
|
|
(4) |
|
|
(5) |
3 Aproximación analítica
3.1 Cargas aplicadas y reacciones
3.1.1 Momentos flectores
Para el cálculo de la distribución de momentos flectores, se va a utilizar la aproximación presentada en [5], que además permite obtener la longitud de grieta sin métodos visuales para cada par de valores de carga-desplazamiento.
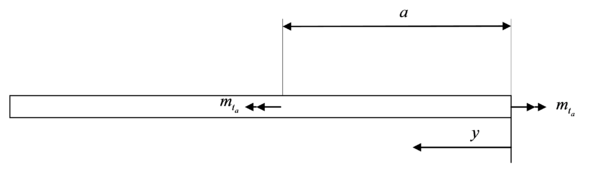
La Figura 3 1 muestra un modelo simplificado de las fuerzas distribuidas en la mitad inferior de la probeta DCB, basado en los resultados obtenidos por otros autores.
Mediante las ecuaciones de la estática, además de la aplicación del teorema de Engesser-Castigliano para hallar los desplazamientos en las secciones 1, 2 y 3 e igualarlos las deformaciones transversales de la probeta, se obtienen los valores de las fuerzas y las distancias . Mientras los valores de no dependen de la longitud de grieta, la variación de con respecto a esta es despreciable para los valores habituales de en los ensayos, y por tanto puede considerarse constante.
Una vez determinados los parámetros del modelo, se calculan las distribuciones de momentos flectores en función de .
Donde y
3.1.2 Momento torsor
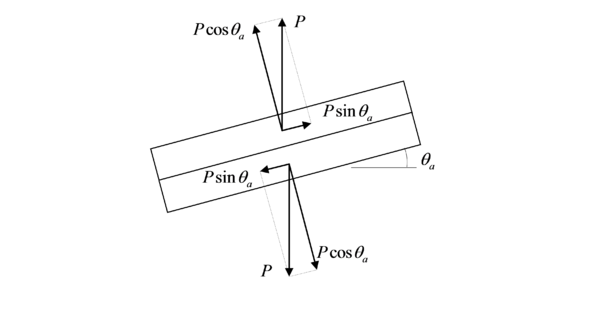
Las tensiones residuales provocan una rotación en cada una de las partes agrietadas de la probeta. Como se observa en la Figura 3 2, mientras que en el caso de los laminados anti-simétricos ambos brazos rotan en el mismo sentido, en los laminados simétricos la rotación es opuesta. En este último caso, teniendo en cuenta que la rotación en el punto de carga está impedido, la propias bisagras están aplicando un momento torsor. De hecho las bisagras aplican una carga no uniforme cuya resultante es la fuerza aplicada y el momento resultante es el momento torsor.
La Figura 3 3 muestra el momento torsor en el punto de aplicación de carga y la reacción en el frente de grieta, relacionada con la distribución no uniforme en la anchura de las fuerzas de la Figura 3 1. Se ha supuesto dicho momento concentrado en el frente de grieta.
Por tanto, las fuerzas y momentos resultantes son:
|
|
(6) |
Se asume que la distribución del momento torsor, es uniforme en la anchura de la probeta. Teniendo en cuenta que el giro es nulo en el punto de plicación de la carga se puede aplicar Engesser-Castigliano para calcular el torsor aplicado por las bisagras. Sustituyendo (6) en (4) y teniendo en cuenta las propiedades de los laminados antisimétricos se obtiene:
Donde
Teniendo en cuenta que la mitad del momento torsor de una sección rectangular corresponde a y la otra mitad al momento resultante de las fuerzas cortantes de fuera del plano [9], se obtiene la siguiente distribución de momentos torsores:
|
|
(7) |
|
|
(8) |
3.1.3 Fuerza cortante
En el caso de los laminados anti-simétricos, el momento torsor higrotérmico genera rotaciones en el mismo sentido en ambos brazos de la parte agrietada de la probeta. Por tanto, la probeta permanece horizontal en el punto de aplicación, pero al estar libre el otro extremo, la probeta se encuentra deformada. Esto quiere decir, como se aprecia en la Figura 3 4 . Componentes de P en el frente de grieta, que en el frente de grieta existirán unas componentes en sentido transversal relacionadas con el modo III de fractura.
Las fuerzas y momentos resultantes en este caso son:
|
|
(9) |
El ángulo girado por el laminado en el frente de grieta se obtiene mediante la siguiente expresión [10]:
|
|
(10) |
Donde es la curvatura del laminado debida a efectos higrotérmicos. Asumiendo que el ángulo es muy pequeño se obtiene la siguiente distribución de la fuerza cortante:
|
|
(11) |
3.2 Tasa de liberación de energía
Con la intención de obtener una expresión para la tasa de liberación de energía en función de la longitud de grieta, las expresiones para las cargas aplicadas y reacciones obtenidas en las secciones anteriores se sustituyen en la ecuación (5).
En el caso de laminados simétricos se obtiene lo siguiente:
Mientras que para los laminados anti-simétricos:
Los factores dependen únicamente de las dimensiones definidas en el modelo. El primer término de cada expresión es la parte de energía debido al modo I de fractura y se puede observar que es el mismo en ambos casos. Sin embargo los segundos términos, relacionados con el modo III de fractura difieren y además en el caso de laminados simétricos es una constante mientras que en el de anti-simétricos es dependiente de la longitud de grieta.
El significado físico del signo negativo de la energía de modo III está relacionado con el hecho de que los efectos higrotérmicos provocan una deformación inicial en modo III sin ninguna carga, como se observa en la Figura 3 2. Por tanto, cuando se aplica la carga se necesita una energía menor para el avance de grieta aunque la cantidad total sea positiva.
4 Material y aparatos
El material usado en este estudio es T6T/F593, una resina epoxi termoestable, reforzada con fibra de carbono y proporcionada por Hexcal Composites. Se han utilizado láminas unidireccionales de este material con un contenido en volumen del 55% para fabricar laminados angulares mediante moldeado por compresión.
Se han producido dos tipos de laminados de dieciseis capas con un film de teflón entre las capas intermedias para producir la grieta inicial. Para la realización de los ensayos, se ha utilizado una máquina universal de ensayos MTS-Insight 10 con una célula de carga de 250N.
5 Resultados
5.1 Propagación de la grieta
Durante la propagación se observa una pronunciada curvatura en el frente de grieta, efecto de la curvatura en el eje y que provoca una deformación máxima en el medio del frente de grieta.
Se observan dos modos diferentes de propagación. Todas las probetas antisimétricas se comportan de la misma manera. La propagación comienza entre las láminas intermedias, pero inmediatamente, en uno de los lados del frente, la grieta pasa a la siguiente lámina propagándose al mismo tiempo por ambas intercaras. Esta última grieta se expande linealmente hasta ocupar todo el frente de grieta, momento en el que se inicia un nuevo salto de lámina. De esta forma los brazos tienen diferente grosor, provocando una rotación similar a la de los ensayos ADCB.
En el caso de los laminados simétricos, aproximadamente la mitad de ellos mostraron el mismo comportamiento que los antisimétricos, mientras que en el resto la grieta se propaga en zig-zag, avanzando simultáneamente en la intercara central y una adyacente.
A la vista de esto el uso de datos obtenidos visualmente y más aún los de propagación es cuestionable. El presente trabajo los datos de longitud de grieta han sido obtenidos mediante el método presentado en [5], que permite obtener una longitud efectiva de grieta para cada par de valores de carga-desplazamiento, basándose en el cambio de la flexibilidad durante el ensayo.
5.2 Tasa de relajación de energía
Teniendo en cuenta el coportamiento durante la propagación y de acuerdo con otros autores, únicamente se considerarán datos de iniciación para calcular la resistencia interlaminar. Con el objetivo de comparar resultados, la tasa de relajación de energía se calculará también mediante el método MBT propuesto por Williams [11] y mediante el método de las áreas. Con respecto a este último, aunque los valores obtenidos no se pueden asociar a una longitud de grieta determinada, ya que corresponde a un valor medio durante un incremento de grieta, se va a usar un incremento mínimo de 1mm para su cálculo. De esta manera, además de evitar valores de propagación aor a 1mm, el valor obtenido se puede asociar a la longitud de grieta inicial.
Figura 51. Tasa crítica de relajación de energía. Laminado simétricoLas figurasFigura 51 y Figura 52 muestran la media para cinco probetas en cada caso de la obtenida mediante los tres métodos descritos anteriormente.
En el caso de las probetas simétricas, Figura 51, los resultados obtenidos mediante MBT son ligeramente superiores a los otros. Esto puede ser debido a que este método no tiene en cuenta los efectos higrotérmicos, que como hemos visto resultan en un término negativo. El valor obtenido para dicho término en los laminados simétricos, y por tanto para la aportación del modo III es .
Con respecto al caso antisimétrico, Figura 52, los resultados obtenidos mediante los tres métodos estudiados son similares. Para esta configuración el término negativo que incluye los efectos higrotérmicos es despreciable, concretamente .
6 Conclusiones
Se ha presentado un estudio analítico y experimental de la tasa crítica de relajación de energía en laminados simétricos y anti-simétricos. En ambos casos cada brazo de la parte agrietada es un sublaminado anti-simétrico.
En ambos casos se ha obtenido una expresión para la energía dependiendo de la longitud de grieta y teniendo en cuenta los efectos higrotérmicos. Estos efectos se traducen en una contribución negativa a la energía, asociada al modo III de fractura.
La consideración de los efectos higrotérmicos en el material estudiado resulta en una disminución del 3% de la tasa de liberación de energía en el caso de laminados simétricos, mientras que el efecto en los antisimétricos es mínimo.
Referencias
| [1] | ISO, « 15024, Fiber-reinforced Plastic Composites – Determination of Mode I Interlaminar Fracture Toughness, GIc, for Unidirectionally Reinforced Materials,» (2001. |
| [2] | M. M. Shokrieh, M. Heidari-Rarani y M. R. Ayatollahi, «Calculation of GI for a multidirectional composite double cantilever beam on two-parametric elastic foundation,» Areospace Science and Technology, vol. 15, pp. 534-543, 2011. |
| [3] | D. Nicholls y J. Gallaguer, «Determination of GIC in Angle Ply Composites Using a Cantilever Beam Test Method,» Journal of Reinforced Plastics and Composites, vol. 2, pp. 2-17, 1983. |
| [4] | J. A. Nairn, «Energy release rate analysis for adhesive and laminate double cantilever beam specimens emphasizing the effect of residual stresses,» International Journal of Adhesion & Adhesives, vol. 20, pp. 59-70, 2000. |
| [5] | J. De Gracia, A. Boyano, A. Arrese y F. Mujika, «A new approach for determining the R-curve in DCB tests without optical measurements,» Engineering Fracture Mechanics, vol. 135, pp. 274-285, 2015. |
| [6] | I. Daniel y O. Ishai, Engineering mechanics of composite materials, New York: Oxford university press , 2006. |
| [7] | F. Mujika, «A novel approach for the three point flexure test of multidirectional laminates,» Journal of Composite Materials, vol. 46, nº 3, pp. 259-274, 2011. |
| [8] | A. Boyano, J. de Gracia, A. Arrese y F. Mujika, «Equivalent energy release rate and crack stability in the End Notched Flexure with inserted roller mixed mode I/II test,» Theoretical and Applied Fracture Mechanics, vol. 87, pp. 99-109, 2017. |
| [9] | V. Vasiliev y E. Morozov, Advanced mechanics of composite materials, 2007. |
| [10] | J. Romera, M. Cantera, I. Adarraga y F. Mujika, «A top-down analytic approach for the analysis of edge effects of angle-ply symmetric laminates,» Composite Structures, vol. 104, pp. 60-70, 2013. |
| [11] | J. G. Williams, «End corrections for orthotropic DCB specimens,» Compos Sci Technol, vol. 35, nº 4, pp. 367-376, 1989. |
Document information
Published on 19/10/17
Accepted on 19/10/17
Submitted on 19/10/17
Volume 01 - Comunicaciones Matcomp17 (2017), Issue Núm. 1 - Comportamiento en Servicio de los Materiales Compuestos, 2017
DOI: 10.23967/r.matcomp.2017.10.017
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?