(Tag: Visual edit) |
|||
| Line 23: | Line 23: | ||
==3 Acondicionamiento de las probetas== | ==3 Acondicionamiento de las probetas== | ||
| − | Las probetas cruciformes para el ensayo de tracción-tracción típicamente presentan el espesor rebajado en la región central para favorecer el fallo en la zona cargada biaxialmente y no en los brazos sometidos a cargas uniaxiales. En la literatura se proponen geometrías [2-19] con diferentes formas, dimensiones y configuraciones de la región central, utilizando transiciones en rampa o escalonadas entre el espesor de los brazos y el de la región central. Las decisiones sobre estos parámetros son relevantes para conseguir experimentos que lleguen a buen término desde el punto de vista de los modos de fallo que deberían localizarse en la región cargada biaxialmente. Por ejemplo la relación entre el grosor de los brazos y el espesor de la región central, definida como <math | + | Las probetas cruciformes para el ensayo de tracción-tracción típicamente presentan el espesor rebajado en la región central para favorecer el fallo en la zona cargada biaxialmente y no en los brazos sometidos a cargas uniaxiales. En la literatura se proponen geometrías [2-19] con diferentes formas, dimensiones y configuraciones de la región central, utilizando transiciones en rampa o escalonadas entre el espesor de los brazos y el de la región central. Las decisiones sobre estos parámetros son relevantes para conseguir experimentos que lleguen a buen término desde el punto de vista de los modos de fallo que deberían localizarse en la región cargada biaxialmente. Por ejemplo la relación entre el grosor de los brazos y el espesor de la región central, definida como <math>t=\frac{t_a}{t_c}</math> es crítica para reducir la concentración de tensiones fuera de la región cargada biaxialmente (inevitable en especímenes bi-traccionados y bi-comprimidos) o para controlar la aparición de pandeo en presencia de compresión. |
Bajo cargas de T-C y C-C el diseño de la probeta cruciforme requiere un acondicionamiento adicional para asegurar resultados satisfactorios. La estabilidad de la muestra se ve favorecida si la longitud de los brazos comprimidos se acorta [13,14]. Además, debe evitarse cualquier imperfección en la geometría de la probeta, ya que tienden a magnificarse en presencia de cargas de compresión. Por lo tanto, debe perseguirse la planitud y el paralelismo de las áreas de contacto de la probeta con las diferentes partes del dispositivo, así como una perpendicularidad precisa entre las superficies de carga y los ejes del brazo. | Bajo cargas de T-C y C-C el diseño de la probeta cruciforme requiere un acondicionamiento adicional para asegurar resultados satisfactorios. La estabilidad de la muestra se ve favorecida si la longitud de los brazos comprimidos se acorta [13,14]. Además, debe evitarse cualquier imperfección en la geometría de la probeta, ya que tienden a magnificarse en presencia de cargas de compresión. Por lo tanto, debe perseguirse la planitud y el paralelismo de las áreas de contacto de la probeta con las diferentes partes del dispositivo, así como una perpendicularidad precisa entre las superficies de carga y los ejes del brazo. | ||
| Line 42: | Line 42: | ||
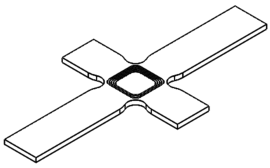
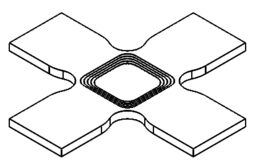
| − | donde ''E'' y <math | + | donde ''E'' y <math>\sigma</math> son el módulo de elasticidad aparente y la tensión límite elástico que exhibe el material cuando se somete a compresión uniaxial, mientras que ''A'' e ''I'' son el área de la sección transversal que presenta la longitud libre del brazo y su momento de inercia calculado en el eje débil, respectivamente. A priori no es necesario establecer ninguna limitación superior en la longitud del brazo si se somete a una carga de tracción, siendo deseable un brazo lo suficientemente largo como para agarrar la muestra sin interacción con la región central. En la Fig. 2 se esquematiza la geometría de las probetas utilizadas en esta investigación para el desarrollo de los ensayos de T-C y C-C. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
Revision as of 12:41, 19 May 2022
1 Introducción
Los ensayos biaxiales son de interés para reproducir casos de carga más cercanos a la realidad en los que el material se puede encontrar cargado en múltiples direcciones simultáneamente. Estos ensayos se consideran cruciales para la caracterización de materiales compuestos con un fuerte comportamiento ortótrópo. En la bibliografía al respecto se han propuesto distintas metodologías para generar estados de tensión y deformación biaxial [1]. En particular, la configuración preferida es la que utiliza probetas planas con una geometría cruciforme [2-18] en las que la intersección de los brazos es la región sometida simultaneamente a cargas perpendiculares. Aunque se comercializan equipos específicos para realizar ensayos biaxiales con probetas cruciformes, aún no existe una norma que recomiende la forma y las dimensiones de las probetas para materiales no metálicos.
La mayor parte de la investigación documentada relacionada con ensayos biaxiales en probetas cruciformes se centra en los casos de carga de tracción-tracción (tracción aplicada en ambos brazos de la muestra) [2-12], evitando en la medida de lo posible implicar la compresión directa de los brazos debido a los problemas de inestabilidad de la probeta. Solo algunas investigaciones sobre materiales compuestos de resina reforzada con fibra o metales [13-19] presentan resultados relacionados con casos de carga en los cuadrantes II, III y IV del plano biaxial.
Este trabajo sugiere la metodología y el acondicionamiento de las probetas para realizar ensayos biaxiales con probetas cruciformes sometidas a cargas de compresión [14], presentando un nuevo dispositivo [20] que reduce la inestabilidad que podría aparecer durante el ensayo. El accesorio limita el pandeo mediante la restricción de los desplazamientos fuera del plano tanto en los casos de carga de tracción-compresión como en compresión-compresión. Hasta donde los autores han podido saber, al menos otros dos dispositivos con distintas características se pueden encontrar en bibliografía [17,18], pero se proponen para una instalación específica y una configuración concreta de la probeta. El accesorio de este trabajo tiene la ventaja de ser ajustable a cualquier equipo y a la geometría de cualquier espécimen cruciforme. Como ejemplo, en esta investigación el diseño del dispositivo se adapta a la geometría de las probetas cruciformes y las características de la máquina de ensayos dados en [8-14].
En una probeta cruciforme el estado biaxial se consigue en la región central, siendo en este trabajo estudiados los casos de carga tracción-compresión (T-C) y compresión-compresión (C-C). Mientras tanto los brazos de la probeta se encuentran cargados uniaxialmente. La inestabilidad de la probeta completa debe estudiarse con la ayuda de modelos numéricos debido a la complejidad de su geometría. Por lo tanto, en la etapa de diseño del experimento el enfoque computacional para describir la inestabilidad elástica del problema se vuelve indispensable para asegurar la viabilidad de los ensayos. Las cargas de bifurcación y el modo de pandeo se obtinenen así del problema de autovalores y autovectores resuelto por medio del Método de Elementos Finitos (MEF). Para ello se realizan simulaciones mediante el MEF evaluando la respuesta completa de la probeta cruciforme y su estabilidad considerando dos escenarios, utilizando o no el dispositivo antipandeo. Uno de los principales objetivos es revisar si la restricción sobre el desplazamiento fuera del plano introducido por el accesorio permite alcanzar mayores tensiones en la región central de la probeta cruciforme un instante antes de la bifurcación. La intención es suprimir la posible influencia del pandeo de los brazos en las mediciones desarrolladas en la región sometida a carga biaxial y favorecer la realización de ensayos biaxiales exitosos con modos de fallo correctos. Asimismo, se revisa la influencia de la relación entre el espesor de los brazos y el espesor central en la carga crítica de la probeta cruciforme.
2 Dispositivo antipandeo
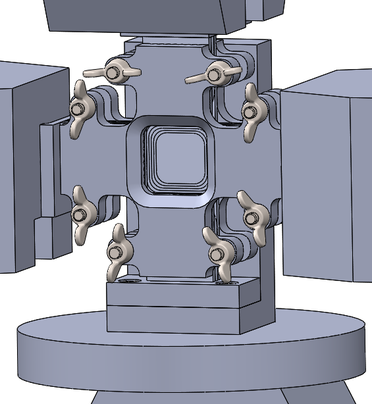
Se ha propuesto un dispositivo antipandeo en la solictud de patente P 2018/109819 [20] para desarrollar ensayos biaxiales de probetas cruciformes con al menos una dirección comprimida. Como principal requisito se ha buscado evitar que los brazos de la probeta cruciforme se desestabilicen debido al pandeo de los mismos. Se debe conseguir una correcta alineación entre la dirección de la carga aplicada y los ejes de los brazos para evitar la aparición de inestabilidades tempranas o inesperadas y para garantizar una carga biaxial pura en la región central de la probeta cruciforme. Además se debe permitir el desplazamiento de la muestra en el plano de carga, asegurando que no haya efectos de fricción durante el ensayo que puedan generar incertidumbres en los resultados o condiciones de carga no deseadas. Es importante evitar que el fallo ocurra sobre la superficie en la que se aplica la carga por medio de platos de compresión o que se produzca el pandeo en la longitud libre de los brazos de la muestra (en la región de aplicación de carga). Es desable disponer de acceso directo y/o visualización de la región cargada biaxialmente para adquirir su estado de deformación por medio de diferentes técnicas, por ejemplo, Correlación Digital de Imagen (DIC), videoextensometría, galgas extensométricas o fibra óptica. Es igualmente recomendable que el útil sea lo suficientemente versátil como para poder estudiar los casos de carga T-C o C-C, para ser adaptable y ajustable a cualquier máquina de ensayos, para ser escalable a la geometría y dimensiones de cualquier tipo de probeta cruciforme y estar basado en un concepto modular que facilite el montaje y desmontaje, así como sus posibilidades de industrialización.
El dispositivo utilizado en este trabajo consiste en dos placas en forma de cruz que restringen los desplazamientos fuera del plano a la muestra situada entre ellos. Estas dos placas están unidas por un conjunto de pernos y tuercas de mariposa de apriete manual, a fin de permitir el movimiento longitudinal de la probeta en la dirección de la carga durante el ensayo. La cara de las placas en contacto con el espécimen contiene una serie de nervios de punta roma para reducir la superficie de fricción entre la probeta y el utillaje. Ambas placas incluyen una ventana cuya posición coincide con la región central de la muestra cruciforme biaxialmente cargada. Las dimensiones de la apertura son suficientes para permitir la visualización de la región de interés, así como su instrumentación para la adquisición de datos. Un soporte en forma de L sirve como fijación y alineación del grupo formado por las placas y la muestra a la máquina de ensayos. Por último recordar que en este trabajo se entiende que la máquina de ensayos aplica las cargas de compresión directamente sobre los brazos de la probeta mediante platos de compresión. La Fig. 1 representa una vista esquemática del sistema antipandeo que aquí se propone.
3 Acondicionamiento de las probetas
Las probetas cruciformes para el ensayo de tracción-tracción típicamente presentan el espesor rebajado en la región central para favorecer el fallo en la zona cargada biaxialmente y no en los brazos sometidos a cargas uniaxiales. En la literatura se proponen geometrías [2-19] con diferentes formas, dimensiones y configuraciones de la región central, utilizando transiciones en rampa o escalonadas entre el espesor de los brazos y el de la región central. Las decisiones sobre estos parámetros son relevantes para conseguir experimentos que lleguen a buen término desde el punto de vista de los modos de fallo que deberían localizarse en la región cargada biaxialmente. Por ejemplo la relación entre el grosor de los brazos y el espesor de la región central, definida como es crítica para reducir la concentración de tensiones fuera de la región cargada biaxialmente (inevitable en especímenes bi-traccionados y bi-comprimidos) o para controlar la aparición de pandeo en presencia de compresión.
Bajo cargas de T-C y C-C el diseño de la probeta cruciforme requiere un acondicionamiento adicional para asegurar resultados satisfactorios. La estabilidad de la muestra se ve favorecida si la longitud de los brazos comprimidos se acorta [13,14]. Además, debe evitarse cualquier imperfección en la geometría de la probeta, ya que tienden a magnificarse en presencia de cargas de compresión. Por lo tanto, debe perseguirse la planitud y el paralelismo de las áreas de contacto de la probeta con las diferentes partes del dispositivo, así como una perpendicularidad precisa entre las superficies de carga y los ejes del brazo.
La adherencia de tacos o talones (“end-tabs” en inglés) en las zonas de aplicación de la carga es opcional, pero es aconsejable en materiales delgados o blandos para evitar el aplastamiento de la región donde se aplica la carga. En caso de que fuera necesario realizar ensayos biaxiales con materiales ultra delgados, el hecho de mecanizar la región central para reducir su espesor podría ser demasiado complejo o incluso desaconsejable en presencia de cargas compresivas debido al mayor riesgo de inestabilidad. En estas circunstancias, las placas estabilizadoras del dispositivo podrían diseñarse sin ventana y con una superficie moleteada para aumentar los puntos de contacto con la muestra, reduciendo las longitudes libres así como la posibilidad de pandeo local. Esto no permitiría medir directamente las deformaciones en la región cargada biaxialmente. Sin embargo, las tensiones y/o las deformaciones en el centro podrían estimarse a partir de los desplazamientos o las cargas aplicados en los brazos de la muestra utilizando las relaciones obtenidas previamente mediante técnicas numéricas como el MEF.
En este trabajo se propone la compresión directa de los brazos de los especímenes mediante placas de compresión [14]. Así es necesaria una cierta distancia inicial d entre las placas de estabilización y los platos de compresión o el soporte en forma de L, que debe planificarse con anticipación para evitar que choquen debido al acortamiento de los brazos sometidos a compresión. Éste es un parámetro crucial que debe elegirse con un valor suficiente para permitir el desarrollo del experimento completo sin colisiones, pero lo suficientemente pequeño para evitar el pandeo local en la longitud libre d debido a la carga de compresión uniaxial que soporta. Por lo tanto, el límite superior de la longitud que queda fuera del accesorio se puede estimar a partir de la teoría de pandeo lineal de Euler, suponiendo que las condiciones de contorno son empotrado-apoyado:
|
|
(1) |
donde E y son el módulo de elasticidad aparente y la tensión límite elástico que exhibe el material cuando se somete a compresión uniaxial, mientras que A e I son el área de la sección transversal que presenta la longitud libre del brazo y su momento de inercia calculado en el eje débil, respectivamente. A priori no es necesario establecer ninguna limitación superior en la longitud del brazo si se somete a una carga de tracción, siendo deseable un brazo lo suficientemente largo como para agarrar la muestra sin interacción con la región central. En la Fig. 2 se esquematiza la geometría de las probetas utilizadas en esta investigación para el desarrollo de los ensayos de T-C y C-C.
4 Modelo numérico
La realización de ensayos biaxiales con materiales compuestos en los que se utilizan probetas cruciformes es un proceso que consume mucho tiempo y dinero desde la concepción de la muestra hasta la interpretación de los resultados, pasando por las etapas de fabricación, mecanizado, acondicionamiento, instrumentación, ensayo y procesado de datos. Además, requiere instalaciones singulares que puedan aplicar carga biaxial en la muestra con garantía. Todas estas características explican la necesidad de ensayos virtuales con el propósito del diseño de los experimentos.
El código comercial de elementos finitos ABAQUS™ [21] se utiliza para analizar el problema de inestabilidad elástica, permitiendo estimar el valor de bifurcación del sistema aplicando un procedimiento de perturbación lineal. De esta forma, el valor propio más bajo será la carga de pandeo y el vector propio correspondiente el modo de pandeo. Se utiliza un modelo 2D en tensión plana con un elemento cuadrático de 8 nudos e integración reducida (el elemento shell S8R). Éste tiene seis grados de libertad por nodo, que son los tres desplazamientos longitudinales (traslaciones) y las tres rotaciones posibles. El modelo se adapta para estudiar el comportamiento biaxial de un laminado simétrico de matriz polimérica reforzado con fibra de carbono (CFRP) con la secuencia de apilamiento [+45º -45º]S. Se ha elegido un enfoque de mesoescala, considerando las propiedades elásticas ortótrópas al nivel de capa del material dadas en la Tabla 1.
|
[GPa] |
[GPa] |
[GPa] |
[GPa] |
[GPa] |
[GPa] |
|
|
|
| 133.00 | 9.14 | 9.14 | 5.42 | 5.42 | 3.10 | 0.19 | 0.19 | 0.03 |
Las probetas se modelan con los brazos de igual ancho y siguiendo las dimensiones de investigaciones anteriores [8-14], pero con la longitud total de los brazos comprimidos acortados para reducir el riesgo de que estos pandeen. Los brazos sometidos a tracción deben ser lo suficientemente largos para evitar que el sistema de agarre interfiera con la región del ensayo, aunque en las simulaciones solo se considera la longitud libre de la dirección sometida a tracción por razones de simplificación. Con respecto al grosor de los brazos y al espesor central, se estudian cuatro relaciones diferentes para revisar su influencia sobre la inestabilidad elástica de la muestra. Luego en la región central de la probeta se examina la respuesta biaxial de la secuencia de apilamiento [+45º -45º]S, considerando en los brazos las configuraciones [+45º -45º]S, [+45º -45º]2S, [+45º -45º]4S o [+45º -45º]8S para evaluar el efecto de las relaciones de espesores t = 1, t = 2, t = 4 y t = 8 respectivamente. Téngase en cuenta que el estudio se centra en la respuesta de laminados CFRP simétricos ±45º, por lo que una vez que se elige el laminado central las opciones para los brazos se reducen debido a la necesidad de mantener la simetría de la secuencia de apilamiento. Se modela la geometría completa, imponiendo condiciones de contorno simétricas a lo largo de las diagonales centrales de +45º y -45º de la probeta en el caso de carga C-C. No se puede introducir simetría o antisimetría en el caso de carga T-C porque se inducirían resultados erróneos, ya que el material y la geometría son simétricos con respecto a las diagonales centrales de +45º y -45º pero no el sentido de las tensiones aplicadas. Por lo tanto, se aplican niveles iguales de tensión uniforme en los brazos de la muestra cruciforme en los casos de carga C-C, mientras que se deben considerar aplicados niveles iguales de desplazamiento uniforme (pero de signo contrario) para los casos de carga T-C. La región de la probeta sobre la que se aplica la carga compresiva se supone que está simplemente apoyada en los platos de compresión, mientras que los brazos traccionados se entienden empotrados debido al sistema de agarre. Además, el análisis se desarrolla considerando la influencia de usar o no el dispositivo anti-pandeo. Teniendo en cuenta que las probetas están rebajadas en su zona central, se considera que las placas estabilizadoras del dispositivo incluyen una apertura para la adquisición de datos. En consecuencia, para modelar la influencia del accesorio, los desplazamientos fuera del plano están restringidos en las caras fuera de la región central rebajada y de la zona de transición entre espesores escalonada.
5 Estabilidad de la probeta cruciforme
La evolución carga-deformación de/para una placa delgada comprimida generalmente presenta una evolución bilineal [28]. Tras pandear la placa no pierde su capacidad de aguantar carga y aún puede soportar una carga mayor que el valor de bifurcación pero con una rigidez menor que en la etapa inicial. En cualquiera de los casos, las imperfecciones geométricas o las desalineaciones de la carga aplicada hacen que el valor crítico deba considerarse simplemente como una mera aproximación. Así, en una situación real, la curva carga-deformación seguiría una trayectoria asintótica desde la pendiente de la primera etapa hasta la segunda respuesta lineal con una rigidez disminuida con respecto a la inicial. De igual forma debe ocurrir con las probetas cruciformes, siendo aconsejable durante el ensayo medir el estado de deformación en las superficies superior e inferior de la región rebajada para reconocer cuándo comienza su diferenciación y, de ese modo, identificar el inicio de la bifurcación.
La mayoría de las instalaciones pueden configurarse para realizar ensayos o bien controlando la carga aplicada sobre la probeta o bien controlando el desplazamiento aplicado. Teniendo en cuenta estas dos posibilidades para el modo de control, en este este trabajo los valores de bifurcación de la muestra se estudiaron en términos de la fuerza aplicada o en términos del desplazamiento aplicado. De cualquier forma, el control por fuerza es más recomendable si se quiere asegurar una relación de carga constante en la región central de la muestra durante todo el ensayo.
En esta sección la estabilidad elástica de la probeta cruciforme se analiza numéricamente, definiendo la carga o el desplazamiento en el momento de la bifurcación como el nivel de fuerza de compresión uniforme o desplazamiento uniforme aplicado en los brazos de la muestra que inicia la inestabilidad [14]. Sin utilizar el dispositivo antipandeo a bajas relaciones de espesor la inestabilidad de la probeta se rige por la respuesta de los brazos. Pero se puede observar un aumento de los valores críticos con mayores relaciones de espesor debido a la reducción de las longitudes de onda de la superficie sinusoidal que aparece en la situación deformada. Esto es consecuencia del aumento de la rigidez de los brazos en relación a la rigidez del centro, imponiendo a la región central una restricción cercana a los bordes empotrados para la relación de espesores t = 8. La presencia del dispositivo antipandeo mejora la estabilidad de la muestra en todas las situaciones, teniendo en cuenta que su efecto no es sustancial cuando la relación de espesores es lo suficientemente alta. Téngase en cuenta que en los casos con t = 1 no se reduce el espesor de la región central y el hecho de no cambiar el grosor en la región libre hace a estos casos más cercanos a asumir una restricción simplemente apoyada en las longitudes críticas.
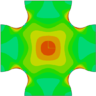
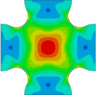
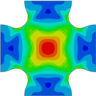
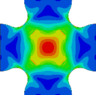
Con respecto a la uniformidad de los campos de tensión en la región central, se evalúa la tensión equivalente . Ésta se calcula como combinando las tensiones promedio , y que actúan sobre la sección transversal expresada en los ejes globales x e y. Los casos estudiados con probetas rebajadas en su zona central, con o sin dispositivo antipandeo, exhiben estados de tensión homogéneos en la región cargada biaxialmente antes del pandeo. La respuesta biaxial del espécimen cruciforme cargado en ambas direcciones bajo compresión presenta concentraciones de tensión y deformación inevitables fuera de la región rebajada, en concreto en las esquinas externas de la unión entre los brazos. Mientras tanto, en el caso de carga de T-C, los niveles más altos de tensiones y deformaciones aparecen en la zona biaxialmente cargada en las probetas con rebaje, pero las muestras sin rebaje desarrollan concentraciones no deseadas fuera de la región de interés. El estudio constata que la relación de espesores es crítica para reducir la concentración de tensiones fuera de la región cargada biaxialmente en especímenes bi-traccionados o bi-comprimidos y para evitar el pandeo en presencia de compresión. A modo de ejemplo, la Fig. 3 representa los mapas de tensión equivalente justo antes de la inestabilidad estructural de la muestra para las distintas relaciones de espesor estudiadas con la presencia del accesorio ante el estado de cargas T-C. En estos casos se ha denominado como a la tensión equivalente obtenida en la zona central de la probeta. En todos los casos mostrados en la Fig. 3 el valor del valor del desplazamiento aplicado necesario para iniciar la inestabilidad fue de . Sin embargo los niveles de tensión conseguidos en la zona central antes de pandear se incrementan al aumentar la relación de espesores. Esto permitiría disponer de medidas fiables del estado tensional en el centro durante más tiempo, además de favorecer la realización de ensayos biaxiales exitosos con modos de fallo correctos. A la luz de los resultados, la configuración preferida para el desarrollo experimental de ensayos con probetas cruciformes en presencia de compresión será una relación de espesores t = 4 combinada con la utilización del dispositivo antipandeo. Una relación de espesores superior complicaría el proceso de fabricación y mecanizado debido al número de capas. Además no aportaría una mejora sustancial en la observación de la respuesta lineal del material, ya que tanto las relaciones de espesores t = 4 y t = 8 permiten conseguir tensiones lo suficientemente altas en la zona central como para observar el comienzo de no linealidades en la respuesta aparente del laminado angle-ply ante cargas T-C.
Para finalizar la discusión sobre las características de pandeo de la probeta cruciforme, vale la pena resaltar su fuerte dependencia, no solo con la geometría y las condiciones de contorno, sino también con las propiedades del material. Si la morfología de la muestra y sus restricciones se mantienen, un cambio en el comportamiento elástico lineal del material en al menos un orden de magnitud puede afectar a los modos de pandeo (y por ende a los valores críticos) incluso para materiales isótropos utilizando un enfoque de macroescala. Por lo tanto, la utilización de las mismas dimensiones y las mismas condiciones de contorno pero un material distinto podrían inducir otros efectos que deberían abordarse antes del ensayo experimental.
| t = 1
|
t = 2
|
t = 4
|
t = 8
|
6 Conclusiones
Este trabajo investiga analítica y numéricamente el fenómeno de inestabilidad elástica de probetas cruciformes formadas por laminados ±45º de CFRP para ensayos biaxiales en presencia de cargas compresivas. Se describen los aspectos principales que se deben tener en cuenta para realizar ensayos biaxiales si la carga de compresión se aplica en los brazos de la muestra por medio de platos de compresión. Para lograr resultados experimentalmente más fiables se demuestra que el uso del dispositivo antipandeo reduce el riesgo de inestabilidad tanto en los brazos como en la zona central de la probeta. A su vez, los ensayos virtuales permiten comprender la influencia de la relación entre el espesor de los brazos y del centro en la carga crítica que desestabiliza la probeta cruciforme y así determinar la geometría óptima para los ensayos ante cargas compresivas.
Agradecimientos
Este trabajo ha sido financiado por el Ministerio de Economía y Competitividad y el Fondo Europeo de Desarrollo Regional con el proyecto de referencia DPI2016-77715-R. Asimismo, S. Horta Muñoz agradece la beca predoctoral SBPLY/16/180501/000263, cofinanciada por la Junta de Comunidades de Castilla La-Mancha y el Fondo Social Europeo.
Referencias
[1] A. Smits, C. Ramault, A. Makris, D. van Hemelrijck, A. Clarke, C. Williamson, M. Gower, R. Shaw, R. Mera, E. Lamkanfi, W. van Paepegem, Exp. Anal. Nano. Eng. Mater. Struct., pág. 933–934 (2007).
[2] Y. Yu, M. Wan, X.D. Xu, J. Mater. Process. Tech., 123, pág. 67-70 (2002).
[3] A. Smits, D. van Hemelrijck, T.P. Philippidis, A. Cardon, Composites Science and Technology, 66, pág. 964-975 (2006).
[4] D. van Hemelrijck, A. Makris, C. Ramault, E. Lamkanfi, W. van Paepegem, D. Lecompte, Proc. Instn. Mech. Engrs. Part L, J. of Mater: Des. Appl., 222, pág. 231-239 (2008).
[5] A.E. Antoniou, D. van Hemelrijck, T.P. Philippidis, Composites Science and Technology, 70, pág. 1232-1241 (2010).
[6] A. Makris, T. Vandenbergh, C. Ramault, D. van Hemelrijck, E. Lamkanfi, W. van Paepegen, Polymer Testing, 29, pág. 216-223 (2010).
[7] M.R.L. Gower, R.M. Shaw, Appl. Mech. Mater., 24-25, pág. 115-120 (2010).
[8] J. Navarro-Zafra, J.L. Curiel-Sosa, M.C. Serna Moreno, Appl. Compos. Mater., 23, pág. 139-154 (2016).
[9] J. Navarro-Zafra, J.L. Curiel-Sosa, M.C. Serna Moreno, Composite Structures, 133, pág. 1093-1100 (2015).
[10] M.C. Serna Moreno, J.J. López Cela, Composites Science and Technology, 72, pág. 91–96 (2011).
[11] M.C. Serna Moreno, J.L. Martínez Vicente, J.J. López Cela, Composite Structures, 103, 27–33 (2013).
[12] M.C. Serna Moreno, J.L. Curiel-Sosa, J. Navarro-Zafra, J.L. Martínez Vicente, J.J. López Cela, Composite Structures, 119, pág. 264–271 (2015).
[13] M.C. Serna Moreno, J.L. Martínez Vicente, Composite Structures, 122, pág. 440–444 (2015).
[14] M.C. Serna Moreno, S. Horta Muñoz, Composites Science and Technology, under review (2019).
[15] J.S. Welsh, J.S. Mayes, A.C. Biskne, Composite Structures, 75, pág. 60-66 (2006).
[16] Y. Huang, S.K. Ha, J. Koyanagi, J.D.D. Melo, H. Kumazawa, I. Susuki, Journal of Composite Materials, 44, pág. 2429–2445 (2010).
[17] P. Hopgood, J. Cook, A. Clarke, Multi-axial testing of planar composite specimens, ICCM12, Paris, France, 1999.
[18] W.J. Vankan, B.H.A.H. Tijs, G.J. de Jong, H.C. de Frel, Journal of Composite Materials, 50, pág. 3477–3500 (2016).
[19] M.A. Iadicola, A.A. Creuziger, T. Foecke, Advanced biaxial cruciform testing at the NIST Center for Automotive Lightweighting, in: M. Rossi, M. Sasso, N. Connesson, R. Singh, A. DeWald, D. Backman, P. Gloeckner (eds), Residual stress thermomechanics infrared imaging hybrid, Tech. Inverse Probl., Springer, pág. 277–285 (2014).
[20] M.C. Serna Moreno, S. Horta Muñoz, Dispositivo para evitar pandeo en ensayos biaxiales de probetas cruciformes, Solicitud de patente, nº de referencia P 2018/109819, 20 Julio 2018.
[21] Hibbitt, Karlsson, Sorensen, Abaqus/Standard User’s Manual 2018, Dassault Systems, Rhode Island, 2018.
[22] M.C.Serna Moreno, A.Romero Gutiérrez, J.L.Martínez Vicente. Composite Structures, 136, pág. 706–711 (2016).
[23] M.C.Serna Moreno, A.Romero Gutiérrez, J.L.Martínez Vicente. Composite Structures,146, pág. 62–68 (2016).
[24] M.C.Serna Moreno, A.Romero Gutiérrez, J.L.Martínez Vicente. Materials Science and Engineering: IOP Conf. Series, 139, article 012047, 8 pages (2016), DOI:10.1088/1757-899X/139/1/012047.
[25] M.C. Serna Moreno, S. Horta Muñoz, A. Romero Gutiérrez, C. Rappold, J.L. Martínez Vicente, P.A. Morales-Rodríguez, J.J. López Cela, Composites Science and Technology, 156, 8–18 (2018).
[26] S. Horta Muñoz, M.C. Serna Moreno, Numerical modelling of the pseudo-ductility effect in ±45° angle-ply laminates under biaxial loading, ECCM18, 23 – 28 Junio 2018.
[27] S. Horta Muñoz, Complexity of the structural response of polymer matrix composites reinforced with fibres, Tesis Doctoral, UCLM, (en proceso).
[28] R.M.Jones. Mechanics of Composite Materials, Taylor & Francis, ISBN: 1-56032-712-X (1999).
Document information
Published on 19/05/22
Accepted on 19/05/22
Submitted on 19/05/22
Volume 05 - Comunicaciones Matcomp19 (2021), Issue Núm. 2 - Caracterización analítica, numérica y experimental de los materiales compuestos. Materiales multifuncionales. Comportamiento de componentes estructurales., 2022
DOI: 10.23967/r.matcomp.2022.05.021
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?