m (Scipediacontent moved page Draft Content 908512468 to Carbajal Mujika 2019a) |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | == | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> |
| − | < | + | N. Carbajal<sup>a</sup>, F. Mujika<sup>a</sup></div> |
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;"><sup>a</sup>GRUPO MATERIALES + TECNOLOGÍAS / MECÁNICA DE MATERIALES, </span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">Departamento de Ingeniería Mecánica, </span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">Escuela de Ingeniería deGipuzkoa, UPV/EHU,</span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;"> Plaza Europa 1, 20018, Donostia-San Sebastián, España.</span></div> | ||
| + | |||
| + | {| style="width: 87%;border-collapse: collapse;" | ||
| + | |- | ||
| + | | colspan='2' style="vertical-align: top;"|<big>Flexión en dos planos de laminados composites unidireccionales</big> | ||
| + | |- | ||
| + | | style="border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:Carbajal_Mujika_2019a-image1.png|54px]] </span> | ||
| + | | style="vertical-align: top;"| | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Historia del artículo:</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Recibido 5 de Mayo 2017</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">En la versión revisada 5 de Mayo 2017</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Aceptado 31 de Mayo 2017</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Accesible online 21 de Junio 2017</span> | ||
| + | | rowspan='4' style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">En este trabajo se propone la flexión en dos planos de laminados unidireccionales de composites reforzados con fibra larga como método de ensayo para conocer el comportamiento del material ante solicitaciones combinadas. Se han fabricado y ensayado diferentes muestras utilizando el material T6T/F593 formado por matriz epoxi reforzado con fibra de carbono. Se han diferenciado tres casos según sea el ratio entre las tensiones normales en dirección de la fibra y las tensiones normales en dirección perpendicular a la fibra: menor, igual o mayor a la unidad. </span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">En todos los casos el fallo está asociado con la la rotura de la matriz, siendo lineal la relación entre tensión y deformación hasta rotura. Los resultados obtenidos se han analizado mediante tres criterios de fallo: Rankine, Tsai-Wu y máxima energía de deformación. El método de Rankine responde bien para los dos primeros casos. Con los resultados obtenidos se ha calculado el parámetro del Criterio Tsai Wu que relaciona las tensiones en dirección de la fibra y en dirección perpendicular a la fibra. Para los casos en que la tensión en dirección de la fibra es bastante mayor que la tensión en dirección perpendicular se puede despreciar esta última en el cálculo de la máxima energía de deformación.</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Palabras clave:</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Flexión en dos planos</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Laminados unidireccionales </span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Criterios de fallo</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;vertical-align: top;"| | ||
| + | |- | ||
| + | | colspan='2' style="vertical-align: top;"|<big>Bending in two planes of unidirectional composite laminates</big> | ||
| + | |- | ||
| + | | style="border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:Carbajal_Mujika_2019a-image2.png|54px]] </span> | ||
| + | | style="vertical-align: top;"| | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Keywords:</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Bending in two planes</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Unidirectional laminates</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Failure criteria</span> | ||
| + | |||
| + | |||
| + | | rowspan='2' style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">In this work bending in two planes of long fiber composite laminates is proposed as a test method for knowing the behaviour of this material in case of combined loads. Different samples have been manufactured and tested using carbon/epoxy T6T/F593 material. Three cases have been considered dendending on the value of the ratio between normal stress in fiber direction and normal stress in direction perpendicular to fibre: less tan 1, equal to 1 and greater than 1.</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">In all cases failure has been related to matrix failure, being a linear relation between stress and deformation until failure. Stress values have been analized by three failure criteria: Rankine, Tsai-Wu and maximum strain energy. Rankine criteria fits well the first two cases. The parameter of Tsai-Wu criteria between normal stresses in fiber direction and normal stresses in direction perpendicular to fibre has been obtained using experimental results. </span><span style="text-align: center; font-size: 75%;">When stress in fiber direction is much greater than stress in direction perpendicular to fiber, this small stress can be ignored in the calculus of maximum strain energy. </span> | ||
| + | |||
| + | |||
| + | |- | ||
| + | | style="border-top: 1pt solid black;vertical-align: top;"| | ||
| + | |} | ||
| + | |||
| + | |||
| + | ==1 Introducción == | ||
| + | |||
| + | <span id='_Ref481775622'></span>Tsai and Wu [<span id='cite-1'></span>[[#1|1]]] propusieron un criterio de fallo para materiales anisótropos sometidos a estados de tensión complejos. Mujika [<span id='cite-2'></span>[[#2|2]]] propuso una nueva aproximación para el ensayo de flexión de 3 puntos de laminados multidireccionales basada en métodos energéticos. En este trabajo se pretende conocer el comportamiento de laminados composite unidireccionales frente a un estado de tensión plano debido a la existencia de momentos flectores en 2 planos. | ||
| + | |||
| + | ==2 Aproximación analítica== | ||
| + | |||
| + | En la figura Figura 1 se muestra la configuración del ensayo realizado con flexión en dos planos. | ||
| + | |||
| + | [[Image:Carbajal_Mujika_2019a-image5.jpeg|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 1.''' Ensayo de flexión en dos planos</span></div> | ||
| + | |||
| + | Se han calculado las tensiones máximas en dirección de la fibra ''σ''<sub>x</sub> y en dirección perpendicular a la fibra ''σ''<sub>y</sub> | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\begin{matrix}{\sigma }_{x}=\frac{3P{L}_{x}}{2b{h}^{2}}\\{\sigma }_{y}=\frac{3P{L}_{y}}{2L{h}^{2}}\end{matrix}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde ''P'' es la máxima carga, ''L''<sub>x</sub> es la luz entre apoyos en dirección de la fibra, ''L''<sub>y</sub> es la luz entre apoyos en dirección perpendicular a la fibra, L es la longitud total en dirección ''x'' y b es la longitud en dirección perpendicular a la pieza del laminado. | ||
| + | |||
| + | Asimismo se define ''B'' como el ratio entre las tensiones σ<sub>x</sub> y σ<sub>y.</sub> | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">B=\frac{{\sigma }_{x}}{{\sigma }_{y}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Sustituyendo las ecuaciones (1) en la ecuación (2) y considerando la condición de L/b = L<sub>x</sub>/ L<sub>y </sub> | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">B={\left( \frac{{L}_{x}}{{L}_{y}}\right) }^{2}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Si se define ''t ''como el ratio entre las luces L<sub>x</sub> y L<sub>y </sub>la ecuación (3) se puede expresar | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">B={t}^{2}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
| + | |} | ||
| + | |||
| + | |||
| + | De acuerdo a la ecuación (4) la relación de tensiones σ<sub>x</sub> y σ<sub>y</sub> es igual al cuadrado de la relación entre luces ''L''<sub>x</sub> y ''L''<sub>y</sub>. | ||
| + | |||
| + | El criterio de Tsai-Wu [<span id='cite-_Ref481775622'></span>[[#_Ref481775622|1]]] para caso de tensión plana cuando las únicas tensiones distintas de cero son σ<sub>x </sub>y σ<sub>y</sub> se expresa | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{{F}_{11}\sigma }_{x}^{2}+{{F}_{22}\sigma }_{y}^{2}+{F}_{1}{\sigma }_{x}+</math><math>{F}_{2}{\sigma }_{y}+{F}_{12}{{\sigma }_{x}\sigma }_{y}=1</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde los parámetros ''F''<sub>11</sub>, ''F''<sub>22</sub>, ''F''<sub>1</sub> y ''F''<sub>2</sub> se obtienen a partir de estados uniaxiales de tensión mediante la siguientes expresiones | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\begin{matrix}{F}_{11}=\frac{1}{{X}_{t}\left| {X}_{c}\right| }&{F}_{22}=\frac{1}{{Y}_{t}\left| {Y}_{c}\right| }\\{F}_{1}=\frac{1}{{X}_{t}}-\frac{1}{\left| {X}_{c}\right| }&{F}_{2}=\frac{1}{{Y}_{t}}-\frac{1}{\left| {Y}_{c}\right| }\end{matrix}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
| + | |} | ||
| + | |||
| + | |||
| + | siendo ''X''<sub>t</sub> la resistencia a tracción longitudinal, ''X''<sub>c </sub>la resistencia a compresión longitudinal, ''Y''<sub>t </sub>la resistencia a tracción transversal e ''Y''<sub>c</sub> la resistencia a compresión transversal. | ||
| + | |||
| + | Sin embargo el parámetro F<sub>12</sub> precisa de un estado biaxial de tensiones para su obtención [<span id='cite-3'></span>[[#3|3]]]. | ||
| + | |||
| + | En la ecuación (5) se puede despejar F<sub>12</sub> | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{F}_{12}=\frac{1-{{F}_{11}\sigma }_{x}^{2}+{{F}_{22}\sigma }_{y}^{2}+{F}_{1}{\sigma }_{x}+{F}_{2}{\sigma }_{y}}{{{\sigma }_{x}\sigma }_{y}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Utilizando el criterio de la máxima energía de deformación para tensión plana cuando las únicas tensiones distintas de cero son σ<sub>x </sub>y σ<sub>y </sub>con valores de B mucho mayores que 1 la máxima energía de deformación por unidad de volumen U<sub>0</sub> se puede aproximar al valor correspondiente al estado uniaxial de tensiones | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{U}_{0}=\frac{{\sigma }_{x}^{2}}{2{E}_{L}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde E<sub>L </sub>es el módulo longitudinal del material. | ||
| + | |||
| + | ==3 Parte experimental== | ||
| + | |||
| + | Se han fabricado laminados de espesores nominales 2 y 3,5 mm y se han ensayado hasta rotura laminados con valores de t 0,25, 1, ,4, 5, 6 y 7 que corresponden a valores de B 0,0625, 1, 16, 25, 36 y 49. | ||
| + | |||
| + | En la Tabla 1 se muestran las dimensiones de las muestras | ||
| + | |||
| + | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| + | |- | ||
| + | | style="border-bottom: 2pt solid black;text-align: center;vertical-align: top;"| | ||
| + | | colspan='4' style="border-bottom: 2pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''Tabla 1.''' Dimensiones de las muestras </span> | ||
| + | |||
| + | |||
| + | | style="border-bottom: 2pt solid black;text-align: center;vertical-align: top;"| | ||
| + | |- | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Muestra</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">L<sub>x</sub>(mm)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">L<sub>y</sub> (mm)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">L(mm)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">b(mm)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">h(mm)</span> | ||
| + | |- | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">0.25-20-2</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">20</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">80</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">25,4</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">101,1</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">2,00</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">1-40-2</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">40</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">20</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">50,7</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">50,3</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">1,99</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">1-60-2</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">60</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">20</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">75,4</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">76,2</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">2,02</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">4-80-2</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">80</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">20</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">100,6</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">26,1</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">2,00</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">4-80-3.5</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">80</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">20</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">100,5</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">25,5</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">3,50</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">5-100-3.5</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">100</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">20</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">125,3</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">25,8</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">3,38</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">6-120-3.5</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">120</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">20</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">150,6</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">25,7</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">3,39</span> | ||
| + | |- | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">7-140-3.5</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">140</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">20</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">175,7</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">25,4</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">3,52</span> | ||
| + | |} | ||
| + | |||
| + | |||
| + | <span id='_Ref478901444'></span>En la tabla 2 aparecen los valores de ''X''<sub>t</sub>, ''X''<sub>c</sub>, ''Y''<sub>t </sub> e''Y''<sub>c</sub>. , donde Xt e Y<sub>t</sub> se han obtenido mediante flexión de 3 puntos utilizando una muestra de espesor nominal 2,53 mm y una luz de 80 mm y otra muestra de espesor nominal 2,69 y una luz de 30 mm respectivamente. Por otro lado X<sub>c</sub> e Y<sub>c</sub> se han obtenido mediante flexión de 3 puntos [<span id='cite-4'></span>[[#4|4]], <span id='cite-5'></span>[[#5|5]]] | ||
| + | |||
| + | {| style="width: 70%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| + | |- | ||
| + | | colspan='4' style="border-bottom: 2pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''Tabla 2.''' Propiedades resistentes de T6T/F593</span> | ||
| + | |||
| + | |||
| + | |- | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">X<sub>t</sub></span><span style="text-align: center; font-size: 75%;">(MPa)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">X<sub>c</sub></span><span style="text-align: center; font-size: 75%;">MPa)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">Y<sub>t</sub></span><span style="text-align: center; font-size: 75%;">(MPa)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Y<sub>c</sub></span><span style="text-align: center; font-size: 75%;">(MPa)</span> | ||
| + | |- | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">1500</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">-1100</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">100</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">-400</span> | ||
| + | |} | ||
| + | |||
| + | |||
| + | En la Tabla 3 se muestran los valores de los coeficientes de Tsai-Wu obtenidos según las ecuaciones (5) a partir de los valores de la Tabla 1. | ||
| + | |||
| + | {| style="width: 73%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| + | |- | ||
| + | | colspan='4' style="border-bottom: 2pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''Tabla 3.''' Valores de coeficientes de Tsai-Wu</span> | ||
| + | |||
| + | |||
| + | |- | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">F<sub>11</sub></span><span style="text-align: center; font-size: 75%;">(MPa<sup>-2</sup></span><span style="text-align: center; font-size: 75%;">)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">F<sub>22</sub></span><span style="text-align: center; font-size: 75%;">(MPa<sup>-2</sup></span><span style="text-align: center; font-size: 75%;">)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">F<sub>1</sub></span><span style="text-align: center; font-size: 75%;">(MPa<sup>-1</sup></span><span style="text-align: center; font-size: 75%;">)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">F<sub>2</sub></span><span style="text-align: center; font-size: 75%;">(MPa<sup>-1</sup></span><span style="text-align: center; font-size: 75%;">)</span> | ||
| + | |- | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">5,56·10<sup>-</sup></span><span style="text-align: center; font-size: 75%;"><sup>7</sup></span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">2,50·10<sup>-</sup></span><span style="text-align: center; font-size: 75%;"><sup>5</sup></span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">-1.67·10<sup>-4</sup></span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">7,50·10<sup>-</sup></span><span style="text-align: center; font-size: 75%;"><sup>3</sup></span> | ||
| + | |} | ||
| + | |||
| + | |||
| + | ==4 Resultados== | ||
| + | |||
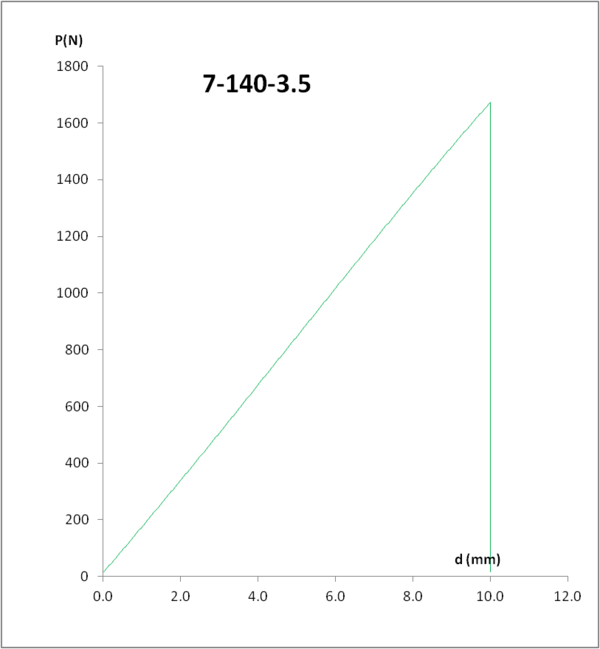
| + | Todas las muestras ensayadas presentan relación lineal entre carga y desplazamiento hasta el momento de la rotura, tal como se observa en la Figura 2, que se produce de forma súbita | ||
| + | |||
| + | [[Image:Carbajal_Mujika_2019a-image6.png|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 2.''' Curva carga –desplazamiento en muestra 7-140-3.5</span></div> | ||
| + | |||
| + | Todas las muestras sufren una rotura en transversal es decir la superficie de rotura es paralela a la dirección de la fibra según se muestra en la Figura 3. | ||
| + | |||
| + | [[Image:Carbajal_Mujika_2019a-image7-c.jpeg|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 3.''' Rotura transversal en la muestra 5-100-3.5</span></div> | ||
| + | |||
| + | En la Tabla 4 se muestran los valores de tensión máxima en dirección de la fibra σ<sub>x </sub>y en dirección perpendicular a la fibra σ<sub>y </sub>para las muestras con distinta valor de B. | ||
| + | |||
| + | {| style="width: 84%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| + | |- | ||
| + | | colspan='4' style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">'''Tabla 4.''' Valores de tensiones </span>σ<sub>x</sub><span style="text-align: center; font-size: 75%;"> y </span>σ<sub>y </sub><span style="text-align: center; font-size: 75%;">para cada muestra</span> | ||
| + | |||
| + | |||
| + | |- | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Muestra</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">B</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">σ<sub>x</sub>(MPa)</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">σ<sub>y</sub>(MPa)</span> | ||
| + | |- | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">0.25-20-2</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">0.0625</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">6</span> | ||
| + | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">101</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">1-40-2</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">1</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">94</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">93</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">1-60-2</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">1</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">89</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">90</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">4-80-2</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">16</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">600</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">39</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">4-80-3.5</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">80</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">695</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">44</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">5-100-3.5</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">25</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">798</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">33</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">6-120-3.5</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">36</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">986</span> | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">28</span> | ||
| + | |- | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">7-140-3.5</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">49</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">1010</span> | ||
| + | | style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">21</span> | ||
| + | |} | ||
| + | |||
| + | |||
| + | Para el caso de B menor que 1 las tensiones σ<sub>y</sub> en dirección perpendicular a la fibra son mayores que la tensión en dirección de la fibra σ<sub>x</sub> , por lo que el criterio de Rankine de la máxima tensión normal explica el fallo transversal en por alcanzarse en primer lugar el valor menor de los de la tabla 2. | ||
| + | |||
| + | Para el caso de B =1 también el criterio de Rankine explica el fallo transversal, aunque sin embargo las tensiones máximas que se obtienen son ligeramente menores que la resistencia a tracción transversal. | ||
| + | |||
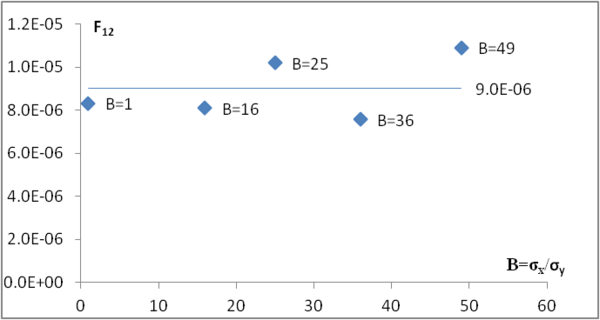
| + | Para el caso de B mayor o igual que 1 se ha utilizado la ecuación (7) del criterio de Rankine para calcular el valor de F12. En la figura 4 se muestra la variación de F<sub>12</sub> con el ratio de tensiones B. Se observa que al aumentar B el valor obtenido de F<sub>12</sub> se hace ligeramente mayor que el valor medio. | ||
| + | |||
| + | [[Image:Carbajal_Mujika_2019a-image8.png|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 4.''' F12 según ecuación (6) en función de B</span></div> | ||
| + | |||
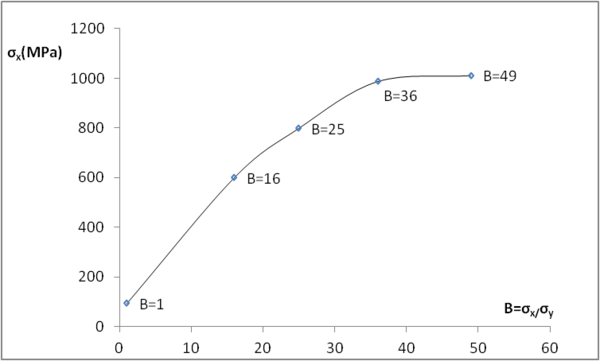
| + | Para el caso de B mayor que 1 en la Figura 5 se muestra la variación de σ<sub>x</sub> con B, observándose que cuando B se hace mucho mayor que 1 σ<sub>x</sub> tiende a un valor de 1000 MPa. | ||
| + | |||
| + | [[Image:Carbajal_Mujika_2019a-image9.png|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 5.''' Tensión en dirección de la fibra en función de B</span></div> | ||
| + | |||
| + | Por último el criterio de la máxima energía de deformación en caso de B mucho mayor que 1 es equivalente al caso uniaxial de tensiones en que σ<sub>y </sub>es nula. | ||
| + | |||
| + | ==5 Conclusiones== | ||
| + | |||
| + | Se ha analizado el comportamiento de laminados composites unidireccionales bajo un estado biaxial de tensiones σ<sub>x</sub> en dirección de la fibra y σ<sub>y</sub> en dirección perpendicular a la fibra ocasionado por flexión en dos planos, pudiendo ser el ratio entre estas tensiones, B, menor, igual o mayor que 1. | ||
| + | |||
| + | En todos los casos el fallo observado es transversal relacionado con el fallo de la matriz, incluso para valores del ratio de tensiones mucho más grandes que 1. | ||
| + | |||
| + | Cuando B es menor que 1 el criterio de Rankine explica bien el fallo transversal. Cuando B es igual a 1 los valores de tensión que se obtienen son ligeramente inferiores a la resistencia a tracción transversal. | ||
| + | |||
| + | Mediante el estado biaxial de tensiones producido por flexión en dos planos se puede obtener el valor del parámetro F<sub>12</sub> del Criterio de Tsai-Wu. | ||
| + | |||
| + | Para valores de B mayores que 1 los valores de tensión en dirección de la fibra aumentan a medida que aumenta B y tienden a un valor próximo al valor de resistencia a compresión longitudinal cuando B es mucho mayor que 1. | ||
| + | |||
| + | Finalmente, para valores de B mucho mayores que 1 la máxima energía de deformación por unidad de volumen en estado biaxial de tensiones es independiente del valor de σ<sub>y</sub>. | ||
| + | |||
| + | ==Agradecimientos== | ||
| + | |||
| + | Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 16/51 en la convocatoria de 2016. | ||
| + | |||
| + | ==Referencias== | ||
| + | |||
| + | <div id="1"></div> | ||
| + | [[#cite-1|[1]]] S.W. Tsai, E.M. Wu. ''Journal of Composite Materials'', '''5, '''pág. 58-80 (1971). | ||
| + | |||
| + | [http://dx.doi.org/ http://dx.doi.org/]10.1177/002199837100500106 | ||
| + | |||
| + | <div id="2"></div> | ||
| + | [[#cite-2|[2]]] F. Mujika, ''Journal of Composite Materials'', '''46, '''pág. 259-274 (2012). | ||
| + | |||
| + | [http://dx.doi.org/10.1177/0021998311412636 http://dx.doi.org/10.1177/0021998311412636] | ||
| + | |||
| + | <div id="3"></div> | ||
| + | [[#cite-3|[3]]] E.M. Wu, ''Journal of Composite Materials'', '''6, '''pág. 472-489 (1972). | ||
| + | |||
| + | [http://dx.doi.org/10.1177/002199837200600304 http://dx.doi.org/10.1177/002199837200600304] | ||
| + | |||
| + | <div id="4"></div> | ||
| + | [[#cite-4|[4]]]N. Carbajal. F. Mujika, ''Polymer Testing'', '''28, '''pág. 618–626 (2009). | ||
| + | |||
| + | [http://dx.doi.org/ http://dx.doi.org/]10.1016/j.polymertesting.2009.05.005 | ||
| + | |||
| + | <div id="5"></div> | ||
| + | [[#cite-5|[5]]]N. Carbajal. F. Mujika, ''Polymer Testing'', '''30, '''pág. 578–584 (2011). | ||
| + | |||
| + | [http://dx.doi.org/ http://dx.doi.org/]10.1016/j.polymertesting.2011.04.012 | ||
Revision as of 11:40, 7 May 2022
1 Introducción
Tsai and Wu [1] propusieron un criterio de fallo para materiales anisótropos sometidos a estados de tensión complejos. Mujika [2] propuso una nueva aproximación para el ensayo de flexión de 3 puntos de laminados multidireccionales basada en métodos energéticos. En este trabajo se pretende conocer el comportamiento de laminados composite unidireccionales frente a un estado de tensión plano debido a la existencia de momentos flectores en 2 planos.
2 Aproximación analítica
En la figura Figura 1 se muestra la configuración del ensayo realizado con flexión en dos planos.
Se han calculado las tensiones máximas en dirección de la fibra σx y en dirección perpendicular a la fibra σy
|
|
(1) |
donde P es la máxima carga, Lx es la luz entre apoyos en dirección de la fibra, Ly es la luz entre apoyos en dirección perpendicular a la fibra, L es la longitud total en dirección x y b es la longitud en dirección perpendicular a la pieza del laminado.
Asimismo se define B como el ratio entre las tensiones σx y σy.
|
|
(2) |
Sustituyendo las ecuaciones (1) en la ecuación (2) y considerando la condición de L/b = Lx/ Ly
|
|
(3) |
Si se define t como el ratio entre las luces Lx y Ly la ecuación (3) se puede expresar
|
|
(4) |
De acuerdo a la ecuación (4) la relación de tensiones σx y σy es igual al cuadrado de la relación entre luces Lx y Ly.
El criterio de Tsai-Wu [1] para caso de tensión plana cuando las únicas tensiones distintas de cero son σx y σy se expresa
|
|
(5) |
donde los parámetros F11, F22, F1 y F2 se obtienen a partir de estados uniaxiales de tensión mediante la siguientes expresiones
|
|
(6) |
siendo Xt la resistencia a tracción longitudinal, Xc la resistencia a compresión longitudinal, Yt la resistencia a tracción transversal e Yc la resistencia a compresión transversal.
Sin embargo el parámetro F12 precisa de un estado biaxial de tensiones para su obtención [3].
En la ecuación (5) se puede despejar F12
|
|
(7) |
Utilizando el criterio de la máxima energía de deformación para tensión plana cuando las únicas tensiones distintas de cero son σx y σy con valores de B mucho mayores que 1 la máxima energía de deformación por unidad de volumen U0 se puede aproximar al valor correspondiente al estado uniaxial de tensiones
|
|
(8) |
donde EL es el módulo longitudinal del material.
3 Parte experimental
Se han fabricado laminados de espesores nominales 2 y 3,5 mm y se han ensayado hasta rotura laminados con valores de t 0,25, 1, ,4, 5, 6 y 7 que corresponden a valores de B 0,0625, 1, 16, 25, 36 y 49.
En la Tabla 1 se muestran las dimensiones de las muestras
| Tabla 1. Dimensiones de las muestras
|
|||||
| Muestra | Lx(mm) | Ly (mm) | L(mm) | b(mm) | h(mm) |
| 0.25-20-2 | 20 | 80 | 25,4 | 101,1 | 2,00 |
| 1-40-2 | 40 | 20 | 50,7 | 50,3 | 1,99 |
| 1-60-2 | 60 | 20 | 75,4 | 76,2 | 2,02 |
| 4-80-2 | 80 | 20 | 100,6 | 26,1 | 2,00 |
| 4-80-3.5 | 80 | 20 | 100,5 | 25,5 | 3,50 |
| 5-100-3.5 | 100 | 20 | 125,3 | 25,8 | 3,38 |
| 6-120-3.5 | 120 | 20 | 150,6 | 25,7 | 3,39 |
| 7-140-3.5 | 140 | 20 | 175,7 | 25,4 | 3,52 |
En la tabla 2 aparecen los valores de Xt, Xc, Yt eYc. , donde Xt e Yt se han obtenido mediante flexión de 3 puntos utilizando una muestra de espesor nominal 2,53 mm y una luz de 80 mm y otra muestra de espesor nominal 2,69 y una luz de 30 mm respectivamente. Por otro lado Xc e Yc se han obtenido mediante flexión de 3 puntos [4, 5]
| Tabla 2. Propiedades resistentes de T6T/F593
| |||
| Xt(MPa) | XcMPa) | Yt(MPa) | Yc(MPa) |
| 1500 | -1100 | 100 | -400 |
En la Tabla 3 se muestran los valores de los coeficientes de Tsai-Wu obtenidos según las ecuaciones (5) a partir de los valores de la Tabla 1.
| Tabla 3. Valores de coeficientes de Tsai-Wu
| |||
| F11(MPa-2) | F22(MPa-2) | F1(MPa-1) | F2(MPa-1) |
| 5,56·10-7 | 2,50·10-5 | -1.67·10-4 | 7,50·10-3 |
4 Resultados
Todas las muestras ensayadas presentan relación lineal entre carga y desplazamiento hasta el momento de la rotura, tal como se observa en la Figura 2, que se produce de forma súbita
Todas las muestras sufren una rotura en transversal es decir la superficie de rotura es paralela a la dirección de la fibra según se muestra en la Figura 3.
En la Tabla 4 se muestran los valores de tensión máxima en dirección de la fibra σx y en dirección perpendicular a la fibra σy para las muestras con distinta valor de B.
| Tabla 4. Valores de tensiones σx y σy para cada muestra
| |||
| Muestra | B | σx(MPa) | σy(MPa) |
| 0.25-20-2 | 0.0625 | 6 | 101 |
| 1-40-2 | 1 | 94 | 93 |
| 1-60-2 | 1 | 89 | 90 |
| 4-80-2 | 16 | 600 | 39 |
| 4-80-3.5 | 80 | 695 | 44 |
| 5-100-3.5 | 25 | 798 | 33 |
| 6-120-3.5 | 36 | 986 | 28 |
| 7-140-3.5 | 49 | 1010 | 21 |
Para el caso de B menor que 1 las tensiones σy en dirección perpendicular a la fibra son mayores que la tensión en dirección de la fibra σx , por lo que el criterio de Rankine de la máxima tensión normal explica el fallo transversal en por alcanzarse en primer lugar el valor menor de los de la tabla 2.
Para el caso de B =1 también el criterio de Rankine explica el fallo transversal, aunque sin embargo las tensiones máximas que se obtienen son ligeramente menores que la resistencia a tracción transversal.
Para el caso de B mayor o igual que 1 se ha utilizado la ecuación (7) del criterio de Rankine para calcular el valor de F12. En la figura 4 se muestra la variación de F12 con el ratio de tensiones B. Se observa que al aumentar B el valor obtenido de F12 se hace ligeramente mayor que el valor medio.
Para el caso de B mayor que 1 en la Figura 5 se muestra la variación de σx con B, observándose que cuando B se hace mucho mayor que 1 σx tiende a un valor de 1000 MPa.
Por último el criterio de la máxima energía de deformación en caso de B mucho mayor que 1 es equivalente al caso uniaxial de tensiones en que σy es nula.
5 Conclusiones
Se ha analizado el comportamiento de laminados composites unidireccionales bajo un estado biaxial de tensiones σx en dirección de la fibra y σy en dirección perpendicular a la fibra ocasionado por flexión en dos planos, pudiendo ser el ratio entre estas tensiones, B, menor, igual o mayor que 1.
En todos los casos el fallo observado es transversal relacionado con el fallo de la matriz, incluso para valores del ratio de tensiones mucho más grandes que 1.
Cuando B es menor que 1 el criterio de Rankine explica bien el fallo transversal. Cuando B es igual a 1 los valores de tensión que se obtienen son ligeramente inferiores a la resistencia a tracción transversal.
Mediante el estado biaxial de tensiones producido por flexión en dos planos se puede obtener el valor del parámetro F12 del Criterio de Tsai-Wu.
Para valores de B mayores que 1 los valores de tensión en dirección de la fibra aumentan a medida que aumenta B y tienden a un valor próximo al valor de resistencia a compresión longitudinal cuando B es mucho mayor que 1.
Finalmente, para valores de B mucho mayores que 1 la máxima energía de deformación por unidad de volumen en estado biaxial de tensiones es independiente del valor de σy.
Agradecimientos
Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 16/51 en la convocatoria de 2016.
Referencias
[1] S.W. Tsai, E.M. Wu. Journal of Composite Materials, 5, pág. 58-80 (1971).
http://dx.doi.org/10.1177/002199837100500106
[2] F. Mujika, Journal of Composite Materials, 46, pág. 259-274 (2012).
http://dx.doi.org/10.1177/0021998311412636
[3] E.M. Wu, Journal of Composite Materials, 6, pág. 472-489 (1972).
http://dx.doi.org/10.1177/002199837200600304
[4]N. Carbajal. F. Mujika, Polymer Testing, 28, pág. 618–626 (2009).
http://dx.doi.org/10.1016/j.polymertesting.2009.05.005
[5]N. Carbajal. F. Mujika, Polymer Testing, 30, pág. 578–584 (2011).
http://dx.doi.org/10.1016/j.polymertesting.2011.04.012
Document information
Published on 20/01/19
Accepted on 20/01/19
Submitted on 20/01/19
Volume 03 - Comunicaciones Matcomp17 (2019), Issue Núm. 1 - Materiales (2), 2019
DOI: 10.23967/r.matcomp.2019.01.008
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?