| Line 317: | Line 317: | ||
|} | |} | ||
| − | donde | + | donde <math display="inline">Y</math> representa la variable de respuesta, <math display="inline">f</math> es la función de respuesta desconocida, <math display="inline">{x}_{1},{x}_{2},\ldots ,{x}_{k}</math> son las variables experimentales independientes y <math display="inline">\epsilon</math> es el error de ajuste que representa otras fuentes de variabilidad no contabilizadas para <math display="inline">f</math>. El objetivo principal del MSR es establecer una función aproximada entre los factores y las respuestas a través de una serie especial de experimentos y análisis estadístico. Para MSR, hay muchos modelos que se pueden utilizar para establecer las funciones para aproximaciones, pero el modelo más común es el polinomio basado en la expansión de la serie de Taylor. En este estudio, la aproximación de <math display="inline">f</math> será propuesta utilizando el modelo de regresión polinomial de segundo orden, que puede escribirse de la siguiente manera: |
{| class="formulaSCP" style="width: 48%;border-collapse: collapse;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 48%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| Line 329: | Line 329: | ||
|} | |} | ||
| − | donde <math display="inline">{\beta }_{0}</math> es la constante del modelo; <math display="inline">{\beta }_{i}</math> representa el término lineal; <math display="inline">{\beta }_{ii}</math> denota el término cuadrático; <math display="inline">{\beta }_{ij}</math> es el término de interacción; | + | donde <math display="inline">{\beta }_{0}</math> es la constante del modelo; <math display="inline">{\beta }_{i}</math> representa el término lineal; <math display="inline">{\beta }_{ii}</math> denota el término cuadrático; <math display="inline">{\beta }_{ij}</math> es el término de interacción; <math display="inline">k</math> es el número de factores o variables; y <math display="inline">\epsilon</math> es el error estadístico. Se debe implementar una serie de experimentos reales o de simulación para obtener los valores de la variable de respuesta, que se pueden registrar en el vector <math display="inline">Y</math>. La función aproximada entre las respuestas y los términos del modelo basados en el modelo polinomial cuadrático puede escribirse en la forma matricial de la siguiente manera: |
{| class="formulaSCP" style="width: 47%;border-collapse: collapse;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 47%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| Line 341: | Line 341: | ||
|} | |} | ||
| − | donde | + | donde <math display="inline">X</math> es una matriz de términos de modelo incluyendo los términos lineales, términos cuadrados y términos de interacción; <math display="inline">\beta</math> es un vector de columna que contiene los coeficientes de la pendiente; y <math display="inline">\, \epsilon</math> es el vector de error residual. El MSR se basan en tres tipos de matrices de diseño de experimentos (DOE), incluyendo diseños de compuestos centrales (DCC), diseño de Box-Behnken (DBB) y estimación de error cuadrático medio integrado óptimo (EIMSE-óptimo). Para evaluar el vector de coeficiente de regresión <math display="inline">\beta</math> del modelo predictivo, se puede utilizar el método de mínimos cuadrados. Se puede describir con la siguiente ecuación en la forma matriz: |
{| class="formulaSCP" style="width: 47%;border-collapse: collapse;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 47%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| Line 354: | Line 354: | ||
| − | donde <math display="inline">{X}^{T}</math> es la transpuesta de la matriz | + | donde <math display="inline">{X}^{T}</math> es la transpuesta de la matriz <math display="inline">X</math>. Para evitar la singularidad de la matriz <math display="inline">{X}^{T}X</math>, debe observarse que el número de puntos de diseño experimental debe ser mayor que el número de los coeficientes de la pendiente. |
===4.2. Diseño Box-Behnken=== | ===4.2. Diseño Box-Behnken=== | ||
| − | Para el diseño experimental, se seleccionó el método DBB porque ofrece un equilibrio razonable entre precisión de predicción y economía de ejecución. Requiere tres niveles de cada factor y es siempre de forma esférica. El diseño Box-Behnken fue específicamente seleccionado ya que requiere menos ejecuciones que un DCC en casos de tres o cuatro variables. Este diseño cúbico se caracteriza por un conjunto de puntos que se encuentran en el punto medio de cada borde de un cubo multidimensional y el punto central se replica (<math>n=5</math>) mientras que las "esquinas perdidas" ayudan al experimentador a evitar los factores extremos combinados. Esta propiedad evita una posible pérdida de datos en esos casos. Como se muestra en Figura 3(a), el sistema de calentamiento está definido por cuatro variables: la distancia del centro de la resistencia a la superficie de la cavidad, | + | Para el diseño experimental, se seleccionó el método DBB porque ofrece un equilibrio razonable entre precisión de predicción y economía de ejecución. Requiere tres niveles de cada factor y es siempre de forma esférica. El diseño Box-Behnken fue específicamente seleccionado ya que requiere menos ejecuciones que un DCC en casos de tres o cuatro variables. Este diseño cúbico se caracteriza por un conjunto de puntos que se encuentran en el punto medio de cada borde de un cubo multidimensional y el punto central se replica (<math>n=5</math>) mientras que las "esquinas perdidas" ayudan al experimentador a evitar los factores extremos combinados. Esta propiedad evita una posible pérdida de datos en esos casos. Como se muestra en [[#img-3|Figura 3]](a), el sistema de calentamiento está definido por cuatro variables: la distancia del centro de la resistencia a la superficie de la cavidad, <math display="inline">h</math>; la distancia de centro a centro de las resistencia, <math display="inline">a</math>; el flujo de calor por unidad de área, <math display="inline">q</math>; y el espesor de la placa del sistema de calentamiento, <math display="inline">b</math>. Por lo tanto, se eligió un diseño de ensayo Box-Behnken con 29 ensayos para cuatro factores y tres niveles. Entre los ensayos experimentales, 24 ensayos estan en el borde del espacio experimental y los otros se replicaron en el centro del cubo espacial. Las rangos de los cuatro factores se pueden definir basándose en la experiencia previa y el análisis de ingeniería. |
| − | Los tres niveles de los factores se enumeran en la Tabla 3. -1, 0 y +1 representan los niveles bajo, medio y alto de los factores, respectivamente. El diseño del experimento basado en DBB se puede ver en la Tabla 4. | + | Los tres niveles de los factores se enumeran en la [[#tab-3|Tabla 3]]. -1, 0 y +1 representan los niveles bajo, medio y alto de los factores, respectivamente. El diseño del experimento basado en DBB se puede ver en la [[#tab-4|Tabla 4]]. |
<div class="center" style="font-size: 75%;">'''Tabla 3'''. Niveles de los factores | <div class="center" style="font-size: 75%;">'''Tabla 3'''. Niveles de los factores | ||
</div> | </div> | ||
| − | {| style=" | + | <div id='tab-3'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | !Factor !! Nivel -1 !! Nivel 0 !! Nivel +1 | ||
|- | |- | ||
| − | | style=" | + | | style="vertical-align: top;"|h (''mm'') |
| − | + | | style="text-align: center;vertical-align: top;"|8.00 | |
| − | + | | style="text-align: center;vertical-align: top;"|10.00 | |
| − | + | | style="text-align: center;vertical-align: top;"|12.00 | |
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|- | |- | ||
| style="vertical-align: top;"|a (''mm'') | | style="vertical-align: top;"|a (''mm'') | ||
| Line 387: | Line 385: | ||
| style="text-align: center;vertical-align: top;"|3.00 | | style="text-align: center;vertical-align: top;"|3.00 | ||
|- | |- | ||
| − | | style=" | + | | style="vertical-align: top;"|b (mm) |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|20.00 |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|22.00 |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|24.00 |
|} | |} | ||
| Line 399: | Line 397: | ||
</div> | </div> | ||
| − | {| style=" | + | <div id='tab-4'></div> |
| − | |- | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | + | |-style="text-align:center" | |
| − | + | !No. de exp. !! h (mm) !! a (mm) !! q (w/<math display="inline"> {\mathit{\boldsymbol{m}}}^{\mathit{\boldsymbol{2}}}</math>) !! b (mm) !! <math display="inline">{\mathit{\boldsymbol{t}}}_{\mathit{\boldsymbol{cr}}}</math> (s) !! <math display="inline">{\mathit{\boldsymbol{t}}}_{\mathit{\boldsymbol{d}}}</math> (s) !! <math display="inline">{\mathit{\boldsymbol{\sigma }}}_{\mathit{\boldsymbol{v}}}</math> (MPa) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|1 | | style="border-top: 1pt solid black;text-align: center;vertical-align: top;"|1 | ||
Latest revision as of 16:09, 17 March 2021
Resumen
En el presente trabajo se presenta la optimización del sistema de calentamiento por resistencias eléctricas para un molde de respuesta térmica rápida (MRTR), usando la metodología de superficie de respuesta (MSR) así como una técnica de optimización. Aplicando la técnica de diseño de experimentos Box-Behnken, se diseñó una matriz de experimentos con cuatro factores y tres niveles. Las variables de diseño que se emplean para describir el diseño y la forma del sistema de calentamiento, son el flujo de calor por unidad de área de la resistencia eléctrica, las distancias desde el centro de los calentadores a la superficie de la cavidad, la distancia entre las resistencias eléctricas adyacentes y el espesor de la placa de calentamiento. El tiempo de calentamiento, la variación de la temperatura en la cavidad y los esfuerzos de Von-Mises fueron considerados como las variables del modelo. Se realizan análisis térmicos y de resistencia térmico-estructural del modelo basado en método de elemento finito (FEM por sus siglas en inglés) para adquirir las variables objetivas. Además, se desarrollan modelos matemáticos de superficie de respuesta mediante el modelo de regresión mixta y el modelo de superficie de respuesta y se emplea el método de análisis de varianza (ANOVA por sus siglas en inglés), para comprobar la exactitud de dichos modelos matemáticos. Con los modelos obtenidos, se optimiza la posición de las resistencias eléctricas y se reduce la relación entre masa y el volumen del inserto de la cavidad para minimizar el tiempo de calentamiento dentro de una distribución de temperatura y resistencia estructural razonables, acoplando los modelos de superficie de respuesta desarrollados con el método de optimización de enjambre de partículas (PSO por sus siglas en inglés). Los resultados obtenidos muestran que el tiempo de calentamiento requerido en la superficie de la cavidad se puede reducir significativamente en el ciclo de moldeo, demostrando con estos la efectividad del sistema de calentamiento.
Palabras clave: Molde de Respuesta Térmica Rápida (MRTR), moldeo por inyección, Optimización de Enjambre de Partículas (PSO), análisis térmico
Abstract
The aim of this work to optimization of the heating system by electrical resistances for a rapid thermal response mold (MRTR), using the response surface methodology (MSR). Applying the design technique of the Box-Behnken experiments, a matrix of experiments with four factors and three levels was designed. The design variables that are used to describe the design and shape of the heating system are the heat flux per unit area of the electrical resistance, the distances from the center of the heaters to the surface of the cavity, the distance between the adjacent electrical resistors and the thickness of the heating plate. The heating time, the variation of the temperature in the cavity and the Von-Mises stress were considered as the variables of the model. Thermal and thermal-structural resistance analyzes of the model based on finite element method (FEM) are performed to acquire the objective variables. Mathematical response surface models are developed using the mixed regression model and the response surface model and the variance analysis method (ANOVA) is used to verify the accuracy of these mathematical models. With the obtained models, the position of the electric resistances is optimized and the ratio between mass and volume of the cavity insert is reduced to minimize the heating time within a reasonable temperature distribution and structural strength, coupling the surface models of response developed with the method of particle swarm optimization (PSO). The results obtained indicate that the required heating time on the surface of the cavity can be significantly reduced in the molding cycle, demonstrating with these the effectiveness of the heating system.
Keywords: Rapid thermal response molding (RTRM), injection molding, Particle Swarm Optimization (PSO), thermal analysis
1. Introducción
Recientemente, la industria de los polímeros está creciendo de manera sorprendente, sobre todo en las últimas décadas, por lo que es necesario estudiar nuevas técnicas que mejoren los procesos de manufactura de partes plásticas, como inyección y extrusión. Las mejoras al proceso se han visto en tres principales áreas, las máquinas de inyección, los moldes y los polímeros. La temperatura del molde es un parámetro de procesamiento importante en el tiempo de ciclo, además, de afectar significativamente la calidad superficial de la pieza moldeada. Si la temperatura del molde es baja en el proceso de moldeado, se acorta el tiempo de ciclo, sin embargo, esto provocará que polímero fundido solidifique prematuramente, por lo tanto, da lugar a una calidad superficial pobre en la superficie de la pieza, rugosidad, líneas de soldadura, rechupes, entre otros defectos [1,2]. Para minimizar estos problemas desde el punto de vista de proceso, se requiere aumentar la presión y/o la velocidad de inyección [3]. Si la parte de plástico requiere de un alto aspecto de brillo, los defectos superficiales requieren ser eliminados mediante operaciones secundarias como el lijado y pulido. Estas operaciones aumentan el costo de producción, el tiempo total del proceso de producción y requieren energía consumida en procesos secundarios. Aumentar la temperatura en la superficie de la cavidad del molde hasta la temperatura de cristalización () mejora la calidad de la superficie de la pieza [4], pero esto extenderá el tiempo de ciclo en el proceso de moldeo regular.
Por esta razón, recientemente se ha desarrollado una nueva tecnología de moldeo llamada MRTR para satisfacer las exigencias cada vez más estrictas de las piezas de plástico. En este proceso de moldeo, la temperatura de la cavidad del molde se cambia alternativamente mediante un rápido calentamiento y enfriamiento en cada ciclo de moldeo. Debido a la elevada temperatura de la cavidad del molde, el polímero fundido llena fácilmente la superficie de la cavidad del molde y por lo tanto pueden moldearse piezas de alto brillo. Para variar la temperatura de la cavidad del molde sin un aumento significativo en el tiempo de ciclo, se requiere una técnica rápida de calentamiento del molde. En los últimos años, se han propuesto algunos métodos rápidos de calentamiento del molde. Estos métodos se pueden dividir principalmente en dos categorías: calefacción externa y calefacción interna. La primera categoría incluye principalmente calentamiento por inducción [5], calentamiento asistido por gas [6], calentamiento con alta frecuencia [7], calentamiento por infrarrojos [8], entre otros métodos de calentamiento. En cuanto a la segunda categoría, se tiene el calentamiento asistida por vapor [9], calentamiento por fluido [10-12] y calentamiento por resistencias eléctricas [13-15] son los métodos más utilizados.
Los métodos de calentamiento externos tienen una buena eficiencia en el calentamiento, así como un costo elevado, además la estructura compleja de los moldes limita sus aplicaciones en la producción real. En aplicaciones prácticas, los métodos de calentamiento interno son preferidos en términos de su mejor adaptabilidad y estabilidad, particularmente para el molde con un volumen relativamente grande. Algunos canales se perforan dentro del molde para transportar el medio caliente o instalar los elementos de calentamiento eléctrico.Los métodos de calentamiento por fluido [10-12] han mostrado una eficiencia mayor en el calentamiento; sin embargo, la infraestructura y costo para su funcionamiento es mayor que la que se requiere en un sistema de calentamiento por resistencias eléctricas, éstas presentan además de las ventajas mencionadas, el mantenimiento casi nulo y el reemplazo de cualquier componente en caso de avería es mínimo y económico. Para obtener el mejor rendimiento del sistema de calentamiento en términos de la distribución de la temperatura en la superficie de la cavidad del molde y la eficiencia de calentamiento, es necesario optimizar la posición de los elementos de calentamiento en el molde. Para solucionar este problema, se han propuesto algunos métodos de diseño de optimización. Li et al. [16], propusieron la estrategia de optimización combinando la metodología de la superficie de respuesta (MSR) con el algoritmo genético (AG) para optimizar el diseño de los canales de calentamiento para un molde de inyección de calentamiento rápido con calentamiento asistido por vapor. Una red neuronal artificial (RNA) [17], suele construir para las variables definidas de un proceso o sistema ajustando una ecuación polinomial, muy semejante a la obtenida por la MSR y estar acoplada a un AG para su optimización [18]. Sin embargo, se ha demostrado que el método de búsqueda estocástico para la optimización, llamado PSO resulta ser más rápido y mejor que las redes neuronales y los algoritmos genéticos [19-22].
En este artículo se presenta la optimización del sistema de calentamiento por resistencias eléctricas para un molde de respuesta térmica rápida (MRTR), usando la metodología de superficie de respuesta (MSR) así como una técnica de optimización. Aplicando la técnica de diseño de experimentos Box-Behnken, se diseñó una matriz de experimentos con cuatro factores y tres niveles. Las variables de diseño que se emplean para describir el diseño y la forma del sistema de calentamiento, son el flujo de calor por unidad de área de la resistencia eléctrica, las distancias desde el centro de los calentadores a la superficie de la cavidad, la distancia entre las resistencias eléctricas adyacentes y el espesor de la placa de calentamiento. El tiempo de calentamiento, la variación de la temperatura en la cavidad y los esfuerzos de Von-Mises fueron considerados como las variables del modelo. Se realizan análisis térmicos y de resistencia térmico-estructural del modelo basado en método de elemento finito (MEF) para adquirir las variables objetivas. Además, se desarrollan modelos matemáticos de superficie de respuesta mediante el modelo de regresión mixta y el modelo de superficie de respuesta y se emplea el método de análisis de varianza (ANOVA), para comprobar la exactitud de dichos modelos matemáticos. Con los modelos obtenidos, se optimiza la posición de las resistencias eléctricas y se reduce la relación entre masa y el volumen del inserto de la cavidad para minimizar el tiempo de calentamiento dentro de una distribución de temperatura y resistencia estructural razonables, acoplando los modelos de superficie de respuesta desarrollados con el método de optimización de enjambre de partículas (PSO, por sus siglas en inglés). Los resultados obtenidos muestran que el tiempo de calentamiento requerido en la superficie de la cavidad se puede reducir significativamente en el ciclo de moldeo, demostrando con estos la efectividad del sistema de calentamiento.
2. Modelo físico y matemático del molde de respuesta térmica rápida (MRTR)
En la presente sección se presenta la estructura física del molde a evaluar, se muestra la cavidad del molde, las resistencias eléctricas, los canales de enfriamiento, los materiales utilizados y las condiciones de frontera, además, los fundamentos matemáticos necesarios para la evaluación de la respuesta térmica en el molde de inyección.
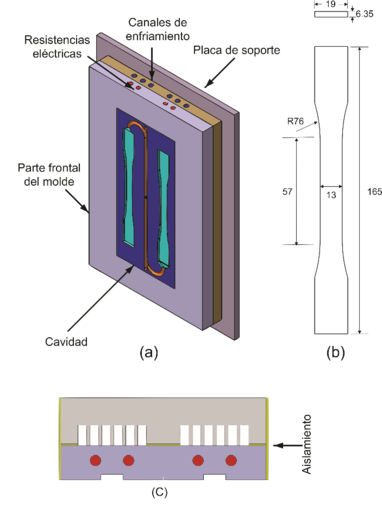
La principal diferencia entre el moldeo por inyección convencional (MIC) y el moldeo con un MRTR es la estrategia de control de la temperatura del molde. En el MRTR, el molde debe calentarse y enfriarse rápidamente para lograr un moldeo por inyección a alta temperatura sin aumentar demasiado el tiempo de ciclo de moldeo. La Figura 1 muestra de manera esquemática el MRTR que se diseña y propone en este trabajo. En la Figura 1(a), se observan los componentes principales del molde, canales de enfriamiento, resistencias eléctricas, placa retenedora, inserto, entre otros, el molde propuesto está bajo dimensiones estandarizadas de la empresa HASCO®, de . La Figura 1(b), se especifica las dimensiones de la pieza final, así como la cavidad del MRTR. Para este trabajo se propuso una probeta de tensión en base a la norma ASTM D638-03 [23], tipo I. La Figura 1(c) muestra un plano de corte trasversal del MRTR, el corte se realizó en el centro de la probeta de tensión.
Un control dinámico de la temperatura del molde se implementa calentando y enfriando el molde en cada ciclo del proceso, por lo que la transferencia de calor es muy diferente a la del proceso MIC. En la etapa de calentamiento del molde, este debe ser calentado hasta la temperatura preestablecida utilizando resistencias eléctricas. Wang propone que, para una mejor apariencia de la pieza plastica, la temperatura en la superficie de la cavidad del molde debe ser en promedio la temperatura de cristalización del polímero en la etapa del llenado [4]. El calor generado se transfiere principalmente al acero del molde a través de la conducción del calor, solamente una pequeña cantidad de calor se acumula en las resistencias eléctricas así como el marco del molde y el resto se disipa al ambiente.
| Figura 1. Esquema del MRTR para una probeta de tensión. (a) Isométrico del MRTR. (b) Probeta de tensión, unidades en mm, (c) Corte de sección transversal del MRTR |
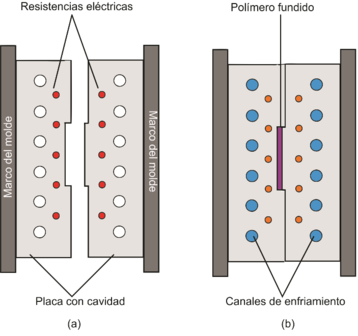
La Figura 20(a), ilustra esquemáticamente la transferencia de calor en la etapa de calentamiento del MRTR con calentamiento eléctrico. Basándose en la ley de conservación de energía, la ecuación de equilibrio de transferencia de calor del molde durante la etapa de calentamiento puede expresarse:
|
|
(1) |
donde es el calor generado por las resistencias eléctricas; es el calor transferido al acero del molde; indica el calor acumulado en las resistencias; y representan el calor disipado al ambiente y al marco del molde en la etapa de calentamiento del molde, respectivamente.
Los , y son bastante pequeños en comparación con el y por lo tanto tienen efectos despreciables sobre el campo de temperatura del molde durante el calentamiento. Así, la ec. (1) se puede simplificar como [24,25]:
|
|
(2) |
donde y puede ser representado como:
|
|
(3) |
|
|
(4) |
donde es la potencia total de las resistencias eléctricas; es el tiempo de calentamiento requerido; es la temperatura inicial del molde; es la temperatura media del molde en el tiempo ; , y representan el calor especifico, densidad y volumen del molde, respectivamente.
Sustituyendo las ecs. (3) y (4) en (2) se obtiene la siguiente expresión:
|
|
(5) |
Cuando se moldea una pieza de plástico específica usando un MRTR, las y están generalmente predeterminadas y por lo tanto pueden considerarse constantes. De aquí que, depende principalmente de los parámetros , , y . La eficiencia de calentamiento del molde se puede mejorar, es decir, el en la ec. (5) se puede minimizar reduciendo los valores de , , y/o aumentando el valor del .
El producto de y para la mayoría de los materiales del molde tiene poca diferencia, por lo que la forma de seleccionar el material del molde con menor y para mejorar la eficiencia de calefacción del molde no es la adecuada [26]. Por lo tanto, bajo la condición de resistencia y rigidez estructural del molde adecuadas, el volumen del molde calentado debe reducirse tanto como sea posible para reducir la capacidad calorífica del molde. Además, aumentar el número y/o potencia de las resistencias eléctricas adecuadamente puede mejorar aún más la eficiencia de calentamiento del molde.
En la Figura 2(b), se muestra la etapa de enfriamiento del molde, en esta, se bombea refrigerante a los canales de enfriamiento del molde para enfriar rápidamente el molde y la pieza moldeada. El calor acumulado en el molde de acero y las resistencias eléctricas en la etapa de calentamiento, así como el calor liberado de la masa fundida de polímero, durante el enfriamiento son eliminados por el refrigerante en circulación; además, una pequeña cantidad de calor se disipa al ambiente y al marco del molde.
| Figura 2. Esquemas de transferencia de calor del MRTR con calentamiento eléctrico. (a) Calentamiento. (b) Enfriamiento |
La ecuación de equilibrio de transferencia de calor del molde durante el enfriamiento puede expresarse como:
|
|
(6) |
donde es el calor liberado del polímero fundido; representa el calor removido por el refrigerante; y representan el calor disipado al ambiente y al marco del molde en la etapa de enfriamiento del molde, respectivamente [27,28].
El y pueden ser representados por las siguientes expresiones:
|
|
(7) | ||
| (8) | |||
donde , y representan el calor específico, la densidad y el volumen de la masa fundida de polímero, respectivamente; es la temperatura inicial del polímero fundido; es la temperatura de eyección de la pieza; es el coeficiente de transferencia de calor por convección en la interfase entre el refrigerante y los canales de enfriamiento; es la superficie interna de los canales de refrigeración; representa el tiempo de enfriamiento requerido; indica la temperatura media de la pared de los canales de refrigeración en el instante t; y es el valor promedio de la temperatura del refrigerante.
Al sustituir las ecs. (4), (7) y (8) en (6), se puede obtener la siguiente expresión:
|
|
(9) |
Los efectos de , y en el campo de temperatura del molde durante el enfriamiento pueden ser despreciables, de modo que la ec. (10) se puede expresar como:
|
|
(10) |
Mediante el uso del teorema del valor medio de las integrales, la ec. (10) se puede representar como la siguiente expresión:
|
|
(11) |
para valores .
Para el moldeo de una parte de plástico específica, se predetermina el material polimérico correspondiente, el volumen de pieza y los parámetros de procesamiento, es decir, el , , , , , , en la ec. (11) pueden considerarse constantes. Por lo tanto, el depende principalmente de los parámetros , , , y . Para mejorar la eficiencia de enfriamiento del molde, es decir, acortar el valor de en la ec. (11), se necesita disminuir los valores de , , y y/o aumentar los valores de y . La opción de minimizar el volumen del molde para mejorar la eficiencia de calentamiento del molde también puede mejorar la eficiencia de enfriamiento del molde. Además, la eficiencia de enfriamiento del molde puede mejorarse adicionalmente aumentando el caudal de refrigerante, bajando la temperatura del refrigerante y aumentando el área de enfriamiento del molde.
3. Análisis térmico y estructural (Análisis térmico-estructural)
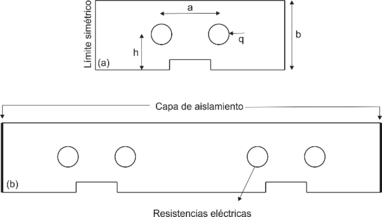
El análisis térmico transitorio y el análisis estructural se implementaron con base en un software comercial de ANSYS® para analizar la respuesta térmica y la resistencia estructural del MRTR. Para este molde, el sistema de calentamiento por resistencias eléctricas se puede utilizar para un calentamiento uniforme y eficiente. La geometría propuesta para la cavidad del molde es una probeta de tensión, la sección de mayor importancia es donde se concentra la carga y se provoca la falla (cuello de la probeta) y por consecuencia es el área de análisis de este trabajo. La Figura 3(a), muestra la geometría total del inserto de la cavidad que será calentado, en la Figura 3(b), se observa la simplificación de la geometría para la simulación térmica-estructural, esta simplificación es el resultado de parte central de la probeta de tensión, que es donde se concentra los esfuerzos y la falla mecánica.
En esta ilustración , y representan la distancia de centro a centro de las resistencias, la altura del centro de la resistencia a la superficie de la cavidad y el flujo de calor por unidad de área, respectivamente.
| Figura 3. Geometría del inserto de la cavidad. (a) Geometría simétrica para la simulación. (b) Geometría total |
El material del molde es un acero pre-endurecido (AISI P20) y sus propiedades físicas se describen en la Tabla 1.
| Propiedad física | Valor |
|---|---|
| Material | AISI P-20 |
| Densidad | 7850 kg/ |
| Calor específico | 460 kJ/°C |
| Conductividad térmica | 34 W/m°C |
| Módulo de elasticidad | 205 GPa |
| Coeficiente de Poisson | 0.285 |
3.1. Análisis de respuesta térmica
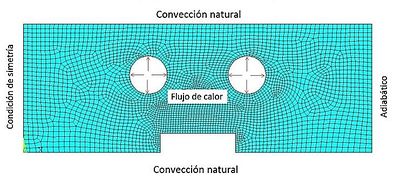
El modelo de malla y las condiciones de frontera en el análisis transitorio de transferencia de calor se muestran en la Figura 4. Se considera la temperatura inicial de 60°C, equivalente a la temperatura de trabajo en un proceso industrial en un periodo transitorio estable.
| Figura 4. Modelo de malla y condiciones de frontera para análisis transitorio de transferencia de calor |
El ciclo de moldeo en el MRTR inicia abierto y sin fluido refrigerante en el sistema de enfriamiento, el sistema de enfriamiento y calentamiento está dividido por una delgada capa de aislamiento (Figura 3c), se eleva la temperatura del molde por medio de las resistencias eléctricas hasta alcanzar la promedio en la superficie de la cavidad, la condición de convección de aire libre se cargó en la superficie externa del molde y el coeficiente de transferencia de calor convectivo correspondiente fue de 20 °C [30]. Para la parte lateral izquierda se implementó una condición de simetría que permite reducir el modelo de malla, en cuanto a la parte lateral derecha, se aplicó un flujo de calor de cero por defecto debido a la capa de aislamiento. El medio para calentar el inserto del molde son resistencias eléctricas.
3.2. Análisis térmico-estructural
En la fase de llenado y empaquetamiento, la superficie de la cavidad del molde sufrira una presión de cavidad grande. Por lo tanto, el molde debe ser lo suficientemente fuerte para reducir la deformación de la superficie de la caviad y mejorar su durabilidad. La posicion de las resistencias electricas tiene un gran efecto sobre la eficiencia de la respuesta termica del molde, ademas de tener un efecto significativo en su resistencia estructural. Por ejemplo, situar las resistencias eléctricas mucho cerca de la supercie del molde puede aumentar la eficiencia de calentamiento, pero disminuir la resistencia estructural del molde. El volumen de la placa de acero que se desea calentar es otro factor importante que se requiere estudiar para reducir el tiempo de calentamiento en el ciclo de moldeo, al reducir el volumen de la placa del sistema de calentamiento, en consecuencia, el tiempo de calentamiento se reducirá. Como resultado, es necesario estudiar el espesor de la placa del sistema de calentamiento y el efecto de la posición de las resistencias eléctricas sobre la resistencia estructural del molde. La presión del polímero causada por la etapa de llenado se calculó mediante una simulación de moldeo por inyección usando Moldex3D. Los parámetros de moldeo por inyección se eligieron considerando el uso de un polietileno de alta densidad (PEMEX, PADMEX 60120-U) con condiciones de trabajo mostradas en la Tabla 2.
| Parámetro | Valor |
|---|---|
| Temperatura de inyección | 200 0C |
| Temperatura del molde | 60 0C |
| Tiempo de inyección de moldeo | 1 s |
| Llenado de cavidad | 98% del volumen total de llenado |
| Presión de empaquetamiento | 80MPa |
| T. de presión de empaquetamiento | 5.13 s |
En la Figura 5, se muestra el perfil de presión de la cavidad a lo largo del tiempo. La presión de inyección máxima, alcanzada en correspondencia con el corredor principal, fue de 65 MPa. A través de esta simulación por volumenes finitos, la distribución de carga se determinó y se usó como condición de frontera en la simulación estructural subsiguiente. Sin embargo, para simplificar la configuración de la simulación estructural y por razones de seguridad, se consideró una presión de inyección de 90 MPa aplicada en la superficie de la cavidad, aunque el valor maximo de la presion de inyección se alcanzó solo en la posición central, debajo del bebedero.
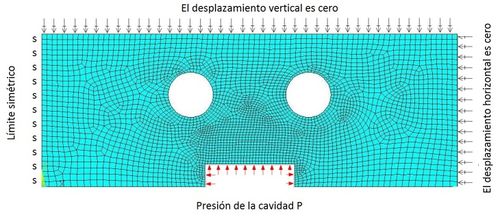
La Figura 6, muestra el modelo de malla y las condiciones de frontera para el análisis de resistencia estructural. En esta ilustración, P representa la presión de inyección.
| Figura 5. Perfil de presión de la cavidad del molde en la etapa de llenado |
| Figura 6. Modelo de malla y condiciones del análisis térmico-estructural |
En el límite izquierdo del modelo, la condición de simetría es implementada, en le límite derecho, el desplazamiento en la dirección normal es cero. Dado que los insertos de molde son soportados por la placa de retención para la fijación, el desplazamiento en el borde inferior del modelo es también cero en la dirección vertical.
4. Trabajo experimental
Para estudiar la relación entre el espesor del inserto del sistema de calentamiento, la posición de las resistencias eléctricas, la eficiencia de respuesta térmica, uniformidad de temperatura y resistencia estructural del MRTR, se implementó la metodología de la superficie de respuesta combinada con la regresión mixta para obtener los correspondientes modelos matemáticos.
4.1. Modelo de superficie de respuesta
El modelo de superficie de respuesta es una función analítica útil para describir la relación numérica entre las variables experimentales controlables y las variables de respuesta. En MSR, la forma cuantitativa de relación entre las variables experimentales y la variable de respuesta deseada puede expresarse mediante la siguiente expresión:
|
|
(12) |
donde representa la variable de respuesta, es la función de respuesta desconocida, son las variables experimentales independientes y es el error de ajuste que representa otras fuentes de variabilidad no contabilizadas para . El objetivo principal del MSR es establecer una función aproximada entre los factores y las respuestas a través de una serie especial de experimentos y análisis estadístico. Para MSR, hay muchos modelos que se pueden utilizar para establecer las funciones para aproximaciones, pero el modelo más común es el polinomio basado en la expansión de la serie de Taylor. En este estudio, la aproximación de será propuesta utilizando el modelo de regresión polinomial de segundo orden, que puede escribirse de la siguiente manera:
|
|
(13) |
donde es la constante del modelo; representa el término lineal; denota el término cuadrático; es el término de interacción; es el número de factores o variables; y es el error estadístico. Se debe implementar una serie de experimentos reales o de simulación para obtener los valores de la variable de respuesta, que se pueden registrar en el vector . La función aproximada entre las respuestas y los términos del modelo basados en el modelo polinomial cuadrático puede escribirse en la forma matricial de la siguiente manera:
|
|
(14) |
donde es una matriz de términos de modelo incluyendo los términos lineales, términos cuadrados y términos de interacción; es un vector de columna que contiene los coeficientes de la pendiente; y es el vector de error residual. El MSR se basan en tres tipos de matrices de diseño de experimentos (DOE), incluyendo diseños de compuestos centrales (DCC), diseño de Box-Behnken (DBB) y estimación de error cuadrático medio integrado óptimo (EIMSE-óptimo). Para evaluar el vector de coeficiente de regresión del modelo predictivo, se puede utilizar el método de mínimos cuadrados. Se puede describir con la siguiente ecuación en la forma matriz:
|
|
(15) |
donde es la transpuesta de la matriz . Para evitar la singularidad de la matriz , debe observarse que el número de puntos de diseño experimental debe ser mayor que el número de los coeficientes de la pendiente.
4.2. Diseño Box-Behnken
Para el diseño experimental, se seleccionó el método DBB porque ofrece un equilibrio razonable entre precisión de predicción y economía de ejecución. Requiere tres niveles de cada factor y es siempre de forma esférica. El diseño Box-Behnken fue específicamente seleccionado ya que requiere menos ejecuciones que un DCC en casos de tres o cuatro variables. Este diseño cúbico se caracteriza por un conjunto de puntos que se encuentran en el punto medio de cada borde de un cubo multidimensional y el punto central se replica () mientras que las "esquinas perdidas" ayudan al experimentador a evitar los factores extremos combinados. Esta propiedad evita una posible pérdida de datos en esos casos. Como se muestra en Figura 3(a), el sistema de calentamiento está definido por cuatro variables: la distancia del centro de la resistencia a la superficie de la cavidad, ; la distancia de centro a centro de las resistencia, ; el flujo de calor por unidad de área, ; y el espesor de la placa del sistema de calentamiento, . Por lo tanto, se eligió un diseño de ensayo Box-Behnken con 29 ensayos para cuatro factores y tres niveles. Entre los ensayos experimentales, 24 ensayos estan en el borde del espacio experimental y los otros se replicaron en el centro del cubo espacial. Las rangos de los cuatro factores se pueden definir basándose en la experiencia previa y el análisis de ingeniería.
Los tres niveles de los factores se enumeran en la Tabla 3. -1, 0 y +1 representan los niveles bajo, medio y alto de los factores, respectivamente. El diseño del experimento basado en DBB se puede ver en la Tabla 4.
| Factor | Nivel -1 | Nivel 0 | Nivel +1 |
|---|---|---|---|
| h (mm) | 8.00 | 10.00 | 12.00 |
| a (mm) | 14.00 | 18.00 | 22.00 |
| q (w/ ) | 1.00 | 2.00 | 3.00 |
| b (mm) | 20.00 | 22.00 | 24.00 |
Para evaluar la influencia del sistema en la eficiencia de calentamiento, la uniformidad de la temperatura y la resistencia estructural, se definen tres variables de respuesta. Se utilizó el tiempo de calentamiento requerido, , para que toda la superficie del molde se calentara a la temperatura designada.
| No. de exp. | h (mm) | a (mm) | q (w/) | b (mm) | (s) | (s) | (MPa) |
|---|---|---|---|---|---|---|---|
| 1 | 10.00 | 14.00 | 2.00 | 20.00 | 17.8 | 10.68 | 448 |
| 2 | 12.00 | 22.00 | 2.00 | 22.00 | 28.9 | 3.564 | 545 |
| 3 | 8.00 | 18.00 | 2.00 | 20.00 | 18.85 | 4.564 | 499 |
| 4 | 8.00 | 18.00 | 1.00 | 22.00 | 49.7 | 2.665 | 525 |
| 5 | 10.00 | 18.00 | 1.00 | 20.00 | 47.25 | 3.921 | 511 |
| 6 | 12.00 | 18.00 | 2.00 | 24.00 | 28.45 | 5.756 | 505 |
| 7 | 10.00 | 22.00 | 2.00 | 24.00 | 29.4 | 1.891 | 543 |
| 8 | 10.00 | 18.00 | 3.00 | 20.00 | 13.7 | 7.22 | 505 |
| 9 | 10.00 | 18.00 | 3.00 | 24.00 | 15.8 | 6.083 | 502 |
| 10 | 12.00 | 18.00 | 3.00 | 22.00 | 16.95 | 7.814 | 530 |
| 11 | 10.00 | 22.00 | 2.00 | 20.00 | 24.45 | 2.892 | 538 |
| 12 | 10.00 | 18.00 | 2.00 | 22.00 | 23.4 | 5.716 | 500 |
| 13 | 10.00 | 18.00 | 2.00 | 22.00 | 23.4 | 5.713 | 499 |
| 14 | 10.00 | 14.00 | 1.00 | 22.00 | 48.65 | 5.795 | 473 |
| 15 | 10.00 | 18.00 | 2.00 | 22.00 | 23.4 | 5.714 | 499 |
| 16 | 10.00 | 18.00 | 2.00 | 22.00 | 23.4 | 5.711 | 499 |
| 17 | 12.00 | 18.00 | 2.00 | 20.00 | 22.55 | 7.166 | 578 |
| 18 | 8.00 | 18.00 | 3.00 | 22.00 | 12.5 | 3.882 | 502 |
| 19 | 10.00 | 22.00 | 1.00 | 22.00 | 57.6 | 1.431 | 542 |
| 20 | 8.00 | 14.00 | 2.00 | 22.00 | 15.95 | 9.935 | 449 |
| 21 | 12.00 | 14.00 | 2.00 | 22.00 | 22.85 | 9.148 | 482 |
| 22 | 10.00 | 22.00 | 3.00 | 22.00 | 17.85 | 2.416 | 548 |
| 23 | 10.00 | 14.00 | 3.00 | 22.00 | 12.15 | 11.86 | 447 |
| 24 | 10.00 | 18.00 | 1.00 | 24.00 | 58.45 | 2.983 | 515 |
| 25 | 8.00 | 18.00 | 2.00 | 24.00 | 21.8 | 3.564 | 507 |
| 26 | 12.00 | 18.00 | 1.00 | 22.00 | 55.85 | 3.571 | 509 |
| 27 | 10.00 | 18.00 | 2.00 | 22.00 | 23.4 | 5.716 | 499 |
| 28 | 10.00 | 14.00 | 2.00 | 24.00 | 21.3 | 9.462 | 450 |
| 29 | 8.00 | 22.00 | 2.00 | 22.00 | 24.65 | 0.814 | 540 |
El polímero inyectado es un PADMEX 60120-U suministrado por la empresa PEMEX, el cual presenta una de 116 [31,32], temperatura que se utiliza para evaluar la eficiencia de calentamiento en el presente trabajo. El esfuerzo máximo de Von Mises, , ejercido sobre el molde se utilizó para evaluar la resistencia estructural. La diferencia de las temperaturas máxima y mínima superficial del molde, . Los resultados de la simulación con los parámetros iniciales, es decir, todos los factores en nivel cero, muestran que la mayoría de la superficie de la cavidad se ha calentado a la temperatura designada después de un calentamiento de 23.4 s.
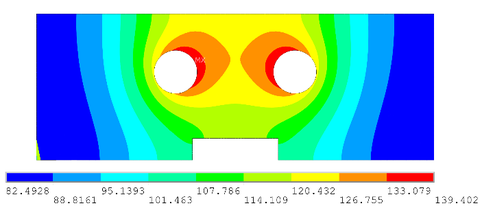
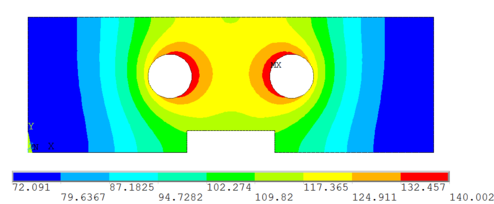
La Figura 7 muestra la gráfica de contorno de la distribución de la temperatura en la superficie de la cavidad cuando se termina el proceso de calentamiento para el sistema de calentamiento del molde con los parámetros iniciales. El largo tiempo de calentamiento y diferencia de temperatura de la superficie de la cavidad fuera de norma conducirá a un largo tiempo de ciclo de moldeo y baja calidad del producto.
| Figura 7. Gráfica de contorno de distribución de temperaturas con parámetros iniciales |
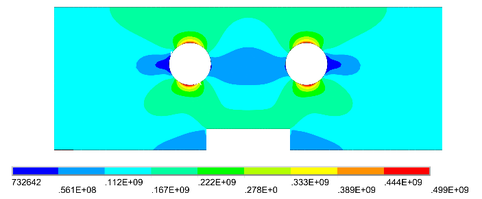
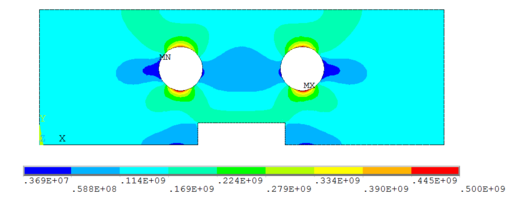
La Figura 8 muestra la distribución de los esfuerzos de Von Mises en la placa de calentamiento en los parámetros iniciales del diseño de experimentos, se observa en la posición de las resistencias eléctricas es donde se concentra los esfuerzos máximos.
| Figura 8. Esfuerzos de Von Mises con parámetros iniciales |
5. Resultados y discusión
De acuerdo con el resultado de DBB, se realizaron análisis de respuesta térmica y análisis de resistencia estructural basado en análisis de elementos finitos (FEA, por sus siglas en inglés) para obtener los valores de las diferentes variables de respuesta. Los resultados experimentales se presentan en la Tabla 4. Las variables de respuesta obtenidas de los experimentos se analizaron por regresión múltiple lineal para determinar los modelos matemáticos con mejores resultados. La adecuación y fiabilidad de los modelos de regresión también se probaron mediante el análisis de varianza (ANOVA).
5.1 Análisis de varianza
Se aplicó un ANOVA para examinar la importancia de los términos del modelo cuadrático. Los resultados de la ANOVA para el modelo cuadrático del tiempo de calentamiento requerido, , se presentan en la Tabla 5.
| Fuente | Sum. de cuadrados | DF | M. de Cuadrado | Valor F | Valor P (Prob>F) | |
| Modelo | 5511.50 | 9 | 612.39 | 2019.83 | < 0.0001 | |
| A-h | 85.87 | 1 | 85.87 | 283.21 | < 0.0001 | |
| B-a | 162.44 | 1 | 162.44 | 535.76 | < 0.0001 | |
| C-w | 4352.93 | 1 | 4352.93 | 14357.1 | < 0.0001 | |
| D-b | 78.03 | 1 | 78.03 | 257.36 | < 0.0001 | |
| AB | 1.76 | 1 | 1.76 | 5.79 | 0.0265 | |
| AD | 2.18 | 1 | 2.18 | 7.18 | 0.0149 | |
| BC | 2.64 | 1 | 2.64 | 8.71 | 0.0082 | |
| CD | 20.70 | 1 | 20.70 | 68.28 | < 0.0001 | |
| 804.97 | 1 | 804.97 | 2655.02 | < 0.0001 | ||
| Residual | 5.76 | 19 | 0.30 | |||
| F. de ajuste | 5.76 | 15 | 0.38 | |||
| Error puro | 0.000 | 4 | 0.000 | |||
| Total | 5517.27 | 28 | ||||
| Desv. Est. | 0.55 | R-Cuadrada | 0.9990 | |||
| Media | 27.60 | R-Cuadrada ajustada | 0.9985 | |||
| C.V.% | 2.00 | R-Cuadrada de la predicción | 0.9969 | |||
| PRESS | 17.20 | Precisión adecuada | 141.596 | |||
La suma de cuadrados en la tabla se refiere a la suma de cuadrados para cada término, que mide la variabilidad en los datos aportados por el término. DF representa el número de términos que contribuirán a la predicción del error. El valor del modelo F de 2019.83 indica que el modelo se considera estadísticamente significativo. Los valores de Valor P (Prob>F) inferiores a 0.0500 indican que los términos del modelo son significativos. En este caso A, B, C, D, AB, AD, BC, CD, son términos de modelo significativos. Los valores superiores a 0.1000 indican que los términos del modelo no son significativos. La R-Cuadrada de la predicción es de 0.9969 está en un acuerdo razonable con la R-Cuadrada ajustada de 0.9985. La Precisión adecuada mide la relación señal/ruido. Es deseable una relación mayor que 4. La relación es de 141.596 lo que indica una señal adecuada. Este modelo se puede utilizar para navegar por el espacio de diseño.
Los resultados del análisis de ANOVA para la diferencia de las temperaturas máxima y mínima superficial del molde, , se presentan en la Tabla 6. El valor del modelo F es de 188.18 implica que el modelo es significativo. Los valores de Valor P (Prob>F) inferiores a 0.0500 indican que los términos del modelo son significativos. En este caso A, B, C, D, AB, AC, BC, , y son términos de modelo significativos. La R-Cuadrada de la predicción de 0.9557 está en un acuerdo razonable con la R-Cuadrada ajustada de 0.9853. La Precisión adecuada mide la relación señal/ruido. Es deseable una relación mayor que 4. La relación de 54.749 indica una señal adecuada. Este modelo se puede utilizar para navegar por el espacio de diseño.
| Fuente | Sum. de cuadrados | DF | M. de Cuadrado | Valor F | Valor P (Prob>F) | |
| Modelo | 224.98 | 10 | 22.50 | 188.18 | < 0.0001 | |
| A-h | 11.20 | 1 | 11.20 | 93.71 | < 0.0001 | |
| B-a | 160.43 | 1 | 160.43 | 1341.9 | < 0.0001 | |
| C-w | 29.80 | 1 | 29.80 | 249.22 | < 0.0001 | |
| D-b | 3.75 | 1 | 3.75 | 31.37 | < 0.0001 | |
| AB | 3.13 | 1 | 3.13 | 26.16 | < 0.0001 | |
| AC | 2.29 | 1 | 2.29 | 19.15 | 0.0004 | |
| BC | 6.45 | 1 | 6.45 | 53.96 | < 0.0001 | |
| 1.29 | 1 | 1.29 | 10.76 | 0.0042 | ||
| 1.64 | 1 | 1.64 | 13.73 | 0.0016 | ||
| 4.17 | 1 | 4.17 | 34.89 | < 0.0001 | ||
| Residual | 2.15 | 18 | 0.12 | |||
| F. de ajuste | 2.15 | 14 | 0.15 | 34158 | < 0.0001 | |
| Error puro | 1.800E-005 | 4 | 4.5 E-6 | |||
| Total | 227.13 | 28 | ||||
| Desv. Est. | 0.35 | R-Cuadrada | 0.9905 | |||
| Media | 5.44 | R-Cuadrada ajustada | 0.9853 | |||
| C.V.% | 6.36 | R-Cuadrada de la predicción | 0.9557 | |||
| PRESS | 10.07 | Precisión adecuada | 54.749 | |||
Los resultados del análisis de ANOVA para la los Esfuerzos de Von Mises se presentan en la Tabla 7. El valor del modelo F es de 26.89 implica que el modelo es significativo. Los valores de Valor P (Prob>F) inferiores a 0.0500 indican que los términos del modelo son significativos.
| Fuente | Sum. de cuadrados | DF | M. de Cuadrado | Valor F | Valor P (Prob>F) | |
| Modelo | 27053.77 | 8 | 3381.72 | 26.89 | < 0.0001 | |
| A-h | 1344.08 | 1 | 1344.08 | 10.69 | 0.0038 | |
| B-a | 21420.75 | 1 | 21420.75 | 170.31 | < 0.0001 | |
| C-w | 140.08 | 1 | 140.08 | 1.11 | 0.3038 | |
| D-b | 270.75 | 1 | 270.75 | 2.15 | 0.1579 | |
| AC | 484.00 | 1 | 484.00 | 3.85 | 0.0639 | |
| AD | 1640.25 | 1 | 1640.25 | 13.04 | 0.0017 | |
| 992.00 | 1 | 992.00 | 7.89 | 0.0109 | ||
| 529.80 | 1 | 529.80 | 4.21 | 0.0534 | ||
| Residual | 2515.47 | 20 | 125.77 | |||
| F. de ajuste | 2514.67 | 16 | 157.17 | 785.83 | < 0.0001 | |
| Error puro | 0.80 | 4 | 0.20 | |||
| Total | 29569.24 | 28 | ||||
| Desv. Est. | 11.21 | R-Cuadrada | 0.9149 | |||
| Media | 506.52 | R-Cuadrada ajustada | 0.8809 | |||
| C.V.% | 2.21 | R-Cuadrada de la predicción | 0.7453 | |||
| PRESS | 7531.18 | Precisión adecuada | 17.898 | |||
En este caso A, B, C, D, AC, AD, y son términos significativos del modelo. Los valores superiores a 0.1000 indican que los términos del modelo no son significativos. La R-Cuadrada de la predicción de 0.753 está en un acuerdo razonable con la R-Cuadrada ajustada de 0.8809. La Precisión adecuada mide la relación señal/ruido. Es deseable una relación mayor que 4. La relación de 17.898 indica una señal adecuada. Este modelo se puede utilizar para navegar por el espacio de diseño.
5.2. Modelo de regresión de las respuestas
Los modelos de regresión de la superficie de respuesta para evaluar el tiempo de calentamiento requerido, la variación de la temperatura superficial del molde y los esfuerzos máximos de Von Mises se expresan como:
|
(16) |
|
(17) |
|
(18) |
Los modelos matemáticos de las ecs. (16)-(18) pueden usarse para predecir el tiempo de calentamiento requerido, , la variación de la temperatura superficial del molde, , los esfuerzos máximos de Von Mises, . Los modelos matemáticos desarrollados anteriormente producen una forma simple y eficiente de predecir los valores de las variables de respuesta dentro de los límites de los factores estudiados.
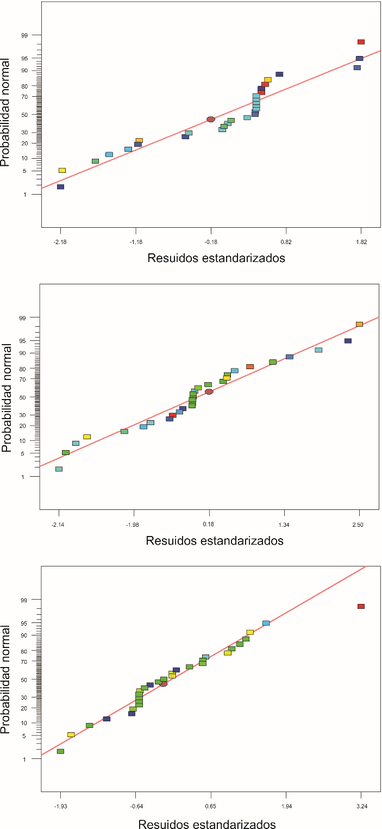
Esto será útil para la optimización de parámetros de diseño en el siguiente paso. Antes de la aplicación de los modelos polinomiales cuadráticos, es necesario verificar su precisión confirmando que los modelos han extraído toda la información relevante de los resultados experimentales. Por esta razón, se seleccionó el análisis residual como la herramienta de diagnóstico [33]. Los diagramas de probabilidad normal de los residuales para el tiempo de calentamiento requerido (), diferencia de temperatura de superficie de cavidad máxima () y los esfuerzos de Von Mises ( se muestran en la Figura 9(a)-(c), respectivamente. Se puede encontrar que los residuos para cada variable de respuesta generalmente caen en una línea recta que implica que los errores se distribuyen normalmente y las adecuaciones de estos modelos matemáticos se ajustan mediante técnicas de regresión de mínimos cuadrados.
| Figura 9. Gráficas de probabilidad normal. (a) Tiempo de calentamiento requerido. (b) Diferencia máxima de temperaturas de la superficie de la cavidad. (c) Esfuerzos de Von Mises | |
Se realizó una prueba de confirmación con un conjunto de parámetros de diseño aleatorios para verificar los modelos matemáticos desarrollados. La Tabla 8 muestra los conjuntos de datos aleatorios para la verificación y la comparación de los resultados de cálculo por los modelos desarrollados y la simulación numérica. Se puede observar que los errores porcentuales calculados son muy pequeños. Las desviaciones porcentuales para las tres variables de respuesta entre los resultados estimados y los experimentales son de 1.85%,0.095% y 0.308%, respectivamente.
Estos pequeños errores indican que los modelos polinomiales desarrollados son adecuados y pueden usarse para predecir las variables objetivas con buena precisión. Se puede deducir, que es razonable usar estos modelos matemáticos para la optimización.
| Parámetros | h
mm |
a
mm |
qw/ | b
mm |
s |
°C |
MPa |
| V. modelo | 11.00 | 19.50 | 1.50 | 23.00 | 40.14 | 3.760 | 519.6 |
| V. simulación | 11.00 | 19.50 | 1.50 | 23.00 | 39.40 | 3.757 | 518 |
| % Error | - | - | - | - | 1.85 | 0.095 | 0.308 |
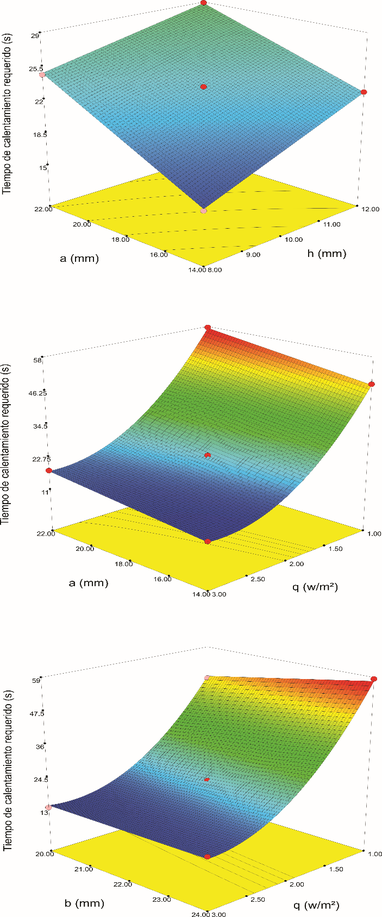
Para visualizar el efecto de las variables en las respuestas, los diagramas de superficie de respuesta tridimensional se pueden usar para describir los modelos matemáticos extraídos. Para la respuesta establecida del tiempo de calentamiento requerido las superficies de respuesta correspondientes se muestran en la Figura 10. La Figura 10(a) muestra la gráfica de superficie de respuesta del efecto del término interactivo, la distancia de centro a centro de las resistencias y la altura del centro de la resistencia a la superficie de la cavidad (ah) en el tiempo de calentamiento requerido, se puede observar el tiempo de calentamiento requerido se puede reducir a medida que se reduce la distancia de centro a centro de las resistencias y la altura del centro de la resistencia a la superficie y aumenta de manera contraria.
El tiempo de calentamiento mínimo requerido sería de 12.15 s, correspondiente a la distancia más pequeña de la distancia de centro a centro de las resistencias () y la menor la altura del centro de la resistencia a la superficie de la cavidad (). En la Figura 10(b) se observa la gráfica de superficie de respuesta del efecto del término interactivo, la distancia de centro a centro de las resistencias y el flujo de calor por unidad de área (aq) en el tiempo de calentamiento requerido, se puede interpretar que el aumento del flujo de calor da como resultado la reducción del tiempo de calentamiento requerido, especialmente cuando la distancia de centro a centro de las resistencias (a) está en su nivel bajo.
La Figura 10(c) muestra la gráfica de superficie de respuesta del efecto del término interactivo, el espesor de la placa de calentamiento y el flujo de calor por unidad de área en el tiempo de calentamiento requerido, el tiempo mínimo de calentamiento requerido se puede obtener con el nivel bajo del espesor de la placa de calentamiento () y el nivel alto del flujo de calor por unidad de área ().
| Figura 10. Gráficas de superficie de los efectos combinados de (a) la distancia de centro a centro de las resistencias y la altura del centro de la resistencia a la superficie de la cavidad (ah), (b) la distancia de centro a centro de las resistencias y el flujo de calor por unidad de área (aq) y (c) el espesor de la placa de calentamiento y el flujo de calor por unidad de área (bq) para el tiempo de calentamiento |
6. Optimización del sistema de calentamiento
Según la discusión anterior, se podría concluir que el espesor de la placa y la posición las resistencias eléctricas tienen efectos significativos y complejos sobre la eficiencia de calentamiento, la uniformidad de temperatura en cavidad del molde y la resistencia del molde.
Dado que la productividad es un indicador importante en la industria de moldeo por inyección, se desea que el tiempo de calentamiento sea lo más corto posible. Por lo tanto, el propósito de esta optimización es minimizar el tiempo de calentamiento requerido para mejorar la eficiencia de calentamiento. Al mismo tiempo, la variación de la temperatura de la superficie del molde de acuerdo a la norma ASTM-D 3641–02 y D 4703–03 [34,35], debe ser inferior a 5°C para garantizar la calidad de la superficie de la pieza. Los esfuerzos máximos de Von Mises no deben ser superiores a 500 MPa. Además, los valores de las tres variables de diseño están todos en el espacio de diseño designado, como se muestra en la Tabla 3. El problema de optimización se puede representar mediante las siguientes ecuaciones:
- Encontrar: h, a, q, b
- Minimizar:
|
|
(19) |
- Sujeto a restricciones:
|
|
(20) |
- Dentro de los rangos:
|
(21) |
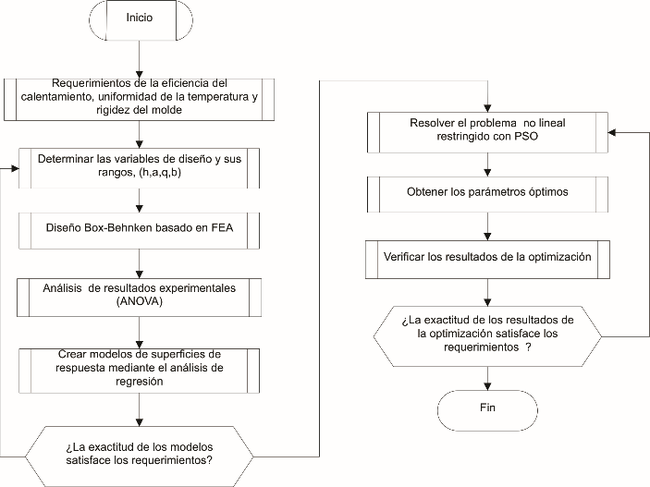
El problema de optimización expresado con las ecuaciones anteriores se resolvió acoplando los modelos matemáticos desarrollados con el algoritmo PSO. El diagrama de flujo del diseño de optimización se muestra en la Figura 11.
| Figura 11. Metodología de diseño óptimo basado en DOE, MSR y PSO |
Los valores de las variables dependientes y las variables de respuesta correspondientes antes y después de la optimización se presentan en la Tabla 9.
| Parámetros | h
mm |
a
mm |
q
w/ |
b
mm |
s |
°C |
MPa |
| V. inicial | 10.0 | 18.00 | 2.00 | 22.00 | 23.4 | 5.714 | 499 |
| V. optimizado | 8.00 | 18.03 | 2.82 | 20.00 | 12.15 | 4.99 | 479.54 |
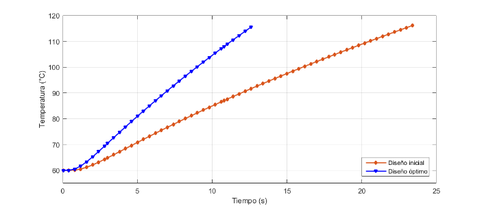
En la Figura 12 se puede observar que el tiempo de calentamiento requerido optimizado en el centro de la superficie de la cavidad de 12.15 s representa una reducción de 92.59 % en comparación con el tiempo de calentamiento requerido inicial de 23.4 s.
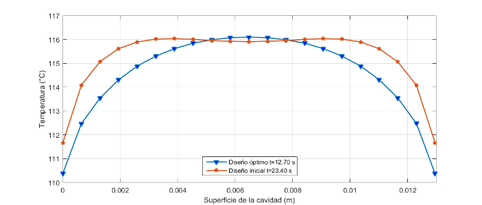
La Figura 13 muestra la variación de la temperatura a lo largo de la superficie del molde se mejora aproximadamente 14.50 % del valor de referencia de 5.714 °C al valor optimizado de 4.999 °C, y el esfuerzo máximo de Von Mises disminuye 4.05 % con respecto al valor inicial de 499 MPa, quedando en 479.54 MPa, por debajo del valor predefinido en la optimización mediante PSO.
| Figura 12. Respuestas de temperatura en el centro de la superficie de la cavidad en etapa de calentamiento |
| Figura 13. Distribución de la temperatura en la superficie de la cavidad entre el caso de diseño óptimo y el inicial |
Se realizó la simulación respuesta térmica y el análisis térmico-estructural con el parámetro optimizado para validar los resultados de optimización. Los resultados de la simulación muestran que el tiempo de calentamiento requerido, la variación de la temperatura superficial del molde y los esfuerzos máximos de Von Mises son 12.70 s, 4.762 °C y 500 MPa, respectivamente.
Los valores en porcentaje de errores entre los valores optimizados y experimentales de , y son 4.25%, 4.78 %, 4.09 %, respectivamente.
Las gráficas de contorno de la distribución de la temperatura y la distribución de esfuerzos de Von Mises basada en los parámetros óptimos se muestran en las Figura 14 y 15, respectivamente.
| Figura 14. Gráfica de contorno de distribución de temperaturas con valores optimizados |
| Figura 15. Esfuerzos de Von Mises con valores optimizados |
7. Conclusiones
El moldeo por respuesta térmica rápida es una nueva tecnología de moldeo por inyección desarrollada en los últimos años. El ciclo de moldeo es relativamente largo debido a la baja eficiencia de calentamiento, el bajo rendimiento de producción es debido a la distribución de temperatura no uniforme en la superficie de la cavidad y vida de servicio relativamente corta debido a la fatiga termo-mecánica son tres preocupaciones principales para el MRTR. Teniendo en cuenta tantos factores y limitaciones en el diseño de MRTR, implica la aplicación de análisis y optimización computarizados avanzados para la optimización del diseño de MRTR.
En este estudio se investigó la respuesta térmica y la resistencia estructural del MRTR por análisis térmico y estructural. Los resultados del análisis térmico muestran que el sistema de calentamiento del molde de inyección tiene la capacidad potencial para ser calentado rápida y uniformemente usando resistencias eléctricas. Los resultados del análisis de campos acoplados térmico-estructural indican que la distribución de los esfuerzos en el bloque de la cavidad es muy desigual. Existen concentraciones de esfuerzos en los bordes de las resistencias eléctricas cerca de la superficie de la cavidad del molde. Tal concentración de esfuerzo y relajación durante el proceso de calentamiento y enfriamiento frecuente en el MRTR puede conducir a la iniciación de la microfisura en el orificio donde se posiciona la resistencia eléctrica y se podría extender hasta la fatiga térmico-mecánica después de ciertos ciclos de moldeo.
Por lo tanto, para el sistema de calentamiento del molde, el espesor de la placa y la posición de las resistencias eléctricas son muy cruciales para el MRTR y debe ser cuidadosamente diseñado considerando la eficiencia de la respuesta térmica, la uniformidad de temperatura, la resistencia estructural del MRTR. La metodología de superficie de respuesta (MSR) basada en el diseño experimental de Box-Behnken y el experimento numérico se utilizó para explorar la relación numérica entre los parámetros de diseño y las variables de respuesta. Se implementó el método PSO para acoplar los modelos matemáticos desarrollados y así encontrar las variables de diseño óptimas para minimizar el tiempo de calentamiento requerido y, al mismo tiempo, asegurar uniformidad de temperatura aceptable y resistencia estructural al molde. Se obtuvo la posición óptima de las resistencias eléctricas del molde para probetas de tensión, se predijeron y verificaron los valores mínimos de , y realizando experimentos de confirmación. Después de la optimización, el tiempo de calentamiento requerido se redujo en 92.59 %, la uniformidad de la temperatura superficial de la cavidad se mejoró en 14.50 %, y la resistencia estructural del molde se mejoró ligeramente 4.05 %. Los modelos de superficie de respuesta cuadrática desarrollados pueden obtener resultados razonables con errores de menos de 5 % entre los datos predichos y los experimentales en experimentos de confirmación. Estos modelos pueden utilizarse para describir la relación entre factores experimentales ( y ) y variables de respuesta (, y ).
El método de optimización desarrollado por el acoplamiento MSR y PSO ha demostrado ser eficaz y será una poderosa herramienta para guiar el diseño de optimización de la posición de las resistencias eléctricas del MRTR, reduciendo así el tiempo de ciclo de moldeo, mejorando el rendimiento de producción y la vida útil del MRTR.
Agradecimientos
Los autores agradecen al Consejo Nacional de Ciencia y Tecnología (CONACyT) por la beca doctoral No. 428731.
Agradecemos a CoreTech System Co., Ltd. (Moldex3D) por su generoso suministro de licencias para esta investigación a través de su distribuido en el Estado de Guanajuato Lic. Salvador López de 3DCAD.
Referencias
| [1] | Kutz M. Applied plastics engineering handbook. Processing, Materials and Aplications, Second ed., Elsevier, Ed., William Andrew, Oxford, 2017. |
| [2] | Kennedy P., Zheng R., Flow analysis of injection molds. Second ed., Henser, Munich, 2013. |
| [3] | Shoemaker J. Moldflow design guide: a resource for plastics engineers. First Edition ed., Hanser Verlag, Massachusetts, 2006. |
| [4] | Wang W., Zhao G., Guan Y., Wu X., Hui Y. Effect of rapid heating cycle injection mold temperature on crystal structures, morphology of polypropylene and surface quality of plastic parts. Journal of Polymer Research, 22:84, 2015. |
| [5] | Chen S.C., Jong W.R., Chang J.A. Dynamic mold surface temperature control using induction heating and its effects on the surface appearance of weld line. Journal of Applied Polymer Science, 101:1174-1180, 2006. |
| [6] | Chen S.C., Minh P.S., Chang J.A. Gas-assisted mold temperature control for improving the quality of injection molded parts with fiber additives. International Communications in Heat and Mass Transfer, 38:304-312, 2011. |
| [7] | Yao D., Kimerling T.E., Kim B. High‐frequency proximity heating for injection molding applications. Polymer Engineering & Science, 46:938-945, 2006. |
| [8] | Chang P.C., Hwang S.J. Experimental investigation of infrared rapid surface heating for injection molding. Journal of Applied Polymer Science, 102:3704-3713, 2006. |
| [9] | Wang G., Zhao G., Li H., Guan Y. Research on a new variotherm injection molding technology and its application on the molding of a large LCD panel. Polymer-Plastics Technology and Engineering, 48:671-681, 2009. |
| [10] | Xu R.X., Sachs E. Rapid thermal cycling with low thermal inertia tools. Polymer Engineering & Science, 49:305-316, 2009. |
| [11] | Collomb J., Balland P., Francescato P., Gardet Y., Leh D., Saffré P. Thermo-mechanical simulations for the comparison of heating channels geometries for composite material injection tools. Applied Thermal Engineering, 126:204-211, 2017. |
| [12] | Shayfull Z., Sharif S., Zain A.M., Saad R.M., Fairuz M.A. Milled groove square shape conformal cooling channels in injection molding process. Materials and Manufacturing Processes, 28:884-891, 2013. |
| [13] | Zhao G., Wang G., Guan Y., Li H. Research and application of a new rapid heat cycle molding with electric heating and coolant cooling to improve the surface quality of large LCD TV panels. Polymers for Advanced Technologies, 22:476-487, 2011. |
| [14] | Xiao C.L., Huang H.X. Multiobjective optimization design of heating system in electric heating rapid thermal cycling mold for yielding high gloss parts. Journal of Applied Polymer Science, 131(6), 2014. |
| [15] | Xiao C.L., Huang H.X. Development of a rapid thermal cycling molding with electric heating and water impingement cooling for injection molding applications. Applied Thermal Engineering, 73:712-722, 2014. |
| [16] | Li X. P., Zhao G. Q., Guan Y. J. and Ma M. X., Optimal design of heating channels for rapid heating cycle injection mold based on response surface and genetic algorithm, Materials & Design, 30:4317-4323, 2009. |
| [17] | Huang H. X., Li J. C., Li D. and Huang G. Q., New strategies for predicting parison dimensions in extrusion blow molding, Polymer-Plastics Technology and Engineering, 50:1329-1337, 2011. |
| [18] | Shen C., Wang L., Li Q. Optimization of injection molding process parameters using combination of artificial neural network and genetic algorithm method. Journal of Materials Processing Technology, 183:412-418, 2007. |
| [19] | Hassan R., Cohanim B., De Weck O., Venter G.A comparison of particle swarm optimization and the genetic algorithm. In 46th AIAA/ASME/ASCE/AHS/ASC structures, Structural Dynamics and Materials Conference, 1897, 2005. |
| [20] | Park J.B., Lee K.S., Shin J.R., Lee K.Y. A particle swarm optimization for economic dispatch with nonsmooth cost functions. IEEE Transactions on Power systems, 20:34-42, 2005. |
| [21] | Settles M., Rodebaugh B., Soule T. Comparison of genetic algorithm and particle swarm optimizer when evolving a recurrent neural network. In Genetic and Evolutionary Computation Conference, Springer, Berlin, 148-149, 2003. |
| [22] | Eberhart R.C., Shi Y. Comparison between genetic algorithms and particle swarm optimization. In International Conference on Evolutionary Programming, Springer, Berlin, 611-616, 1998. |
| [23] | ASTM, ASTM D638, ASTM Standard test method for tensile properties of plastics. In D638-03., West Conshohocken: ASTM International, 2003. |
| [24] | Menges G., Michaeli W., Mohren P. How to make injection molds. 3rd edn., Henser, Munich, 2001. |
| [25] | Rao N.S., Schumacher G. Design formulas for plastics engineers. Carl Hanser Verlag GmbH Co KG, Munich, 2014. |
| [26] | Yao D., Chen S.C., Kim B.H. Rapid thermal cycling of injection molds: an overview on technical approaches and applications. Advances in Polymer Technology, 27:233-255, 2008. |
| [27] | Park S.J., Kwon T.H. Optimal cooling system design for the injection molding process. Polymer Engineering & Science, 38:1450-1462, 1998. |
| [28] | Rao N.S., Schumacher G., Schott N.R., O’brien K.T. Optimization of cooling systems in injection molds by an easily applicable analytical model. Journal of Reinforced Plastics and Composites, 21:451-459, 2002. |
| [29] | Xiao C.L., Huang H.X. Development of a rapid thermal cycling molding with electric heating and water impingement cooling for injection molding applications. Applied Thermal Engineering, 73:712-722, 2014. |
| [30] | Cengel Y., Boles M. Thermodynamics: An engineering approach. 4th ed., McGraw-Hill, New York, 2002. |
| [31] | Dorigato A., D'Amato M., Pegoretti A. Thermo-mechanical properties of high density polyethylene-fumed silica nanocomposites: effect of filler surface area treatment. Journal of Polymer Research, 19:9889, 2012. |
| [32] | Al Ashraf A. Thermal analysis of polymer by DSC. Center for Advanced Materials, 2:5, 2015. |
| [33] | Montgomery D.C. Introduction to statistical quality control. Seventh ed., John Wiley & Sons, Arizona, 2009. |
| [34] | ASTM, ASTM D3641, ASTM standard practice for injection molding test specimens of thermoplastic molding and extrusion materials. In ASTM D3641-15, West Conshohocken: ASTM INTERNATIONAL, 2003. |
| [35] | ASTM, ASTM D4703, ASTM standard practice for compression molding thermoplastic materials into test specimens, plaques, or sheets. In D4703-10a., West Conshohocken: ASTM International, 2010. |
Document information
Published on 16/09/19
Accepted on 11/09/19
Submitted on 06/06/19
Volume 35, Issue 3, 2019
DOI: 10.23967/j.rimni.2019.09.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?