| Line 170: | Line 170: | ||
|} | |} | ||
| − | In order to assure the continuation point of the first node (No. 0) and the last node (No. <math>n+1</math>), the drill pipe need to be extended upward and downward respectively, as shown in [[#img-2|Figure 2]]. Then, (<math>n+5</math>) nodes in total can be obtained including the fictitious extended nodes of No. -1, No. -2, No.<math>n+1</math> and No. <math>n+2</math>. There are (<math>n+5 </math>) unknown parameters representing the displacements of each node of drill pipe during SPT installation (<math>x_{-2}</math>, <math>x_{-1}</math>, <math>x_{0}</math>, <math>x_1,\cdots , x_{n+1}</math>, <math>x_{n+ | + | In order to assure the continuation point of the first node (No. 0) and the last node (No. <math>n+1</math>), the drill pipe need to be extended upward and downward respectively, as shown in [[#img-2|Figure 2]]. Then, (<math>n+5</math>) nodes in total can be obtained including the fictitious extended nodes of No. -1, No. -2, No.<math>n+1</math> and No. <math>n+2</math>. There are (<math>n+5 </math>) unknown parameters representing the displacements of each node of drill pipe during SPT installation (<math>x_{-2}</math>, <math>x_{-1}</math>, <math>x_{0}</math>, <math>x_1,\cdots , x_{n+1}</math>, <math>x_{n+2}</math>). |
| − | Then, the (<math>n+5 </math>) unknown parameters can be solved according to the (<math>n+5 </math>) obtained equations including the (<math>n+1 </math>) equations deduced from the governing equation Eq.[[#eq-9|(9)]] and 4 equations in the boundary conditions of Eq.[[#eq-10|(10)]]. The matrix form of these equations can be expressed as, | + | Then, the (<math>n+5 </math>) unknown parameters can be solved according to the (<math>n+5</math>) obtained equations including the (<math>n+1</math>) equations deduced from the governing equation Eq.[[#eq-9|(9)]] and 4 equations in the boundary conditions of Eq.[[#eq-10|(10)]]. The matrix form of these equations can be expressed as, |
<span id="eq-11"></span> | <span id="eq-11"></span> | ||
| Line 185: | Line 185: | ||
|} | |} | ||
| − | where | + | where <math>[M]</math> is the coefficient matrix, <math>[X]=[x_{-2} x_{-1} x_0 x_1\cdots x_{n+1} x_{n+2}]^T</math> is the unknown matrix of deformation of the installation pipe at each discrete node, and <math>[q]=[q_0 q_1 q_2 \cdots q^n 0 0 0 h^2q(z_L]^T</math> is the matrix of known parameters. The coefficient matrix formed according to the governing equation and boundary equations belongs to large sparse matrix. In order to solve the deformation of each discrete node of pipe, an augmented matrix need to be established as, |
<span id="eq-12"></span> | <span id="eq-12"></span> | ||
| Line 198: | Line 198: | ||
|} | |} | ||
| − | Then, establish an array | + | Then, establish an array <math>pos[n]</math> and initialize the array which is used to preserve the pivot element of each row of the established augmented matrix. Assuming <math>pos[k]=p</math> (where <math>k=1, 2, 3,\cdots , n</math>) and an intermediate variable <math>a_{pk}</math> as, |
<span id="eq-13"></span> | <span id="eq-13"></span> | ||
| Line 234: | Line 234: | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (15) | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) | ||
|} | |} | ||
| − | where, | + | |
| + | where, <math>j=1,2,\cdots ,p-1,p+1,\cdots ,n</math> and <math>l=k,k+1,\cdots ,n</math>. Then, the augmented matrix is transferred into the upper triangular matrix and the deformation of each discrete node of the drill pipe <math>[X]</math> is be obtained. | ||
==3. Case study and discussion== | ==3. Case study and discussion== | ||
| Line 250: | Line 251: | ||
! Parameters !! Value !! Parameters !! Value | ! Parameters !! Value !! Parameters !! Value | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|Density of seawater | + | | style="text-align: center;vertical-align: top;"|Density of seawater <math>\rho _{w} </math> (kg.m<math>^{-3}</math>) |
| style="text-align: center;vertical-align: top;"|1030 | | style="text-align: center;vertical-align: top;"|1030 | ||
| − | | style="text-align: center;vertical-align: top;"|Density of pipe | + | | style="text-align: center;vertical-align: top;"|Density of pipe <math>\rho _{s} </math> is (kg.m<math>^{-3}</math>) |
| style="text-align: center;vertical-align: top;"|7850 | | style="text-align: center;vertical-align: top;"|7850 | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|Tidal velocity | + | | style="text-align: center;vertical-align: top;"|Tidal velocity <math>V_t</math> (m.s<math>^{-1}</math>) |
| style="text-align: center;vertical-align: top;"|1.5 | | style="text-align: center;vertical-align: top;"|1.5 | ||
| − | | style="text-align: center;vertical-align: top;"|Submerged weight SPT | + | | style="text-align: center;vertical-align: top;"|Submerged weight SPT <math>P_{SPT}</math> (kN) |
| style="text-align: center;vertical-align: top;"|300 | | style="text-align: center;vertical-align: top;"|300 | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|Wind-generated current velocity | + | | style="text-align: center;vertical-align: top;"|Wind-generated current velocity <math>V_{CW}</math> |
| style="text-align: center;vertical-align: top;"|1.0 | | style="text-align: center;vertical-align: top;"|1.0 | ||
| − | | style="text-align: center;vertical-align: top;"|Drag force coefficient | + | | style="text-align: center;vertical-align: top;"|Drag force coefficient <math>C_D</math> |
| style="text-align: center;vertical-align: top;"|1.2 | | style="text-align: center;vertical-align: top;"|1.2 | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|Wave height | + | | style="text-align: center;vertical-align: top;"|Wave height <math>H_{w} </math> (m) |
| style="text-align: center;vertical-align: top;"|6 | | style="text-align: center;vertical-align: top;"|6 | ||
| − | | style="text-align: center;vertical-align: top;"|Inertia force coefficient | + | | style="text-align: center;vertical-align: top;"|Inertia force coefficient <math>C_M</math> |
| style="text-align: center;vertical-align: top;"|1.0 | | style="text-align: center;vertical-align: top;"|1.0 | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|Wave period | + | | style="text-align: center;vertical-align: top;"|Wave period <math>T_{w} </math> (s) |
| style="text-align: center;vertical-align: top;"|8 | | style="text-align: center;vertical-align: top;"|8 | ||
| − | | style="text-align: center;vertical-align: top;"|Outer diameter of the pipe | + | | style="text-align: center;vertical-align: top;"|Outer diameter of the pipe <math>(D_{o}</math> ''(mm) |
| style="text-align: center;vertical-align: top;"|127 | | style="text-align: center;vertical-align: top;"|127 | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|Water depth | + | | style="text-align: center;vertical-align: top;"|Water depth <math>L</math> (m) |
| style="text-align: center;vertical-align: top;"|1000 | | style="text-align: center;vertical-align: top;"|1000 | ||
| − | | style="text-align: center;vertical-align: top;"|Inner diameter of the pipe | + | | style="text-align: center;vertical-align: top;"|Inner diameter of the pipe <math>(D_{i}</math> (mm) |
| style="text-align: center;vertical-align: top;"|101.6 | | style="text-align: center;vertical-align: top;"|101.6 | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"|Young’s modulus of the pipe | + | | style="text-align: center;vertical-align: top;"|Young’s modulus of the pipe <math>E</math> (GPa) |
| style="text-align: center;vertical-align: top;"|210 | | style="text-align: center;vertical-align: top;"|210 | ||
| style="text-align: center;vertical-align: top;"| | | style="text-align: center;vertical-align: top;"| | ||
| Line 287: | Line 288: | ||
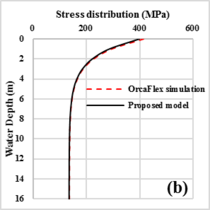
| − | The lateral deformation and total stress of drill pipe obtained by OrcaFlex simulation and the proposed model have the same variation during the SPT installation process, as shown in [[#img-3|Figure 3]] . The lateral deformation of the pipe increased obviously at shallow water and varied slowly at deep water. And the largest lateral deformation of the pipe appears near the bottom end of the pipe. The stress of the pipe decrease dramatically with water depth and remains unchanged while the pipe at below 10''m''. Contrary to the largest value of the lateral deformation of pipe, the maximum stress of the pipe located at the lift-off point of the pipe. However, all the variations of deformation and stress of the pipe with installation depth show a trend of dramatically incensement at shallow water and increase slowly at deep water. The maximum values of the lateral deformation, bending moment and total stress obtained by the OrcaFlex simulation are 28. | + | The lateral deformation and total stress of drill pipe obtained by OrcaFlex simulation and the proposed model have the same variation during the SPT installation process, as shown in [[#img-3|Figure 3]] . The lateral deformation of the pipe increased obviously at shallow water and varied slowly at deep water. And the largest lateral deformation of the pipe appears near the bottom end of the pipe. The stress of the pipe decrease dramatically with water depth and remains unchanged while the pipe at below 10''m''. Contrary to the largest value of the lateral deformation of pipe, the maximum stress of the pipe located at the lift-off point of the pipe. However, all the variations of deformation and stress of the pipe with installation depth show a trend of dramatically incensement at shallow water and increase slowly at deep water. The maximum values of the lateral deformation, bending moment and total stress obtained by the OrcaFlex simulation are 28.7m, 35.6kN.m and 414.1MPa, respectively. And the maximum values of these parameters obtained by the proposed model are 30.2m, 33.6kN.m and 399.1MPa, respectively. The errors noted between the two results then can be ignored. However, the calculation efficiency of the proposed model is much higher than that of the OrcaFlex simulation. |
<div id='img-1'></div> | <div id='img-1'></div> | ||
| Line 302: | Line 303: | ||
====3.2.1 Effect of ocean wave==== | ====3.2.1 Effect of ocean wave==== | ||
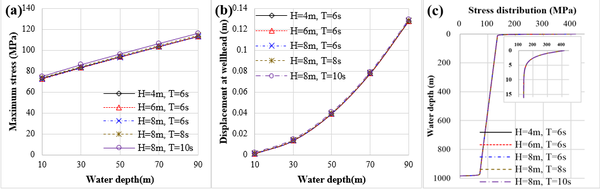
| − | To evaluate the effect of ocean wave to the drill pipe during SPT installation, different wave height (which ranges from | + | To evaluate the effect of ocean wave to the drill pipe during SPT installation, different wave height (which ranges from 4m to 8m) and wave period (which ranges from 6s to 10s) are applied on the drill pipe. The performances of stress and deformation of the drill pipe under different ocean wave conditions are shown in [[#img-4|Figure 4]]. The maximum stress that located at the lift-point and the displacement at wellhead on the mud line varied significantly with water depth while varied few with the ocean wave conditions, as shown in [[#img-4|Figures 4]](a) and (b). Moreover, the stress distribution of the pipe under different ocean wave conditions almost remained unchanged, as shown in [[#img-4|Figure 4]](c). |
<div id='img-4'></div> | <div id='img-4'></div> | ||
| Line 317: | Line 318: | ||
====3.2.2 Effect of ocean current==== | ====3.2.2 Effect of ocean current==== | ||
| − | The ocean wave is one of important factors that affects mechanical properties of the drill pipe during the SPT installation. The effect of ocean current on the deformation and stress of the drill pipe predicted by the proposed model derived in this article are depicted in [[#img-5|Figure 5]]. The tidal velocity was considered as varying from 0. | + | The ocean wave is one of important factors that affects mechanical properties of the drill pipe during the SPT installation. The effect of ocean current on the deformation and stress of the drill pipe predicted by the proposed model derived in this article are depicted in [[#img-5|Figure 5]]. The tidal velocity was considered as varying from 0.4m/s to 1.2m/s, which cover most ocean environment. |
<div id='img-4'></div> | <div id='img-4'></div> | ||
| Line 328: | Line 329: | ||
| − | The displacement at wellhead and the maximum stress located at the lift-off point of the pipe, contrary to the effect of ocean wave on the drill pipe, increase significantly with the current velocity. The last node of the pipe, which adjusted the SPT at the bottom end, is away from the subsea wellhead 62. | + | The displacement at wellhead and the maximum stress located at the lift-off point of the pipe, contrary to the effect of ocean wave on the drill pipe, increase significantly with the current velocity. The last node of the pipe, which adjusted the SPT at the bottom end, is away from the subsea wellhead 62.4m. And the maximum total stress which appears at the lift-off point is 757.6MPa which approaches to the yield strength of the drill pipe. Therefore, the lateral deformation and total stress of the pipe need to be accurately evaluated before SPT is lowered in each SPT installation process to prevent excessive bending deformation of the drill pipe. |
====3.2.3 Effect of water depth==== | ====3.2.3 Effect of water depth==== | ||
| − | As the SPT need to be lowered underwater with different depth gradually, five depth points vary from | + | As the SPT need to be lowered underwater with different depth gradually, five depth points vary from 600m to 1400m were selected to evaluate the deformation and mechanical behavior of the drill pipe. |
The mechanical behaviours of the drill pipe with different water depth during SPT installation predicted by the proposed model are shown in [[#img-6|Figure 6]]. The displacement at wellhead and the maximum stress at lift-off point increase gradually with the installation depth of the SPT, as shown in [[#img-6|Figure 6]](a). According to the stress distribution of the pipe under different water depth, as shown in [[#img-6|Figure 6]](b), the displacement of SPT is roughly away from subsea wellhead in a linear relationship with the water depth. | The mechanical behaviours of the drill pipe with different water depth during SPT installation predicted by the proposed model are shown in [[#img-6|Figure 6]]. The displacement at wellhead and the maximum stress at lift-off point increase gradually with the installation depth of the SPT, as shown in [[#img-6|Figure 6]](a). According to the stress distribution of the pipe under different water depth, as shown in [[#img-6|Figure 6]](b), the displacement of SPT is roughly away from subsea wellhead in a linear relationship with the water depth. | ||
| Line 349: | Line 350: | ||
Five specification of drill pipe (ranging from 4''in ''to 6 5/8''in'') that used in ocean oil and gas exploration are selected to analyze the effect of drill pipe size on the mechanical behaviors of the pipe. | Five specification of drill pipe (ranging from 4''in ''to 6 5/8''in'') that used in ocean oil and gas exploration are selected to analyze the effect of drill pipe size on the mechanical behaviors of the pipe. | ||
| − | As shown in [[#img-7|Figure 7]], the displacement of the last node of the drill pipe increase with the drill pipe size from 25. | + | As shown in [[#img-7|Figure 7]], the displacement of the last node of the drill pipe increase with the drill pipe size from 25.7m to 30.4m and the maximum stress at the lift-off point increase with the drill pipe size from 285MPa to 492MPa. For the reason that the deformation and stress of the pipe mainly caused by the ocean current and weight of the pipe, the larger size of the pipe would encounter larger loads during SPT installation. It would be better to chosen drill pipe with the smaller size therefore under the same ocean condition to assure the safety (safely) operation. |
<div id='img-7'></div> | <div id='img-7'></div> | ||
| Line 361: | Line 362: | ||
====3.2.5 Effect of SPT weight==== | ====3.2.5 Effect of SPT weight==== | ||
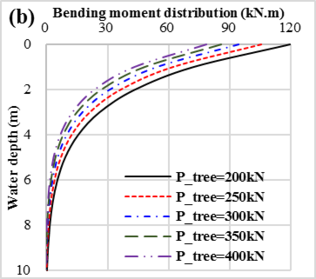
| − | In order to analyze the effect of SPT on the mechanical behaviors of pipe during SPT installation, different SPTs with weight ranged from | + | In order to analyze the effect of SPT on the mechanical behaviors of pipe during SPT installation, different SPTs with weight ranged from 200kN to 400kN that cover most of the SPT used under water are selected in this model. For the reason that the axial load caused by the SPT weight would reduce the bending moment of the pipe when the drill pipe encounter the same ocean conditions, the displacement of the pipe at wellhead and the maximum stress at the lift-off point decrease with the weight of SPT slowly, as shown in [[#img-8|Figure 8]](a). As the axial loads are mainly caused by the weight of the pipe, changes in SPT weight have less effect on the mechanical behaviors of the pipe and the bending moment decrease sharply with water depth, as shown in [[#img-8|Figure 8]](b). |
<div id='img-8'></div> | <div id='img-8'></div> | ||
| Line 374: | Line 375: | ||
===3.3 Operability envelopes of the SPT installation=== | ===3.3 Operability envelopes of the SPT installation=== | ||
| − | According to the mechanical behaviors evaluation for pipe during SPT installation, the factors that mostly affect the strength and deformation of the drill pipe are the ocean current, water depth, drill pipe size and SPT weight. In order to decrease the risks of destructive failure happens to the installation components under extreme ocean environment, the operability envelopes for SPT installation have been proposed considering the factors that might dominate the safety for the SPT installation. The operability envelopes established were based on the wind-generated current velocity | + | According to the mechanical behaviors evaluation for pipe during SPT installation, the factors that mostly affect the strength and deformation of the drill pipe are the ocean current, water depth, drill pipe size and SPT weight. In order to decrease the risks of destructive failure happens to the installation components under extreme ocean environment, the operability envelopes for SPT installation have been proposed considering the factors that might dominate the safety for the SPT installation. The operability envelopes established were based on the wind-generated current velocity <math>V_{CW}</math> and the tidal velocity <math>V_t</math>, as shown in [[#img-9|Figures 9]]-[[#img-11|11]], and the permissible installation areas are marked with green. Obviously, according to the operability envelopes obtained from [[#img-9|Figures 9]]-[[#img-11|11]], the variation tendencies of the operability envelopes with different ocean conditions for the SPT installation are the same. |
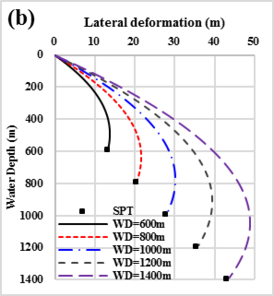
| − | The operability envelopes of the SPT installation with different water depths ranged from | + | The operability envelopes of the SPT installation with different water depths ranged from 600m to 1400''m'' that covers most of the installation water depth are obtained. As shown in [[#img-9|Figures 9]], the permissible ocean conditions for SPT installation decrease with the water depth. The permissible wind-generated current velocities under 600m, 800m, 1000m and 1200m are 1.72m/s, 1.51m/s, 1.34m/s, 1.21m/s and 1.19m/s, respectively. The permissible tidal velocities under 600m, 800m, 1000m and 1200m are 2.58 m/s, 2.40m/s, 2.18m/s, 2.10m/s and 2.01m/s, respectively. Due to the wind-generated current velocity and tidal velocity decrease with water depth and almost remain unchanged under deep-water, the areas of operability envelopes for SPT installation decrease with the water depth sharply in shallow water ([[#img-9|Figures 9]](a)-(c)). On the contrary, the areas of operability envelopes decrease slowly in deep water ([[#img-9|Figures 9]](c)-(e)). |
<div id='img-9'></div> | <div id='img-9'></div> | ||
| Line 387: | Line 388: | ||
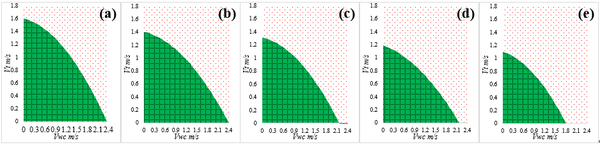
| − | As shown in [[#img-10|Figure 10]], the permissible ocean conditions for SPT installation with specification of drill pipe ranging from | + | As shown in [[#img-10|Figure 10]], the permissible ocean conditions for SPT installation with specification of drill pipe ranging from 4in to 6 5/8in decrease with the drill pipe size are obtained. The permissible wind generated current velocities are ranging from 1.63m/s to 1.12m/s and the permissible tidal velocities are ranging from 2.38m/s to 1.8'm/s. The larger the drill pipe size, the smaller permissible wind-generated current velocity and tidal velocity of the ocean condition. Then, it would be much better to choose smaller pipe to obtain larger permissible ocean conditions such as in [[#img-10|Figure 10]](a). |
<div id='img-10'></div> | <div id='img-10'></div> | ||
| Line 398: | Line 399: | ||
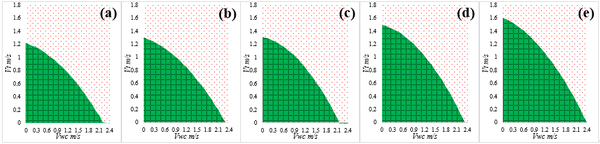
| − | Contrary to variations of the operability envelopes with different water depth and drill pipe size, as shown in [[#img-11|Figure 11]], the permissible wind-generated current velocity and tidal velocity increase with the SPT weight. The permissible wind-generated current velocities are ranging from 1. | + | Contrary to variations of the operability envelopes with different water depth and drill pipe size, as shown in [[#img-11|Figure 11]], the permissible wind-generated current velocity and tidal velocity increase with the SPT weight. The permissible wind-generated current velocities are ranging from 1.21m/s to 1.58m/s and the permissible tidal velocities are ranging from 2.25m/s to 2.41m/s. |
<div id='img-11'></div> | <div id='img-11'></div> | ||
| Line 412: | Line 413: | ||
Based on the analysis of the quantitatively strength-related factors such as the stresses and deformations of the drill pipe, this research established a mathematical model to investigate the operability envelopes for SPT installation using drill pipe. The ocean environments, drill pipe size, and SPT weight that might dominate the deformation and mechanical behavior of the pipe have been evaluated based on the proposed model. Based on the work done in this research, the following results and conclusions were obtained. | Based on the analysis of the quantitatively strength-related factors such as the stresses and deformations of the drill pipe, this research established a mathematical model to investigate the operability envelopes for SPT installation using drill pipe. The ocean environments, drill pipe size, and SPT weight that might dominate the deformation and mechanical behavior of the pipe have been evaluated based on the proposed model. Based on the work done in this research, the following results and conclusions were obtained. | ||
| − | (a) The accuracy of the established mathematical model was verified using OrcaFlex simulation. The variation tendencies of the mechanical behaviors obtained by the proposed model were in good agreement with those obtained by the OrcaFlex simulation. | + | * (a) The accuracy of the established mathematical model was verified using OrcaFlex simulation. The variation tendencies of the mechanical behaviors obtained by the proposed model were in good agreement with those obtained by the OrcaFlex simulation. |
| − | (b) The ocean wave applied on the drill pipe during SPT installation rarely affects the maximum stress (located at the lift-off point of pipe) and the displacement at wellhead (location where the SPT needed to be adjusted) in deep-water where the SPT installed. | + | * (b) The ocean wave applied on the drill pipe during SPT installation rarely affects the maximum stress (located at the lift-off point of pipe) and the displacement at wellhead (location where the SPT needed to be adjusted) in deep-water where the SPT installed. |
| − | (c) The displacement of the pipe at wellhead and the maximum stress at lift-off point of the pipe increase gradually with ocean current, water depth and drill pipe size while decrease slowly with SPT weight. In addition, the displacement of SPT is roughly away from subsea wellhead in a linear relationship with the water depth. | + | * (c) The displacement of the pipe at wellhead and the maximum stress at lift-off point of the pipe increase gradually with ocean current, water depth and drill pipe size while decrease slowly with SPT weight. In addition, the displacement of SPT is roughly away from subsea wellhead in a linear relationship with the water depth. |
| − | (d) According to the variations of the operability envelopes, which were established based on the wind-generated current velocity and the tidal velocity, changes of depths in deep water and SPT weight have few effects on the operation ocean conditions and it would be better to choose smaller pipe to obtain larger permissible ocean conditions. | + | * (d) According to the variations of the operability envelopes, which were established based on the wind-generated current velocity and the tidal velocity, changes of depths in deep water and SPT weight have few effects on the operation ocean conditions and it would be better to choose smaller pipe to obtain larger permissible ocean conditions. |
==Acknowledgements== | ==Acknowledgements== | ||
Revision as of 12:45, 20 October 2020
Abstract
The article presents a mathematical model to investigate the operability envelopes for subsea production tress (SPT) installation using drill pipe. The finite differential method was used to solve the established governing equations in which the ocean conditions were considered. Based on the evaluations of the ocean wave, ocean current, water depth, specification of drill pipe and SPT weight that might dominate the mechanical behaviors of the pipe, the operability envelopes with permissible ocean conditions for SPT installation were obtained. The results indicate that changes of depths in deep water and SPT weight have few effects on the operation conditions and it would be better to choose smaller pipe to obtain larger permissible ocean conditions during SPT installation.
Keywords: Operability envelope, SPT installation, drill pipe, ocean conditions, mechanical behavior
1. Introduction
Due to the installation of subsea production tree (SPT) directly affects the success of deep-water oil production and economic efficiency of the whole project, the analysis of deformation and strength of structures that the SPT is attached at the bottom end has caught much attention in ocean engineering. According to the actual application of different methods of SPT installation, such as installation of moon pool method, hoister installation method and transport barge installation method, the installation of moon pool method is the most widely used application due to its high effectiveness and economic efficiency [1-3]. However, destructive accident might be caused under extreme ocean environment during the installation process of the SPT. The operability envelopes, which were used to determine the environmental conditions of SPT installation, therefore need to be carefully analyzed to assure the safety of the structure over the duration of installation process.
The literatures offer many research studies on the installation of the SPT. Robert et al. [4-5] introduced the main processes of different installation methods as well as the technological problems concerned in SPT installation and found that the installation of moon pool method, in which the drill pipe to lower the SPT to the subsea wellhead, has better safety performance. Hu et al. [6] analyzed the variations of deformation and strength of drill pipe based on the analysis of environment loads the drill pipe encounter when installing the SPT. Khan [7] analyzed the variation of pipe bending stress with ABAQUS software when the pipe subjected to the wave loads. Gardner and Kotch [8] introduced an efficient and accurate solution for the response of pipe during SPT installation by establishing the computational model. Gong [9] established an analytical model of the pipe with boundary conditions at different installation stages and examined the model using the finite element method.
The researches mentioned above were obtained by the FEM method whose effectiveness has been accepted by the engineering community. Nevertheless, each application case need to be carried out and the nonlinear calculations with local defective element will be inefficient by using this method. The theoretical analysis therefore is necessary. Raman-Nair and Baddour [10] established a mathematical model to analyze the response of the pipe during SPT installation by using Kane’s formalism, where the pipe is modelled using lumped masses connected by extensional and rotational springs, including structural damping. Fan et al. [11] applied the Newmark-β method and Newton-Raphson iteration method to obtain the numerical solution for the hand-off drill pipe. Bai et al. [12] performed mechanical research on a manifold installation by the drill pipe in deep water that considered the wave loads and lowering velocity. Based on the archived documents available to the authors, it seems that there are very few research studies investigating the operability envelopes for SPT installation, although the importance of them is recognized by researchers and engineers.
The aim of the research reported here was to investigate the operability envelopes for SPT installation using moon pool method. Based on the analysis of the axial and lateral loads loaded on the drill pipe, a mathematical model was established to analyze quantitatively strength-related factors such as the stresses and deformations of the drill pipe under ocean wave and current during SPT installation. The operability envelopes for SPT installation were proposed considering the environments, drill pipe size, and SPT weight that might dominate the deformation and mechanical behavior of the pipe. It is anticipated that the results of this research may decrease the risks of SPT installation and enhance the efforts of researchers and engineers in designing safer and more reliable SPT installation process.
2. Mechanical Model
2.1 Analysis model
Figure 1 shows the schematic of the SPT installation string system, which serves as the link between the platform positioned at sea surface and the SPT needed to be installed at subsea wellhead. The SPT is attached to the bottom end of the drill pipe and lowered together with the drill pipe from the float platform to the subsea wellhead under water after the conductor has been installed. The drill pipe is subjected to the axial tension force (generated by the float platform, weight of drill pipe and SPT) and lateral force (generated by ocean wave and current) during the process of SPT installation. As shown in Figure 1, a global coordinate system () is set with its origin at (0, 0) of the lift-off point of the float platform, the axis is parallel to the sea surface with positive direction same as the direction of lateral force, the axis is vertical pointing the mudline underwater.
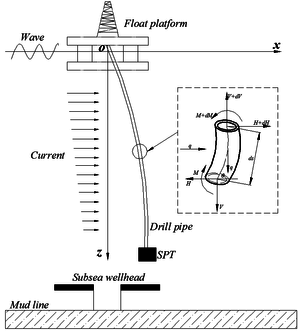
|
| Figure 1. Model of SPT installation system |
A differential segment of the drill pipe with length is selected to analyze the mechanical behavior of the drill pipe during SPT installation, as shown in Figure 1. Considering the equilibrium of the lateral force , the vertical force and the bending moment loaded on the drill pipe, the equilibrium equations for the drill pipe segment can be set as,
|
|
(1) |
where is the inclination slop of the pipe, is the vertical force generated by submerged weight of the pipe and SPT, is the lateral force generated by ocean wave and current. The geometric relationship of these parameters mentioned in Eq.(1) can be obtained as , , . And the bending moment of the drill pipe can be obtained by multiplying the bending stiffness and the curvature as . Then, governing equation of the proposed model can be obtained as,
|
|
(2) |
Due to there has a fixed connection with the float platform at the top end of drill pipe, there has no deformation and slope at the lift-off point. For the lateral force on the SPT is far less than that of the drill pipe, the size effect of SPT (attached to the bottom end of the drill pipe) on the mechanical behavior of the drill pipe might be ignored. The boundary conditions of the governing equation in Eq.(2) therefore can be obtained as,
|
|
(3) |
where is the depth of ocean, and are the vertical force generated by each segment submerged weight of the pipe and the lateral force generated by ocean wave and current, respectively. For the gravity of SPT that suspended at the bottom end of the pipe might be considered as a mass point distributed on the lower end, the vertical force loaded on the pipe can be obtained as,
|
|
(4) |
where is submerged weight of the SPT, is the density of the installation pipe, is the density of sea water, is outer diameter of the pipe, is inner diameter of the pipe. According to the Morison theory [13], the lateral force generated by ocean wave and current can be obtained as,
|
|
(5) |
where, is the drag force coefficient, is the inertia force coefficient, is the horizontal velocity of ocean wave particle at depth, is the ocean current velocity at depth and is the horizontal acceleration of ocean wave particle. Based on the Airy wave theory [14], the horizontal velocity and acceleration of ocean wave particle can be obtained as,
|
|
(6) |
|
|
(7) |
where is the wave height, is the wave period, is the wave number, is the wave circular frequency. The ocean current velocity can be obtained according to the Ekman transport theory [15] as,
|
|
(8) |
where is the tidal velocity, is the wind-generated current velocity, , which is recommended by DNV RP C205.
2.2 Model solution
The analytical solution of the above equation can hardly be obtained directly for the vertical force and lateral force loaded on the drill pipe vary with water depth, wave height, wave period and surface current velocity. By using the finite differential method, the drill pipe can be divided into number of segments starting from the lift-off point of the float platform which denoted the first node (No. 0) to the pipe end connecting with SPT which denoted the last node (No. ), as shown in Figure 2.
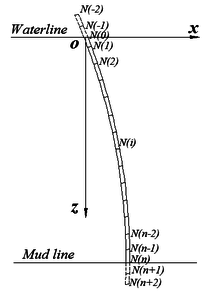
|
| Figure 2. Schematic diagram of drill pipe discretization |
By taking place the derivatives with difference quotient term, the governing equation of Eq.(2) can be expressed as,
|
|
(9) |
where is the length of each segment of the installation pipe, and are the coordinate of the No. () Node on the axis and axis, respectively. And the boundary conditions in Eq.(3) can be expressed as,
|
|
(10) |
In order to assure the continuation point of the first node (No. 0) and the last node (No. ), the drill pipe need to be extended upward and downward respectively, as shown in Figure 2. Then, () nodes in total can be obtained including the fictitious extended nodes of No. -1, No. -2, No. and No. . There are () unknown parameters representing the displacements of each node of drill pipe during SPT installation (, , , , ).
Then, the () unknown parameters can be solved according to the () obtained equations including the () equations deduced from the governing equation Eq.(9) and 4 equations in the boundary conditions of Eq.(10). The matrix form of these equations can be expressed as,
|
|
(11) |
where is the coefficient matrix, is the unknown matrix of deformation of the installation pipe at each discrete node, and is the matrix of known parameters. The coefficient matrix formed according to the governing equation and boundary equations belongs to large sparse matrix. In order to solve the deformation of each discrete node of pipe, an augmented matrix need to be established as,
|
|
(12) |
Then, establish an array and initialize the array which is used to preserve the pivot element of each row of the established augmented matrix. Assuming (where ) and an intermediate variable as,
|
|
(13) |
Calculate the following equations,
|
|
(14) |
|
|
(15) |
where, and . Then, the augmented matrix is transferred into the upper triangular matrix and the deformation of each discrete node of the drill pipe is be obtained.
3. Case study and discussion
3.1 Case study
To illustrate the previous model with examples, an actual installation of SPT is selected with its basic parameters as shown in Table 1.
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Density of seawater (kg.m) | 1030 | Density of pipe is (kg.m) | 7850 |
| Tidal velocity (m.s) | 1.5 | Submerged weight SPT (kN) | 300 |
| Wind-generated current velocity | 1.0 | Drag force coefficient | 1.2 |
| Wave height (m) | 6 | Inertia force coefficient | 1.0 |
| Wave period (s) | 8 | Outer diameter of the pipe (mm) | 127 |
| Water depth (m) | 1000 | Inner diameter of the pipe (mm) | 101.6 |
| Young’s modulus of the pipe (GPa) | 210 |
The lateral deformation and total stress of drill pipe obtained by OrcaFlex simulation and the proposed model have the same variation during the SPT installation process, as shown in Figure 3 . The lateral deformation of the pipe increased obviously at shallow water and varied slowly at deep water. And the largest lateral deformation of the pipe appears near the bottom end of the pipe. The stress of the pipe decrease dramatically with water depth and remains unchanged while the pipe at below 10m. Contrary to the largest value of the lateral deformation of pipe, the maximum stress of the pipe located at the lift-off point of the pipe. However, all the variations of deformation and stress of the pipe with installation depth show a trend of dramatically incensement at shallow water and increase slowly at deep water. The maximum values of the lateral deformation, bending moment and total stress obtained by the OrcaFlex simulation are 28.7m, 35.6kN.m and 414.1MPa, respectively. And the maximum values of these parameters obtained by the proposed model are 30.2m, 33.6kN.m and 399.1MPa, respectively. The errors noted between the two results then can be ignored. However, the calculation efficiency of the proposed model is much higher than that of the OrcaFlex simulation.
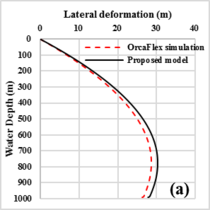
|
|
| Figure 3. Comparisons of (a) lateral deformation of drill pipe. (b) Stress distribution of drill pipe | |
3.2 Mechanical behavior evaluation for drill pipe
3.2.1 Effect of ocean wave
To evaluate the effect of ocean wave to the drill pipe during SPT installation, different wave height (which ranges from 4m to 8m) and wave period (which ranges from 6s to 10s) are applied on the drill pipe. The performances of stress and deformation of the drill pipe under different ocean wave conditions are shown in Figure 4. The maximum stress that located at the lift-point and the displacement at wellhead on the mud line varied significantly with water depth while varied few with the ocean wave conditions, as shown in Figures 4(a) and (b). Moreover, the stress distribution of the pipe under different ocean wave conditions almost remained unchanged, as shown in Figure 4(c).
In ocean engineering, the SPT need to be installed mostly underwater to gathering oil and gas in deep water area. Then, the effect of the ocean wave applied on the drill pipe can be ignored during analyzing deformation and mechanical behavior of pipe in the SPT installation process.
3.2.2 Effect of ocean current
The ocean wave is one of important factors that affects mechanical properties of the drill pipe during the SPT installation. The effect of ocean current on the deformation and stress of the drill pipe predicted by the proposed model derived in this article are depicted in Figure 5. The tidal velocity was considered as varying from 0.4m/s to 1.2m/s, which cover most ocean environment.
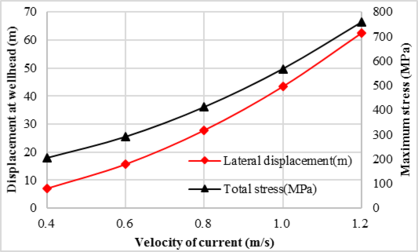
|
| Figure 5. Variation of displacement at wellhead and stress at lift-off point with velocity of current |
The displacement at wellhead and the maximum stress located at the lift-off point of the pipe, contrary to the effect of ocean wave on the drill pipe, increase significantly with the current velocity. The last node of the pipe, which adjusted the SPT at the bottom end, is away from the subsea wellhead 62.4m. And the maximum total stress which appears at the lift-off point is 757.6MPa which approaches to the yield strength of the drill pipe. Therefore, the lateral deformation and total stress of the pipe need to be accurately evaluated before SPT is lowered in each SPT installation process to prevent excessive bending deformation of the drill pipe.
3.2.3 Effect of water depth
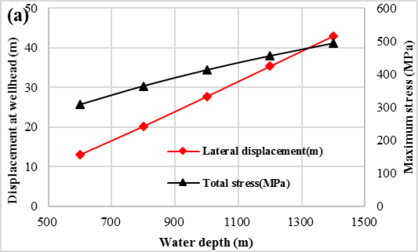
As the SPT need to be lowered underwater with different depth gradually, five depth points vary from 600m to 1400m were selected to evaluate the deformation and mechanical behavior of the drill pipe.
The mechanical behaviours of the drill pipe with different water depth during SPT installation predicted by the proposed model are shown in Figure 6. The displacement at wellhead and the maximum stress at lift-off point increase gradually with the installation depth of the SPT, as shown in Figure 6(a). According to the stress distribution of the pipe under different water depth, as shown in Figure 6(b), the displacement of SPT is roughly away from subsea wellhead in a linear relationship with the water depth.
|
|
| Figure 6. Mechanical behaviours of drill pipe with different water depth: (a) variation of displacement at wellhead and stress at lift-off point, (b) stress distribution of the drill pipe | |
3.2.4 Effect of drill pipe size
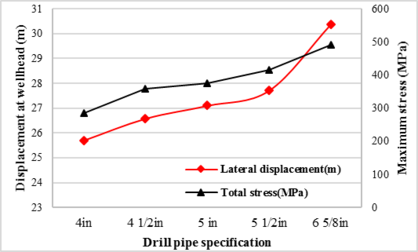
Five specification of drill pipe (ranging from 4in to 6 5/8in) that used in ocean oil and gas exploration are selected to analyze the effect of drill pipe size on the mechanical behaviors of the pipe.
As shown in Figure 7, the displacement of the last node of the drill pipe increase with the drill pipe size from 25.7m to 30.4m and the maximum stress at the lift-off point increase with the drill pipe size from 285MPa to 492MPa. For the reason that the deformation and stress of the pipe mainly caused by the ocean current and weight of the pipe, the larger size of the pipe would encounter larger loads during SPT installation. It would be better to chosen drill pipe with the smaller size therefore under the same ocean condition to assure the safety (safely) operation.
|
| Figure 7. Variation of displacement at wellhead and stress at lift-off point with drill pipe specification |
3.2.5 Effect of SPT weight
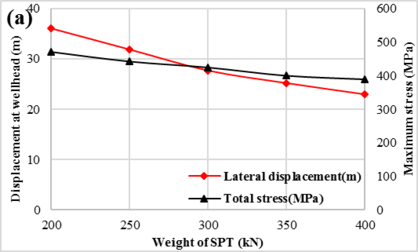
In order to analyze the effect of SPT on the mechanical behaviors of pipe during SPT installation, different SPTs with weight ranged from 200kN to 400kN that cover most of the SPT used under water are selected in this model. For the reason that the axial load caused by the SPT weight would reduce the bending moment of the pipe when the drill pipe encounter the same ocean conditions, the displacement of the pipe at wellhead and the maximum stress at the lift-off point decrease with the weight of SPT slowly, as shown in Figure 8(a). As the axial loads are mainly caused by the weight of the pipe, changes in SPT weight have less effect on the mechanical behaviors of the pipe and the bending moment decrease sharply with water depth, as shown in Figure 8(b).
|
|
| Figure 8. Variation of drill pipe’s mechanical behaviours with SPT weight. (a) Variation of displacement at wellhead and stress at lift-off point. (b) Variation of bending moment distribution | |
3.3 Operability envelopes of the SPT installation
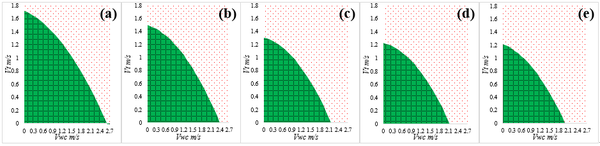
According to the mechanical behaviors evaluation for pipe during SPT installation, the factors that mostly affect the strength and deformation of the drill pipe are the ocean current, water depth, drill pipe size and SPT weight. In order to decrease the risks of destructive failure happens to the installation components under extreme ocean environment, the operability envelopes for SPT installation have been proposed considering the factors that might dominate the safety for the SPT installation. The operability envelopes established were based on the wind-generated current velocity and the tidal velocity , as shown in Figures 9-11, and the permissible installation areas are marked with green. Obviously, according to the operability envelopes obtained from Figures 9-11, the variation tendencies of the operability envelopes with different ocean conditions for the SPT installation are the same.
The operability envelopes of the SPT installation with different water depths ranged from 600m to 1400m that covers most of the installation water depth are obtained. As shown in Figures 9, the permissible ocean conditions for SPT installation decrease with the water depth. The permissible wind-generated current velocities under 600m, 800m, 1000m and 1200m are 1.72m/s, 1.51m/s, 1.34m/s, 1.21m/s and 1.19m/s, respectively. The permissible tidal velocities under 600m, 800m, 1000m and 1200m are 2.58 m/s, 2.40m/s, 2.18m/s, 2.10m/s and 2.01m/s, respectively. Due to the wind-generated current velocity and tidal velocity decrease with water depth and almost remain unchanged under deep-water, the areas of operability envelopes for SPT installation decrease with the water depth sharply in shallow water (Figures 9(a)-(c)). On the contrary, the areas of operability envelopes decrease slowly in deep water (Figures 9(c)-(e)).
|
| Figure 9. Operability envelopes with water depth of (a) 600m, (b) 800m, (c) 1000m, (d) 1200m and (e) 1400m |
As shown in Figure 10, the permissible ocean conditions for SPT installation with specification of drill pipe ranging from 4in to 6 5/8in decrease with the drill pipe size are obtained. The permissible wind generated current velocities are ranging from 1.63m/s to 1.12m/s and the permissible tidal velocities are ranging from 2.38m/s to 1.8'm/s. The larger the drill pipe size, the smaller permissible wind-generated current velocity and tidal velocity of the ocean condition. Then, it would be much better to choose smaller pipe to obtain larger permissible ocean conditions such as in Figure 10(a).
|
| Figure 10. Operability envelopes with drill pipe size of (a) 4in, (b) 4 1/2in, (c) 5in, (d) 5 1/2in and (e) 6 5/8in |
Contrary to variations of the operability envelopes with different water depth and drill pipe size, as shown in Figure 11, the permissible wind-generated current velocity and tidal velocity increase with the SPT weight. The permissible wind-generated current velocities are ranging from 1.21m/s to 1.58m/s and the permissible tidal velocities are ranging from 2.25m/s to 2.41m/s.
|
| Figure 11. Operability envelopes with SPT weight of (a) 200kN, (b) 250kN, (c) 300kN, (d) 350kN and (e) 400kN |
Conclusion
Based on the analysis of the quantitatively strength-related factors such as the stresses and deformations of the drill pipe, this research established a mathematical model to investigate the operability envelopes for SPT installation using drill pipe. The ocean environments, drill pipe size, and SPT weight that might dominate the deformation and mechanical behavior of the pipe have been evaluated based on the proposed model. Based on the work done in this research, the following results and conclusions were obtained.
- (a) The accuracy of the established mathematical model was verified using OrcaFlex simulation. The variation tendencies of the mechanical behaviors obtained by the proposed model were in good agreement with those obtained by the OrcaFlex simulation.
- (b) The ocean wave applied on the drill pipe during SPT installation rarely affects the maximum stress (located at the lift-off point of pipe) and the displacement at wellhead (location where the SPT needed to be adjusted) in deep-water where the SPT installed.
- (c) The displacement of the pipe at wellhead and the maximum stress at lift-off point of the pipe increase gradually with ocean current, water depth and drill pipe size while decrease slowly with SPT weight. In addition, the displacement of SPT is roughly away from subsea wellhead in a linear relationship with the water depth.
- (d) According to the variations of the operability envelopes, which were established based on the wind-generated current velocity and the tidal velocity, changes of depths in deep water and SPT weight have few effects on the operation ocean conditions and it would be better to choose smaller pipe to obtain larger permissible ocean conditions.
Acknowledgements
The authors acknowledge the support of grant No. 2017QHZ010 from the scientific research-starting project of SWPU China.
References
[1] Kaiser, M., MARK, J. Deepwater subsea well spuds on the decline: Dry tree versus wet tree trends examined. Offshore. 79: 26-27, 2019.
[2] Kanhua, S., Jilin, L., Li, F, W., Meng, L. Measures to Prevent Subsea Wellhead Instability for Deepwater Drilling: Proceedings of the 4th Annual International Conference on Materials Science and Environmental Engineering. Mater. Environ. Eng., Proc. Annu. Int. Conf. Mater. Sci. Environ. Eng., 4th. Mater. Environ. Eng. 1245-1256, 2017.
[3] Dennis, D. Subsea-Hardware Installation from an FDPSO. J. Pet. Technol. 62(8): 60-62, 2010.
[4] Robert, E. Subsea tree installations. World Oil. 221(11): 27, 2000.
[5] Chris, C. Development of Installation Pipe-Riser-Intervention Systems Offshore West Africa. J. Pet. Technol. 67(6): 104-106, 2003.
[6] Hu, Y., Cao, J., Yao, B., Zeng, Z. Dynamic behaviors of a marine riser with variable length during the installation of a subsea production tree. J. Mar. Sci. Technol. 23(2): 378-388, 2018.
[7] Khan R. Nonlinear dynamic analysis of deep-water marine risers. Ships and Offshore Struct. 13(1): 10-19, 2006.
[8] Gardner T., Kotch A. Dynamic analysis of riser and caissons by the element method. OTC. 2651: 405-413, 1976.
[9] Gong, X., Liu, S., Duan, L., Wang, G. Research on the running instalment process of deep sea underwater Christmas tree. China Petrol Machinery. 41(4): 50-54, 2013.
[10] Raman, N. W., Baddour, E. Three-dimensional dynamics of a flexible marine riser undergoing large elastic deformations. Multibody Syst Dyn. 10(4): 393-423, 2003.
[11] Fan, H., Li, C., Wang, Z. Dynamic analysis of a hang-off drilling riser considering internal solitary wave and vessel motion. J. Nat. Gas Sci. Eng. 37: 512-522, 2017.
[12] Bai, Y., Ruan, S., Yuan, X. 3D mechanical analysis of subsea manifold installation by drill pipe in deep water. Ships and Offshore Struct. 9(3): 333-343, 2014.
[13] Donald, L. New Research Supports a Modification of Samuel Eliot Morison’s Theory Concerning Columbus’s Inter-Island Route Through the Bahamas. Terrae Incognitae., 49(2):114-131, 2017.
[14] Ortega, A., Rivera, A., Larsen, M. Slug flow and waves induced motions in flexible riser. J. Energy Resour. Technol., 140(1):0892-7219, 2018.
[15] Michael, A., Joseph, P. Interaction of Ekman Layers and Islands. J Phys Oceanogr., 43(5):1028-1041, 2013.
Document information
Published on 12/01/21
Accepted on 06/10/20
Submitted on 05/06/20
Volume 37, Issue 1, 2021
DOI: 10.23967/j.rimni.2020.10.004
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?