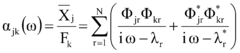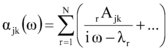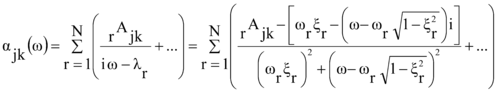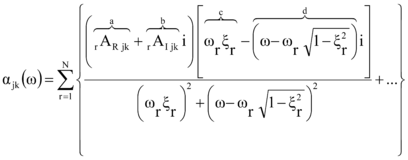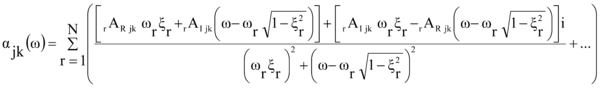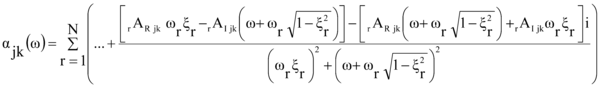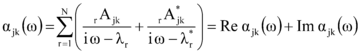| Line 313: | Line 313: | ||
A continuación se sigue el procedimiento expuesto en este trabajo: en primer lugar se identifica el sistema dinámico, mediante procedimientos de optimización, desde el modelo de respuesta (matriz de FRF), hasta el modelo modal (frecuencias naturales, razones de amortiguamiento y matriz modal normalizada respecto a la masa). | A continuación se sigue el procedimiento expuesto en este trabajo: en primer lugar se identifica el sistema dinámico, mediante procedimientos de optimización, desde el modelo de respuesta (matriz de FRF), hasta el modelo modal (frecuencias naturales, razones de amortiguamiento y matriz modal normalizada respecto a la masa). | ||
| − | Se ha simulado ruido numéricamente en el modelo de respuesta, añadiendo un ruido blanco a cada una de las componentes de la matriz de las FRF, de la siguiente manera [ | + | Se ha simulado ruido numéricamente en el modelo de respuesta, añadiendo un ruido blanco a cada una de las componentes de la matriz de las FRF, de la siguiente manera [13,19] |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 328: | Line 328: | ||
Donde α<sub>jk</sub>(ω) es la componente jk de la matriz de FRF, que contiene los datos usados para la identificación, E<sub>p</sub> es el nivel de ruido (en %), y N<sub>ruido</sub> es una distribución normal estándar, con un valor medio de 0 y una desviación típica de 1, es decir N(0,1). Ambas magnitudes, real y compleja, de la matriz de FRF, se ven perturbadas por este ruido blanco. | Donde α<sub>jk</sub>(ω) es la componente jk de la matriz de FRF, que contiene los datos usados para la identificación, E<sub>p</sub> es el nivel de ruido (en %), y N<sub>ruido</sub> es una distribución normal estándar, con un valor medio de 0 y una desviación típica de 1, es decir N(0,1). Ambas magnitudes, real y compleja, de la matriz de FRF, se ven perturbadas por este ruido blanco. | ||
| − | Se han identificado los cuatro primeros modos en flexión vertical (Figura 4). Para ilustrar gráficamente el modelo de respuesta de la estructura, y al objeto de no ocupar un espacio excesivo, en la | + | Se han identificado los cuatro primeros modos en flexión vertical (Figura 4). Para ilustrar gráficamente el modelo de respuesta de la estructura, y al objeto de no ocupar un espacio excesivo, en la Figura 5 se representa en el dominio de la frecuencia una de las componentes α<sub>jk</sub>(ω) de la diagonal principal de la matriz de las FRF (con un nivel de ruido en la señal del 20%), correspondiente a la sección 32 del puente, para un g.d.l. vertical (evidentemente perpendicular al eje longitudinal del mismo), muy próximo a la clave y a la sección intermedia del vano principal (central) del puente. |
| − | En la práctica, el rango de interés del análisis está limitado por las frecuencias asociadas a los modos de vibración que se quieren estimar. Es decir, se trata de obtener residuos en modelos incompletos | + | En la práctica, el rango de interés del análisis está limitado por las frecuencias asociadas a los modos de vibración que se quieren estimar. Es decir, se trata de obtener residuos en modelos incompletos. En la referencia [14] se describe la alternativa empleada, basada en técnicas de optimización, que consiste en utilizar complementos residuales móviles (tanto para la parte real como para la imaginaria), para así tener en cuenta el efecto de los modos fuera de rango. |
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| Line 340: | Line 340: | ||
| − | Asimismo, una vez obtenidos los residuos, en [15] | + | Asimismo, una vez obtenidos los residuos, se describe en la referencia [15] la alternativa de cálculo empleada para obtener la matriz modal del sistema dinámico, utilizando técnicas de optimización a partir de aquellos. |
| − | Es necesario hacer notar, que los procedimientos citados en [14] y [15] se realizaron para amortiguamiento independiente de la frecuencia (histerético), pero también son válidos en el presente trabajo para el caso general de amortiguamiento viscoso, con ajustes menores (en la primera referencia se muestra como se obtienen los parámetros modales a través de las FRF, mientras que en la segunda, se describe la determinación de la matriz modal desde los residuos, ambas utilizando técnicas de optimización). | + | Es necesario hacer notar, que los procedimientos citados en las referencias [14] y [15] se realizaron para amortiguamiento independiente de la frecuencia (histerético), pero también son válidos en el presente trabajo para el caso general de amortiguamiento viscoso, con ajustes menores (en la primera referencia se muestra como se obtienen los parámetros modales a través de las FRF, mientras que en la segunda, se describe la determinación de la matriz modal desde los residuos, ambas utilizando técnicas de optimización). |
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| Line 352: | Line 352: | ||
| − | + | La Tabla 1 muestra los resultados de las frecuencias naturales y factores de amortiguamiento correspondientes a los 4 primeros modos de vibración, así como las magnitudes de los mismos en las secciones: 4, 7, 17, 22, 27, 32, 37, 42, 47, y 54; normalizados estos respecto de la masa. Estos parámetros modales, que caracterizan el comportamiento dinámico del puente analizado, se han obtenido en un estudio anterior [13]. | |
<div class="center" style="font-size: 75%;">'''Tabla 1'''. Magnitudes de referencia de los parámetros modales</div> | <div class="center" style="font-size: 75%;">'''Tabla 1'''. Magnitudes de referencia de los parámetros modales</div> | ||
| Line 441: | Line 441: | ||
| − | + | Las Tablas 2 y 3 muestran los resultados estimados, utilizando las técnicas de optimización descritas previamente en el apartado 2, mediante el programa informático GAMS: sistema de modelado para la programación matemática y la optimización [20]. | |
<div class="center" style="font-size: 75%;">'''Tabla 2'''. Magnitudes estimadas de los parámetros modales, obtenidas mediante técnicas de optimización, con un nivel de ruido en la señal nulo</div> | <div class="center" style="font-size: 75%;">'''Tabla 2'''. Magnitudes estimadas de los parámetros modales, obtenidas mediante técnicas de optimización, con un nivel de ruido en la señal nulo</div> | ||
| Line 530: | Line 530: | ||
| − | Finalmente, los valores estimados de las Tablas 2 y 3 (con y sin, ruido en la señal respectivamente), frente a los de la Tabla 1 (para las magnitudes de referencia), ponen de manifiesto que ambos conjuntos de parámetros dinámicos (estimados y de referencia) se corresponden perfectamente entre ellos | + | Finalmente, los valores estimados de las Tablas 2 y 3 (con y sin, ruido en la señal respectivamente), frente a los de la Tabla 1 (para las magnitudes de referencia), ponen de manifiesto que ambos conjuntos de parámetros dinámicos (estimados y de referencia) se corresponden perfectamente entre ellos, lo cual permite apreciar que se alcanza una precisión razonable para su aplicación práctica, y se deriva que el modelo está bien calibrado. |
<div class="center" style="font-size: 75%;">'''Tabla 3'''. Magnitudes estimadas de los parámetros modales, obtenidas mediante técnicas de optimización, con un nivel de ruido en la señal del 15% | <div class="center" style="font-size: 75%;">'''Tabla 3'''. Magnitudes estimadas de los parámetros modales, obtenidas mediante técnicas de optimización, con un nivel de ruido en la señal del 15% | ||
Revision as of 12:53, 25 September 2019
Resumen
En este artículo, se desarrolla la aplicación de técnicas de optimización -a través de las funciones de respuesta en frecuencia (FRF)- para la determinación de parámetros modales por el método de identificación, orientadas a: sistemas con amortiguamiento viscoso, niveles de amortiguamiento bajos, y alternativas que operan en el dominio de la frecuencia.
Se proponen técnicas de descomposición para trabajar con magnitudes complejas, que permiten tratar separadamente la parte real e imaginaria (las cuales, de esta forma, pueden ser implementadas en programas comerciales de optimización), incluso en operaciones matriciales producto. La influencia de los modos altos y bajos, se tiene en cuenta de forma rigurosa, a través del mismo algoritmo de optimización.
Para ilustrar el trabajo se ha analizado una estructura singular por su esbeltez, el Puente de la Cartuja (Sevilla, España), que además constituye una estructura muy ligera y poco amortiguada. Su diseño, aportó en su día, un nuevo esquema estructural de complicadas geometrías; mediante el empleo de un nuevo material, como es el acero de alto límite elástico.
Palabras clave: Dinámica estructural, análisis modal, identificación, optimización
Abstract
In the present paper, the application of optimization techniques –via frequency response functions (FRF)– is developed for determining modal parameters by means of the identification method that are exclusively limited to: systems with viscous damping, low levels of damping, and methods that work within the frequency domain.
Decomposition techniques are proposed for working with complex magnitudes that allow the real and imaginary parts to be treated separately (which can, in this way, be implemented in commercial optimization programs), even in matrix product operations. The influence of high and low modes is rigorously taken into consideration via the selfsame optimization algorithm.
To illustrate this work we have analyzed a structure unique in its slenderness, La Cartuja Bridge (Seville, Spain), which also constitutes a very light structure with very little damping. Its design contributed in its day a new structural framework of complicated geometries through the use of a new material: high yield strength steel.
Keywords: Structural dynamics, modal analysis, identification, optimization
1. Introducción
Hay diferentes técnicas que permiten deducir las características modales de un sistema dado desde el modelo de respuesta obtenido experimentalmente. El procedimiento es conocido como “identificación modal” [1]. Debido al gran volumen y complejidad de los resultados experimentales, habitualmente estos se recogen como funciones de respuesta en frecuencia (FRF), a partir de las cuales se estiman los parámetros modales [2].
Para la excitación de la estructura, se pueden dar dos opciones: excitación forzada, o natural (debida a las fuerzas ambientales presentes: viento, tráfico, peatones, etc.).
A su vez, estos registros (habitualmente de aceleración) recolectados experimentalmente en cada grado de libertad (g.d.l.), son tratados posteriormente con diferentes técnicas para proceder a la identificación de datos.
Una primera clasificación -la más elemental posible-, divide en dos grandes grupos a las técnicas utilizadas:
- Análisis modal clásico: en donde hay un conocimiento, tanto de la respuesta de la estructura como de la excitación aplicada (habitualmente generada por equipos electrohidráulicos); por lo que se puede determinar la relación entre ambas y obtener modos normalizados respecto de la matriz de masa [2,3,4].
- Análisis modal operacional: no requiere una excitación artificial, ya que utiliza la del ambiente (tráfico, viento, peatones, etc.), y solo emplea la respuesta de la estructura [5]. Los modos de vibración obtenidos, no están normalizados, al no poder medir/registrar la excitación de entrada [6,7,8].
Entre ambos grupos de métodos, normalmente es preferible el primero, siempre y cuando estemos hablando de pequeñas estructuras y conjuntos mecánicos que se pueden ensayar en laboratorio, o también en el caso de grandes estructuras cuyos modos de vibración de interés pueden ser excitados artificialmente sin dificultades significativas [2].
La ventaja de utilizar el análisis modal clásico frente al operacional, no radica solo en que la excitación (artificial) sea conocida, sino en que se dispone de más procedimientos para estimar los parámetros modales [9,10] y caracterizar los sistemas; y a su vez con mayor precisión en la identificación de ciertas magnitudes, como en el caso de las razones de amortiguamiento.
La estimación del amortiguamiento, en el caso de una excitación de baja amplitud (como generalmente es la producida por las acciones ambientales), es menos precisa, y sus resultados presentan mayor dispersión debido a que si las oscilaciones de la estructura son muy reducidas, la influencia del ruido se hace más notable, llegando incluso a ser del mismo orden de magnitud que aquellas. Por otra parte, el amortiguamiento de cada modo no es una magnitud constante, varía con el nivel de carga (afectando esta última a la amplitud de aceleración); este comportamiento se ha documentado en otros trabajos [11,12]. A mayor excitación, mayor amortiguamiento; incluso con un cierto comportamiento no lineal entre ambos.
Los parámetros modales que definen el comportamiento dinámico del Puente de la Cartuja, así como su modelo de respuesta, se han obtenido en un trabajo anterior [13]. Para ello se ha modelizado el puente, al objeto de someterlo a una serie de simulaciones numéricas.
La principal aportación del presente estudio, es abrir un nuevo camino para la resolución del problema inverso en análisis modal (determinar el modelo modal a partir del modelo de respuesta del sistema), utilizando métodos de optimización y técnicas de descomposición que permiten trabajar con magnitudes complejas, para tratar separadamente la parte real e imaginaria [14,15], las cuales, de esta forma, pueden ser implementadas en programas comerciales de optimización.
El objeto del trabajo presentado, es estimar de la forma más fiable posible los parámetros modales [9], con unos resultados más óptimos, incluso con la presencia de un alto nivel de ruido en la señal. Y está orientado a sistemas con amortiguamiento viscoso, niveles de amortiguamiento bajos, y alternativas que operan en el dominio de la frecuencia.
2. Determinación de parámetros modales aplicando técnicas de optimización
La receptancia expresada en el dominio de la frecuencia (analíticamente es habitual trabajar con receptancias, mientras experimentalmente lo es con acelerancias) [1], como cociente entre la respuesta del sistema (desplazamiento), en el grado de libertad g.d.l. j, y la fuerza de excitación, en el g.d.l. k, para el caso general de amortiguamiento viscoso (no proporcional) viene dada por
|
(1) |
donde
|
(2) |
es una cantidad compleja conocida como constante modal o residuo para el modo r. Por definición, cada residuo es el resultado del producto de dos componentes de una misma columna de la matriz modal; asimismo, los polos λr vienen dados por
|
(3) |
siendo ωr y ξr la frecuencia natural y la razón de amortiguamiento para el modo r, respectivamente; donde * denota conjugado complejo.
La expresión anterior (1) muestra, que la respuesta total es el resultado de la suma de las contribuciones de los diferentes modos de vibración.
Las características principales, de la técnica de optimización que se describe en este apartado, son las siguientes:
- Trabaja en el dominio de la frecuencia.
- Indirecta, es decir, el modelo modal se determina a partir del modelo de respuesta.
- Se aplica a sistemas con múltiples g.d.l.
- Los parámetros a estimar son:
- A nivel local: frecuencias naturales ωr , y factores de amortiguamiento ξr , en cada FRF.
- A nivel global: matriz modal [Φ] , utilizando los resultados conjuntos de las FRF (los modos de vibración pueden ser complejos).
- No es necesario cálculo previo alguno para estimar los valores iniciales de los parámetros modales; ya que no hace falta suministrar buenas estimaciones de partida para que el proceso converja.
El conjunto de datos para la obtención de residuos, está constituido por la parte real y compleja de cada una de las FRF. Analíticamente se suele trabajar con receptancias, como ya se ha indicado
- dR i: magnitud de la receptancia (parte real), a la frecuencia i
- dI i: magnitud de la receptancia (parte compleja), a la frecuencia i
A continuación se enumeran el conjunto de variables involucradas en el problema, incluyendo las frecuencias naturales comprendidas dentro de cada uno de los intervalos identificados manualmente, en los que se encuentran cada uno de los modos que se quieren estimar (picos de las curvas):
- ωr: frecuencia natural para el modo r
- AR r: residuo de alfa (parte real) para el modo r
- AI r: residuo de alfa (parte compleja) para el modo r
- ξr: razón de amortiguamiento para el modo r
- εR i: error asociado con al dato i (parte real)
- εI i: error asociado con al dato i (parte compleja)
- z: función objetivo
εR i y εI i son siempre positivos, debido a la metodología del análisis de regresión efectuado.
La receptancia αjk(ω) tiene componentes real y compleja -y asumiendo que los grandes paquetes de software para optimización sólo trabajan con magnitudes reales (véase por ejemplo: GAMS, AMPL y AIMMS)-, es necesario -en primer lugar-, racionalizar dicho quebrado, para posteriormente realizar las estimaciones de la expresión resultante (parte real y compleja) por separado. De esta manera, se evitan los problemas que surgen al tener que operar con la magnitud y la fase de la receptancia, en lugar de operar con su parte real y compleja, en el proceso de optimización. Tal como se ha visto en (1), para el primer quebrado de αjk(ω), se tiene que
|
(4) |
Racionalizando este primer quebrado (multiplicando ambos miembros del mismo por el conjugado del denominador), resulta
|
(5) |
Para separar el producto de magnitudes reales y complejas del numerador de la receptancia αjk(ω), se recurre a agrupar las componentes reales e imaginarias de acuerdo con la descomposición
|
(6) |
Identificando términos a ambos lados de la igualdad anterior, al objeto de separar el residuo rAjk, en sus componentes real rAR jk e imaginaria rAI jk
|
(7) |
de donde finalmente se obtiene, para el primer quebrado
|
(8) |
Siguiendo el mismo procedimiento, y utilizando el conjugado de a + bi en la expresión (6) se obtiene, para el segundo quebrado
|
(9) |
del conjunto de ambos quebrados de (1), agrupando sus partes real e imaginaria, en cada una de sus expresiones (8) y (9), se alcanza la partición buscada.
|
(10) |
Para ajustar cada una de las FRF, se utiliza un análisis de regresión, según el método de estimación del mínimo valor absoluto [16]; este método tiene la ventaja de asignar una importancia semejante a todos los errores. Otros métodos, como el de mínimos cuadrados (dado que los errores van elevados al cuadrado), penaliza los errores grandes con respecto a los pequeños; el método minimax, por su parte, se centra solo en el error máximo.
|
(11) |
La estimación de los parámetros modales, se realiza a través de la resolución del siguiente problema de programación no lineal
|
(12) |
Sujeto al siguiente conjunto de restricciones no lineales del problema, que definen el conjunto de soluciones admisibles
|
(13) |
donde n es el número de muestras o de puntos en los que se ha medido la respuesta y αR i , αI i la estimación, respectivamente, de la parte real e imaginaria de la receptancia αjk(ω) considerada (10).
Finalmente, es digno de mencionar, que las condiciones de ortogonalidad [1] se cumplen rigurosamente para los parámetros calculados a través de este método. Esto ha sido verificado mediante simulaciones de modelos analíticos previos; partiendo del modelo espacial, formado por las matrices de masa, rigidez y amortiguamiento.
Las características de los lenguajes de programación citados más arriba (GAMS, AMPL y AIMMS) son similares; para resolver este trabajo se ha elegido el primero, por la familiaridad del autor con este lenguaje, pero en principio los otros dos también serían válidos.
Sin embargo, en cuanto a la definición del problema, la descripción matemática del modelo coincide prácticamente con el problema de optimización (código) de GAMS. Y además, el proceso de modelado está separado del proceso de resolución del problema; de esta manera el usuario se despreocupa del funcionamiento interno del algoritmo que precisa para resolverlo. Ambas características son propias del paquete GAMS.
El modelo se resuelve utilizando un optimizador de programación no lineal (nlp). Entre la información que ofrece del programa sobre el modelo resuelto (véase apartado 4), destacan los sufijos:
- modelstat, que informa sobre la calidad de la solución obtenida, asignándole un valor de 2: localmente óptimo (esto es debido a la naturaleza del problema -de tipo nlp- asociado a ese valor).
- solvestat, que informa sobre el estado del optimizador al finalizar la resolución, asignándole un valor de 1: finalización normal.
Una vez finalizada la exposición del procedimiento de cálculo, se ilustra el mismo, en su aplicación a una estructura actualmente en uso.
3. Características del puente analizado
El puente de La Cartuja, está ubicado en el Meandro de San Jerónimo, en Sevilla (España), sobre el río Guadalquivir [17,18], se trata de un puente de tipo viga cajón continua de sección variable, con tablero ortótropo, totalmente metálico, que respeta la visibilidad del entorno mediante una estructura discreta y elegante.
Consta de 3 vanos, con una longitud total de 238 m: 42.5 m en el vano lado Expo, 170 m en el vano central, y 25.5m en el vano lado Sevilla. La viga cajón o viga principal del puente, está rigidizada mediante marcos de rigidización transversal cada 4.25 m, los cuales dividen el puente en 56 módulos. El peso acabado del puente es de 1869 t, equivalente a 714 kp/m2 (Figuras 1 y 2).

|
| Figura 1. Alzado general del Puente de la Cartuja |

|
| Figura 2. Vista del vano principal (central) del Puente de la Cartuja |
El ancho del tablero es de 11 m y el canto de la viga variable: desde los 1.92m del estribo lado Expo que aumenta progresivamente hasta llegar a los 6 m en la pila del mismo margen, para disminuir hasta alcanzar los 3 m manteniéndose prácticamente constante en buena parte del vano central y vano lateral lado Sevilla; lo cual representa una relación luz/canto de 56.6: este valor en su día fue el menor registrado en un puente, por lo que se convirtió en el puente más esbelto del mundo. Haciendo gala de una elegancia inédita hasta entonces. Figura desde el año 2007 en el Libro Guinnes de los records.
La continuidad de la viga del puente en los tres vanos, permite alcanzar esta esbeltez, gracias a los vanos laterales relativamente cortos y a las ménsulas ubicadas en el tablero y en los estribos, a través de los cuales se trasmiten reacciones negativas (Figura 1).
4. Análisis de resultados
Utilizando la metodología de cálculo desarrollada en el Apartado 2, seguidamente se muestran los resultados obtenidos, modelizando el Puente de la Cartuja mediante 56 tramos de 4.25 m cada uno (Figura 3); en total 57 secciones. El efecto del arrastre del esfuerzo cortante en las diferentes secciones transversales, se ha tenido en cuenta en la modelización del esqueleto resistente (Figura 3) del Puente de la Cartuja.

|
| Figura 3. Modelización del Puente de la Cartuja: viga cajón continua de sección variable, con tablero ortótropo |
A continuación se sigue el procedimiento expuesto en este trabajo: en primer lugar se identifica el sistema dinámico, mediante procedimientos de optimización, desde el modelo de respuesta (matriz de FRF), hasta el modelo modal (frecuencias naturales, razones de amortiguamiento y matriz modal normalizada respecto a la masa).
Se ha simulado ruido numéricamente en el modelo de respuesta, añadiendo un ruido blanco a cada una de las componentes de la matriz de las FRF, de la siguiente manera [13,19]
|
(14) |
Donde αjk(ω) es la componente jk de la matriz de FRF, que contiene los datos usados para la identificación, Ep es el nivel de ruido (en %), y Nruido es una distribución normal estándar, con un valor medio de 0 y una desviación típica de 1, es decir N(0,1). Ambas magnitudes, real y compleja, de la matriz de FRF, se ven perturbadas por este ruido blanco.
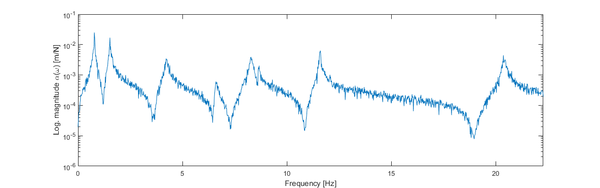
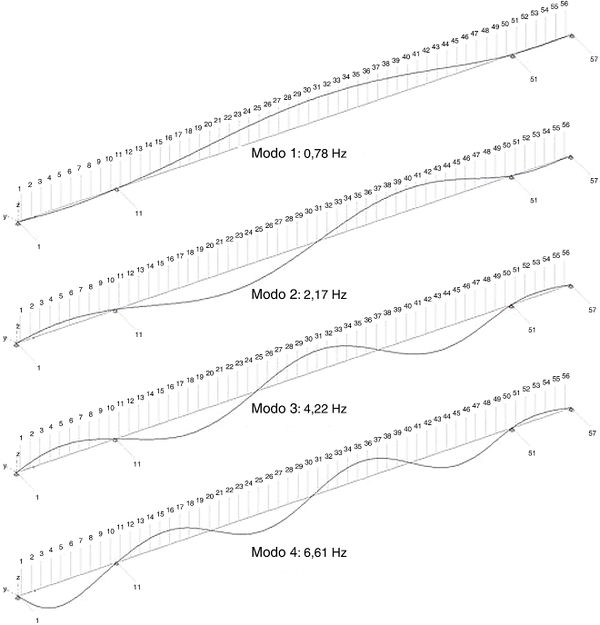
Se han identificado los cuatro primeros modos en flexión vertical (Figura 4). Para ilustrar gráficamente el modelo de respuesta de la estructura, y al objeto de no ocupar un espacio excesivo, en la Figura 5 se representa en el dominio de la frecuencia una de las componentes αjk(ω) de la diagonal principal de la matriz de las FRF (con un nivel de ruido en la señal del 20%), correspondiente a la sección 32 del puente, para un g.d.l. vertical (evidentemente perpendicular al eje longitudinal del mismo), muy próximo a la clave y a la sección intermedia del vano principal (central) del puente.
En la práctica, el rango de interés del análisis está limitado por las frecuencias asociadas a los modos de vibración que se quieren estimar. Es decir, se trata de obtener residuos en modelos incompletos. En la referencia [14] se describe la alternativa empleada, basada en técnicas de optimización, que consiste en utilizar complementos residuales móviles (tanto para la parte real como para la imaginaria), para así tener en cuenta el efecto de los modos fuera de rango.
|
| Figura 4. Flexión vertical: primeros cuatro modos de oscilación |
Asimismo, una vez obtenidos los residuos, se describe en la referencia [15] la alternativa de cálculo empleada para obtener la matriz modal del sistema dinámico, utilizando técnicas de optimización a partir de aquellos.
Es necesario hacer notar, que los procedimientos citados en las referencias [14] y [15] se realizaron para amortiguamiento independiente de la frecuencia (histerético), pero también son válidos en el presente trabajo para el caso general de amortiguamiento viscoso, con ajustes menores (en la primera referencia se muestra como se obtienen los parámetros modales a través de las FRF, mientras que en la segunda, se describe la determinación de la matriz modal desde los residuos, ambas utilizando técnicas de optimización).
La Tabla 1 muestra los resultados de las frecuencias naturales y factores de amortiguamiento correspondientes a los 4 primeros modos de vibración, así como las magnitudes de los mismos en las secciones: 4, 7, 17, 22, 27, 32, 37, 42, 47, y 54; normalizados estos respecto de la masa. Estos parámetros modales, que caracterizan el comportamiento dinámico del puente analizado, se han obtenido en un estudio anterior [13].
| PARÁMETROS MODALES DE REFERENCIA | |||||||||||||
| MODO | ω [rad/s] | ξ [%] | [Φ] | COMPONENTES | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
| 1 | 4.92 | 0.0173 | Φ1 | -0.0035 | -0.0042 | 0.0128 | 0.0297 | 0.0387 | 0.0427 | 0.0373 | 0.0243 | 0.0088 | -0.0013 |
| 2 | 13.64 | 0.0098 | Φ2 | 0.0086 | 0.0100 | -0.0259 | -0.0394 | -0.0281 | 0.0038 | 0.0333 | 0.0393 | 0.0197 | -0.0035 |
| 3 | 26.50 | 0.0165 | Φ3 | 0.0179 | 0.0194 | -0.0343 | -0.0183 | 0.0170 | 0.0368 | 0.0053 | -0.0351 | -0.0297 | 0.0063 |
| 4 | 41.51 | 0.0072 | Φ4 | -0.0409 | -0.0382 | 0.0248 | -0.0221 | -0.0308 | 0.0125 | 0.0302 | -0.0139 | -0.0315 | 0.0084 |
Las Tablas 2 y 3 muestran los resultados estimados, utilizando las técnicas de optimización descritas previamente en el apartado 2, mediante el programa informático GAMS: sistema de modelado para la programación matemática y la optimización [20].
| PARÁMETROS MODALES ESTIMADOS (NIVEL DE RUIDO EN LA SEÑAL 0 %) | |||||||||||||
| MODO | ω [rad/s] | ξ [%] | [Φ] | COMPONENTES | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
| 1 | 4.92 | 0.0173 | Φ1 | -0.0035 | -0.0042 | 0.0128 | 0.0297 | 0.0387 | 0.0427 | 0.0373 | 0.0243 | 0.0088 | -0.0013 |
| 2 | 13.65 | 0.0110 | Φ2 | 0.0086 | 0.0100 | -0.0259 | -0.0394 | -0.0281 | 0.0038 | 0.0333 | 0.0393 | 0.0197 | -0.0034 |
| 3 | 26.50 | 0.0164 | Φ3 | -0.0179 | -0.0194 | 0.0343 | 0.0226 | -0.0158 | -0.0368 | -0.0051 | 0.0352 | 0.0294 | -0.0062 |
| 4 | 41.51 | 0.0071 | Φ4 | 0.0409 | 0.0382 | -0.0248 | 0.0221 | 0.0308 | -0.0125 | -0.0302 | 0.0139 | 0.0315 | -0.0084 |
Finalmente, los valores estimados de las Tablas 2 y 3 (con y sin, ruido en la señal respectivamente), frente a los de la Tabla 1 (para las magnitudes de referencia), ponen de manifiesto que ambos conjuntos de parámetros dinámicos (estimados y de referencia) se corresponden perfectamente entre ellos, lo cual permite apreciar que se alcanza una precisión razonable para su aplicación práctica, y se deriva que el modelo está bien calibrado.
| PARÁMETROS MODALES ESTIMADOS (NIVEL DE RUIDO EN LA SEÑAL 15 %) | |||||||||||||
| MODO | ω [rad/s] | ξ [%] | [Φ] | COMPONENTES | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
| 1 | 4.92 | 0.0193 | Φ1 | -0.0033 | -0.0040 | 0.0128 | 0.0292 | 0.0392 | 0.0432 | 0.0373 | 0.0249 | 0.0086 | -0.0013 |
| 2 | 13.65 | 0.0058 | Φ2 | 0.0084 | 0.0098 | -0.0260 | -0.0399 | -0.0286 | 0.0038 | 0.0325 | 0.0400 | 0.0195 | -0.0034 |
| 3 | 26.55 | 0.0159 | Φ3 | -0.0150 | -0.0206 | 0.0329 | 0.0174 | -0.0168 | -0.0372 | -0.0050 | 0.0145 | 0.0276 | -0.0060 |
| 4 | 41.50 | 0.0061 | Φ4 | 0.0408 | 0.0377 | -0.0251 | 0.0219 | 0.0314 | -0.0121 | -0.0298 | 0.0137 | 0.0314 | -0.0085 |
En consecuencia, para simular la respuesta dinámica de la estructura, es posible trabajar con modos normalizados respecto de la masa, aplicando superposición modal de un número finito y reducido de modos de vibración.
5. Conclusiones
A continuación se exponen las conclusiones más destacadas, resultantes de los apartados previos:
- La resolución del problema inverso en análisis modal -a través de los procedimientos expuestos de optimización, y en concreto del programa Gams-, abre un nuevo camino para determinar el modelo modal a partir del modelo de respuesta del sistema estructural, en el caso general de amortiguamiento viscoso.
- Los métodos de descomposición propuestos, permiten trabajar con magnitudes complejas, para tratar separadamente la parte real e imaginaria, un requisito ineludible, en su implementación en programas comerciales de optimización.
- Se tiene en cuenta la influencia de los modos altos y bajos de forma rigurosa, a través del mismo algoritmo de optimización, que se encarga de ajustar la solución mediante complementos residuales móviles, tanto para los modos altos y bajos, como para la parte real y compleja de los modos por separado. Esto tiene un interés práctico, dado que el análisis se centra en un rango de frecuencias determinado, e incluso, en ocasiones dicho rango se encuentra condicionado por las limitaciones de los sensores de captación y/o del equipo analizador.
- El procedimiento propuesto es mucho más estable, frente al error cometido, ante la presencia de un elevado nivel de ruido en la señal.
- Si se excitan adecuadamente los modos de vibración de los que se pretenden extraer sus propiedades dinámicas, se alcanzan unas estimaciones de los resultados muy buenas. A su vez, dichos resultados permiten simular la respuesta dinámica de una gran estructura sin necesidad de utilizar otros procedimientos con más auge en la actualidad, como son el ajuste de un modelo de elementos finitos de la estructura analizada [5].
- Por otra parte, si se pretende graduar un amortiguador de masa sintonizado, es necesaria una estimación óptima de la masa modal, para ello la mejor opción es utilizar un análisis modal tradicional, mediante el ajuste de FRF obtenidas experimentalmente.
6. Referencias
[1] Maia N.M.M., Silva J.M.M. Modal analysis identification techniques. Philosophical Transactions of the Royal Society of London Series A: Mathematical, Physical & Engineering Sciences, 359(1778):29–40, 2001.
[2] Cacho-Pérez M., Frechilla N., Lorenzana A. Estimación de parámetros modales de estructuras civiles a partir de la función de respuesta en frecuencia. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 33(3-4):197-203, 2017.
[3] Coppotelli G. On the estimate of the FRFs from operational data. Mechanical Systems and Signal Processing, 23:288-299, 2009.
[4] D'ambrogio W., Sestieri A. Coupling theoretical data and translational FRFs to perform distributed structural modification. Mechanical Systems and Signal Processing, 15(1):157-172, 2001.
[5] Foti D., Gattulli V., Potenza F. Output-only modal identification in unfavourable testing conditions and finite element model updating of a seismically damaged building. Computer-Aided Civil And Infrastructure Engineering, 29(9):659-675, 2014.
[6] Parloo E., Cauberghe B., Benedettini F., Alaggio R., Guillaume P. Sensitivity-based operational mode shape normalisation: Application to a bridge. Mechanical Systems and Signal Processing (MSSP), 19:43-55, 2005.
[7] Villa L.M. Error analysis in obtaining scale factors with operational modal analysis and mass change. Rev. Fac. Ing. Univ. de Antioquía, 75:84-92, 2015.
[8] Khatibi M.M., Ashory M.R., Malekjafarian A., Brincker R. Mass–stiffness change method for scaling of operational mode shapes. Mechanical Systems and Signal Processing, 26:34-59, 2012.
[9] Sitarz P., Powałka B. Modal parameters estimation using ant colony optimisation algorithm. Mechanical Systems and Signal Processing, 76-77:531–554, 2016.
[10] Lardiès J. Modal parameter identification by an iterative approach and by the state space model. Mechanical Systems and Signal Processing, 95:239–251, 2017.
[11] Sebastián J., Díaz I.M., Casado C.M., Poncela A.V., Lorenzana A. Evaluación de la predicción de aceleraciones debidas al tránsito peatonal en una pasarela en servicio. Informes de la Construcción, 65-531:335-348, 2013.
[12] Cappellini A., Manzoni S., Vanali M. Experimental and numerical studies of the people effects on a structure modal parameters. Proc. 30th International Modal Analysis Conference IMAC XXX, Jacksonville, USA, (2012).
[13] Villa L.M. Comparación entre la estimación de parámetros modales de estructuras a partir de análisis modal clásico y operacional con modificaciones de masa. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 33(3-4):188–196: 2017.
[14] Villa L.M. Aplicación de técnicas de optimización para la determinación de parámetros modales a través de las funciones de respuesta en frecuencia. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 23(4):395-414, 2007.
[15] Villa L.M., cálculo de la matriz modal de un sistema dinámico a partir de las constantes modales utilizando técnicas de optimización. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 24(1):13-23, 2008.
[16] Castillo E., Hadi A.S., Lacruz B. Regresion diagnostic for the least absolute value and the minimax methods. Communications in Statistics, Theory and Methods, 30:381-395, 2001.
[17] Asensio-Cerver F. Bridges. Atrium, Barcelona, 1992.
[18] Sevilla: Puentes del 92. Colegio de Ingenieros de Caminos, Canales y Puertos de Andalucía (Sección de Publicaciones), 1992.
[19] Zhu X.Q., Law S.S. Time domain identification of moving loads on bridge deck. Journal of Vibration and Acoustics, 125(2):187-198, 2003.
[20] Castillo E., Conejo J.A., Pedregal P., García R., Alguacil N. Building and solving mathematical programming models in engineering and science. Research Studies Press Ltd., 2001.
Document information
Published on 30/09/19
Accepted on 26/09/19
Submitted on 03/12/18
Volume 35, Issue 3, 2019
DOI: 10.23967/j.rimni.2019.09.010
Licence: CC BY-NC-SA license