| Line 482: | Line 482: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image11.jpeg| | + | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image11.jpeg|700px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" style="padding:10px;"| '''Figura 11'''. Gráficos de secciones tipo (i) y de espesores de chapa considerados en ala superior, ala inferior y alma (d) | | colspan="1" style="padding:10px;"| '''Figura 11'''. Gráficos de secciones tipo (i) y de espesores de chapa considerados en ala superior, ala inferior y alma (d) | ||
| Line 490: | Line 490: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image12.jpg| | + | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image12.jpg|700px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" style="padding:10px;"| '''Figura 12'''. Gráficos de factores de reducción '' <math display="inline">\psi</math> '' para determinar el ancho eficaz de la losa (i) y de inercias de las secciones en el modelo de ELS (d) | | colspan="1" style="padding:10px;"| '''Figura 12'''. Gráficos de factores de reducción '' <math display="inline">\psi</math> '' para determinar el ancho eficaz de la losa (i) y de inercias de las secciones en el modelo de ELS (d) | ||
| Line 498: | Line 498: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image13.jpg| | + | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image13.jpg|700px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" style="padding:10px;"| '''Figura 13'''. Gráficos de posición de eje neutro plástico (i) y de clases de los elementos estructurales en momentos negativos (d) | | colspan="1" style="padding:10px;"| '''Figura 13'''. Gráficos de posición de eje neutro plástico (i) y de clases de los elementos estructurales en momentos negativos (d) | ||
| Line 506: | Line 506: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image14.jpeg| | + | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image14.jpeg|700px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" style="padding:10px;"| '''Figura 14'''. Gráficos de combinación de flectores pésimos (i) y de combinaciones de tensiones de Von Misses pésimas en un punto de control (d) | | colspan="1" style="padding:10px;"| '''Figura 14'''. Gráficos de combinación de flectores pésimos (i) y de combinaciones de tensiones de Von Misses pésimas en un punto de control (d) | ||
| Line 514: | Line 514: | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image15.jpeg| | + | |style="padding:10px;"|[[Image:review_Baraibar_Baraibar_2018a-image15.jpeg|700px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" style="padding:10px;"| '''Figura 15'''. Gráficos de ley de esfuerzos cortantes dimensionantes y resistencias asociadas (i) y comprobación de la conexión acero-hormigón (d) | | colspan="1" style="padding:10px;"| '''Figura 15'''. Gráficos de ley de esfuerzos cortantes dimensionantes y resistencias asociadas (i) y comprobación de la conexión acero-hormigón (d) | ||
| Line 520: | Line 520: | ||
| − | La descripción de las prestaciones completas del programa, así como su código fuente, puede encontrarse en la referencia [1]. | + | La descripción de las prestaciones completas del programa, así como su código fuente, puede encontrarse en la referencia [1]. |
==3. Búsqueda del diseño óptimo== | ==3. Búsqueda del diseño óptimo== | ||
Revision as of 11:12, 17 September 2019
Resumen
Las estructuras mixtas no han sido capaces de competir en España con las obras de hormigón pretensado en el rango inferior de las luces medias (30 - 90 m). En este contexto, la sección bijácena se erige como tipología más competente por su sobriedad, facilidad constructiva y buen rendimiento estructural.
En la actualidad raramente se cuestiona el carácter óptimo de los diseños propuestos en los proyectos de estructuras. En el presente estudio se desarrolla un análisis profundo de la tipología bijácena, planteándose la optimización completa de un tablero definido con todas sus variables de forma estricta. Para ello se desarrolla un modelo específico de emparrillado plano, que integra el carácter mixto y evolutivo de los tableros con sección bijácena, así como los fenómenos de inestabilidad propios de las estructuras confeccionadas con chapas delgadas.
Tras efectuar un cálculo paramétrico en abanico y empleando un método de optimización combinatoria se extraen diversas conclusiones relativas a las dimensiones óptimas de las variables que definen la tipología bijácena. Estas conclusiones se cristalizan con una serie de fórmulas de proyecto que pueden servir de guía de diseño a la hora de plantear la idoneidad de esta tipología.
Palabras clave:
Abstract
Composite structures have not been able to compete in Spain with more conventional prestressed concrete bridges in the lower range of medium spans. In this context, twin-girder sections are revealed as a more competent typology because of its sobriety, ease of construction and good structural performance.
At present the optimal character of the designs in structural projects is rarely challenged. The present study undertakes an in-depth analysis of the twin-girder section, involving a complete optimisation for the deck. To this end a specific 2D grillage model has been developed, integrating the composite and evolutive character of twin-girder decks, as well as the instability phenomena inherent to thin-walled structures.
Several conclusions are drawn after a parametric calculation using this model, regarding the optimum dimensions of all the variables that define the twin-girder section. These conclusions crystallise in a series of formulas that can be used as a design guide.
Keywords: Bridge, twin-girder, optimisation, deck, grillage
1. Diseño de secciones bijácena
1.1 Introducción
Frente al empleo de la sección cajón, de utilización prácticamente sistemática en España en el rango inferior de las luces medias (30–90 m.), que está expuesta a la distorsión y a las reducciones de ancho colaborante de las alas, la sección bijácena se erige como tipología más competente por su sobriedad, facilidad constructiva y buen rendimiento estructural.
Por otra parte, en la actualidad raramente se cuestiona el carácter óptimo de los diseños propuestos en los proyectos de estructuras. Aunque las técnicas de optimización han experimentado una evolución enorme en los últimos años, sólo suelen emplearse en ámbitos académicos y asociadas a problemas muy concretos. En el presente artículo se expone el trabajo desarrollado para diseñar un modelo mecánico específico adaptado al cálculo de este tipo de secciones, que permite plantear la optimización completa de un tablero bijáceno definido con todas sus variables de forma estricta y sometido a todos los estados límite que imponen las reglamentaciones de referencia [1], empleando un método de optimización combinatoria.
1.2 La sección bijácena actual
1.2.1. La sección bijácena clásica
La sección resistente que corresponde a la tipología bijácena está compuesta por dos vigas continuas y armadas de alma llena, de canto y espesores de chapa constantes o variables, sobre las que se apoya una losa superior de hormigón, armada transversalmente y longitudinalmente sobre apoyos internos (Figura 1). La tipología bijácena es la última etapa de la evolución de la distribución de rigidez transversal en la sección estructural, ya que la concentra únicamente en dos líneas paralelas, resultando una sección caracterizada por su limpieza, sobriedad y eficacia que destaca por poseer un buen rendimiento estructural, al emplear mecanismos de flexión diferencial entre las vigas como respuesta estructural frente a sobrecargas excéntricas [2].
La losa superior de hormigón armado, además de colaborar en la inercia longitudinal de las vigas y distribuir la carga entre las mismas, procura estabilidad al conjunto, actuando como elemento de arriostramiento superior. Las vigas principales, no obstante, se ligan transversalmente de acuerdo con dos posibles variantes: una viga transversal independiente, de alma llena, situada a media altura de la sección metálica o una viga mixta transversal situada bajo la losa. Las acciones horizontales son recogidas por estos marcos transversales en H que, a través de la flexión en su plano, las transmiten a los diafragmas de apoyo. Estos elementos rigidizan además, aunque en menor medida, la sección frente a fenómenos de flexión transversal y distorsión.
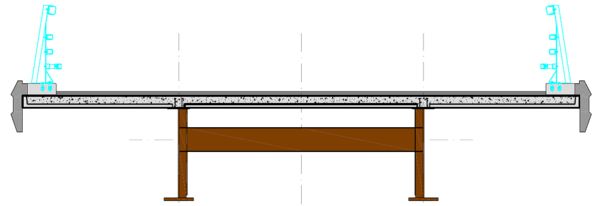
|
| Figura 1. Sección bijácena clásica actual |
La solución descrita en los parágrafos anteriores suele denominarse “bijácena francesa”, ya que precisamente en Francia ha sido ampliamente utilizada en el rango de las luces medias a partir de los años 90, tanto en sus aplicaciones para carretera como para ferrocarril de alta velocidad. El sistema se emplea habitualmente en toda Europa en las luces medias, dominando el mercado de los puentes mixtos por encima de los 30 m. de luz. Por debajo de este valor son las soluciones formadas por vigas múltiples laminadas o por perfiles embebidos quienes compiten con las estructuras de hormigón pretensado [3].
En la Tabla 1 se resumen las características propias de la sección bijácena clásica que suele emplearse en la actualidad.
| Elemento | Características principales |
| Estructura principal – subsección metálica | Formada por dos vigas armadas de alma llena, sin rigidización longitudinal o muy reducida, de canto y espesores de chapa constantes o variables, que se adaptan en cada sección a las necesidades resistentes de la estructura. Normalmente la anchura de las alas suele mantenerse constante. |
| Losa superior | De hormigón, armada transversalmente y longitudinalmente sobre apoyos, para controlar la fisuración. El canto es constante en la dirección longitudinal al puente y puede ser variable en la dirección transversal, variando entre 24 cm. y 40 cm., permitiendo una distancia transversal entre vigas del orden de 6-8 m. y unos voladizos laterales del orden de 2.50-3.00 m. [4]. |
| Elementos de estabilización transversal | Entre vigas longitudinales, a media altura, espaciados en el entorno de los 6-8 metros, estando constituidos por marcos con sección en H. Normalmente el espaciamiento es constante, si bien es habitual acercarlos cerca de los apoyos y alejarlos en el centro de vano, para evitar el pandeo lateral de las vigas [5].
El elemento estabilizador se encuentra constituido normalmente por perfiles laminados comerciales o armados, que se unen a los rigidizadores transversales de las almas, para los que se adoptan secciones en T. Esta disposición permite el uso de encofrados móviles que facilitan el encofrado de la losa. Todos los detalles de unión entre elementos se han simplificado, buscando una mayor sencillez de ejecución así como un comportamiento adecuado frente a la fatiga. La disposición de estos arriostramientos permite la visita de la parte inferior de la losa y el alojamiento de todo tipo de conducciones. Las vigas transversales a nivel de los apoyos son normalmente más rígidas y deben disponerse siempre. Para luces inferiores a 30.00 m., los elementos de estabilización transversal entre apoyos pueden suprimirse [4]. |
| Conexión acero-hormigón | Normalmente se materializa con conectores soldados sobre la cara externa del ala superior de las vigas metálicas, que quedan embebidos en la losa de hormigón armado. Su misión es fundamental, ya que aseguran el comportamiento mixto de la sección. |
Cuando el peralte de la carretera es simétrico, las dos vigas principales son idénticas y posicionadas a la misma altura (Figura 2a). Sin embargo, cuando el peralte es constante (Figura 2b) no se suele alterar el diseño de la losa superior, consiguiéndose con un decalaje en vertical cuyo valor es el producto entre su interdistancia y el peralte. En este caso la viga de estabilización transversal suele ser paralela a la cara superior de la losa [5].
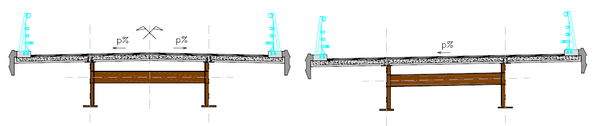
|
| Figura 2. Peralte simétrico (a) o constante (b) en secciones bijácena |
1.2.2. Variantes tipológicas de la sección bijácena actual
La sección bijácena es muy versátil, ya que se adapta fácilmente a diversas anchuras de plataforma, lo que propicia la aparición de ciertas variantes de su sección transversal. Para el ámbito del tráfico carretero, al que está circunscrito el presente estudio, las principales variantes se ilustran en la Figura 3. Pueden combinarse con todos los criterios de configuración longitudinal del viaducto: canto o espesores de chapa constantes o variables, lo que permite una gran variedad de posibilidades a la hora de concebir la estructura [5].
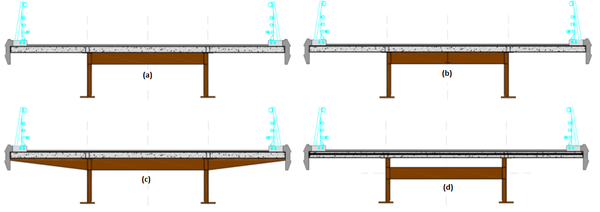
|
| Figura 3. Variantes tipológicas principales de la sección bijácena actual |
La sección bijácena clásica se adapta a anchuras de tablero inferiores a 14.00 m. Para anchuras de tablero mayores pueden adoptarse configuraciones como las que ilustra la Figura 3. En la Figura 3a se eleva la posición de las vigas transversales hasta llegar al nivel inferior de la losa, para transformarlas en vigas mixtas. En este tipo de variante, la distancia entre las vigas principales se incrementa en la misma proporción que lo hace la anchura de la plataforma, sin necesidad de aumentar el canto de la losa, que puede permanecer en el rango 0.20- 0.24 cm. [4]. En la Figura 3b se añade a la anterior una nueva viga longitudinal, denominada stringer en el ámbito anglosajón y longeron en el francófono, que permite incrementar la separación entre las vigas principales y secundarias, si bien sus uniones con estas últimas han de estudiarse con detenimiento para evitar problemas de fatiga [2].
En plataformas de mayor anchura puede combinarse la elevación de las vigas transversales con la presencia de jabalcones laterales que les dan continuidad, según se indica en la Figura 3c. De este modo se posibilitan zonas voladas de la sección de mayor longitud, reduciendo la interdistancia entre las vigas principales y disminuyendo la anchura de los elementos de la subestructura.
Finalmente, para tableros de anchura mayor (hasta 18 m.) existe una variante que aprovecha la tipología de la sección clásica introduciendo un postesado transversal a la losa de hormigón (Figura 3d). Esta característica permite mayores separaciones entre vigas principales y voladizos de mayor longitud. La implementación de este postesado resulta una tarea ardua, que ha provocado que esta variante haya caído en desuso en los últimos años, favoreciéndose para este tipo de plataformas la tipología de vigas transversales elevadas con jabalcones en sus extremos (Figura 3c).
2. Análisis de la respuesta resistente de las secciones bijácena
2.1 Principales mecanismos resistentes presentes en la sección bijácena
El estudio del conjunto de mecanismos resistentes de una estructura es fundamental para comprender su funcionamiento y poder acometer con garantías su comprobación y dimensionamiento, ya que contribuye a formar un fondo intuitivo del fenómeno resistente.
Los mecanismos resistentes son inherentes a cada elemento estructural. La combinación de diferentes elementos estructurales en una misma sección constructiva permite identificar nuevos mecanismos resistentes que pueden interpretarse a nivel global. Las leyes de distribución de esfuerzos en cualquier estructura son el resultado de la superposición de muchos mecanismos resistentes con mayor o menor influencia [6].
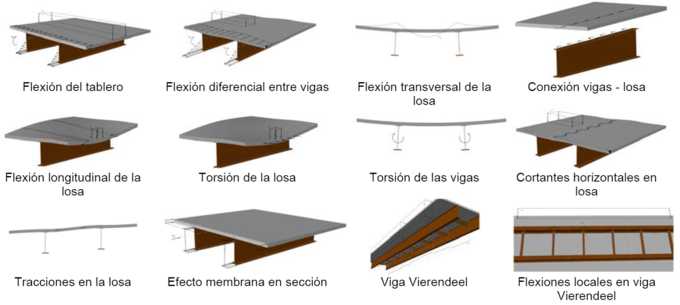
|
| Figura 4. Mecanismos resistentes presentes en la sección bijácena |
En [1] se recopilan los mecanismos resistentes presentes en la sección bijácena (Figura 4), asociándose al tipo de cargas que desencadenan su funcionamiento. Se identifican hasta 12 mecanismos resistentes, 4 principales (flexión general del tablero, flexión diferencial entre las vigas, flexión transversal de la losa, conexión entre las vigas y la losa superior) y 8 secundarios (flexión longitudinal de la losa, torsión de la losa, torsión de las vigas, efecto de membrana en la losa-cortantes horizontales, efecto de membrana en la losa-tracción en la losa, efecto de membrana en la sección, efecto de viga Vierendeel frente a cargas horizontales, flexiones locales en la viga Vierendeel).
2.2. Aproximaciones al comportamiento estructural de la sección bijácena
Los tableros de puente son estructuras tridimensionales que pueden analizarse a partir de modelos más o menos simplificados. El estudio de la resistencia de una construcción comienza por la elección de un esquema de funcionamiento y de cálculo. Esta elección no es generalmente única y depende del grado de precisión requerido para el análisis. Normalmente, por su mayor sencillez en el análisis y la herencia de las verificaciones a efectuar en la normativa en vigor, la principal simplificación consiste en reducir la forma geométrica de las estructuras a esquemas de viga. El estudio se completa con un análisis en el sentido transversal, para apreciar de este modo el carácter tridimensional de su funcionamiento [7].
En [1] se recogen los métodos que se han empleado tradicionalmente para el análisis del comportamiento estructural de los tableros bijácena, que van desde el modelo más sencillo de viga hasta los modelos más sofisticados de elementos finitos, pasando por modelos adaptados de viga, modelos de lámina plegada, de losa ortótropa o de emparrillado plano, el cual, como veremos, se adapta perfectamente a los objetivos perseguidos en el trabajo. Las particularidades de estos modelos se resumen en la Tabla 2.
| Modelo de comportamiento | Sección indeformable | Viga fibras paralelas | Sección compacta | Validez del principio de Saint-Venant | Validez del principio de Navier-Bernouillil | Adaptabilidad a vigas de sección variable | Integra mecanismo de rigidez a torsión pura | Integra efectos análogos a la torsión alabeada |
| Modelo de viga I (Resistencia de Materiales clásica) | SÍ | SÍ | SÍ | SÍ | SÍ | SÍ | SÍ | NO |
| Modelo de viga II (Integra torsión no uniforme) | SÍ | SÍ | NO | NO | NO | NO | SÍ | SÍ |
| Modelo de vigas transversales rígidas | SÍ | SÍ | NO | NO | NO | SÍ | NO | SÍ |
| Modelo de lámina plegada | NO | SÍ | NO | NO | NO | NO | NO | SÍ |
| Modelo losa ortótropa | NO | SÍ | NO | NO | NO | SÍ | SÍ | SÍ |
| Modelo Cart-Fauchart | NO | SÍ | NO | NO | NO | NO | NO | SÍ |
| Modelo emparrillado plano | NO | SÍ | NO | NO | NO | SÍ | SÍ | SÍ |
| Modelo de elementos finitos | NO | NO | NO | NO | NO | SÍ | SÍ | SÍ |
Cabe destacarse que en los tableros bijácena, cuya sección está constituida por paredes delgadas, los modos de carga simétricos no provocan ningún alabeo de la sección, de forma que las tensiones originadas por este tipo de modos pueden calcularse por los métodos usuales de la Resistencia de Materiales clásica. Por el contrario, los modos de carga no simétricos sí originan tensiones importantes que no captan los métodos usuales de la Resistencia de Materiales (Figura 5). Por tanto cualquier modelo que se precie de representar fielmente el comportamiento estructural de este tipo de estructuras ha de ser capaz de integrar este fenómeno resistente.
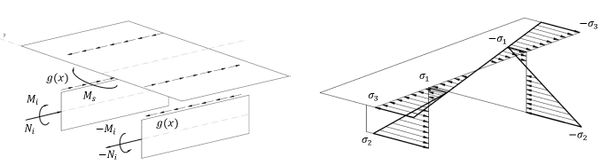
|
| Figura 5. Ejemplo de lámina plegada para sección bijácena (i) y aspecto de las tensiones originadas por cargas antimétricas en secciones bijácena (d) |
2.3. Elección y desarrollo del modelo de cálculo
2.3.1. Descripción del modelo
Para determinar la respuesta resistente de la sección bijácena se construye un modelo de cálculo específico de emparrillado plano (Figura 6), que es capaz de integrar el carácter mixto y evolutivo de los tableros con sección bijácena, así como los fenómenos de inestabilidad propios de las estructuras confeccionadas con chapas delgadas. Este modelo, que se calibra según [8], se adapta perfectamente a la linealidad de los componentes principales de la tipología, lo que implica un empleo racional y contenido de los recursos de cálculo, y posibilita el análisis de múltiples esquemas estáticos con técnicas sencillas de minería de datos. Este modelo permite, frente a la rigidez del MEF al respecto, configurar fácilmente los estados evolutivos que atraviesa la estructura y obtener de forma integrada los esfuerzos dimensionantes de las secciones, respetando los criterios de las diferentes normas de referencia (IAP98, IAP2011 y Eurocódigo) en cuanto a las zonas eficaces de sección, bien sea por arrastre de cortante o por abolladura.
|
| Figura 6. Modelos de emparrillado plano para representar el funcionamiento de los tableros bijácena |
La estructura del emparrillado plano que se desarrolla como modelo de cálculo para alcanzar los objetivos del estudio está compuesta por dos vigas principales longitudinales y una serie de vigas secundarias transversales. Habida cuenta de la simetría de la sección, el análisis se centra en la jácena más cargada de la sección bijácena, sobre la que el modelo efectúa un reparto transversal de las cargas actuantes. El modelo genera la envolvente de esfuerzos más desfavorables que determinan el dimensionamiento de las secciones que componen la jácena.
Las cargas que el modelo considera en el reparto transversal se toman en función de la normativa de acciones adoptada, bien sea la vigente Instrucción sobre las acciones a considerar en el proyecto de puentes de carretera (IAP, 2011) o la inmediatamente anterior (IAP, 1998), que se considera de interés por haber sido norma de referencia en el último ciclo expansivo de obra pública en nuestro país (2000 – 2007), o el Eurocódigo 1, sobre el que se basa plenamente en lo que nos concierne la vigente Instrucción española (IAP, 2011).
En todos los casos se considera una geometría de la sección simétrica, con ambas jácenas iguales. En la IAP 98, el tren vertical de cargas puede configurar conjuntos de cargas actuantes excéntricos, que han de posicionarse “en la situación más desfavorable para el elemento en estudio”. Como el elemento en estudio puede ser cada una de las jácenas por separado, existen casos de carga excéntricos, simétricos entre sí, que conducen a los mismos esfuerzos más desfavorables y por tanto a un análogo dimensionamiento de ambas jácenas. En la IAP 11 y en el Eurocódigo 1, sin embargo, la asignación de la carga variable vertical de tráfico es diferente en función de la posición de ciertos carriles virtuales dentro de la sección. En este caso se considera como condición de proyecto que el tráfico puede circular en ambos sentidos, por lo que en algún momento de su tiempo de servicio cada jácena puede estar situada cerca del carril más cargado, lo que en este supuesto provoca que las condiciones de dimensionamiento resulten iguales para ambas jácenas.
En efecto el comportamiento de los tableros bijácena, que no presentan diafragmas en las secciones del interior de la luz, puede representarse por un emparrillado en el que se conjuga la simple combinación de dos vigas longitudinales y un entramado equivalente de vigas secundarias a modo de losa superior (Figura 6 (d)). La losa flecta transversalmente transfiriendo la carga hacia las vigas vecinas, y éstas se transfieren hacia los apoyos principalmente mediante un mecanismo de flexión longitudinal, en el que las vigas trabajan de forma mixta junto con la zona más próxima de la losa a su ala superior. En el modelo de emparrillado no se considera la influencia de las vigas de estabilización transversal, ya que como se sitúan cada 6-8 m. su contribución a la rigidez transversal no es significativa. El efecto de la contribución de estas vigas de estabilización en la movilización de la rigidez transversal de la sección se comprueba en los modelos de ejemplo que ilustra la Figura 7. El modelo “A” representa un tablero con sección bijácena sin elementos de estabilización transversal. El modelo “B” es una copia del anterior pero incluye vigas de estabilización transversal, que se sitúan cada 6 m. Ambos se someten a un caso de carga excéntrico, que moviliza la flexión transversal.
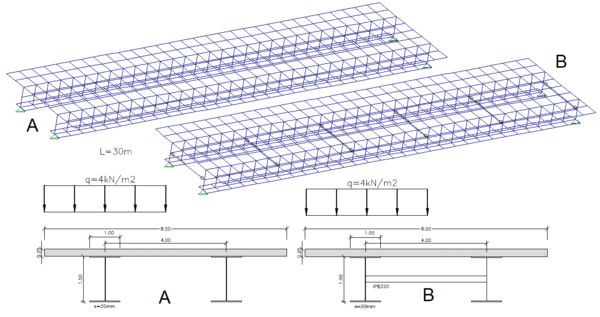
|
| Figura 7. Modelos de comprobación de la contribución de las vigas de estabilización a la flexión transversal |
En la Figura 8 se ilustra la ley de movimientos verticales de la fibra inferior para ambos modelos, tanto de la jácena izquierda, bajo la que se sitúa la carga, como de la jácena derecha. Las diferencias en los movimientos obtenidos con ambos modelos son inferiores al 1%.
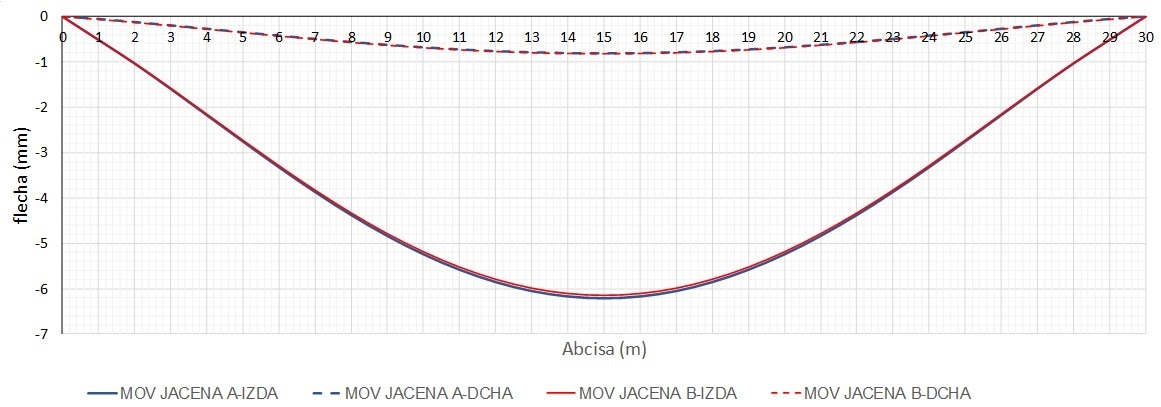
|
| Figura 8. Desplazamientos verticales en las jácenas consideradas en el los modelos de la Figura 7 |
En la Tabla 3 se incluyen las tensiones en la fibra inferior de las jácenas del modelo descrito en la Figura 7, en centro luz. Las diferencias que se obtienen con ambos modelos son inferiores al 2%.
| MODELO | σ(MPa)
JÁCENA IZQUIERDA |
σ(MPa)
JÁCENA DERECHA |
| MODELO A | 13.629 | 1.783 |
| MODELO B | 13.555 | 1.817 |
| DIFERENCIA (%) | 0.54% | 1.90% |
Estas vigas de estabilización transversal sí juegan un papel importante en la comprobación de la resistencia de la estructura frente al pandeo lateral.
Como la losa presenta una rigidez a flexión muy inferior a la de las vigas, flecta con mucha mayor curvatura transversalmente que longitudinalmente. Por ello el comportamiento de la losa entre vigas es mucho más parecido al de un gran número de traviesas. Sólo en las proximidades de una carga concentrada el orden de magnitud de los momentos torsores y flectores en sentido longitudinal en la losa es comparable a la magnitud de sus momentos transversales [9].
En la Figura 9 se muestran las fuerzas diferenciales en un elemento del modelo simplificado de emparrillado formado por viga y losa superior. Se omiten la torsión en la losa, comparativamente muy pequeña en losas de pequeño espesor, la torsión en las vigas y la flexión longitudinal en la losa, por los motivos comentados anteriormente [10].
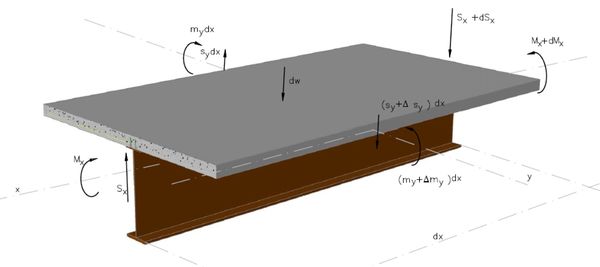
|
| Figura 9. Inventario de fuerzas elementales y predominantes sobre un elemento del modelo de viga y losa superior |
Siempre que se analicen los efectos locales de las cargas exteriores para determinar el armado de la losa superior, el modelo de losa puede reducirse, del lado de la seguridad, a una viga transversal continua soportada por apoyos elásticos que representan cada jácena (Figura 10).
El problema principal de este modelo consiste en aplicar a cada jácena sus características apropiadas, asociadas a cada etapa de cálculo, dado el carácter evolutivo de la sección, y teniendo en cuenta el riesgo de inestabilidad de las secciones y el fenómeno de arrastre de cortante inducido por las concentraciones de rigidez que suponen las propias vigas dentro de la sección. Cuando la variación de cortante en una sección produce flexiones en la misma, las tensiones procedentes de esta flexión se introducen como rasantes al ala, para aumentar o disminuir el axil en ese ala, produciendo en la misma, por la flexibilidad en su plano, una ley de tensiones de compresión o tracción no uniforme [10].
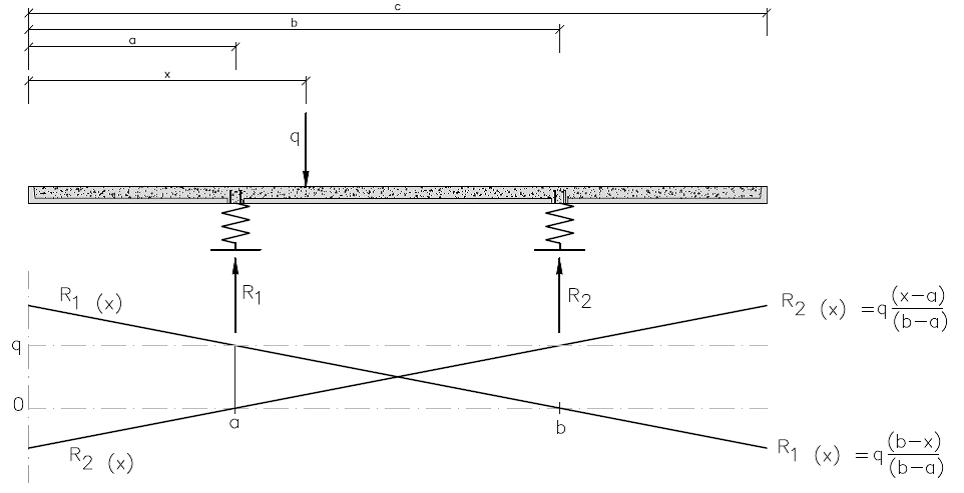
|
| Figura 10. Modelo de viga transversal con apoyos elásticos a la altura de las jácenas y líneas de influencia |
A efectos prácticos y de un modo análogo al empleado en incorporar la consideración de los fenómenos de inestabilidad, el arrastre de cortante se integra en el modelo reduciendo el ancho de la semiala central entre almas o voladizo del ala a un valor , de tal forma que el producto del área comprendida en el ancho eficaz por la tensión máxima es igual al axil que resulta del área real por la distribución real de tensiones.
2.3.2. Comprobación del modelo
El modelo de cálculo se calibra con los datos expuestos en la Monografía M-10. Comprobación de un tablero mixto, publicada por la Asociación Científico-técnica del Hormigón Estructural [8], correspondientes a la comprobación de un puente mixto de tres vanos, empleando un modelo de elementos finitos.
En la Tabla 4 se muestra la comparativa para diferentes casos de carga en Estado Límite de Servicio de las tensiones en los puntos de control de la sección en apoyo propuestas por [8] y las obtenidas con el modelo desarrollado en el trabajo. En general, las diferencias obtenidas son inferiores al 2%, y pueden deberse al modo de aplicar las cargas al modelo.
| CASO DE CARGA | TENSIÓN (Mpa) | MONOGRAFÍA M10 | PROGRAMA | VARIACIÓN |
| Peso Propio Estructura Metálica | σ(MPa) ‐ SUP | 22.6 | 22.42 | 0.8% |
| Peso Propio Estructura Metálica | σ(MPa) ‐ INF | 11.8 | 11.75 | 0.4% |
| Peso Propio Estructura Metálica | τ(MPa) | 4 | 3.95 | 1.3% |
| Peso Propio LOSA + RETRACCIÓN | σ(MPa) ‐ SUP | 150.5 | 149.93 | 0.4% |
| Peso Propio LOSA + RETRACCIÓN | σ(MPa) ‐ INF | 80.1 | 80.20 | ‐0.1% |
| Peso Propio LOSA + RETRACCIÓN | τ(MPa) | 24.68 | 25 | 1.3% |
| CARGA MUERTA | σ(MPa) ‐ SUP | 22.3 | 21.73 | 2.6% |
| CARGA MUERTA | σ(MPa) ‐ INF | 14.9 | 15.01 | ‐0.7% |
| CARGA MUERTA | τ(MPa) | 6.4 | 6.32 | 1.3% |
| ACCIÓN TÉRMICA MMAX NEGATIVO | σ(MPa) ‐ SUP | 11.9 | 12.21 | ‐2.6% |
| ACCIÓN TÉRMICA MMAX NEGATIVO | σ(MPa) ‐ INF | 8 | 8.43 | ‐5.4% |
| SC UNIFORME EXCÉNTRICA MMAX. NEGATIVO | σ(MPa) ‐ SUP | 55.4 | 54.65 | 1.4% |
| SC UNIFORME EXCÉNTRICA MMAX. NEGATIVO | σ(MPa) ‐ INF | 37.5 | 37.75 | ‐0.7% |
| SC UNIFORME EXCÉNTRICA MMAX. NEGATIVO | τ(MPa) | 16.8 | 16.61 | 1.1% |
| VEHÍCULO POSICIÓN EXCÉNTRICA MMAX. NEGATIVO | σ(MPa) ‐ SUP | 41.8 | 41.74 | 0.2% |
| VEHÍCULO POSICIÓN EXCÉNTRICA MMAX. NEGATIVO | σ(MPa) ‐ INF | 28.3 | 28.83 | ‐1.9% |
| VEHÍCULO POSICIÓN EXCÉNTRICA MMAX. NEGATIVO | τ(MPa) | 14.3 | 14.98 | -4.8% |
2.3.3. Programación del modelo
La puesta a punto del modelo se plantea con el clásico método matricial de la rigidez o método de los desplazamientos, según ilustra la Eq. (1), en el que la sección mixta se modeliza mediante barras que presentan características homogeneizadas
|
|
(1) |
En el proceso evolutivo de construcción de la estructura, el análisis de plantea como la suma de modelos en régimen lineal para los que, en el caso de secciones homogeneizadas, las características inerciales de la sección se actualizan en función de sus diagramas momento-curvatura. El principal aspecto específico del modelo en régimen lineal de las estructuras mixtas, como la bijácena, es la incidencia de las deformaciones diferidas del hormigón y en la redistribución de los posibles esfuerzos hiperestáticos, que se integran en el cálculo a través de los coeficientes de equivalencia acero-hormigón [11].
En todos los casos que contempla el programa de cálculo desarrollado para alcanzar los objetivos planteados en el estudio, las cargas introducidas en el modelo, tanto fuerzas como momentos, han sido nodales en todos los supuestos considerados, lo cual es suficientemente representativo en caso de barras cortas, de 0.50 m. de longitud, como las empleadas. Del mismo modo, sólo se han contemplado condiciones concordantes homogéneas para la generación de los apoyos y la determinación de las reacciones.
El programa de cálculo empleado para ensamblar el modelo se ha escrito en archivos .m del entorno MATLAB®, desarrollado por la compañía The MathWorks, Inc.. Su funciones principales son la comprobación automática de los estados límite según los criterios de la normativa española de referencia (RPX, 1995) y los Eurocódigos estructurales (EC3, 2010) y (EC4, 2011), así como la obtención de su coste a partir de las mediciones completas de todos sus componentes.
MATLAB® presenta ciertas ventajas que han facilitado la programación del modelo: lenguaje incorporado de alto nivel, gran capacidad de cálculo matricial, capacidad de intercambiar información con otras aplicaciones de uso común, como MS Excel y capacidad de gestionar grandes cantidades de información en formato vectorial y matricial, entre otras.
Se emplea la versión 2012 sobre un ordenador común de sobremesa (procesador Intel® Core™ i5 a 2.50 Ghz, con 4 Gb de memoria RAM), que puede desarrollar una potencia en megaflops (millones de operaciones por segundo) de aproximadamente 25. El tiempo usual de cálculo en estas condiciones para un sistema estructural de 5 vanos y longitudes de barra de 0.5 m. es de aproximadamente 80’’.
El programa propuesto integra para cada conjunto de variables a verificar en cada esquema estático comprobado la generación de dos submodelos: uno para el análisis global en ELU y otro para el análisis global en ELS. El submodelo para al análisis global en ELS tienen en cuenta la reducción de anchos eficaces por arrastre de cortante y la disminución de ancho eficaz en secciones de clase 4 sometidas a momento negativo. La programación del modelo responde a un esquema de tipo modular, en el que las diferentes piezas van entrando al compilador de forma lógica [1].
2.3.4. Prestaciones del programa
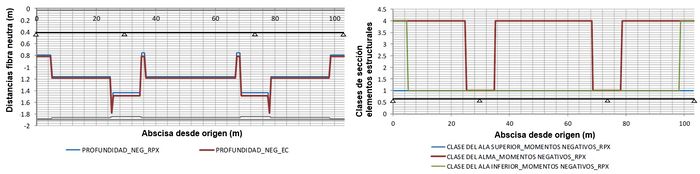
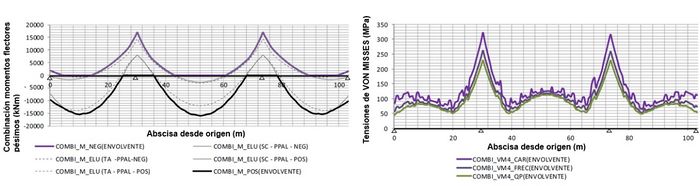
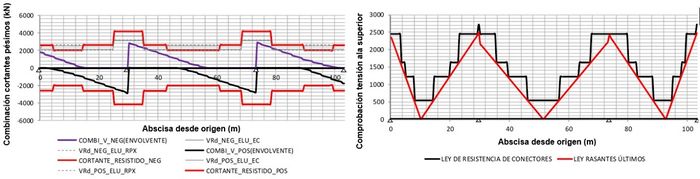
Se muestran a continuación algunas de las salidas del programa desarrollado para llevar a cabo el estudio, relativas a la geometría inicial del caso de estudio (Figura 11), las propiedades mecánicas de las secciones (Figura 12), clases de las secciones (Figura 13), esfuerzos y tensiones combinadas asociados a casos de carga (Figura 14), y comprobación de estados límite últimos y de servicio (Figura 15).
Los gráficos corresponden al ejemplo resuelto en la Monografía M-10. Comprobación de un tablero mixto, publicada por la Asociación Científico-técnica del Hormigón Estructural [8].
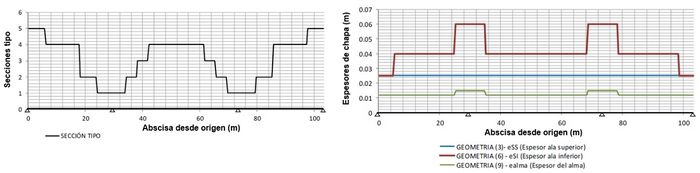
|
| Figura 11. Gráficos de secciones tipo (i) y de espesores de chapa considerados en ala superior, ala inferior y alma (d) |
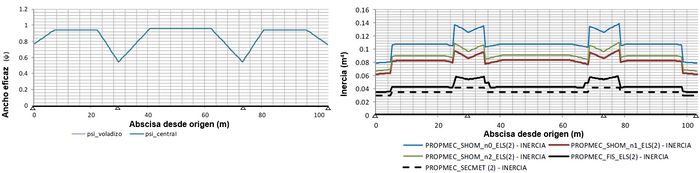
|
| Figura 12. Gráficos de factores de reducción para determinar el ancho eficaz de la losa (i) y de inercias de las secciones en el modelo de ELS (d) |
|
| Figura 13. Gráficos de posición de eje neutro plástico (i) y de clases de los elementos estructurales en momentos negativos (d) |
|
| Figura 14. Gráficos de combinación de flectores pésimos (i) y de combinaciones de tensiones de Von Misses pésimas en un punto de control (d) |
|
| Figura 15. Gráficos de ley de esfuerzos cortantes dimensionantes y resistencias asociadas (i) y comprobación de la conexión acero-hormigón (d) |
La descripción de las prestaciones completas del programa, así como su código fuente, puede encontrarse en la referencia [1].
3. Búsqueda del diseño óptimo
3.1 Planteamiento del problema de diseño óptimo
Se formula el problema de diseño óptimo, clásico de la ingeniería, como la selección de un conjunto de variables de diseño de forma que se minimice una función de coste generalizado, o función objetivo (Eq. (2)). Esta función constituye la base para seleccionar uno de entre los muchos diseños aceptables, y el criterio para discernir hasta qué punto es satisfactorio
|
|
(2) |
En la Eq. (2), es la función objetivo, es el vector de variables de decisión, y es un vector de parámetros que no son objeto de optimización. Además han de verificarse ciertas restricciones que deben satisfacer las variables, que pueden ser condiciones de comportamiento o de diseño [12]. La función objetivo y las restricciones dependen de los parámetros, que se fijan de antemano. es el espacio factible de soluciones y es el espacio posible de soluciones.
3.1.1. Parámetros del problema
Los parámetros del problema contemplados en el análisis se detallan en la Tabla 5. Si bien los parámetros no son objeto de optimización, los efectos de sus diferentes valores sí son determinantes para evaluar las condiciones de determinación del conjunto de variables óptimas. El modelo de cálculo se ha diseñado para integrar los valores de estos parámetros, de modo que puede efectuarse un análisis cuantitativo de la influencia de sus valores sobre la solución óptima.
| Nº | Parámetro | Valores que puede adoptar el parámetro |
| 1 | Método de construcción de la sección metálica | -Ley de momentos flectores análoga a viga continua
-Izado paulatino de vanos sin apeos -Izado de vanos con apeos provisionales -Izado de vanos con soldaduras en pilas |
| 2 | Método de construcción de la losa de H.A. | -Una única fase
-Construcción por fases -Paso de peregrino -Construcción con empleo de cimbra |
| 3 | Número de vanos | -Entre 1 y 5 vanos |
| 4 | Relación luz vano lateral / luz vano interior | -Entre 60% y 80% |
| 5 | Anchura de tablero | -10 m. – 13.50 m. |
| 6 | Cambios en sección tipo por vano | -Entre 2 y 4 en platabanda inferior |
| 7 | Calidad del acero | -S460 – S690 |
| 8 | Calidad del hormigón | -30 MPa |
| 9 | Armaduras pasivas | -B500S |
| 10 | Normativa de referencia | -Combinación RPX-95 / IAP-98
-Combinación RPX-95 / IAP-11 -Eurocódigo |
3.1.2. Variables de diseño
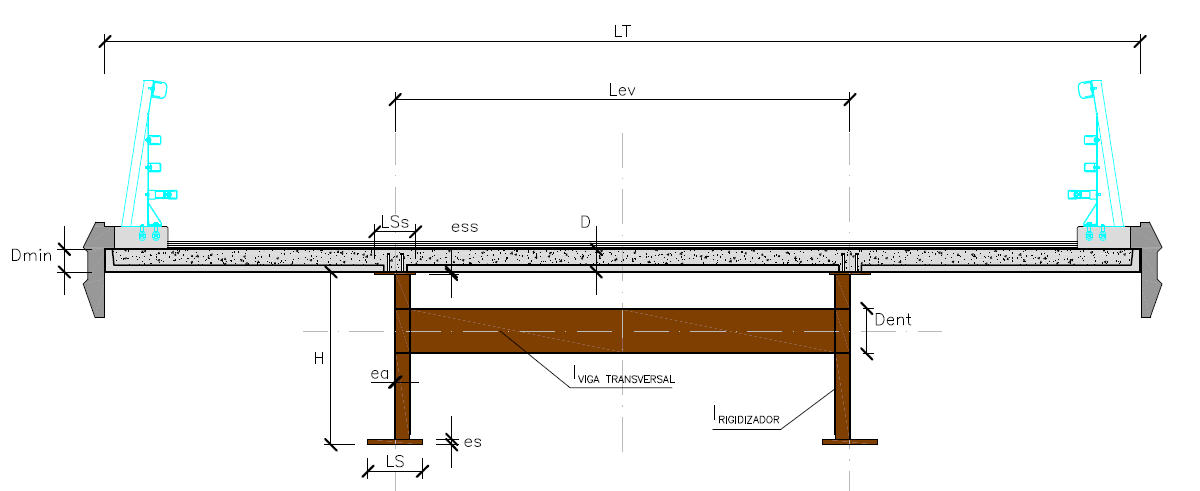
El conjunto de variables objeto de optimización se refiere a la geometría de los componentes de la sección (Figura 16). Adoptan valores discretos, dentro de unos rangos ingenieriles definidos de forma apriorística. Los valores de espesores varían además en función de su posición longitudinal.
|
| Figura 16. Variables determinantes del problema |
3.1.3. Función objetivo
La función objetivo se expresa como la suma de los costes correspondientes a las unidades de obra que configuran la sección bijácena: acero estructural, pernos conectadores, prelosas armadas, hormigón de losa superior y armadura pasiva (Eq. (3))
|
|
(3) |
En la expresión anterior, cada uno de los sumandos expresa el coste obtenido por agregación de los costes elementales de cada componente. Estos costes se generan multiplicando la medición por su precio unitario, y repercutiéndolos al metro cuadrado de tablero. Los precios elementales unitarios medios, correspondientes al método de construcción de izado con torres de apeo provisionales, se ilustran en la Tabla 6.
| Nº | Ud | Definición | Precio unitario (€-2016) |
| 1 | kg | Acero estructural de las vigas principales y secundarias | 2.02 € |
| 2 | ud | Perno conectador Φ19mm, h=150 mm. | 1.95 € |
| 3 | m2 | Prelosa armada con diferentes cuantías según norma | 48.06 € – 59.64 € |
| 4 | m3 | Hormigón de la losa superior HA-30/B/20/IIa – HA40/B/20/IIa | 86.90 € - 95.50 € |
| 5 | kg | Acero B500S en barras corrugadas | 0.76 € |
3.2. Propuesta de metodología de resolución
Se propone como metodología de resolución del problema de diseño óptimo una técnica de optimización combinatoria. Esta técnica consiste en evaluar la aptitud de miles de soluciones previamente definidas en subespacios formados por aquellas que son potencialmente construibles con criterios ingenieriles, empleando una estrategia de tipo prueba-error. Esta técnica, ilustrada en la Figura 17, además de evitar la focalización en óptimos locales, permite asegurar la factibilidad de los diseños a nivel constructivo, determinar cuáles son las características tendenciales de los diseños óptimos y analizar las causas de inaptitud de los diseños no válidos [13].
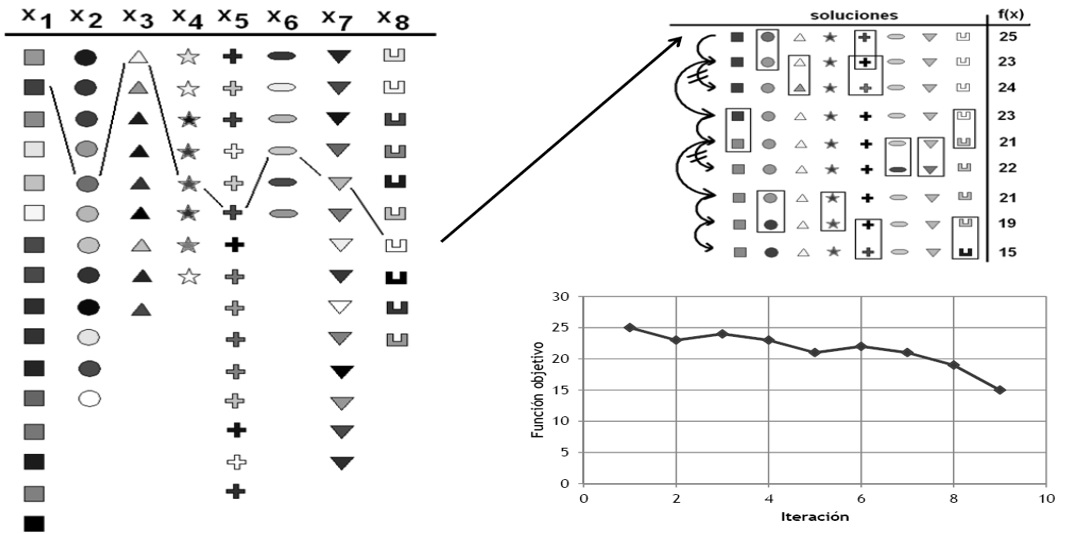
|
| Figura 17. Explicación gráfica de los movimientos en optimización combinatoria [13] |
3.3. Generación de conjuntos de variables potencialmente óptimas
La determinación inicial de las dimensiones de los elementos que forman parte de una estructura implica el uso de ratios geométricos, experiencia previa y comprobaciones aproximadas [14]. En los siguientes parágrafos se da cuenta de la estrategia para definir los conjuntos de variables que pueden determinar potencialmente configuraciones de mínimo coste.
Bajo la hipótesis de rigidez constante, en un tablero de tres vanos compensados los esfuerzos de diseño pueden aproximarse empleando diversas expresiones básicas provenientes de la Resistencia de Materiales clásica, según se ilustra en la referencia [15]. A modo de ejemplo, en la Eq. (4) se da cuenta del momento de diseño en pila en la fase de construcción, en donde es el peso lineal de cada jácena metálica y la carga permanente originada por la prelosa y resto de losa de hormigón
|
|
(4) |
Al objeto de poder determinar los espesores iniciales de las chapas que conforman la sección metálica y sus dimensiones (platabanda superior, inferior y alma de cada una de las secciones tipo) se adaptan las expresiones sugeridas en [16]. Es ilustrativa la expresión propuesta para determinar el área necesaria en la platabanda inferior en la sección de apoyo (Eq. (5))
|
|
(5) |
Como el momento de diseño exacto actuante en la zona de pilas es a priori desconocido, la expresión planteada integra dos parámetros que se evalúan para diversos rangos de valores. De este modo, al canto de la sección metálica se le hace variar entre y y al parámetro se le hace variar entre 1 y 6. La disminución del límite elástico se justifica como reserva ante los efectos de concentración del momento en la zona de pilas por el incremento local de rigidez así como para integrar los efectos no contemplados en la estimación inicial de la fluencia, retracción y gradiente térmico.
3.3.1. Estrategia de selección
En la Figura 18 se aprecia de forma cualitativa la variación de área consumida en función del canto cuando se dimensiona una jácena metálica para resistir un momento flector de valor conocido. El área de la platabanda inferior disminuye rápidamente con el canto mientras que el área del alma, de espesor constante, crece linealmente con el mismo.
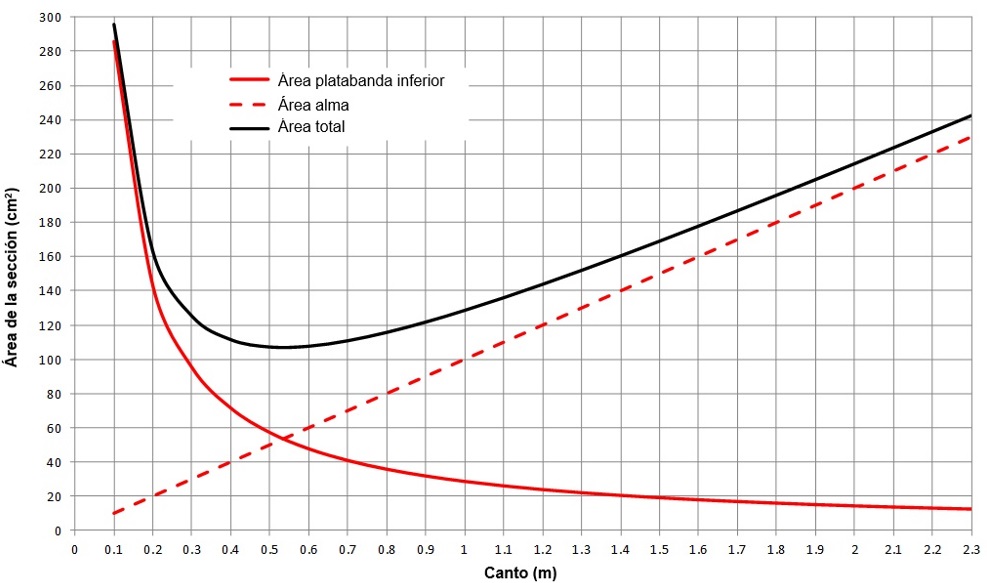
|
| Figura 18. Evolución del área de la sección en función del canto para un momento de diseño conocido |
Existe un cierto rango de cantos (en la Figura 18 entre los valores 0.3 y 0.9) en los que el consumo de área, y por tanto de peso, en la sección es mínimo. Para las particularidades del problema que estamos tratando, se evalúan cantos entre y .
Empleando el modelo de cálculo descrito en el presente artículo se evalúa el cumplimiento de todos los estados límite para cada conjunto de parámetros y variables propuesto, que se caracteriza por la variación de cantos comentada y una variación del parámetro entre 1 y 6, al objeto de poder ajustar los esfuerzos de diseño por los efectos de la concentración local de rigidez en las pilas y la consideración de la fluencia, retracción y gradiente térmico.
El conjunto de variables óptimo seleccionado es aquel que proporciona un coste mínimo cumpliendo con todos los estados límite impuestos por la reglamentación de referencia.
4. Análisis de sensibilidad y resultados del modelo
4.1 Obtención de leyes de coste y cuantías mínimas
En la Figura 19 se muestra el menor coste por m2 asociado a aquellos tableros con un diseño válido, en términos de cumplimiento de estados límite, para cada luz de referencia, obtenido tras evaluar todos los conjuntos de variables definidos como potencialmente óptimos. Esta ley de costes mínimos en función de la luz de referencia se asocia a un conjunto de parámetros determinado (Tabla 7).
| Parámetro | Valor en el caso base |
| Método de construcción de la sección metálica | Izado con torres de apeo provisionales |
| Método de construcción de la losa de H.A. | Una única fase |
| Número de vanos | 3 |
| Relación luz vano lateral / luz vano interior | 70% |
| Anchura de tablero | 10 m. |
| Cambios de sección tipo por vano | 5 (4 en platabanda inferior) |
| Calidad del acero | S355 (S460 en platabanda inferior) |
| Calidad del hormigón | HA-30 |
| Armaduras pasivas | B-500S |
| Normativa de referencia | Combinación RPX-95 / IAP-11 |
Se toma como referencia un caso base, asociado a parámetros que pueden representar un caso habitual o de más probable ocurrencia. Por su interés, en la Figura 17 se comparan los costes mínimos asociados a las diferentes posibilidades contempladas para el parámetro “Normativa de referencia”.
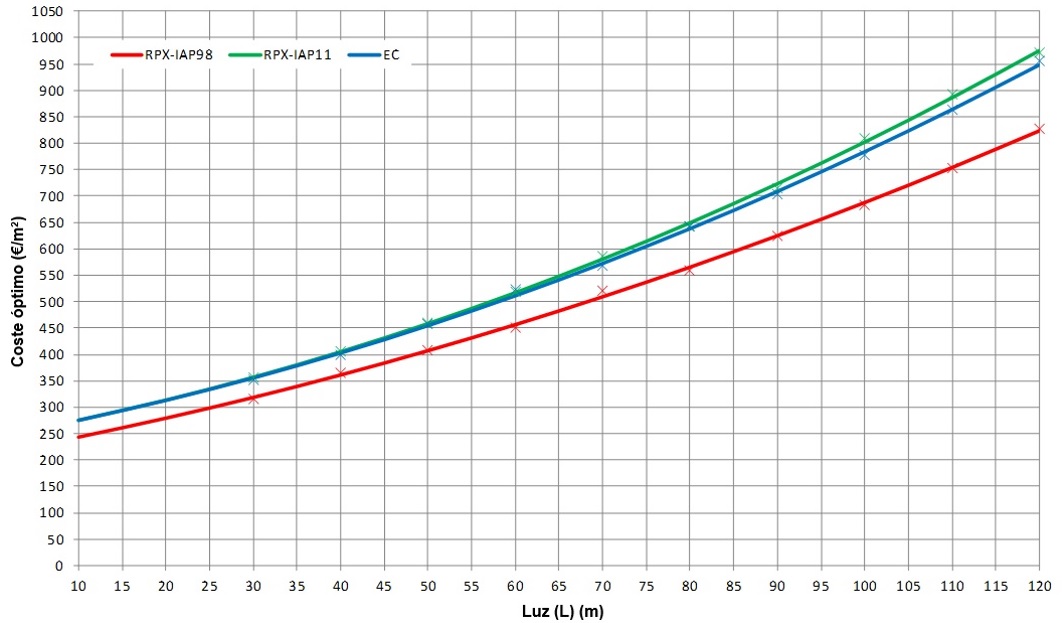
|
| Figura 19. Coste mínimo en función de la luz, para diferentes normativas de referencia |
Las cuantías de consumo de acero estructural están directamente relacionadas con el coste mínimo por m2 de tablero. En la Figura 20 se ilustran las cuantías de consumo de acero estructural asociadas a los diseños con coste mínimo. Los datos obtenidos en [1] se comparan con las principales referencias bibliográficas [2,4,5].
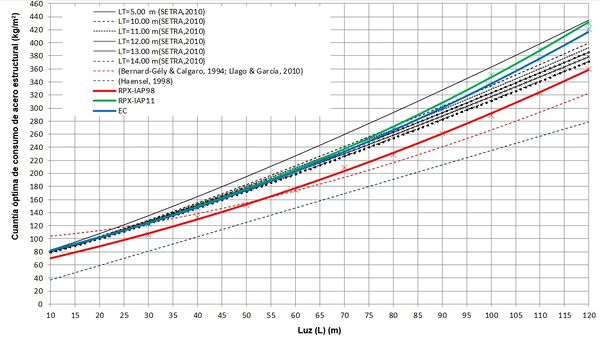
|
| Figura 20. Cuantía óptima de acero estructural por metro cuadrado de plataforma |
En la Figura 21 se muestra la distribución del coste asociado a cada elemento que conforma la sección bijácena. Puede apreciarse que la proporción del coste de la subsección metálica respecto al coste global es creciente con la luz. Para luces del entorno de 30 m. la proporción es del orden del 70% del coste global, hasta alcanzar una proporción del 90% en luces de 120 m.
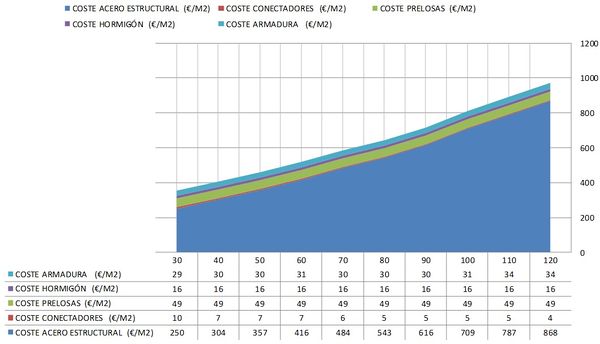
|
| Figura 21. Distribución del coste óptimo entre los componentes de la sección bijácena |
4.2. Fórmulas de proyecto
Las conclusiones del análisis de sensibilidad se cristalizan con una serie de fórmulas de proyecto de modo que puedan servir de guía de diseño y de sustento para valorar de forma apriorística la conveniencia o no del empleo de la tipología bijácena en cada caso particular. Las fórmulas son expresiones matemáticas sencillas válidas para predimensionar soluciones que proporcionan un coste mínimo por metro cuadrado de tablero.
En [1] se proponen expresiones para determinar: momentos negativos de diseño en pila y positivos en centro luz; esfuerzos cortantes de diseño; cantos de la sección metálica; anchura y espesores de ala superior, tanto en pila como en centro luz; anchura y espesores del ala inferior, tanto en pila como en centro luz, espesores de alma; cuantías de rigidización transversal y cuantías de armaduras de refuerzo en zona de momentos negativos.
Como ejemplo, se muestran las expresiones propuestas para determinar los cantos asociados a diseños óptimos, cuando el parámetro “Normativa de referencia” adopta los valores “Combinación RPX-95 / IAP-98” (Eq. (6)), “Combinación RPX-95 / IAP-98” (Eq. (7)), y Eurocódigo (Eq. (8))
|
|
(6) |
|
|
(7) |
|
|
(8) |
Además se incluyen las expresiones obtenidas para determinar los espesores de alma en pila asociadas a diseños óptimos, en función de la luz, cuando el parámetro “Normativa de referencia” adopta los valores “Combinación RPX-95 / IAP-98” (Eq. (9)), “Combinación RPX-95 / IAP-98” (Eq. (10)), y Eurocódigo (Eq. (11))
|
|
(9) |
|
|
(10) |
|
|
(11) |
Finalmente se incluyen las expresiones obtenidas para determinar las cuantías de consumo de acero estructural por metro cuadrado de plataforma asociadas a diseños óptimos (Figura 18), cuando el parámetro “Normativa de referencia” adopta los valores “Combinación RPX-95 / IAP-98” (Eq. (12)), “Combinación RPX-95 / IAP-98” (Eq. (13)), y Eurocódigo (Eq. (14))
|
|
(12) |
|
|
(13) |
|
|
(14) |
5. Conclusiones
Tras haber sometido al algoritmo de optimización con criterios ingenieriles a más de 2.500 configuraciones estáticas de tableros bijácenos, se obtienen las siguientes conclusiones principales:
- El coste mínimo obtenido por m2 de tablero es del mismo orden si consideramos como normativa de referencia la combinación RPX-95/IAP-11 o el Eurocódigo. Se detectan diferencias en el rango superior de las luces medias, hasta alcanzar un 3% más de coste empleando la normativa española respecto a los Eurocódigos para luces del entorno de los 120 m. Los diseños óptimos asociados a la normativa vigente, ya sea la española o la de ámbito europeo, sí presentan un coste significativamente superior al asociado a la normativa anterior, vigente hasta 2011. Las diferencias relativas de coste se sitúan en torno al 12% en el rango inferior de las luces medias, ascendiendo hasta un 18% para luces del entorno de los 120 m.
- En los diseños óptimos, el 75% del peso de la sección metálica recae sobre los elementos que conforman la jácena principal y el 25% del peso sobre los elementos de estabilización (rigidizadores y vigas de estabilización transversal).
- La construcción por izado de la subsección metálica empleando torres de apeo provisionales se revela como la más ventajosa respecto a otras estrategias de izado, que pueden suponer hasta un incremento de coste del 30% sobre esta solución. Las diferentes estrategias de hormigonado de la losa superior (por fases, en “paso de peregrino”, etc.) no provocan diferencias significativas de coste respecto a su construcción en una única fase de hormigonado.
- El coste por m2 de tablero de las configuraciones estáticas de dos vanos resulta entre un 20% y un 60% mayor que el obtenido para configuraciones estáticas de 3 vanos, en el rango de luces de 30 m. a 120 m. Si se consideran configuraciones estáticas de un único vano, el porcentaje de incremento de coste es incluso superior, entre un 45% y un 85% para el rango de luces antedicho.
- Una estrategia de asignación de secciones tipo en el tablero en la que permite dos cambios de platabanda inferior por vano en lugar de cuatro puede suponer un incremento de coste de hasta un 6% para luces de referencia de 120 m. sobre este último caso.
- En los conjuntos de diseños óptimos, el espesor del alma viene determinado por criterios de tensión máxima hasta el rango de 60 a 80 m. de luz de referencia. A partir de este valor de luz, el espesor de alma lo determina el criterio de estabilidad límite para evitar el uso de rigidizadores longitudinales.
- Los conjuntos de diseños óptimos para configuraciones estáticas de tres o más vanos corresponden con secciones compactas, capaces de desarrollar resistencias últimas plásticas.
- El límite de inaptitud más cercano a los conjuntos de diseños óptimos en el rango entre 70 y 120 m. de luz lo determinan los criterios de resistencia última de las secciones. Para luces inferiores el límite de validez de los conjuntos propuestos lo determinan los límites tensionales en las fibras extremas. Las comprobaciones de estados límite de vibraciones y de fatiga, si bien nunca constituyen las fronteras de los diseños óptimos, comienzan a suponer un factor cercano al límite de validez en luces inferiores a 60 m.
Referencias
[1] Baraibar, J.M. (2015). Diseño óptimo de puentes bijácena de ámbito carretero. Tesis Doctoral. Santander: Universidad de Cantabria.
[2] Llago, R., García, P. (2010). Los puentes mixtos bijácena: una solución competitiva en las luces medias. Revista de obras públicas, 3516, 29-46.
[3] COMBRI (2008). COMBRI Design Manual. Part II. State of the art and conceptual design of steel and composite bridges. Stuttgart: Institute for Structural Design. Universität Stuttgart.
[4] Bernard-Gély, A., Calgaro, J. (1994). Conception des ponts (1ª ed.). París: Presses de l’École Nationale des Ponts et Chaussées.
[5] SETRA (2010). Steel-Concrete Composite Bridges Sustainable Design Guide. Bagneux: Service d’études sur les transports, les routes et leurs aménagements (SETRA).
[6] Schanack, F. (2008). Puentes en Arco Tipo Network. Tesis Doctoral. Santander: Universidad de Cantabria.
[7] Calgaro, J., Virlogeux, M. (1988). Projet et construction des ponts: Analyse structural des tabliers des ponts (1a ed.) París: Presses de l’École Nationale des Ponts et Chaussées.
[8] ACHE (2006). Monografía M-10 Comprobación de un tablero mixto. Madrid: ACHE.
[9] Hambly, E.C. (1991). Bridge Deck Behaviour. London: E&FN Spon.
[10] Monleón, S. (1996). Ingeniería de puentes: análisis estructural (ed. 2015). Valencia: Editorial Universitat Politècnica de València.
[11] Martínez, J., Viñuela, L. (2009). Proyecto y Construcción de Puentes Metálicos y Mixtos. Madrid: Publicaciones APTA (Asociación para la Promoción Técnica del Acero).
[12] Hernández, S. (1990). Métodos de diseño óptimo de estructuras. Colección Seinor. Madrid: Colegio de Ingenieros de Caminos, Canales y Puertos.
[13] Yepes, V. (2013). Introducción a la optimización heurística en ingeniería. Santiago de Chile:Chile.
[14] Collings, D. (2005). Steel-concrete composite bridges. London: Thomas Telford Publishing
[15] RPX (2000). Manual de aplicación de las recomendaciones RPM-RPX/95. Madrid: Ministerio de Fomento. Dirección General de Carreteras.
[16] RPX (1995). Recomendaciones para el Proyecto de puentes mixtos para carreteras. Madrid: Ministerio de Fomento. Dirección General de Carreteras.
Document information
Published on 18/09/19
Accepted on 16/09/19
Submitted on 26/03/18
Volume 35, Issue 3, 2019
DOI: 10.23967/j.rimni.2019.09.005
Licence: CC BY-NC-SA license