| Line 11: | Line 11: | ||
[mailto:leilsonjoaquim@gmail.com; leilsonjoaquim@gmail.com;] [mailto:agnovieira@yahoo.com.br agnovieira@yahoo.com.br]; [mailto:danielag@utfpr.edu.br danielag@utfpr.edu.br] | [mailto:leilsonjoaquim@gmail.com; leilsonjoaquim@gmail.com;] [mailto:agnovieira@yahoo.com.br agnovieira@yahoo.com.br]; [mailto:danielag@utfpr.edu.br danielag@utfpr.edu.br] | ||
--> | --> | ||
| − | |||
==Abstract == | ==Abstract == | ||
Concrete gravity dams have trapezoidal shape in their cross section and shall guarantee the global stability against acting loads like hydrostatic and uplift pressures through his gravitational actions (self-weight and others). This study focuses on the shape optimization of concrete gravity dams using genetic algorithms. In this case, the dam cross section area is considered as the objective function and the design variables are the geometric parameters of the gravity dam. The optimum cross-section of a concrete gravity dam is achieved by the Genetic Algorithm (GA) through a Matlab routine developed by the author. Sliding, overturning and floating verifications are implemented in the program. In order to assess the efficiency of the proposed methodology for gravity dams optimization, one application is presented adopting the concrete gravity dam of Belo Monte Hydropower Plant (HPP), considering normal loading condition and others assumptions presented. | Concrete gravity dams have trapezoidal shape in their cross section and shall guarantee the global stability against acting loads like hydrostatic and uplift pressures through his gravitational actions (self-weight and others). This study focuses on the shape optimization of concrete gravity dams using genetic algorithms. In this case, the dam cross section area is considered as the objective function and the design variables are the geometric parameters of the gravity dam. The optimum cross-section of a concrete gravity dam is achieved by the Genetic Algorithm (GA) through a Matlab routine developed by the author. Sliding, overturning and floating verifications are implemented in the program. In order to assess the efficiency of the proposed methodology for gravity dams optimization, one application is presented adopting the concrete gravity dam of Belo Monte Hydropower Plant (HPP), considering normal loading condition and others assumptions presented. | ||
| − | '''Keywords | + | '''Keywords''': Optimization, concrete gravity dams, genetic algorithm, design optimization |
| − | ==1 Introduction== | + | ==1. Introduction== |
Concrete gravity dams are hydraulic structures widely used as water reservoir to hydroelectric power plants in general. These structures have trapezoidal shape in their cross section and shall guarantee the global stability against hydrostatic and uplift pressures by means of gravitational actions (as self-weight and others) [32]. Hence, finding a proper design for the cross-section can remarkably reduce the construction costs [3]. | Concrete gravity dams are hydraulic structures widely used as water reservoir to hydroelectric power plants in general. These structures have trapezoidal shape in their cross section and shall guarantee the global stability against hydrostatic and uplift pressures by means of gravitational actions (as self-weight and others) [32]. Hence, finding a proper design for the cross-section can remarkably reduce the construction costs [3]. | ||
| Line 26: | Line 25: | ||
In order to assure the structural global stability and the allowable stress criteria for the concrete gravity dam design, as discussed in Gutstein [19] and [20] a trial and error procedure process is usually carried out from a preliminary cross section defined in the design initial phases, followed by stability and stress analysis studies. Then, if the chosen cross section does not meet the security criteria, it shall be modified and analyzed again. Also, once safety criteria are met, a new study can be conducted with the purpose of optimizing the design (minimizing the dam cross section area). | In order to assure the structural global stability and the allowable stress criteria for the concrete gravity dam design, as discussed in Gutstein [19] and [20] a trial and error procedure process is usually carried out from a preliminary cross section defined in the design initial phases, followed by stability and stress analysis studies. Then, if the chosen cross section does not meet the security criteria, it shall be modified and analyzed again. Also, once safety criteria are met, a new study can be conducted with the purpose of optimizing the design (minimizing the dam cross section area). | ||
| − | To achieve this purpose, several alternatives can be used to obtain a number of feasible shapes. Finally, the cross section with minimum area (also with lower cost), that meets the structural considerations and design criteria, is selected as the final shape. In order to reliably achieve an optimal shape for dams in this study, instead of this trial and error procedure, optimization techniques have been effectively utilized [23 | + | To achieve this purpose, several alternatives can be used to obtain a number of feasible shapes. Finally, the cross section with minimum area (also with lower cost), that meets the structural considerations and design criteria, is selected as the final shape. In order to reliably achieve an optimal shape for dams in this study, instead of this trial and error procedure, optimization techniques have been effectively utilized [23,24,34]. |
Genetic Algorithms (GA) are heuristic search approaches applicable to a wide range of optimization problems [4]. This flexibility makes them attractive for many optimization problems in practice. They represent one branch of the field of study called evolutionary computation, which imitate the biological processes of reproduction and natural selection to solve for the fittest solutions [7]. | Genetic Algorithms (GA) are heuristic search approaches applicable to a wide range of optimization problems [4]. This flexibility makes them attractive for many optimization problems in practice. They represent one branch of the field of study called evolutionary computation, which imitate the biological processes of reproduction and natural selection to solve for the fittest solutions [7]. | ||
| − | GA can solve a broad class of engineering problems encountered in practice, involving a large number of design parameters (integer, discrete, continuous and integer/discrete-continuous) and a large number of constraints. It has been highly successful as one of evolutionary computation techniques in searching for a broad class of stacking sequence, size, topology optimization problems for composite structures [18 | + | GA can solve a broad class of engineering problems encountered in practice, involving a large number of design parameters (integer, discrete, continuous and integer/discrete-continuous) and a large number of constraints. It has been highly successful as one of evolutionary computation techniques in searching for a broad class of stacking sequence, size, topology optimization problems for composite structures [18,29,30,31]. |
Designing and constructing concrete gravity dams can be considered as a typical optimization problem, since the cross section geometry with lowest area that meets the design criteria is searched for, with the final aim of reducing cost. [35]. | Designing and constructing concrete gravity dams can be considered as a typical optimization problem, since the cross section geometry with lowest area that meets the design criteria is searched for, with the final aim of reducing cost. [35]. | ||
| − | Optimizing this cost requires cross-section optimization. The main aim of this paper is to present and discussed an optimization study for concrete gravity dams based on GA and Matlab application. The present work brings a simple implementation using GA in Matlab for usual loading condition, contrasting with the complexity presented in | + | Optimizing this cost requires cross-section optimization. The main aim of this paper is to present and discussed an optimization study for concrete gravity dams based on GA and Matlab application. The present work brings a simple implementation using GA in Matlab for usual loading condition, contrasting with the complexity presented in [2,3,13,14,23,24,35] which bring approaches with high complexity computational methods. |
The dam's geometry and the acting loads must be considered in its design analysis procedure. In order to reduce the computational cost of the optimization process, the stopping criteria is limited to satisfactory values. To demonstrate the efficiency of GAs in finding the optimum design of concrete gravity dams, the cross-section from Belo Monte Hydropower Plant is presented as an example of application, considering normal loads and hypothetical resistance parameters for the foundation. | The dam's geometry and the acting loads must be considered in its design analysis procedure. In order to reduce the computational cost of the optimization process, the stopping criteria is limited to satisfactory values. To demonstrate the efficiency of GAs in finding the optimum design of concrete gravity dams, the cross-section from Belo Monte Hydropower Plant is presented as an example of application, considering normal loads and hypothetical resistance parameters for the foundation. | ||
| − | ==2 Stability Analysis of Concrete Gravity Dams== | + | ==2. Stability Analysis of Concrete Gravity Dams== |
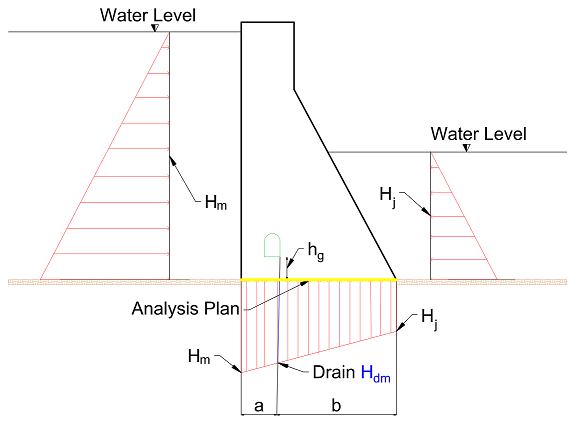
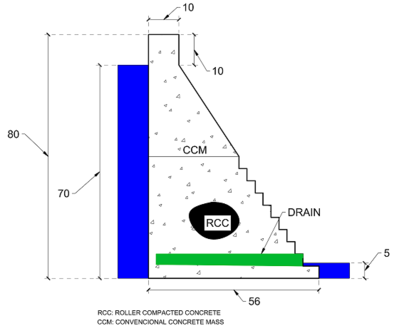
Figure 1 shows the usual loads acting in a dam considering drainage. Water pressure is the major external load acting on such a dam. The horizontal water pressure, exerted by the weight of the water stored on the upstream side on the dam can be estimated from rule of hydrostatic pressure distribution. | Figure 1 shows the usual loads acting in a dam considering drainage. Water pressure is the major external load acting on such a dam. The horizontal water pressure, exerted by the weight of the water stored on the upstream side on the dam can be estimated from rule of hydrostatic pressure distribution. | ||
| Line 88: | Line 87: | ||
where h<sub>g</sub> is the gallery height, H<sub>m</sub> is the upstream water level, H<sub>j</sub> is the downstream water level and all of them in relation to the concrete-rock contact (analysis plan). Those expressions considerer the 66% drainage curtain efficiency adopted for the Bureau of Reclamation [33]. | where h<sub>g</sub> is the gallery height, H<sub>m</sub> is the upstream water level, H<sub>j</sub> is the downstream water level and all of them in relation to the concrete-rock contact (analysis plan). Those expressions considerer the 66% drainage curtain efficiency adopted for the Bureau of Reclamation [33]. | ||
| − | ==3 Geometrical Model of Concrete Gravity Dams and Problem Formulation== | + | ==3. Geometrical Model of Concrete Gravity Dams and Problem Formulation== |
Based on the model of concrete gravity dam depicted in Figure 2, the cross-section of concrete gravity dam studied is defined by the four parameters given by Equation 5. | Based on the model of concrete gravity dam depicted in Figure 2, the cross-section of concrete gravity dam studied is defined by the four parameters given by Equation 5. | ||
| Line 164: | Line 163: | ||
<math display="inline">\,</math> <math display="inline">\,</math> </div> | <math display="inline">\,</math> <math display="inline">\,</math> </div> | ||
| − | ==4 The Optimization Algorithm (Optdam)== | + | ==4. The Optimization Algorithm (Optdam)== |
===4.1 Genetic Algorithm (GA)=== | ===4.1 Genetic Algorithm (GA)=== | ||
| Line 312: | Line 311: | ||
Figure 6. Optimization Algorithm</div> | Figure 6. Optimization Algorithm</div> | ||
| − | ==5 Example: Idealized Cross-Section of the Belo Monte HPP== | + | ==5. Example: Idealized Cross-Section of the Belo Monte HPP== |
The Belo Monte Hydropower Plant has a retaining wall between the main intake and the earth/rockfill dam, which is usually designed following the same criteria as a concrete gravity dam. In order to present the applicability of the Optdam programa in a practical situation, an optimization study using Optdam program is applied on cross-section of the retaining wall. The initial design of Belo Monte cross-section is shown in Figure 7. | The Belo Monte Hydropower Plant has a retaining wall between the main intake and the earth/rockfill dam, which is usually designed following the same criteria as a concrete gravity dam. In order to present the applicability of the Optdam programa in a practical situation, an optimization study using Optdam program is applied on cross-section of the retaining wall. The initial design of Belo Monte cross-section is shown in Figure 7. | ||
| Line 465: | Line 464: | ||
It is worth noting that this is an example that refers to a dam designed and executed, not being configured as a case study, since the values of the constants (cohesion, angle of friction, specific gravity of concrete, etc.) among other specificities of the project are not known with exactness. | It is worth noting that this is an example that refers to a dam designed and executed, not being configured as a case study, since the values of the constants (cohesion, angle of friction, specific gravity of concrete, etc.) among other specificities of the project are not known with exactness. | ||
| − | ==6 Results== | + | ==6. Results== |
The optimum design of the cross-section based on retaining-wall of Belo Monte HPP is given in Table 4. By comparing the solution obtained for the cross-section with the GA it's possible to note that the concrete volume can be significantly reduced. | The optimum design of the cross-section based on retaining-wall of Belo Monte HPP is given in Table 4. By comparing the solution obtained for the cross-section with the GA it's possible to note that the concrete volume can be significantly reduced. | ||
| Line 549: | Line 548: | ||
Figure 10. Optimized Section. Dimensions in meters.</div> | Figure 10. Optimized Section. Dimensions in meters.</div> | ||
| − | ==7 Conclusions== | + | ==7. Conclusions== |
Cross-section optimization is one goal of dam designers. Dam designing must be such that not only satisfies sustaining condition, but also leads to minimum costs and excessive concrete volumes. An efficient optimization procedure is introduced to find the optimal shapes of concrete gravity dams using genetic algorithm in Matlab software. The concrete gravity dam body is treated as a two-dimensional structure. | Cross-section optimization is one goal of dam designers. Dam designing must be such that not only satisfies sustaining condition, but also leads to minimum costs and excessive concrete volumes. An efficient optimization procedure is introduced to find the optimal shapes of concrete gravity dams using genetic algorithm in Matlab software. The concrete gravity dam body is treated as a two-dimensional structure. | ||
| Line 561: | Line 560: | ||
Although some authors suggest that once the overall stability criteria are met, the stress criterion will also be satisfied [19], in real design situations, the cross-section obtained with Optdam should be later evaluated for stress criteria (usually using finite elements) and specific conditions that vary with each project (earthquakes, silting, etc.). | Although some authors suggest that once the overall stability criteria are met, the stress criterion will also be satisfied [19], in real design situations, the cross-section obtained with Optdam should be later evaluated for stress criteria (usually using finite elements) and specific conditions that vary with each project (earthquakes, silting, etc.). | ||
| − | == | + | ==Acknowledgments== |
The research described in this paper was financially supported by the Federal Institute of Education, Science and Technology of Goias. | The research described in this paper was financially supported by the Federal Institute of Education, Science and Technology of Goias. | ||
| Line 567: | Line 566: | ||
<span id='_Ref523227263'></span> | <span id='_Ref523227263'></span> | ||
| − | == | + | ==References== |
[1] Ackley, David H. (1987). "The model." In A Connectionist Machine for Genetic Hillclimbing, pp. 29-70. Springer, Bos-ton, MA. | [1] Ackley, David H. (1987). "The model." In A Connectionist Machine for Genetic Hillclimbing, pp. 29-70. Springer, Bos-ton, MA. | ||
Revision as of 11:32, 11 June 2019
Abstract
Concrete gravity dams have trapezoidal shape in their cross section and shall guarantee the global stability against acting loads like hydrostatic and uplift pressures through his gravitational actions (self-weight and others). This study focuses on the shape optimization of concrete gravity dams using genetic algorithms. In this case, the dam cross section area is considered as the objective function and the design variables are the geometric parameters of the gravity dam. The optimum cross-section of a concrete gravity dam is achieved by the Genetic Algorithm (GA) through a Matlab routine developed by the author. Sliding, overturning and floating verifications are implemented in the program. In order to assess the efficiency of the proposed methodology for gravity dams optimization, one application is presented adopting the concrete gravity dam of Belo Monte Hydropower Plant (HPP), considering normal loading condition and others assumptions presented.
Keywords: Optimization, concrete gravity dams, genetic algorithm, design optimization
1. Introduction
Concrete gravity dams are hydraulic structures widely used as water reservoir to hydroelectric power plants in general. These structures have trapezoidal shape in their cross section and shall guarantee the global stability against hydrostatic and uplift pressures by means of gravitational actions (as self-weight and others) [32]. Hence, finding a proper design for the cross-section can remarkably reduce the construction costs [3].
For stability requirements, the dam must be safe against overturning, sliding and floating. Moreover, the acting stresses in the concrete of the dam or in the foundation material shall attend the limits stabilized by design criteria. The potential failure plans as concrete-foundation contact, horizontal plans through the dam body or through the foundation, can be considered, according to the rupture mechanisms identified by the geotechnical model [11].
In order to assure the structural global stability and the allowable stress criteria for the concrete gravity dam design, as discussed in Gutstein [19] and [20] a trial and error procedure process is usually carried out from a preliminary cross section defined in the design initial phases, followed by stability and stress analysis studies. Then, if the chosen cross section does not meet the security criteria, it shall be modified and analyzed again. Also, once safety criteria are met, a new study can be conducted with the purpose of optimizing the design (minimizing the dam cross section area).
To achieve this purpose, several alternatives can be used to obtain a number of feasible shapes. Finally, the cross section with minimum area (also with lower cost), that meets the structural considerations and design criteria, is selected as the final shape. In order to reliably achieve an optimal shape for dams in this study, instead of this trial and error procedure, optimization techniques have been effectively utilized [23,24,34].
Genetic Algorithms (GA) are heuristic search approaches applicable to a wide range of optimization problems [4]. This flexibility makes them attractive for many optimization problems in practice. They represent one branch of the field of study called evolutionary computation, which imitate the biological processes of reproduction and natural selection to solve for the fittest solutions [7].
GA can solve a broad class of engineering problems encountered in practice, involving a large number of design parameters (integer, discrete, continuous and integer/discrete-continuous) and a large number of constraints. It has been highly successful as one of evolutionary computation techniques in searching for a broad class of stacking sequence, size, topology optimization problems for composite structures [18,29,30,31].
Designing and constructing concrete gravity dams can be considered as a typical optimization problem, since the cross section geometry with lowest area that meets the design criteria is searched for, with the final aim of reducing cost. [35].
Optimizing this cost requires cross-section optimization. The main aim of this paper is to present and discussed an optimization study for concrete gravity dams based on GA and Matlab application. The present work brings a simple implementation using GA in Matlab for usual loading condition, contrasting with the complexity presented in [2,3,13,14,23,24,35] which bring approaches with high complexity computational methods.
The dam's geometry and the acting loads must be considered in its design analysis procedure. In order to reduce the computational cost of the optimization process, the stopping criteria is limited to satisfactory values. To demonstrate the efficiency of GAs in finding the optimum design of concrete gravity dams, the cross-section from Belo Monte Hydropower Plant is presented as an example of application, considering normal loads and hypothetical resistance parameters for the foundation.
2. Stability Analysis of Concrete Gravity Dams
Figure 1 shows the usual loads acting in a dam considering drainage. Water pressure is the major external load acting on such a dam. The horizontal water pressure, exerted by the weight of the water stored on the upstream side on the dam can be estimated from rule of hydrostatic pressure distribution.
In other to meet the safety requirements, the dam cross section is verified against floating, overturning and sliding.
Floating safety factor has the function to guarantee the stability of structure against the forces that tend to make the body float. It is calculated by Equation 1 [12].
Where FSF is safety factor against floating, should be greater than 1.3. ΣV is resultant vertical force and ΣU is total uplift force.
The overturning of a gravity dam may be calculated by dividing the total resisting moments by the total moments tending to cause overturning about the downstream toe, it is defined as the ratio between the resisting moments and overturning moments [33].
FSO is the safety factor against overturning, should be greater than 1.5. are moments resisting and moments overturning.
A dam will fail in sliding at its base, or at any other level, if the horizontal forces causing sliding are greater than the resistance available to it at that level. The resistance against sliding may be due to friction alone, or due to friction and shear strength of the joint. The sliding stability is based on a safety factor as a measure of determining the resistance of the structure against sliding [12].
FSS is the safety factor against sliding which should also be greater than 1.0. µ is reduced coefficient of friction, ΣV is total vertical force acting on dam and ΣH is total horizontal force acting on dam.
According to Eletrobras [12], the calculation of the uplift pressure acting in the analysis plan is made considering the uplift pressure reduction (Hdm) in the drainage curtain according to (4):
where hg is the gallery height, Hm is the upstream water level, Hj is the downstream water level and all of them in relation to the concrete-rock contact (analysis plan). Those expressions considerer the 66% drainage curtain efficiency adopted for the Bureau of Reclamation [33].
3. Geometrical Model of Concrete Gravity Dams and Problem Formulation
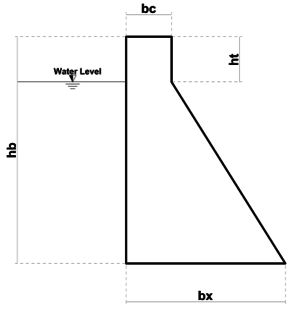
Based on the model of concrete gravity dam depicted in Figure 2, the cross-section of concrete gravity dam studied is defined by the four parameters given by Equation 5.
Where bc is a parameter required to define the dam crest. Also, the downstream slope is specified by the bx and ht design variables and hb is the dam’s height.
The process of evaluating the overall stability of a concrete dam, makes use of the static equations to evaluate the equilibrium of rigid body of the part. In order to automate the calculation of the global stability of a concrete gravity dam, an evaluation program was developed in the Matlab language. This program will be used as a starting point of the research.
The evaluation program has the ability to calculate overall stability and dam stress from the dimensions and conditions provided by the designer. This algorithm returns the values of the safety factors, calculated by equations 2,3 and 4.
After completing the calculations, the program displays the values obtained for FSF, FSO and FSS with a message indicating whether these values meet the design criteria, or whether the study section should be resized.
Gravity dam optimization problem is explained in this section. The cross-sectional area of the dam is considered as an objective function to be minimized. An optimization problem subjected to design constraints can be expressed as follows:
Where and are the objective function and the constraints, respectively. and are the lower bound and the upper bound of the design variables, , respectively [23].
In this optimization problem of concrete gravity dams, the cross-section area of gravity dam body is considered as objective function, , that should be minimized. The cross-section area of concrete gravity dam can be determined as follows:
Where is cross-section area, and hb, bc, bx and ht are design variables showed in figure 2.
In the present study, the behavior and stability constraints are considered as the problem constraints, . The behavior constraints consist on the safety factor against floating, overturning and sliding, calculated by equations 2, 3 and 4.
4. The Optimization Algorithm (Optdam)
4.1 Genetic Algorithm (GA)
Genetic algorithm (GA) is a method for solving both constrained and unconstrained optimization problems that is based on natural selection, the process that drives biological evolution. It is an optimization and search technique based on the principles of genetics and natural selection [21]. An individual is any point fitness function can be evaluated [1].
The value of the fitness function for an individual is its score. A population is an array of individuals. At each iteration, the genetic algorithm performs a series of computations on the current population to produce a new population. Each successive population is called a new generation. The best fitness value for a population is the smallest fitness value for any individual in the population [15].
To create the next generation, the genetic algorithm selects certain individuals in the current population, called parents, and uses them to create individuals in the next generation, called children. Typically, the algorithm is more likely to select parents that have better fitness values [28].
A GA allows a population composed of many individuals to evolve under specified selection rules to a state that maximizes the fitness (minimizes the cost function). The genetic algorithm repeatedly modifies a population of individual solutions [27].
Evolution is the basis of Genetic Algorithms. The current variety and success of species is a good reason for believing in the power of evolution. Species are able to adapt to their environment. They have developed to complex structures that allow the survival in different kinds of environments. Mating and getting offspring to evolve belong to the main principles of the success of evolution. These are good reasons for adapting evolutionary principles to solving optimization problems [25].
It presumes that the potential solution of a problem is an individual and can be represented by a set of parameters. These parameters are regarded as the genes of a chromosome and can be structured by a string of values in binary form. A positive value, generally known as fitness value, is used to reflect the degree of “good-ness” of the chromosome for solving the problem, and this value is closely related to its objective value [26].
At each step, the genetic algorithm selects individuals at random from the current population to be parents and uses them to produce the children for the next generation. They combine survival of the fittest among string structures with a structured yet randomized information exchange search algorithm with some of innovative flair of human search [16]. Over successive generations, the population evolves toward an optimal solution.
It can be applied to solve a variety of optimization problems that are not well suited for standard optimization algorithms, including problems in which the objective function is discontinuous, nondifferentiable, stochastic, or highly nonlinear. The genetic algorithm can address problems of mixed integer programming, where some components are restricted to be integer-valued [10].
The genetic algorithm differs from a classical, derivative-based, optimization algorithm in two main ways. First, classical algorithms generate a single point at each iteration. The sequence of points approaches an optimal solution, GA generates a population of points at each iteration and the best point in the population approaches an optimal solution. The second difference is that classical algorithms selects the next point in the sequence by a deterministic computation. Instead, GA selects the next population by computation which uses random number generators.
4.2 Penalty Function
In generic search methods, most applications of GAs to constraint optimization problems have used the penalty function approach of handling constraints. The penalty function approach involves a number of penalty parameters which must be set right in any problem to obtain feasible solutions [22].
It uses the penalty function in Equation 7, where infeasible solutions are compared based only on their constraint violation [8].
Where is the penalty function, and , as shown in section 3, are the objective function and the constraints, respectively. Hence, denotes the absolute value of the operand, if the operand is negative and returns a value zero, otherwise. The parameter is the penalty parameter of the jh inequality constraint. The purpose of a penalty parameter is to make the constraint violation of the same order of magnitude as the objective function value [9].
The parameter is the objective function value of the worst feasible solution in the population. Thus, the fitness of an infeasible solution not only depends on the amount of constraint violation, but also on the population of solutions at hand. However, the fitness of a feasible solution is always fixed and is equal to its objective function value.
4.3 Optdam
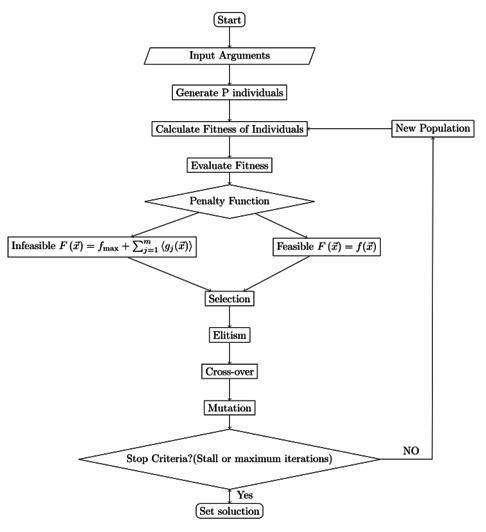
Bearing in mind the importance of studying dams and application for evolutionary computing methods of optimization, the aim now is to comment on the Optdam program developed in Matlab. This program allows finding an optical dam’s cross section. The program was developed to cover general cross sections of dams in terms of geometry as showed in figure 2.
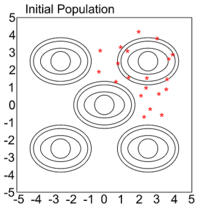
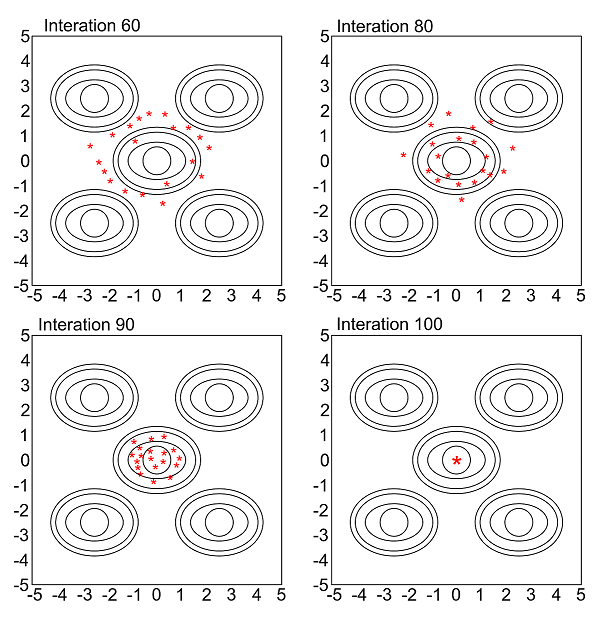
First, a set of solutions is initialized and denoted as the initial population. This initialization is recommended to randomly cover the whole solution space or to model and incorporate expert knowledge. The representation determines the initialization process. Initial population is shown in figure 3 [16].
After initial population, GA scores each member of the current population by computing its fitness value, scales the raw fitness scores to convert them into a more usable range of values, then selects members, called parents, based on their fitness.
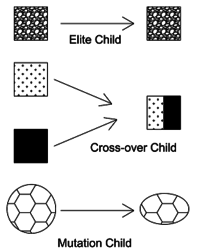
Some of the individuals in the current population that have lower fitness are chosen as elite [17]. These elite individuals are taken as parents for the next population. Hence, children are produced either by making random changes to a single parent, mutation, or by combining the vector entries of a pair of parents, crossover. Therefore, GA replaces the current population with the children to form the next generation [5] and [6]. The conception of the new generations is presented in figure 4.
In summary, the GA in Matlab uses three main types of rules at each step to create the next generation from the current population:
- Selection rules select the individuals, called parents, that contribute to the population at the next generation.
- Crossover rules combine two parents to form children for the next generation.
- Mutation rules apply random changes to individual parents to form children.
The algorithm stops when one of the stopping criteria is met. Figure 5 shown the convergence process. The GA parameters of Optdam program are shown in table 1. Figure 6 shows a flowchart illustrating the process.
| GA Parameters | ||
| Parameters | Adopted | |
| Population type | Double vector | |
| Population size | 100 | |
| Fitness scaling | Rank | |
| Elite count | 40 | |
| Cross-over fraction | 0.8 | |
| Mutation function | Constraint dependent | |
| Cross-over function | Constraint dependent | |
| Migration direction | forward | |
| Migration fraction | 0.2 | |
| Migration interval | 20 | |
| Initial penalty | 10 | |
| Penalty factor | 100 | |
| Maximum number of generations | 100 | |
| Stall generations | 50 | |
| Function tolerance | 10-6 | |
| Constraint tolerance | 10-3 | |
| Stall time | 60 (s) | |
| Compile timeout | 180 (s) | |
5. Example: Idealized Cross-Section of the Belo Monte HPP
The Belo Monte Hydropower Plant has a retaining wall between the main intake and the earth/rockfill dam, which is usually designed following the same criteria as a concrete gravity dam. In order to present the applicability of the Optdam programa in a practical situation, an optimization study using Optdam program is applied on cross-section of the retaining wall. The initial design of Belo Monte cross-section is shown in Figure 7.
The material properties for the calculation were taken from commonly used values for dams built in the Belo Monte region. They are included in Table 2.
| The properties of materials | ||
| Material | Value | Unit |
| Concrete’s Young Modulus | 240.00 | MPa |
| Concrete resistance | 25.00 | MPa |
| Poison’s ratio of concrete | 0.2 | - |
| Mass density of concrete | 2500 | Kg/m³ |
| Speed of pressure wave | 1440 | m/s |
| Wave reflection coefficient | 0.9 | - |
| Rock friction angle | π/5 | rad |
| Partial friction safety factor | 1.5 | - |
| Reduced coefficient of friction | 0.7 | - |
| Elasticity modulus of rock | 27.580 | MPa |
| Poison’s ratio of foundation | 0.2 | - |
The analyzed section presents the geometric parameters shown in table 3 which also includes other important parameters for optimizing the section, such as hydrostatic loads and the search space defined from the minimum dimensions defined by the project specifications (such as free-board).
In this way, the lower boundary of the section is defined by the hydrological parameters, topographic conditions, terrain and other specific constraints that change. Hence, the upper boundary is defined by the designer, based on experience. In case little information is available, wide ranges can be adopted, since the program is able to search for the optimal.
Since the actual values of the hydrological parameters and other constraints are not known, for the example discussed here the dimensions for the lower boundary were hypothetically defined. In the other hand, the values of the upper border were defined by the values of the real section executed.
Table 3 also shows the safety factors obtained for the initial cross section. Since they are higher than those recommended by the design criteria, the geometry can be optimized, finding safety factors close to the minimum required.
| Geometry parameters | ||
| Parameter | Value | Unit |
| Cross section area | 2410 | m² |
| Concrete volume | 2410000 | m³ |
| Hydrostatic loads | ||
| Parameter | Value | Unit |
| Upstream water | 70 | m |
| Downstream water | 5 | m |
| Search Space | ||
| Design variable | Lower bound (m) | Upper bound (m) |
| hb | 75 | 80 |
| bc | 2 | 10 |
| bx | 16 | 56 |
| ht | 2 | 10 |
| Safety factors | ||
| Factor | Design criteria request | Achieved values |
| FSF | 3.00 | 4.52 |
| FSO | 1.50 | 2.08 |
| FSS | 1.00 | 1.32 |
It is worth noting that this is an example that refers to a dam designed and executed, not being configured as a case study, since the values of the constants (cohesion, angle of friction, specific gravity of concrete, etc.) among other specificities of the project are not known with exactness.
6. Results
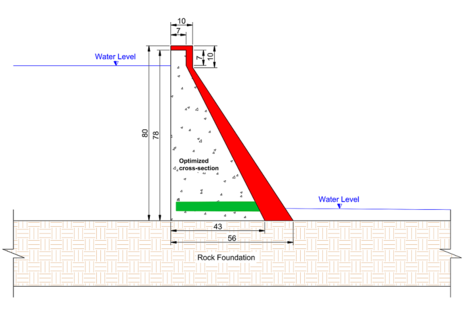
The optimum design of the cross-section based on retaining-wall of Belo Monte HPP is given in Table 4. By comparing the solution obtained for the cross-section with the GA it's possible to note that the concrete volume can be significantly reduced.
| Optimum designs of the dam obtained by Optdam (GA) | ||
| Design variable | Value | Unit |
| hb | 78 | m |
| bc | 7 | m |
| bx | 43 | m |
| ht | 7 | m |
| FSF | 4.5062 | - |
| FSO | 1.5001 | - |
| FSS | 1.0030 | - |
| Cross section area | 1824 | m² |
| Concrete savings | 586000 | m³ |
| savings percentage | 24.31 | % |
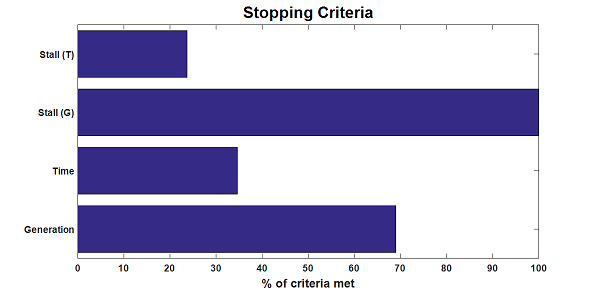
In order to limit the computational cost and to streamline the section optimization process, four stop criteria were defined for Optdam. They are presented in table 1 along with the other program information. In order to make the program's functionality clearer, the stopping criteria are further analyzed here. The Optdam’s stopping criteria are stall generations, stall time, maximum number of generations and compile timeout.
Stall generations defines the number of generations in which there is no significant gain in the optimization of the objective function. Stall time defines the timeout in which there are generations without significant gain in optimization. Maximum number of generations specifies the maximum number of iterations the genetic algorithm performs and compile timeout defines the maximum time the program can take to find the optimal solution. Figure 8 shows the operation of the stop criteria in the example.
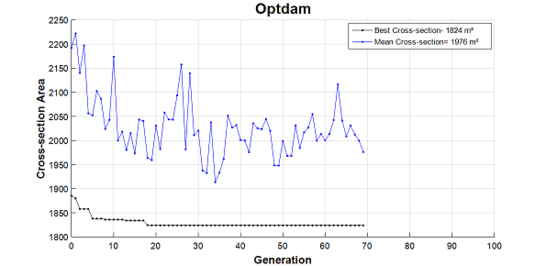
Due to the rapid convergence of GA, already in the first generations tends to obtain satisfactory results. This makes the number of fifty stall generations a high measure of reliability that global minimum has been achieved. Since stall generations is the decisive stopping criterion, it is noted that the stopping criteria validate each other. The graph in Figure 9 presents the best cross section area value of the objective function in each generation versus the generation number. The best values and mean values are highlighted for each iteration.
It can be concluded that the methodology is robust for the problem at hand (reduction of area): As mentioned before, the best individuals in the first generations already feature low values of the cross section area.
Figure 10 shows the optimized cross section within the actual section. The red area shows the savings of area obtained in the use of Optdam. The optimal shape shown in Figure 10 implies a 24.31% reduction in cross-section area, considering the shear resistance adopted.
7. Conclusions
Cross-section optimization is one goal of dam designers. Dam designing must be such that not only satisfies sustaining condition, but also leads to minimum costs and excessive concrete volumes. An efficient optimization procedure is introduced to find the optimal shapes of concrete gravity dams using genetic algorithm in Matlab software. The concrete gravity dam body is treated as a two-dimensional structure.
An example based on a real structure has been presented. Results demonstrated the ability of these algorithms for this type of continuous optimization problem. Status of optimally designed dam for the algorithm is also provided for better assessment of safety factors. It is shown that all the constraints are satisfied.
This research provides useful optimization formulations for concrete gravity dams and can be extended to other hydraulic structures. The final result is a genetic algorithm program for shape optimization of concrete gravity dams, that is simple from a mathematical point of view and is able to work with dams under different load and boundary conditions. In the presented example, the proposed method resulted in more than 20% reduction in cross-section area and consequently resulted in more than 20% reduction in with low computational effort.
However, it is worth mentioning that the program developed here makes use of the global stability conditions as limiting for the evaluation and selection of the cross sections, being this necessary but not sufficient condition in a concrete dam design by gravity.
Although some authors suggest that once the overall stability criteria are met, the stress criterion will also be satisfied [19], in real design situations, the cross-section obtained with Optdam should be later evaluated for stress criteria (usually using finite elements) and specific conditions that vary with each project (earthquakes, silting, etc.).
Acknowledgments
The research described in this paper was financially supported by the Federal Institute of Education, Science and Technology of Goias.
References
[1] Ackley, David H. (1987). "The model." In A Connectionist Machine for Genetic Hillclimbing, pp. 29-70. Springer, Bos-ton, MA.
[2] Ali, Pr Dr Ahmed AM, Pr Dr Rafa HS Al-Suhaili, and Shamil AK Behaya. (2014) "A genetic algorithm optimization model for the gravity dam section under seismic excitation with reservoir-dam-foundation interactions." Amer J Eng Res 3, no. 6: 143-53.
[3] Baghlani, Abdolhossein, Mohsen Sattari, and Mohammad Hadi Makiabadi. (2014) "Application of genetic program-ming in shape optimization of concrete gravity dams by metaheuristics." Cogent Engineering 1, no. 1: 982348.
[4] Bento, Eduardo Prevedello, and Nelson Kagan. (2008) "Algoritmos genéticos e variantes na solução de problemas de configuração de redes de distribuição." Sba: Controle & Automação Sociedade Brasileira de Automatica 19, no. 3: 302-315.
[5] Conn, Andrew R., Nicholas IM Gould, and Philippe Toint. (1991) "A globally convergent augmented Lagrangian algo-rithm for optimization with general constraints and simple bounds." SIAM Journal on Numerical Analysis 28, no. 2: 545-572.
[6] Conn, Andrew R., and Luís N. Vicente. "Bilevel derivative-free optimization and its application to robust optimization." Optimization Methods and Software 27, no. 3 (2012): 561-577.
[7] Carr, Jenna. "An introduction to genetic algorithms." Senior Project 1: 40. Personal report, Udesc, Joinvile-SC, Brasil, 2014.
[8] Deb, Kalyanmoy. (2000) "An efficient constraint handling method for genetic algorithms." Computer methods in ap-plied mechanics and engineering 186, no. 2-4: 311-338.
[9] Deb, K. (1995) "Optimization for Engineering Design: Algorithms and Examples Prentice-Hall." New Delhi.
[10] Deep, Kusum, Krishna Pratap Singh, Mitthan Lal Kansal, and C. Mohan. (2009) "A real coded genetic algorithm for solving integer and mixed integer optimization problems." Applied Mathematics and Computation 212, no. 2: 505-518.
[11] Durieux, Johan Hendrik. (2009). "Development of a practical methodology for the analysis of gravity dams using the non-linear finite element method." PhD diss., University of Pretoria.
[12] ELETROBRÁS, Centrais Elétricas Brasileiras S.A. "Critérios de projeto civil de usinas hidrelétricas". Rio de Janeiro: ELETROBRAS e CBDB, 2003
[13] Ghaffari, Yousef, Fereshteh Nouri Zonouz, Vahid Mahdavifar, Ramin Taghinezhad, and Vafa Soltangharaei. "Shape Optimization of Gravity Dams Using Genetic Algorithm." Journal, International Journal of Science and Engineering Investigations , 2018,
[14] Gen, Mitsuo, and Runwei Cheng. (2000). Genetic algorithms and engineering optimization. Vol. 7. John Wiley & Sons.
[15] Gen, Mitsuo, Runwei Cheng, and Lin Lin. Network models and optimization: Multiobjective genetic algorithm approach. Springer Science & Business Media, 2008.
[16] Goldberg, David E., and John H. Holland. (1988) "Genetic algorithms and machine learning." Machine learning 3, no. 2: 95-99.
[17] Guide, MATLAB User’S. (1998) "The mathworks." Inc., Natick, MA 5: 333.
[18] Gurba, W. (2001) "Probabilistic Methods of Composite Structures Optimization." PhD diss., Ph. D. Thesis, Cracow University of Technology, Krakówm (in Polish).
[19] Gutstein, Daniela. "Estudo das tensões em fundações de barragens de gravidade de concreto pelo método de elementos finitos". 2003. Dissertação de Mestrado (Masters dissertation). Universidade Federal de Santa Catarina.
[20] Gutstein, Daniela. "Projeto de estruturas de barragens de gravidade de concreto por meio de métodos computacionais: visão geral e metodologia". 2011. Tese de doutorado (Doctoral thesis). Universidade Federal de Santa Catarina.
[21] Haupt, Randy L., Sue Ellen Haupt, and Sue Ellen Haupt. (1998) Practical genetic algorithms. Vol. 2. New York: Wiley.
[22] Homaifar, Abdollah, Charlene X. Qi, and Steven H. Lai. "Constrained optimization via genetic algorithms." Simulation 62, no. 4 (1994): 242-253.
[23] Khatibinia, M., H. Chiti, A. Akbarpour, and H. R. Naseri. (2016) "Shape optimization of concrete gravity dams considering dam–water–foundation interaction and nonlinear effects." Iran University of Science & Technology 6, no. 1: 115-134.
[24] Khosravi, Sh, and M. Khatibinia. (2016). "Optimal Shape Design of Concrete Gravity Dams Including." Iranian Journal of Structural Engineering 3, no. 2.
[25] Kramer, Oliver. (2017). Genetic algorithm essentials. Vol. 679. Springer.
[26] Man, Kim-Fung, Kit-Sang Tang, and Sam Kwong. (1996) "Genetic algorithms: concepts and applications [in engineer-ing design]." IEEE transactions on Industrial Electronics 43, no. 5: 519-534.
[27] Michalewicz, Zbigniew, and Stephen J. Hartley. (1996) "Genetic algorithms+ data structures= evolution programs." Mathematical Intelligencer 18, no. 3: 71.
[28] Mitchell, Melanie. (1998). An introduction to genetic algorithms. MIT press.
[29] Muc, A. (1997) "Transverse shear effects in discrete optimization of laminated compressed cylindrical shells." Compo-site structures 38, no. 1-4: 489-497.
[30] Muc, A. W. Gurba, (2001) Genetic algorithms and finite element analysis in optimization of composite structures, Composite Structures, vol. 54, ss. 275-81.
[31] Muc, A. (2018) Evolutionary design of engineering constructions, Latin American Journal of Solids and Structures.
[32] Usace, Manual Engineer. (1995) "Gravity dam design." Engineer 20020626: 116.
[33] USBR - United States Bureau of Reclamation (1976). “Design of gravity dams”. Denver: United States Department of the Interior – Bureau of Reclamation.
[34] Vianna, Luis Claudio Coelho. (2003). "Otimização de seções transversais de concreto armado: aplicação a pórticos." PhD diss., Universidade de São Paulo.
[35] Yazd, Hamidreza Golkar Hamzee, Seyed Jafar Arabshahi, Mojtaba Tavousi, and Abbas Alvani. (2015) "Optimal de-signing of concrete gravity dam using Particle Swarm Optimization Algorithm (PSO)." Indian Journal of Science and Technology 8, no. 12: 1.
Document information
Published on 05/07/19
Accepted on 04/06/19
Submitted on 19/10/18
Volume 35, Issue 3, 2019
DOI: 10.23967/j.rimni.2019.06.002
Licence: CC BY-NC-SA license