(a)
|
|
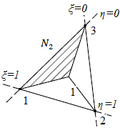
(b)
|
|
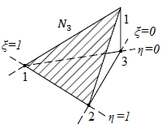
(c)
|
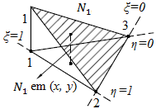
Figura 4 - Representação das funções de forma no nó 1 (a), nó 2 (b) e nó 3 (c)
Os deslocamentos dos elementos são escritos usando as funções de forma e os valores nodais do campo de deslocamento desconhecido.
Sendo , e expressos pelas equações 9.1, 9.2 e 9.3, as equações 10.1 e 10.2 ficam representadas, na forma simplificada, por:
As coordenadas x e y também podem ser representadas em termos de coordenadas nodais pelo uso das mesmas funções de forma. Essa é a chamada representação isoparamétrica. As representações isoparamétricas relacionam as coordenadas cartesianas x e y às coordenadas naturais e .
Na avaliação das deformações específicas, as derivadas parciais de e devem ser tomadas com relação a x e y. Pelas representações isoparamétricas verifica-se que , , x e y são funções de e . Logo, podem ser representadas por:
Usando-se a regra da cadeia para derivadas de u, obtém-se a matriz quadrada (2x2) denotada como Jacobiana de transformação, logo:
Realizando-se as derivadas da matriz Jacobiana e algumas manipulações matemáticas chegam-se às relações deformação específica-deslocamento, que pela definição de xij e yij demonstra-se que yij = -yji e yij = yik - yjk, podendo ser escrita, de forma sucinta, da seguinte forma:
A energia potencial do sistema é dada por:
Sendo que os termos correspondem à energia de deformação do elemento, força de corpo, força de superfície e carregamento pontual, respectivamente. Por meio de triangulação, a energia potencial total pode ser escrita da seguinte forma, sendo que representa a energia de deformação do elemento.
A matriz de rigidez do elemento é obtida por meio da energia de deformação do elemento. Substituindo-se a Equação 14 na energia de deformação do elemento, tem-se:
Considerando a espessura do elemento ( 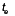 ) e discretizando com triângulos a área a ser analisada, a matriz de rigidez do elemento pode ser obtida a partir da Equação 17, e é dada por: ) e discretizando com triângulos a área a ser analisada, a matriz de rigidez do elemento pode ser obtida a partir da Equação 17, e é dada por:
Considerando-se a energia de deformação, os termos de força, as condições de contorno e realizando-se as modificações de rigidez e forças, a equação 16 fica definida como:
Sendo que refere-se à matriz de rigidez da estrutura analisada, ao vetor de deslocamentos nodais da estrutura e ao vetor de cargas globais aplicadas.
Como as deformações específicas são constantes em um elemento CST, as suas componentes de tensões também permanecem constantes. Os valores das tensões devem ser calculados para cada elemento, usando as relações de deformação específica-deslocamento do elemento. Substituindo-se a equação 14 na equação 6, tem-se que a tensão em cada elemento é dada por:
A conectividade será utilizada para extrair os deslocamentos nodais do elemento do vetor de deslocamentos globais . Para fim de interpolação, as tensões obtidas pela equação 20 podem ser usadas como um valor referente ao centroide do elemento analisado. Finalmente, vale ressaltar que as tensões principais e suas direções principais são determinadas a partir das relações do Círculo de Mohr.
4. Aplicações
4.1 Introdução
Neste capítulo são mostradas as aplicações do presente trabalho, representando de forma numérica o Modelo de Bielas e Tirantes. Inicialmente realizou-se a análise, representando os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por MONTOYA et al. [1], além de modelar numericamente via MEF uma viga-parede com uma grande abertura, desenvolvida por SCHLAICH et al. [2]. E por fim analisou-se um consolo curto, um bloco de fundação sob duas estacas de concreto e uma sapata rígida, realizando seus dimensionamentos via MEF e comparando com resultados de expressões normativas e exemplos clássicos encontrados na literatura. Menciona-se ainda que todos os resultados das análises realizadas pelo programa computacional desenvolvido são comparados com resultados determinados por meio da utilização do software ANSYS 17.
Vale ressaltar que em todos os exemplos analisados neste trabalho foi necessário um maior refinamento de malha, em virtude, da utilização do elemento finito plano adotado, Constant Strain Triangle (CST), que no ANSYS 17 corresponde ao elemento sólido “Plane 182”. Esse elemento apresenta campos de deslocamentos menos refinados que os elementos quadrilaterais com quatro nós, ou elementos lineares e que o elemento quadrilateral com nove nós conhecido na literatura como elemento parabólico. Com isso, realizou-se um maior refinamento da malha utilizada com os elementos CST e assim foi possível obter bons resultados, mesmo utilizando um elemento mais simples que os demais.
4.2 Modelo desenvolvido por Montoya
O modelo desenvolvido por MONTOYA et al. [1] foi implementado analisando-se o comportamento das tensões de compressão nas bielas de uma viga fletida, a partir da discretização da região correspondente (Figura 5a), submetida a um carregamento de superfície igual a 0,797 kN/cm², e não de todo o elemento estrutural.
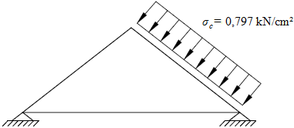
Figura 5a - Região da viga analisada pelo Modelo de MONTOYA
|
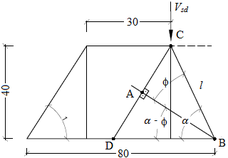
Figura 5b - Modelo de MONTOYA (cm)
|
Na Figura 5b mostram-se as propriedades geométricas da região analisada, sendo submetida a um carregamento pontual aplicado no ponto C. Utilizou-se o modelo de cálculo I da ABNT NBR 6118 [9] para a definição dos ângulos e , com e . A seção transversal da região analisada é igual a 40 x 25 cm, com altura útil (d) igual a 36 cm e com (d’) igual a 4 cm.
Em relação às propriedades físicas dos materiais, foram utilizados módulo de elasticidade (E) igual a 2800 kN/cm², coeficiente de Poisson ( ) igual a 0,25 e o concreto com resistência característica à compressão ( ) igual a 30MPa.
Com auxílio do software ANSYS 17 a região analisada foi mapeada, gerando uma malha com 1200 elementos finitos triangulares (CST) e 641 nós, representada pela Figura 6.
É importante informar que em todas as aplicações realizadas, o programa ANSYS serviu como um gerador de malha, ou seja, os dados da malha gerada no ANSYS, coordenadas nodais e elementos com as suas respectivas incidências, foram inseridos como dados de entrada no programa computacional desenvolvido.
Figura 6 - Malha mapeada pelo modelo de MONTOYA – ANSYS
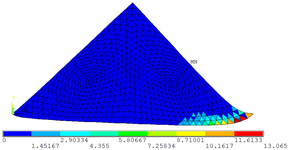
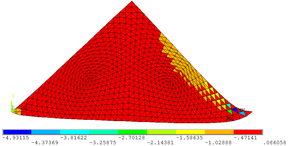
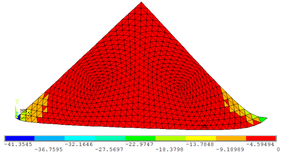
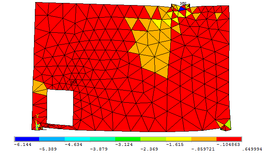
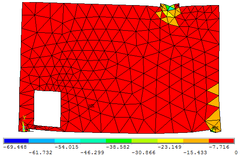
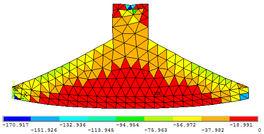
As Figuras 7a, 7b e 7c permitem observar as configurações deformadas da região comprimida quando estão submetidas às três tensões principais , e , respectivamente. Os valores das tensões encontrados na escala de referência das figuras são dados em kN/cm².
Nas Tabelas 1, 2, 3, 4 e 5 apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e a partir do software ANSYS 17. Percebe-se que a precisão obtida pelas simulações numéricas é satisfatória tanto para as tensões elementares ( , e ) quanto para as tensões principais ( , ).
Tabela 1 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-0,7552
|
-0,3896
|
-0,8807
|
-0,4279
|
-0,9961
|
-0,5038
|
-1,1000
|
-0,6030
|
-1,1890
|
-0,7143
|
| ANSYS
|
-0,7552
|
-0,3896
|
-0,8807
|
-0,4279
|
-0,9961
|
-0,5038
|
-1,0996
|
-0,6030
|
-1,1892
|
-0,7143
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0001
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0004
|
1,0000
|
0,9998
|
1,0000
|
Tabela 2 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-0,6156
|
-0,3985
|
-0,5535
|
-0,4054
|
-0,4849
|
-0,3993
|
-0,4118
|
-0,3782
|
-0,3364
|
-0,3435
|
| ANSYS
|
-0,6156
|
-0,3985
|
-0,5535
|
-0,4054
|
-0,4849
|
-0,3993
|
-0,4118
|
-0,3782
|
-0,3364
|
-0,3435
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0000
|
0,9999
|
1,0000
|
1,0000
|
0,9999
|
1,0000
|
1,0000
|
0,9999
|
1,0000
|
Tabela 3 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-0,1374
|
-0,4087
|
-0,1107
|
-0,4096
|
-0,0990
|
-0,4069
|
-0,1009
|
-0,4040
|
-0,1150
|
-0,4031
|
| ANSYS
|
-0,1374
|
-0,4088
|
-0,1107
|
-0,4096
|
-0,0990
|
-0,4069
|
-0,1009
|
-0,4040
|
-0,1150
|
-0,4031
|
| Presente Trabalho/ ANSYS
|
1,0002
|
0,9999
|
0,9996
|
1,0000
|
1,0000
|
1,0000
|
1,0005
|
1,0000
|
0,9999
|
0,9999
|
Tabela 4 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-0,5313
|
0,0147
|
-0,5196
|
-0,0069
|
-0,4664
|
-0,0413
|
-0,3973
|
-0,0713
|
-0,3212
|
-0,0852
|
| ANSYS
|
-0,5313
|
0,0147
|
-0,5196
|
-0,0069
|
-0,4664
|
-0,0413
|
-0,3973
|
-0,0713
|
-0,3212
|
-0,0852
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0002
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
Tabela 5 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-0,8395
|
-0,8028
|
-0,9146
|
-0,8264
|
-1,0150
|
-0,8618
|
-1,1140
|
-0,9100
|
-0,1204
|
-0,9726
|
| ANSYS
|
-0,8395
|
-0,8028
|
-0,9147
|
-0,8264
|
-1,0150
|
-0,8618
|
-1,1140
|
-0,9100
|
-0,1204
|
-0,9726
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0000
|
0,9999
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
Comparando as tensões positivas com a resistência à tração do concreto ( ), verifica-se que há formação de fissuras em algumas regiões específicas na viga. A Tabela 6 comprova esse fato, pois há valores de tensão que ultrapassam 0,30 kN/cm², correspondente à resistência do concreto à tração.
Tabela 6 - Verificação das tensões de fissuras (kN/cm²)
| Elemento
|
18
|
19
|
20
|
200
|
201
|
202
|
203
|
204
|
205
|
206
|
| Presente Trabalho
|
0,0155
|
0,0028
|
0,0147
|
0,0871
|
2,021
|
3,025
|
2,41
|
3,791
|
2,818
|
4,7445
|
| ANSYS
|
0,0155
|
0,0028
|
0,0147
|
0,0871
|
2,0205
|
3,0251
|
2,4103
|
3,7912
|
2,8178
|
4,7452
|
| Ocorrência de Trincas
|
NÃO
|
NÃO
|
NÃO
|
NÃO
|
SIM
|
SIM
|
SIM
|
SIM
|
SIM
|
SIM
|
Nas Figuras 8a e 8b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido nesta pesquisa e dos resultados encontrados com auxílio do software ANSYS 17. Neste caso, é possível verificar a precisão entre os resultados dos deslocamentos nas duas direções dos eixos de referências (x e y), validando dessa forma a implementação numérica desenvolvida.

Figura 8a - Deslocamentos nodais em x
|

Figura 8b - Deslocamentos nodais em y
|
4.3 Representação numérica do Modelo de Schäfer & Schläich
Neste exemplo é analisado numericamente o modelo de SCHÄFER & SCHLÄICH [2] que corresponde a uma viga-parede com abertura submetida a um carregamento pontual. Na Figura 9 se apresenta de forma detalhada a viga-parede, que está sujeita à carga de 800 kN. Neste exemplo, o concreto apresenta um módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25.
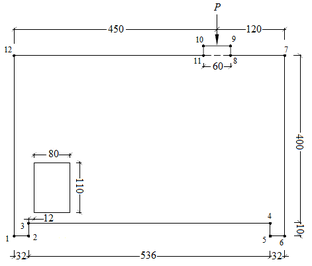
Figura 9 - Viga-parede Modelo de SCHÄFER & SCHLÄICH
|
A viga-parede foi discretizada no software ANSYS 17, gerando-se uma malha livre com 414 elementos finitos triangulares (CST) e 249 nós, conforme mostrado na Figura 10.
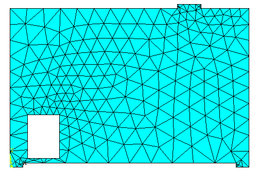
Figura 10 - Malha livre da Viga-parede – ANSYS
|
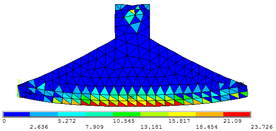
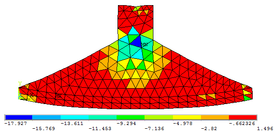
Com auxílio do ANSYS 17 verifica-se o comportamento e as deformações da viga-parede submetida às tensões principais ( , e ). Essas configurações deformadas são mostradas nas Figuras 11a, 11b e 11c, respectivamente, cujas escalas de referências encontram-se em kN/cm².
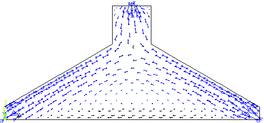
Refinando a malha utilizada, aumentando o número de elementos finitos de forma excessiva, obtendo uma nova malha com 26496 elementos finitos triangulares (CST) e com 13584 nos, é possível visualizar as regiões comprimidas que formam as bielas na viga-parede, representadas na cor azul na Figura 12, demonstrando assim a concentração de tensões de compressão em algumas regiões da viga-parede.
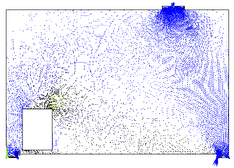
Figura 12 - Representação vetorial das tensões na viga-parede com a malha refinada ANSYS
|
Nas Tabelas 7, 8, 9, 10 e 11 apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e o software ANSYS 17. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas.
Tabela 7 - Tensões (kN/cm²)
| Elemento
|
1
|
50
|
100
|
150
|
200
|
250
|
300
|
350
|
400
|
414
|
| Presente Trabalho
|
-0,3167
|
1,0030
|
-0,1158
|
-0,1362
|
-0,3266
|
0,0105
|
-0,3654
|
0,5519
|
-3,8440
|
-3,9420
|
| ANSYS
|
-0,3167
|
1,0035
|
-0,1158
|
-0,1362
|
-0,3266
|
0,0105
|
-0,3654
|
0,5519
|
-3,8442
|
-3,9423
|
| Presente Trabalho/ ANSYS
|
1,0001
|
0,9995
|
1,0004
|
1,0001
|
0,9999
|
0,9998
|
1,0000
|
1,0000
|
0,9999
|
0,9999
|
Tabela 8 - Tensões (kN/cm²)
| Elemento
|
1
|
50
|
100
|
150
|
200
|
250
|
300
|
350
|
400
|
414
|
| Presente Trabalho
|
-0,0766
|
-0,0818
|
-0,5528
|
-2,8170
|
-2,3570
|
0,1902
|
0,1591
|
0,3279
|
-4,7240
|
-3,1630
|
| ANSYS
|
-0,0766
|
-0,0818
|
-0,5528
|
-2,8169
|
-2,3570
|
0,1902
|
0,1591
|
0,3279
|
-4,7244
|
-3,1627
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0003
|
1,0001
|
1,0000
|
0,9999
|
1,0001
|
Tabela 9 - Tensões (kN/cm²)
| Elemento
|
1
|
50
|
100
|
150
|
200
|
250
|
300
|
350
|
400
|
414
|
| Presente Trabalho
|
-0,7080
|
-0,2509
|
-0,3003
|
1,6410
|
-0,5192
|
-0,5483
|
-0,7349
|
-0,6071
|
-3,9740
|
-4,3650
|
| ANSYS
|
-0,7080
|
-0,2510
|
-0,3003
|
1,6406
|
-0,5192
|
-0,5483
|
-0,7349
|
-0,6071
|
-3,9744
|
-4,3650
|
| Presente Trabalho/ ANSYS
|
1,0001
|
0,9998
|
1,0000
|
1,0002
|
1,0000
|
1,0000
|
0,9999
|
1,0000
|
0,9999
|
1,0000
|
Tabela 10 - Tensões (kN/cm²)
| Elemento
|
1
|
50
|
100
|
150
|
200
|
250
|
300
|
350
|
400
|
414
|
| Presente Trabalho
|
0,5215
|
1,0590
|
0,0371
|
0,6420
|
-0,2016
|
0,6559
|
0,6772
|
1,0570
|
-0,2857
|
0,8299
|
| ANSYS
|
0,5215
|
1,0587
|
0,0371
|
0,6420
|
-0,2016
|
0,6559
|
0,6772
|
1,0573
|
-0,2857
|
0,8299
|
| Presente Trabalho/ ANSYS
|
1,0001
|
1,0003
|
1,0001
|
1,0000
|
1,0002
|
0,9999
|
1,0001
|
0,9997
|
1,0002
|
1,0000
|
Tabela 11 - Tensões (kN/cm²)
| Elemento
|
1
|
50
|
100
|
150
|
200
|
250
|
300
|
350
|
400
|
414
|
| Presente Trabalho
|
-0,9147
|
-0,1370
|
-0,7057
|
-3,5950
|
-2,4820
|
-0,4553
|
-0,8835
|
-0,1775
|
-8,2830
|
-7,9350
|
| ANSYS
|
-0,9147
|
-0,1370
|
-0,7057
|
-3,5950
|
-2,4820
|
-0,4553
|
-0,8835
|
-0,1775
|
-8,2830
|
-7,9348
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0002
|
1,0001
|
1,0000
|
1,0000
|
1,0001
|
1,0000
|
1,0001
|
1,0000
|
1,0000
|
Nas Figuras 13a e 13b mostram-se comparações gráficas entre os deslocamentos nodais obtidos por meio do programa desenvolvido e os resultados fornecidos a partir do software ANSYS 17, sendo os nós localizados na parte inferior da viga-parede.

Figura 13a - Deslocamento em x
|

Figura 13b - Deslocamento em y
|
4.4 Sapata rígida
A sapata rígida em análise cujas dimensões são mostradas na Figura 14 está submetida a um carregamento pontual igual a 800 kN. Neste exemplo o concreto apresenta um módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25.
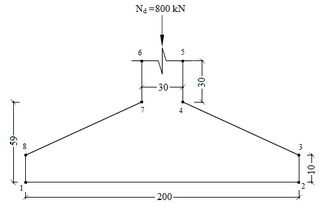
Figura 14 - Dimensões da sapata rígida (cm)
|
Em sua modelagem, a sapata foi dividida em duas áreas para que o Software ANSYS 17 pudesse gerar a malha. A parte superior foi mapeada de forma livre e a parte inferior, correspondente à fôrma, foi mapeada de forma estruturada, realizando três análises distintas dividindo a parte inferior em 10, 20 e 25 divisões com o fim de se comparar eventuais alterações nos resultados numéricos. As respectivas malhas geradas no software ANSYS 17, são mostradas nas Figuras 15a, 15b e 15c. No primeiro caso analisado, a malha gerada apresenta 164 elementos finitos triangulares (CST) e 111 nós. A segunda malha gerada apresenta 272 elementos finitos triangulares (CST) e com 170 nós. Já a malha final apresenta 329 elementos finitos triangulares (CST) e com 201 nós.
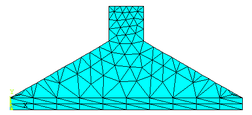
Figura 15a - Malha da sapata rígida – 10 divisões
|
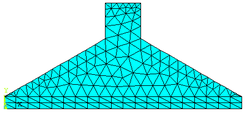
Figura 15b - Malha da sapata rígida – 20 divisões
|
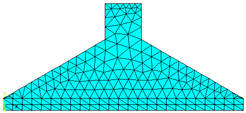
Figura 15c - Malha da sapata rígida - 25 divisões
|
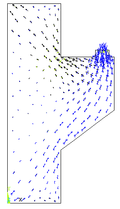
A malha com 25 divisões apresentou melhores resultados em suas análises, podendo observar o comportamento e as deformações da sapata rígida nas Figuras 16a, 16b e 16c, cujas escalas de referências encontram-se em kN/cm². Na Figura 16d, mostra-se, de forma vetorial, a transferência dos esforços internos.
Nas Tabelas 12, 13, 14, 15 e 16, apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e por meio do software ANSYS 17 para a sapata com 25 divisões na parte inferior. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas.
Tabela 12 - Tensões (kN/cm²)
| Elemento
|
1
|
40
|
80
|
120
|
160
|
200
|
240
|
280
|
320
|
329
|
| Presente Trabalho
|
-21,38
|
5,2410
|
23,300
|
-16,370
|
-26,26
|
-22,84
|
-30,280
|
-1,7730
|
-2,2510
|
-31,9300
|
| ANSYS
|
-21,384
|
5,2406
|
23,301
|
-16,372
|
-26,260
|
-22,837
|
-30,280
|
-1,7731
|
-2,2509
|
-31,9250
|
| Presente Trabalho/ ANSYS
|
0,9998
|
1,0001
|
1,0000
|
0,9999
|
1,0000
|
1,0001
|
1,0000
|
0,9999
|
1,0000
|
1,0002
|
Tabela 13 - Tensões (kN/cm²)
| Elemento
|
1
|
40
|
80
|
120
|
160
|
200
|
240
|
180
|
320
|
329
|
| Presente Trabalho
|
-23,550
|
0,4340
|
1,1660
|
-2,8400
|
-4,9580
|
-9,6150
|
-8,6300
|
-15,700
|
-4,7820
|
-15,1900
|
| ANSYS
|
-23,555
|
0,4340
|
1,1661
|
-2,8401
|
-4,9584
|
-9,6153
|
-8,6303
|
-15,703
|
-4,7821
|
-15,1900
|
| Presente Trabalho/ ANSYS
|
0,9998
|
1,0000
|
0,9999
|
1,0000
|
0,9999
|
1,0000
|
1,0000
|
0,9998
|
1,0000
|
1,0000
|
Tabela 14 - Tensões (kN/cm²)
| Elemento
|
1
|
40
|
80
|
120
|
160
|
200
|
240
|
180
|
320
|
329
|
| Presente Trabalho
|
24,970
|
-0,4914
|
2,4540
|
4,1260
|
-11,510
|
5,7290
|
15,950
|
5,6540
|
-6,6560
|
25,5700
|
| ANSYS
|
24,969
|
-0,4914
|
24,538
|
4,1257
|
-11,511
|
5,7293
|
15,947
|
5,6545
|
-66,562
|
25,5710
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0001
|
1,0000
|
1,0001
|
0,9999
|
1,0000
|
1,0002
|
1,0000
|
1,0000
|
1,00000
|
Tabela 15 - Tensões (kN/cm²)
| Elemento
|
1
|
40
|
80
|
120
|
160
|
200
|
240
|
280
|
320
|
329
|
| Presente Trabalho
|
2,5240
|
5,2900
|
23,570
|
-1,6810
|
0,0732
|
-7,4780
|
-0,1815
|
0,2332
|
3,2590
|
3,3480
|
| ANSYS
|
2,5236
|
5,2903
|
23,570
|
-16,814
|
0,0732
|
-7,4781
|
-0,1815
|
0,2332
|
3,2590
|
3,3479
|
| Presente Trabalho/ ANSYS
|
1,0002
|
0,9999
|
1,0000
|
0,1000
|
1,0000
|
1,0000
|
1,0001
|
0,9999
|
1,0000
|
1,0000
|
Tabela 16 - Tensões (kN/cm²)
| Elemento
|
1
|
40
|
80
|
120
|
160
|
200
|
240
|
280
|
320
|
329
|
| Presente Trabalho
|
-47,460
|
0,3843
|
0,8974
|
-17,530
|
-31,290
|
-24,970
|
-38,730
|
-17,710
|
-10,290
|
-47,4600
|
| ANSYS
|
-47,462
|
0,3843
|
0,8974
|
-17,530
|
-31,292
|
-24,974
|
-38,729
|
-17,709
|
-10,292
|
-47,4620
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
0,9999
|
0,9998
|
1,0000
|
1,0001
|
0,9998
|
1,0000
|
Em relação aos deslocamentos nodais, as Figuras 17a e 17b mostram as comparações gráficas entre os deslocamentos na parte inferior da sapata rígida obtida por meio do programa desenvolvido e pelos resultados determinados via software ANSYS 17, utilizando um maior número de nós entre as simulações realizadas.

Figura 17a - Deslocamento em x
|
 Figura 17b - Deslocamento em y Figura 17b - Deslocamento em y
|
4.4 Consolo curto
O consolo curto analisado, cujas dimensões são mostradas na Figura 18a, está submetido a um carregamento pontual igual a 400 kN. Nesta aplicação, o concreto apresenta módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. O consolo curto foi discretizado pelo software ANSYS 17, gerando uma malha livre com 223 elementos finitos triangulares (CST) e com 139 nós, conforme mostrado na Figura 18b.
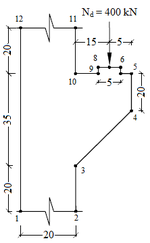
Figura 18a - Dimensões do consolo curto (cm)
|
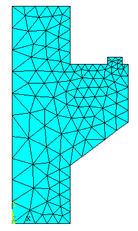
Figura 18b - Malha livre do consolo curto ANSYS
|
As configurações deformadas do elemento em análise submetido às tensões principais ( , e ) são mostradas nas Figuras 19a, 19b e 19c, respectivamente.
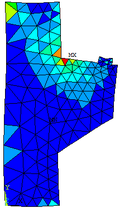
Figura 19a - Tensão principal
|
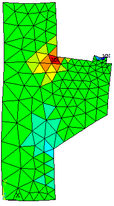
Figura 19b - Tensão principal
|
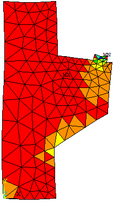
Figura 19c - Tensão principal
|
Logo é possível visualizar a transferência dos esforços internos por meio de uma representação vetorial mostrada na Figura 20, determinando as regiões tracionadas e comprimidas do consolo curto.
Figura 20 - Representação vetorial das tensões no consolo curto – ANSYS
Nas Tabelas 17, 18, 19, 20 e 21 apresentam-se comparações entre os resultados numéricos determinados pelo programa computacional desenvolvido e a partir do software ANSYS 17.
Tabela 17 - Tensões (kN/cm²)
| Elemento
|
10
|
30
|
50
|
70
|
90
|
110
|
130
|
150
|
170
|
200
|
| Presente Trabalho
|
5,3280
|
8,7690
|
-6,1200
|
3,0680
|
-11,290
|
-4,3290
|
-0,7243
|
14,700
|
3,8040
|
15,9100
|
| ANSYS
|
5,3283
|
8,7687
|
-6,1197
|
3,0675
|
-11,295
|
-4,3285
|
-0,7243
|
14,699
|
3,8043
|
15,9080
|
| Presente Trabalho/ ANSYS
|
0,9999
|
1,0000
|
1,0000
|
1,0002
|
0,9996
|
1,0001
|
1,0000
|
1,0001
|
0,9999
|
1,0001
|
Tabela 18 - Tensões (kN/cm²)
| Elemento
|
10
|
30
|
50
|
70
|
90
|
110
|
130
|
150
|
170
|
200
|
| Presente Trabalho
|
17,540
|
-93,230
|
-8,4660
|
-0,4384
|
-12,800
|
-17,730
|
-16,790
|
-1,3020
|
-24,540
|
2,0090
|
| ANSYS
|
17,536
|
-93,228
|
-8,4661
|
-0,4384
|
-12,799
|
-17,732
|
-16,790
|
-1,3024
|
-24,541
|
2,0092
|
| Presente Trabalho/ ANSYS
|
1,0002
|
1,0000
|
1,0000
|
1,0001
|
1,0001
|
0,9999
|
1,0000
|
0,9997
|
1,0000
|
0,9999
|
Tabela 19 - Tensões (kN/cm²)
| Elemento
|
10
|
30
|
50
|
70
|
90
|
110
|
130
|
150
|
170
|
200
|
| Presente Trabalho
|
- 7,415
|
1,372
|
-12,960
|
- 3,417
|
-14,01
|
- 8,805
|
- 3,796
|
- 4,128
|
-13,000
|
- 9,3750
|
| ANSYS
|
- 7,415
|
1,371
|
-12,959
|
- 3,416
|
-14,012
|
- 8,804
|
- 3,795
|
- 4,127
|
-12,999
|
- 9,3747
|
| Presente Trabalho/ ANSYS
|
0,9999
|
1,0002
|
1,0001
|
1,0001
|
0,9999
|
1,0000
|
1,0001
|
1,0001
|
1,0001
|
1,0000
|
Tabela 20 - Tensões (kN/cm²)
| Elemento
|
10
|
30
|
50
|
70
|
90
|
110
|
130
|
150
|
170
|
200
|
| Presente Trabalho
|
12,890
|
8,7870
|
5,7190
|
5,1550
|
1,9850
|
0,0349
|
0,1274
|
15,700
|
8,8630
|
20,6300
|
| ANSYS
|
12,889
|
8,7871
|
5,7192
|
5,1546
|
1,9850
|
0,0349
|
0,1274
|
15,701
|
8,8627
|
20,6280
|
| Presente Trabalho/ ANSYS
|
1,0001
|
1,0000
|
1,0000
|
1,0001
|
1,0000
|
0,9999
|
1,0000
|
0,9999
|
1,0000
|
1,0001
|
Tabela 21 - Tensões (kN/cm²)
| Elemento
|
10
|
30
|
50
|
70
|
90
|
110
|
130
|
150
|
170
|
200
|
| Presente Trabalho
|
-45,300
|
-93,250
|
-20,310
|
-2,5250
|
-26,080
|
-22,100
|
-17,640
|
-2,3040
|
-29,600
|
-2,7110
|
| ANSYS
|
-45,298
|
-93,246
|
-20,305
|
-2,5255
|
-26,079
|
-22,096
|
-17,641
|
-2,3043
|
-29,599
|
-2,7109
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0000
|
1,0002
|
0,9998
|
1,0000
|
1,0002
|
0,9999
|
0,9999
|
1,0000
|
1,0000
|
Nas Figuras 21a e 21b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido e os resultados do ANSYS 17, sendo os nós referentes à parte superior do consolo curto. Lembrando que nessa região ficam localizadas as armaduras de tração.

Figura 21a - Deslocamento em x
|

Figura 21b - Deslocamento em y
|
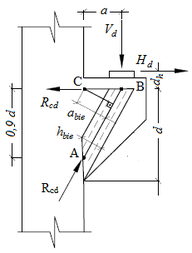
Por fim, realizou-se o dimensionamento do consolo curto e os resultados foram comparados com as respostas determinadas pelo presente trabalho que é baseado no Método dos Elementos Finitos, sendo os valores das tensões elementares extraídos da modelagem numérica realizada. Para a realização do dimensionamento, considerou-se a altura útil do consolo igual a =31cm, =4cm, a distância entre o ponto de aplicação da carga e a face do pilar igual =15,5cm e =43,47kN/cm². Na Tabela 22 mostra-se a boa aproximação entre os resultados encontrados.
Tabela 22 – Área de Aço (cm²)
| Resultado Normativo
|
Presente Trabalho
|
Presente Trabalho/ Resultado Normativo
|
| 5,11
|
4,64
|
0,91
|
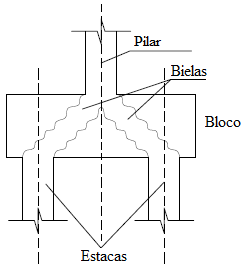
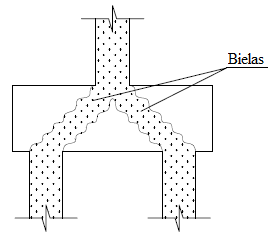
4.5 Bloco de fundação sob duas estacas de concreto
O bloco de fundação com duas estacas está submetido a um carregamento pontual igual a 1500 kN, suas dimensões são mostradas na Figura 22a. Considerou-se neste exemplo que o concreto apresenta módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. Por sua vez, o bloco de fundação foi discretizado com quatro malhas distintas, sendo apresentados os resultados das análises realizadas com a malha estruturada de 328 elementos finitos triangulares (CST) e 202 nós mostrada na Figura 22b.
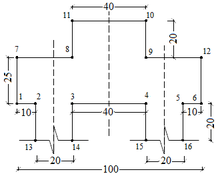
Figura 22a - Dimensões do bloco de (cm)
|

Figura 22b - Malha do bloco de fundação – ANSYS
|
Com auxílio do software ANSYS 17 é possível observar o comportamento e as deformações do bloco de fundação. Essas configurações deformadas são mostradas nas Figuras 23a, 23b e 23c, respectivamente, cujas escalas de referências encontram-se em kN/cm². Na Figura 23d, mostra-se, de forma vetorial, as tensões de tração e compressão no bloco de fundação.

Figura 23a - Tensão principal
|
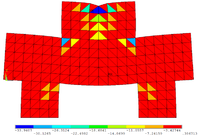
Figura 23b - Tensão principal
|

Figura 23c - Tensão principal
|

Figura 23d - Representação vetorial de tensões no bloco de fundação – ANSYS
|
Nas Tabelas 23, 24, 25, 26 e 27, apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e do software ANSYS 17. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas.
Tabela 23 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-15,420
|
-22,870
|
-12,000
|
-46,660
|
-2,0900
|
-22,540
|
-7,0360
|
5,9950
|
27,660
|
58,5300
|
| ANSYS
|
-15,417
|
-22,870
|
-11,995
|
-46,665
|
-2,0905
|
-22,538
|
-7,0356
|
5,9951
|
27,660
|
58,5320
|
| Presente Trabalho/ ANSYS
|
1,0002
|
1,0000
|
1,0004
|
0,9999
|
0,9998
|
1,0001
|
1,0001
|
1,0000
|
1,0000
|
1,0000
|
Tabela 24 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-7,5970
|
-59,470
|
-74,980
|
-216,30
|
-21,670
|
-29,710
|
-27,160
|
-18,920
|
-15,220
|
0,5455
|
| ANSYS
|
-7,5974
|
-59,474
|
-74,979
|
-216,26
|
-21,666
|
-29,715
|
-27,161
|
-18,916
|
-15,221
|
0,5455
|
| Presente Trabalho/ ANSYS
|
0,9999
|
0,9999
|
1,0000
|
1,0002
|
1,0002
|
0,9998
|
1,0000
|
1,0002
|
0,9999
|
1,0001
|
Tabela 25 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
2,8870
|
-29,430
|
-12,660
|
48,170
|
15,420
|
27,870
|
16,820
|
6,8850
|
26,970
|
11,7500
|
| ANSYS
|
2,8874
|
-29,435
|
-12,662
|
48,165
|
15,424
|
27,872
|
16,820
|
6,8846
|
26,971
|
11,7460
|
| Presente Trabalho/ ANSYS
|
0,9999
|
0,9998
|
0,9998
|
1,0001
|
0,9997
|
0,9999
|
1,0000
|
1,0001
|
1,0000
|
1,0003
|
Tabela 26 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-6,6470
|
-6,5110
|
-9,5450
|
-33,940
|
6,3890
|
1,9750
|
2,5020
|
7,7710
|
40,670
|
60,8200
|
| ANSYS
|
-6,6467
|
-6,5111
|
-9,5453
|
-33,941
|
6,3890
|
1,9754
|
2,5019
|
7,7711
|
40,674
|
60,8200
|
| Presente Trabalho/ ANSYS
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
1,0000
|
0,9998
|
1,0000
|
1,0000
|
0,9999
|
1,0000
|
Tabela 27 - Tensões (kN/cm²)
| Elemento
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
| Presente Trabalho
|
-16,370
|
-75,830
|
-77,430
|
-229,00
|
-30,150
|
-54,230
|
-36,700
|
-20,690
|
-28,240
|
-1,7430
|
| ANSYS
|
-16,367
|
-75,832
|
-77,429
|
-228,99
|
-30,146
|
-54,229
|
-36,698
|
-20,692
|
-28,236
|
-1,7435
|
| Presente Trabalho/ ANSYS
|
1,0002
|
1,0000
|
1,0000
|
1,0000
|
1,0001
|
1,0000
|
1,0001
|
0,9999
|
1,0001
|
0,9997
|
Nas Figuras 24a e 24b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido e os resultados obtidos via ANSYS 17, sendo os nós referentes à parte inferior do bloco de fundação, localizados entre as duas estacas de concreto.

Figura 24a: Deslocamento em x
|

Figura 24b: Deslocamento em y
|
Por fim, encontrou-se a área de aço da armadura tracionada a partir do Método de Blévot & Frémy e os resultados foram confrontados com respostas obtidas a partir do Método dos Elementos Finitos para as quatro malhas analisadas. Para a realização do dimensionamento, considerou-se:  =25cm, =4cm, =40cm, =60cm e =43,47 kN/cm². Os resultados são mostrados na Tabela 28, verificando uma melhora na aproximação dos resultados com o refinamento da malha. =25cm, =4cm, =40cm, =60cm e =43,47 kN/cm². Os resultados são mostrados na Tabela 28, verificando uma melhora na aproximação dos resultados com o refinamento da malha.
Tabela 28 - Área de Aço (cm²)
| Bloco de Fundação
|
Blévot & Frémy
|
Presente Trabalho
|
Presente Trabalho/ Blévot & Frémy
|
| 328 elementos
|
18,25
|
16,35
|
0,90
|
| 360 elementos
|
18,25
|
16,91
|
0,92
|
| 392 elementos
|
18,25
|
18,17
|
0,99
|
| 654 elementos
|
18,25
|
18,46
|
1,01
|
5. Conclusão
Em todas as aplicações realizadas, observou-se uma ótima convergência entre os resultados numéricos obtidos com o programa computacional implementado e as respostas encontradas por meio do software ANSYS 17. Logo, verifica-se que a implementação desenvolvida foi bem sucedida, contribuindo com valores precisos de tensões elementares, tensões principais e deslocamentos das estruturas planas com comportamento elástico-linear.
O objetivo principal prático da pesquisa desenvolvida foi dimensionar as armaduras de aço tracionadas em alguns elementos estruturais estudados, utilizando como base um programa computacional implementado em linguagem FORTRAN com formulação baseada no Método dos Elementos Finitos e realiza um comparativo com algumas prescrições normativas vigentes, com o intuito de verificar a precisão dessas respostas.
Na análise feita por meio do modelo desenvolvido por MONTOYA el al. [1], verificaram-se também de forma numérica via Método dos Elementos Finitos, diversos pontos em que há o surgimento de trincas, visto que, os valores de tensões obtidos ultrapassaram a resistência à tração do concreto.
Com relação à análise da viga-parede verificou-se a formação das bielas e tirantes a partir da representação vetorial, comprovando dessa forma as regiões comprimidas e tracionadas do elemento estrutural.
Em relação ao dimensionamento, em duas aplicações (consolos curtos e bloco de fundação) verificou-se boa aproximação ao serem comparados os resultados numéricos com a metodologia desenvolvida por Blévot & Frémy.
Para a análise realizada no bloco de fundação, verificou-se que o refinamento na malha de elementos finitos proporcionou maior aproximação entre o valor de área de aço calculado numericamente e o resultado determinado a partir do método clássico desenvolvido por BLÉVOT & FRÉMY [8].
Referências
[1] MONTOYA, P.J.; MESEGER, A.G.; CABRÉ, F.M., (1991) Hormigón Armado. 13.ed. Barcelona: Editorial Gustavo Gili.
[2] SCHLAICH, J.; SCHAFER, K., (1988) Consistent Design of Structural Concrete Using Strut and Tie Model. 5º Colóquio sobre comportamento e Projeto de estruturas. PUC/RJ.
[3] SOUZA, R. A., (2006) Análise, dimensionamento e verificação de elementos especiais em concreto armado utilizando o método dos elementos finitos e o método das bielas. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería.
[4] FONTES, F. F., (2005) Análise Estrutural de elementos lineares segundo a NBR 6118:2003. Dissertação de Mestrado, Escola de Engenharia de São Carlos, USP, São Carlos, São Paulo, Brasil.
[5] VICENTE, W. M.; OLIVEIRA, W. C., (2009). Análise de Tensões em Placas Circulares Utilizando elementos Finitos Axissimétricos. Trabalho Final de Graduação de Engenharia Mecânica, Universidade Federal de Itajubá, Itajubá, MG, Brasil.
[6] DELALIBERA, R. G.. (2005). Estudo experimental e analítico de blocos sobre estacas submetidos a momento e normal. Qualificação de Doutorado, Escola de Engenharia de São Carlos, USP, São Carlos, São Paulo, Brasil.
[7] HOBBS, N. B.; STEIN, P., (1957). An investigation into the stress distribution in pile caps with some notes on design. Proceedings of the Institution of Civil Engineers.
[8] BLÉVOT, J., FRÉMY, R.,(1967). Semelles sur piex. Analles d’ Institut Techique du Bâtiment et des Travaux Publlics Paris.
[9] NBR-6118., (2014). Projeto de Estruturas de Concreto – Procedimento, ABNT – Associação Brasileira de Normas Técnicas, Rio de Janeiro, Brasil.
[10] FERNANDES, R. M., EL DEBS, M. K., (2005). Análise da capacidade resistente de consolos de concreto armado considerando a contribuição da armadura de costura. Cadernos de Engenharia de Estruturas da UFSCar.
[11] NBR-9062., (2006). Projeto e execução de estruturas de concreto pré-moldado, ABNT – Associação Brasileira de Normas Técnicas, Rio de Janeiro, Brasil.
[12] CHANDRUPATLA, T.R.; BELEGUNDU, A.D., (2014). Elementos Finitos. Pearson Education do Brasil, São Paulo.
|