| Line 153: | Line 153: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Zarate_969633417-image8-c.png|438px]] | + | |style="padding:10px;"|[[Image:Draft_Zarate_969633417-image8-c.png|438px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 8:''' Ensayo de compresión simple. a) Probeta y maquina universal b) Fractura experimental | | colspan="1" | '''Figura 8:''' Ensayo de compresión simple. a) Probeta y maquina universal b) Fractura experimental | ||
| Line 166: | Line 166: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Zarate_969633417-image9-c.png|462px]] | + | |style="padding:10px;"|[[Image:Draft_Zarate_969633417-image9-c.png|462px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 9:''' Superficies de daño. a) Rankine b) Mohr Coulomb | | colspan="1" | '''Figura 9:''' Superficies de daño. a) Rankine b) Mohr Coulomb | ||
| Line 201: | Line 201: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Zarate_969633417-image12-c.png|312px]] | + | |style="padding:10px;"|[[Image:Draft_Zarate_969633417-image12-c.png|312px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 12:''' Ensayo de compresión simple. Probeta y malla utilizada en el ensayo 2D | | colspan="1" | '''Figura 12:''' Ensayo de compresión simple. Probeta y malla utilizada en el ensayo 2D | ||
| Line 218: | Line 218: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Zarate_969633417-image13.png|510px]] | + | |style="padding:10px;"|[[Image:Draft_Zarate_969633417-image13.png|510px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 13:''' Ensayo de compresión simple. Probeta biempotrada, malla no estructurada | | colspan="1" | '''Figura 13:''' Ensayo de compresión simple. Probeta biempotrada, malla no estructurada | ||
| Line 227: | Line 227: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Zarate_969633417-image14.png|504px]] | + | |style="padding:10px;"|[[Image:Draft_Zarate_969633417-image14.png|504px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 14:''' Ensayo de compresión simple. Probeta con dos caras deslizantes, resultados numéricos y teóricos | | colspan="1" | '''Figura 14:''' Ensayo de compresión simple. Probeta con dos caras deslizantes, resultados numéricos y teóricos | ||
| Line 238: | Line 238: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 70%;max-width: 70%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Zarate_969633417-image15.png|378px]] | + | |style="padding:10px;"|[[Image:Draft_Zarate_969633417-image15.png|378px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figura 15:''' Ensayo de compresión simple. Probeta con una cara deslizante, resultados numéricos, teóricos y experimentales | | colspan="1" | '''Figura 15:''' Ensayo de compresión simple. Probeta con una cara deslizante, resultados numéricos, teóricos y experimentales | ||
Revision as of 14:52, 25 January 2019
Resumen
Este trabajo describe una metodología de cálculo para evaluar la rotura de piezas y estructuras de hormigón y su aplicación a cuatro ensayos típicos en laboratorios de resistencia de materiales. Los resultados de los ensayos son comparados y analizados desde el punto de vista experimental y numérico a fin de poner de manifiesto la necesidad de que los ensayos experimentales se basen en resultados numéricos, y en contrapartida que los modelos numéricos sigan fielmente el comportamiento y la física que ocurre en los experimentos de laboratorio. Esta comparativa permite explicar los mecanismos que ocurren a lo largo del experimento y también verificar la integridad e idoneidad del código de cálculo y del modelo numérico a utilizar.
Palabras clave: Ensayo Experimental, Método de elementos discretos, Método de elementos finitos, Mecánica de fractura, Estrategia FEM-DEM.
Abstract
This paper describes a computation methodology to evaluate the ultimate strength and fracture of concrete samples and structures and its application to four typical tests of experimental laboratories of strength of materials. The tests results are compared and analysed from the experimental and numerical points of view in order to highlight the need for experimental trials to use the information derived from numerical results and, in turn, to validate that numerical models follow the behaviour and physics that occur in laboratory tests This comparison allows to explain the different mechanisms that occur throughout the experiments.
Keywords: Experimental model test, Discrete Element Method, Finite Element Method, Fracture mechanics, FEM-DEM technique
Introducción
Existen tres formas bien definidas para analizar y resolver un problema de ingeniera: Métodos Analíticos, Métodos Experimentales y Métodos Numéricos. El primero de ellos obtiene soluciones resolviendo analíticamente las ecuaciones matemáticas que gobiernan la física del problema bajo estudio. Algunos ejemplos se encuentran en las sencillas fórmulas disponibles en la literatura de ingeniería, o procedimientos descritos en normas técnicas de organizaciones clasificadoras como la American Society of Mechanical Engineers (ASME), American Society of Testing Materials (ASTM), Det Norske Veritas (DNV), o la Asociación Española de Normalización y Certificación (AENOR), entre otras. Se trata de una metodología simple, en general de bajo costo y poca complejidad, que proporciona una respuesta rápida y directa [1]. En general, este tipo de soluciones suelen ser muy aproximadas a la respuesta física del problema, debido principalmente a la gran cantidad de simplificaciones que contienen [2].
Los Métodos Experimentales se pueden clasificar en ensayos a escala real y a escala reducida, y en función de la supervivencia de la probeta en ensayos destructivos o no destructivos. Sin embargo, estos métodos solo se aplican sobre probetas de geometría sencilla, o a elementos estructurales muy concretos, aplicando cargas y condiciones que representan una determinada situación práctica. Todo ello con la finalidad de observar y medir parámetros asociados a la física del problema que se desea reproducir. Estos ensayos son bien aceptados por la comunidad científico-técnica, pero en contrapartida son costosos, requieren de una infraestructura muy específica y en ocasiones el experimento suele durar mucho tiempo.
Finalmente, los Métodos Numéricos resuelven de forma numérica las ecuaciones matemáticas que gobiernan los fenómenos físicos. La solución de dichas ecuaciones se realiza utilizando métodos aproximados como los de Elementos Finitos (MEF) [3], Diferencias Finitas y Volúmenes Finitos, y otros menos populares. Estos métodos requieren el uso intensivo de herramientas de cálculo (software y ordenadores) y actualmente su aplicación se encuentra muy difundida debido a la gran variedad de software de uso académico o industrial, que existe.
La tendencia actual en la solución de los problemas de ingeniería se inclina hacia el uso de los Métodos Numéricos, que se aplican prácticamente a todo tipo de problemas de ingeniera, dejando de lado los Métodos Analíticos y haciendo relativamente poco uso de los Métodos Experimentales. De hecho, los Métodos Analíticos se utilizan casi exclusivamente como herramienta de diseño aproximado de estructuras y para verificación de normativas.
Por otro lado, los Métodos Experimentales tienen dos utilidades muy concretas e interesantes: la verificación de la capacidad resistente de nuevos elementos estructurales, y el control de la calidad de materiales y elementos constructivos, desde el punto de vista de su resistencia. En el primer caso se hace un uso intensivo de los Métodos Numéricos para minimizar el costo de la experimentación y garantizar la precisión de los resultados. Mientras que en el segundo existe muy poca vinculación entre ambos métodos.
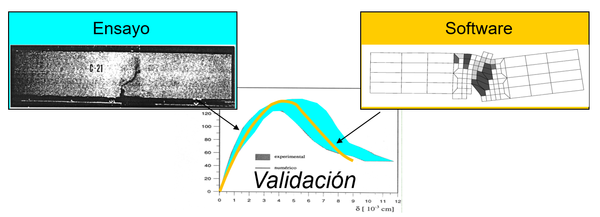
En este trabajo se pone de manifiesto que el uso de los Métodos Numéricos y los Métodos Experimentales no está desvinculado, sino que ambos métodos son complementarios en campos como la validación de los Métodos Numéricos y los códigos de cálculo asociados (Figura 1), el diseño de nuevos Métodos Experimentales y la consolidación de los ensayos de laboratorio existentes, además de la correcta caracterización numérica de los materiales utilizados.
|
| Figura 1: Vinculación entre los Métodos Experimentales y Numéricos |
En este trabajo se utiliza la técnica numérica FEM-DEM [4 - 6] para predecir la rotura de piezas y estructuras de hormigón. Dicha técnica se aplica a cuatro ensayos experimentales con el fin de poner de manifiesto la utilidad de los Métodos Numéricos en el ámbito experimental y viceversa.
El primero ensayo es el de tracción indirecta que permite cuantificar de manera simple la tracción máxima que un material frágil es capaz de soportar.
El segundo ensayo es la compresión simple de una probeta cilíndrica. Este ensayo complementa al primero, y ambos sirven para caracterizar los parámetros numéricos de los modelos constitutivos más comunes para representar un material, tales como el módulo de elasticidad, la tracción y compresión máxima a la rotura, etc. Por otra parte, el uso de los Métodos Numéricos permite dilucidar sobre los diferentes mecanismos de rotura que se presentan en el ensayo experimental.
El tercer ensayo es la rotura por cortante de una probeta entallada. Este ensayo pone de manifiesto que cambios mínimos en la geometría de las probetas pueden inducir comportamientos no previstos y obtener resultados poco fiables o atribuibles al fenómeno físico que se desee capturar. El uso de Métodos Numéricos en la reproducción de este ensayo permite observar los fenómenos físicos involucrados con más detalle.
Finalmente, se presenta un el ensayo de extracción de un elemento metálico de un bloque de hormigón con el objetivo de poner de nuevo en evidencia que el fenómeno físico que se desea capturar no es precisamente el que ocurre, aun a pesar de que los resultados obtenidos experimentalmente sean congruentes con los esperados. En este caso, como en otros, es clara la necesidad de usar Métodos Numéricos para diseñar correctamente los ensayos a realizar con Métodos Experimentales.
Los ensayos experimentales han sido realizados en el Laboratorio de Resistencia de Materiales de la Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos de la Universidad Politécnica de Cataluña y por la empresa Geotecnia y Calidad Liccsa, S. A. de C. V. (Figura 2).

|
| Figura 2: Ensayos de compresión en las instalaciones del laboratorio de Geotecnia y Calidad Liccsa S.A. C.V. |
La técnica FEM-DEM
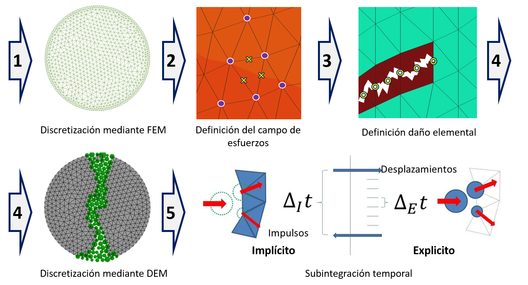
Para los experimentos numéricos se ha hecho uso del método FEM-DEM y del código implícito FEM2DEM desarrollado en CIMNE [4]. El método FEM-DEM está basado en la formulación propuesta por Zárate et al. [5,6] y se puede resumir en las cinco etapas siguientes, esquematizadas en la Figura 3.
- 1. Inicialmente se parte de una malla de elementos finitos (triángulos de 3 nodos en 2D y tetraedros de 4 nodos en 3D) que discretiza el dominio de la pieza o la estructura a analizar.
- 2. Se somete a la pieza a una carga de valor creciente en el tiempo y se evalúa por el método de elementos finitos (FEM, por sus siglas en inglés) la respuesta de la pieza o la estructura bajo estudio mediante un esquema de integración en el tiempo implícito. Para cada nivel de carga se evalúan las tensiones en el punto medio de las aristas de cada elemento, utilizando una parcela súper-convergente [37]. Con dichas tensiones se evalúa el daño en el centro de cada arista de todos los elementos, utilizando un sencillo modelo de daño isótropo [38]
- 3. El daño en cada uno de los elementos de la malla se evalúa como el promedio de los dos mayores valores del daño calculado sobre las aristas del elemento.
- 4. Cuando el daño elemental alcanza un valor muy próximo a la unidad se elimina el elemento y en sus vértices se generan elementos discretos (discos circulares en 2D y esferas en 3D). A partir de ese momento el dominio de estudio contiene elementos finitos y elementos discretos.
- 5. La integración temporal de los elementos discretos se realiza mediante un esquema explicito, en el que se parte de la posición inicial de los elementos discretos y se acumula el impulso provocado por todos los contactos a lo largo de un incremento de tiempo de la integración implícita utilizada para encontrar la solución en la malla de elementos finitos. De esta manera, el impulso encontrado, dividido por el incremento de tiempo implícito, se usa como una fuerza en el siguiente paso de tiempo de la solución implícita. El contacto friccional entre los elementos discretos y los lados (en 2D) o las caras y las aristas (en 3D) de los elementos se trata con técnicas usuales del método de elementos discretos (DEM, por sus siglas en inglés) [7,8].
|
| Figura 3: Descripción esquemática de la técnica FEM DEM |
La formulación FEM-DEM utilizada en éste trabajo ha sido ampliamente verificada en diversas aplicaciones de rotura de estructuras de hormigón y mampostería [7 – 10], demostrando en todos los casos su robustez, versatilidad y exactitud.
Ensayo de tracción indirecta
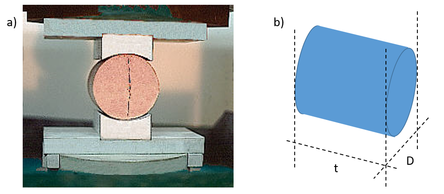
El ensayo brasileño, o de tracción indirecta (BTS, de Brazilian Tensile Strength) es una forma práctica y sencilla de evaluar la resistencia a la tracción de materiales frágiles. Este ensayo se desarrolló de manera simultánea, pero independiente, por Carneiro y Barcellos [12] en Brasil y Akazawa [13] en Japón. El ensayo consiste en aplicar a una probeta cilíndrica fuerzas de compresión hasta alcanzar la rotura del material. Dichas fuerzas se encuentran distribuidas a lo largo de la probeta y son diametralmente opuestas como se puede observar en la Figura 4(a) y de forma esquemática en la Figura 5.
|
| Figura 4: Ensayo de tracción indirecta. a) Ensayo en el laboratorio b) Dimensiones de la probeta |
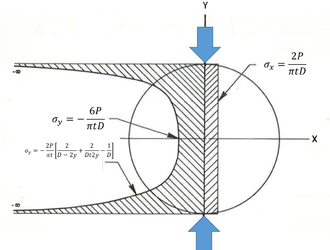
|
| Figura 5: Ensayo de tracción indirecta. Distribución teórica de las tensiones |
Esta condición de carga provoca una tensión de tracción relativamente uniforme a lo largo del plano diametral que contiene las cargas aplicadas (Figura 5). El fallo generalmente ocurre al romper la probeta a lo largo de ese plano.
La principal desventaja del ensayo BTS es que las condiciones de carga de la prueba no coinciden con las que ocurren en una estructura real. Sin embargo, es un ensayo idóneo para caracterizar la resistencia a tracción de un material frágil. Las seis principales ventajas atribuidas al ensayo BTS son [14]:
- Es un ensayo relativamente simple de llevar a cabo.
- El tipo de probeta cilíndrica y el equipo experimental son los mismos que los utilizados para ensayos de compresión simple.
- Los resultados son poco sensibles a las condiciones de la superficie de la probeta.
- El fallo del material se origina en una región de tensión relativamente uniforme.
- El rango de variación de los resultados del ensayo es pequeño.
- Los resultados obtenidos son aplicables a una gran variedad de modelos numéricos para materiales frágiles.
Este ensayo se encuentra normalizado de acuerdo con las normas ASTM C496/C496M – 17 [16], UNE 22950-2:1990 [17] e ISO 1920-4 [18], en la que se caracteriza el tamaño de las probetas, los tipos de apoyo y la velocidad de carga.
Diversos autores han caracterizado la distribución de esfuerzos dentro de la probeta cilíndrica. La formulación más aceptada es la propuesta por Froch [15] la cual evalúa la distribución de tensiones para una probeta de diámetro D y espesor t (Figura 4b) sometida a una carga diametralmente opuesta P. La Figura 5 muestra dicha distribución de tensiones y sus valores en el centro de la probeta.
La aplicación de la mecánica computacional a este ensayo es doblemente útil. Por un lado, permite caracterizar un estado tensional de rotura para un material frágil, aplicable a la definición del modelo numérico que se usa para caracterizar el material (junto con el ensayo de compresión simple). Por otro lado, permite validar los códigos numéricos mediante la reproducción del ensayo en el ordenador.
La Figura 6 muestra los resultados numéricos obtenidos mediante el programa FEM2DEM 2D [4] en donde se observa claramente que el valor de las tensiones se encuentra en total concordancia con los valores teóricos esperados.
Finalmente, la Figura 7 muestra el mecanismo de falla obtenido experimentalmente para una probeta de hormigón y el resultado de un ensayo numérico. Es clara la correspondencia entre ambos resultados, constatando que el código numérico captura de manera correcta los fenómenos físicos que intervienen en el experimento.
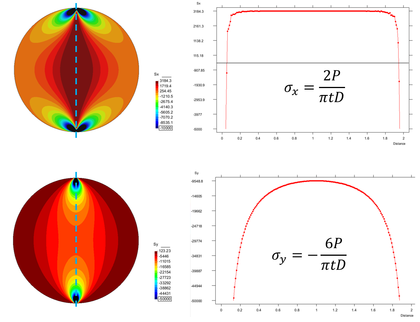
|
| Figura 6: Ensayo de tracción indirecta. resultados numéricos obtenidos mediante el programa FEM2DEM 2D [4] |
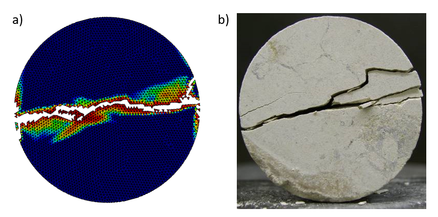
|
| Figura 7: Ensayo de tracción indirecta. Distribución teórica de las tensiones |
Ensayo de compresión simple
Los primeros ensayos de compresión realizados de manera científica y sistemática se atribuyen a Galileo [19]. Sin embargo, seguramente las civilizaciones más antiguas (entre 4000 y 2000 años AC) debieron haber realizado experimentos similares para caracterizar los materiales utilizados y evitar el colapso de sus obras de ingeniería [20].
El ensayo de compresión actualmente se realiza de acuerdo con la instrucción de hormigón estructural (EHE-08) [21] la cual hace referencia a la norma UNE-EN 12390-3.2009 [22] en la que se especifica las dimensiones de las probetas y las condiciones del ensayo. También se utilizan las normas ISO 1920-4 [18] y ASTM C39/C39M – 18 [23], muy similares a la anterior. En la Figura 8 se muestra una prensa universal utilizada en el ensayo experimental, así como una probeta típica de hormigón en la que se puede observar uno de los mecanismos de fallo típicos en este tipo de ensayos.

|
| Figura 8: Ensayo de compresión simple. a) Probeta y maquina universal b) Fractura experimental |
El experimento permite determinar la resistencia máxima a compresión simple y también el módulo de elasticidad a compresión del material ensayado.
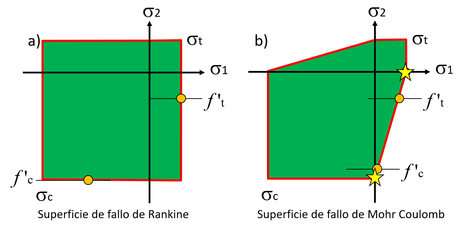
Si tomamos en cuenta la resistencia máxima a tracción ( ) conjuntamente con la resistencia máxima a compresión ( ) es posible modelar el comportamiento del material mediante los modelos de fallo más populares para materiales frágiles como los de Rankine o Mohr Coulomb. En la Figura 9 se muestran la interpretación gráficas de ambas teorías representadas en ejes principales ( y ), donde , y, corresponden a las tensiones máximas de tracción y compresión, respectivamente.
|
| Figura 9: Superficies de daño. a) Rankine b) Mohr Coulomb |
Aunque las normas permiten el uso de probetas cubicas, este ejemplo considera probetas cilíndricas las cuales, al final del ensayo, deben de presentar fisuras similares a las que se muestran en la Figura 10 de acuerdo con la norma ISO 1920-4 [18].

|
| Figura 10: Ensayo de compresión simple. Mecanismos de fractura aceptados como correctos en el ensayo de compresión [18] |
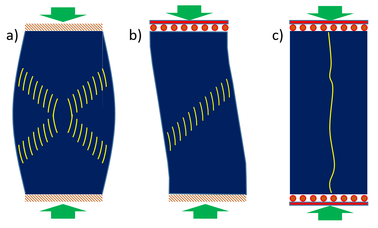
La diversificación de la tipología de fisuras obtenida en los resultados experimentales ha sido estudiada con detalle [24] y el diferente comportamiento se atribuye a las condiciones de contorno en los extremos de la probeta, tal como se muestra en la Figura 11. Sin embargo, controlar de forma adecuada las condiciones de apoyo en el laboratorio es una tarea difícil y complicada, pues basta que el refrentado de la probeta no quede lo suficientemente compacto u horizontal para generar un apoyo deslizante o una carga excéntrica al eje de la probeta.
|
| Figura 11: Ensayo de compresión simple. Mecanismos de fractura en función de las condiciones de apoyo. a) biempotrada. b) un apoyo deslizante. c) dos apoyos deslizantes |
El experimento numérico que se presenta se realiza primero en 2D utilizando probetas hexaédricas en tensión plana y probetas cilíndricas normalizadas para el caso 3D. El objetivo es reproducir los valores de la tensión máxima del hormigón a compresión y obtener los tres tipos de fracturas en función de las condiciones de apoyo.
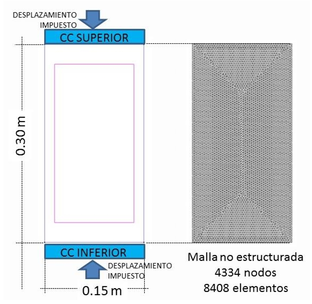
El ensayo en 2D consiste en comprimir la probeta cuyas dimensiones y condiciones de carga se muestran en la Figura 12 y en la que también se presenta la malla de elementos finitos utilizada.
|
| Figura 12: Ensayo de compresión simple. Probeta y malla utilizada en el ensayo 2D |
Las propiedades del hormigón utilizadas son. = 30.0 × 109 Pa, = 0.20, = 24 × 103 N/m3, = 2000 MPa, = 20.0 MPa y G = 105 × 10-3 J/m2 La tensión máxima de compresión es de 20 × MPa.
El resultado numérico obtenido con la técnica FEM-DEM para la tensión máxima es de 19 MPa. Este valor se aproxima mucho al resultado esperado, lo que confirma el buen comportamiento del modelo de cálculo utilizado.
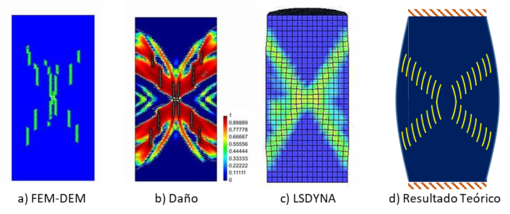
En las siguientes figuras se analiza el patrón de grietas generado en la probeta. Para una probeta bi-empotrada la Figura 13 muestra claramente como los resultados numéricos reproducen el patrón de grieta en cruz. La Figura 13(a) muestra las grietas obtenidas con el programa FEM2DEM [4] y la Figura 13(b) el daño en los elementos. Estos resultados se pueden comparar con la Figura 13(d) que corresponde a los resultados teóricos [24], o bien con la Figura 13(c) que corresponde a los resultados obtenidos con el código comercial LS-DYNA [25]. Es importante observar que, aunque ambos programas presentan patrones de daño similares, solo el primero es capaz de reproducir las micro-grietas en la dirección de las bandas de daño, tal como sugieren los resultados teóricos. De manera que no todos los modelos numéricos, por similares que sean, son válidos para reproducir este complejo fenómeno de rotura del hormigón.
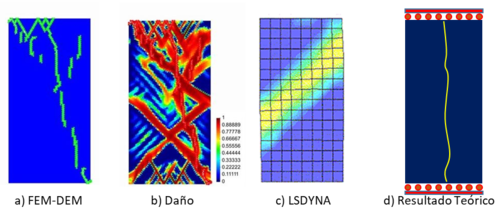
La Figura 14 corresponde al caso en que ambas superficies de carga tienen un desplazamiento horizontal no nulo. Teóricamente [24], como se muestra en la 14(d), la fisura debe ser vertical. La Figura 14(a) muestra un conjunto de fisuras verticales que claramente coinciden con los resultados teóricos y de laboratorio (Figura 10). El patrón de daño es el mostrado en la Figura 14(b). Se observa en la Figura 14(c) que los resultados obtenidos con el código LS_DYNA [25] no reproducen correctamente las grietas en la probeta, a pesar de capturar correctamente los valores máximos de carga.
|
| Figura 13: Ensayo de compresión simple. Probeta biempotrada, malla no estructurada |
|
| Figura 14: Ensayo de compresión simple. Probeta con dos caras deslizantes, resultados numéricos y teóricos |
Finalmente, la Figura 15 muestra una probeta 3D analizada con el programa FEM2DEM [4] y los resultados teóricos [24] y experimentales. Se aprecia que el modelo numérico es capaz de reproducir adecuadamente el mecanismo de fallo de acuerdo a lo esperado y en concordancia con los resultados experimentales.

|
| Figura 15: Ensayo de compresión simple. Probeta con una cara deslizante, resultados numéricos, teóricos y experimentales |
Ensayo de cortante
El objetivo de este ensayo es mostrar los diferentes resultados que se pueden obtener cuando la geometría utilizada no es la correcta, aunque experimentalmente no se puedan observar las diferencias. El uso de los Métodos Numéricos permite poner de manifiesto que la física del problema no siempre es la se intuye.
El ensayo de cortante realizado está diseñado para aplicar un esfuerzo de cizalladura sobre una probeta de modo que se produzca el fallo por deslizamiento a lo largo de un plano paralelo a las fuerzas aplicadas. Por lo general las fuerzas de cizallamiento provocan que una de las superficies de fallo del material se mueva en una dirección y la otra superficie en dirección opuesta, de manera que el material se encuentra sometido a un estado de corte. El objetivo final del ensayo es obtener la resistencia del material al esfuerzo cortante.
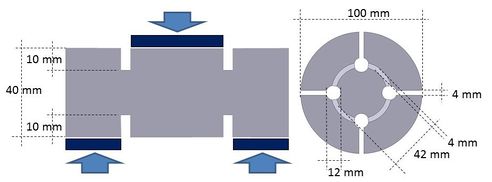
El ensayo de cortante seleccionado ha sido propuesto por Luong M.P. [26]. La probeta tiene forma tubular cuyo eje coincide con el eje z = 0 presenta varias entallas y se encuentra sujeta a una carga central en una de sus caras y otra excéntrica en la cara opuesta de manera que se genere un esfuerzo cortante paralelo al eje z = 0, tal y como se describe en la Figura 16, en la que adicionalmente se muestran las condiciones de contorno impuestas. La profundidad de la entalla es de 10 mm y su ancho es de 4 mm. La carga se aplica mediante un desplazamiento impuesto de velocidad constante e igual a 1 mm/s hasta llegar a la fractura.
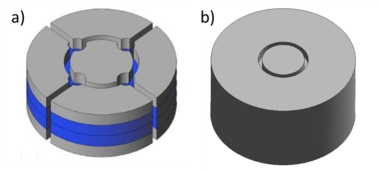
Como se aprecia en la Figura 16, la geometría propuesta para el ensayo presenta cuatro entallas rematadas por sendos taladros de manera que la superficie de corte sea lo más diáfana posible. En la Figura 17 (a) se observa la geometría de la probeta de acuerdo con el ensayo original, mientras que la Figura 17 (b) define la probeta utilizada comúnmente y adoptada como estándar en muchos laboratorios. Aparentemente los esfuerzos de cizalladura que se generan en esta probeta son los mismos que en la probeta original, permitiendo extraer el corazón cilíndrico al final del ensayo, como se muestra en la Figura 18.
Observando con detalle el corazón extraído en todas las probetas, se puede ver que no es perfectamente cilíndrico; siendo su geometría ligeramente cónica.
Realizando el ensayo de cortante con el código FEM2DEM [4] con las dos geometrías propuestas se puede observar que el mecanismo de rotura no es similar y por tanto el resultado cuantitativo tampoco lo puede ser.
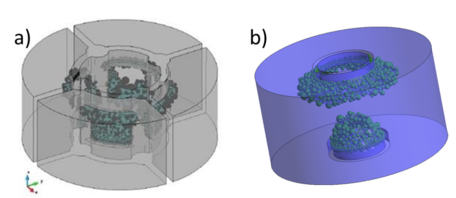
En la Figura 19 se pueden observar los dos mecanismos de rotura. Para la geometría original (Figura 19 (a)) los planos de corte son claros y bien definidos, ocurriendo justo en la zona correcta y permitiendo la extracción del corazón de la probeta de forma totalmente cilíndrica. La Figura 19 (b) muestra que en el caso de la geometría simplificada la superficie inicial de la fractura no es inicialmente cilíndrica, sino en forma de abanico. Esto origina que el corazón extraído no sea del todo cilíndrico sino cónico. También se puede observar que en la parte inferior del corazón de la probeta también se forma un cono de falla
Cuantitativamente la diferencia entre la resistencia al cortante obtenida en ambos ensayos es de un 20%, lo que en ocasiones puede no ser detectable dada la alta variabilidad de los resultados de los ensayos experimentales.
Ensayo de extracción
En algunos países, como Italia y Dinamarca, el ensayo de extracción es una prueba muy común para estimar la resistencia a la compresión del hormigón in situ. Una de las variantes más populares de este ensayo corresponde al denominado LOK-TEST [27] el cual mide de forma indirecta la resistencia a la compresión del hormigón al correlacionarla con la fuerza necesaria para extraer un inserto de acero incrustado en el hormigón. A pesar de ser un ensayo que requiere su planificación antes de fabricar la pieza de hormigón, resulta una forma útil y aproximada para conocer el comportamiento del hormigón en la obra, añadiendo el hecho de que se trata de una prueba no destructiva. Actualmente este ensayo se encuentra estandarizado y descrito en la norma ASTM C900-15, la British Standard 1881-207 y la norma europea UNE-EN 12504-3 [28 - 30].
Este ensayo se ha estudiado de forma numérica y con gran detalle con el método FEM-DEM con la finalidad de conocer los mecanismos de fallo que ocurren durante el proceso de extracción del inserto metálico. Adicionalmente y debido a que experimentalmente proporciona valores muy acertados de la tensión máxima de rotura de forma totalmente indirecta, resulta un ejemplo muy complejo para ser simulado en el ordenador.
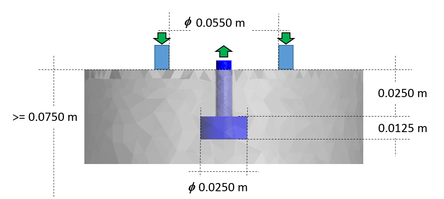
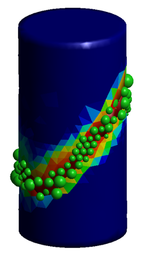
El inserto de acero requerido por este ensayo corresponde a un disco de 0.025 m de diámetro y colocado a 0.025 m de profundidad como se muestra en la Figura 20. Una varilla que no se encuentra encastrada en el hormigón sujeta el disco de acero y permite tirar de este apoyándose en un disco de sujeción de 0.055 m de diámetro. El dispositivo de extracción mide la fuerza necesaria para sacar el inserto metálico.
Este proceso no solo extrae el inserto metálico, sino que además separa un cono de hormigón del resto de la pieza (Figura 21). Las dimensiones de dicho cono dependen del diámetro del inserto, el anillo de compresión y la profundidad a la que se encuentra el inserto de acero.
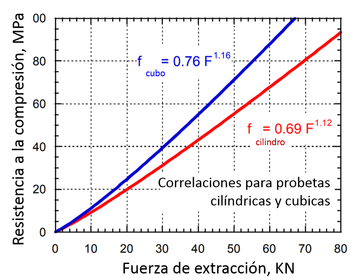
Como se ha comentado, este ensayo mide de forma indirecta la resistencia a compresión del hormigón en función de la fuerza de extracción. En general es necesario realizar una gran cantidad de pruebas para establecer la relación existente entre ambas magnitudes [27]. Actualmente la relación más aceptada es la mostrada en la Figura 22, donde se representa la fuerza de extracción en función de la tensión ultima de compresión del material tanto para probetas cubicas como cilíndricas [31].
En un inicio, durante el proceso de diseño del ensayo, se pensó que el mecanismo de rotura para la formación del cono de hormigón durante la extracción del inserto, era el mismo que el que ocurre en los ensayos de compresión [27]. No obstante, aunque existe una cierta correlación entre los resultados de ambos ensayos, la investigación llevada a cabo en las últimas décadas no llega a definir adecuadamente el mecanismo de colapso interno en el bloque de hormigón asociado con el proceso de extracción del inserto metálico [32].
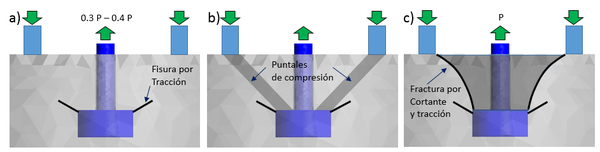
El mecanismo que parece más cercano a la evidencia real define tres etapas bien diferenciadas, cada una con diferentes tipos de fractura [33 – 35].
- Inicialmente se origina una fisura por tracción desde el borde del inserto a un nivel de carga de 30-40% de la fuerza máxima de extracción, como se muestra en la Figura 23 (a).
- La propagación de la primera grieta se detiene mediante la activación de una serie de microgrietas localizadas en los puntales de compresión entre el inserto y el anillo de sujeción, Figura 23 (b).
- Finalmente, el puntal de compresión colapsa y la superficie de fractura final en forma de cono se activa, formando una grieta de tracción/cortante que discurre desde el exterior del borde del disco hasta el borde interior del anillo de sujeción. Como se muestra en la Figura 23 (c), el ángulo final del cono formado es de unos 52 grados.
Una vez definidos los pormenores de este ensayo se realizó la simulación numérica con la técnica FEM-DEM. Para ello se simularon los ensayos de extracción y de compresión simple utilizando las mismas propiedades del material. Todo ello con la finalidad de verificar si se cumple la correlación mostrada en la Figura 22.
Las propiedades del hormigón consideradas son. E0 = 27.0 × 109 Pa, ν = 0.20, γ = 22.2 × 103 N/m3, σc = 48.18 MPa, σt = 4.818 MPa y G = 70 J/m2. El inserto metálico, así como el perno de extracción se modelan en acero con las siguientes propiedades: E0 = 161.0 × 109 Pa, ν = 0.20, γ = 78.2 × 103 N/m3, σc = 575.00 MPa, σt = 575.00 MPa y G = 300 J/m2.
La geometría utilizada y sus dimensiones se muestran en la Figura 20. Haciendo uso de la simetría de la geometría, solo se analiza una cuarta parte de ella discretizada en 478,164 elementos: 19,537 tetraedros de acero y 458,627 tetraedros de hormigón. El ensayo se realiza extrayendo el inserto a velocidad constante de 0.04 m/s y restringiendo el movimiento vertical del hormigón en contacto con el cilindro de sujeción. Es importante remarcar que el perno de extracción no se encuentra unido solidariamente al hormigón; no ocurre así con el disco de extracción.
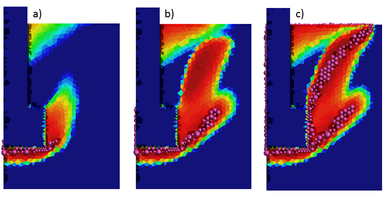
La fuerza máxima de extracción obtenida con el método FEM-DEM ha sido de 24,506 N. Un aspecto importante es que a un valor de 7,350 N se visualiza el inicio de la fisura de tracción mediante una banda de elementos dañados alrededor de la parte inferior del disco. Esta fisuración se inicia en la parte inferior del disco principalmente debido a que éste se encuentra unido al hormigón, como se muestra en la Figura 24 (a). Hay que destacar que son pocos los ensayos numéricos consultados que llegan a detectar el desarrollo de esta fisura [31, 36].
La Figura 24 (b) muestra como la fisura por tracción se detiene y se desarrollan los puntales de compresión, mientras que la Figura 24 (c) muestra cómo se genera la fractura que permite extraer el cono de hormigón. Es destacable que el ensayo numérico reproduce adecuadamente el comportamiento real del ensayo.
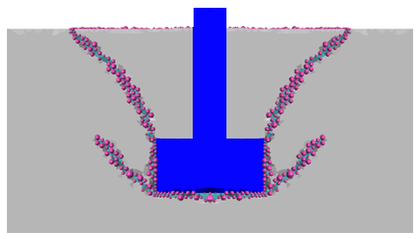
La Figura 25 muestra una vista simétrica de la fisuración ultima del ensayo. En la Figura 26, también en vista simétrica, se puede observar la fisura por tracción y la superficie de fallo en donde se pone de manifiesto la forma cónica de la pieza de hormigón extraída.
Una vez realizado el ensayo de extracción se procedió a realizar un ensayo numérico de compresión simple con el método FEM-DEM utilizando las mismas propiedades del material, tal y como se ha descrito en el apartado anterior correspondiente a este ensayo.
La probeta utilizada para el ensayo de compresión simple se discretiza en 38,296 tetraedros lineales. La Figura 27 muestra el daño y la fisura obtenida en la probeta con una tensión de compresión máxima de 28.92 MPa. Más información al respecto de este ensayo utilizando la técnica FEM-DEM se puede encontrar en [11].
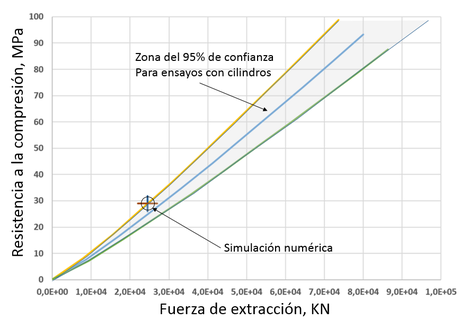
Las correlaciones mostradas en la Figura 22 son el resultado de aplicar una regresión sobre una nube de puntos experimentales, en los que la dispersión de la resistencia a compresión de los ensayos de probetas cilíndricas fue del ± 6%, mientras que la fuerza de extracción presentó una dispersión del ±8%. De esta forma se puede definir una zona que corresponde al 95% de fiabilidad de los datos experimentales tal y como se muestra en la Figura 28.
En la Figura 28 también se puede observar el punto correspondiente a los valores de la fuerza de extracción y de la tensión de compresión máxima obtenidos con la técnica FEM-DEM (24,506 N, 28.92 MPa. Dicho punto se encuentra dentro de la zona correspondiente al 95% de fiabilidad.
El resultado mostrado constata que la técnica FEM-DEM es capaz de reproducir el complejo comportamiento del hormigón, no solo de manera cualitativa al capturar adecuadamente la dirección y tipo de fisuras, sino también de forma cuantitativa.
En cuanto a los resultados experimentales, es interesante observar que a pesar de que inicialmente se pensaba que el mecanismo de fallo estaba ligado a la formación de pilares de compresión durante la extracción, se ha verificado que el proceso de fallo real es una combinación de modos de fractura no considerados en el diseño de la prueba. Sin embargo, la correlación propuesta entre la fuerza de extracción y la tensión a compresión máxima del hormigón proporciona resultados muy útiles del valor de dicha tensión a efectos prácticos.
Conclusiones
Los resultados de los estudios realizados demuestran que el código numérico basado en la técnica FEM-DEM y un sencillo modelo constitutivo de daño isótropo permite reproduce adecuadamente la física de los ensayos de rotura de probetas de hormigón. La técnica FEM-DEM es, por tanto, un procedimiento fiable para estudiar el comportamiento en servicio y en rotura de estructuras de hormigón [5,6].
Se han presentado cuatro ejemplos donde la información proveniente de los Métodos Experimentales y los Métodos Numéricos permite enriquecer ambos campos de estudio. Ambos procedimientos son complementarios, por lo que se debe de potenciar el uso de Métodos Numéricos en los laboratorios de resistencia de materiales y en la verificación de ensayos y normativas. Por su parte, los Métodos Experimentales proporcionan información relevante para definir el modelo del material y también para la formulación, calibración y validación de nuevos métodos numéricos.
Agradecimientos
Los autores agradecen a la Asociación Nacional de Laboratorios Independientes al Servicio de la Construcción, A.C. (ANALISEC), delegación Guanajuato (México), su apoyo en la presentación de este trabajo en el marco del segundo seminario “Los Laboratorios en la Sustentabilidad de la Construcción” realizado en la ciudad de Guanajuato el 3 y 4 de Mayo de 2018.
Referencias
[1] Silva, R. Método Numérico, Analítico y Experimental: Concurrentes o complementarios en la ingeniería. ESS https://www.esss.co/blog/es/metodo-numerico-analitico-y-experimental (13 de septiembre 2018)
[2] Zárate F., Cuellar J.J., Regalado A.E., La simplificación en ingeniería, ventajas e inconvenientes. 2 Revista Mexicana de Métodos Numéricos (2018).
[3] Zienkiewicz O.C., Cheung Y.K.; The Finite Element Method in Structural and Continuum Mechanics”, 1967
[4] Zarate, F. FEM2DEM 3D, Finite-Discrete element code, CIMNE (2017) Barcelona.
[5] Zárate, F., Oñate, E. A simple FEM–DEM technique for fracture prediction in materials and structures. Comp. Part. Mech. (2015) 2: 301-314. https://doi.org/10.1007/s40571-015-0067-2
[6] Zárate, F., Cornejo, A., Oñate, E. A three-dimensional FEM–DEM technique for predicting the evolution of fracture in geomaterials and concrete, Comp. Part. Mech. (2018) 5:3 411-420. https://doi.org/10.1007/s40571-017-0178-z
[7] Oñate E., Labra C., Zárate F., Rojek J. and Miquel J., Avances en el desarrollo de los métodos de elementos discretos y de elementos finitos para el análisis de problemas de fractura. Anales de Mecánica de Fractura (2005) 22 27-34
[8] Oñate E., Zárate F., Celigueta M.A., González J.M., Miquel J., Carbonell J.M., Arrufat F., Latorre S., Santasusana M., Advances in the DEM and Coupled DEM and FEM Techniques in Non Linear Solid Mechanics. In: Oñate E., Peric D., de Souza Neto E., Chiumenti M. (eds) Advances in Computational Plasticity. Computational Methods in Applied Sciences, Vol. 46. Springer (2018)
[9] González, J.M., Zárate, F. & Oñate, E. Pulse fracture simulation in shale rock reservoirs: DEM and FEM–DEM approaches. Comp. Part. Mech. (2018) 5: 355. https://doi.org/10.1007/s40571-017-0174-3
[10] Zárate F., Gonzalez J.M., Miquel J., Lohner R., Oñate E., A coupled FEM-DEM technique for predicting blasting operations in tunnels. Aceptado para su publicación en Underground Space, Elsevier (2018) https://doi.org/10.1016/j.undsp.2018.09.002
[11] Zárate F., Oñate E.. Predicción de fracturas en estructuras de hormigón combinando los métodos de elementos finitos y de elementos discretos, Aceptado para su publicación en Hormigón y Acero (2018), https://doi.org/10.1016/j.hya.2018.05.002
[12] Carniero F.L.L.B, Barcellos A., Concrete Tensile Strength, Bulletin No 13, International Association of Testing and Research Laboratories for Materials and Structures, Paris, (March 1953), pp 97- 127.
[13] Akazawa T., Tension Test Method for Concrete, Bulletin No 16, International Association of Testing and Research Laboratories, Paris, (November 1953), pp 11-23.
[14] Hudson W.R., Kennedy T.W., An indirect tensile test for stabilized materials, Research Report Number 98-1 Research Project 3-8-66-98 The Texas Highway Department, U. S. Department of Transportation Federal Highway Administration Bureau of Public Roads (January 1968)
[15] Frocht M.M., “Photoelasticity”, Vol 2, John Wiley & Sons, Inc., New York, (1957).
[16] AMERICAN SOCIETY FOR TESTING AND MATERIALS C900-15, Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens, West Conshohocken, PA, (2017)
[17] UNE 22950-2:1990 Propiedades mecánicas de las rocas. Ensayos para la determinación de la resistencia. Parte 2: resistencia a tracción. Determinación indirecta (ensayo brasileño). Asociación Española de Normalización y Certificación AENOR (1990)
[18] ISO 1920-4 Testing of concrete - Part 4: Strength of hardened concrete International Organization for Standardization ISO (2005)
[19] Galilei G. ´´Diálogo y demostración matemática sobre dos nuevas ciencias". 1638. Traducción al español de Editora Nacional. (1976)
[20] Straub H.: ´´A history of civil engineering". Leonard Hill Ltd. (1960)
[21] Norma a Instrucción de Hormigón Estructural (EHE-08)
[22] UNE-EN 12390-3.2009 Ensayos de hormigón endurecido. Parte 3. Determinación de la resistencia a compresión de probetas. (2009) Asociación Española de Normalización y Certificación AENOR
[23] AMERICAN SOCIETY FOR TESTING AND MATERIALS C39/C39M - 18, Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens, West Conshohocken, PA, 2018
[24] Bazant Z.P., Planas J., Fracture and Size Effect in Concrete and Other Quasibrittle Materials CRC Press LLC (1998). ISBN 9780849382840
[25] Murray Y.D., Abu-Odeh A. and Bligh R., Evaluation of LS-DYNA Concrete Material Model 159 Publication No. FHWA-HRT-05-063, (2007) US Department of Transportation.
[26] Luong M., Tensile and shear strengths of concrete and rock, Engineering Fracture Mechanics 1-3 (1990), no. 35, 127–135.
[27] Kierkegaard-Hansen, P.: "Lok-Strength", Nordisk Betong, #3-4, (1977), Stockholm, Sweden
[28] AMERICAN SOCIETY FOR TESTING AND MATERIALS C900-15, Standard Test Method for Pullout Strength of Hardened Concrete, ASTM International, West Conshohocken, PA, 2015, DOI: 10.1520/C0900-15
[29] BRITISH STANDARDS INSTITUTION. BS 1881-207 Testing concrete. Recommendations for the assessment of concrete strength by near-to-surface tests (1992)
[30] ASOCIACION ESPAÑOLA DE NORMALIZACION Y CERTIFICACION. UNE-EN 12504-3 Ensayos de hormigón en estructuras. Parte 3: Determinación de la fuerza de arrancamiento (2006)
[31] Petersen C.G., “LOK-Test and CAPO-Test Pullout Testing: Twenty Years Experience,” Conference on Non-Destructive Testing in Civil Engineering, Liverpool, UK, April 1997, British Institute of Non-Destructive Testing
[32] A. Brencich A post-installed insert for pull-out tests on concrete up to 70 MPa. Construction and Building Materials, (2015) Vol 95, pp 788-801
[33] Krenchel H., Bickley J.A. Pullout testing of concrete: historical background and scientific level today Nord. Betong, 6 (1987), p. 155
[34] Krenchel, H. & Shah, S.P.: "Fracture analysis of the pullout test", RILEM, Materials & Structures, No. 108, (1985)
[35] Stone W.C., Carino N.J., Deformation and failure in large-scale pull-out test ACI J., (1983), 80 (6) p. 501-513
[36] Stone W.C., Carino N.J., Comparison of analytical with experimental strain distribution for the pull-out test ACI J., (1984) 81 (1), p. 3-12
[37] O.C Zienkiewicz and J.Z. Zhu, The superconvergent patch recovery (SPR) and adaptive finite element refinement., Comput. Methods App. Mech. Engng. (1992) 101, 207 –224.
[38] Oller S., Oliver J., Lubliner J. y Oñate E., Un modelo constitutivo de daño plástico para materiales friccionales. Parte I: Variables fundamentales, Rev. Int. de Métodos Numéricos para Cálculo y Diseño en Ingeniería, (1988) Vol. 4, No. 4, pp. 397-431,
Document information
Published on 08/02/19
Accepted on 24/01/19
Submitted on 09/12/18
Volume 35, Issue 1, 2019
DOI: 10.23967/j.rimni.2019.01.004
Licence: CC BY-NC-SA license