Revision as of 17:51, 5 December 2018 (view source) Valdesjg (talk | contribs) (Created page with "==Una formulación acoplada sólido-estructura para el análisis de vigas de concreto postensado == '''''' ==Resumen== Se presenta una formulación numérica en base al m...")	Revision as of 17:56, 5 December 2018 (view source) Valdesjg (talk | contribs) m (Valdesjg moved page Draft Valdes-Vazquez 571746928 to Review 438063361961) Newer edit →
(No difference)

---

Revision as of 17:56, 5 December 2018

Una formulación acoplada sólido-estructura para el análisis de vigas de concreto postensado

'

Resumen

Se presenta una formulación numérica en base al método de los elementos finitos para obtener los esfuerzos y desplazamientos de vigas de concreto postensado. La formulación acopla los cables de postensado con la formulación del sólido, considerando al cable como estructura con apoyos intermedios embebidos en el sólido, lo que es una alternativa novedosa y la principal aportación de este trabajo, ya que no sólo es factible de implementarse con elementos finitos como aquí se muestra, sino que es versátil, en el sentido de que cualquier combinación de carga común y condiciones de apoyo puede representarse con el modelo; pero además, el modelo también es de aplicación práctica para el análisis y diseño de trabes de concreto postensado. El método es validado comparándolo con una alternativa reportada en la literatura, y mediante tres ejemplos con cargas diferentes, con los que se muestra que la formulación propuesta da muy buenos resultados. Está alternativa mediante métodos numéricos, puede extenderse a casos más complejos en el futuro, ya que explota la conveniencia de los elementos finitos, que son más precisos y de más amplia aplicación que otros métodos simplificados, comúnmente usados para diseñar vigas de concreto postensado.

Palabras clave: postensado, vigas de concreto, elementos finitos, formulación acoplada

1 Introducción

Las estructuras de concreto postensado son ampliamente usadas para la construcción de obras de ingeniería civil, ya que pueden reducir las dimensiones de estructuras diseñadas mediante refuerzo convencional en el concreto, están ligadas a la construcción de elementos prefabricados lo que acelera el proceso constructivo y conllevan a un mejor control de calidad, entre otras ventajas. Como todo sistema constructivo, los elementos de concreto postensado también presentan desventajas, por ejemplo, la dificultad de predecir las pérdidas en la fuerza de postensado. El hecho es que estos elementos son usados en la construcción de estructuras nuevas, y además existen numerosas estructuras que fueron diseñadas con este método constructivo. Es por lo anterior, que este tema sigue siendo motivo de amplia investigación en el mundo, ya sea en investigaciones experimentales y/o analíticas (e.g. [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13]), así como en temas de revisión, evaluación, diseño, colapso, instrumentación y monitoreo de estructuras de concreto postensado existentes (e.g. [14], [15], [16], [17], [18], [19]). Cabe mencionar que en muchos estudios experimentales normalmente se llevan a cabo estudios analíticos y numéricos con fines de comparación y/o validación. Otros temas de investigación recientes en elementos de concreto postensado incluyen temas de sustentabilidad (e.g. [20]), de ciclo de vida y optimización (e.g. [21]), del uso de redes neuronales (e.g. [22]), entre otros temas.

Si bien el concreto postensado e investigaciones relacionadas abarcan una amplia gama de elementos estructurales, como muros, columnas, y sistemas de soporte de aerogeneradores (e.g. [23], [24]), entre otras estructuras, esta investigación se centra en trabes sometidas a flexión (si bien podría extenderse la formulación a otro tipo de elementos sometidos a momento flexionante, como losas).

Respecto al caso específico de elementos en flexión, la mayoría de las investigaciones citadas arriba usan el método de elementos finitos (MEF) para sus análisis, y en algunos casos se proponen métodos simplificados (e.g. [5]). Sin embargo, ninguno de estos métodos presenta un análisis de elementos finitos considerando por separado el análisis estructural unidimensional en el plano del postensado y acoplándolo al análisis bidimensional con elementos de la mecánica de sólidos. Entonces, aquí se presenta una formulación acoplada que incluya una estructura con apoyos intermedios para el cable, interactuando con la formulación de sólidos del resto de la viga.

Por lo tanto el objetivo principal de este trabajo es presentar una formulación alternativa para el análisis de vigas de concreto postensado. La metodlogía consiste en realizar el análisis de la parte estructural con elementos unidimensionales que consideran solamente fuerzas axiales, las cuales representarán las fuerzas a las que está sometido el cable postensado. Los resultados de este análisis se utilizan como fuerzas externas a las que estará sometida la viga bidimensional, que será analizada con elementos finitos en el plano. La forma de proceder se describe a detalle más adelante, pero se puede resumir como: desarrollar una formulación novedosa para el analísis de trabes postensadas, representando los cables como estructuras a tensión con apoyos intermedios, acopladas con un sólido para obtener desplazamientos y esfuerzos del elemento estructural en su conjunto, útiles para fines de diseño.

Los resultados del presente estudio podrían ser útiles para ingenieros de la práctica, en tanto un método relativamente fácil de implementar con herramientas conocidas, pero también a investigadores y desarrolladores de códigos de diseño, quienes podrían disponer del método descrito en este artículo y sus resultados para futuros reglamentos y/o actualizaciones de los existentes.

2 Formulación Acoplada Sólido-Estructura

2.1 Elemento Estructural

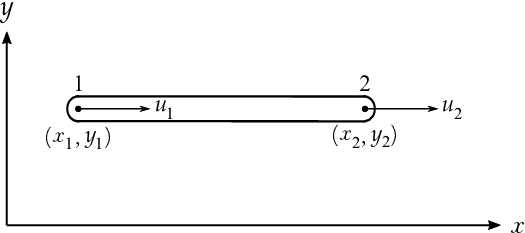
El elemento estructural que se utiliza para simular el cable de presfuerzo es un elemento unidimensional de dos nodos, tal y como aparece en la figura 1, (e.g. [25], [26]).

Figura 1: Cable de 2 nodos

cuyo campo de desplazamientos es

${\displaystyle \mathbf {u} =u_{x}=u}$

(1)

La solución exacta ${\textstyle \mathbf {u} }$ para el desplazamiento se aproxima por ${\textstyle \mathbf {u} ^{h}}$ de tal forma que

${\displaystyle \mathbf {u} \approx \mathbf {u} ^{h}=u_{x}^{h}=u^{h}}$

(2)

La formulación del elemento finito de dos nodos usa polinomios lineales de primer orden, con lo que

${\displaystyle u^{h}=u^{h}(x)=N_{1}(x)\,u_{1}+N_{2}(x)\,u_{2}}$

(3)

donde ${\textstyle N_{I}}$ ${\textstyle (I=1,2)}$ son conocidas como funciones de forma, también llamadas funciones de interpolación, las cuales se calculan con

${\displaystyle {\begin{matrix}N_{1}(x)={\dfrac {x_{2}-x}{x_{2}-x_{1}}}\\\\N_{2}(x)={\dfrac {x-x_{1}}{x_{2}-x_{1}}}\\\\\end{matrix}}}$

(4)

Con el cálculo del campo de los desplazamientos con elementos finitos, se procede a calcular las deformaciones, resultando

${\displaystyle \varepsilon ^{h}=-{\frac {1}{L}}\,u_{1}+{\frac {1}{L}}\,u_{2}={\begin{bmatrix}-{\dfrac {1}{L}}&,&{\dfrac {1}{L}}\end{bmatrix}}\cdot {\begin{bmatrix}u_{1}\\\\u_{2}\end{bmatrix}}=\mathbf {B} \cdot \mathbf {u} ^{h}}$

(5)

donde ${\textstyle L=x_{2}-x_{1}}$. Los esfuerzos en el cable están relacionados con las deformaciones mediante el módulo de elasticidad del cable, ${\textstyle E_{c}}$, de forma que tenemos

${\displaystyle \sigma ^{h}=E_{c}\,\,\varepsilon ^{h}=E_{c}\,\,\mathbf {B} \cdot \mathbf {u} ^{h}}$

(6)

Una vez que se obtiene el esfuerzo normal sobre el elemento, se procede a calcular las fuerzas internas con

${\displaystyle \mathbf {f} ^{\,int}=\int _{L}\mathbf {B} ^{T}\,\sigma ^{h}\,A_{c}\,\,dx=\int _{L}E_{c}\,A_{c}\,\,\mathbf {B} ^{T}\cdot \mathbf {B} \cdot \mathbf {u} ^{h}\,\,dx={\dfrac {E_{c}\,A_{c}}{L}}{\begin{bmatrix}1&&-1\\\\-1&&1\end{bmatrix}}\cdot {\begin{bmatrix}u_{1}\\\\u_{2}\end{bmatrix}}}$

(7)

donde ${\textstyle A_{c}}$ es el area de la sección transversal del cable. El cálculo de la matriz de rigidez se efectúa con

${\displaystyle \mathbf {K} ={\dfrac {\partial \mathbf {f} ^{\,int}}{\partial \mathbf {u} ^{h}}}=\int _{L}E_{c}\,A_{c}\,\,\mathbf {B} ^{T}\cdot \mathbf {B} \,\,dx={\dfrac {E_{c}\,A_{c}}{L}}{\begin{bmatrix}1&&-1\\\\-1&&1\end{bmatrix}}}$

(8)

la cual es necesaria para realizar el primer paso del acoplamiento que más adelante se detalla.

2.2 Elemento Sólido

El sólido que se utiliza en este trabajo es un elemento bidimensional, y se particularizó para un elemento triangular de tres nodos de esfuerzo plano, también conocido como elemento de esfuerzo constante (CST) por sus siglás en inglés, (e.g. [25], [26]). De esta manera el campo de los desplazamientos del elemento se encuentra definido por

${\displaystyle \mathbf {u} ={\begin{bmatrix}u_{x}\\\\u_{y}\end{bmatrix}}={\begin{bmatrix}u\\\\v\end{bmatrix}}}$

(9)

La solución exacta dada por ${\textstyle \mathbf {u} }$ se aproxima mediante elementos finitos por ${\textstyle \mathbf {u} ^{h}}$, de manera que

${\displaystyle \mathbf {u} \approx \mathbf {u} ^{h}={\begin{bmatrix}u_{x}^{h}\\\\u_{y}^{h}\end{bmatrix}}={\begin{bmatrix}u^{h}\\\\v^{h}\end{bmatrix}}}$

(10)

La solución con elementos finitos se hace mediante polinomios de primer orden en el espacio bidimensional. De esta manera, la aproximación polinomial del campo de los desplazamientos del elemento triangular de tres nodos en el espacio Euclideo se puede escribir por

${\displaystyle {\begin{matrix}u^{h}=u^{h}(x,y)=N_{1}(x,y)\,u_{1}+N_{2}(x,y)\,u_{2}+N_{3}(x,y)\,u_{3}\\\\v^{h}=v^{h}(x,y)=N_{1}(x,y)\,v_{1}+N_{2}(x,y)\,v_{2}+N_{3}(x,y)\,v_{3}\end{matrix}}}$

(11)

donde las funciones de forma, también conocidas como funciones de interpolación, se encuentran definidas para cada nodo del elemento por ${\textstyle N_{I}}$ ${\textstyle (I=1,2,3)}$, siendo

${\displaystyle N_{I}={\frac {1}{2A}}\left(a_{_{I}}+b_{_{I}}\,x+c_{_{I}}\,y\right)}$

(12)

en las que

${\displaystyle a_{_{I}}=x_{_{J}}\,y_{_{K}}-x_{_{K}}\,y_{_{J}}}$ ${\displaystyle b_{_{I}}=y_{_{J}}-y_{_{K}}}$ ${\displaystyle c_{_{I}}=x_{_{K}}-x_{_{J}}}$

(13)

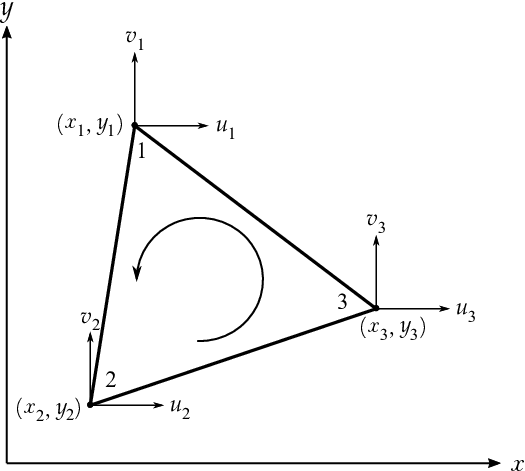
donde ${\textstyle I,J,K=1,2,3}$ con ${\textstyle I\neq J\neq K}$ y además ${\textstyle I,J,K}$ deben ir en sentido antihorario, como se representa en la figura 2.

Figura 2: Triángulo de 3 nodos

Una vez definido el campo de los desplazamientos, se encuentra que el campo de las deformaciones es

${\displaystyle {\boldsymbol {\varepsilon }}^{h}={\begin{bmatrix}\varepsilon _{x}^{h}\\\\\varepsilon _{y}^{h}\\\\\gamma _{xy}^{h}\end{bmatrix}}=\mathbf {B} \,\mathbf {u} ^{h}}$

(14)

donde la matriz ${\textstyle \mathbf {B} }$ es la matriz de la derivada de las funciones de forma, compuesta por las submatrices ${\textstyle \mathbf {B} =\left[\mathbf {B} _{1},\mathbf {B} _{2},\mathbf {B} _{3}\right]}$, y cada submatriz se define por

${\displaystyle \mathbf {B} _{I}={\begin{bmatrix}{\dfrac {\partial N_{I}}{\partial x}}&0\\\\0&{\dfrac {\partial N_{I}}{\partial y}}\\\\{\dfrac {\partial N_{I}}{\partial y}}&{\dfrac {\partial N_{I}}{\partial x}}\end{bmatrix}}}$

(15)

Por otro lado, el campo de los esfuerzos se define por

${\displaystyle {\boldsymbol {\sigma }}^{h}={\begin{bmatrix}\sigma _{x}^{h}\\\\\sigma _{y}^{h}\\\\\tau _{xy}^{h}\end{bmatrix}}=\mathbf {C} \,{\boldsymbol {\varepsilon }}^{h}}$

(16)

donde la ecuación constitutiva viene definida por un problema bidimensional de esfuerzo plano, la cual es

${\displaystyle \mathbf {C} ={\dfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&&\nu &0\\\\\nu &&1&0\\\\0&&0&{\dfrac {1-\nu }{2}}\end{bmatrix}}}$

(17)

donde se utilizan las propiedades del concreto: ${\textstyle E}$ siendo el módulo de elasticidad y ${\textstyle \nu }$ el coeficiente de Poisson. Con los resultados anteriores, se procede al cálculo de las fuerzas internas con

${\displaystyle \mathbf {f} ^{\,int}=\int _{A}\mathbf {B} ^{T}\cdot {\boldsymbol {\sigma }}^{h}\,t\,dA}$

(18)

donde ${\textstyle t}$ es el espesor de la viga. Finalmente, el cálculo de la matriz de rigidez es

${\displaystyle \mathbf {K} ={\dfrac {\partial \mathbf {f} ^{\,int}}{\partial \mathbf {u} ^{h}}}=\int _{A}\mathbf {B} ^{T}\cdot \mathbf {C} \cdot \mathbf {B} \,t\,dA}$

(19)

y servirá para realizar el segundo paso del acoplamiento que a continuación se presenta.

2.3 Acoplamiento

La idea principal del acoplamiento sólido-estructura consiste en resolver el problema en dos partes: primero se resuelve solamente la parte estructural debida al cable de postensado, y en segundo lugar se resuelve el modelo de la viga bidimensional usando elementos finitos triangulares, tomando como fuerzas de postensado, los resultados del paso anterior.

2.3.1 Solución Estructural

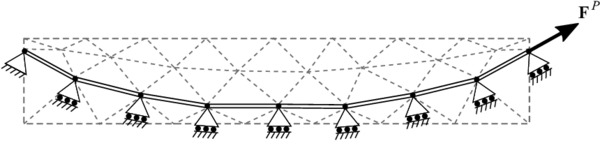
Ya que la solución del puro cable sin el sólido es prácticamente imposible, se procede a generar un modelo como a continuación se describe. Se toma la geometría del cable tal y como está embebida en el concreto. En un extremo se agrega un apoyo simple fijo y en el otro extremo se pone el valor de la fuerza calculada de pretensado ${\textstyle \mathbf {F} ^{P}}$. En los nodos intermedios restantes, se colocarán apoyos inclinados como se aprecia en la figura 3. En la misma figura y con linea punteada, se aprecia tanto el dominio bidimensional de la viga así como su mallado con elementos finitos triangulares. Hasta donde los autores conocen, no existe una formulación como está para el analísis de cables postensados. Esta formulación para el cable, vinculada a la formulación del sólido que se presenta más abajo, es la principal aportación del presente estudio, ya que conlleva a una formulación práctica de elementos finitos, que al mismo tiempo da resultados precisos, como se verá adelante en la sección de Validación.

Figura 3: Cable de postensado embebido en viga en el espacio bidimensional

Previo a realizar el acoplamiento, tenemos que transformar la matriz de rigidez del elemento unidimensional a una matriz de rigidez local del mismo elemento pero en un espacio bidimensional. La matriz de rigidez local del elemento unidimensional en el espacio bidimensional, y su respectivo campo de desplazamientos son

${\displaystyle \mathbf {K} ^{l}={\dfrac {E_{c}\,A_{c}}{L}}{\begin{bmatrix}1&0&-1&0\\0&0&0&0\\-1&0&1&0\\0&0&0&0\end{bmatrix}},\mathbf {u} ^{l}={\begin{bmatrix}{\bar {u}}_{1}\\{\bar {v}}_{1}\\{\bar {u}}_{2}\\{\bar {v}}_{2}\end{bmatrix}}}$

(20)

Para poder resolver el problema, la matriz de rigidez local ${\textstyle \mathbf {K} ^{l}}$ se tiene que poder acoplar a un sistema coordenado global definido por vectores unitarios ${\textstyle {\hat {\mathbf {e} }}_{1}}$ y ${\textstyle {\hat {\mathbf {e} }}_{2}}$ que están en dirección de los ejes globales ${\textstyle x}$ y ${\textstyle y}$. La componentes de la matriz de rotación para transformar de ejes locales a ejes globales está definida por

${\displaystyle M_{ij}^{LtG}={\hat {\mathbf {e} }}_{i}\cdot {\bar {\mathbf {e} }}_{j}}$

(21)

en la que ${\textstyle {\bar {\mathbf {e} }}_{j}}$ ${\textstyle \left(j=1,2\right)}$ representa los vectores unitarios del elemento unidimensional en ejes locales, como se aprecia en la figura 4. Dada la propiedad de ortogonalidad de las matrices de rotación, podemos escribir

${\displaystyle \mathbf {M} _{(2\times 2)}^{GtL}=\left[\mathbf {M} ^{LtG}\right]_{(2\times 2)}^{-1}=\left[\mathbf {M} ^{LtG}\right]_{(2\times 2)}^{T}}$

(22)

De esta forma, se obtiene la matriz de rigidez global con

${\displaystyle \mathbf {K} _{(4\times 4)}^{G}={\begin{bmatrix}\mathbf {M} _{(2\times 2)}^{LtG}&&\mathbf {0} _{(2\times 2)}\\\\\mathbf {0} _{(2\times 2)}&&\mathbf {M} _{(2\times 2)}^{LtG}\end{bmatrix}}\cdot \mathbf {K} _{(4\times 4)}^{l}\cdot {\begin{bmatrix}\mathbf {M} _{(2\times 2)}^{GtL}&&\mathbf {0} _{(2\times 2)}\\\\\mathbf {0} _{(2\times 2)}&&\mathbf {M} _{(2\times 2)}^{GtL}\end{bmatrix}}}$

(23)

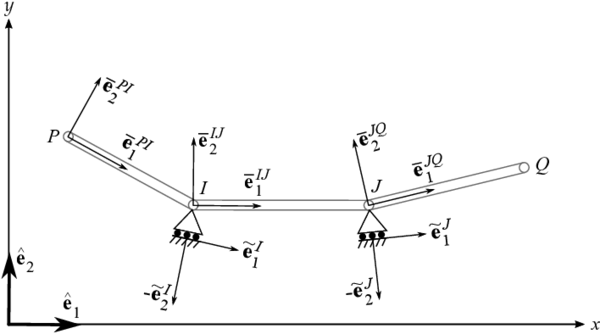
Finalmente, se tienen que incluir el efecto de los apoyos inclinados en la matriz de rigidez. De acuerdo con la figura 4, los vectores unitarios del apoyo sobre el nodo ${\textstyle I}$ son ${\textstyle {\tilde {\mathbf {e} }}_{i}^{I}}$ ${\textstyle (i=1,2)}$, cuyo valor es

${\displaystyle {\tilde {\mathbf {e} }}_{i}^{I}={\dfrac {1}{2}}\left({\bar {\mathbf {e} }}_{i}^{PI}+{\bar {\mathbf {e} }}_{i}^{IJ}\right)}$

(24)

en la que ${\textstyle {\bar {\mathbf {e} }}_{1}^{PI}}$ hace referencia al vector local unitario del elemento que va del nodo ${\textstyle P}$ al nodo ${\textstyle I}$, y el vector ${\textstyle {\bar {\mathbf {e} }}_{2}^{PI}}$ es su componente perpendicular. Con la finalidad de no complicar la información de la figura 4, se optó por mostrar la dirección ${\textstyle {\tilde {\mathbf {e} }}_{2}^{I}}$ de forma negativa, al igual que ${\textstyle {\tilde {\mathbf {e} }}_{2}^{J}}$.

Figura 4: Ejes locales de cable y apoyos inclinados

Con los valores de los vectores unitarios en los apoyos ${\textstyle I}$ y ${\textstyle J}$, se calculan las matrices de rotación para cada uno, siendo sus componentes respectivas

${\displaystyle \left[M_{I}^{LtG}\right]_{ij}={\hat {\mathbf {e} }}_{i}\cdot {\tilde {\mathbf {e} }}_{j}^{I},\left[M_{J}^{LtG}\right]_{ij}={\hat {\mathbf {e} }}_{i}\cdot {\tilde {\mathbf {e} }}_{j}^{J}}$

(25)

De esta manera, la matriz de rigidez del cable ${\textstyle \mathbf {K} ^{C}}$ para el elemento que va del nodo ${\textstyle I}$ al nodo ${\textstyle J}$ considerando los apoyos inclinados es

${\displaystyle \mathbf {K} _{IJ}^{C}={\begin{bmatrix}\mathbf {M} _{I}^{GtL}&&\mathbf {0} \\\\\mathbf {0} &&\mathbf {M} _{J}^{GtL}\end{bmatrix}}\cdot \mathbf {K} _{IJ}^{G}\cdot {\begin{bmatrix}\mathbf {M} _{I}^{LtG}&&\mathbf {0} \\\\\mathbf {0} &&\mathbf {M} _{J}^{LtG}\end{bmatrix}}}$

(26)

El sistema de ecuaciones que se tiene que resolver después del ensamblaje de todos los elementos es

${\displaystyle \mathbf {K} ^{C}\cdot \mathbf {u} =\mathbf {F} ^{P}}$

(27)

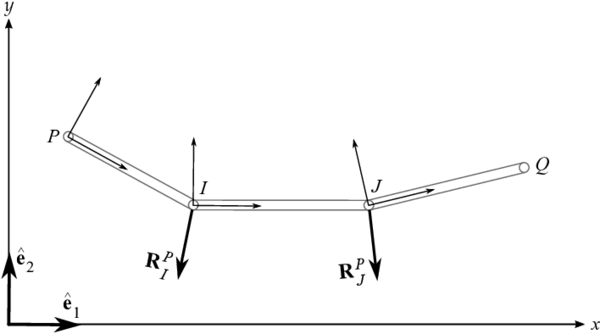
Con los resultados dados en la ecuación (27), se calculan las reacciones en los apoyos, que en este caso llamaremos ${\textstyle \mathbf {R} ^{P}}$. En cada apoyo, la reacción se representará como se muestra en la figura 5.

Figura 5: Reacciones en apoyos inclinados

2.3.2 Solución del Sólido

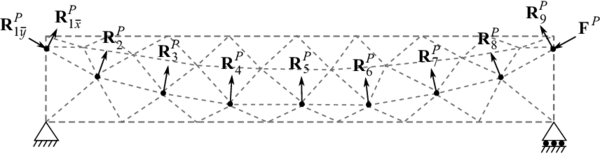
Finalmente, acoplamos los resultados del cálculo estructural en un segundo paso en el cual resolveremos el cálculo del sólido. Para ello, las reacciones del presforzado se pasarán igual y de sentido contrario al problema de sólidos, como se aprecia en la figura 6. También se deberá incluir el valor de la fuerza de presfuerzo ${\textstyle \mathbf {F} ^{P}}$ igual pero en sentido contrario. En la misma figura, se puede observar como se han incluido un par de apoyos, ya que éstos son necesarios para poder resolver el problema. Los apoyos del sólido podrán ser de cualquier tipo que lo permita el análisis bidimensional, así como también se podrá añadir cualquier tipo de carga externa sobre el sólido a modelar (por ejemplo: cargas muertas, cargas vivas, o alguna combinación), a parte de las fuerzas de pretensado. Esto significa que la propuesta de este estudio es muy versatil, y de evidente aplicación práctica, ya que puede cubrir condiciones de apoyo y combinaciones de carga comunes en el ámbito de la ingeniería estructural. Por lo tanto, la propuesta descrita no sólo es novedosa, sino útil para diseñadores de estructuras reales. Esto será más evidente en la siguiente sección, en la que un ejemplo de aplicación se utiliza para fines de validación.

Figura 6: Reacciones en apoyos inclinados

El problema acoplado final a resolver para el cálculo de desplazamientos y esfuerzos en la viga debidas al postensado es

${\displaystyle \mathbf {K} \cdot \mathbf {u} =-\mathbf {R} ^{p}}$

(28)

Si bien la fuerza ${\textstyle \mathbf {F} ^{P}}$ y las reacciones ${\textstyle \mathbf {R} _{I}^{P}}$ en cada nodo ${\textstyle I}$ están en ejes locales, éstas se pueden rotar al sistema de coordenadas global ${\textstyle x}$ y ${\textstyle y}$ utilizando las mismas matrices de rotación introducidas en la ecuación (25).

3 Validaciones

Para validar nuestra propuesta de análisis, hemos tomado el ejemplo del libro [27], el cual se detalla en la tesis [28]. Se trata del análisis de una viga postensada que será usada en el primer nivel de una construcción de 3 niveles de altura. Las cargas del segundo y tercer nivel ya consideradas en las cargas puntuales sobre la viga del primer nivel, se muestran en la figura 7. En la tabla 1 se encuentran las cargas tanto muertas como vivas por unidad de longitud ${\textstyle W}$ correspondientes al primer nivel, así como las cargas muertas y vivas de los niveles segundo y tercero, las cuales serán cargas puntuales ${\textstyle P}$ por cada columna (i.e., ${\textstyle P=P_{m}+P_{v}}$ entre otras combinaciones).

Tabla. 1 Cargas en estructura

	Carga muerta	Carga viva
Primer piso	${\displaystyle W_{m}=}$37 kg/cm	${\displaystyle W_{v}=}$22 kg/cm
Segundo piso	${\displaystyle P_{m}=}$18,200 kg	${\displaystyle P_{v}=}$9,100 kg
Tercer piso	${\displaystyle P_{m}=}$18,200 kg	${\displaystyle P_{v}=}$9,100 kg

La fuerza total de presfuerzo aplicada proporcionada en [27] es de 700,000 ${\textstyle kg}$, la cual ya está reducida por las pérdidas. Esta fuerza se aplicará dividida entre cuatro, ya que es el número de cables que está presente por cada plano del modelo bidimensional.

La longitud total de la viga es de ${\textstyle 18}$.${\textstyle 30}$ ${\textstyle m}$, la cual se encuentra simplemente apoyada, como se aprecia en la parte izquierda de la figura 7. En la parte derecha de la misma figura se encuentra la sección transversal de la viga, la cual es una sección T. La ubicación exacta del acero de presfuerzo se encuentra representada en la figura 8, y corresponde a los extremos de la viga, así como a la parte central donde el presfuerzo es recto.

Figura 7: Definición del problema ${\displaystyle [cm]}$

Tabla. 2 Propiedades de los materiales

	Acero	Concreto
${\textstyle E}$	2.1${\textstyle \times 10^{6}}$ ${\textstyle kg/cm^{2}}$	2.62${\textstyle \times 10^{5}}$ ${\textstyle kg/cm^{2}}$
${\displaystyle A}$	28.8 ${\textstyle cm^{2}}$	–-
${\displaystyle t_{1}}$	–-	114 ${\textstyle cm}$
${\displaystyle t_{2}}$	–-	46 ${\textstyle cm}$

Las propiedades de los materiales se encuentran en la tabla 2 tal y como se necesitan para el análisis acoplado por elementos finitos. Hay que destacar que en esta última tabla aparecen dos espesores (${\textstyle t_{1}}$ y ${\textstyle t_{2}}$), debido a que se trata de una sección ${\textstyle T}$. Se utilizaron tres combinaciones de carga, (correspondientes a los tres ejemplos dados abajo), para validar los resultados de esta propuesta de análisis.

Figura 8: Ubicación del refuerzo ${\displaystyle [cm]}$

3.1 Ejemplo 1

Con los datos geométricos y del material proporcionados anteriormente, se procede a hacer un primer análisis considerando carga muerta ${\textstyle W_{m}}$ sobre la viga, a la cual se agrega la carga muerta puntual del segundo piso ${\textstyle P_{m}}$ más el 50% de la fuerza de presfuerzo (por cada capa, que en total son 4). Estas cargas aparecen en la tabla 3. La malla de elementos finitos utilizada para el modelo acoplado se muestra en la figura 9, con 833 nodos, 1501 elementos triangulares de 3 nodos y 420 elementos unidimensionales de 2 nodos.

Figura 9: Modelo de elementos finitos

El primer caso de carga se puede resumir como:

• Carga muerta ${\textstyle W_{m}}$ + 50% de presfuerzo + cargas puntuales del 2${\textstyle ^{do}}$ piso ${\textstyle P_{m}}$

Tabla. 3 Cargas para ejemplo 1

	Cargas	Cargas	Fuerzas
	Uniformes	Puntuales	Presfuerzo
	${\displaystyle [kg/cm]}$	${\displaystyle [kg]}$	${\displaystyle [kg]}$
Carga muerta	37	18,200	–-
Carga viva	0	0	–-
Presfuerzo	–-	–-	87,500
Totales	${\displaystyle W=}$37	${\displaystyle P=}$18,200	${\displaystyle F^{p}=}$87,500

Después de realizar el análisis con la metodología propuesta, se encuentra que el valor de los desplazamientos es de 0.16 ${\textstyle cm}$ hacia abajo en el centro del claro, y de 0.12 ${\textstyle cm}$ hacia abajo en la zona de las columnas (es decir, en la zona de las cargas puntuales). Estos resultados se muestran en la figura 10. Los resultados reportados en [27] son de 0.16 ${\textstyle cm}$ y 0.11 ${\textstyle cm}$ respectivamente.

Figura 10: Desplazamientos ${\displaystyle [cm]}$

Por otro lado, el valor del esfuerzo en la parte de arriba de la viga al centro del claro es de 45.9 ${\textstyle kg/cm^{2}}$ a compresión, mientras que en la parte baja de la viga es de 18.1 ${\textstyle kg/cm^{2}}$ (figura 11). El resultado de la referencia [27] es de 50.5 ${\textstyle kg/cm^{2}}$ y 15.9 ${\textstyle kg/cm^{2}}$ respectivamente.

Los esfuerzos correspondientes a la zona de columnas son de 41.8 ${\textstyle kg/cm^{2}}$ a compresión en la parte de arriba, mientras que se encontró un valor de 26.6 ${\textstyle kg/cm^{2}}$ en la parte de abajo. Los resultados reportados por [27] son de 44.9 ${\textstyle kg/cm^{2}}$ y 24.7 ${\textstyle kg/cm^{2}}$ respectivamente.

Figura 11: Esfuerzos ${\displaystyle [kg/cm^{2}]}$

Para este ejemplo, se puede ver como los desplazamientos son prácticamente los mismos, mientras que existen ligeras diferencias en los esfuerzos (del orden de 9% Sin embargo, la precisión del método de los elementos finitos frente a métodos simplificados nos hace pensar que nuestra aproximación es más precisa.

3.2 Ejemplo 2

Para el segundo análisis, se agregan las siguientes cargas a las ya consideradas en el ejemplo 1, es decir, se suma la carga muerta puntual del tercer piso ${\textstyle P_{m}}$ más el 33% de la fuerza de presfuerzo (por cada capa, que en total son 4). Estas cargas se aprecian en la tabla 4.

El segundo caso de carga se puede resumir como los valores mostrados a continuación, sumandos a las cargas del caso anterior:

• Se suma el 33% de presfuerzo + cargas puntuales del 3${\textstyle ^{er}}$ piso ${\textstyle P_{m}}$

Tabla. 4 Cargas para ejemplo 2

	Cargas	Cargas	Fuerzas
	Uniformes	Puntuales	Presfuerzo
	${\displaystyle [kg/cm]}$	${\displaystyle [kg]}$	${\displaystyle [kg]}$
Carga muerta	37	36,400	–-
Carga viva	0	0	–-
Presfuerzo	–-	–-	145,250
Totales	${\displaystyle W=}$37	${\displaystyle P=}$36,400	${\displaystyle F^{p}=}$145,250

Después de realizar el análisis con la metodología propuesta, se encuentra que el valor de los desplazamientos es de 0.233 ${\textstyle cm}$ hacia abajo en el centro del claro, y de 0.235 ${\textstyle cm}$ hacia abajo en la zona de las columnas (es decir, en la zona de las cargas puntuales). Estos resultados se muestran en la figura 12. Los resultados reportados en [27] son de 0.25 ${\textstyle cm}$ y 0.26 ${\textstyle cm}$ respectivamente.

Figura 12: Desplazamientos ${\displaystyle [cm]}$

Por otro lado, el valor del esfuerzo en la parte de arriba de la viga al centro del claro es de 62.1 ${\textstyle kg/cm^{2}}$ a compresión, mientras que en la parte baja de la viga es de 59.5 ${\textstyle kg/cm^{2}}$ (figura 13). El resultado de la referencia [27] es de 62.4 ${\textstyle kg/cm^{2}}$ y 59.9 ${\textstyle kg/cm^{2}}$ respectivamente.

Los esfuerzos correspondientes a la zona de columnas son de 57.7 ${\textstyle kg/cm^{2}}$ a compresión en la parte de arriba, mientras que se encontró un valor de 69.0 ${\textstyle kg/cm^{2}}$ en la parte de abajo. Los resultados reportados por [27] son de 56.8 ${\textstyle kg/cm^{2}}$ y 68.7 ${\textstyle kg/cm^{2}}$ respectivamente.

Figura 13: Esfuerzos ${\displaystyle [kg/cm^{2}]}$

Para este ejemplo, se puede ver como los esfuerzos son prácticamente los mismos, mientras que existen ligeras diferencias en los desplazamientos (del orden de 9%

3.3 Ejemplo 3

Para el tercer análisis, se agregan las siguientes cargas a las ya consideradas en el ejemplo 1 y 2, es decir, se suman las cargas vivas puntuales del segundo y tercer piso ${\textstyle P_{v}}$ más la carga viva del primer nivel, más el 17% de la fuerza de presfuerzo (por cada capa, que en total son 4). Estas cargas se aprecian en la tabla 4.

El tercer caso de carga se puede resumir como los valores mostrados a continuación, sumandos a las cargas de los casos anteriores:

• Se suma la carga viva ${\textstyle W_{v}}$ + cargas puntuales del 2${\textstyle ^{do}}$ y 3${\textstyle ^{er}}$ piso ${\textstyle P_{v}}$ + 17% del presfuerzo

Tabla. 5 Cargas para ejemplo 3

	Cargas	Cargas	Fuerzas
	Uniformes	Puntuales	Presfuerzo
	${\displaystyle [kg/cm]}$	${\displaystyle [kg]}$	${\displaystyle [kg]}$
Carga muerta	37	36,400	–-
Carga viva	22	18,200	–-
Presfuerzo	–-	–-	175,000
Totales	${\displaystyle W=}$59	${\displaystyle P=}$54,600	${\displaystyle F^{p}=}$175,000

Después de realizar el análisis con la metodología propuesta, se encuentra que el valor de los desplazamientos es de 0.72 ${\textstyle cm}$ hacia abajo en el centro del claro, y de 0.59 ${\textstyle cm}$ hacia abajo en la zona de las columnas (es decir, en la zona de las cargas puntuales). Estos resultados se muestran en la figura 14. Los resultados reportados en [27] son de 0.71 ${\textstyle cm}$ y 0.56 ${\textstyle cm}$ respectivamente.

Figura 14: Desplazamientos ${\displaystyle [cm]}$

Por otro lado, el valor del esfuerzo en la parte de arriba de la viga al centro del claro es de 102.4 ${\textstyle kg/cm^{2}}$ a compresión, mientras que en la parte baja de la viga es de 14.1 ${\textstyle kg/cm^{2}}$ (figura 15). El resultado de la referencia [27] es de 117.6 ${\textstyle kg/cm^{2}}$ y 5.8 ${\textstyle kg/cm^{2}}$ respectivamente.

Los esfuerzos correspondientes a la zona de columnas son de 95.6 ${\textstyle kg/cm^{2}}$ a compresión en la parte de arriba, mientras que se encontró un valor de 28.9 ${\textstyle kg/cm^{2}}$ en la parte de abajo. Los resultados reportados por [27] son de 108.6 ${\textstyle kg/cm^{2}}$ y 20.1 ${\textstyle kg/cm^{2}}$ respectivamente.

Figura 15: Esfuerzos ${\displaystyle [kg/cm^{2}]}$

Para este último ejemplo, se puede ver como los desplazamientos son prácticamente los mismos, mientras que existen algunos cambios en los desplazamientos. Nuevamente, la precisión del método de los elementos finitos frente a métodos simplificados nos hace pensar que nuestra aproximación es más precisa.

4 Conclusiones

En este trabajo se encontró una forma alternativa de reproducir el efecto que producen los postensados en estructuras de concreto, mediante la utilización de una formulación acoplada de sólidos bidimensionales y elementos estructurales unidimensionales en el plano. Mediante ejemplos de validación, se mostró que los resultados obtenidos son prácticamente los mismos que aquellos utilizados con formulaciones tradicionales. Esta propuesta tiene además la ventaja de que, con simples cambios en la geometría, se pueden explorar otros tipos de soluciones para una misma estructura.

Lo anterior se demostró mediante un ejemplo de aplicación con tres condiciones de carga distintas. En la formulación se usó una malla de elementos finitos con 833 nodos, 1501 elementos triangulares de 3 nodos y 420 elementos unidimensionales de 2 nodos. En el primer caso se realizó un análisis considerando carga muerta sobre la viga, a la cual se agregó la carga muerta puntual del segundo piso más el 50% de la fuerza de presfuerzo. Los resultados tanto en términos de desplazamientos, como en términos de esfuerzos son muy similares a lo reportado en la literatura, e incluso pueden ser más precisos, ya que se sabe en ingeniería estructural que el método de elementos finitos da mejores resultados que los métodos simplificados de análisis normalmente empleados por los diseñadores. De los otros dos casos de carga se obtienen conclusiones análogas.

Finalmente, se considera que la alternativa plateada en términos de métodos numéricos puede extenderse a casos más complejos y variados, pues se basa en el método de los elementos finitos, de conocido potencial para problemas poco comunes, ya que es más preciso y mucho más versátil que otros métodos simplificados para el diseño de vigas de concreto postensado y otros elementos estructurales. Por lo tanto, se considera ampliamente recomendable desarrollar investigación futura con el método propuesto para el caso de muros, losas, sistemas de soporte de aerogeneradores, y otras estructuras postensadas de común uso en ingeniería estructural.

5 Agradecimientos

Estamos agradecidos con el Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE) por proporcionarnos una licencia de su pre y post-procesador GiD [29] en nuestra Aula-CIMNE en el Departamento de Ingeniería Civil de la Universidad de Guanajuato.

BIBLIOGRAFÍA

[1] Seung-Jun Kwon and Keun-Hyeok Yang and Ju-Hyun Mun. (2018) "Flexural tests on externally post-tensioned lightweight concrete beams", Volume 164. Engineering Structures 128-140

[2] M.P. Limongelli and D. Siegert and E. Merliot and J. Waeytens and F. Bourquin and R. Vidal and V. Le Corvec and I. Gueguen and L.M. Cottineau. (2016) "Damage detection in a post tensioned concrete beam - Experimental investigation", Volume 128. Engineering Structures 15-25

[3] D. Noble and M. Nogal and A.-J. O'Connor and V. Pakrashi. (2015) "The effect of post-tensioning force magnitude and eccentricity on the natural bending frequency of cracked post-tensioned concrete beams", Volume 628. Journal of Physics: Conference Series

[4] Ho Park and Seungmin Jeong and Seong-Cheol Lee and Jae-Yeol Cho. (2016) "Flexural behavior of post-tensioned prestressed concrete girders with high-strength strands", Volume 112. Engineering Structures 90-99

[5] N.R. Brenkus and J. Tatar and H.R. Hamilton and G.R. Consolazio. (2019) "Simplified finite element modeling of post-tensioned concrete members with mixed bonded and unbonded tendons", Volume 179. Engineering Structures 387-397

[6] Min Sook Kim and Young Hak Lee. (2016) "Flexural Behavior of Posttensioned Flat Plates Depending on Tendon Layout", Volume. Hindawi Publishing Corporation Advances in Materials Science and Engineering 1-11

[7] Abbas H. Mohammed and Nildem Taysi and Dia Eddin Nassani and Ali K. Hussein. (2017) "Finite element analysis and optimization of bonded post-tensioned concrete slabs", Volume 4. Cogent Engineering

[8] Keun-Hyeok Yang and Yongjei Lee and Dae-Bong Joo. (2016) "Flexural Behavior of Post-tensioned Lightweight Concrete Continuous One-Way Slabs", Volume 10-4. International Journal of Concrete Structures and Materials 425-434

[9] B. Vakhshouri. (2018) "Experimental and numerical analysis of deflection of posttensioned lightweight concrete slabs", Volume 24. Mechanics of Advanced Materials and Structures 1-9

[10] M. Maghsoudi and A. A. Maghsoudi. (2017) "Experimental and Theoretical Serviceability of Strengthened and Nonstrengthened Unbonded Posttensioned Indeterminate I-Beams", Volume 22-7. Journal of Bridge Engineering

[11] A. Taoum and H. Jiao and D. Holloway. (2015) "Flexural behaviour of locally post-tensioned reinforced concrete beams", Volume 16-3. Australian Journal of Structural Engineering 180-186

[12] J.-W. Hwang and J.-H. Kwak and H.-G. Kwak. (2015) "Finite-Element Model to Evaluate Nonlinear Behavior of Posttensioned Composite Beams with Partial Shear Connection", Volume 141-8. Journal of Structural Engineering

[13] T. H. Kang and Y. Huang and M. Shin and J. D. Lee and A. S. Cho. (2015) "Experimental and numerical assessment of bonded and unbonded post-tensioned concrete members", Volume 112-6. ACI Structural Journal 735-748

[14] Roberto Gomez and J. Alberto Escobar and Hector Guerrero. (2017) "Instrumentation and monitoring of segmental post-tensioned girders", Volume 236. IOP Conf. Series: Materials Science and Engineering

[15] Laura Anania and Antonio Badalà and Giuseppe D'Agata. (2018) "Damage and collapse mode of existing post tensioned precast concrete bridge: The case of Petrulla viaduct", Volume 162. Engineering Structures 226-244

[16] Maximilian Fuchs and Gregor Blank and Andreas Schneider and Florian Paukner. (2017) "An integral post-tensioned concrete bridge (in German)", Volume. Verlag für Architektur und technische Wissenschaften GmbH and Co. KG

[17] Patrick Huber and Kurt Kratzer and Tobias Huber and Michael Kleiser and Johann Kollegger. (2016) "Assessment of the shear strength of an existing posttensioned concrete bridge with a low amount of shear reinforcement - First application of the "Flexural Shear Crack" model in practice (in German)", Volume. Verlag für Architektur und technische Wissenschaften GmbH and Co. KG

[18] Lukasz Slawski and Lukasz Kosno and Grzegorz Swit. (2016) "Evaluation of precast pre- post-tensioned concrete bridge beams with the use of GPR method", Volume 156. Procedia Engineering 443-450

[19] B. D. Hedegaard and C. E. W. French and C. K. Shield. (2017) "Long-Term Monitoring Strategy for Time-Dependent Deflections of Posttensioned Concrete Bridges", Volume 22-11. Journal of Bridge Engineering

[20] Tatiana García-Segura and Víctor Yepes and Julián Alcalá and Eloy Pérez-López. (2015) "Hybrid harmony search for sustainable design of post-tensioned concrete box-girder pedestrian bridges", Volume 92. Engineering Structures 112-122

[21] Tatiana García-Segura and Víctor Yepes and Dan M. Frangopol and David Y. Yang. (2017) "Lifetime reliability-based optimization of post-tensioned box-girder bridges", Volume 145. Engineering Structures 381-391

[22] Tatiana García-Segura and Víctor Yepes and Dan M. Frangopol. (2017) "Multi-objective design of post-tensioned concrete road bridges using artificial neural networks", Volume 56. Struct Multidisc Optim 139-150

[23] A. Kenna and B. Basu. (2015) "A finite element model for pre-stressed or post-tensioned concrete wind turbine towers", Volume 18. Wind Energy 1593-1610

[24] Christian Gläser and Niklas Puttendörfer and Sven Brockmann and Thomas Hartwig. (2015) "Post-Tensioning for Onshore-Wind Energy Plants - From New Construction to retrofitting of existing structures (in German)", Volume. Verlag für Architektur und technische Wissenschaften GmbH and Co. KG

[25] Eugenio Oñate. (1992) "Cálculo de Estructuras por el Método de Elementos Finitos". CIMNE

[26] Jesús Gerardo Valdés-Vázquez. (2017) "El ABC del Método de los Elementos Finitos". GEMEC - UG

[27] Prestressed-Concrete-Institute. (1983) "Fundamentals of Prestressed Concrete Design". CIMNE, 2 Edition

[28] Carlos Daniel Andrade-Moreno. (2018) "Análisis acoplado de elementos finitos sólido-estructura aplicado a vigas postensadas". Tesis de licenciatura. Universidad de Guanajuato

[29]. (2017) "GiD – The personal pre and post processor". CIMNE, 13 Edition