Revision as of 05:37, 19 October 2018 (view source) Srriverar (talk | contribs) (Created page with "<!-- metadata commented in wiki content ==Formulación Matemática y Validación Numérica de Costos de Incertidumbre para Demandas Controlables Considerando su Estocasticidad...")	Revision as of 05:42, 19 October 2018 (view source) Srriverar (talk | contribs) m (Srriverar moved page Draft Rivera 955067782 to Review 691124104615) Newer edit →
(No difference)

---

Revision as of 05:42, 19 October 2018

Abstract

This document presents an analysis in the development of a new mathematical formulation with which it will be possible to determine, through probabilistic approaches, the cost that can be generated if a diversified electricity market existed, in which the demand is able to actively participate. For this, it is considered that the electrical demand in a moment of time has associated a probability distribution and a system that makes it controllable. The cost of uncertainty of demand is mathematically developed by calculating the expected cost of supplying the most convenient demand value for the power system. The validation of the analytical formula is done through the Monte Carlo method, which allows us to compare the penalty costs in the case of underestimating or overestimating the demand for electrical energy.

Resumen. Este documento presenta un análisis en el desarrollo de una nueva formulación matemática con la cual será posible determinar, a través de enfoques probabilísticos, el costo que puede generarse si existiera un mercado eléctrico diversificado, en el cual la demanda pueda participar activamente. Para ello, se considera que la demanda eléctrica en un instante de tiempo tiene asociada cierta distribución de probabilidad y un sistema que la hace controlable. Se desarrolla matemáticamente el costo de incertidumbre de la demanda calculando el costo esperado de suplir el valor de demanda mas conveniente para el sistema de potencia. La validación de la fórmula analítica se realiza a través del método de Monte Carlo, que nos permite comparar los costos de penalización en el caso de subestimar o sobreestimar la demanda de energía eléctrica.

Controllable demand, electric market, uncertainty costs, probabilistic studies, Monte Carlo simulation.

9 Introducción

Existen formas de calcular los costos de la energía eléctrica cuando se utilizan fuentes alternativas para su producción, algunos de estos costos están asociados al tipo de tecnología utilizada para la conversión de otros tipos de energía, en energía eléctrica [1], [2], [3] Sin embargo, hay un costo que puede llegar a ser parte importante en la toma de decisiones cuando la demanda se comporta activamente en el mercado eléctrico y es el costo de incertidumbre de las demandas controlables [2].El costo de incertidumbre viene ligado a la oportunidad de entregar la energía generada a través de medios no convencionales por la red, por lo tanto, se deben conocer los diferentes tipos de componentes [1] que se pueden analizar para obtener un panorama completo de los tipos de costos por los cuales se ve influenciado el sistema eléctrico.

Otra variable que actualmente toma más fuerza y crea incertidumbre sobre un sistema de energía moderno es la incorporación de cargas controlables en la red. El comportamiento de poder de estos elementos se puede describir probabilísticamente a través del modelado matemático de los patrones de consumo. De esta manera, es posible obtener una estimación de los costos asociados con la incertidumbre de estos agentes energéticos, en particular hablando del valor esperado de una función de costo de incertidumbre. El concepto de estas funciones se exploró primero para la energía eólica en la investigación presentada en [3A]. Las primeras cargas controlables que se estudiaron con respecto al costo de incertidumbre fuerón los vehículos eléctricos (PEVs), en [3B] se presenta el estudio combinado de energía eólica y PEVs. Una aplicación del concepto para energía eólica y solar se presenta en [3C].

En los estudios mencionados anteriormente [3A]-[3C], se menciona la necesidad de ampliar el estudio de los costos de incertidumbre que se generan cuando el pronóstico de la demanda es estocástico para diferentes horas del día. Está demanda se modela a través de funciones de distribución de probabilidad y el costo de penalización se presenta al conectar generación distribuida a la red para suplir demanda o cuando no se tiene como suplir la demanda [3B]. De esta manera, se tiene que extraer energía de la red, debido a que la generación distribuida no tiene como definir su operación en términos de energía firme, y por lo tanto es difícil pronosticar cuándo y cómo será la participación para suplir la demanda. Para este caso en particular tenemos un estudio previo el cual presenta el costo de incertidumbre con una demanda fija [2].

En este estudio tenemos una idea concreta de como realizar el modelamiento y conexión de diferentes tecnologías a la red [2]. También se tienen consideraciones previas que se deben definir para poder realizar un análisis que pueda comparar los resultados como en los casos que se presentan con la generación hidráulica y térmica. Para cada uno de los casos anteriormente mencionados se tienen costos de incertidumbre por la cantidad de agua que se puede almacenar y por el tiempo de calentamiento de la planta, respectivamente. Se debe recordar que, al realizar el estudio para el caso que se presenta en varios países en vias de desarrollo [3A]-[3C], se tiene un problema debido a que la reglamentación para definir a los auto generadores todavía no está clara, por lo tanto, no se tiene certeza de cómo se van a pagar los intercambios de energía y el uso de la red para estos nuevos participantes.

De esta manera en [2], primero se definen los comportamientos de la generación distribuida en términos de la capacidad de energía que es capaz de satisfacer a través de cada tecnología, y se definen límites de sobrestimación y subestimación de la demanda a suplir. A partir de estos dos parámetros es posible modelar estáticamente la capacidad de generación a través de funciones de distribución de probabilidad (FDP), con lo cual, podemos realizar un análisis estocástico del comportamiento para el caso de generación fotovoltaica (GF), generación eólica (GE), y conexión de vehículos eléctricos a la red (VE), para este último caso en particular se tiene una mayor incertidumbre ya que estos vehículos pueden ser conectados a la red para suplir carga en cualquier momento o para ser cargados [2]. El antecedente mas reciente de costos de incertidumbre se refiere a centrales hidroeléctricas presentado en [4]

10 Estado del arte y antecedentes

10.1 Costos de Incertidumbre y su Validación Númerica

Para realizar la formulación de los costos de incertidumbre, primero hay que encontrar datos históricos del comportamiento de la fuente primaria y patrones de consumo que se utilizará para la transformación en energía eléctrica [2]-[3C]. De acuerdo a las investigaciones realizadas con respecto a los costos de incertidumbre en generación renovable, es necesario determinar la conducta de la generación en diferentes instantes de tiempo, considerando el clima de la región donde se ubica la planta de generación. Este procedimiento se hace para encontrar los puntos máximos y mínimos de generación para cualquier fuente de energía renovable no convencional. Está metodología se conoce en la literatura técnica como subestimar y sobreestimar la potencia generada por plantas las cuales dependen de factores externos como el clima, el viento, la temperatura ambiente y el caudal de los ríos [2]-[4]. Estos antecedentes se centran en la generación, y en este articulo se extenderá a las demandas eléctricas controlables.

La validación númerica de los costos de incertidumbre se realiza mendiante simulaciones de Monte Carlo. Donde el objetivo es comparar el costo esperado de la subestimación y sobreestimación dada por los escenarios de Monte Carlo y el costo esperado analítico. Las simulaciones de Monte Carlo son apropiadas para simular la variabilidad de la energía solar, eólica y recursos de vehículos eléctricos, ya que estos recursos pueden ser modelados por funciones de probabilidad conocidas [2], [4]. La novedad del enfoque propuesto es una formulación analítica para el costo de incertidumbre. Con esta formulación, es posible una evaluación determinista, a través del costo esperado para ser incluido en un despacho económico (por ejemplo, en un despacho de una microred, como en [4A], [4B]), que considere las distribuciones de probabilidad de la velocidad del viento, irradiación solar y patrones de conducción y consumo.

En este documento, las simulaciones de Monte Carlo se utilizan para simular varios escenarios de la energía inyectada o consumida de las fuentes de energía primaria mencionadas, en cada escenario se calcula un costo de penalización y, finalmente, el valor esperado del costo de penalización se obtiene utilizando el valor medio del histograma del coste de penalización. Para la demanda se supone conocida la distribución de los patrones de consumo.

10.2 Demandas Controlables y su Necesidad en los Nuevos Sistemas de Potencia

Las plantas térmicas en este momento producen gases de efecto invernadero los cuales emiten en el medio ambiente partículas que generan enfermedades y contribuyen al cambio climático, por lo cual, es necesario utilizar nuevas fuentes de generación de energía eléctrica, cómo las fuentes renovables no convencionales. Para permitir la penetración de estas nuevas tecnologías y bajar los niveles de contaminación, se necesita programar los despachos de energía de las nuevas formas de generación, con esto, se debe realizar un análisis profundo para el despacho de las fuentes renovables, sin embargo, esto no es suficiente, la demanda juega un papel importante para determinar el balance en los intercambios de energía y por consiguiente el despacho óptimo [5].

El funcionamiento de las Fuentes Renovables de Energía (FRE), muestran un problema al realizar un análisis del comportamiento de las fuentes de generación, sin embargo, una de las fuentes que presenta mayor variabilidad, por lo tanto, mayor incertidumbre, es la generación eólica, esto conlleva a la difícil incorporación de esta fuente de energía en los mercados eléctricos [6]. Existen dos formas para que la participación de la generación eólica sea eficiente en el desarrollo de los mercados eléctricos, la primera es hacer programable el despacho de las plantas eólicas, el segundo es la no programación del despacho para estas plantas. Una de las frmas de atacar esta intermitencia es mediante la gestión de la demanda.

La respuesta de la demanda ha sido una de las soluciones propuestas para mantener el balance entre la demanda y la generación, sin embargo, algunas de estas soluciones no están directamente ligadas a las transferencias de energía, ni a la atención de la demanda, sino al mercado financiero de intercambios de energía [6], por lo tanto, la forma en la que se tranza la energía ha dado al sistema una manera de controlar el balance de energía, haciendo que los precios en los mercados reflejen de manera real las posiciones de los generadores y la demanda.

Para predecir el comportamiento de la demanda se debe tener en cuenta tanto la situación económica del país como la ubicación geográfica y su desarrollo industrial, algunos de los estudios para determinar estos comportamientos se basan en realizar o utilizar modelos de regresión lineal, sin embargo, esto no es suficiente para determinar el comportamiento. En varios paises el clima afecta directamente el consumo de energía eléctrica, y debido a la alta dependencia de la generación hidráulica los precios pueden aumentar en épocas de sequía, y la demanda puede presentar comportamientos erráticos como los vistos en zonas donde existen estaciones climáticas, por lo tanto, se deben encontrar algunos patrones que permitan definir algunos límites en la conducta que tiene la demanda [7].

De esta manera una solución viable para operar los nuevos sistemas de potencia que tienen alta penetración de energía renovable es también utilizando demandas controlables. Estas son demandas capaces de adaptar lo que necesitan de la red en un instante de tiempo determinado [8], [9]. Para ello deben contar con un backup capaz de suplir lo faltante en caso que el operador de red suministre en el nodo de demanda menos de lo que se necesita. O el backup también debe ser capaz de almacenar energía en caso que el operador de red suministre mas de lo que necesita.

11 Formulación para Costos de Incertidumbre en Demanda Controlable

Para definir el comportamiento de la demanda en términos de funciones de distribución de probabilidad se tiene la función normal [8] y la función beta [9], además se presenta la formulación analítica correspondiente para determinar los costos de penalización para cada caso:

• Costo de penalización debido a subestimar

Este costo de penalización se presenta por subestimar la potencia que es capaz de demandar el usuario, en otras palabras el generador de energía eléctrica no es capaz de suplir la cantidad de energía que el usuario necesita, por lo tanto, se debe aplicar una penalización por no atender toda la demanda. Sin embargo, puede ocurrir un segundo escenario, el cual representaría un contrato entre el generador de energía eléctrica y la demanda, donde esta última se compromete a no sobrepasar un límite de potencia, potencia contratada. Este caso es el que vamos a abordar debido a que se necesita realizar un análisis donde la demanda o el usuario no cumple con los contratos de energía bilaterales, entonces se debe penalizar a la demanda y por esto se debe encontrar el costo de penalización asociado.

En términos de la potencia demandada, tenemos el costo por subestimar representado como:

${\displaystyle W_{s,i}<W_{c,d}{33-1}}$

(1)

Donde ${\textstyle W_{s,i}}$ es la potencia programada por el modelo del despacho económico y ${\textstyle W_{c,d}}$ es la potencia contratada por la demanda.

• Costo de penalización debido a sobrestimar

Este costo de penalización se presenta por sobrestimar la demanda de energía eléctrica, por lo tanto, cuando se realiza el despacho de energía, al generador que suple esa carga puede sobrarle enegía ya que la demanda o el usuario no fue capaz de preveer la cantidad real de energía que se prentendía consumir y por la cual se realizó el contrato.

En términos de la potencia demandada, tenemos el costo por sobrestimar representado como:

${\displaystyle W_{c,d}<W_{s,i}{33-2}}$

(2)

Donde ${\textstyle W_{s,i}}$ es la potencia programada por el modelo del despacho económico y ${\textstyle W_{c,d}}$ es la potencia contratada por la demanda.

• Formulación Matemática de los Costos por Subestimar

Se realiza una aproximación a través de una función lineal para calcular los costos de penalización por subestimar la demanda de energía eléctrica.

${\displaystyle C_{u,i}(W_{s,i},W_{c,d})=C_{u,i}(W_{c,d}-W_{s,i}){33-3}}$

(3)

Donde:

• ${\textstyle C_{u,i}}$ se tiene como coeficiente del costo de penalización por subestimar.
• ${\textstyle C_{u,i}(W_{s,i},W_{c,d})}$ se denomina función de costo debido a subestimar.

A través de estos términos se puede determinar el costo de penalización como:

${\displaystyle E[C_{u,i}(W_{s,i},W_{c,d})]=\int _{W_{s,i}}^{W_{\infty ,i}}C_{u,i}(W_{c,d}-W_{s,i})\cdot f_{W}(W_{c,d})\cdot dW_{c,d}{33-4}}$

(4)

Donde:

• ${\textstyle E[C_{u,i}(W_{s,i},W_{c,d})]}$ es el valor esperado de los costos por subestimar.
• ${\textstyle f_{W}(W_{c,d})}$ es la FDP que determina el comportamiento de la demanda.
• ${\textstyle {W_{\infty ,i}}}$ es la potencia máxima suministrada por el generador i.

• Formulación Matemática de los Costos por Sobrestimar

Se realiza una aproximación a través de una función lineal para calcular los costos de penalización por sobrestimar la demanda de energía eléctrica.

${\displaystyle C_{o,i}(W_{s,i},W_{c,d})=C_{o,i}(W_{s,i}-W_{c,d}){33-5}}$

(5)

Donde:

• ${\textstyle C_{o,i}}$ se tiene como coeficiente del costo de penalización por sobrestimar.
• ${\textstyle C_{o,i}(W_{s,i},W_{c,d})}$ se denomina función de costo debido a sobrestimar.

A través de estos términos se puede determinar el costo de penalización como:

${\displaystyle E[C_{o,i}(W_{s,i},W_{c,d})]=\int _{W_{min,i}}^{W_{s,i}}C_{o,i}(W_{s,i}-W_{c,d})\cdot f_{W}(W_{c,d})\cdot dW_{c,d}{33-6}}$

(6)

Donde:

• ${\textstyle E[C_{o,i}(W_{s,i},W_{c,d})]}$ es el valor esperado de los costos por sobrestimar.
• ${\textstyle f_{W}(W_{c,d})}$ es la FDP que determina el comportamiento de la demanda.
• ${\textstyle {W_{\infty ,i}}}$ es la potencia mínima suministrada por el generador i.

11.1 Desarrollo Analítico de los Costos para la Demanda (FDP NORMAL)

El comportamiento de la demanda de energía eléctrica en la red se puede representar a través de FDP con una función normal, que se presenta a continuación:

${\displaystyle f_{Pe}(Pe)={\frac {1}{\sqrt {2\pi \phi ^{2}}}}*e^{{\bigg (}{\frac {P_{e}-\mu }{{\sqrt {2}}\phi }}{\bigg )}^{2}}{33-7}}$

(7)

Donde ${\textstyle f_{Pe}}$ es la FDP de la demanda, ${\textstyle P_{e}}$ representa la potencia demandada, ${\textstyle \mu }$ y ${\textstyle \phi }$ son la media y la desviación estándar respectivamente del comportamiento probabilístico.

Se desarrolla la siguiente integral para relacionar el costo de penalización debido a subestimar la demanda con su respectiva FDP.

• Costo de penalidad por subestimar la demanda de energía eléctrica

${\displaystyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]=\int _{P_{e,s,i}}^{P_{e,\infty }}C_{e,u,i}\cdot (P_{e,i}-P_{e,s,i})\cdot f_{P_{e}}(P_{e})\cdot dP_{e,i}{33-8}}$

(8)

Donde:

• ${\textstyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]}$ es el valor esperado para el costo de penalidad debido a la subestimación en la demanda.
• ${\textstyle f_{P_{e}}(P_{e})}$ Es la FDP de la potencia de la demanda en el nodo i.
• ${\textstyle C_{e,u,i}}$ Es el coeficiente del costo de penalidad a través de la subestimación en la demanda en el nodo i.
• ${\textstyle {P_{e,\infty }}}$ Es la potencia máxima de salida causada por la demanda en el nodo i.
• ${\textstyle P_{e,s,i}}$ Es la potencia programada para modelar la demanda en el nodo i.
• ${\textstyle P_{e,i}}$ Es la potencia entregada por un generador en el nodo i.

Para determinar el costo de penalización reemplazamos 33-7 en la ecuación 33-8 y comenzamos con el desarrollo de la integral:

${\displaystyle E[C_{e,u,i}(P_{e,i},P_{e,s,i}]=\int _{P_{e,s,i}}^{P_{e,\infty }}C_{e,u,i}(P_{e,i}-P_{e,s,i})\cdot {\frac {1}{\sqrt {2\pi \phi ^{2}}}}\cdot e^{-{\bigg (}{\frac {P_{e}-\mu }{{\sqrt {2}}\cdot \phi }}{\bigg )}^{2}}\cdot dP_{e,i}{33-9}}$

(9)

Para el desarrollo, primero utilizamos el teorema de cambio de variable para reducir la integral:

${\displaystyle U={\frac {P_{e,i}-\mu }{{\sqrt {=}}\cdot \phi }}\longrightarrow P_{e,i}=U\cdot {\sqrt {=}}\cdot \phi +\mu {33-10}}$

(10)

${\displaystyle dU={\frac {dP_{e,i}}{{\sqrt {=}}\cdot \phi }}\longrightarrow dP_{e,i}=dU\cdot {\sqrt {=}}\cdot \phi {33-11}}$

(11)

Debido al cambio de variable se hace necesario cambiar los límites de integración a las nuevas variables:

Failed to parse (unknown function "\enspace"): Si \enspace P_{e,i} = P_{e,s,i} \longrightarrow U_{a} = \frac{P_{e,s,i} - \mu }{\sqrt= \cdot \phi } {33-12}

(12)

Failed to parse (unknown function "\enspace"): Si \enspace P_{e,i} = \infty ^+ \longrightarrow U_{b} = \frac{\infty ^+ - \mu }{\sqrt= \cdot \phi } {33-13}

(13)

A través del cambio de variable se procede a desarrollar la ecuación 33-9.

${\displaystyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]=\int _{U_{a}}^{U_{b}}C_{e,u,i}(U\cdot {\sqrt {=}}\cdot \phi +\mu -P_{e,s,i})\cdot {\frac {1}{{\sqrt {=}}\phi }}\cdot e^{-U^{2}}\cdot {\sqrt {=}}\cdot \phi \cdot dU{33-14}}$

(14)

${\displaystyle =\int _{U_{a}}^{U_{b}}C_{e,u,i}{\bigg (}{\frac {{\sqrt {=}}\cdot \phi }{\sqrt {=}}}\cdot Ue^{-U^{2}}\cdot dU{\bigg )}+\int _{U_{a}}^{U_{b}}C_{e,u,i}{\frac {(\mu -P_{e,s,i})}{\sqrt {=}}}\cdot e^{-U^{2}}\cdot dU{33-15}}$

(15)

Para la primera parte de la integral se tiene el siguiente resultado:

${\displaystyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]=C_{e,u,i}{\frac {\sqrt {=}}{\sqrt {=}}}\cdot \phi \cdot {\frac {1}{2}}\cdot {\bigg (}e^{-U_{a}^{2}}-e^{-U_{b}^{2}}{\bigg )}{33-16}}$

(16)

Para el caso del desarrollo de la función ${\textstyle e^{-U^{2}}}$ de la segunda parte de la integral utilizamos la función error, con la cual se puede resolver esta parte de la ecuación.

Entonces:

${\displaystyle e^{-U^{2}}={\frac {\sqrt {=}}{2}}\cdot erf(x)+C{33-17}}$

(17)

Al reemplazar en la segunda parte de la integral, tenemos:

${\displaystyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]=C_{e,u,i}{\frac {(\mu -P_{e,s,i})}{\sqrt {=}}}\cdot {\bigg (}erf(U_{b})-erf(U_{a}){\bigg )}{33-18}}$

(18)

Al final el resultado de la ecuación 33-15 realizando el cambio de variable, es:

${\displaystyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]=C_{e,u,i}\cdot (\mu -P_{e,s,i})\cdot {\bigg (}1+erf{\bigg (}{\frac {\mu -P_{e,s,i}}{{\sqrt {=}}\cdot \phi }}{\bigg )}{\bigg )}+{\frac {C_{e,u,i}\cdot \phi }{\sqrt {=}}}\cdot e^{-{\bigg (}{\frac {\mu {-}P_{e,s,i}}{{\sqrt {2}}\cdot \phi }}{\bigg )}^{2}}{33-19}}$

(19)

• Costo de penalidad por sobrestimar la demanda de energía eléctrica

${\displaystyle E[C_{e,o,i}(P_{e,i},P_{e,s,i})]=\int _{0}^{P_{e,s,i}}C_{e,o,i}\cdot (P_{e,s,i}-P_{e,i})\cdot f_{P_{e}}(P_{e})\cdot dP_{e,i}{33-20}}$

(20)

Donde:

• ${\textstyle E[C_{e,o,i}(P_{e,i},P_{e,s,i})]}$ es el valor esperado para el costo de penalidad debido a la sobrestimación en la demanda.
• ${\textstyle f_{P_{e}}(P_{e})}$ Es la FDP de la potencia de la demanda en el nodo i.
• ${\textstyle C_{e,u,i}}$ Es el coeficiente del costo de penalidad a través de la subestimación en la demanda en el nodo i.
• ${\textstyle P_{e,s,i}}$ Es la potencia programada para modelar la demanda en el nodo i.
• ${\textstyle P_{e,i}}$ Es la potencia entregada por un generador en el nodo i.

Para determinar el costo de penalización reemplazamos 33-7 en la ecuación 33-20 y comenzamos con el desarrollo de la integral:

${\displaystyle E[C_{e,o,i}(P_{e,i},P_{e,s,i}]=\int _{0}^{P_{e,s,i}}C_{e,o,i}(P_{e,s,i}-P_{e,i})\cdot {\frac {1}{\sqrt {2\pi \phi ^{2}}}}\cdot e^{-{\bigg (}{\frac {P_{e,i}-\mu }{{\sqrt {2}}\cdot \phi }}{\bigg )}^{2}}\cdot dP_{e,i}{33-21}}$

(21)

Para el desarrollo, primero utilizamos el teorema de cambio de variable para reducir la integral:

${\displaystyle U={\frac {P_{e,i}-\mu }{{\sqrt {=}}\cdot \phi }}\longrightarrow P_{e,i}=U\cdot {\sqrt {=}}\cdot \phi +\mu {33-22}}$

(22)

${\displaystyle dU={\frac {dP_{e,i}}{{\sqrt {=}}\cdot \phi }}\longrightarrow dP_{e,i}=dU\cdot {\sqrt {=}}\cdot \phi {33-23}}$

(23)

Debido al cambio de variable se hace necesario cambiar los límites de integración a las nuevas variables:

Failed to parse (unknown function "\enspace"): Si \enspace P_{e,i} = 0 \longrightarrow U_{a} = \frac{0 - \mu }{\sqrt= \cdot \phi } {33-24}

(24)

Failed to parse (unknown function "\enspace"): Si \enspace P_{e,i} = P_{e,s,i} \longrightarrow U_{b} = \frac{P_{e,s,i} - \mu }{\sqrt= \cdot \phi } {33-25}

(25)

A través del cambio de variable se procede a desarrollar la ecuación 33-21.

${\displaystyle E[C_{e,o,i}(P_{e,i},P_{e,s,i})]=\int _{U_{a}}^{U_{b}}C_{e,o,i}(P_{e,s,i}-U\cdot {\sqrt {=}}\cdot \phi -\mu )\cdot {\frac {1}{{\sqrt {=}}\phi }}\cdot e^{-U^{2}}\cdot {\sqrt {=}}\cdot \phi \cdot dU{33-26}}$

(26)

${\displaystyle =\int _{U_{a}}^{U_{b}}C_{e,o,i}{\frac {(P_{e,s,i}-\mu )}{\sqrt {=}}}\cdot e^{-U^{2}}\cdot dU-\int _{U_{a}}^{U_{b}}C_{e,o,i}{\bigg (}{\frac {{\sqrt {=}}\cdot \phi }{\sqrt {=}}}\cdot Ue^{-U^{2}}\cdot dU{\bigg )}{33-27}}$

(27)

Para el caso del desarrollo de la función ${\textstyle e^{-U^{2}}}$ de la primera parte de la integral utilizamos la función error, con la cual se puede resolver esta parte de la ecuación. Entonces:

${\displaystyle e^{-U^{2}}={\frac {\sqrt {=}}{2}}\cdot erf(x)+C{33-28}}$

(28)

Al reemplazar en la primera parte de la integral, tenemos:

${\displaystyle E[C_{e,o,i}(P_{e,i},P_{e,s,i})]=C_{e,o,i}{\frac {(P_{e,s,i}-\mu )}{2}}\cdot {\bigg (}erf(U_{b})-erf(U_{a}){\bigg )}{33-29}}$

(29)

Para la segunda parte de la integral se tiene el siguiente resultado:

Failed to parse (unknown function "\enspace"): E[C_{e,o,i}(P_{e,i},P_{e,s,i})] = - \enspace C_{e,o,i} \frac{\phi }{\sqrt=} \cdot \bigg(e^{-U_{a}^2} - e^{-U_{b}^2} \bigg) {33-30}

(30)

Al final el resultado de la ecuación 33-27 realizando el cambio de variable, es:

${\displaystyle E[C_{e,o,i}(P_{e,i},P_{e,s,i})]=}$ ${\displaystyle =C_{e,o,i}\cdot {\frac {(P_{e,s,i}-\mu )}{2}}\cdot {\bigg (}erf{\bigg (}{\frac {\mu }{{\sqrt {=}}\cdot \phi }}{\bigg )}-erf{\bigg (}{\frac {\mu -P_{e,s,i}}{{\sqrt {=}}\cdot \phi }}{\bigg )}{\bigg )}}$ Failed to parse (unknown function "\enspace"): + \enspace C_{e,o,i}\cdot \frac{\phi }{\sqrt=} \cdot \bigg(e^{-\bigg(\frac{P_{e,s,i} - \mu }{\sqrt= \cdot \phi }\bigg)^2} -e^{\bigg(-\frac{\mu }{\sqrt= \cdot \phi }\bigg)}\bigg) {33-31}

(31)

Por lo tanto, es posible obtener el costo de incertidumbre para el caso de la demanda como la suma de 33-19 y 33-31.

11.2 Desarrollo Analítico de los Costos para la Demanda (FDP BETA)

El comportamiento de la demanda de energía eléctrica en la red se puede representar a través de FDP con una función beta, que se presenta a continuación:

${\displaystyle f_{Pe}(Pe)={\frac {\Gamma (\alpha {-\beta })}{\Gamma (\alpha )\cdot \Gamma (\beta )}}\cdot (P_{e,i})^{\alpha {-1}}\cdot (1-P_{e,i})^{\beta {-1}}{33-32}}$

(32)

Donde ${\textstyle \Gamma }$ representa la función gama, ${\textstyle \alpha }$ y ${\textstyle \beta }$ son dos parámetros que varían entre 0 y 1, y ${\textstyle P_{e,i}}$ es la potencia demandada.

Se desarrolla la siguiente integral para relacionar el costo de penalización debido a subestimar la demanda con su respectiva FDP.

• Costo de penalidad por subestimar la demanda de energía eléctrica

${\displaystyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]=\int _{P_{e,s,i}}^{P_{e,\infty }}C_{e,u,i}\cdot (P_{e,i}-P_{e,s,i})\cdot f_{P_{e}}(P_{e})\cdot dP_{e,i}{33-33}}$

(33)

Donde:

• ${\textstyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]}$ es el valor esperado para el costo de penalidad debido a la subestimación en la demanda.
• ${\textstyle f_{P_{e}}(P_{e})}$ Es la FDP de la potencia de la demanda en el nodo i.
• ${\textstyle C_{e,u,i}}$ Es el coeficiente del costo de penalidad a través de la subestimación en la demanda en el nodo i.
• ${\textstyle {P_{e,\infty }}}$ Es la potencia máxima de salida causada por la demanda en el nodo i.
• ${\textstyle P_{e,s,i}}$ Es la potencia programada para modelar la demanda en el nodo i.
• ${\textstyle P_{e,i}}$ Es la potencia entregada por un generador en el nodo i.

Para determinar el costo de penalización reemplazamos 33-32 en la ecuación 33-33 y comenzamos con el desarrollo de la integral:

Forma general:

${\displaystyle E[C_{e,u,i}(P_{e,i},P_{e,s,i})]=\int _{P_{e,s,i}}^{P_{e,\infty }}C_{e,u,i}\cdot (P_{e,i}-P_{e,s,i})\cdot {\frac {\Gamma (\alpha {-\beta })}{\Gamma (\alpha )\cdot \Gamma (\beta )}}\cdot (P_{e,i})^{\alpha {-1}}\cdot (1-P_{e,i})^{\beta {-1}}\cdot dP_{e,i}{33-34}}$

(34)

Desarrollando se tiene una forma generalizada de la función hipergeométrica con la cual se aproxima el resultado:

${\displaystyle {\frac {C_{k+1}}{C_{k}}}={\frac {P(k)}{Q(k)}}={\frac {(k+a_{1})(k+a_{2})...(k+a_{p})}{(k+b_{1})(k+b_{2})...(k+b_{q})(k+1)}}\cdot x.{33-35}}$

(35)

El factor de ${\textstyle k+1}$ en el denominador se presenta como razón de notación histórica.

La función ${\textstyle 2f_{1}(a,b;c;x)}$ correspondiente a p = 2, q = 1 es la primera función hipergeométrica que se estudiará, debido a que es la más frecuente en problemas físicos.

Las funciones hipergeométricas son soluciones de la ecuación diferencial hipergeométrica, la cual tiene un punto regular singular en el origen. Para derivar la función hipergeométrica de la ecuación diferencial hipergeométrica se tiene:

Failed to parse (unknown function "\enspace"): z(1-z)\enspace y'' + [c-(a+b+1)z]\enspace y' -aby = 0 {33-36}

(36)

El método de Frobenius permite crear una solución en serie de potencias de esa ecuación diferencial, con Failed to parse (unknown function "\enspace"): p(z) \enspace y \enspace q(z)

analíticas en 0 o, siendo analíticas, si sus límites en 0 existen (si son finitos).

Se usa el método de Frobenius para reducir la expresión:

Failed to parse (unknown function "\enspace"): \sum _{n=0}^{\infty } \bigg[(n+1) \cdot (n+c)\enspace A_{n+1} - \bigg[n^2 + (a+b)\enspace n + a\cdot b \bigg]A_{n}\bigg]\cdot z^n = 0 {33-37}

(37)

Teniendo la ecuación inicial:

${\displaystyle A_{n+1}={\frac {(n+a)(n+b)}{(n+1)(n+c)}}\cdot A_{n}{33-38}}$

(38)

Utilizando la solución de series de potencia:

${\displaystyle y=\sum _{n=0}^{\infty }A_{z}\cdot z^{n}{33-39}}$

(39)

Entonces tenemos la solución:

${\displaystyle y=A_{0}\cdot {\bigg [}1+{\frac {a\cdot b}{1!\cdot c}}\cdot z+{\frac {a\cdot (a+1)b\cdot (b+1)}{2!\cdot c\cdot (c+1)}}\cdot z^{2}+...{\bigg ]}.{33-40}}$

(40)

Esta es la llamada solución regular, denotada como:

${\displaystyle F_{1}(a,b;c;z)=1+{\frac {a\cdot b}{1!\cdot c}}\cdot z+{\frac {a\cdot (a+1)b\cdot (b+1)}{2!\cdot c\cdot (c+1)}}\cdot z^{2}+...}$ ${\displaystyle =\sum _{n=0}^{\infty }{\frac {(a)_{n}\cdot (b)_{n}}{(c)_{n}}}\cdot {\frac {z^{n}}{n!}}{33-41}}$

(41)

La cual converge si c no es un entero negativo (1) para todo ${\textstyle \mid z\mid <1}$ y (2) en el circulo unitario Failed to parse (unknown function "\enspace"): {\textstyle \mid z \mid = 1 \enspace si \enspace R\enspace [c-a-b]>0}

. Aquí, ${\textstyle (a)_{n}}$ es un símbolo de Pochhammer. El simbolo de Pochhammer introducido por Leo August Pochhammer es la notación ${\displaystyle (x)_{n}}$ donde n es un entero no negativo.

Por lo tanto el resultado final de la expresión es:

${\displaystyle \int _{P_{e,s,i}}^{P_{e,\infty }}C_{e,u,i}\cdot (P_{e,i}-P_{e,s,i})\cdot {\frac {\Gamma (\alpha {-\beta })}{\Gamma (\alpha )\cdot \Gamma (\beta )}}\cdot (P_{e,i})^{\alpha {-1}}\cdot (1-P_{e,i})^{\beta {-1}}\cdot dP_{e,i}}$ Failed to parse (unknown function "\enspace"): = -\frac{(P_{e,i})^\alpha \cdot ((1+\alpha )\cdot P_{e,s,i}\cdot Hypergeometric\enspace 2F1 [a,-b,1+a,x]}{\alpha \cdot (1+\alpha )} \enspace + Failed to parse (unknown function "\enspace"): \frac{\alpha \cdot (-1+P_{e,s,i})\cdot x \cdot Hypergeometric\enspace 2F1 [a,-b,1+a,x]}{\alpha \cdot (1+\alpha )} {33-42}

(42)

El cual representa el costo por subestimar la demanda con la función de distribución de probabilidad beta.

• Costo de penalidad por sobrestimar la demanda de energía eléctrica

${\displaystyle E[C_{e,o,i}(P_{e,i},P_{e,s,i})]=\int _{0}^{P_{e,s,i}}C_{e,o,i}\cdot (P_{e,s,i}-P_{e,i})\cdot f_{P_{e}}\cdot (P_{e})\cdot dP_{e,i}{33-43}}$

(43)

Donde:

• ${\textstyle E[C_{e,o,i}(P_{e,i},P_{e,s,i})]}$ es el valor esperado para el costo de penalidad debido a la sobrestimación en la demanda.
• ${\textstyle f_{P_{e}}(P_{e})}$ Es la FDP de la potencia de la demanda en el nodo i.
• ${\textstyle C_{e,u,i}}$ Es el coeficiente del costo de penalidad a través de la subestimación en la demanda en el nodo i.
• ${\textstyle P_{e,s,i}}$ Es la potencia programada para modelar la demanda en el nodo i.
• ${\textstyle P_{e,i}}$ Es la potencia entregada por un generador en el nodo i.

Para determinar el costo de penalización reemplazamos 33-32 en la ecuación 33-43 y comenzamos con el desarrollo de la integral:

Forma general:

${\displaystyle E[C_{e,o,i}(P_{e,i},P_{e,s,i})]=\int _{0}^{P_{e,s,i}}C_{e,o,i}\cdot (P_{e,s,i}-P_{e,i})\cdot {\frac {\Gamma (\alpha {-\beta })}{\Gamma (\alpha )\cdot \Gamma (\beta )}}\cdot (P_{e,i})^{\alpha {-1}}\cdot (1-P_{e,i})^{\beta {-1}}\cdot dP_{e,i}{33-44}}$

(44)

Se utilizan las ecuaciones presentadas para el análisis de la función hipergeométrica desde la ecuación 33-35 hasta la ecuación 33-41.

Finalmente el costo por subestimar la demanda con la función de distibución beta es:

${\displaystyle \int _{P_{e,s,i}}^{P_{e,\infty }}C_{e,u,i}\cdot (P_{e,i}-P_{e,s,i})\cdot {\frac {\Gamma (\alpha {-\beta })}{\Gamma (\alpha )\cdot \Gamma (\beta )}}\cdot (P_{e,i})^{\alpha {-1}}\cdot (1-P_{e,i})^{\beta {-1}}\cdot dP_{e,i}}$ Failed to parse (unknown function "\enspace"): = (P_{e,i})^\alpha \cdot \bigg[-\frac{P_{e,s,i}\cdot Hypergeometric\enspace 2F1 [a,-b,1+a,x]}{\alpha } \enspace + Failed to parse (unknown function "\enspace"): \frac{(-1+P_{e,s,i})\cdot x \cdot Hypergeometric\enspace 2F1 [a,-b,1+a,x]}{(1+\alpha )}\bigg] {33-45}

(45)

12 Validación Númerica con Simulación de Monte Carlo

Se presenta la metodología con la cual se desarrollo la validación de los resultados reportados a continuación (subsecciones A y B). Para este caso se realizarón un total de 25 simulaciones para encontrar el error para un caso en particular con cada función de distribución de probabilidad.

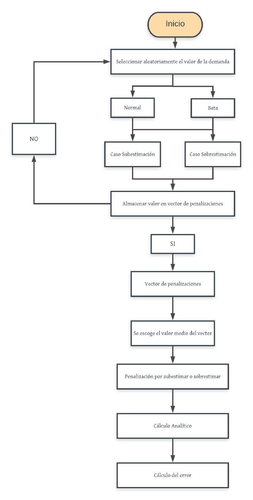
Figure 1: Diagrama de flujo para la validación de resultados

12.1 FUNCIÓN DE DISTRIBUCIÓN NORMAL

• Caso 1: El costo de incertidumbre hallado analíticamente fue de $ 317.5790. En este caso se supone que la demanda tiene un valor medio (${\textstyle \mu }$) de 19.54 MW y un desviación estandar (${\textstyle \phi }$) de 0.54 MW. La potencia programada (${\textstyle P_{e,s}}$) es 18.5 MW. En la tabla 1 se presentan los 25 casos simulados, y en la figura 2 la comparación entre el método analítico y la simulación de Monte Carlo.

Table. 1 Resultados Simulación Caso 1, Distribución Normal

Simulación	Monte Carlo	Simulación	Monte Carlo
1	318.2913	14	318.0775
2	317.9161	15	317.3798
3	318.4017	16	318.9341
4	317.3396	17	317.4439
5	317.5135	18	317.4791
6	317.2197	19	317.2286
7	317.9858	20	317.6289
8	318.7582	21	317.5556
9	316.8641	22	318.3687
10	317.9871	23	317.6681
11	317.3757	24	317.3042
12	317.3007	25	318.2144
13	318.7174

1

Figure 2: Comparación Costos para el Caso 1, Distribución Normal

En la tabla 2T el error porcentual en los 25 casos, y la tabla 3T el análisis estadístico.

Table. 2 Error Calculado, Caso 1, Distribución Normal

Simulación	Error (%)	Simulación	Error (%)
1	0.223789	14	0.156723
2	0.106034	15	0.062764
3	0.258384	16	0.424884
4	0.075440	17	0.042559
5	0.020629	18	0.031467
6	0.113265	19	0.110457
7	0.127930	20	0.015710
8	0.369936	21	0.007369
9	0.225617	22	0.248046
10	0.128339	23	0.028048
11	0.064057	24	0.086605
12	0.087709	25	0.199677
13	0.357182

2T

     

Table. 3 Datos Estadísticos, Error Calculado, Caso 1, Distribución Normal

Varianza	0.013770
Media	0.094694
Promedio	0.142905
Desviación Estándar	0.117344

3T

Las figuras 3 y 4 presentan los histogramas de los escenarios simulados de Monte Carlo.

Figure 3: Escenarios para la potencia, costos de subestimación y sobrestimación, Caso 1, Función Normal.

Figure 4: Costo de incertidumbre (UCF), bajo los parámetros de simulación, Caso 1, Función Normal.

12.2 FUNCIÓN DE DISTRIBUCI BETA

• Caso 1: El costo de incertidumbre hallado analíticamente fue de $ 181.4107. En este caso se supone que la demanda puede variar entre 0 y 1 MW; y los parametrs de la disribuci´n beta son: ${\textstyle \alpha }$=2 y ${\textstyle \beta }$=1.5. La potencia programada (${\textstyle P_{e,s}}$) es 0.9 MW. En la tabla 4T se presentan los 25 casos simulados, y en la figura 5 la comparación entre el método analítico y la simulación de Monte Carlo.

 

Table. 4 Resultados Simulación Caso 1, Distribución Beta

Simulación	Monte Carlo	Simulación	Monte Carlo
1	181.4460	14	181.4098
2	181.4191	15	181.4099
3	181.3914	16	181.3515
4	181.3818	17	181.3818
5	181.4180	18	181.4601
6	181.4480	19	181.4114
7	181.4148	20	181.4097
8	181.4163	21	181.3926
9	181.3573	22	181.4198
10	181.4730	23	181.4055
11	181.4235	24	181.4310
12	181.4277	25	181.4227
13	181.3645

4T

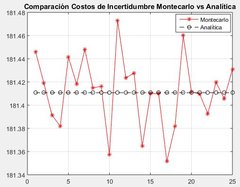
Figure 5: Comparación Costos para el Caso 1, Distribución Beta

En la tabla 5-17 el error porcentual en los 25 casos, y la tabla 5-18 el análisis estadístico.

Table. 5 Error Calculado, Caso 1, Distribución Beta

Simulación	Error (%)	Simulación	Error (%)
1	0.019455	14	0.025474
2	0.004630	15	0.000496
3	0.010640	16	0.000441
4	0.015933	17	0.032644
5	0.016920	18	0.015933
6	0.004024	19	0.027224
7	0.020557	20	0.000386
8	0.002260	21	0.000551
9	0.003087	22	0.009978
10	0.029445	23	0.005016
11	0.034330	24	0.002867
12	0.007055	25	0.011189
13	0.009370

5-17

Table. 6 Datos Estadísticos, Error Calculado, Caso 1, Distribución Beta

Varianza	0.000117
Media	0.006564
Promedio	0.012396
Desviación Estándar	0.010833

5-18

Las figuras 6 y 7 presentan los histogramas de los escenarios simulados de Monte Carlo.

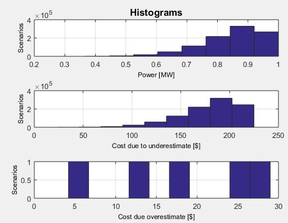
Figure 6: Escenarios para la potencia, costos de subestimación y sobrestimación, Caso 1, Función Beta.

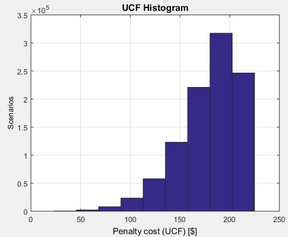
Figure 7: Costo de incertidumbre (UCF), bajo los parámetros de simulación, Caso 1, Función Beta.

13 Análisis de Resultados y Conclusiones

El principal resultado encontrado en esta investigación es la formulación matemática del costo de incertidumbre de cargas controlables. El costo de incertidumbre evaluad con la formula analítica resulta ser el mismo que el costo esperad de las simulaciones de Monte Carlo. Las conclusiones de este estudio son:

• A través del modelamiento de la demanda con funciones de distribución de probabilidad es posible encontrar un patrón de consumo, que permite definir los costos de incertidumbre que se generan en el sistema por la subestimación y la sobrestimación de la demanda de energía eléctrica.
• Es posible encontrar valores muy cercanos a las simulaciones a través de la formulación analática, como se puede ver a través de los resultados, los valores encontrados se aproximan al método de Monte Carlo, por lo tanto, se tiene una nueva herramienta para definir los costos de incertidumbre sin emplear grandes tiempos de simulación.
• Con la formulación analítica presentada se pueden hallar los costos de incertidumbre por subestimar o sobrestimar a la demanda de energía eléctrica, sin diferenciar esta y teniendo rangos amplios para el modelamiento de cualquier tipo de demanda.
• Con el modelamiento de la demanda de energía eléctrica a través de las funciones de distribución normal y beta, se demostró que el algoritmo desarrollado es capaz de adaptarse a cualquier tipo de variación de la demanda y que no se tienen errores significativos en la adquisición de resultados.
• Se ha encontrado una manera simple y sencilla de definir el costo de penalización que debe ser asumido por el sistema o la demanda cuando alguno de las partes falla en los compromisos adquiridos en el mercado de energía eléctrica.
• Las variaciones de los datos de simulación y del error encontradas son menores al 1%, evidenciando la facilidad y utilidad de la formula analítica desarrollada en este documento.

BIBLIOGRAPHY

[3] 1 V. Siriariyaporn, D. J. Gotham, and F. T. Sparrow, "Determining the cost of uncertainty to electric utilities in serving highly varying loads," Electr. Util. Deregulation, Restruct. Power Technol. 2004. (DRPT 2004). Proc. 2004 IEEE Int. Conf., vol. 2, no. April, p. 580–585 Vol.2, 2004. [4] 2 F. Santos, J. Arévalo and S. Rivera, "Uncertainty Cost Functions for Solar Photovoltaic Generation, Wind Energy, and Plug-In Electric Vehicles: Mathematical Expected Value and Verification by Monte Carlo Simulation," International Journal of Power and Energy Conversion (in press) 2019. [5] 3 J. Cardell, L. Anderson, "Analysis of the System Costs of Wind Variability Through Monte Carlo Simulation," Proceedings of the 43rd Hawaii International Conference on System Sciences, 2010. [6] 3A J. Hetzer, C. Yu and K. Bhattarai, "An economic dispatch model incorporating wind power," IEEE Transactions on Energy Conversion, vol. 23, no. 2, 603-611, 2008. [7] 3B S. Surender, P. Bijwe and A. Abhyankar, "Real-time economic dispatch considering renewable power generation variability and uncertainty over scheduling period," IEEE Systems Journal, vol. 9, no. 4, 1440-1451, 2015.

[8] 3C J. Zhao, F. Wen, Z. Dong, Y. Xue and K. Wong, "Optimal dispatch of electric vehicles and wind power using enhanced particle swarm optimization," IEEE Transactions on Industrial Informatics, vol. 8, no. 4, 889-899, 2012.

[9] 4 F. Molina, S. Pérez and S. Rivera, "Uncertainty Cost Function Formulation in Small Hydropower Plants Inside a Microgrid," Ingenierías USBMed, Vol. 8, No. 1, Enero-Junio 2017. [10] 4A E. Mojica-Nava, S. Rivera and N. Quijano, "Distributed dispatch control in microgrids with network losses," 2016 IEEE Conference on Control Applications (CCA), Buenos Aires, 2016, pp. 285-290.

[11] 4B E. Mojica-Nava, S. Rivera and N. Quijano, "Game-theoretic dispatch control in microgrids considering network losses and renewable distributed energy resources integration," in IET Generation, Transmission & Distribution, vol. 11, no. 6, pp. 1583-1590, 2017.

[12] 5 R. Mehri and M. Kalantar, “Multi-objective Scheduling of Electric Vehicles Considering Wind and Demand Uncertainties,” no. Sgc, pp. 23–24, 2015. [13] 6 Ernst and Young, “Información de los mercados mayoristas de energía electrica del Reino Unido, Nord Pool, PJM y CAISO discriminado los principales aspectos normativos, operativos y comerciales,” p. 246, 2015. [14] 7 I. El, R. Bann, and A. Abouabdellah, “Modeling and Forecasting Energy Demand,” 2016. [15] 8 J. J. Chen, Q. H. Wu, L. L. Zhang, and P. Z. Wu, “Multi-objective mean–variance–skewness model for nonconvex and stochastic optimal power flow considering wind power and load uncertainties,” Eur. J. Oper. Res., vol. 263, no. 2, pp. 719–732, 2017. [16] 9 Nick T. Thomopoulos. Essentials of Monte Carlo Simulation: statistical methods for building simulation models. Springer, Chicago, Illinois, USA, 2013. ISBN: 978-1-4614-6022-0.

[17] 10 S. Simbaqueba, “Costos de Incertidumbre con Generación Distribuida Considerando la Estocasticidad de la Demanda Controlable,”, Director: S. Rivera, 2018