Revision as of 13:52, 9 October 2018 (view source) Cinmemj (talk | contribs) ← Older edit		Latest revision as of 15:14, 10 October 2018 (view source) Move page script (talk | contribs) m (Move page script moved page Draft Samper 249588187 to Onate et al 2006a)
(2 intermediate revisions by one other user not shown)
Line 1:		Line 1:
−	<!-- metadata commented in wiki content	+	Published in ''Comput. Meth. Appl. Mech. Engng. '', Vol. 195, pp. 339-362, 2006<br />
−	==ERROR ESTIMATION AND MESH ADAPTIVITY IN INCOMPRESSIBLE VISCOUS FLOWS USING  A RESIDUAL POWER APPROACH ==	+	doi: 10.1016/j.cma.2004.07.054
−	'''Eugenio Oñate, Joaquin Arteaga, Julio García and Roberto Flores
−
−	~&nbsp;
−
−	International Center for Numerical Methods in Engineering (CIMNE)
−
−	Universidad Politécnica de Cataluña
−
−	Campus Norte UPC, 08034 Barcelona, Spain
−
−	E-mail: cimne@cimne.upc.es, web page: http://www.cimne.upc.es/'''
−	-->
	==Abstract==		==Abstract==

---

Latest revision as of 15:14, 10 October 2018

Published in Comput. Meth. Appl. Mech. Engng. , Vol. 195, pp. 339-362, 2006
doi: 10.1016/j.cma.2004.07.054

Abstract

A methodology for error estimation and mesh adaptation for finite element (FE) analysis of incompressible viscous flow is presented. The error estimation method is based on the evaluation of the energy rate (the power) of the FE residuals of the momentum and incompressibility equations. The residuals are computed using recovered values of the derivatives of the velocity and pressure variable obtained via a nodal derivative recovery technique. Two mesh adaptation procedures based on: a) the equi-distribution of the residual power among the elements in the mesh and b) the equi-distribution of the density of the total residual power are presented. The stabilized form of the Navier-Stokes equations using a finite calculus (FIC) formulation is solved with a fractional step FE scheme. This allows the use of linear triangles and tetrahedra with an equal order interpolation for the velocity and pressure variables. A nodal-based approach is used for computing the residual power integrals. The examples show the ability of the error estimation and the mesh adaptation process to capture the high gradients of the solution in the vecinity of boundary layers and in zones of high vorticity of the fluid for both steady state and transient flow situations.

1 INTRODUCTION

The estimation of the error in the finite element solution of the Navier-Stokes equations for an incompressible fluid is a difficult problem [1]. The presence of convective terms in the momentum equations prevents the use of standard error estimators based on the energy norm of the error developed for elliptic type problems typical of solid mechanics and heat transfer analysis [2-4]. Extension of these methods to fluid mechanics problems have been reported in [5]. A different class of mesh refinement procedures for fluid flow problems based on error indicators using approximations of the Hessian operator has been reported in [6-10]. Alternative error estimation approaches for fluid flow problems can be found in [11-16].

The error estimation method presented in this paper is based on the evaluation of a particular form of the energy rate (the power) of the finite element residuals of the momentum and mass balance (incompressibility) equations. The residuals are computed using recovered values of the derivatives of the velocity and pressure variable obtained via a nodal derivative recovery technique. Two mesh adaptation processes based on: a) the equi-distribution of the residual power among the elements in the mesh and b) the equi-distribution of the density of the total residual power are presented. The stabilized form of the Navier-Stokes equations using a finite calculus (FIC) procedure developed by the authors [17-21] is used for the FE solution of the examples presented in the paper using a fractional step scheme. This allows the use of linear triangles and tetrahedra with an equal order interpolation for the velocity and pressure variables. A nodal-based approach is used for computation of the residual power error and the total power generated by the viscous stresses and the pressure terms in the mesh. The residual power form derived from the FIC approach includes power terms emanating from the velocity field and from the gradient of the velocity field. It is shown that accounting for the terms involving the velocity gradient provides an effective error estimation and mesh adaptation procedure for CFD problems. Also the FIC form of the residual power expression can be effectively extended for error estimation and mesh adaptivity of other problems in computational mechanics [22].

The examples show the ability of the error estimation and the mesh adaptation process to capture the high gradients of the solution in the vecinity of boundary layers and in zones of high vorticity of the fluid for both steady state and transient flow situations.

2 STABILIZED FINITE ELEMENT SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATIONS

We consider here the solution of the Navier-Stokes equations for an incompressible fluid written as

Momentum

${\displaystyle r_{m_{i}}=0\qquad {\hbox{in }}\Omega }$

(1)

Mass balance

${\displaystyle r_{v}=0\qquad {\hbox{in }}\Omega }$

(2)

For the transient case

${\displaystyle r_{m_{i}}=\rho \left[{\partial u_{i} \over \partial t}+u_{j}{\partial u_{i} \over \partial x_{j}}\right]+{\partial p \over \partial x_{i}}-{\partial \tau _{ij} \over \partial x_{j}}-b_{i}}$

(3)

${\displaystyle r_{v}={\partial u_{i} \over \partial x_{i}}}$

(4)

with ${\textstyle i,j=1,n_{d}}$ when ${\textstyle n_{d}}$ is the number of space dimensions (${\textstyle n_{d}=2}$ for 2D flow problems).

In eq.(3) ${\textstyle \rho }$ is the fluid density (here assumed to be constant), ${\textstyle u_{i}}$ is the velocity component in the ${\textstyle i}$-th direction, ${\textstyle p}$ the pressure, ${\textstyle b_{i}}$ the body forces and ${\textstyle \tau _{ij}}$ the viscous stress tensor components related to the velocity gradients through the fluid viscosity ${\textstyle \mu }$ by

${\displaystyle \tau _{ij}=2\mu \left(\varepsilon _{ij}-{1 \over 3}{\partial u_{k} \over \partial x_{k}}\delta _{ij}\right)}$

(5a)

with

${\displaystyle \varepsilon _{ij}={1 \over 2}\left({\partial u_{i} \over \partial x_{j}}+{\partial u_{j} \over \partial x_{i}}\right)}$

(5b)

Summation convention for repeated indexes in products and derivatives is used unless otherwise specified.

The field equations are completed by the standard boundary conditions

${\displaystyle \sigma _{ij}n_{j}-t_{i}^{p}=0\quad {\hbox{ on }}\Gamma _{t}}$ (6) ${\displaystyle u_{i}-u_{i}^{p}=0\quad {\hbox{ on }}\Gamma _{u}}$ (7)

where ${\textstyle t_{i}^{p}}$ and ${\textstyle u_{i}^{p}}$ are prescribed tractions and the prescribed displacement at the Neuman and Dirichlet boundaries ${\textstyle \Gamma _{t}}$ and ${\textstyle \Gamma _{u}}$, respectively.

We will choose an equal order finite element (FE) approximation for the velocity and pressure

${\displaystyle u_{i}\simeq {\hat {u}}_{i}=\sum \limits _{j=1}^{n}N_{j}({\hat {u}}_{i})_{j}={\bf {N}}{\hat {\bf {u}}}_{i}}$

(8a)

${\displaystyle p\simeq {\hat {p}}=\sum \limits _{j=1}^{n}N_{j}{\hat {p}}_{j}={\bf {N}}{\hat {\bf {p}}}}$

(8b)

where ${\textstyle {\hat {(\cdot )}}}$ denotes approximate values, ${\textstyle N_{j}}$ are the shape functions, ${\textstyle (\cdot )_{j}}$ are nodal values and ${\textstyle n}$ is the number of nodes in the mesh [1]. Standard three node linear triangles are used in the examples given in the paper.

It is well known that stabilized finite element schemes are needed for overcoming the numerical instabilities induced by high values of the convective terms and by the incompressibility constraint when equal order interpolation for the velocities and the presure are used. A number of stabilized FE methods are available in the literature and most of them can be casted in the following form

${\displaystyle \int _{\Omega }N_{k}{\hat {r}}_{m_{i}}d\Omega +\int _{\Gamma _{t}}N_{k}({\hat {\sigma }}_{ij}n_{j}-t_{i}^{p})d\Gamma +\sum _{e}\int _{\Omega ^{e}}\tau _{m_{i}}^{e}P_{m_{i}}(N_{k}){\hat {r}}_{m_{i}}d\Omega =0}$

(9)

${\displaystyle \int _{\Omega }N_{k}{\hat {r}}_{v}d\Omega +\sum _{e}\int _{\Omega ^{e}}\tau _{v}^{e}P_{v}(N_{k}){\hat {r}}_{v}d\Omega =0}$

(10)

In above ${\textstyle {\hat {r}}_{m_{i}}\equiv r_{m_{i}}({\hat {u}}_{j},{\hat {p}})}$ and ${\textstyle {\hat {r}}_{v}=r_{v}({\hat {u}}_{j},{\hat {p}})}$ denote the approximate finite element residuals for the momentum and mass balance equations, respectively, ${\textstyle P_{m_{i}}(N_{k})}$ and ${\textstyle P_{v}(N_{k})}$ are appropriate functions of the shape functions ${\textstyle N_{k}}$ and ${\textstyle \tau _{m_{i}}^{e}}$ and ${\textstyle \tau _{v}^{e}}$ are stabilization parameters which depend on the element dimensions and the physical variables of the problem.

Eqs.(9) and (10) can be interpreted as extended Galerkin expressions where the last integrals over the element interiors has been added to the standard Galerkin forms of the momentum and mass balance equations in order to get a physically meanful (stabilized) numerical solution. Many popular stabilized methods (SUPG, GLS, SGS, etc.) can be written in the form of Eqs.(9) and (10) and they just differ in the choice of the weighting functions ${\textstyle P_{m_{i}}}$ and ${\textstyle P_{v}}$ and in the values of the stabilization parameters [1,24-30].

A somehow different class of stabilized method developed by the authors is based on a finite calculus (FIC) formulation [17-21]. Here the standard momentum and mass balance equations are modified by enforcing the balance laws in a domain of finite size. The modified governing equations contain additional terms which play the role of stabilizing terms in the numerical solution. The Galerkin FE form of the FIC equations of an incompressible fluid can also be written by integral forms analogous to Eqs.(9) and (10) and hence we will retain these equations as general expressions applicable to any stabilized method. Details on the FIC formulation used for the solution of the examples presented in the paper are given in a later section.

3 RESIDUAL POWER FORMS BASED ON THE RECOVERED BALANCE EQUATIONS

We will assume that a finite element solution has been found for the velocity and pressure variables using any stabilized FE scheme. The next step in the error estimation and mesh adaptivity method proposed is to compute the enhanced recovered values of the derivatives of the velocity and the pressure at the element nodes. The derivative recovery procedure used here is explained in the next section.

The recovered nodal derivative fields of the velocities and the pressure are used now to compute the finite element residuals of the discretized momentum and mass balance equations (1) and (2) and the Neumann boundary conditions (6) as:

${\displaystyle {\begin{array}{c}\displaystyle R_{m_{i}}={\bar {\hat {r}}}_{m_{i}}\\~~\\\displaystyle R_{v}={\bar {\hat {r}}}_{v}\\~~\\\displaystyle R_{\Gamma _{i}}=n_{j}{\bar {\hat {\sigma }}}_{ij}-t_{i}^{p}\end{array}}}$

(11)

where ${\textstyle {\bar {\hat {(\cdot )}}}}$ denote values computed using the recovered derivative fields. In Eqs.(11) ${\textstyle R_{m_{i}}}$ can be interpreted as the ith component of an out-of-balance body force, whereas ${\textstyle R_{v}}$ represents an spurious non-zero volumetric strain rate. Similarly, the recovered residuals ${\textstyle R_{\Gamma _{i}}}$ are out-of-balance tractions at the Neuman boundary.

The power due to the recovered residuals can be written as

${\displaystyle \displaystyle P_{m_{i}}=\int _{\Omega }W_{i}^{u}R_{m_{i}}d\Omega +\int _{\Gamma _{t}}{\bar {W}}_{i}^{u}R_{\Gamma _{i}}d\Gamma \qquad {\hbox{no sum in }}i}$

(12a)

${\displaystyle \displaystyle P_{v}=\int _{\Omega }{\bar {W}}^{p}R_{v}d\Omega }$

(12b)

where the weights ${\textstyle (W_{i}^{u},{\bar {W}}_{i}^{u})}$ and ${\textstyle W^{p}}$ are functions of the approximate velocity vector field and the pressure, respectively. Indeed the simplest choice is ${\textstyle W_{i}^{u}={\bar {W}}_{i}^{u}={\hat {u}}_{i}}$ and ${\textstyle W^{p}={\hat {p}}}$. However, many other options are possible. In this work we have chosen

${\displaystyle W_{i}^{u}={\hat {u}}_{i}+{h_{j} \over 2}{\partial {\hat {u}}_{i} \over \partial x_{j}}\quad ,\quad {\bar {W}}_{i}^{u}=0\quad {\hbox{and}}\quad W^{p}={\hat {p}}+{h_{j} \over 2}{\partial {\hat {p}} \over \partial x_{j}}}$

(13)

where ${\textstyle h_{j}}$ is a characteristic length of the order of the element size. This choice is a result of the finite calculus formulation described in a next section.

Note that at the solid boundaries ${\textstyle {\hat {u}}=0}$ and at the exterior boundary ${\textstyle {\hat {\sigma }}_{ij}n_{j}\simeq t_{i}}$ on ${\textstyle \Gamma _{t}}$. This justifies neglecting the boundary integral in Eq.(12a) by choosing ${\textstyle {\bar {W}}_{i}^{u}=0}$.

The weights ${\textstyle W_{i}^{u}}$ and ${\textstyle W^{p}}$ as defined in Eq.(13) are discontinuous for standar finite element interpolations. A continuous discrete form of these weights can be found by using the recovered values of the derivatives of ${\textstyle {\hat {u}}_{i}}$ and ${\textstyle {\hat {p}}}$ as explained in Section 4.

The integrals over the domain can be computed by summing up the individual element contributions in the usual manner. However in the examples presented in the paper the volume integrals in Eqs.(12) are computed using a nodal integration scheme as

${\displaystyle {\begin{array}{l}\displaystyle P_{m_{i}}=\sum \limits _{k=1}^{\bar {N}}[P_{m_{i}}]_{k}=\sum \limits _{k=1}^{\bar {N}}\left|\left[W_{i}^{u}R_{m_{i}}\right]_{k}\right|\Omega _{k}\quad {\hbox{no sum in }}i\\\\\displaystyle P_{v}=\sum \limits _{k=1}^{\bar {N}}[P_{v}]_{k}=\sum \limits _{k=1}^{\bar {N}}\left|\left[W_{i}^{p}R_{v}\right]_{k}\right|\Omega _{k}\end{array}}}$

(14)

where ${\textstyle [\cdot ]_{k}}$ denotes values computed at node ${\textstyle k}$, ${\textstyle {\bar {N}}}$ is the number of internal nodes in the mesh and ${\textstyle \Omega _{k}}$ is the tributary area of node ${\textstyle k}$ (Figure 1). In Eqs.(14) absolute values are used to avoid random cancelation of the residual power terms. Indeed Eqs.(14) imply nodal continuity of the weighting functions obtained via the derivative recovery process explained in the next Section. The global error for a given mesh is estimated as

${\displaystyle \Vert P\Vert _{\Omega }=\sum \limits _{k=1}^{\bar {N}}\Vert P\Vert _{\Omega ^{k}}}$

(15)

where ${\textstyle \Vert P\Vert _{\Omega ^{k}}}$ is the estimated error value for an individual node defined as

${\displaystyle \Vert P\Vert _{\Omega ^{k}}=\sum \limits _{i=1}^{n_{d}}[P_{m_{i}}]_{k}+[P_{v}]_{k}}$

(16)

Remark

We note that the residual power expressions chosen can be interpreted as the projection of the recovered residuals of the momentum and incompressibility equations against the weighting functions ${\textstyle P_{m_{i}}}$ and ${\textstyle P_{v}}$, respectively. In this sense, Eqs.(12) can be viewed as a particular class of residual projection method. A review of these procedures can be found in [15] and references herein.

4 RECOVERY OF THE NODAL DERIVATIVES OF THE VELOCITIES AND THE PRESSURE

The recovered derivative field ${\textstyle \left(\displaystyle {\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)}$ is defined so as to satisfy the following variational form

${\displaystyle \int _{\Omega }N_{k}\left[\left({\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)-{\partial {\hat {u}}_{i} \over \partial x_{j}}\right]d\Omega =0\quad {\hbox{no sum in }}i}$

(17)

where ${\textstyle N_{k}}$ are the same shape functions used to approximate the velocity field and ${\textstyle \displaystyle {\partial {\hat {u}}_{i} \over \partial x_{j}}}$ are known derivatives values directly obtained from the finite element solution.

A standard finite element approximation is chosen for the recovered derivative field; i.e.

${\displaystyle \left({\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)=\sum \limits _{k}N_{k}\left({\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)_{k}}$

(18)

Substituting Eq.(18) into (17) gives the following system of equations from which the recovered nodal derivative values can be obtained

${\displaystyle {\bf {M}}{\bar {\hat {\bf {d}}}}_{ij}={\bf {f}}_{ij}}$

(19)

with

${\displaystyle {\bar {\hat {\bf {d}}}}_{ij}=\left[\left({\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)_{1},\left({\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)_{2},\cdots ,\left({\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)_{N}\right]^{T}}$

(20)

where ${\textstyle N}$ is the number of nodes in the mesh.

The element contributions to ${\textstyle {\bf {M}}}$ and ${\textstyle {\bf {f}}}$ are

${\displaystyle M_{kl}^{e}=\int _{\Omega ^{e}}N_{k}N_{l}d\Omega \quad ,\quad (f_{ij}^{e})_{k}=\int _{\Omega ^{e}}N_{k}{\partial {\hat {u}}_{i} \over \partial x_{j}}d\Omega }$

(21)

We recall that in above ${\textstyle \displaystyle {\partial {\hat {u}}_{i} \over \partial x_{j}}}$ is the (discontinuous) derivative field obtained from the finite element solution and ${\textstyle \left(\displaystyle {\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)_{k}}$ are the recovered derivative values at node ${\textstyle k}$. The process is repeated for ${\textstyle i,j=1,n_{d}}$.

The full form of matrix ${\textstyle {\bf {M}}}$ is used for the solution of Eq.(19) using a standard Jacobian iterative scheme.

The same procedure is followed in order to recover the nodal derivatives of the pressure and the nodal second derivatives of the velocity field ${\textstyle \left(\displaystyle {\partial ^{2}{\hat {u}}_{k} \over \partial x_{i}\partial x_{j}}\right)}$ needed for computation of all the terms in the recovered momentum equations ${\textstyle R_{m_{i}}}$.

5 ERROR INDICATORS AND MESH ADAPTATION PROCEDURES

A global error parameter is defined as

${\displaystyle \xi _{g}={\Vert P\Vert _{\Omega } \over \mu U}}$

(22)

where ${\textstyle \mu }$ is the prescribed global error value and ${\textstyle U}$ is the total power in the mesh defined here as

${\displaystyle U=\int _{\Omega }\left[\tau _{ij}\varepsilon _{ij}+{\partial p \over \partial x_{i}}u_{i}\right]d\Omega }$

(23)

The first term in Eq.(23) is the power of the viscous stresses, whereas the second one is the power of the pressure gradient terms. The integral in Eq.(23) is computed using nodal information by an expression analogous to Eq.(15).

The mesh adaption process aims to reduce the global error (leading to a value of ${\textstyle \xi _{g}=1}$) while satisfying a local error condition for each individual element. The two options considered in this work for the local error condition are presented next.

5.1 Mesh adaptation based on the equidistribution of the global error

A local error parameter ${\textstyle \xi _{g}}$ is defined for each element as

${\displaystyle \xi ^{e}={\Vert P\Vert _{\Omega ^{e}}N \over \Vert P\Vert _{\Omega }}}$

(24)

where ${\textstyle \Vert P\Vert _{\Omega ^{e}}}$ is the residual power error for element ${\textstyle e}$ and ${\textstyle N}$ is the total number of elements in the mesh. Eq.(24) is based in the so called equi-distribution of the global error, i.e. if ${\textstyle \xi ^{e}=1}$ for all elements then the total residual power error is uniformly distributed in the mesh [4].

The error indicator for the element is defined as

${\displaystyle \gamma ^{e}=(\xi ^{e})^{\alpha }(\xi _{g})^{\beta }}$

(25)

Parameters ${\textstyle \alpha }$ and ${\textstyle \beta }$ are found by analyzing the convergence rate of the global and local error parameters as described in [4]. In the examples presented in the paper the following values of ${\textstyle \alpha }$ and ${\textstyle \beta }$ have been used

${\displaystyle \alpha ={1 \over p+n_{d}}\quad ,\quad \beta ={1 \over p+1}}$

(26)

where ${\textstyle p}$ is the order of the finite element interpolation (i.e. ${\textstyle p=1}$ for linear elements).

The new element size ${\textstyle h_{new}}$ is computed in terms of the error indicator ${\textstyle \gamma ^{e}}$ and the current element size as

${\displaystyle h_{new}=h_{old}[\gamma ^{e}]^{-1}}$

(27)

5.2 Mesh adaptation based on the equidistribution of the error density

An alternative local error parameter based on the equidistribution of the density of the residual power can be defined as

${\displaystyle \xi ^{e}={\Omega \Vert P\Vert _{\Omega ^{e}} \over \Omega ^{e}\Vert P\Vert _{\Omega }}}$

(28)

where ${\textstyle \Omega }$ and ${\textstyle \Omega ^{e}}$ are the area of the analysis domain and the area of an individual element, respectively. Now ${\textstyle \xi ^{e}=1}$ if the density of the error (error per unit area) is uniformly distributed over the mesh.

The expression for the error indicator for the element is again given by Eq.(25). The following values of ${\textstyle \alpha }$ and ${\textstyle \beta }$ are now chosen as deduced following the procedure described in [4]

${\displaystyle \alpha ={1 \over p}\quad ,\quad \beta ={1 \over p}}$

(29)

The new element sizes are computed from Eq.(27).

This mesh adaptation criteria leads to meshes where the smaller elements are concentrated in zones where the higher gradients of the velocity and pressure occur, whereas much larger elemens are placed in other zones of the domain [4]. This is adequate for capturing accurate solutions in the vecinity of boundary layers or singularity zones. The drawback of this procedure is that it tends to refine progressively (and very fast) the mesh in these zones until ${\textstyle \xi ^{e}=1}$. This leads to regions with very small elements and hence to an extremely large number of elements in the mesh. A limiting value in the size of the smallest element in the new mesh is mandatory in these cases.

Alternatively the criterium based on the equidistribution of the global error described in the previous section leads to meshes with a “smoother” distribution of the element sizes between the regions where high gradients occur and the other zones in the domain.

A comparison of these two mesh adaptions procedures for linear structural analysis can be found in [4].

5.3 Mesh refinement strategy

The mesh refinement strategy is as follows.

Step 1 Compute the nodal recovered values of the derivatives of the velocity and pressure fields using the algorithm described in Section 4.

Step 2 Compute the residual power error for each element in the mesh and the total residual power error using Eqs.(15) and (16).

Step 3 Compute the global and local (element) error parameters ${\textstyle \xi _{g}}$ and ${\textstyle \xi ^{e}}$.

Step 4 Compute the new element sizes using Eq.(27). Perform a smoothing of the new element sizes to avoid problems during the regeneration of the mesh.

Step 5 Regenerate a new mesh. Minimum and maximum sizes of the elements in the mesh are prescribed in order to have a better control of the mesh generation process. The mesh generation is carried out using the GiD pre/postprocessing system [23].

Above mesh refinement strategy is equally applicable for the two mesh adaption procedures explained in the previous sections.

For steady-state flow problems the error estimation and the mesh refinement process are performed after a steady state solution has been found. For transient problems the mesh refinement is performed after a prescribed number of time steps.

6 STABILIZED FEM FOR THE NAVIER-STOKES EQUATIONS USING FINITE CALCULUS

6.1 Finite calculus form of the Navier-Stokes equations

The FIC governing equations for incompressible viscous flows are obtained by applying the standard conservation laws expressing balance of momentum and mass over a control domain. Assuming that the control domain has finite dimensions and expressing the variation of mass and momentum over the domain using Taylor series expansions of one order higher than those used in the standard infinitesimal theory, the following expressions are found [17-21]:

Momentum

${\displaystyle r_{m_{i}}-{\underline {{1 \over 2}h_{j}{\partial r_{m_{i}} \over \partial x_{j}}}}{1 \over 2}h_{j}{\partial r_{m_{i}} \over \partial x_{j}}=0\qquad {\hbox{in }}\Omega }$

(30)

Mass balance

${\displaystyle r_{v}-{\underline {{1 \over 2}h_{j}{\partial r_{v} \over \partial x_{j}}}}{1 \over 2}h_{j}{\partial r_{v} \over \partial x_{j}}=0\qquad {\hbox{in }}\Omega }$

(31)

where ${\textstyle r_{m_{i}}}$ and ${\textstyle r_{v}}$ were defined in Eqs.(3) and (4), respectively.

Eqs.(30) and (31) are the FIC forms of the governing differential equations for an incompressible flow. The terms underlined in Eqs.(30) and (31) introduce naturally the necessary stabilization at the discretization level. The so called characteristic length vector ${\textstyle {h}}$ is defined as (for 2D problems)

${\displaystyle {h}=\left\{{\begin{matrix}h_{1}\\h_{2}\\\end{matrix}}\right\}}$

(32)

where ${\textstyle h_{1}}$ and ${\textstyle h_{2}}$ are characteristic dimensions of the finite control domain where balance of momentum and mass conservation is enforced. The components of vector ${\textstyle {h}}$ introduce the necessary stabilization along the streamline and transverse directions to the flow in the discrete problem [17-21].

The method to derive the modified differential equations (30) and (31) incorporating the stabilization terms is termed finite calculus (FIC) as a reference to the standard infinitesimal calculus where the size of the domain where balance of mass and momentum is enforced is assumed to be negligible. Note that for ${\textstyle {h}\to 0}$ the standard infinitesimal form of the momentum and mass balance equations is recovered [1].

Eqs.(30) and (31) are completed by the following FIC boundary conditions [17].

Equilibrium of surface tractions at the boundary ${\textstyle \Gamma _{t}}$

${\displaystyle n_{j}\sigma _{ij}-t_{i}^{p}+{\underline {{1 \over 2}h_{j}n_{j}r_{m_{i}}}}{1 \over 2}h_{j}n_{j}r_{m_{i}}=0\qquad {\hbox{on}}~~\Gamma _{t}}$

(33)

Prescribed velocity at the boundaries

${\displaystyle u_{t}=u_{t}^{p}\qquad {\hbox{on}}~~\Gamma _{u_{t}}}$

(34)

${\displaystyle u_{n}-{\underline {{1 \over 2}h_{i}n_{i}r_{v}}}{1 \over 2}h_{i}n_{i}r_{v}=u_{n}^{p}\qquad {\hbox{on}}~~\Gamma _{u_{n}}}$

(35)

In eq.(34) ${\textstyle u_{t}}$ and ${\textstyle u_{t}^{p}}$ denote the tangential velocity to the boundary and its prescribed value, respectively.

Eq.(35) expresses the balance of mass on an arbitrary domain next to the boundary and ${\textstyle u_{n}}$ and ${\textstyle u_{n}^{p}}$ denote the velocity normal to the boundary and its prescribed value, respectively. The value of ${\textstyle u_{n}^{p}}$ is zero on solid walls and stationary free surfaces.

Also in eqs.(34) and (35) ${\textstyle \Gamma _{u_{t}}}$ and ${\textstyle \Gamma _{u_{n}}}$ are the parts of the boundary ${\textstyle \Gamma }$ of ${\textstyle \Omega }$ where the tangential and normal velocities are prescribed, respectively. The Dirichlet boundary is defined as ${\textstyle \Gamma _{u}=\Gamma _{u_{t}}\cup \Gamma _{u_{n}}}$.

The underlined terms in eqs.(33) and (35) introduce the necessary stabilization at the boundaries in a form consistent with that of eqs.(30) and (31). Details of the derivation of eqs.(30–35) can be found in [17] whereas the derivation of eq.(9) is shown in [18].

6.2 Residual power forms of FIC equations

We will choose again an equal order finite element approximation for the velocity and pressure variables given by Eqs.(8)

Again we will assume that a finite element solution has been found for the velocity and the pressure variables. The finite element algorithm used for the examples solved in this paper is based on a fractional step scheme [19-21,30]. The next step is to obtain enhanced recovered values of the derivatives of the velocity and the pressure at the element nodes as explained in previouss section.

The recovered nodal derivative fields of the velocities and the pressure are used now to compute the FIC residuals of the momentum and mass balance equations (1) and (2):

${\displaystyle {\begin{array}{c}\displaystyle R_{m_{i}}={\bar {\hat {r}}}_{m_{i}}-{h_{j} \over 2}{\partial {\bar {\hat {r}}}_{m_{i}} \over \partial x_{j}}\\\\\displaystyle R_{v}={\bar {\hat {r}}}_{v}-{h_{j} \over 2}{\partial {\bar {\hat {r}}}_{v} \over \partial x_{j}}\end{array}}}$

(36)

where once more ${\textstyle {\bar {\hat {(\cdot )}}}}$ denote values computed using the recovered derivative fields.

The total power due to the FIC residuals can be written as

${\displaystyle {\begin{array}{c}\displaystyle P_{m_{i}}=\int _{\Omega }{\hat {u}}_{i}R_{m_{i}}d\Omega +\int _{\Gamma _{t}}{\hat {u}}_{i}\left(n_{j}{\bar {\hat {\sigma }}}_{ij}-t_{i}+{h_{j} \over 2}n_{j}{\bar {\hat {r}}}_{m_{i}}\right)d\Gamma \\\\\displaystyle P_{v}=\int _{\Omega }{\hat {p}}R_{v}d\Omega -\int _{\Gamma _{u_{n}}}{\hat {p}}\left({\hat {u}}_{n}-u_{n}^{p}-{h_{j} \over 2}n_{j}{\bar {\hat {r}}}_{v}\right)d\Gamma \end{array}}}$

(37)

Substituting the expressions of ${\textstyle R_{m_{i}}}$ and ${\textstyle R_{v}}$ of Eqs.(36) into (37) and integrating by parts some derivative terms gives

${\displaystyle P_{m_{i}}=\int _{\Omega }\left[{\hat {u}}_{i}+{h_{j} \over 2}\left({\partial {\hat {u}}_{i} \over \partial x_{j}}\right)\right]{\bar {\hat {r}}}_{m_{i}}d\Omega +\int _{\Gamma _{t}}{\hat {u}}_{i}\left({\bar {\hat {\sigma }}}_{ij}n_{j}-t_{i}\right)d\Gamma -\int _{\Gamma _{u}}{h_{j} \over 2}n_{j}{\hat {u}}_{i}{\bar {\hat {r}}}_{m_{i}}d\Gamma \quad {\hbox{no sum in }}i}$

(38a)

${\displaystyle P_{v}=\int _{\Omega }\left[{\hat {p}}+{h_{j} \over 2}\left({\partial {\hat {p}} \over \partial x_{j}}\right)\right]{\bar {\hat {r}}}_{v}d\Omega -\int _{\Gamma _{u_{n}}}{\hat {p}}({\hat {u}}_{n}-u_{n}^{p})d\Gamma -\int _{\Gamma -\Gamma _{u_{n}}}{\hat {p}}{h_{j} \over 2}n_{j}{\bar {\hat {r}}}_{v}d\Gamma }$

(38b)

Numerical experiments have shown that the contribution of the boundary integrals in Eqs.(38) is negligible versus the value of the integrals over the domain. Hence the contribution of the surface integrals in Eqs.(38) will not be taken into account from now onwards. An explanation for this is that at the solid boundaries in a viscous flow ${\textstyle {\hat {u}}_{j}=0}$ and hence the line integrals in Eq.(38a) vanish there. Note also that at the exterior boundary ${\textstyle {\hat {\sigma }}_{ij}n_{j}\simeq t_{i}}$ on ${\textstyle \Gamma _{t}}$ and ${\textstyle r_{m_{i}}\simeq 0}$ on ${\textstyle \Gamma _{u}}$ and this justifies neglecting the line integral at those boundaries. In Eq.(38b) the first line integral vanishes if ${\textstyle {\hat {u}}_{n}}$ is made equal to the prescribed normal velocity ${\textstyle u_{n}^{p}}$ when solving the system of discretized equations. The second integral in Eq.(38b) can be neglected by accepting that either ${\textstyle p=0}$ (external boundary) or ${\textstyle {\bar {\hat {r}}}_{v}\simeq 0}$ at the ${\textstyle \Gamma -\Gamma _{u_{n}}}$ boundary.

In summary, the relevant residual power terms for the FIC momentum and mass balance equations are

${\displaystyle \displaystyle P_{m_{i}}=\int _{\Omega }\left[{\hat {u}}_{i}+{h_{j} \over 2}\left({\partial {\hat {u}}_{i} \over \partial x_{j}}\right)\right]{\bar {\hat {r}}}_{m_{i}}d\Omega \qquad {\hbox{no sum in }}i}$

(39a)

${\displaystyle \displaystyle P_{v}=\int _{\Omega }\left[{\hat {p}}+{h_{j} \over 2}\left({\partial {\hat {p}} \over \partial x_{j}}\right)\right]{\bar {\hat {r}}}_{v}d\Omega }$

(39b)

In the examples presented in the paper the integrals in Eq.(39) are computed using a nodal integration scheme. This requires computing the recovered nodal value of the derivative of the velocity and pressure field. This is an unexpensive task as the recovered nodal values are needed to evaluate the recovered residual. The nodal computation of the residual power expressions is therefore written as

${\displaystyle {\begin{array}{l}\displaystyle P_{m_{i}}=\sum \limits _{k=1}^{\bar {N}}\left|\left[\left({\hat {u}}_{i}+{h_{j} \over 2}\left({\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)\right){\bar {\hat {r}}}_{m_{i}}\right]_{k}\right|\Omega _{k}\\\\\displaystyle P_{v}=\sum \limits _{k=1}^{\bar {N}}\left|\left[\left({\hat {p}}+{h_{j} \over 2}\left({\overline {\partial {\hat {p}} \over \partial x_{j}}}\right)\right){\bar {\hat {r}}}_{v}\right]_{k}\right|\Omega _{k}\end{array}}}$

(40)

the different terms have the meaning explained for Eq.(14).

We note that in the examples presented next the characteristic length parameters have been defined as the characteristic sizes of each tributary domain for a node (see Figure 1).

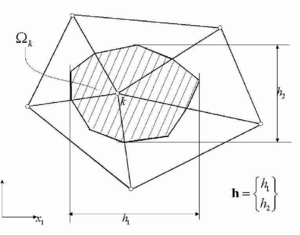
Figure 1: Tributary domain for a node ${\displaystyle k}$ and definition of characteristic lengths.

The global and element error norm are defined by Eqs.(15) and (16), respectively. The error estimation process and the mesh adaptivity scheme follow precisely the steps explained in Section 5.

Remark

Eqs.(40) define the weighting functions in the general residual power forms of Eqs.(12) and (13) as

${\displaystyle {\begin{array}{l}\displaystyle {W_{i}^{u}={\hat {u}}_{i}+{h_{j} \over 2}\left({\overline {\partial {\hat {u}}_{i} \over \partial x_{j}}}\right)}\quad ,\quad {\bar {W}}_{i}^{u}=0\\\\\displaystyle {W^{p}={\hat {p}}+{h_{j} \over 2}\left({\overline {\partial {\hat {p}} \over \partial x_{j}}}\right)}\end{array}}}$

(41)

These expressions, obtained using arguments from the FIC formulation, can be used to compute variational residual forms of the error in order to derive effective mesh refinement procedures for other problems of computational mechanics using the general scheme presented in Section 5.3 [19].

We note again however that Eqs.(41) are not the only option for ${\textstyle W_{i}^{u}}$ and ${\textstyle W^{p}}$ and some other choices are explored in [22] to derive a variety of error estimation and mesh refinement procedures for convection-diffusion problems. Numerical results reported in [22] show that the expressions given by Eqs.(41) have a better performance.

7 EXAMPLES

Typical parameters used for the examples presented are: prescribed global error ${\textstyle \mu =1\%}$, maximum and minimum sizes of the new elements generated ${\textstyle h_{max}=0.3}$m and ${\textstyle h_{min}=0.001}$m.

7.1 Flow past a NACA airfoil

This a transient problem. The mesh refinement process has been carried out at a time ${\textstyle t=2s}$. The value of the Reynolds number for this problem is 100. Figure 2 shows the initial mesh of 2574 nodes and 5148 linear elements used.

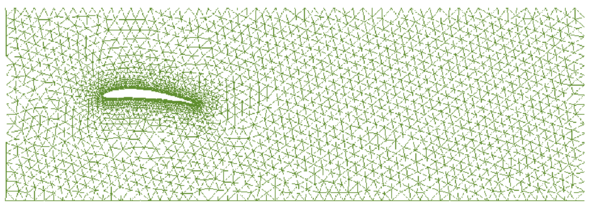
Figure 2: Flow past a NACA airfoil. Characteristic length =1m, ${\displaystyle Re=100}$. Original mesh

The mesh adaptation procedure chosen first is that of equidistribution of the global error. Figures 3 and 4 show the mesh obtained after five refinement steps. The distribution of the velocity field for that mesh is shown in Figures 5 and 6. Table 1 shows the value of the global error and the evolution of the number of elements and nodes during the mesh refinement process. The percentage errors in the drag and lift values are also given in Table 1. We note that the solution was found using a laminar flow model. Therefore some error in the drag values is to be expected even for fine meshes. The error of 6.4% obtained in this case is quite acceptable.

Figure 3: Mesh obtained after five refinement steps using the equidistribution of the global error.

Figure 4: Details of the refined mesh of Figure 3 in the vecinity of the airfoil

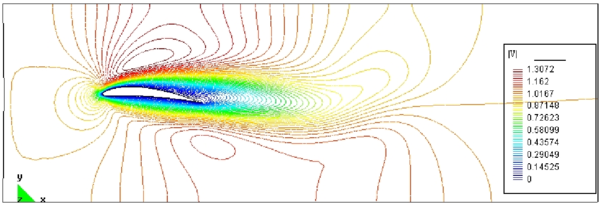
Figure 5: Velocity field after five refinement steps

Figure 6: Detail of the velocity field

Table. 1 Flow past a NACA airfoil (equidistribution of global error). Convergence of the global error with the mesh refinement. Minimum element size = 0.001m

Mesh	Global error ${\textstyle \left({\Vert P\Vert _{\Omega } \over U}\right)}$(%)	Nodes	Elements	Drag error %	Lift error%
1	5.55	2574	4784	29.1810942	2.99902143
2	2.93	5340	10680	28.7443059	2.5500113
3	2.87	7942	15884	22.1078024	2.00851784
4	2.77	11948	23896	15.2893198	1.54898957
5	1.81	17142	34284	10.6478917	1.17033653
6	1.81	17255	34510	8.54878424	1.02567233
7	1.71	17372	34744	6.93290243	0.86514698
8	1.72	16729	33458	6.40377809	0.97782406

The same problem was solved using the criterium of the equidistribution of error density. The same maximum and minimum sizes for the generated elements are used (i.e., ${\textstyle h_{max}=0.3}$m and ${\textstyle h_{min}=0.001}$m). In this case, after the third step the mesher was unable to generate a new grid from the element size distributions given by the method. Figures 7 and 8 show the mesh obtained after the second step. The failure of the mesh generator is due to the very large gradients of the element size field leading to an extremely high density of elements concentrated near the airfoil.

Figure 7: Mesh obtained after two refinement steps using the equidistribution of the error density (min size = 0.001m)

Figure 8: Detail of the refined mesh shown in the previous figure

Table. 2 Flow past a NACA profile (equidistribution of error density). Convergence of the global error with the mesh refinement (min. element size = 0.001m)

Mesh	Global error ${\textstyle \left({\Vert P\Vert _{\Omega } \over U}\right)}$(%)	Nodes	Elements	Drag error %	Lift error%
1	5.55	2574	4784	29.1810942	201.915023
2	2.18	10594	21188	10.4796861	1.16034921
3	2.14	39895	79790	3,17339951	0.5988364

Figure 9: Mesh obtained after four refinement steps using the equidistribution of the error density (min size = 0.002m).

Figure 10: Detail of the refined mesh of Figure 9.

Table 2 shows that the criterium of equidistribution of error density leads to a smaller error for the drag and lift in fewer time steps. Note however the increase in the number of elements and nodes with respect to that of Table 1. In order to avoid this problem, the minimum element size was increased next to 0.002m. This allowed to complete the mesh refinement process and the results are shown in Table 3 and Figures 9 and 10. Note that the drag and lift errors have now slightly increased, showing the dependence of these values with the minimum element size. Again we note that these errors can be reduced using a turbulence model.

Table. 3 Flow past a NACA airfoil (equidistribution of error density). Convergence of the global error with the mesh refinement. Minimum element size = 0.002m

Mesh	Global error ${\textstyle \left({\Vert P\Vert _{\Omega } \over U}\right)}$(%)	Nodes	Elements	Drag error %	Lift error%
1	6.38	2574	4784	29.1810942	2.99902143
2	3.42	9871	19742	11.4092413	1.21135183
3	2.23	29414	58828	6.34299015	0.78983056
4	2.11	50062	100124	6.31490459	0.78318179
5	2.15	71826	143652	6.76638966	0.79634854

Finally Figures 11 and 12 respectively show the evolution of the drag and lift errors for the three cases considered and Figure 13 shows the convergence of the global error.

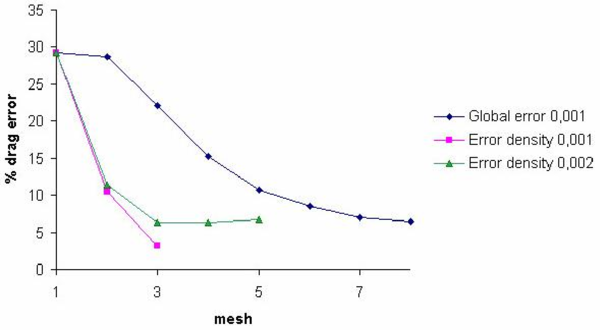
Figure 11: Flow past a NACA airfoil. Convergence of the drag error for both refinement methods

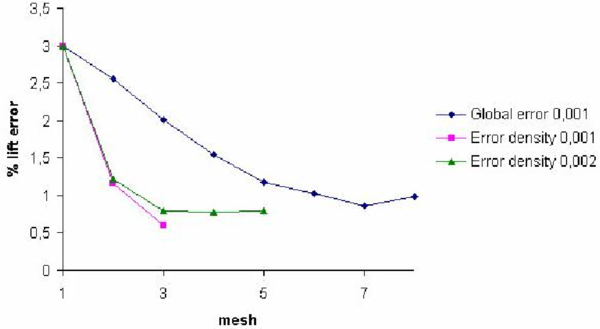
Figure 12: Flow past a NACA airfoil. Convergence of the lift error for both refinement methods. Numbers next to legend denote the minimum element size prescribed

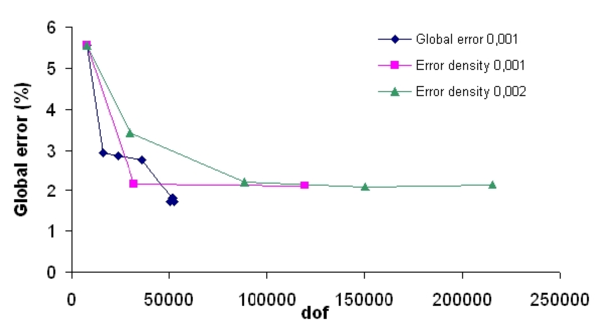
Figure 13: Convergence of the global error for both refinement methods

7.2 Flow past a cylinder Re=100

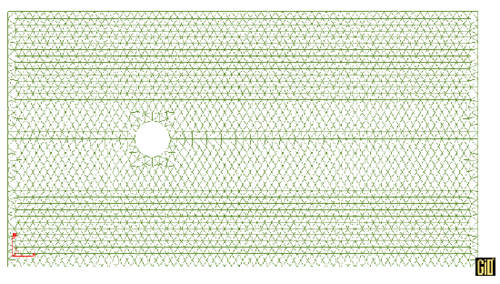
The mesh refinement process for this transient problem has been carried out at a time ${\textstyle t=60s}$. Figure 14 shows the original mesh of 2135 nodes and 5365 linear elements used.

Using the equidistribution of the global error, the maximum and minimum size of the elements to be generated are 0.3m and 0.001m, respectively. Figures 15 and 16 show the mesh obtained after two refinement steps. Figures 17 and 18 show the velocity field for the third mesh. Table 4 shows the value of the global error and the evolution of the number of elements and nodes during the mesh refinement process.

Figure 14: Flow past a cylinder. Radius=1m, ${\displaystyle Re=100}$. Original mesh

Figure 15: Mesh obtained after two refinement steps using the equidistribution of the global error

Figure 16: Detail of the refined mesh in the neighbourhood of the cylinder

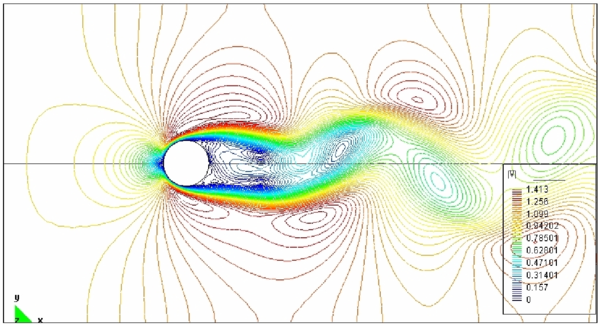
Figure 17: Velocity field after two refinement steps. Equidistribution of global error

Figure 18: Detail of the velocity field

Table. 4 Flow past a cylinder (equidistribution of global error). Convergence of the global error with the mesh refinement

Mesh	Global error ${\textstyle \left({\Vert P\Vert _{\Omega } \over U}\right)}$(%)	Nodes	Elements
1	8.72	2135	5365
2	2.67	7863	15875
3	2.05	12035	24264
4	2	14448	29114
5	1.86	16661	33539

The same problem was solved using the criterium based on the equidistribution of the error density. Now the minimum size of the elements generated is increased to 0.003m, in order to avoid problems in the regeneration of the mesh. The mesh obtained after two steps is shown in Figures 19 and 20. Table 5 shows the evolution of the global error and the number of elements and nodes during the mesh refinement process.

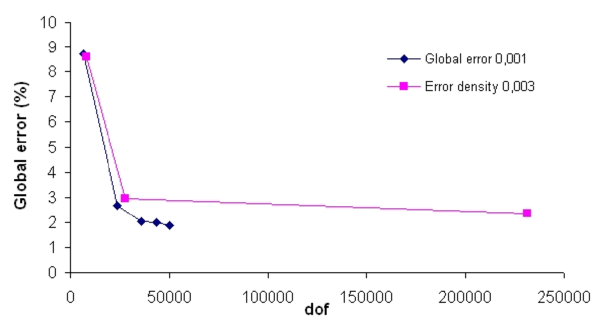
Figure 21 shows the convergence of the global error for both cases.

Figure 19: Mesh obtained after two refinement steps using the equidistribution of the error density

Figure 20: Details of the refined mesh of Figure 19

Table. 5 Flow past a cylinder (equidistribution of error density). Convergence of the global error with the mesh refinement

Mesh	Global error ${\textstyle \left({\Vert P\Vert _{\Omega } \over U}\right)}$(%)	Nodes	Elements
1	8.6	2653	5092
2	2.96	9198	18057
3	2.37	77064	153190

Figure 21: The convergence of the global error for both cases.

7.3 Driven cavity flow

This is another well known benchmark problem in the CFD literature. The problem is solved for a Reynolds number of 1000. The mesh regeneration was performed at the time ${\textstyle t=2s}$.

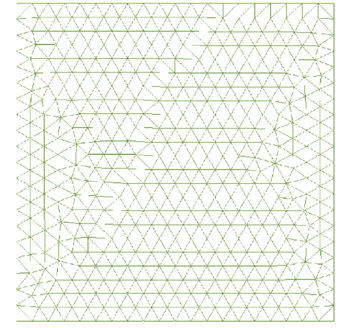
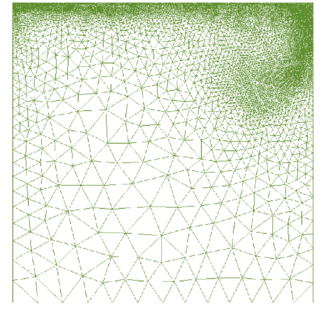
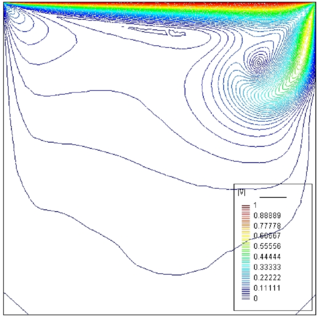
The initial mesh of 477 nodes and 952 linear elements is shown in Figure 22. The mesh obtained after three refinement steps and the corresponding velocity field are shown in Figure 23. The mesh adaptation criterium based on the equidistribution of the global error was used. Table 6 shows the value of the global error and the evolution of the number of elements and nodes during the mesh refinement process.

Figure 24 shows the convergence of the global error.

Figure 22: Driven cavity flow. Side length =1m, ${\displaystyle Re=1000}$. Original mesh

Figure 23: Mesh obtained after three refinement steps (equidistribution of the global error) and velocity field.

Table. 6 Driven cavity flow (equidistribution of global error). Convergence of the global error with the mesh refinement

Mesh	Global error ${\textstyle \left({\Vert P\Vert _{\Omega } \over U}\right)}$(%)	Nodes	Elements
1	26.88	477	872
2	14.5	3089	5985
3	9.56	6475	12521
4	9.42	8103	15700
5	9.14	9411	18280
6	6.63	12997	25207

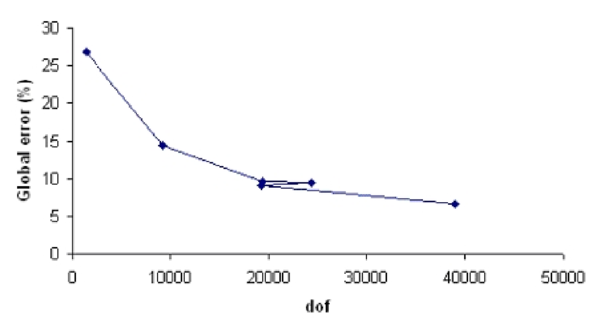
Figure 24: Convergence of the global error in the cavity problem.

Figure 25: High-lift airfoil configuration. Characteristic length =0.6m, Re=100. Initial mesh

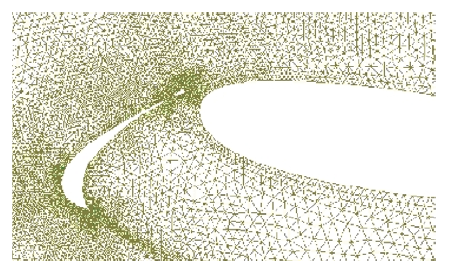
Figure 26: Mesh obtained after two refinement steps using equiditribution of global error (${\displaystyle \mu =0.01}$)

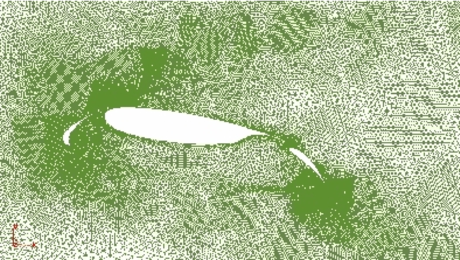
Figure 27: Mesh obtained in the fith after changing ${\displaystyle \mu =0.01}$ to ${\displaystyle \mu =0.005}$ in the fourth step

7.4 Flow past a wing in high-lift configuration

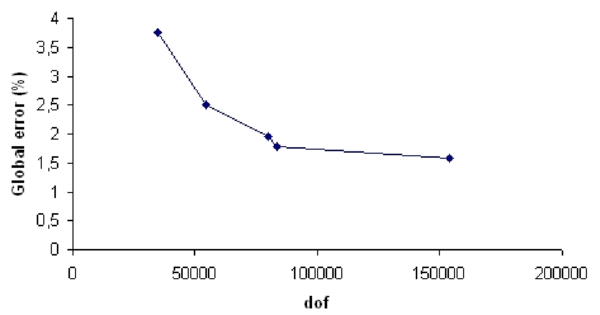
This last example is a multiple airfoil configuration including slat, wing and flap. The problem has been solved with a laminar solver and a Reynolds number of 100. In this example the maximum size of the generated elements has been reduced to 0.05m. The initial mesh of 11703 nodes and 23480 elements is shown in Figure 25. The resulting mesh after two refinement steps is shown in Figure 26. The convergence of the global error with the mesh refinement is shown in Table 7. The algorithm based on the equidistribution of the global error has been used in this example.

Table. 7 High-lift configuration (equidistribution of global error). Convergence of the global error with the mesh refinement

Mesh	Global error ${\textstyle \left({\Vert P\Vert _{\Omega } \over U}\right)}$(%)	Nodes	Elements
1	3.76	11703	22874
2	2.51	18334	35909
3	1.95	26718	52487
4	1.79	27845	54810
5	1.58	51361	101532

After the fourth step the prescribed global error was reduced from ${\textstyle \mu =0.01}$ to ${\textstyle \mu =0.005}$. The result is shown in Figure 27.

The velocity field for the fifth step is shown in Figure 28.

Figures 29 and 30 show the convergence of the drag and lift error, respectively. Figure 31 shows the evolution of the global error.

Figure 28: Velocity field obtained after five refinement steps

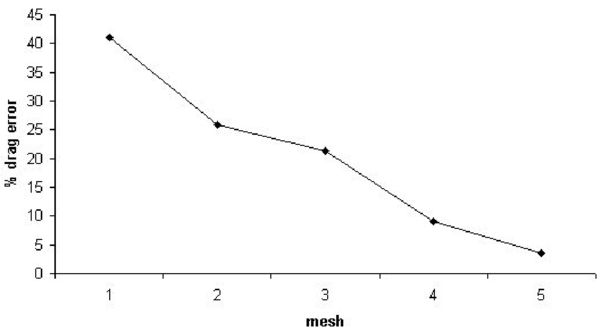
Figure 29: The convergence of the drag error

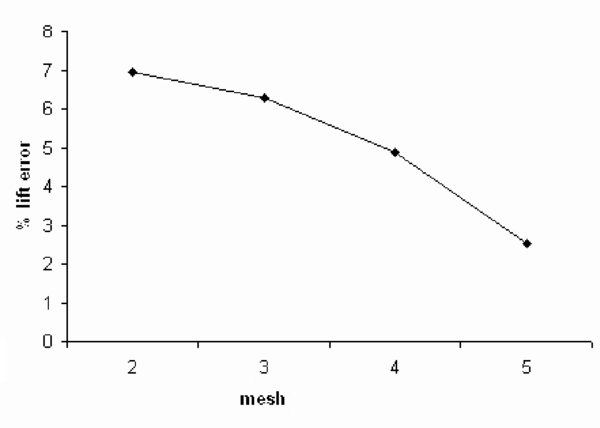
Figure 30: The convergence of the lift error

Figure 31: The convergence of the global error

8 CONCLUDING REMARKS

An error estimator for the finite element analysis of incompressible fluid flow problems has been proposed. The estimator is based on the weigthed form (the power) of the residuals of the stabilized momentum and mass balance equations. The particular form of the weighting functions used has been found from a finite calculus formulation of the Navier-Stokes equations. This weighted residual form derived is also applicable for error estimation and mesh adaptivity in other problems in computational mechanics [22].

A simple mesh refinement strategy based on the equal distribution of the total residual power among the elements in the mesh has been presented. The refinement strategy has proven to be more cost-effective than that based on the equal distribution of the density of the error also presented in the paper. The efficiency of the error estimation and the mesh adaptation process has been verified in the solution of steady state and transient flow problems using a FIC stabilized formulation for the Navier-Stokes equations and a standard fractional step scheme.

The method yields refined meshes which capture very well the features of the velocity and pressure fields in high gradient zones near the solid boundaries and within the analysis domain. Note that in the problems presented here the global error is not reduced below its limited value. The reason is that a minimun element size has been prescribed in order to facilitate the mesh generation process. Should this limit be reduced then the global error would be subsequently reduced.

Further work in this field will focus in the relationship of the residual power error values and the error in selected individual variables (velocity, pressure, etc) or other solutions outputs target (drag, lift, etc.).

ACKNOWLEDGEMENTS

The numerical results were obtained using the finite element code Tdyn provided by the company COMPASS Ingeniería y Sistemas SA [31]. Thanks are also given to Dassault Aviation for providing the multiple airfoil geometry for the last example.

REFERENCES

[1] O.C. Zienkiewicz and R.L. Taylor. The finite element method. 5th Edition, 3 Volumes, Butterworth–Heinemann, 2000.

[2] O.C. Zienkiewicz and J.Z. Zhu. A simple error estimator and adaptive procedure for practical engineering analysis. Int. J. Num. Meth. Eng., 24, 337-57, 1987.

[3] J.Z. Zhu and O.C. Zienkiewicz. Adaptive techniques in the finite element method. Comm. App. Num. Math., 4, 197–204, 1988.

[4] Oñate E. and G. Bugeda. A study of mesh optimality criteria in adaptive finite element analysis. Engineering Computations, Vol. 3, 307-321, 1994.

[5] J. Wu, Z.J. Zhu, J. Szmelter and O.C. Zienkiewicz. Error estimation and adaptivity in Navier-Stokes incompressible flows. Comput Mechancis, 6, 254–70, 1990.

[6] R. Löhner, K. Morgan and O.C. Zienkiewicz. An adaptive finite element procedure for compressible high speed flows. Comp. Meth. Appl. Mech. Eng., 51, 441–65, 1985.

[7] R. Löhner, K Morgan and O.C. Zienkiewicz. Adaptive grid refinement for the Euler and compressible Navier-Stokes equations. in Accuracy Estimates and Adaptive Refinements in Finite Element Computations (eds I. Babuska, O.C. Zienkiewicz, J. Gago y E.R. de A. Oliveira), cap. 15, pp. 281–98, Wiley, Chichester, 1986.

[8] J. Peraire, M. Vahdati, K. Morgan and O.C. Zienkiewicz. Adaptive remeshing for compressible flow computations. J. Comp. Phys., 72, 449–66, 1987.

[9] J.T. Oden, T. Strouboulis and P. Devloo. Adaptive finite element methods for high speed compressible flows. Int. J. Num. Meth. Eng., 7, 1211–28, 1987.

[10] R. Löhner. Adaptive remeshing for transient problems. Comput. Meth. Appl. Mech. Eng., 75, 195–214, 1989.

[11] J.T. Oden, W. Wu and M. Ainsworth. An a posteriori error estimate for finite element approximations of the Navier-Stokes equations, Comput. Meth. Appl. Mech. Eng., 111, 185–202, 1993.

[12] C. Johnson, R. Rannacher and M. Boman. Numerics and hydrodynamic stability: Towards error control in CFD. SIAM J. Numer. Anal., 32, 1058–1079, 1995.

[13] R.C. Almeida, R.A. Feijoo, A.C. Galeao, C. Padra and R.S. Silva. Adaptive finite element computational fluid dynamics using an anisotropic error estimator. Comput. Meth. Appl. Mech. Eng., 182, 379–400, 2000.

[14] J.M. Cascón, G.C. García and R. Rodríguez. A priori and a posteriori error analysis for a large-scale ocean circulation finite element model. Comput. Meth. Appl. Mech. Eng., 192, 5305–5327, 2003.

[15] W. Bangerth and R. Rannacher. Adaptive finite elements for differential equations. Birkhäuser Verlag, Basel, 2003.

[16] D.L. Darmofal, D.A. Venditti. Anisotropic grid adaptation for functional outputs: Application to two-dimensional viscous flows. Journal of Computational Physics, 187, 22–66, 2003.

[17] E. Oñate. Derivation of stabilized equations for advective-diffusive transport and fluid flow problems. Comput. Methods Appl. Mech. Engrg., 151:1-2, 233–267, 1998.

[18] E. Oñate. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput. Methods Appl. Mech. Engrg., 182:1–2, 355–370, 2000.

[19] E. Oñate and J. García. A finite element method for fluid-structure interaction with surface waves using a finite calculus formulation. in Comput. Methods Appl. Mech. Engrg., 191:6-7, 635-660, 2001.

[20] E. Oñate, J. García, G. Bugeda and S.R. Idelsohn. A general stabilized formulation for incompressible fluid flow using finite calculus and the FEM. In Towards a new fluid dynamics with its challenges in aeronautics, J. Periaux, D. Chamption, O. Pironneau and Ph. Thomas (Eds.), CIMNE, Barcelona, Spain 2002.

[21] E. Oñate, J. García, S.R. Idelsohn and F. Del Pin. FIC formulations for finite element analysis of incompressible flows. Eulerian, ALE and Lagrangian approaches, Submitted to Comput. Methods Appl. Mech. Engng., July 2004.

[22] E. Oñate, J. Arteaga and R. Flores. A weigthed recovered residual method for error estimation and mesh adaptivity in convection-diffusion problems. Research Report CIMNE, Barcelona, September 2004.

[23] GiD. The personal pre/postprocessing system. CIMNE, Barcelona, www.gidhome.com, 2004.

[24] M.A. Cruchaga and E. Oñate. A finite element formulation for incompressible flow problems using a generalized streamline operator. Comput. Methods Appl. Mech. Engng., 143, 49–67, 1997.

[25] T.J.R. Hughes and M. Mallet. A new finite element formulations for computational fluid dynamics: III. The generalized streamline operator for multidimensional advective-diffusive systems. Comput Methods Appl. Mech. Engrg., 58, 305–328, (1986a).

[26] T.J.R. Hughes, L.P. Franca and G.M. Hulbert. A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations. Comput. Methods Appl. Mech. Engrg., 73, 173–189, (1989).

[27] T.J.R. Hughes. Multiscale phenomena: Green functions, subgrid scale models, bubbles and the origins of stabilized methods. Comput. Methods Appl. Mech. Engrg, 127, 387–401, (1995).

[28] R. Codina. Comparison of some finite element methods for solving the diffusion-convection-reaction equation. Comput. Methods Appl. Mech. Engrg., 156, 185–210, (1998).

[29] R. Codina. Stabilization of incompressibility and convection through orthogonal sub-scales in finite element method. Comput. Methods Appl. Mech. Engrg., 190, 1579–1599, (2000).

[30] O.C. Zienkiewicz and R. Codina. A general algorithm for compressible and incompressible flow. Part I: The split characteristic based scheme. Int. J. Num. Meth. in Fluids, 20, 869-85, (1995).

[31] Tdyn. An unstructured finite element code for fluid dynamic analysis, COMPASS Ingeniería y Sistemas SA, www.compassis.com, 2003.