| (49 intermediate revisions by 2 users not shown) | |||
| Line 9: | Line 9: | ||
In previous works, the nonlinear localization was first presented and studied in the case of large displacements but only for globally stable structural responses. In this paper, the parallelization of this computational strategy using a Balancing Domain Decomposition by Constrains (BDD-C) is presented. Finally, a validation of this implementation is carried out in lineal elasticity, verifying the ''speed-up'' and the numerical extensibility. | In previous works, the nonlinear localization was first presented and studied in the case of large displacements but only for globally stable structural responses. In this paper, the parallelization of this computational strategy using a Balancing Domain Decomposition by Constrains (BDD-C) is presented. Finally, a validation of this implementation is carried out in lineal elasticity, verifying the ''speed-up'' and the numerical extensibility. | ||
| − | ==1 Introducción== | + | ==1. Introducción== |
En estructuras aeronáuticas como fuselajes la mayor no linealidad que ocurre corresponde a pandeo localizado en elementos esbeltos. Durante los ensayos estructurales de certificación llevados a cabo en un fuselaje completo, se observa pandeo en la piel entre los rigidizadores. Al aumentar las cargas, estos fenómenos se pueden expandir y provocar redistribuciones de esfuerzos en la estructura. Para cargas normales de trabajo, estos fenómenos son reversibles, el material se mantiene dentro del rango lineal. De todas formas, pueden provocar concentraciones de esfuerzo alrededor de las bases de los rigidizadores que pueden ser el origen de daños locales conducentes a fallas completas de las estructuras. Realizar cálculos de estos fenómenos para grandes estructuras como un fuselaje completo, conlleva mallas con aprox. <math display="inline">10^8</math> grados de libertad (g.d.l.), incluso con mallas adaptadas. Debido al gran número de incógnitas y a las limitaciones tanto de memoria como de los procesadores, la resolución directa de este tipo de problemas mediante el Método de Elementos Finitos (MEF) es impracticable. Es por esta razón, que los ingenieros usan métodos de aproximación basados en super-elementos (condensación lineal de g.d.l. internos) o análisis global-local, que corresponden a un cálculo lineal global de toda la estructura seguido de análisis locales no lineales. Si bien estos métodos permiten realizar ciertos cálculos, no toman en cuenta fenómenos como redistribuciones de esfuerzos o expansión de zonas con no linealidades, debido a que solo ofrecen un diálogo en una sola dirección debido a las escalas introducidas. Como resultado, solo pueden tratar no linealidades localizadas que no tengan una influencia en la respuesta global de la estructura. Nuevos avances, utilizando máquinas en paralelo y cluster, nos permiten hoy en día distribuir el costo computacional y requerimientos de memoria en varios procesadores. Problemas muy complejos son abordables siempre que los métodos de resolución puedan tomar ventaja del paralelismo inherente de los hardwares disponibles. En este estudio, se exploran las posibilidades relacionadas con estrategias de cálculo en paralelo y multiescala en el contexto de problemas no lineales geométricamente. | En estructuras aeronáuticas como fuselajes la mayor no linealidad que ocurre corresponde a pandeo localizado en elementos esbeltos. Durante los ensayos estructurales de certificación llevados a cabo en un fuselaje completo, se observa pandeo en la piel entre los rigidizadores. Al aumentar las cargas, estos fenómenos se pueden expandir y provocar redistribuciones de esfuerzos en la estructura. Para cargas normales de trabajo, estos fenómenos son reversibles, el material se mantiene dentro del rango lineal. De todas formas, pueden provocar concentraciones de esfuerzo alrededor de las bases de los rigidizadores que pueden ser el origen de daños locales conducentes a fallas completas de las estructuras. Realizar cálculos de estos fenómenos para grandes estructuras como un fuselaje completo, conlleva mallas con aprox. <math display="inline">10^8</math> grados de libertad (g.d.l.), incluso con mallas adaptadas. Debido al gran número de incógnitas y a las limitaciones tanto de memoria como de los procesadores, la resolución directa de este tipo de problemas mediante el Método de Elementos Finitos (MEF) es impracticable. Es por esta razón, que los ingenieros usan métodos de aproximación basados en super-elementos (condensación lineal de g.d.l. internos) o análisis global-local, que corresponden a un cálculo lineal global de toda la estructura seguido de análisis locales no lineales. Si bien estos métodos permiten realizar ciertos cálculos, no toman en cuenta fenómenos como redistribuciones de esfuerzos o expansión de zonas con no linealidades, debido a que solo ofrecen un diálogo en una sola dirección debido a las escalas introducidas. Como resultado, solo pueden tratar no linealidades localizadas que no tengan una influencia en la respuesta global de la estructura. Nuevos avances, utilizando máquinas en paralelo y cluster, nos permiten hoy en día distribuir el costo computacional y requerimientos de memoria en varios procesadores. Problemas muy complejos son abordables siempre que los métodos de resolución puedan tomar ventaja del paralelismo inherente de los hardwares disponibles. En este estudio, se exploran las posibilidades relacionadas con estrategias de cálculo en paralelo y multiescala en el contexto de problemas no lineales geométricamente. | ||
| − | En este trabajo se presenta la paralelización de una estrategia de cálculo basada en el método de descomposición de dominio llamado Newton-Krylov-Schur (NKS) | + | En este trabajo se presenta la paralelización de una estrategia de cálculo basada en el método de descomposición de dominio llamado Newton-Krylov-Schur (NKS) [1,2], el cual es uno de los métodos paralelos de referencia para la resolución de problemas no lineales para el caso del post-pandeo. Este método NKS se ha modificado integrando una etapa de localización no lineal [3], además de introducir una descomposición de dominio mixta. Esta etapa de localización no lineal consiste en realizar iteraciones adicionales en los subdominios después de cada iteración global de manera de obtener el comportamiento no lineal y el equilibrio en ellos. En trabajos anteriores [3,4,5] se ha demostrado la eficacia de esta estrategia de cálculo para problemas con no linealidades locales y desbalanceadas. En una primera parte, se presenta la estrategia de localización no lineal, para luego en una segunda parte, presentar la paralelización de la estrategia mediante un método BDDC [6] junto con una validación de la misma en el caso de elasticidad lineal. |
| − | ==2 Métodos de descomposición de dominio== | + | ==2. Métodos de descomposición de dominio== |
| − | Los métodos de descomposición de dominio (MDD) | + | Los métodos de descomposición de dominio (MDD) [7] permiten resolver grandes problemas en computadores paralelos. Existen diferentes MDD dependiendo de las condiciones que transmiten entre los subdominios. Los métodos primales [8,9] favorecen la continuidad de desplazamientos mientras que los métodos duales [10] favorecen ''a-priori'' el equilibrio de fuerzas entre los subdominios. Los métodos mixtos [11,12,13,14] utilizan relaciones de tipo Robin entre los desplazamientos y fuerzas en las interfaces, sin favorecer a ninguno de los dos. Cuando los MDD son utilizados con el procedimiento iterativo de Newton para resolver problemas no lineales, estas estrategias se llaman métodos NKS [1]. Estos métodos se basan en: |
* Método de Newton para la linearización del problema no lineal y el esquema iterativo incremental. | * Método de Newton para la linearización del problema no lineal y el esquema iterativo incremental. | ||
| Line 24: | Line 24: | ||
La Figura [[#img-1|1]] presenta las diferentes etapas del método NKS clásico. Estos métodos involucran un gran número de sistemas lineales, que producen una gran cantidad de comunicaciones entre los procesadores (ensamblaje del residuo global). Cuando son aplicados a grandes problemas no lineales un importante esfuerzo computacional se utiliza en regiones lineales cuando las no linealidades no están igualmente distribuidas. <div id='img-1'></div> | La Figura [[#img-1|1]] presenta las diferentes etapas del método NKS clásico. Estos métodos involucran un gran número de sistemas lineales, que producen una gran cantidad de comunicaciones entre los procesadores (ensamblaje del residuo global). Cuando son aplicados a grandes problemas no lineales un importante esfuerzo computacional se utiliza en regiones lineales cuando las no linealidades no están igualmente distribuidas. <div id='img-1'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | |[[Image:draft_Samper_613894993-fignks_esp.png|450px|Método NKS clásico.]] | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-fignks_esp.png|450px|Método NKS clásico.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 1:''' Método NKS clásico. | + | | colspan="1" style="padding-bottom:10px;"| '''Figura 1:''' Método NKS clásico. |
|} | |} | ||
| − | ==3 Principio de la localización no lineal== | + | ==3. Principio de la localización no lineal== |
| − | Cuando el problema inicial es descompuesto en subdominios antes de la linearización, el equilibrio no lineal de cada subdominio se debe asegurar en cada iteración. Los problemas no lineales son resueltos en cada subdominio para valores de interfaz dados. Lo que conlleva a la estrategia presentada en la Figura [[#img-2|2]]. Con respecto a los MDD clásicos utilizados para resolver problemas no lineales, en las etapas locales de los subdominios se resuelven problemas no lineales. Es este paso el que llamaremos localización no lineal. Esta estrategia ha sido evaluada para el cálculo de estructuras con pandeo localizado, con MDD primales y duales, y comparado con la estrategia clásica NKS | + | Cuando el problema inicial es descompuesto en subdominios antes de la linearización, el equilibrio no lineal de cada subdominio se debe asegurar en cada iteración. Los problemas no lineales son resueltos en cada subdominio para valores de interfaz dados. Lo que conlleva a la estrategia presentada en la Figura [[#img-2|2]]. Con respecto a los MDD clásicos utilizados para resolver problemas no lineales, en las etapas locales de los subdominios se resuelven problemas no lineales. Es este paso el que llamaremos localización no lineal. Esta estrategia ha sido evaluada para el cálculo de estructuras con pandeo localizado, con MDD primales y duales, y comparado con la estrategia clásica NKS [3]. La versión dual se ha aplicado a daño [15]. La versión mixta ha sido aplicada en delaminación de materiales compuestos [16], para la interacción delaminación/pandeo en materiales compuestos [17] y para la simulación de fractura en madera [18]. <div id='img-2'></div> |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | |[[Image:draft_Samper_613894993-fignks2_esp.png|330px|Método NKS con etapa de localización no lineal.]] | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-fignks2_esp.png|330px|Método NKS con etapa de localización no lineal.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 2:''' Método NKS con etapa de localización no lineal. | + | | colspan="1" style="padding-bottom:10px;"| '''Figura 2:''' Método NKS con etapa de localización no lineal. |
|} | |} | ||
===3.1 Estrategia de localización no lineal mixta=== | ===3.1 Estrategia de localización no lineal mixta=== | ||
| − | Dos clases de MDD mixto se pueden encontrar en la literatura: Uno basado en la introducción de condiciones mixtas mediante una formulación Lagrangiana aumentada, que asume la existencia de un potencial para la energía de deformación. Tres campos de interfaces son introducidos: la traza en las interfaces del desplazamiento de los subdominios, el multiplicador de Lagrange y un desplazamiento de interfaz adicional | + | Dos clases de MDD mixto se pueden encontrar en la literatura: Uno basado en la introducción de condiciones mixtas mediante una formulación Lagrangiana aumentada, que asume la existencia de un potencial para la energía de deformación. Tres campos de interfaces son introducidos: la traza en las interfaces del desplazamiento de los subdominios, el multiplicador de Lagrange y un desplazamiento de interfaz adicional [13,19]. En la otra clase, se introducen algoritmos con dos direcciones de búsqueda, sin recurrir a los multiplicadores de Lagrange. Dos juegos de interfaces son introducidas: las fuerzas y los desplazamientos de las interfaces. Ambas cumpliendo un rol simétrico [20]. Los MDD basados en el método LATIN [21] corresponden a este tipo de métodos. También se pueden mencionar los trabajos de [12] que propuso un algoritmo con dos direcciones de búsqueda, versión ALG3 [20]. |
====3.1.1 Etapa local no lineal==== | ====3.1.1 Etapa local no lineal==== | ||
| − | La primera etapa consiste en encontrar los campos de fuerzas y desplazamiento <math display="inline">\underline{f} | + | La primera etapa consiste en encontrar los campos de fuerzas y desplazamiento <math display="inline">\underline{f}</math> y <math display="inline">\underline{u}</math> para cada subdominio <math display="inline">\Omega ^s</math> que verifiquen el comportamiento no lineal y las condiciones de contorno mixtas, conociendo las fuerzas <math display="inline">\underline{F}^s</math> (equilibradas) y los desplazamientos <math display="inline">\underline{U}^s</math> (continuos en las interfaces) de la etapa lineal global (vea sección [[#3.1.2 Etapa global lineal|3.1.2]]) precedente resuelta en las interfaces (o una etapa de inicialización): |
<span id="eq-1"></span> | <span id="eq-1"></span> | ||
| − | <span id="eq-3"></span> | + | <span id="(eq-3)"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 56: | Line 56: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\underline{f} | + | | style="text-align: center;" | <math>\underline{f}_{int}^s (\underline{u}^s) + \overline{\underline{g}}^s + \underline{f}^s = \underline{0} \qquad \hbox{on} ~ \Omega ^s </math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | (1) | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> \underline{u} | + | | style="text-align: center;" | <math> \underline{u} ^s = \underline{\overline{u}}^s \qquad \qquad\hbox{on} ~ \partial _1 \Omega ^s </math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | (2) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> (\underline{f} | + | | style="text-align: center;" | <math> (\underline{f}^s - \underline{F}^s) + \mathbf{k}^s(\underline{u} ^s_b - \underline{U}^s) = \underline{0} \qquad \hbox{on} ~ \Gamma ^s </math> |
| style="width: 5px;text-align: right;white-space: nowrap;" | (3) | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">\underline{f} | + | donde <math display="inline">\underline{f}_{int}^s</math> es la parte correspondiente a los grados de libertad (g.d.l.) internos del vector fuerza que soporta el subdominio <math display="inline">{}^s</math>, <math display="inline">\overline{\underline{g}}^s</math> son las cargas externas, <math display="inline">\underline{\overline{u}}^s</math> a los desplazamientos impuestos, <math display="inline">\partial _1 \Omega ^s</math> condiciones de contorno, <math display="inline">\mathbf{k}^s</math> es el parámetro de tipo Robin que corresponde a una dirección de búsqueda y el subíndice <math display="inline">{}_b</math> a los nodos de interfaz de cada subdominio. La ecuación [[#(eq-3)|(3)]] corresponde a una condición de tipo Robin. Las variables en mayúscula se refieren a cantidades de interfaz que son conocidas (vea sección [[#3.1.2 Etapa global lineal|3.1.2]]). |
| − | Linearizando la ecuación [[#eq-1|1]] con la [[#eq-3|3]] se obtiene el siguiente problema tangente por subdominio: | + | Linearizando la ecuación [[#eq-1|(1)]] con la [[#eq-3|(3)]] se obtiene el siguiente problema tangente por subdominio: |
| − | <span id="eq- | + | <span id="eq-4"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 77: | Line 77: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\left[ \begin{array}{cc}{\mathbf{K}}^s_{Tii}(\underline{u} | + | | style="text-align: center;" | <math>\left[ \begin{array}{cc}{\mathbf{K}}^s_{Tii}(\underline{u}^s) & {\mathbf{K}}^s_{Tib} (\underline{u}^s)\\ {\mathbf{K}}^s_{Tbi}(\underline{u}^s) & {\mathbf{K}}^s_{Tbb} (\underline{u}^s) + {\mathbf{k}^s}\\ \end{array} \right] \left[ \begin{array}{c}{\delta \underline{u}^s_i} \\ {\delta \underline{u}^s_b}\\ \end{array} \right]= \left[ \begin{array}{c}{\underline{r}^s_i} \\ {\underline{r}^s_b}+{\mathbf{k}^s} \cdot{\Delta \underline{U}^s + \underline{F}^s}\\ \end{array} \right] </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) |
|} | |} | ||
| − | donde el subíndice <math display="inline">{}_i</math> referencia los g.d.l. interiores de los subdominios, <math display="inline">{\mathbf{K}}^s_{T}</math> representa la matriz tangente del subdominio <math display="inline">{}^s</math>, <math display="inline">{\delta \underline{u} | + | donde el subíndice <math display="inline">{}_i</math> referencia los g.d.l. interiores de los subdominios, <math display="inline">{\mathbf{K}}^s_{T}</math> representa la matriz tangente del subdominio <math display="inline">{}^s</math>, <math display="inline">{\delta \underline{u}^s}</math> es un incremento de desplazamientos, <math display="inline">{\underline{r}^s}</math> es un residuo y <math display="inline">{\Delta \underline{U}^s}</math> es el salto de desplazamientos entre la interfaz y el subdominio (al tratarse de un método mixto, las interfaces y los subdominios pueden estar separadas durante el proceso iterativo). Las condiciones de contorno, son tomadas en cuenta por medio de un método de eliminación directa. |
| − | El parámetro de tipo Robin, <math display="inline">\mathbf{k}^s</math>, es un parámetro del método. Este parámetro corresponde a un operador linear simétrico definido positivo y representa la rigidez de la vecindad del subdominio en cuestión. Normalmente, se define como parte del complemento de Schur primal de los subdominios vecinos asociados con los g.d.l. considerados en la interfaz del subdominio analizado, <math display="inline">{\mathbf{k}^s} = {\mathbf{S}^s}</math>. Este operador se obtiene ensamblando las diferentes contribuciones de los subdominios vecinos en la interfaz considerada, cuando todos sus otras interfaces están empotradas. Para mayores detalles en cuanto a la definición, como en la influencia del parámetro Robin en el desempeño de la estrategia, el lector se puede referir a | + | El parámetro de tipo Robin, <math display="inline">\mathbf{k}^s</math>, es un parámetro del método. Este parámetro corresponde a un operador linear simétrico definido positivo y representa la rigidez de la vecindad del subdominio en cuestión. Normalmente, se define como parte del complemento de Schur primal de los subdominios vecinos asociados con los g.d.l. considerados en la interfaz del subdominio analizado, <math display="inline">{\mathbf{k}^s} = {\mathbf{S}^s}</math>. Este operador se obtiene ensamblando las diferentes contribuciones de los subdominios vecinos en la interfaz considerada, cuando todos sus otras interfaces están empotradas. Para mayores detalles en cuanto a la definición, como en la influencia del parámetro Robin en el desempeño de la estrategia, el lector se puede referir a [4]. En [22], se demuestra que una buena elección del parámetro de tipo Robin es fundamental para obtener un método eficiente. |
====3.1.2 Etapa global lineal==== | ====3.1.2 Etapa global lineal==== | ||
| − | La segunda etapa consiste en asegurar la admisibilidad de las incógnitas de interfaz: equilibrio de fuerzas <math display="inline">\underline{F} | + | La segunda etapa consiste en asegurar la admisibilidad de las incógnitas de interfaz: equilibrio de fuerzas <math display="inline">\underline{F}</math> y continuidad de desplazamientos <math display="inline">\underline{U}</math> , además de transmitir la información mecánica a través de toda la estructura, de manera de asegurar la escalabilidad del algoritmo. Más precisamente, conociendo <math display="inline">\underline{f}^s</math> y <math display="inline">\underline{u}^s</math> (fuerzas y desplazamientos provenientes de la etapa local precedente, vea sección [[#3.1.1 Etapa local no lineal|3.1.1]]) o una etapa de inicialización, <math display="inline">\underline{F}</math> y <math display="inline">\underline{U}</math> deben verificar la continuidad de desplazamientos [[#eq-5|(5)]] y el equilibrio de fuerzas [[#eq-6|(6)]] para cada interfaz <math display="inline">\Gamma ^{ss'}</math> que conecta dos subdominios <math display="inline">{}^{s}</math> y <math display="inline">{}^{s'}</math>: |
| − | <span id="eq- | + | <span id="eq-5"></span> |
| − | <span id="eq- | + | <span id="eq-6"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 97: | Line 97: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\underline{U} | + | | style="text-align: center;" | <math>\underline{U}^s = \underline{U}^{s'} \quad \hbox{ on} \quad \Gamma ^{ss'} </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \underline{F} | + | | style="text-align: center;" | <math> \underline{F}^s + \underline{F}^{s'} = \underline{0} \quad \quad \hbox{ on} \quad \Gamma ^{ss'} </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) |
|} | |} | ||
|} | |} | ||
| Line 112: | Line 112: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\mathbf{S}_T^s(\underline{U} | + | | style="text-align: center;" | <math>\mathbf{S}_T^s(\underline{U}^s - \underline{u}^s_b) = \underline{F}^s - \underline{f}^s_b</math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \mathbf{S}_T^{s'}(\underline{U} | + | | style="text-align: center;" | <math> \mathbf{S}_T^{s'}(\underline{U}^{s'} - \underline{u}^{s'}_b) = \underline{F}^{s'} - \underline{f}^{s'}_b </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) |
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">\underline{u} | + | donde <math display="inline">\underline{u}^s_b</math>, <math display="inline">\underline{u}^{s'}_b</math>, <math display="inline">\underline{f}^s_b</math> y <math display="inline">\underline{f}^{s'}_b</math> son conocidas. La elección de la dirección de búsqueda <math display="inline">\mathbf{S}_T^s</math> se basa en los trabajos de [3] en donde se utiliza para propagar información global entre los subdominios, donde <math display="inline">\mathbf{S}_T</math> corresponde al complemento primal de Schur del subdominio <math display="inline">{^s}</math>, que conecta todos los g.d.l. del subdominio <math display="inline">{^s}</math> y se calcula: |
| − | <span id="eq- | + | <span id="eq-9"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 130: | Line 130: | ||
| style="text-align: center;" | <math>\mathbf{S}_T^s = \mathbf{K}^s_{bb} - \mathbf{K}^s_{bi} {\mathbf{K}^s_{ii}}^{-1} \mathbf{K}^s_{ib} </math> | | style="text-align: center;" | <math>\mathbf{S}_T^s = \mathbf{K}^s_{bb} - \mathbf{K}^s_{bi} {\mathbf{K}^s_{ii}}^{-1} \mathbf{K}^s_{ib} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) |
|} | |} | ||
El problema mixto no lineal condensado que se obtiene desde el equilibrio de las interfaces se puede resolver con un Newton-Raphson. Luego de la linearización y utilizando una formulación en desplazamientos, se obtiene: | El problema mixto no lineal condensado que se obtiene desde el equilibrio de las interfaces se puede resolver con un Newton-Raphson. Luego de la linearización y utilizando una formulación en desplazamientos, se obtiene: | ||
| − | <span id="eq- | + | <span id="eq-10"></span> |
| − | <span id="eq- | + | <span id="eq-11"></span> |
| − | <span id="eq- | + | <span id="eq-12"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 143: | Line 143: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\mathbf{S}_T \delta{\underline{U} | + | | style="text-align: center;" | <math>\mathbf{S}_T \delta{\underline{U}} = \underline{R}</math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \underline{U} | + | | style="text-align: center;" | <math> \underline{U}^s = {\underline{U}^s}_{\hbox{old}} + \delta \underline{U}^s </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (11) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \underline{F} | + | | style="text-align: center;" | <math> \underline{F}^s = \underline{f}^s_b + \mathbf{S}_T^s (\underline{U}^s-\underline{u}^s_b) </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (12) |
|} | |} | ||
|} | |} | ||
| − | donde <math display="inline">\mathbf{S}_T</math> y <math display="inline">\underline{R} | + | donde <math display="inline">\mathbf{S}_T</math> y <math display="inline">\underline{R}</math> corresponden al ensamblaje de los problemas condensados y los residuos de cada subdominio respectivamente, según: |
| − | <span id="eq- | + | <span id="eq-14"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 163: | Line 163: | ||
|- | |- | ||
| style="text-align: center;" | <math>\mathbf{S}_T = \sum _s \big(A^s \mathbf{S}^s_T {A^s}^t\big)</math> | | style="text-align: center;" | <math>\mathbf{S}_T = \sum _s \big(A^s \mathbf{S}^s_T {A^s}^t\big)</math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (13) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \underline{R} | + | | style="text-align: center;" | <math> \underline{R} = \sum _sA^s \Big({\mathbf{S}_T^s} \underline{u}^s_b +\underline{r}^s_b - \mathbf{K}^s_{bi} {\mathbf{K}^s_{ii}}^{-1} \underline{r}^s_i \Big) </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (14) |
|} | |} | ||
|} | |} | ||
| Line 172: | Line 172: | ||
donde <math display="inline">A^s</math> corresponde al operador de ensamblaje, que conecta los g.d.l. de borde del subdominio <math display="inline">(s)</math> con las incógnitas del problema global. | donde <math display="inline">A^s</math> corresponde al operador de ensamblaje, que conecta los g.d.l. de borde del subdominio <math display="inline">(s)</math> con las incógnitas del problema global. | ||
| − | Esto implica la solución de problemas no lineales locales en cada subdominio para las cantidades de interfaz (<math display="inline">\underline{F} | + | Esto implica la solución de problemas no lineales locales en cada subdominio para las cantidades de interfaz (<math display="inline">\underline{F}^s</math>, <math display="inline">\underline{U}^s</math>) y para la condición de tipo Robin [[#eq-3|(3)]]. Resolviendo el problema de interfaces global [[#eq-10|(10)]], se obtiene <math display="inline">\delta{\underline{U}}</math>, que corresponde al incremento del desplazamiento en las interfaces <math display="inline">\underline{U}</math> [[#eq-11|(11)]]. Las fuerzas balanceadas de las interfaces <math display="inline">\underline{F}</math> se obtienen a partir de la ecuación [[#eq-12|(12)]] cuando los desplazamientos <math display="inline">\underline{U}</math> son conocidos. Los problemas [[#eq-11|(11)]] y [[#eq-12|(12)]] pueden ser resueltos independientemente en cada subdominio. El sistema [[#eq-10|(10)]] puede ser resuelto de la misma manera que los métodos NKS clásicos, incluso utilizando los mismos precondicionadores y procedimientos iterativos. Para más detalles sobre la estrategia, el lector puede referirse a [4]. |
| − | ==4 Paralelización de la estrategia de localización no lineal mixta== | + | ==4. Paralelización de la estrategia de localización no lineal mixta== |
Las estrategia de localización no lineal, como los métodos NKS clásicos, están adaptados a la arquitectura en paralelo de las máquinas de computo modernas. El problema tangente de interfaz, etapa global, se puede resolver utilizando un procedimiento iterativo de Krylov que solo realiza productos matriz-vector. El intercambio de información entre subdominios es necesario a cada iteración. Por el contrario, la etapa no lineal, consiste en cálculos totalmente independientes en cada subdominio. Una implementación en paralelo clásica, consiste en asociar cada subdominio a un procesador distinto, por ejemplo en un Cluster. Algunos procesadores pueden requerir esperar un largo tiempo a que los otros terminen sus tareas. Estos tiempos de espera afectan le efectividad del método y, en general, se busca repartir de la mejor manera posible las tareas entre los distintos procesadores. Esta problemática ya ha sido tratada en la implementación de MDD clásicos. En estos casos la descomposición del dominio se hace de manera automática de forma de que cada problema local (factorización y resolución del sistema lineal) represente un costo de cálculo lo más uniforme posible; Esto se logra con algoritmos de particionamiento, por ejemplo METIS. | Las estrategia de localización no lineal, como los métodos NKS clásicos, están adaptados a la arquitectura en paralelo de las máquinas de computo modernas. El problema tangente de interfaz, etapa global, se puede resolver utilizando un procedimiento iterativo de Krylov que solo realiza productos matriz-vector. El intercambio de información entre subdominios es necesario a cada iteración. Por el contrario, la etapa no lineal, consiste en cálculos totalmente independientes en cada subdominio. Una implementación en paralelo clásica, consiste en asociar cada subdominio a un procesador distinto, por ejemplo en un Cluster. Algunos procesadores pueden requerir esperar un largo tiempo a que los otros terminen sus tareas. Estos tiempos de espera afectan le efectividad del método y, en general, se busca repartir de la mejor manera posible las tareas entre los distintos procesadores. Esta problemática ya ha sido tratada en la implementación de MDD clásicos. En estos casos la descomposición del dominio se hace de manera automática de forma de que cada problema local (factorización y resolución del sistema lineal) represente un costo de cálculo lo más uniforme posible; Esto se logra con algoritmos de particionamiento, por ejemplo METIS. | ||
| − | En el caso del presente trabajo, es mucho más difícil poder evaluar ''a-priori'' el costo de cálculos no lineales por subdominio, que dependen de los operadores, pero también del nivel de cargas externas sobre los subdominios. Una estimación posible consiste en considerar el número de iteraciones de la etapa no lineal precedente. De todas formas, este costo puede variar entre distintas iteraciones. En esos casos, se puede utilizar métodos de repartición dinámica. Utilizando un número inferior de procesadores que de subdominios puede facilitar esa tarea. Algunas alternativas a estos problemas han sido desarrolladas por | + | En el caso del presente trabajo, es mucho más difícil poder evaluar ''a-priori'' el costo de cálculos no lineales por subdominio, que dependen de los operadores, pero también del nivel de cargas externas sobre los subdominios. Una estimación posible consiste en considerar el número de iteraciones de la etapa no lineal precedente. De todas formas, este costo puede variar entre distintas iteraciones. En esos casos, se puede utilizar métodos de repartición dinámica. Utilizando un número inferior de procesadores que de subdominios puede facilitar esa tarea. Algunas alternativas a estos problemas han sido desarrolladas por [23,24]. |
===4.1 Principios de paralización y dificultades=== | ===4.1 Principios de paralización y dificultades=== | ||
| Line 190: | Line 190: | ||
===4.3 Paralelización de la etapa global=== | ===4.3 Paralelización de la etapa global=== | ||
| − | La paralelización del problema global de interfaz se puede hacer de diferente formas. Una solución consiste en la utilización de librerías paralelas de resolución de sistemas lineares por ejemplo: MUMPS (MUltifrontal Massively Parallel Sparse direct Solver), HIPS (Hierarchical Iterative Parallel Solver), PaStiX (Parallel Sparse matriX package). El principal problema con estas librerías es que los resultados no son extensibles en función del número de procesadores. De todas formas estas librerías mantienen sus eficiencias para un número moderado de procesadores (del orden de 10 a 100), el ''speed-up'' se ve afectado para un número creciente de procesadores. Otra opción consiste en la utilización de procedimientos de solución paralelos de tipo BDD o FETI. Como el problema de interfaces está formulado en desplazamientos, el método BDD | + | La paralelización del problema global de interfaz se puede hacer de diferente formas. Una solución consiste en la utilización de librerías paralelas de resolución de sistemas lineares por ejemplo: MUMPS (MUltifrontal Massively Parallel Sparse direct Solver), HIPS (Hierarchical Iterative Parallel Solver), PaStiX (Parallel Sparse matriX package). El principal problema con estas librerías es que los resultados no son extensibles en función del número de procesadores. De todas formas estas librerías mantienen sus eficiencias para un número moderado de procesadores (del orden de 10 a 100), el ''speed-up'' se ve afectado para un número creciente de procesadores. Otra opción consiste en la utilización de procedimientos de solución paralelos de tipo BDD o FETI. Como el problema de interfaces está formulado en desplazamientos, el método BDD [9] será utilizado y mejorado con la implementación de un precondicionador de tipo BDDC (Balancing Domain Decomposition by Constraints) [6]. Las restricciones adicionales introducidas por el precondicionador corresponden a la continuidad de desplazamientos en los nodos esquina de los subdominios. El problema está escrito con una formulación corrotacional [25] lo que genera sistemas no simétricos, debido a lo cual se utiliza un algoritmo de tipo GMRES. |
====4.3.1 Paralelización de la etapa global con un método BDD==== | ====4.3.1 Paralelización de la etapa global con un método BDD==== | ||
| − | El residuo global consiste en ensamblar los residuos locales. El cálculo de los distintos residuos locales condensados se realiza en cada procesador, <math display="inline">(\underline{r} | + | El residuo global consiste en ensamblar los residuos locales. El cálculo de los distintos residuos locales condensados se realiza en cada procesador, <math display="inline">(\underline{r}^s_b - \mathbf{K}^s_{bi} {\mathbf{K}^s_{ii}}^{-1} \underline{r}^s_i)</math>. Además se deben considerar los saltos de desplazamiento entre los subdominios <math display="inline">({\mathbf{S}_T^s} \underline{u}^s_b)</math>. Finalmente se deben ensamblar todas estas contribuciones (ecuación [[#eq-14|(14)]]). |
El objetivo de este procedimiento es no realizar multiplicaciones entre matrices, si no productos matriz-vector. Para eso, es necesario construir dos matrices, <math display="inline">\overline{\mathbf{K}}^s_{ii}\mathbf{I}</math> y <math display="inline">\overline{\mathbf{K}}^s_{bi}\mathbf{I}</math> para poder realizar las siguientes operaciones por subdominio: | El objetivo de este procedimiento es no realizar multiplicaciones entre matrices, si no productos matriz-vector. Para eso, es necesario construir dos matrices, <math display="inline">\overline{\mathbf{K}}^s_{ii}\mathbf{I}</math> y <math display="inline">\overline{\mathbf{K}}^s_{bi}\mathbf{I}</math> para poder realizar las siguientes operaciones por subdominio: | ||
| Line 203: | Line 203: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\underline{b} | + | | style="text-align: center;" | <math>\underline{b}^s = -\underbrace{\left[ \begin{array}{cc} {\mathbf{K}}^s_{bi} & -\mathbf{I} \end{array} \right]}_{\overline{\mathbf{K}}^s_{bi}\mathbf{I}} \underbrace{\left[ \begin{array}{cc} {\mathbf{K}}^s_{ii} & \mathbf{0}\\ \mathbf{0} & \mathbf{I} \end{array} \right]^{-1}}_{\overline{\mathbf{K}}^s_{ii}\mathbf{I}} \left( \begin{array}{c}\underline{r}^s_i\\ \underline{r}^s_b \end{array} \right) </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) |
|} | |} | ||
| − | Es necesario tener presente la multiplicidad de cada g.d.l. de interfaz. Los nodos compartidos por 2 subdominios tienen multiplicidad 2, los compartidos por 3 subdominios, tienen multiplicidad 3, etc. Antes de ensamblar, cada termino del vector <math display="inline">\underline{b} | + | Es necesario tener presente la multiplicidad de cada g.d.l. de interfaz. Los nodos compartidos por 2 subdominios tienen multiplicidad 2, los compartidos por 3 subdominios, tienen multiplicidad 3, etc. Antes de ensamblar, cada termino del vector <math display="inline">\underline{b}^s</math> debe ser dividido por la multiplicidad correspondiente. |
| − | Los saltos de desplazamiento entre los subdominios <math display="inline">({\mathbf{S}_T^s} \underline{u} | + | Los saltos de desplazamiento entre los subdominios <math display="inline">({\mathbf{S}_T^s} \underline{u}^s_b)</math> se obtiene mediante un procedimiento similar al anterior, en donde se utilizan las mismas dos matrices descritas para el residuo como también <math display="inline">\overline{{\mathbf{K}}}^s_{ib/bb}</math>. El procedimiento consiste en realizar las siguientes multiplicaciones matriz-vector (de derecha a izquierda): |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 217: | Line 217: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>{\mathbf{S}_T^s} \underline{u} | + | | style="text-align: center;" | <math>{\mathbf{S}_T^s} \underline{u}^s_b= -\underbrace{\left[ \begin{array}{cc} {\mathbf{K}}^s_{bi} & -\mathbf{I} \end{array} \right]}_{\overline{\mathbf{K}}^s_{bi}\mathbf{I}} \underbrace{\left[ \begin{array}{cc} {\mathbf{K}}^s_{ii} & \mathbf{0}\\ \mathbf{0} & \mathbf{I} \end{array} \right]^{-1}}_{\overline{\mathbf{K}}^s_{ii}\mathbf{I}} \underbrace{\left[ \begin{array}{cc} {\mathbf{K}}^s_{ib} \\ {\mathbf{K}}^s_{bb} \end{array} \right]}_{\overline{{\mathbf{K}}}^s_{ib/bb}} \underline{u}^s </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) |
|} | |} | ||
| − | Todas estas operaciones son independientes por subdominios, por lo tanto paralelizables. La etapa final consiste en ensamblar los distintos resultados locales condensados [[#eq- | + | Todas estas operaciones son independientes por subdominios, por lo tanto paralelizables. La etapa final consiste en ensamblar los distintos resultados locales condensados [[#eq-14|(14)]], mediante la función <math display="inline">MPI\_Allreduce ~ (sum,a)</math> de Open MPI, la cual optimiza este procedimiento. Las tres matrices (<math display="inline">\overline{\mathbf{K}}^s_{bi}\mathbf{I}</math>, <math display="inline">\overline{\mathbf{K}}^s_{ii}\mathbf{I}</math> y <math display="inline">\overline{{\mathbf{K}}}^s_{ib/bb}</math>) son almacenadas, ya que son utilizadas iterativamente para resolver el sistema. |
====4.3.2 Construcción e implementación de un precondicionador basado en una BDDC==== | ====4.3.2 Construcción e implementación de un precondicionador basado en una BDDC==== | ||
| − | El método GMRES utilizado para resolver el problema global necesita la utilización de un precondicionador para ser eficaz. Para esta implementación se eligió el precondicionador del método BDDC | + | El método GMRES utilizado para resolver el problema global necesita la utilización de un precondicionador para ser eficaz. Para esta implementación se eligió el precondicionador del método BDDC [6,26]. El método BDDC es muy similar al método FETI-DP [27] ya que funciona como un método primal. |
El método BDDC introduce restricciones suplementarias (continuidad de desplazamientos) en las esquinas de los subdominios durante la etapa de precondicionamiento. Este método es una respuesta a los problemas de pérdida de extensibilidad debido a las singularidades observadas en nodos esquina en problemas de placas. Desde un punto de vista práctico, las esquinas son definidas como puntos múltiples (nodos compartidos por varios subdominios). La selección de estos nodos esquina debe hacerse de manera de bloquear los movimientos y rotaciones de cuerpo rígido de cada subdominio. | El método BDDC introduce restricciones suplementarias (continuidad de desplazamientos) en las esquinas de los subdominios durante la etapa de precondicionamiento. Este método es una respuesta a los problemas de pérdida de extensibilidad debido a las singularidades observadas en nodos esquina en problemas de placas. Desde un punto de vista práctico, las esquinas son definidas como puntos múltiples (nodos compartidos por varios subdominios). La selección de estos nodos esquina debe hacerse de manera de bloquear los movimientos y rotaciones de cuerpo rígido de cada subdominio. | ||
| Line 239: | Line 239: | ||
| style="text-align: center;" | <math>\widetilde{\mathbf{S}}^{-1} (\mathbf{S}_Tx_0-b) = \widetilde{\mathbf{S}}^{-1} r = \mathbf{A} \mathbf{D}_P (\Psi u_c + z) </math> | | style="text-align: center;" | <math>\widetilde{\mathbf{S}}^{-1} (\mathbf{S}_Tx_0-b) = \widetilde{\mathbf{S}}^{-1} r = \mathbf{A} \mathbf{D}_P (\Psi u_c + z) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) |
|} | |} | ||
donde | donde | ||
| − | <span id="eq- | + | <span id="eq-18"></span> |
| − | <span id="eq- | + | <span id="eq-19"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 252: | Line 252: | ||
|- | |- | ||
| style="text-align: center;" | <math>\Psi ^T \mathbf{S} \Psi u_c = \Psi ^T \mathbf{D}_P \mathbf{A} r </math> | | style="text-align: center;" | <math>\Psi ^T \mathbf{S} \Psi u_c = \Psi ^T \mathbf{D}_P \mathbf{A} r </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (18) |
|- | |- | ||
| style="text-align: center;" | <math> \mathbf{S}z + \mathbf{C}^T \mu = \mathbf{D}_P^T \mathbf{A} r, \qquad \mathbf{C}z = 0 </math> | | style="text-align: center;" | <math> \mathbf{S}z + \mathbf{C}^T \mu = \mathbf{D}_P^T \mathbf{A} r, \qquad \mathbf{C}z = 0 </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (19) |
|- | |- | ||
| style="text-align: center;" | <math> \mathbf{A} = \begin{bmatrix}A^1 & \dots & A^n \end{bmatrix} </math> | | style="text-align: center;" | <math> \mathbf{A} = \begin{bmatrix}A^1 & \dots & A^n \end{bmatrix} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) |
|} | |} | ||
|} | |} | ||
| Line 282: | Line 282: | ||
| style="text-align: center;" | <math>\mathbf{A} \mathbf{D}_P \mathbf{A}^T = \mathbf{I} </math> | | style="text-align: center;" | <math>\mathbf{A} \mathbf{D}_P \mathbf{A}^T = \mathbf{I} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) |
|} | |} | ||
| Line 294: | Line 294: | ||
| style="text-align: center;" | <math>\begin{bmatrix}\mathbf{S} & \mathbf{C}^T\\ \mathbf{C} & \mathbf{0}\\ \end{bmatrix} \left( \begin{matrix}\Psi \\ \Lambda \end{matrix} \right) = \begin{bmatrix}\mathbf{0} \\ \mathbf{I}_c \end{bmatrix} </math> | | style="text-align: center;" | <math>\begin{bmatrix}\mathbf{S} & \mathbf{C}^T\\ \mathbf{C} & \mathbf{0}\\ \end{bmatrix} \left( \begin{matrix}\Psi \\ \Lambda \end{matrix} \right) = \begin{bmatrix}\mathbf{0} \\ \mathbf{I}_c \end{bmatrix} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) |
|} | |} | ||
| Line 314: | Line 314: | ||
Finalmente, <math display="inline">\Psi _j^s</math> representa la respuesta de la interfaz cuando un nodo esquina (<math display="inline">j</math>) es cargado con una fuerza unitaria (desplazamiento o rotación) y todos los otros g.d.l. de los todos nodos esquinas están bloqueados (Figura [[#img-3a|3a]]). | Finalmente, <math display="inline">\Psi _j^s</math> representa la respuesta de la interfaz cuando un nodo esquina (<math display="inline">j</math>) es cargado con una fuerza unitaria (desplazamiento o rotación) y todos los otros g.d.l. de los todos nodos esquinas están bloqueados (Figura [[#img-3a|3a]]). | ||
| − | <math display="inline">\Psi ^s</math> es ensamblado haciendo, <math display="inline">\Psi ^s = \left(\begin{matrix} \Psi ^s_1 & \Psi ^s_2 & \dots & \Psi ^s_j\\ \end{matrix} \right)</math>. <math display="inline">u_c</math> en [[#eq- | + | <math display="inline">\Psi ^s</math> es ensamblado haciendo, <math display="inline">\Psi ^s = \left(\begin{matrix} \Psi ^s_1 & \Psi ^s_2 & \dots & \Psi ^s_j\\ \end{matrix} \right)</math>. <math display="inline">u_c</math> en [[#eq-18|(18)]] representa el desplazamiento de los nodos esquina, a su vez <math display="inline">z</math> en [[#eq-19|(19)]] representa el desplazamiento del resto de los nodos de interfaz bajo la acción del residuo local ponderado (<math display="inline">{\widetilde{A^s}}^T r </math>), mientras se mantienen los nodos esquina empotrados (Figura [[#img-3b|3b]]). <div id='img-3a'></div> |
| + | |||
<div id='img-3b'></div> | <div id='img-3b'></div> | ||
<div id='img-3'></div> | <div id='img-3'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | |[[Image:draft_Samper_613894993-Psi2.png| | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-Psi2.png|160px|Representación gráfica de Ψ<sub>j</sub><sup>s</sup>.]] |
| − | |[[Image:draft_Samper_613894993-z.png| | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-z.png|300px|Representación gráfica de z.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) Representación gráfica de <math>\Psi _j^s</math>. | + | | style="padding-bottom:10px;"|(a) Representación gráfica de <math>\Psi _j^s</math>. |
| − | | (b) Representación gráfica de <math>z</math>. | + | | style="padding-bottom:10px;"|(b) Representación gráfica de <math>z</math>. |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 3:''' Casos de carga analizados | + | | colspan="2" style="padding-bottom:10px;"| '''Figura 3:''' Casos de carga analizados |
|} | |} | ||
| − | La ecuación [[#eq- | + | La ecuación [[#eq-19|(19)]] se puede escribir, |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 336: | Line 337: | ||
| style="text-align: center;" | <math>\begin{bmatrix}\mathbf{K}_{ii}^s & \mathbf{K}_{ir}^s & \mathbf{0}\\ \mathbf{K}_{ri}^s & \mathbf{K}_{rr}^s & \mathbf{0}\\ \mathbf{0} & \mathbf{0} & \mathbf{I}_{cc}^s\\ \end{bmatrix} \left( \begin{matrix}u_i^s\\ z^s \end{matrix} \right) = \begin{bmatrix}\mathbf{0} \\ {\widetilde{A^s}}^T r \\ \mathbf{0} \end{bmatrix} </math> | | style="text-align: center;" | <math>\begin{bmatrix}\mathbf{K}_{ii}^s & \mathbf{K}_{ir}^s & \mathbf{0}\\ \mathbf{K}_{ri}^s & \mathbf{K}_{rr}^s & \mathbf{0}\\ \mathbf{0} & \mathbf{0} & \mathbf{I}_{cc}^s\\ \end{bmatrix} \left( \begin{matrix}u_i^s\\ z^s \end{matrix} \right) = \begin{bmatrix}\mathbf{0} \\ {\widetilde{A^s}}^T r \\ \mathbf{0} \end{bmatrix} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) |
|} | |} | ||
| − | Por último, <math display="inline">\mu </math> en [[#eq- | + | Por último, <math display="inline">\mu </math> en [[#eq-19|(19)]] corresponde a un multiplicador de Lagrange usado para imponer la continuidad entre los nodos esquina. |
La implementación del método BDDC permite reducir, de manera importante, el número de iteraciones GMRES. En la sección siguiente, se presenta un estudio de validación de la implementación del BDDC en elasticidad lineal. En particular análisis de extensibilidad y ''speed-up''. | La implementación del método BDDC permite reducir, de manera importante, el número de iteraciones GMRES. En la sección siguiente, se presenta un estudio de validación de la implementación del BDDC en elasticidad lineal. En particular análisis de extensibilidad y ''speed-up''. | ||
| − | ==5 Validación de la implementación en elasticidad lineal== | + | ==5. Validación de la implementación en elasticidad lineal== |
===5.1 Extensibilidad numérica de la implementación=== | ===5.1 Extensibilidad numérica de la implementación=== | ||
| − | Para verificar la extensibilidad numérica del método implementado en elasticidad lineal, se estudia la influencia en el aumento del número de subdominios en el número de iteraciones GMRES para resolver el sistema global. Cada subdominio tiene la misma relación <math display="inline">H/h</math>, siendo <math display="inline">H</math> una longitud característica de un subdominio y <math display="inline">h</math> una longitud característica de un elemento. En todos los cálculos un subdominio es calculado por un procesador. La estructura analizada consiste en una placa plana, empotrada en un extremo y sometida a dos tipos de cargas: uno de tracción y flexión en el plano (Figura [[#img-4a|4a]]) y otro de flexión fuera del plano (Figura [[#img-4b|4b]]). Distintos números de subdominios se han generado, pero siempre descomponiendo en ambas direcciones. La Figura [[#img-5|5]] presenta los resultados para cada caso analizado. El número de iteraciones para cada relación H/h parece tender a una asíntota. Estos resultados son muy similares a los obtenidos por | + | Para verificar la extensibilidad numérica del método implementado en elasticidad lineal, se estudia la influencia en el aumento del número de subdominios en el número de iteraciones GMRES para resolver el sistema global. Cada subdominio tiene la misma relación <math display="inline">H/h</math>, siendo <math display="inline">H</math> una longitud característica de un subdominio y <math display="inline">h</math> una longitud característica de un elemento. En todos los cálculos un subdominio es calculado por un procesador. La estructura analizada consiste en una placa plana, empotrada en un extremo y sometida a dos tipos de cargas: uno de tracción y flexión en el plano (Figura [[#img-4a|4a]]) y otro de flexión fuera del plano (Figura [[#img-4b|4b]]). Distintos números de subdominios se han generado, pero siempre descomponiendo en ambas direcciones. La Figura [[#img-5|5]] presenta los resultados para cada caso analizado. El número de iteraciones para cada relación H/h parece tender a una asíntota. Estos resultados son muy similares a los obtenidos por [7] y [28] para placas en flexión fuera del plano. Se puede decir que por la definición de nodos esquina utilizada, lo ideal es mantener una relación <math display="inline">H/h<32</math>, la cual permite asegurar una buena extensibilidad del método. <div id='img-4a'></div> |
<div id='img-4b'></div> | <div id='img-4b'></div> | ||
<div id='img-4'></div> | <div id='img-4'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | |[[Image:draft_Samper_613894993-Ext_cas1.png| | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-Ext_cas1.png|270px|Placa en tracción y flexión en el plano.]] |
| − | |[[Image:draft_Samper_613894993-Ext_cas2.png| | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-Ext_cas2.png|300px|Placa en flexión fuera del plano.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) Placa en tracción y flexión en el plano. | + | | style="padding-bottom:10px;"|(a) Placa en tracción y flexión en el plano. |
| − | | (b) Placa en flexión fuera del plano. | + | | (style="padding-bottom:10px;"|b) Placa en flexión fuera del plano. |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 4:''' Casos de carga analizados | + | | colspan="2" style="padding:10px;"| '''Figura 4:''' Casos de carga analizados |
|} | |} | ||
<div id='img-5a'></div> | <div id='img-5a'></div> | ||
<div id='img-5b'></div> | <div id='img-5b'></div> | ||
<div id='img-5'></div> | <div id='img-5'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | |[[Image:draft_Samper_613894993-Exten_caseA2_esp.png| | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-Exten_caseA2_esp.png|525px|Placa en tracción y flexión en el plano.]] |
| − | |[[Image:draft_Samper_613894993-Exten_caseB2_esp.png| | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-Exten_caseB2_esp.png|525px|Placa en flexión fuera del plano.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) Placa en tracción y flexión en el plano. | + | | style="padding-bottom:10px;"|(a) Placa en tracción y flexión en el plano. |
| − | | (b) Placa en flexión fuera del plano. | + | | (style="padding-bottom:10px;"|b) Placa en flexión fuera del plano. |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 5:''' Estudio de extensibilidad. | + | | colspan="2" style="padding:10px;"| '''Figura 5:''' Estudio de extensibilidad. |
|} | |} | ||
===5.2 Speed-up de la implementación=== | ===5.2 Speed-up de la implementación=== | ||
| − | El ''speed-up'' de un algoritmo en paralelo se define como la relación entre la velocidad de un cálculo cuando se utiliza un solo procesador y cuando se utilizan <math display="inline">N</math> procesadores para resolver un problema de tamaño fijo (<math display="inline">h</math> constante y <math display="inline">H</math> variable). No todas las etapas son paralelizables, por lo que generalmente este número es inferior a <math display="inline">N</math> y se define según la ley de Amdahl | + | El ''speed-up'' de un algoritmo en paralelo se define como la relación entre la velocidad de un cálculo cuando se utiliza un solo procesador y cuando se utilizan <math display="inline">N</math> procesadores para resolver un problema de tamaño fijo (<math display="inline">h</math> constante y <math display="inline">H</math> variable). No todas las etapas son paralelizables, por lo que generalmente este número es inferior a <math display="inline">N</math> y se define según la ley de Amdahl [29]: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 385: | Line 386: | ||
| style="text-align: center;" | <math>S(N)= \frac{T(1)}{T(N)}= \frac{T_s + T_p}{T_s + T_p/N} </math> | | style="text-align: center;" | <math>S(N)= \frac{T(1)}{T(N)}= \frac{T_s + T_p}{T_s + T_p/N} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (24) |
|} | |} | ||
| Line 391: | Line 392: | ||
Para verificar el ''speed-up'' del método, se estudia el efecto del número de subdominios sobre el tiempo de cálculo total del problema. La malla de la estructura se deja fijo. A medida que el número de subdominios aumenta el tamaño del problema global aumenta, mientras que los problemas locales se reducen. La estructura analizada corresponde a la misma que para el estudio de extensibilidad (Figura [[#img-4a|4a]]) pero solo para una carga de tracción solamente. En este estudio, tres niveles de refinamiento de malla se han analizado. Para cada cálculo, cada procesador se encarga de un solo subdominio. Los resultados del estudio, considerando los tres niveles de refinamiento, se presentan en la Figura [[#img-6|6]]. Se verifica, un ''speed-up'' muy cercano al óptimo al menos para valores de <math display="inline">H/h</math> razonables (al aumentar el número de subdominios el valor de <math display="inline">H</math> se aproxima a <math display="inline">h</math>). Se aprecia que para los tres casos de refinamiento existe un número óptimo de procesadores (subdominios) que da el mejor ''speed-up''. Este número depende de la malla de la estructura (parámetro <math display="inline">H/h</math>). Para valores de <math display="inline">H/h>20</math>, el ''speed-up'' está sobre la curva óptima. Por el contrario cuando <math display="inline">H/h<20</math>, el ''speed-up'' se deteriora (se pasa más tiempo comunicando los procesos que resolviendo el problema). <div id='img-6'></div> | Para verificar el ''speed-up'' del método, se estudia el efecto del número de subdominios sobre el tiempo de cálculo total del problema. La malla de la estructura se deja fijo. A medida que el número de subdominios aumenta el tamaño del problema global aumenta, mientras que los problemas locales se reducen. La estructura analizada corresponde a la misma que para el estudio de extensibilidad (Figura [[#img-4a|4a]]) pero solo para una carga de tracción solamente. En este estudio, tres niveles de refinamiento de malla se han analizado. Para cada cálculo, cada procesador se encarga de un solo subdominio. Los resultados del estudio, considerando los tres niveles de refinamiento, se presentan en la Figura [[#img-6|6]]. Se verifica, un ''speed-up'' muy cercano al óptimo al menos para valores de <math display="inline">H/h</math> razonables (al aumentar el número de subdominios el valor de <math display="inline">H</math> se aproxima a <math display="inline">h</math>). Se aprecia que para los tres casos de refinamiento existe un número óptimo de procesadores (subdominios) que da el mejor ''speed-up''. Este número depende de la malla de la estructura (parámetro <math display="inline">H/h</math>). Para valores de <math display="inline">H/h>20</math>, el ''speed-up'' está sobre la curva óptima. Por el contrario cuando <math display="inline">H/h<20</math>, el ''speed-up'' se deteriora (se pasa más tiempo comunicando los procesos que resolviendo el problema). <div id='img-6'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | |[[Image:draft_Samper_613894993-Speed-up_esp.png| | + | |style="padding:10px;"|[[Image:draft_Samper_613894993-Speed-up_esp.png|370px|Estudio de ''Speed-up'', placa en tracción.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 6:''' Estudio de ''Speed-up'', placa en tracción. | + | | colspan="1" style="padding-bottom:10px;"| '''Figura 6:''' Estudio de ''Speed-up'', placa en tracción. |
|} | |} | ||
==Conclusiones== | ==Conclusiones== | ||
| − | En este trabajo se ha paralelizado una estrategia de localización no lineal mixta, mediante un método de tipo BDD, resuelto con un procedimiento de tipo GMRES. Este procedimiento necesita muchas iteraciones del algoritmo GMRES, por lo que se incorpora un precondicionador de tipo BDDC. Posteriormente se ha validado esta implementación analizando en elasticidad lineal, la extensibilidad y el speed-up del método. Se ha constatado que las curvas de extensibilidad numérica tienen un comportamiento asintótico, similar al observado en | + | En este trabajo se ha paralelizado una estrategia de localización no lineal mixta, mediante un método de tipo BDD, resuelto con un procedimiento de tipo GMRES. Este procedimiento necesita muchas iteraciones del algoritmo GMRES, por lo que se incorpora un precondicionador de tipo BDDC. Posteriormente se ha validado esta implementación analizando en elasticidad lineal, la extensibilidad y el speed-up del método. Se ha constatado que las curvas de extensibilidad numérica tienen un comportamiento asintótico, similar al observado en [7] y [28] para una placa en flexión. Para el speed-up, se constató que para diferentes tamaños de malla se obtienen valores máximos diferentes. Este valor máximo se debe a que la resolución del problema global se vuelve menos importante, en términos de tiempos de cálculos, por lo que no se gana nada al aumentar la paralelización (número de subdominios). Esto depende del tamaño del problema (número de g.d.l.). Finalmente, se deben utilizar relaciones de <math display="inline">20<H/h<32</math>, que permiten asegurar la extensibilidad del método y un ''speed-up'' cercano al óptimo. |
==Agradecimientos== | ==Agradecimientos== | ||
| Line 411: | Line 412: | ||
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | [1] De Roeck Y.H., Le Tallec P. and Vidrescu M. 1992. | + | [1] De Roeck Y.H., Le Tallec P. and Vidrescu M. (1992). A domain-decomposition solver for nonlinear elasticity. Computer Methods in Applied Mechanics and Engineering 99: 187–207. |
<div id="cite-2"></div> | <div id="cite-2"></div> | ||
| − | [2] Farhat C., Lesoinne M. and Pierson K. 2000. | + | [2] Farhat C., Lesoinne M. and Pierson K. (2000). A scalable dual-primal domain decomposition method. Numerical Linear Algebra with application 7: 687–714. |
<div id="cite-3"></div> | <div id="cite-3"></div> | ||
| − | [3] Cresta P., Allix O., Rey C. and Guinard, S. 2007. | + | [3] Cresta P., Allix O., Rey C. and Guinard, S. (2007). Nonlinear localization strategies for domain decomposition methods: application to post-buckling analyses. Computer Methods in Applied Mechanics and Engineering 196: 1436–1446. |
<div id="cite-4"></div> | <div id="cite-4"></div> | ||
| − | [4] Hinojosa J., Allix O., Guidault P.-A. and Cresta P. 2014. | + | [4] Hinojosa J., Allix O., Guidault P.-A. and Cresta P. (2014). Domain decomposition methods with nonlinear localization for the buckling and post-buckling analyses of large structures. Advances in Engineering Software 70: 13–24. |
<div id="cite-5"></div> | <div id="cite-5"></div> | ||
| − | [5] Hinojosa J., Allix O., Guidault P.-A., Cresta Ph., and Saavedra K. 2017. | + | [5] Hinojosa J., Allix O., Guidault P.-A., Cresta Ph., and Saavedra K. (2017). Mixed nonlinear localization strategy for the buckling and post-buckling analyses of structures: Parameter optimization and path following implementation. Engineering Optimization 49(2): 269–289. |
<div id="cite-6"></div> | <div id="cite-6"></div> | ||
| − | [6] Dohrmann C. R. 2003. | + | [6] Dohrmann C. R. (2003). A preconditioner for substructuring based on constrained energy minimization. SIAM Journal on Scientific Computing 25(1):246–258. |
<div id="cite-7"></div> | <div id="cite-7"></div> | ||
| − | [7] Gosselet P. and Rey C. 2006. | + | [7] Gosselet P. and Rey C. (2006). Non-overlapping domain decomposition methods in structural mechanics. Archives of Computational Methods in Engineering 13(4): 515–572. |
<div id="cite-8"></div> | <div id="cite-8"></div> | ||
| − | [8] Le Tallec P., De Roeck Y.H. and Vidrascu M. 1991. | + | [8] Le Tallec P., De Roeck Y.H. and Vidrascu M. (1991). Domain decomposition methods for large linearly elliptic three-dimension problems. Journal of Computational and Applied Mathematics 34(1): 93–117. |
<div id="cite-9"></div> | <div id="cite-9"></div> | ||
| − | [9] Mandel J. 1993. | + | [9] Mandel J. (1993). Balancing domain decomposition. Communications in Applied Numerical Methods 9: 233–241. |
<div id="cite-10"></div> | <div id="cite-10"></div> | ||
| − | [10] Farhat C. and Roux F.-X. 1991. | + | [10] Farhat C. and Roux F.-X. (1991). A method of finite element tearing and interconnecting and its parallel solution algorithm. International Journal for Numerical Methods in Engineering 32: 1205–1227. |
<div id="cite-11"></div> | <div id="cite-11"></div> | ||
| − | [11] Ladevèze P. 1985. | + | [11] Ladevèze P. (1985). Sur une famille d'algorithmes en mécanique des structures. Compte rendu de l'académie de Sciences 300(2): 41–4 |
<div id="cite-12"></div> | <div id="cite-12"></div> | ||
| − | [12] Glowinski R. and Le Tallec P. 1990. | + | [12] Glowinski R. and Le Tallec P. (1990). Augmented Lagrangian interpretation of the non overlapping Schwarz alternating method. in: Third International Symposium on Domain Decomposition Methods for Partial Differential Equations, SIAM 224–231. |
<div id="cite-13"></div> | <div id="cite-13"></div> | ||
| − | [13] Series L., Feyel F. and Roux F.-X. 2003. | + | [13] Series L., Feyel F. and Roux F.-X. (2003). Une méthode de décomposition de domaine avec deux multiplicateurs de Lagrange, application au calcul des structures, cas du contact. Actes du Sixieme Colloque National en Calcul des Structures 373–380. |
<div id="cite-14"></div> | <div id="cite-14"></div> | ||
| − | [14] Pavarino L. F. and Widlund O. B. 2002. | + | [14] Pavarino L. F. and Widlund O. B. (2002). Balancing Neumann-Neumann methods for incompressible Stokes equations. Communications on Pure and Applied Mathematics 55(3): 302–335. |
<div id="cite-15"></div> | <div id="cite-15"></div> | ||
| − | [15] Pebrel J., Rey C., and Gosselet P. 2008. | + | [15] Pebrel J., Rey C., and Gosselet P. (2008). A nonlinear dual domain decomposition method: application to structural problems with damage. International Journal for Multiscale Computational Engineering 6(3): 251–262. |
<div id="cite-16"></div> | <div id="cite-16"></div> | ||
| − | [16] Allix O., Kerfriden P. and Gosselet P. 2010. | + | [16] Allix O., Kerfriden P. and Gosselet P. (2010). A relocalization technique for the multi scale computation of delamination in composite structures. Computer Modeling in Engineering and Sciences 55: 271–292 |
<div id="cite-17"></div> | <div id="cite-17"></div> | ||
| − | [17] Saavedra K., Allix O. and Gosselet P. 2012. | + | [17] Saavedra K., Allix O. and Gosselet P. (2012). On a multi scale strategy and its optimization for the simulation of combined delamination and buckling. International Journal for Numerical Methods in Engineering 91(7): 772–798. |
<div id="cite-18"></div> | <div id="cite-18"></div> | ||
| − | [18] Saavedra E., Saavedra K., Hinojosa J., Chandra Y., and Das R. 2016. | + | [18] Saavedra E., Saavedra K., Hinojosa J., Chandra Y., and Das R. (2016). Multi-scale modeling of rolling shear failure in cross-laminated timber structures by homogeneisation and cohesive models. International Journal of Solids and Structures 81: 219–232. |
<div id="cite-19"></div> | <div id="cite-19"></div> | ||
| − | [19] Brezzi F. and Marini L.D. 2005. | + | [19] Brezzi F. and Marini L.D. (2005). The three-field formulation for elasticity problems. GAMM Mitteilungen 28: 124–153. |
<div id="cite-20"></div> | <div id="cite-20"></div> | ||
| − | [20] Fortin M. and Glowinski R. 1983. | + | [20] Fortin M. and Glowinski R. (1983). Chapter1: Augmented Lagrangian Methods in Quadratic Programming, in: Fortin M. and Glowinski R. (Eds), Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary Value Problems. Studies in Mathematics and Its Applications, Elsevier vol. 15: 1–46. |
<div id="cite-21"></div> | <div id="cite-21"></div> | ||
| − | [21] Ladeveze P. 1999. | + | [21] Ladeveze P. (1999). Nonlinear computational structural mechanics - New Approaches and Non-incremental Methods of Calculation. Springer Verlarg, Berlin. |
<div id="cite-22"></div> | <div id="cite-22"></div> | ||
| − | [22] Saavedra K., Allix O., Gosselet P., Hinojosa J., and Viard A. 2017. | + | [22] Saavedra K., Allix O., Gosselet P., Hinojosa J., and Viard A. (2017). An enhanced non-linear multi-scale strategy for the simulation of buckling and delamination on 3D composite plates. Computer Methods in Applied Mechanics and Engineering 317: 952–969. |
<div id="cite-23"></div> | <div id="cite-23"></div> | ||
| − | [23] Diekmann R., Monien B. and Preis R. 1997. | + | [23] Diekmann R., Monien B. and Preis R. (1997). Load balancing strategies for distributed memory machines. In Satz H., Karsch F. and Monien B. editors: Multi-Scale Phenomena and Their Simulation. World Scientific 255–266. |
<div id="cite-24"></div> | <div id="cite-24"></div> | ||
| − | [24] Lottiaux R., Gallard P., Vallée G., Morin C. and Boissinot B. 2005. | + | [24] Lottiaux R., Gallard P., Vallée G., Morin C. and Boissinot B. (2005). Openmosix, openssi ans kerrighed: a comparative study. In CCGRID'05: Proceedings of the Fifth IEEE International Symposiun on Cluster Computing and the Grip vol. 2: 1016–1023, Washington, DC, USA. IEEE Computer Society. |
<div id="cite-25"></div> | <div id="cite-25"></div> | ||
| − | [25] Felippa C.A. and Haugen B. 2005. | + | [25] Felippa C.A. and Haugen B. (2005). A unified formulation of small-strain corotational finite elements: 1. Theory. Computer Methods in Applied Mechanics and Engineering 194(21-24): 2285–2335. |
<div id="cite-26"></div> | <div id="cite-26"></div> | ||
| − | [26] Mandel J., Dohrmann C. R., and Tezaur R. 2004. | + | [26] Mandel J., Dohrmann C. R., and Tezaur R. (2004). An algebraic theory for primal and dual substructuring methods by constraints. Applied Numerical Mathematics 54(2): 167–193. 6th IMACS. |
<div id="cite-27"></div> | <div id="cite-27"></div> | ||
| − | [27] Farhat C., Lesoinne M., Le Tallec P., Pierson K., and Rixen D. 2001. | + | [27] Farhat C., Lesoinne M., Le Tallec P., Pierson K., and Rixen D. (2001). FETI-DP: A dual-primal unified FETI method - Part I: A faster alternative to the two-level FETI method. International Journal for Numerical Methods in Engineering 50: 1523–1544. |
<div id="cite-28"></div> | <div id="cite-28"></div> | ||
| − | [28] Beirão da Veiga L., Chinosi C., Lovadina C. and Pavarino L. F. 2010. | + | [28] Beirão da Veiga L., Chinosi C., Lovadina C. and Pavarino L. F. (2010). Robust BDDC preconditioners for Reissner-Mindlin plate bending problems and MITC elements. SIAM J. Numerical Analysis 47(6): 4214–4238. |
<div id="cite-29"></div> | <div id="cite-29"></div> | ||
| − | [29] Amdahl G. M. 1988. | + | [29] Amdahl G. M. (1988). Limits of expectation. International Journal of High Performance Computing Applications 2: 88–94. |
</div> | </div> | ||
Latest revision as of 12:47, 20 July 2018
Resumen
En trabajos previos la localización no lineal fue presentada y estudiada para casos de grandes desplazamientos pero solo para problemas de estructuras con respuestas globales estables y resueltos de manera secuencial. En este trabajo se presenta la paralelización de esta estrategia de cálculo mediante el método Balancing Domain Decomposition by Constrains (BDD-C). Finalmente, se realiza una validación de la implementación en elasticidad lineal, mediante la comprobación del speed-up y la extensibilidad numérica.
Palabras clave: multiescala, método de descomposición, BDDC, paralelisación, cálculo no lineal.
Abstract
In previous works, the nonlinear localization was first presented and studied in the case of large displacements but only for globally stable structural responses. In this paper, the parallelization of this computational strategy using a Balancing Domain Decomposition by Constrains (BDD-C) is presented. Finally, a validation of this implementation is carried out in lineal elasticity, verifying the speed-up and the numerical extensibility.
1. Introducción
En estructuras aeronáuticas como fuselajes la mayor no linealidad que ocurre corresponde a pandeo localizado en elementos esbeltos. Durante los ensayos estructurales de certificación llevados a cabo en un fuselaje completo, se observa pandeo en la piel entre los rigidizadores. Al aumentar las cargas, estos fenómenos se pueden expandir y provocar redistribuciones de esfuerzos en la estructura. Para cargas normales de trabajo, estos fenómenos son reversibles, el material se mantiene dentro del rango lineal. De todas formas, pueden provocar concentraciones de esfuerzo alrededor de las bases de los rigidizadores que pueden ser el origen de daños locales conducentes a fallas completas de las estructuras. Realizar cálculos de estos fenómenos para grandes estructuras como un fuselaje completo, conlleva mallas con aprox. grados de libertad (g.d.l.), incluso con mallas adaptadas. Debido al gran número de incógnitas y a las limitaciones tanto de memoria como de los procesadores, la resolución directa de este tipo de problemas mediante el Método de Elementos Finitos (MEF) es impracticable. Es por esta razón, que los ingenieros usan métodos de aproximación basados en super-elementos (condensación lineal de g.d.l. internos) o análisis global-local, que corresponden a un cálculo lineal global de toda la estructura seguido de análisis locales no lineales. Si bien estos métodos permiten realizar ciertos cálculos, no toman en cuenta fenómenos como redistribuciones de esfuerzos o expansión de zonas con no linealidades, debido a que solo ofrecen un diálogo en una sola dirección debido a las escalas introducidas. Como resultado, solo pueden tratar no linealidades localizadas que no tengan una influencia en la respuesta global de la estructura. Nuevos avances, utilizando máquinas en paralelo y cluster, nos permiten hoy en día distribuir el costo computacional y requerimientos de memoria en varios procesadores. Problemas muy complejos son abordables siempre que los métodos de resolución puedan tomar ventaja del paralelismo inherente de los hardwares disponibles. En este estudio, se exploran las posibilidades relacionadas con estrategias de cálculo en paralelo y multiescala en el contexto de problemas no lineales geométricamente.
En este trabajo se presenta la paralelización de una estrategia de cálculo basada en el método de descomposición de dominio llamado Newton-Krylov-Schur (NKS) [1,2], el cual es uno de los métodos paralelos de referencia para la resolución de problemas no lineales para el caso del post-pandeo. Este método NKS se ha modificado integrando una etapa de localización no lineal [3], además de introducir una descomposición de dominio mixta. Esta etapa de localización no lineal consiste en realizar iteraciones adicionales en los subdominios después de cada iteración global de manera de obtener el comportamiento no lineal y el equilibrio en ellos. En trabajos anteriores [3,4,5] se ha demostrado la eficacia de esta estrategia de cálculo para problemas con no linealidades locales y desbalanceadas. En una primera parte, se presenta la estrategia de localización no lineal, para luego en una segunda parte, presentar la paralelización de la estrategia mediante un método BDDC [6] junto con una validación de la misma en el caso de elasticidad lineal.
2. Métodos de descomposición de dominio
Los métodos de descomposición de dominio (MDD) [7] permiten resolver grandes problemas en computadores paralelos. Existen diferentes MDD dependiendo de las condiciones que transmiten entre los subdominios. Los métodos primales [8,9] favorecen la continuidad de desplazamientos mientras que los métodos duales [10] favorecen a-priori el equilibrio de fuerzas entre los subdominios. Los métodos mixtos [11,12,13,14] utilizan relaciones de tipo Robin entre los desplazamientos y fuerzas en las interfaces, sin favorecer a ninguno de los dos. Cuando los MDD son utilizados con el procedimiento iterativo de Newton para resolver problemas no lineales, estas estrategias se llaman métodos NKS [1]. Estos métodos se basan en:
- Método de Newton para la linearización del problema no lineal y el esquema iterativo incremental.
- MDD y condensación de Schur del problema tangente definido en las interfaces.
- Procedimiento iterativo en paralelo de tipo Krylov, para resolver el problema lineal condensado en las interfaces.
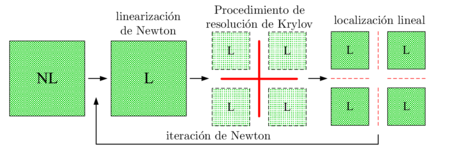
|
| Figura 1: Método NKS clásico. |
3. Principio de la localización no lineal
Cuando el problema inicial es descompuesto en subdominios antes de la linearización, el equilibrio no lineal de cada subdominio se debe asegurar en cada iteración. Los problemas no lineales son resueltos en cada subdominio para valores de interfaz dados. Lo que conlleva a la estrategia presentada en la Figura 2. Con respecto a los MDD clásicos utilizados para resolver problemas no lineales, en las etapas locales de los subdominios se resuelven problemas no lineales. Es este paso el que llamaremos localización no lineal. Esta estrategia ha sido evaluada para el cálculo de estructuras con pandeo localizado, con MDD primales y duales, y comparado con la estrategia clásica NKS [3]. La versión dual se ha aplicado a daño [15]. La versión mixta ha sido aplicada en delaminación de materiales compuestos [16], para la interacción delaminación/pandeo en materiales compuestos [17] y para la simulación de fractura en madera [18].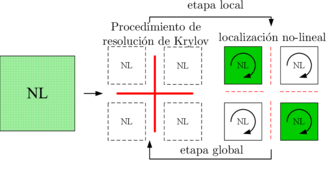
|
| Figura 2: Método NKS con etapa de localización no lineal. |
3.1 Estrategia de localización no lineal mixta
Dos clases de MDD mixto se pueden encontrar en la literatura: Uno basado en la introducción de condiciones mixtas mediante una formulación Lagrangiana aumentada, que asume la existencia de un potencial para la energía de deformación. Tres campos de interfaces son introducidos: la traza en las interfaces del desplazamiento de los subdominios, el multiplicador de Lagrange y un desplazamiento de interfaz adicional [13,19]. En la otra clase, se introducen algoritmos con dos direcciones de búsqueda, sin recurrir a los multiplicadores de Lagrange. Dos juegos de interfaces son introducidas: las fuerzas y los desplazamientos de las interfaces. Ambas cumpliendo un rol simétrico [20]. Los MDD basados en el método LATIN [21] corresponden a este tipo de métodos. También se pueden mencionar los trabajos de [12] que propuso un algoritmo con dos direcciones de búsqueda, versión ALG3 [20].
3.1.1 Etapa local no lineal
La primera etapa consiste en encontrar los campos de fuerzas y desplazamiento y para cada subdominio que verifiquen el comportamiento no lineal y las condiciones de contorno mixtas, conociendo las fuerzas (equilibradas) y los desplazamientos (continuos en las interfaces) de la etapa lineal global (vea sección 3.1.2) precedente resuelta en las interfaces (o una etapa de inicialización):
|
donde es la parte correspondiente a los grados de libertad (g.d.l.) internos del vector fuerza que soporta el subdominio , son las cargas externas, a los desplazamientos impuestos, condiciones de contorno, es el parámetro de tipo Robin que corresponde a una dirección de búsqueda y el subíndice a los nodos de interfaz de cada subdominio. La ecuación (3) corresponde a una condición de tipo Robin. Las variables en mayúscula se refieren a cantidades de interfaz que son conocidas (vea sección 3.1.2).
Linearizando la ecuación (1) con la (3) se obtiene el siguiente problema tangente por subdominio:
|
|
(4) |
donde el subíndice referencia los g.d.l. interiores de los subdominios, representa la matriz tangente del subdominio , es un incremento de desplazamientos, es un residuo y es el salto de desplazamientos entre la interfaz y el subdominio (al tratarse de un método mixto, las interfaces y los subdominios pueden estar separadas durante el proceso iterativo). Las condiciones de contorno, son tomadas en cuenta por medio de un método de eliminación directa.
El parámetro de tipo Robin, , es un parámetro del método. Este parámetro corresponde a un operador linear simétrico definido positivo y representa la rigidez de la vecindad del subdominio en cuestión. Normalmente, se define como parte del complemento de Schur primal de los subdominios vecinos asociados con los g.d.l. considerados en la interfaz del subdominio analizado, . Este operador se obtiene ensamblando las diferentes contribuciones de los subdominios vecinos en la interfaz considerada, cuando todos sus otras interfaces están empotradas. Para mayores detalles en cuanto a la definición, como en la influencia del parámetro Robin en el desempeño de la estrategia, el lector se puede referir a [4]. En [22], se demuestra que una buena elección del parámetro de tipo Robin es fundamental para obtener un método eficiente.
3.1.2 Etapa global lineal
La segunda etapa consiste en asegurar la admisibilidad de las incógnitas de interfaz: equilibrio de fuerzas y continuidad de desplazamientos , además de transmitir la información mecánica a través de toda la estructura, de manera de asegurar la escalabilidad del algoritmo. Más precisamente, conociendo y (fuerzas y desplazamientos provenientes de la etapa local precedente, vea sección 3.1.1) o una etapa de inicialización, y deben verificar la continuidad de desplazamientos (5) y el equilibrio de fuerzas (6) para cada interfaz que conecta dos subdominios y :
|
En estas estrategias, se introducen las siguientes direcciones de búsquedas por interfaz:
|
donde , , y son conocidas. La elección de la dirección de búsqueda se basa en los trabajos de [3] en donde se utiliza para propagar información global entre los subdominios, donde corresponde al complemento primal de Schur del subdominio , que conecta todos los g.d.l. del subdominio y se calcula:
|
|
(9) |
El problema mixto no lineal condensado que se obtiene desde el equilibrio de las interfaces se puede resolver con un Newton-Raphson. Luego de la linearización y utilizando una formulación en desplazamientos, se obtiene:
|
donde y corresponden al ensamblaje de los problemas condensados y los residuos de cada subdominio respectivamente, según:
|
donde corresponde al operador de ensamblaje, que conecta los g.d.l. de borde del subdominio con las incógnitas del problema global.
Esto implica la solución de problemas no lineales locales en cada subdominio para las cantidades de interfaz (, ) y para la condición de tipo Robin (3). Resolviendo el problema de interfaces global (10), se obtiene , que corresponde al incremento del desplazamiento en las interfaces (11). Las fuerzas balanceadas de las interfaces se obtienen a partir de la ecuación (12) cuando los desplazamientos son conocidos. Los problemas (11) y (12) pueden ser resueltos independientemente en cada subdominio. El sistema (10) puede ser resuelto de la misma manera que los métodos NKS clásicos, incluso utilizando los mismos precondicionadores y procedimientos iterativos. Para más detalles sobre la estrategia, el lector puede referirse a [4].
4. Paralelización de la estrategia de localización no lineal mixta
Las estrategia de localización no lineal, como los métodos NKS clásicos, están adaptados a la arquitectura en paralelo de las máquinas de computo modernas. El problema tangente de interfaz, etapa global, se puede resolver utilizando un procedimiento iterativo de Krylov que solo realiza productos matriz-vector. El intercambio de información entre subdominios es necesario a cada iteración. Por el contrario, la etapa no lineal, consiste en cálculos totalmente independientes en cada subdominio. Una implementación en paralelo clásica, consiste en asociar cada subdominio a un procesador distinto, por ejemplo en un Cluster. Algunos procesadores pueden requerir esperar un largo tiempo a que los otros terminen sus tareas. Estos tiempos de espera afectan le efectividad del método y, en general, se busca repartir de la mejor manera posible las tareas entre los distintos procesadores. Esta problemática ya ha sido tratada en la implementación de MDD clásicos. En estos casos la descomposición del dominio se hace de manera automática de forma de que cada problema local (factorización y resolución del sistema lineal) represente un costo de cálculo lo más uniforme posible; Esto se logra con algoritmos de particionamiento, por ejemplo METIS.
En el caso del presente trabajo, es mucho más difícil poder evaluar a-priori el costo de cálculos no lineales por subdominio, que dependen de los operadores, pero también del nivel de cargas externas sobre los subdominios. Una estimación posible consiste en considerar el número de iteraciones de la etapa no lineal precedente. De todas formas, este costo puede variar entre distintas iteraciones. En esos casos, se puede utilizar métodos de repartición dinámica. Utilizando un número inferior de procesadores que de subdominios puede facilitar esa tarea. Algunas alternativas a estos problemas han sido desarrolladas por [23,24].
4.1 Principios de paralización y dificultades
El objetivo consiste en la paralelización completa del código de cálculo: paralización de todas las etapas y paralelización/distribución de los datos del problema. Para realizar la paralelización de los datos del problema, cada procesador debe almacenar solamente la información de sus subdominios. Esta paralelización permite reducir el uso de memoria, pero complejiza la comunicación entre los diferentes procesadores. De esta forma un subdominio debe acceder a la información que necesita de los subdominios vecinos (interfazz, direcciones de búsqueda, etc.). Para paralelizar el código, se utiliza la librería de cálculo en paralelo Open MPI, que permite una paralelización completa de cada etapa. Una lista de todas las funciones junto con sus descripciones se pueden encontrar en el sitio de Open MPI (www.open-mpi.org).
4.2 Precisiones para la resolución en paralelo de la etapa local
Los problemas locales, resueltos a la etapa de localización no lineal, son naturalmente paralelisables, debido a que no requieren comunicarse con ningún otro subdominio, ni interfaz durante su resolución. Para esta implementación se ha elegido como dirección de búsqueda el complemento de Schur del subdominio vecino. Este operador modifica la matriz durante la operación que genera un aumento del tiempo de cálculo para la primera iteración local. Para las iteraciones locales sucesivas, la estructura de la matriz no cambia, aunque la dirección de búsqueda cambie. De modo de disminuir el tiempo de cálculo de esta operación, la suma de las matrices se ha hecho directamente sobre la definición de la matriz , lo que ha disminuido el tiempo de cálculo en un . Una potencial mejora consiste en determinar a-priori el tamaño de esta matriz para asignar correctamente la memoria el inicio del cálculo.
4.3 Paralelización de la etapa global
La paralelización del problema global de interfaz se puede hacer de diferente formas. Una solución consiste en la utilización de librerías paralelas de resolución de sistemas lineares por ejemplo: MUMPS (MUltifrontal Massively Parallel Sparse direct Solver), HIPS (Hierarchical Iterative Parallel Solver), PaStiX (Parallel Sparse matriX package). El principal problema con estas librerías es que los resultados no son extensibles en función del número de procesadores. De todas formas estas librerías mantienen sus eficiencias para un número moderado de procesadores (del orden de 10 a 100), el speed-up se ve afectado para un número creciente de procesadores. Otra opción consiste en la utilización de procedimientos de solución paralelos de tipo BDD o FETI. Como el problema de interfaces está formulado en desplazamientos, el método BDD [9] será utilizado y mejorado con la implementación de un precondicionador de tipo BDDC (Balancing Domain Decomposition by Constraints) [6]. Las restricciones adicionales introducidas por el precondicionador corresponden a la continuidad de desplazamientos en los nodos esquina de los subdominios. El problema está escrito con una formulación corrotacional [25] lo que genera sistemas no simétricos, debido a lo cual se utiliza un algoritmo de tipo GMRES.
4.3.1 Paralelización de la etapa global con un método BDD
El residuo global consiste en ensamblar los residuos locales. El cálculo de los distintos residuos locales condensados se realiza en cada procesador, . Además se deben considerar los saltos de desplazamiento entre los subdominios . Finalmente se deben ensamblar todas estas contribuciones (ecuación (14)).
El objetivo de este procedimiento es no realizar multiplicaciones entre matrices, si no productos matriz-vector. Para eso, es necesario construir dos matrices, y para poder realizar las siguientes operaciones por subdominio:
|
|
(15) |
Es necesario tener presente la multiplicidad de cada g.d.l. de interfaz. Los nodos compartidos por 2 subdominios tienen multiplicidad 2, los compartidos por 3 subdominios, tienen multiplicidad 3, etc. Antes de ensamblar, cada termino del vector debe ser dividido por la multiplicidad correspondiente.
Los saltos de desplazamiento entre los subdominios se obtiene mediante un procedimiento similar al anterior, en donde se utilizan las mismas dos matrices descritas para el residuo como también . El procedimiento consiste en realizar las siguientes multiplicaciones matriz-vector (de derecha a izquierda):
|
|
(16) |
Todas estas operaciones son independientes por subdominios, por lo tanto paralelizables. La etapa final consiste en ensamblar los distintos resultados locales condensados (14), mediante la función de Open MPI, la cual optimiza este procedimiento. Las tres matrices (, y ) son almacenadas, ya que son utilizadas iterativamente para resolver el sistema.
4.3.2 Construcción e implementación de un precondicionador basado en una BDDC
El método GMRES utilizado para resolver el problema global necesita la utilización de un precondicionador para ser eficaz. Para esta implementación se eligió el precondicionador del método BDDC [6,26]. El método BDDC es muy similar al método FETI-DP [27] ya que funciona como un método primal.
El método BDDC introduce restricciones suplementarias (continuidad de desplazamientos) en las esquinas de los subdominios durante la etapa de precondicionamiento. Este método es una respuesta a los problemas de pérdida de extensibilidad debido a las singularidades observadas en nodos esquina en problemas de placas. Desde un punto de vista práctico, las esquinas son definidas como puntos múltiples (nodos compartidos por varios subdominios). La selección de estos nodos esquina debe hacerse de manera de bloquear los movimientos y rotaciones de cuerpo rígido de cada subdominio.
El precondicionador se define como:
|
|
(17) |
donde
|
es una matriz diagonal por bloques que se construye a partir de las matrices de ponderaciones de cada subdominio,
|
|
la diagonal de cada matriz de ponderación, representa el reciproco de la multiplicidad de cada g.d.l. de interfaz. Se considera que estas matrices cumplen con,
|
|
(21) |
el operador se define como:
|
|
(22) |
donde es el ensamblaje de cada por subdominio. Se usa para obtener el desplazamiento de los nodos esquina desde el vector que contiene los desplazamientos de todos los nodos de interfaz.
corresponde al ensamblaje de los diferentes , y se obtiene para cada subdominio haciendo,
|
|
donde representa a los nodos internos del subdominio (nodos no pertenecientes a ninguna interfaz), son los nodos de interfaz que no son de nodos esquina y son los nodos esquina.
Finalmente, representa la respuesta de la interfaz cuando un nodo esquina () es cargado con una fuerza unitaria (desplazamiento o rotación) y todos los otros g.d.l. de los todos nodos esquinas están bloqueados (Figura 3a).
es ensamblado haciendo, . en (18) representa el desplazamiento de los nodos esquina, a su vez en (19) representa el desplazamiento del resto de los nodos de interfaz bajo la acción del residuo local ponderado (), mientras se mantienen los nodos esquina empotrados (Figura 3b).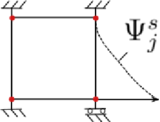
|
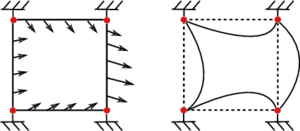
|
| (a) Representación gráfica de . | (b) Representación gráfica de . |
| Figura 3: Casos de carga analizados | |
La ecuación (19) se puede escribir,
|
|
(23) |
Por último, en (19) corresponde a un multiplicador de Lagrange usado para imponer la continuidad entre los nodos esquina.
La implementación del método BDDC permite reducir, de manera importante, el número de iteraciones GMRES. En la sección siguiente, se presenta un estudio de validación de la implementación del BDDC en elasticidad lineal. En particular análisis de extensibilidad y speed-up.
5. Validación de la implementación en elasticidad lineal
5.1 Extensibilidad numérica de la implementación
Para verificar la extensibilidad numérica del método implementado en elasticidad lineal, se estudia la influencia en el aumento del número de subdominios en el número de iteraciones GMRES para resolver el sistema global. Cada subdominio tiene la misma relación , siendo una longitud característica de un subdominio y una longitud característica de un elemento. En todos los cálculos un subdominio es calculado por un procesador. La estructura analizada consiste en una placa plana, empotrada en un extremo y sometida a dos tipos de cargas: uno de tracción y flexión en el plano (Figura 4a) y otro de flexión fuera del plano (Figura 4b). Distintos números de subdominios se han generado, pero siempre descomponiendo en ambas direcciones. La Figura 5 presenta los resultados para cada caso analizado. El número de iteraciones para cada relación H/h parece tender a una asíntota. Estos resultados son muy similares a los obtenidos por [7] y [28] para placas en flexión fuera del plano. Se puede decir que por la definición de nodos esquina utilizada, lo ideal es mantener una relación , la cual permite asegurar una buena extensibilidad del método.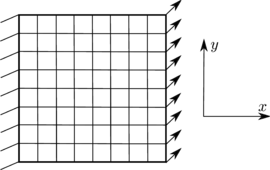
|
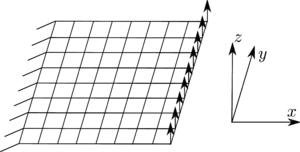
|
| (a) Placa en tracción y flexión en el plano. | b) Placa en flexión fuera del plano. |
| Figura 4: Casos de carga analizados | |
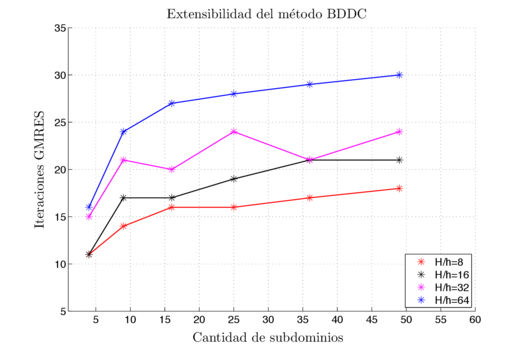
|
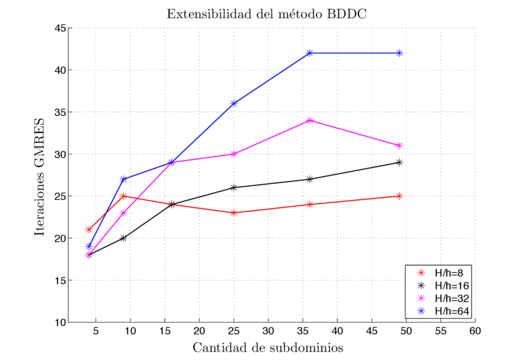
|
| (a) Placa en tracción y flexión en el plano. | b) Placa en flexión fuera del plano. |
| Figura 5: Estudio de extensibilidad. | |
5.2 Speed-up de la implementación
El speed-up de un algoritmo en paralelo se define como la relación entre la velocidad de un cálculo cuando se utiliza un solo procesador y cuando se utilizan procesadores para resolver un problema de tamaño fijo ( constante y variable). No todas las etapas son paralelizables, por lo que generalmente este número es inferior a y se define según la ley de Amdahl [29]:
|
|
(24) |
donde corresponde al tiempo de la parte paralelizable y a la parte secuencial, no paralelizable.
Para verificar el speed-up del método, se estudia el efecto del número de subdominios sobre el tiempo de cálculo total del problema. La malla de la estructura se deja fijo. A medida que el número de subdominios aumenta el tamaño del problema global aumenta, mientras que los problemas locales se reducen. La estructura analizada corresponde a la misma que para el estudio de extensibilidad (Figura 4a) pero solo para una carga de tracción solamente. En este estudio, tres niveles de refinamiento de malla se han analizado. Para cada cálculo, cada procesador se encarga de un solo subdominio. Los resultados del estudio, considerando los tres niveles de refinamiento, se presentan en la Figura 6. Se verifica, un speed-up muy cercano al óptimo al menos para valores de razonables (al aumentar el número de subdominios el valor de se aproxima a ). Se aprecia que para los tres casos de refinamiento existe un número óptimo de procesadores (subdominios) que da el mejor speed-up. Este número depende de la malla de la estructura (parámetro ). Para valores de , el speed-up está sobre la curva óptima. Por el contrario cuando , el speed-up se deteriora (se pasa más tiempo comunicando los procesos que resolviendo el problema).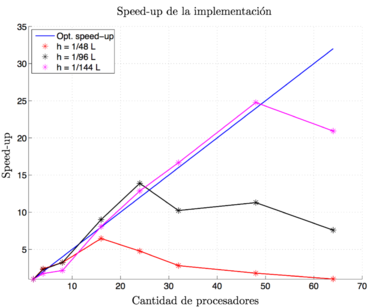
|
| Figura 6: Estudio de Speed-up, placa en tracción. |
Conclusiones
En este trabajo se ha paralelizado una estrategia de localización no lineal mixta, mediante un método de tipo BDD, resuelto con un procedimiento de tipo GMRES. Este procedimiento necesita muchas iteraciones del algoritmo GMRES, por lo que se incorpora un precondicionador de tipo BDDC. Posteriormente se ha validado esta implementación analizando en elasticidad lineal, la extensibilidad y el speed-up del método. Se ha constatado que las curvas de extensibilidad numérica tienen un comportamiento asintótico, similar al observado en [7] y [28] para una placa en flexión. Para el speed-up, se constató que para diferentes tamaños de malla se obtienen valores máximos diferentes. Este valor máximo se debe a que la resolución del problema global se vuelve menos importante, en términos de tiempos de cálculos, por lo que no se gana nada al aumentar la paralelización (número de subdominios). Esto depende del tamaño del problema (número de g.d.l.). Finalmente, se deben utilizar relaciones de , que permiten asegurar la extensibilidad del método y un speed-up cercano al óptimo.
Agradecimientos
La investigación que han permitido obtener los resultados aquí presentados han recibido financiamiento de CONICYT, FONDECYT de Iniciación n11160108.
Referencias
[1] De Roeck Y.H., Le Tallec P. and Vidrescu M. (1992). A domain-decomposition solver for nonlinear elasticity. Computer Methods in Applied Mechanics and Engineering 99: 187–207.
[2] Farhat C., Lesoinne M. and Pierson K. (2000). A scalable dual-primal domain decomposition method. Numerical Linear Algebra with application 7: 687–714.
[3] Cresta P., Allix O., Rey C. and Guinard, S. (2007). Nonlinear localization strategies for domain decomposition methods: application to post-buckling analyses. Computer Methods in Applied Mechanics and Engineering 196: 1436–1446.
[4] Hinojosa J., Allix O., Guidault P.-A. and Cresta P. (2014). Domain decomposition methods with nonlinear localization for the buckling and post-buckling analyses of large structures. Advances in Engineering Software 70: 13–24.
[5] Hinojosa J., Allix O., Guidault P.-A., Cresta Ph., and Saavedra K. (2017). Mixed nonlinear localization strategy for the buckling and post-buckling analyses of structures: Parameter optimization and path following implementation. Engineering Optimization 49(2): 269–289.
[6] Dohrmann C. R. (2003). A preconditioner for substructuring based on constrained energy minimization. SIAM Journal on Scientific Computing 25(1):246–258.
[7] Gosselet P. and Rey C. (2006). Non-overlapping domain decomposition methods in structural mechanics. Archives of Computational Methods in Engineering 13(4): 515–572.
[8] Le Tallec P., De Roeck Y.H. and Vidrascu M. (1991). Domain decomposition methods for large linearly elliptic three-dimension problems. Journal of Computational and Applied Mathematics 34(1): 93–117.
[9] Mandel J. (1993). Balancing domain decomposition. Communications in Applied Numerical Methods 9: 233–241.
[10] Farhat C. and Roux F.-X. (1991). A method of finite element tearing and interconnecting and its parallel solution algorithm. International Journal for Numerical Methods in Engineering 32: 1205–1227.
[11] Ladevèze P. (1985). Sur une famille d'algorithmes en mécanique des structures. Compte rendu de l'académie de Sciences 300(2): 41–4
[12] Glowinski R. and Le Tallec P. (1990). Augmented Lagrangian interpretation of the non overlapping Schwarz alternating method. in: Third International Symposium on Domain Decomposition Methods for Partial Differential Equations, SIAM 224–231.
[13] Series L., Feyel F. and Roux F.-X. (2003). Une méthode de décomposition de domaine avec deux multiplicateurs de Lagrange, application au calcul des structures, cas du contact. Actes du Sixieme Colloque National en Calcul des Structures 373–380.
[14] Pavarino L. F. and Widlund O. B. (2002). Balancing Neumann-Neumann methods for incompressible Stokes equations. Communications on Pure and Applied Mathematics 55(3): 302–335.
[15] Pebrel J., Rey C., and Gosselet P. (2008). A nonlinear dual domain decomposition method: application to structural problems with damage. International Journal for Multiscale Computational Engineering 6(3): 251–262.
[16] Allix O., Kerfriden P. and Gosselet P. (2010). A relocalization technique for the multi scale computation of delamination in composite structures. Computer Modeling in Engineering and Sciences 55: 271–292
[17] Saavedra K., Allix O. and Gosselet P. (2012). On a multi scale strategy and its optimization for the simulation of combined delamination and buckling. International Journal for Numerical Methods in Engineering 91(7): 772–798.
[18] Saavedra E., Saavedra K., Hinojosa J., Chandra Y., and Das R. (2016). Multi-scale modeling of rolling shear failure in cross-laminated timber structures by homogeneisation and cohesive models. International Journal of Solids and Structures 81: 219–232.
[19] Brezzi F. and Marini L.D. (2005). The three-field formulation for elasticity problems. GAMM Mitteilungen 28: 124–153.
[20] Fortin M. and Glowinski R. (1983). Chapter1: Augmented Lagrangian Methods in Quadratic Programming, in: Fortin M. and Glowinski R. (Eds), Augmented Lagrangian Methods: Applications to the Numerical Solution of Boundary Value Problems. Studies in Mathematics and Its Applications, Elsevier vol. 15: 1–46.
[21] Ladeveze P. (1999). Nonlinear computational structural mechanics - New Approaches and Non-incremental Methods of Calculation. Springer Verlarg, Berlin.
[22] Saavedra K., Allix O., Gosselet P., Hinojosa J., and Viard A. (2017). An enhanced non-linear multi-scale strategy for the simulation of buckling and delamination on 3D composite plates. Computer Methods in Applied Mechanics and Engineering 317: 952–969.
[23] Diekmann R., Monien B. and Preis R. (1997). Load balancing strategies for distributed memory machines. In Satz H., Karsch F. and Monien B. editors: Multi-Scale Phenomena and Their Simulation. World Scientific 255–266.
[24] Lottiaux R., Gallard P., Vallée G., Morin C. and Boissinot B. (2005). Openmosix, openssi ans kerrighed: a comparative study. In CCGRID'05: Proceedings of the Fifth IEEE International Symposiun on Cluster Computing and the Grip vol. 2: 1016–1023, Washington, DC, USA. IEEE Computer Society.
[25] Felippa C.A. and Haugen B. (2005). A unified formulation of small-strain corotational finite elements: 1. Theory. Computer Methods in Applied Mechanics and Engineering 194(21-24): 2285–2335.
[26] Mandel J., Dohrmann C. R., and Tezaur R. (2004). An algebraic theory for primal and dual substructuring methods by constraints. Applied Numerical Mathematics 54(2): 167–193. 6th IMACS.
[27] Farhat C., Lesoinne M., Le Tallec P., Pierson K., and Rixen D. (2001). FETI-DP: A dual-primal unified FETI method - Part I: A faster alternative to the two-level FETI method. International Journal for Numerical Methods in Engineering 50: 1523–1544.
[28] Beirão da Veiga L., Chinosi C., Lovadina C. and Pavarino L. F. (2010). Robust BDDC preconditioners for Reissner-Mindlin plate bending problems and MITC elements. SIAM J. Numerical Analysis 47(6): 4214–4238.
[29] Amdahl G. M. (1988). Limits of expectation. International Journal of High Performance Computing Applications 2: 88–94.
Document information
Published on 03/01/18
Accepted on 27/06/17
Submitted on 25/04/17
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.7.004
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?