| (6 intermediate revisions by 2 users not shown) | |||
| Line 24: | Line 24: | ||
We study whether parental education affects the choice of tertiary education in Spain. We analyze two qualitative characteristics of the university studies: the length of the program and its academic prestige. We identify for which individuals parental background matters the most. For the choice of a long program, parental background changes the most likely outcome for students with low grades in the academic track and those with excellent grades in the vocational track. Regarding the prestige of the program, parental background matters the most for the worse performing boys and the girls with rather good grades in the academic track. | We study whether parental education affects the choice of tertiary education in Spain. We analyze two qualitative characteristics of the university studies: the length of the program and its academic prestige. We identify for which individuals parental background matters the most. For the choice of a long program, parental background changes the most likely outcome for students with low grades in the academic track and those with excellent grades in the vocational track. Regarding the prestige of the program, parental background matters the most for the worse performing boys and the girls with rather good grades in the academic track. | ||
| − | |||
| − | |||
| − | |||
| − | |||
<br/> | <br/> | ||
| Line 172: | Line 168: | ||
We first study whether parental background influences the choice between long and short university program. Table 2 reports the logistic estimation coefficients of the probability of studying a long program. In model 1, we include father’s education level. Model 2 includes instead the highest level of education of the parents, while model 3 includes both the education level of father and mother. Apart from parental education, we control for gender, track of secondary education (vocational vs. academic) and ability (average grade in secondary education). All these variables have a significant effect on the choice of study program. Results are as expected. Females and students that followed the vocational track in secondary education are less likely to graduate from a long program, while higher ability and parental education increase chances of studying a long program. | We first study whether parental background influences the choice between long and short university program. Table 2 reports the logistic estimation coefficients of the probability of studying a long program. In model 1, we include father’s education level. Model 2 includes instead the highest level of education of the parents, while model 3 includes both the education level of father and mother. Apart from parental education, we control for gender, track of secondary education (vocational vs. academic) and ability (average grade in secondary education). All these variables have a significant effect on the choice of study program. Results are as expected. Females and students that followed the vocational track in secondary education are less likely to graduate from a long program, while higher ability and parental education increase chances of studying a long program. | ||
| − | |||
'''Table 2.''' Table of coefficients for a logistic estimation. Dependent variable: Long program (1=long, 0=short). | '''Table 2.''' Table of coefficients for a logistic estimation. Dependent variable: Long program (1=long, 0=short). | ||
| Line 223: | Line 218: | ||
Results in Table 2 reveal that parental background influences the probability of studying a long program. However, we need to resort to predicted probabilities to confirm that this effect is strong enough to change the most likely outcome for particular individuals. | Results in Table 2 reveal that parental background influences the probability of studying a long program. However, we need to resort to predicted probabilities to confirm that this effect is strong enough to change the most likely outcome for particular individuals. | ||
| − | |||
| − | |||
'''Figure 1.''' Plot of predicted probabilities of studying a long program by parental background. Cases where EMI is satisfied. | '''Figure 1.''' Plot of predicted probabilities of studying a long program by parental background. Cases where EMI is satisfied. | ||
| − | + | [[Image:Vilalta-Bufi_2018a_9914_figure1.png|center|286px]] | |
| − | [[Image:Vilalta- | + | |
| − | + | ||
a. Academic track in secondary education and average grade ''‘pass’''. | a. Academic track in secondary education and average grade ''‘pass’''. | ||
| − | + | [[Image:Vilalta-Bufi_2018a_9514_figure2.png|center|292px]] | |
| − | [[Image:Vilalta- | + | |
b. Academic track in secondary education and average grade ‘''good''’. | b. Academic track in secondary education and average grade ‘''good''’. | ||
| − | + | [[Image:Vilalta-Bufi_2018a_1504_figure3.png|center|294px]] | |
| − | [[Image:Vilalta- | + | |
| − | + | ||
c. Vocational track in secondary education and average grade ‘''excellent with honors''’. | c. Vocational track in secondary education and average grade ‘''excellent with honors''’. | ||
| Line 313: | Line 301: | ||
|} | |} | ||
''t'' statistics in parentheses <sup>*</sup> ''p'' < 0.1, <sup>**</sup> ''p'' < 0.05, <sup>***</sup> ''p'' < 0.01, McKelvey & Zavoina’s R<sup>2</sup> reported, cutoff points tested for not overlapping. | ''t'' statistics in parentheses <sup>*</sup> ''p'' < 0.1, <sup>**</sup> ''p'' < 0.05, <sup>***</sup> ''p'' < 0.01, McKelvey & Zavoina’s R<sup>2</sup> reported, cutoff points tested for not overlapping. | ||
| − | |||
| − | |||
'''Table 4.''' Predicted probabilities of attending an academically prestigious program (Academic track, ‘Licenciados’ sample). | '''Table 4.''' Predicted probabilities of attending an academically prestigious program (Academic track, ‘Licenciados’ sample). | ||
| Line 523: | Line 509: | ||
'''Figure 2.''' Plots of predicted probabilities for those from academic track where EMI is satisfied. | '''Figure 2.''' Plots of predicted probabilities for those from academic track where EMI is satisfied. | ||
| − | + | {| style="width: 100%;align: center;" | |
| − | {| | + | |
|- | |- | ||
| − | | [[Image:Vilalta- | + | | [[Image:Vilalta-Bufi_2018a_6593_figure2_1.png|center|274px]] |
| − | | [[Image:Vilalta- | + | | [[Image:Vilalta-Bufi_2018a_8292_figure2_2.png|center|285px]] |
|} | |} | ||
| − | |||
Father’s education: 1-without studies, 2-primary education, 3-secondary education and 4-tertiary education. | Father’s education: 1-without studies, 2-primary education, 3-secondary education and 4-tertiary education. | ||
| Line 535: | Line 519: | ||
Table 5 reports the predicted probabilities to study a prestigious program for those individuals who followed a vocational track. We observe that parental background changes the most likely outcome for males with average grades ‘Good’ and ‘Very good’ in the secondary education. In the case of females, the same happens when they have ‘Excellent’ grade in secondary education. Note, however, that females with lower grades who followed a secondary vocational education are not affected by father’s education in their chances for academically prestigious program. This can be an artifact of gender socialization roles apparently still existent in Spain. | Table 5 reports the predicted probabilities to study a prestigious program for those individuals who followed a vocational track. We observe that parental background changes the most likely outcome for males with average grades ‘Good’ and ‘Very good’ in the secondary education. In the case of females, the same happens when they have ‘Excellent’ grade in secondary education. Note, however, that females with lower grades who followed a secondary vocational education are not affected by father’s education in their chances for academically prestigious program. This can be an artifact of gender socialization roles apparently still existent in Spain. | ||
| − | |||
'''Table 5.''' Predicted probabilities of attending an academically prestigious program (vocational track, ‘Licenciados’ sample) | '''Table 5.''' Predicted probabilities of attending an academically prestigious program (vocational track, ‘Licenciados’ sample) | ||
| Line 739: | Line 722: | ||
Figure 3 displays the predicted probabilities for those cases from the vocational track where EMI is satisfied. In contrast to the previous results, parental background changes the most likely outcome for those individuals with rather high average grade in secondary education when they studied vocational track. We observe that, in general, those males with ‘Very good’ average grade get to prestigious programs unless their father has no studies, in which case they get to low prestigious studies. For those males who obtained a ‘Good’ average grade in secondary education, only those with highly educated fathers will be slightly more likely to graduate from highly prestigious programs. In the case of females results show that those with ‘Excellent’ grade whose father has at most primary education will most likely study in a low prestige program, while those whose father has secondary or tertiary education will be more likely to study in a highly prestigious program. | Figure 3 displays the predicted probabilities for those cases from the vocational track where EMI is satisfied. In contrast to the previous results, parental background changes the most likely outcome for those individuals with rather high average grade in secondary education when they studied vocational track. We observe that, in general, those males with ‘Very good’ average grade get to prestigious programs unless their father has no studies, in which case they get to low prestigious studies. For those males who obtained a ‘Good’ average grade in secondary education, only those with highly educated fathers will be slightly more likely to graduate from highly prestigious programs. In the case of females results show that those with ‘Excellent’ grade whose father has at most primary education will most likely study in a low prestige program, while those whose father has secondary or tertiary education will be more likely to study in a highly prestigious program. | ||
| − | |||
| − | |||
'''Figure 3.''' Plots of predicted probabilities for those from vocational track where EMI is satisfied. | '''Figure 3.''' Plots of predicted probabilities for those from vocational track where EMI is satisfied. | ||
| − | {| | + | {| style="align: center; width: 100%;" |
|- | |- | ||
| − | | [[Image:Vilalta- | + | | [[Image:Vilalta-Bufi_2018a_9087_figure3_1.png|center|300px]] |
| − | | [[Image:Vilalta- | + | | [[Image:Vilalta-Bufi_2018a_1704_figure3_2.png|center|300px]] |
| + | |- | ||
| + | | colspan="2" | [[Image:Vilalta-Bufi_2018a_3285_figure3_3.png|center|300px]] | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
Latest revision as of 11:52, 11 July 2018
Abstract
We study whether parental education affects the choice of tertiary education in Spain. We analyze two qualitative characteristics of the university studies: the length of the program and its academic prestige. We identify for which individuals parental background matters the most. For the choice of a long program, parental background changes the most likely outcome for students with low grades in the academic track and those with excellent grades in the vocational track. Regarding the prestige of the program, parental background matters the most for the worse performing boys and the girls with rather good grades in the academic track.
1. Introduction
The literature on intergenerational mobility has for long recognized the importance of education as the key intermediate factor (Breen and Jonsson 2005; Erikson and Goldthorpe 2002; Kerckhoff 1995; Kerckhoff 2001). The main findings resulting from this research are that there is a large increase in educational mobility, which, in time, facilitates also the class mobility across generations. Results, however, are not uniform across countries and have been demonstrated to depend on the country’s structure of schooling and its influence on transitions between levels of education for different social origins (Muller and Karle 1993). In light of this evidence, special attention has to be paid not only to the probabilities of attaining certain levels of education conditioned on the social origin as advanced by the Mare model (Mare 1981), but also to the probabilities of attaining a certain type of education within a given level.
Another result of the literature is that parental background influences tend to fade as transitions to higher levels of education are concerned (Raftery and Hout 1993; Shavit and Blossfeld 1993). Several hypotheses have been advanced to explain the waning family background phenomenon. In the Life Course Perspective (LCP) Muller and Karle (1993) claimed that students at later transitions are less dependent on their parents in financial and cultural terms. This perspective cannot be really embraced in Spain. Especially strong family ties characterize the Spanish society and so the life course perspective would not hold in Spain for cultural reasons. The alternative hypothesis named Maximally Maintained Inequality (MMI) claims that parental effects lose strength in educational mobility equations because education is highly subsidized by governments and enrollment rises so fast that lower social classes are progressively included into levels of education previously closed for them (Raftery and Hout 1993). This situation is much more plausible in Spain given its spectacular democratization of education (especially tertiary education in recent decades). There is, however, empirical evidence that Spanish social mobility is still limited.
The hypothesis that we want to test in this paper is called the Effectively Maintained Inequality (EMI) advanced by Lucas (Lucas 2009; Lucas 2001). According to this theory, the effects of parental background manifest across successive transitions not only through the odds of making a particular transition, but also through qualitative differences within each transition. These qualitative differences can take form of choosing one particular track over another or one type of school over the other. We hypothesize that at tertiary transitions in Spain, parental influences manifest not so much through the likelihood of making that transition, but rather through the qualitative differences associated to this transition in terms of educational program qualities. We analyze two qualitative characteristics of the university studies: the length of the program and its academic prestige.
We can distinguish between long and short programs in the Spanish universities during the 2000s. They differed in several qualitative aspects apart from the years of study they required. The long program, which was called Licenciatura (4-year studies), gave access to doctoral studies. Moreover, it was generally regarded as more prestigious by the labor market and on average offered more and better job opportunities than the short program (called Diplomatura, 3-year studies). In some occupations, it was actually required by law to have a degree from a long program (Engineering, Law, Medicine…).
We look also at the academic prestige of the study program reported by individuals five years after graduation. This variable measures to what extent the program attended by graduates was regarded as prestigious and thus, would give them better chances for a good employment.
The rest of the paper is organized as follows. The next section sketches the historical context in the Spanish educational expansion and provides motivation why one would like to concentrate on the tertiary rather than secondary transition in order to test EMI. We also provide some basic statistics on the demographic situation in Spain and briefly discuss gender and immigrant situation. Section 3 presents the data and analytical methods used for each of the two analyses: program length and academic prestige. Finally, sections 4 and 5 present and discuss results respectively.
2. Historical context of the modern Spanish education system
Modern Spanish education system known today is a product of years of evolution rather than a product of revolution. Changes applied to the education system came through a series of reforms that could be traced back as much as to the middle ninetieth century and the Public Instruction Act (Ley de Instrucción Pública). It was the first comprehensive education law in Spain. In fact, this law laid the basis for all the later laws in Spain. It promoted and reinforced creation of private, most often Catholic, primary and secondary schools, which exist until today and are regarded as offering high quality, prestigious education. The Public Instruction Act made for the first time a strong point on the introduction of sciences into secondary education, which fostered the acquisition of technical skills by Spanish elites. It has to be recognized that until roughly the death of General Franco, Spanish education system above the primary level was largely an elite system. During the major part of the twentieth century (until late sixties) university education was largely a question of a much selected elite rather than the massive phenomenon known today. The expansion of tertiary education started with the General Act on Education and Financing of Educational Reform (Ley General de Educación y Financiamiento de la Reforma Educativa, LGE), a short-lasting reform (EURYDICE 2009b; Perotti 2007).
Secondary level expansion
The secondary education in Spain ceased to be elitist much earlier than the tertiary. Already the Constitution of the Second Republic proclaimed in 1931 provided basis for free and compulsory primary education. Later, in 1953, the dictatorial regime reformed the secondary education finishing its elitist position and introduced the possibility for studying it at two levels: elementary (up to 14 years of age) and higher (up to 16 years). At that time, the pre-university course was also introduced (later changed into university orientation course (COU – Curso de Orientación Universitaria)). It is then when we can already talk about the expansion of the secondary education. However, the real expansion occurred with the introduction of the General Act on Education and Financing of Educational Reform in 1970 (Ley General de Educación y Financiamiento de la Reforma Educativa) which established free and compulsory education for everyone aged 6 to 14 and laid several legislative provisions for an improvement of the quality of education for all pupils. The following reforms that occurred in the decade of eighties were characterized by the same aim – expansion of the secondary education, and constant improvement in its quality. The Act on the Right to Education approved in 1985 provided a basis for publicly funded private schools which were supposed to increase the access to quality secondary education even more (EURYDICE 2009b). All these legislative efforts found their culmination in the Act on the General Organization of the Education System (Ley Orgánica de Ordenación General del Sistema Educativo, LOGSE) issued in 1990. LOGSE extended free and compulsory education until age 16, entailing primary (Educación Primaria) and lower secondary (Educación Secundaria Obligatoria, ESO) education. At present the secondary education in Spain can safely be called universal (EURYDICE 2009a). Participation rate in the secondary education (jointly ISCED 2 and ISCED 3) reached almost 100% (97%) for the population of 15-year-olds in 2006 in Spain. For the 16-year-olds, the participation rate falls to some 93%. Majority of secondary level students are enrolled in academic programs. The ratio for the total population is 57.5% in favor of academic schooling vs. vocational education. For male population the ratio falls to 54% in academic tracks while for females it grows to almost 60%. Participation rate in secondary education falls to 70% after the age of 16 (end of compulsory education), which is similar to the average for the whole European Union (EU-27). It must be noted here that despite the universality of the secondary education in Spain today, the dropout rate from the compulsory secondary education is extremely high, reaching over 30% of all pupils at that level.
Massive tertiary level
Given the universality of the secondary education one gets to ask what is the participation rate in tertiary education in today’s Spain. In tertiary levels, there has occurred a very similar, though much delayed, trend as in secondary education. Participation rate in tertiary education in Spain grew seven times the size of that in the early sixties. In 2008 over 45% of women and 30% of men aged 20 were enrolled in tertiary education. Even more striking are the figures of new enrollments compared to the 18-year-old population in Spain. The participation at this age group grew from 21% in early eighties to over 55% in the end of nineties (Mora, Garcia-Montalvo and Garcia-Aracil 2000). In the age group 25-34, the population ratio holding tertiary degree to the whole population in Spain is 39%. Slightly lower ratio can be found for the active population which is 29% for the year 2007.
Tertiary level expansion roots
To arrive at this participation levels the Spanish tertiary education has undergone several groundbreaking changes over the last decades. The process of reforming tertiary education can be traced back to early seventies when the General Act on Education and Financing of Educational Reform (Ley General de Educación y Financiamiento de la Reforma Educativa) introduced new rules of access to university. All pupils willing to enroll in the university had to pass from then on an entry exam after accomplishing three years of higher secondary education (Bachillerato Universal y Polivalente, BUP) and a one-year university orientation course (Curso de Orientación Universitaria, COU). Meanwhile the upper secondary education was controlled by the secondary school; the university preparatory course’s curriculum was set by universities but still taught by the institutes of secondary education. The 1970 law organized the university system as well. It introduced formally the three cycle system which existed until very recently, with first cycle studies being 3-years long and leading to a title of Diplomatura, or longer 4-year title Licenciatura, second cycle studies usually lasting 1-2 years and awarding titles of Licenciatura, and finally graduate third cycle programs awarding advanced degrees (doctorate).
The key change for the organization of tertiary education in Spain was the introduction of the Act on University Reform (Ley de Reforma Universitaria, LRU) in 1983. It changed several things about university organization giving it, above of all, the long-demanded autonomy in establishing new curricula. This was also the first law to abandon the old financing system assigned to full professor positions and shifted it towards the students enrollment numbers (EURYDICE 2009b; Mora and Vidal 2000; Perotti 2007). Under the new system, universities could enroll more students, create new curricula and introduce certain flexibility in assessment rules. This opened a wide avenue for mass tertiary education for the first time in the history of Spain. This law was reinforced with the provisions of the Act on the General Organization of the Education System (Ley Orgánica de Ordenación General del Sistema Educativo, LOGSE) in 1990. The main contribution of this law to mass tertiary education was establishing that higher vocational education became considered higher non-university education thereafter. The massive inflow of students into the tertiary system called for the need of establishing some quality rules in the tertiary sector. This has been brought by the Act on Universities (Ley Orgánica de Universidades, LOU) from December 2001. Apart from a further strengthening of the university autonomy and the introduction of the National Agency for Quality Assessment and Accreditation (ANECA), LOU expanded also the influence of local autonomous governments on university financing. All these changes led to a rapid and massive expansion of the tertiary education in Spain (Vidal 2003). While in 1982 there were 31 universities in Spain (5 private and 26 public), there were already 71 universities in 2005, 23 of which were private. Such increase shows best the magnitude of the tertiary level expansion in Spain during the last two decades.
Given the massive participation in the secondary education and extremely high levels of enrollment in the tertiary levels (short and long programs), we believe it is most interesting to test the Effectively Maintained Inequality hypothesis with respect to the tertiary level of education. At the secondary level, though, it could also be tested taking into account types of tracks and private/public school distinctions. These differences, however, most likely would reflect more internal Spanish migrant status than social origin per se (Recaño Valverde and Roig Vila 2003). We decide to concentrate on tertiary level education transitions and their qualitative dimension. The REFLEX data offers us unprecedented quality of information on qualitative aspects of educational program, which allow testing EMI hypothesis in much greater depth than other data sets currently available for Spain.
3. Data and Methods
To analyze whether the effectively maintained inequality theory applies to the choice of tertiary level studies in Spain, we use REFLEX data. A detailed description of the REFLEX survey is available at Allen and Van der Velden (2007). This survey consists of information on individuals who graduated in 1999/2000 and were interviewed five years later in 2005. We have detailed information on their graduate studies, their parental level of education and their personal background. All this information is available for 3,522 individuals in Spain.
Parental background is described by the level of education of the father and the mother of the respondent. Each of these variables has four levels: 1-without studies, 2-primary education, 3-secondary education and 4-tertiary education. We also created a variable that collects the highest level of education attained by parents.
We perform two types of analysis. First, we estimate the effect of parental background on the probability to study a short vs. long program. As mentioned above, this distinction does not only refer to number of years of study, but it has a qualitative aspect as well. Graduates from short programs have no access to doctoral studies and generally have more limited job opportunities than graduates from long programs especially in Spain (Mora, Garcia-Montalvo and Garcia-Aracil 2000). We perform a logistic estimation and using predicted probabilities check whether the most likely outcome changes due to parental background.
Second, we analyze a qualitative dimension within each type of program. We have information on six qualitative characteristics of the study program at the tertiary level. The respondent was asked to what extent the program was generally regarded as demanding, was academically prestigious, was vocationally oriented, had a broad focus, employers were familiar with the content and there was freedom in composing own program. Estimation analyses reveal that only Prestige depends on the parental education level. Therefore, our further analysis concentrates exclusively on this characteristic. We define Prestige as a three-category variable (converted from a five-category scale). We perform ordered logistic estimations to learn whether parental background changes the choice of studies of their offspring in terms of this qualitative variable. We run the analysis by level of education: diplomatura (lower tertiary, 3-year studies) and licenciatura (higher tertiary level, 4-year studies).
Table 1 reports the descriptive statistics of the variables per sample. Above 60% of graduates studied a long program. Moreover, the average prestige of long programs (‘Licenciatura’) is slightly higher than that of short programs (‘Diplomatura’). We observe a better parental background for the ‘Licenciatura’ sample, suggesting that parental education will influence the choice between long and short program. Similarly, those who chose long program have on average higher grade in secondary education than those who studied a short program.
As for gender, there are no significant differences across samples. Around 64% of the graduates are female. The highest difference is in the track of secondary education. Those who followed a vocational track are more likely to study a short program. This is due to the tracking system itself that restricts the access of these students to some long programs.
Table 1. Descriptive statistics.
| Whole sample | 'Diplomatura' sample | 'Licenciatura' sample | ||||
| Variable | Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. |
| Long program | 0.601 | 0.490 | 0 | 0.000 | 1 | 0.000 |
| Prestigious program | 2.014 | 0.828 | 1.847 | 0.803 | 2.124 | 0.825 |
| Father’s education level | 2.646 | 0.966 | 2.453 | 0.905 | 2.775 | 0.984 |
| Mother’s education level | 2.444 | 0.885 | 2.268 | 0.824 | 2.560 | 0.905 |
| Highest parental education level | 2.792 | 0.945 | 2.590 | 0.912 | 2.926 | 0.944 |
| Female | 0.645 | 0.479 | 0.653 | 0.476 | 0.639 | 0.480 |
| Vocational track | 0.086 | 0.280 | 0.169 | 0.374 | 0.031 | 0.174 |
| Grade in secondary education | 2.861 | 0.926 | 2.646 | 0.822 | 3.005 | 0.963 |
| Number of observations | 3522 | 1406 | 2116 | |||
4. Results
4.1 Long vs. short program
We first study whether parental background influences the choice between long and short university program. Table 2 reports the logistic estimation coefficients of the probability of studying a long program. In model 1, we include father’s education level. Model 2 includes instead the highest level of education of the parents, while model 3 includes both the education level of father and mother. Apart from parental education, we control for gender, track of secondary education (vocational vs. academic) and ability (average grade in secondary education). All these variables have a significant effect on the choice of study program. Results are as expected. Females and students that followed the vocational track in secondary education are less likely to graduate from a long program, while higher ability and parental education increase chances of studying a long program.
Table 2. Table of coefficients for a logistic estimation. Dependent variable: Long program (1=long, 0=short).
| (1) | (2) | (3) | |
|---|---|---|---|
| Long program | Long program | Long program | |
| Female | -0.118 | -0.128* | -0.128* |
| (-1.54) | (-1.67) | (-1.66) | |
| Vocational track | -1.870*** | -1.858*** | -1.850*** |
| (-12.64) | (-12.54) | (-12.49) | |
| Grade in secondary educ | 0.483*** | 0.476*** | 0.473*** |
| (11.30) | (11.14) | (11.03) | |
| Father's education | 0.276*** | 0.184*** | |
| (7.14) | (3.79) | ||
| Highest parental education | 0.296*** | ||
| (7.51) | |||
| Mother's education | 0.165*** | ||
| (3.07) | |||
| Constant | -1.437*** | -1.508*** | -1.563*** |
| (-8.77) | (-9.05) | (-9.23) | |
| N | 3522 | 3522 | 3522 |
| AIC | 4339.3 | 4333.8 | 4331.8 |
| BIC | 4370.1 | 4364.6 | 4368.8 |
| R-squared mz | 0.151 | 0.153 | 0.155 |
t statistics in parentheses, * p < 0.1, ** p < 0.05, *** p < 0.01.</div>
Results in Table 2 reveal that parental background influences the probability of studying a long program. However, we need to resort to predicted probabilities to confirm that this effect is strong enough to change the most likely outcome for particular individuals.
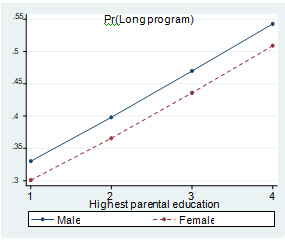
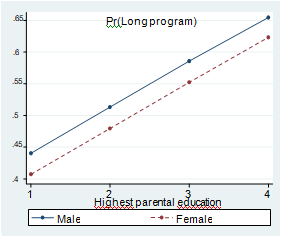
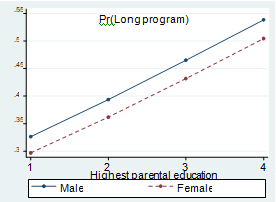
Figure 1. Plot of predicted probabilities of studying a long program by parental background. Cases where EMI is satisfied.
a. Academic track in secondary education and average grade ‘pass’.
b. Academic track in secondary education and average grade ‘good’.
c. Vocational track in secondary education and average grade ‘excellent with honors’.
Parental education: 1-without studies, 2-primary education, 3-secondary education and 4-tertiary education. Crossing the 0.5 line implies a change in the most likely outcome.
Figure 1 shows the three cases that were found to confirm the effectively maintained inequality thesis (Lucas 2001). In the rest of the cases, parental background did not change the most likely outcome of individuals. To compute predicted probabilities we used the estimation that includes the highest level of education of parents (Model 2).
As it becomes clear from the predicted probabilities, parental education helps those individuals with low grades in secondary education that studied an academic track and those individuals with best grades in secondary education that followed a vocational track. Consider, for instance, a male who followed an academic track in secondary education and has an average grade of ‘good’ (Figure 1b). If none of his parents has any studies, he is more likely to study a short program (probability of studying a long program 0.44, vs. probability of studying a short program 0.56). In contrast, had one of his parents secondary or tertiary education, then he would most likely study a long program (probability of studying a long program 0.59 and 0.65 respectively).
4.2 Prestige of the program
In this section, we test whether parental education influences the choice of an academically prestigious program within short and long university programs respectively. We estimate ordered logistic equations separately by each type of program. Table 3 reports the coefficient estimates for three different specifications. In model 1, we include father’s education level. Model 2 includes instead the highest level of education of the parents, while model 3 includes both the education level of father and mother. As before, we control for gender, track in the secondary education and ability.
Results reveal that parental educational background is important only for the ‘licenciados’ group. Moreover, model 1 is preferred as indicated by the Akaike’s and Bayesian information criteria. Therefore, if parental background matters in choosing an academically prestigious program, it occurs in higher tertiary education (long program). Moreover, father’s education level (model 1) is the main determinant of this effect.
Next, we compute the predicted probabilities for different individuals to find out those cases where parental background is strong enough to change their most likely outcome. We do so for the ‘Licenciatura’ sample only, since estimation results show that parental background does not explain prestige of the program in the ‘Diplomatura’ sample. We compute predicted probabilities using model 1, which is the best one according to Akaike’s and Bayesian information criteria.
Tables 4 and 5 report predicted probabilities of attending an academically prestigious program as a function of father’s education and for all combinations of gender and average grade from secondary education. Table 4 considers the probabilities for an individual who followed an academic track in secondary education, while Table 5 reports the probabilities for an individual from a vocational secondary track. Recall that these probabilities are all referring to the sample of ‘Licenciados’ (the long program graduates).
Table 3. Table of coefficients for an ordered logistic estimation. Dependent variable: Academically prestigious program (three levels: low, medium, high prestige).
| Short Prog | Short Prog | Short Prog | Long Pr | Long Pr | Long Pr | |
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (1) | (2) | (3) | |
| Female | -0.89*** | -0.89*** | -0.897*** | -0.472*** | -0.48*** | -0.47*** |
| (-8.36) | (-8.37) | (-8.40) | (-5.52) | (-5.57) | (-5.52) | |
| Vocational track | -0.200 | -0.182 | -0.183 | -0.436* | -0.456** | -0.436* |
| (-1.45) | (-1.32) | (-1.32) | (-1.89) | (-1.98) | (-1.89) | |
| Grade in secondary educ. | 0.374*** | 0.372*** | 0.368*** | 0.340*** | 0.341*** | 0.340*** |
| (5.94) | (5.90) | (5.83) | (7.69) | (7.70) | (7.67) | |
| Father’s education | 0.0434 | -0.0150 | 0.142*** | 0.148*** | ||
| (0.77) | (-0.21) | (3.41) | (2.79) | |||
| Highest parental education | 0.0863 | 0.103** | ||||
| (1.55) | (2.39) | |||||
| Mother’s education | 0.107 | -0.0111 | ||||
| (1.39) | (-0.19) | |||||
| Constant cut1 | 0.0905 | 0.204 | 0.172 | 0.136 | 0.0480 | 0.128 |
| (0.39) | (0.88) | (0.72) | (0.76) | (0.26) | (0.69) | |
| Constant cut2 | 1.601*** | 1.716*** | 1.684*** | 1.468*** | 1.377*** | 1.460*** |
| (6.84) | (7.24) | (6.96) | (8.01) | (7.34) | (7.75) | |
| N | 1406 | 1406 | 1406 | 2116 | 2116 | 2116 |
| AIC | 2947.2 | 2945.4 | 2947.3 | 4496.6 | 4502.5 | 4498.5 |
| BIC | 2978.7 | 2976.9 | 2984.0 | 4530.5 | 4536.4 | 4538.1 |
| MZ R2 | 0.0758 | 0.0772 | 0.0773 | 0.0541 | 0.0513 | 0.0541 |
| Brant χ2 | 1.812 | 1.613 | 2.110 | 5.840 | 6.427 | 6.593 |
| Brant p-val. | 0.770 | 0.806 | 0.834 | 0.211 | 0.169 | 0.253 |
t statistics in parentheses * p < 0.1, ** p < 0.05, *** p < 0.01, McKelvey & Zavoina’s R2 reported, cutoff points tested for not overlapping.
Table 4. Predicted probabilities of attending an academically prestigious program (Academic track, ‘Licenciados’ sample).
| Prestige levels of study program | |||||||
| Grade in secondary educ. | Father's education | high | medium | low | high | medium | low |
| Male in Academic track | Female in Academic track | ||||||
| 1
‘Pass’ |
No studies | 0.27 | 0.31 | 0.41 | 0.19 | 0.28 | 0.53 |
| Primary | 0.30 | 0.32 | 0.38 | 0.21 | 0.29 | 0.50 | |
| Secondary | 0.33 | 0.32 | 0.35 | 0.24 | 0.30 | 0.46 | |
| Tertiary | 0.36 | 0.32 | 0.32 | 0.26 | 0.31 | 0.43 | |
| 2
‘Good’ |
No studies | 0.34 | 0.32 | 0.34 | 0.25 | 0.31 | 0.45 |
| Primary | 0.38 | 0.32 | 0.30 | 0.27 | 0.31 | 0.41 | |
| Secondary | 0.41 | 0.31 | 0.28 | 0.30 | 0.32 | 0.38 | |
| Tertiary | 0.44 | 0.31 | 0.25 | 0.33 | 0.32 | 0.35 | |
| 3
‘Very good’ |
No studies | 0.42 | 0.31 | 0.26 | 0.31 | 0.32 | 0.37 |
| Primary | 0.46 | 0.30 | 0.24 | 0.35 | 0.32 | 0.33 | |
| Secondary | 0.49 | 0.29 | 0.21 | 0.38 | 0.32 | 0.30 | |
| Tertiary | 0.53 | 0.28 | 0.19 | 0.41 | 0.31 | 0.27 | |
| 4
‘Excellent’ |
No studies | 0.51 | 0.29 | 0.20 | 0.39 | 0.32 | 0.29 |
| Primary | 0.54 | 0.28 | 0.18 | 0.43 | 0.31 | 0.26 | |
| Secondary | 0.58 | 0.26 | 0.16 | 0.46 | 0.30 | 0.24 | |
| Tertiary | 0.61 | 0.24 | 0.14 | 0.50 | 0.29 | 0.21 | |
| 5
‘Excellent with honors’ |
No studies | 0.59 | 0.25 | 0.15 | 0.47 | 0.30 | 0.23 |
| Primary | 0.63 | 0.24 | 0.14 | 0.51 | 0.29 | 0.20 | |
| Secondary | 0.66 | 0.22 | 0.12 | 0.55 | 0.27 | 0.18 | |
| Tertiary | 0.69 | 0.20 | 0.11 | 0.58 | 0.26 | 0.16 | |
Underlined the most likely outcome. Bolded where the most likely outcome changes with parental background.
Bolded in Table 4 are all those combinations of gender and secondary average grade from an academic secondary track that give support to the EMI hypothesis. Parental background changes the most likely outcome for males with lowest grade in secondary education. Notice for instance that the most likely outcome for this individual when his father has no studies is to attain a low prestige program (probability 0.41). Had his father had tertiary education, his most likely outcome in terms of program prestige would be a highly prestigious program (with probability 0.36). In the case of females, parental background changes the most likely outcome when they have ‘very good’ grade from their secondary education.
Figure 2 plots the predicted probabilities for these two types of individuals. Results show that male who followed an academic track in their secondary education and have an average grade ‘Pass’ from those studies benefit from having a father with tertiary education. While the most likely outcome is studying a low prestige program for those individuals with father’s education lower than tertiary, those whose father has tertiary education are more likely to study an academically prestigious program. In the second plot from Figure 2 we observe that those females from an academic track who have ‘Very good’ as average grade in secondary education will most likely study a highly prestigious program as long as their father has at least primary education. The differences in predicted probabilities grow with father’s education. In contrast, those females whose father has no studies have more chances to end up in a low prestige study program.
Figure 2. Plots of predicted probabilities for those from academic track where EMI is satisfied.
Father’s education: 1-without studies, 2-primary education, 3-secondary education and 4-tertiary education.
Table 5 reports the predicted probabilities to study a prestigious program for those individuals who followed a vocational track. We observe that parental background changes the most likely outcome for males with average grades ‘Good’ and ‘Very good’ in the secondary education. In the case of females, the same happens when they have ‘Excellent’ grade in secondary education. Note, however, that females with lower grades who followed a secondary vocational education are not affected by father’s education in their chances for academically prestigious program. This can be an artifact of gender socialization roles apparently still existent in Spain.
Table 5. Predicted probabilities of attending an academically prestigious program (vocational track, ‘Licenciados’ sample)
| Prestige levels of study program | ||||||||
| Grade in secondary educ | Father's education | high | medium | low | high | medium | low | |
| Male, Vocational track | Female, Vocational track | |||||||
| 1
‘Pass’ |
No studies | 0.19 | 0.28 | 0.52 | 0.13 | 0.23 | 0.64 | |
| Primary | 0.22 | 0.3 | 0.49 | 0.15 | 0.25 | 0.6 | ||
| Secondary | 0.24 | 0.31 | 0.45 | 0.17 | 0.26 | 0.57 | ||
| Tertiary | 0.27 | 0.31 | 0.42 | 0.19 | 0.28 | 0.53 | ||
| 2
‘Good’ |
No studies | 0.25 | 0.31 | 0.44 | 0.17 | 0.27 | 0.56 | |
| Primary | 0.28 | 0.32 | 0.4 | 0.2 | 0.28 | 0.52 | ||
| Secondary | 0.31 | 0.32 | 0.37 | 0.22 | 0.3 | 0.49 | ||
| Tertiary | 0.34 | 0.32 | 0.34 | 0.24 | 0.31 | 0.45 | ||
| 3
‘Very good’ |
No studies | 0.32 | 0.32 | 0.36 | 0.23 | 0.3 | 0.47 | |
| Primary | 0.35 | 0.32 | 0.33 | 0.25 | 0.31 | 0.44 | ||
| Secondary | 0.39 | 0.32 | 0.3 | 0.28 | 0.32 | 0.4 | ||
| Tertiary | 0.42 | 0.31 | 0.27 | 0.31 | 0.32 | 0.37 | ||
| 4
‘Excellent’ |
No studies | 0.4 | 0.32 | 0.28 | 0.29 | 0.32 | 0.39 | |
| Primary | 0.43 | 0.31 | 0.26 | 0.32 | 0.32 | 0.35 | ||
| Secondary | 0.47 | 0.3 | 0.23 | 0.36 | 0.32 | 0.32 | ||
| Tertiary | 0.51 | 0.29 | 0.21 | 0.39 | 0.32 | 0.29 | ||
| 5
‘Excellent with honors’ |
No studies | 0.48 | 0.3 | 0.22 | 0.37 | 0.32 | 0.31 | |
| Primary | 0.52 | 0.28 | 0.2 | 0.4 | 0.32 | 0.28 | ||
| Secondary | 0.55 | 0.27 | 0.18 | 0.44 | 0.31 | 0.25 | ||
| Tertiary | 0.59 | 0.26 | 0.16 | 0.47 | 0.3 | 0.23 | ||
Underlined the most likely outcome. Bolded where the most likely outcome changes with parental background.
Figure 3 displays the predicted probabilities for those cases from the vocational track where EMI is satisfied. In contrast to the previous results, parental background changes the most likely outcome for those individuals with rather high average grade in secondary education when they studied vocational track. We observe that, in general, those males with ‘Very good’ average grade get to prestigious programs unless their father has no studies, in which case they get to low prestigious studies. For those males who obtained a ‘Good’ average grade in secondary education, only those with highly educated fathers will be slightly more likely to graduate from highly prestigious programs. In the case of females results show that those with ‘Excellent’ grade whose father has at most primary education will most likely study in a low prestige program, while those whose father has secondary or tertiary education will be more likely to study in a highly prestigious program.
Figure 3. Plots of predicted probabilities for those from vocational track where EMI is satisfied.
5. Conclusions
Spain has seen a large educational expansion in the last decades, which has also occurred in tertiary education since the Act on University Reform (Ley de Reforma Universitaria, LRU) in 1983. In 2008 over 45% of women and 30% of men aged 20 were enrolled in tertiary education. Notwithstanding the increase in the access to university experienced during last decades, we have found that equality of opportunities is hindered by the influence of parental background on the choice of tertiary education program. Understanding the role of parental background is especially important in Spain given that more than 47% of parents have at most primary education.
We analyze two educational choices: long vs. short program and prestige of the program. Our results show that those individuals with better-educated parents are more likely to choose a long program. Moreover, among those who chose a long program, having better educated parents, leads to more chances to study in an academically prestigious program.
In order to investigate the strength of the parental influence on educational outcomes of individuals, we compute predicted probabilities and find that for some cases parental background changes the most likely outcome of individuals from short to long program and from low to high prestige tertiary program. These results support the effectively maintained inequality thesis of Lucas (2001).
Our results show that parental education is a strong determinant of studying a long program for those individuals with low grades from academic secondary track as well as for those with high grades from vocational secondary track. With regards to prestige of the program, when individuals followed the academic secondary education track, parental background changes the most likely outcome for those males with the lowest grades and for those females with ‘Very good’ grade. In the case of those who studied the vocational track in secondary education, parental background strongly influences their program prestige for males with ‘Good’ or ‘Very good’ grades and for females with ‘Excellent’ grade in secondary education.
The optimist side from our analysis is that ability (measured as average grade in secondary education) also has an important role in explaining the choice of study program. Those with best grades are always more likely to study a highly academically prestigious program.
After the Bologna process, all undergraduate degrees last 4 years in Spain. Nowadays there is the introduction of new degrees that last 3 years. We believe that the results of this paper shed some light on the implications it might have on educational mobility.
References
Allen, Jim, and Rolf Van der Velden (Eds.). 2007. The Flexible Professional in The Knowledge Society: General Results of the REFLEX Project: Research Centre for Education and the Labour Market.
Breen, Richard, and Jan O. Jonsson. 2005. "Inequality of Opportunity in Comparative Perspective: Recent Research on Educational Attainment and Social Mobility." Annual Review of Sociology 31:223.
Erikson, Robert, and John H. Goldthorpe. 2002. "Intergenerational Inequality: Sociological Perspective." Journal of Economic Perspectives 16:31.
EURYDICE. 2009a. "Key Data on Education in Europe 2009." European Commission.
—. 2009b. "Organisation of the education system in Spain." European Commission.
Kerckhoff, Alan C. 1995. "Institutional Arrangements and Stratification Processes in Industrial Societies." Annual Review of Sociology 21:323.
—. 2001. "Education and Social Stratification Processes in Comparative Perspective." Sociology of Education 74:3.
Lucas, Samuel. 2009. "Stratification Theory, Socioeconomic Background, and Educational Attainment: A Formal Analysis." Rationality and Society 21:459-511.
Lucas, Samuel R. 2001. "Effectively Maintained Inequality: Education Transitions, Track Mobility, and Social Background Effects." American Journal of Sociology 106:1642.
Mare, Robert D. 1981. "Change and Stability in Educational Stratification." American Sociological Review 46:72.
Mora, Jose-Gines, Jose Garcia-Montalvo, and Adela Garcia-Aracil. 2000. "Higher Education and Graduate Employment in Spain." European Journal of Education 35(2):229-37.
Mora, José-Ginés, and Javier Vidal. 2000. "Lifelong Learning in Spanish Universities: The Market Inside the Public System." European Journal of Education 35(3):317-27.
Muller, Walter, and Wolfgang Karle. 1993. "Social Selection in Educational Systems in Europe." European Sociological Review 9:1.
Perotti, Loris. 2007. "Institutional Change in teh Spanish Higher Education System." European Journal of Education 42(3):411-23.
Raftery, Adrian E., and Michael Hout. 1993. "Maximally Maintained Inequality: Expansion, Reform and Opportunity in Irish Education, 1921-75." Sociology of Education 66:41.
Recaño Valverde, Joaquín, and Marta Roig Vila. 2003. "Internal Migration and Inequalities. The Influence of Migrant Origin on Educational Attainment in Spain." European Sociological Review 19(3):299-317.
Shavit, Yossi, and Hans Peter Blossfeld. 1993. Persistent Inequality. Changing Educational Attainment in Thirteen Countries: Boulder CO: Westview.
Vidal, Javier. 2003. "Quality of Assurance, Legal Reforms and the European Higher Education Area in Spain." European Journal of Education 38(3):301-13.
Document information
Published on 10/05/18
Accepted on 10/05/18
Submitted on 22/01/18
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?