Métodos numéricos generales no estándar para la solución directa de ecuaciones diferenciales no despejadas en formas canónicas.

Latest revision as of 10:43, 28 November 2017

Métodos numéricos generales no estándar para la solución directa de ecuaciones diferenciales no despejadas en formas canónicas.

Carlos Oscar Rodríguez Leal

Universidad de Guadalajara. CUCEI.

e-mail: misifu17@gmail.com

Resumen

En este trabajo se desarrollan algoritmos numéricos que se pueden aplicar de manera directa a ecuaciones diferenciales de la forma general ${\textstyle f(t,x,x')=0}$ , sin necesidad de despejar ${\textstyle x'}$ . Mis métodos son algoritmos híbridos entre los métodos estándar de solución de ecuaciones diferenciales y métodos de solución de ecuaciones algebraicas, con los que se despeja numéricamente la variable ${\textstyle x'}$ .

La aplicación de estos métodos va desde ecuaciones diferenciales ordinarias de orden uno, hasta el caso más general de sistemas de ${\textstyle m}$ ecuaciones de orden ${\textstyle n}$ . Dichos algoritmos se aplican a la solución de diversas ecuaciones de la física-matemática.

Por último, se hace el análisis numérico correspondiente de existencia, unicidad, estabilidad, consistencia y convergencia, principalmente para el caso más sencillo de una sola ecuación diferencial ordinaria de primer orden.

Palabras clave Ecuaciones diferenciales, métodos numéricos no estándar, función derivada implícita, método de Euler-bisección, consistencia, estabilidad, convergencia, ecuaciones de estrella de bosones.

Non-standard general numerical methods for the direct solution of differential equations not cleared in canonical forms

Abstract

In this work I develop numerical algorithms that can be applied directly to differential equations of the general form ${\textstyle f(t,x,x')=0}$ , without the need to cleared ${\textstyle x'}$ . My methods are hybrid algorithms between standard methods of solving differential equations and methods of solving algebraic equations, with which the variable ${\textstyle x'}$ is numerically cleared.

The application of these methods ranges from the ordinary differential equations of order one, to the more general case of systems of ${\textstyle m}$ equations of order ${\textstyle n}$ . These algorithms are applied to the solution of different physical-mathematical equations.

Finally, the corresponding numerical analysis of existence, uniqueness, stability, consistency and convergence is made, mainly for the simplest case of a single ordinary differential equation of the first order.

Keywords Differential equations, non-standard numerical methods, implicit derivative function, Euler-bisection method, consistency, stability, convergence, boson star equations.

1 Introducción

En este trabajo se desarrollan algoritmos numéricos que se pueden aplicar de manera directa a ecuaciones diferenciales de la forma general ${\textstyle f(t,x,x')=0}$ , sin necesidad de despejar algebraicamente ${\textstyle x'}$ de la forma ${\textstyle x'=f(t,x)}$ para poder emplear los métodos ordinarios.

Los algoritmos desarrollados son modificaciones de métodos estándar para resolver ecuaciones diferenciales con condiciones iniciales, en particular el método de Euler. La esencia de la modificación consiste en desarrollar algoritmos híbridos entre los métodos estándar de solución de ecuaciones diferenciales y métodos de solución de ecuaciones algebraicas, con los cuales se despejan numéricamente la variable ${\textstyle y'}$ . Los métodos se desarrollan tanto para ecuaciones diferenciales ordinarias de orden uno, como para el caso más general de sistemas de ${\textstyle m}$ ecuaciones con ${\textstyle m}$ incógnitas de orden ${\textstyle n}$ .

La importancia de estos métodos radica en que en la práctica muchas veces es muy difícil hacer los despejes algebraicos de ${\textstyle y'}$ en las ecuaciones diferenciales, si no es que imposible.

Dichos procedimientos directos los aplico a ecuaciones de la física-matemática, entre ellas la ecuación de caída libre con fricción y las ecuaciones de Einstein para las estrellas de bosones.

Por último, realizo el análisis numérico correspondiente de existencia, unicidad, estabilidad, consistencia y convergencia de las soluciones numéricas proporcionadas por mis métodos, principalmente para el caso más sencillo de una sola ecuación diferencial ordinaria de primer orden resuleta por mi método de Euler modificado, dejando para trabajos posteriores el análisis correspondiente de los demás casos.

2 Definiciones y teoremas previos

En esta sección se enunciarán algunos teoremas ya establecidos que serán necesarios para la elaboración de este trabajo.

Teorema 1: Supóngase que el problema de valor inicial

se aproxima por el método de diferencias de un paso de la forma

Considérese también que existe un número ${\textstyle h_{0}>0}$ y ${\textstyle \phi (t,x;h)}$ es continua y satisface una condición de Lipschitz en la variable ${\textstyle x}$ con constante de Lipschitz ${\textstyle L}$ en el conjunto

Entonces el método es estable.

Teorema 2: Si en la ecuación ${\textstyle x'=g(t,x)}$ , ${\textstyle \partial g/\partial t}$ y ${\textstyle \partial g/\partial y}$ existen, entonces

(1)

3 Método de Euler modificado o de Euler-Leal

En esta primera sección, comenzando por los casos más simples, se explican tanto la elaboración como el análisis numérico para el método de Euler modificado, combinando el método de Euler con el método algebraico de bisección.

3.1 Método de Euler-Bisección

En este primer método, como punto de partida, se emplan los dos métodos más simples, intuitivos y fáciles de analizar, los cuales son el método de Euler, para ecuaciones diferenciales, y el método de la bisección.

3.1.1 Desarrollo del algoritmo

Así pues, comenzaremos considerando la ecuación general sin despejar

(2)

para la cual calcularemos los distintos valores aproximados de ${\textstyle x'}$ en un intervalo ${\textstyle t_{0}\leq t\leq t_{f}}$ , con un tamaño de paso ${\textstyle h}$ y con la condición inicial ${\textstyle x(t_{0})=x_{0}}$ ; la cual, al sustituirla en la función ${\textstyle f}$ , generará la expresión

(3)

Entonces, dado que no tenemos despejada de manera explícita la variable ${\textstyle x'}$ , para encontrar su valor, de manera aproximada, usaremos el método de la bisección, donde tomamos dos valores de arranque inamovibles ${\textstyle \alpha _{i}}$ y ${\textstyle \alpha _{d}}$ , ${\textstyle \alpha _{i}<\alpha _{d}}$ , tales que

(4)

Además la diferencia

(5)

deberá ser convenientemente grande en lugar de ser convenientemente pequeña (lo cual se explicará más adelante).

Luego de ello comenzamos las iteraciones del núcleo del algoritmo.

- ${{\tilde {x}}'}_{0}=Biseccion(t_{0},{\tilde {x}}_{0},\alpha _{i},\alpha _{d},\tau )$
- para $(n=0{\hbox{ hasta }}N-1)$

  a)    $t_{n+1}=t_{n}+h$ 
  b)    ${\tilde {x}}_{n+1}={\tilde {x}}_{n}+{{\tilde {x}}'}_{n}h$  
  c)    $\tau =\tau (h)$ 
  d)    ${{\tilde {x}}'}_{n+1}=Biseccion(t_{n+1},{\tilde {x}}_{n+1},\alpha _{i},\alpha _{d},\tau )$

- fin

(6)

donde en la ecuación del inciso c)

(7)

${\textstyle \tau }$ es la tolerancia o error para el método de la bisección, de tal manera que la subrutina de bisección se detendrá cuando ${\textstyle {{\tilde {x}}'}_{{(n+1)}_{m}}-{{\tilde {x}}'}_{{(n+1)}_{m-1}}\leq \tau }$ , para alguna ${\textstyle m}$ -ésima iteración del algoritmo anidado “Biseccion” dentro del núcleo del algoritmo de Euler-biseccion en su iteración ${\textstyle n}$ -ésima. El porqué se ha elegido a la tolerancia ${\textstyle \tau }$ como función de ${\textstyle h}$ será aclararado en la sección del análisis de este método.

Por ahora diremos que la elección de la diferencia (5) debe ser suficientemente amplia, pues si dicha diferencia es pequeña, aunque el teorema del valor intermedio nos garantiza que existe una raiz ${\textstyle x'}$ para ${\textstyle f}$ dados ${\textstyle t_{0}}$ y ${\textstyle x_{0}}$ fijos y cumpliéndose (4) (bajo el supuesto de que la función ${\textstyle f}$ es continua, lo que se analizará más adelante, en la subsección de convergencia), como tal función ${\textstyle f}$ irá variando sus valores ${\textstyle t_{n}}$ y ${\textstyle x_{n}}$ al entrar al núcleo recursivo (6), para esos nuevos valores fijados (con ${\textstyle n}$ suficientemente grande) dicha función podría ya no tener una raiz para ${\textstyle x'}$ dentro del intervalo pequenño ${\textstyle [\alpha _{i},\alpha _{d}]}$ . Pero con un intervalo adecuadamente amplio y donde ${\textstyle {x'}_{0}}$ esté más o menos centrada, disminuirá considerablemente el riesgo de que la raiz se localice fuera de dicho intervalo y el método aborte dándonos un mensaje de error (pues está programado para tolerar ese fallo).

3.1.2 Condiciones generales para un problema bien planteado

Ahora procederemos a hacer el correspondiente análisis de unicidad y buen planteamiento, del método numérico anterior, estableciendo los criterios bajo los cuales se cumplirán ambos requisitos.

Observación 1: En todos los análisis de este artículo siempre tomaremos como punto de partida algún espacio ${\textstyle \mathbb {R} ^{n}}$ , para algún ${\textstyle n\in \mathbb {N} }$ y consideraremos una métrica euclideana, es decir, partiremos de un espacio euclidiano ${\textstyle n}$ -dimensional.

Así pues, emplearemos las condiciones de la sección 3.1.1, con

(8)

Ahora consideraremos las siguientes hipótesis de esta subsección que han de cumplirse, y sus correspondientes tesis.

Definición 1: Definiremos primeramente a ${\textstyle F=[t_{0},t_{f}]\times \mathbb {R} \times \mathbb {R} }$ , lo cual significa que ${\textstyle F}$ es el dominio de definición de ${\textstyle f}$ .

Teorema 3:

Si extendemos el conjunto

, eligiendo

definido como

(9)

de tal forma que ${\textstyle \beta _{i}<t_{0}}$ y ${\textstyle \beta _{d}>t_{f}}$ , tendremos que ${\textstyle G}$ será un subconjunto abierto de ${\textstyle R^{3}}$ que contendrá a ${\textstyle F}$ .

Por lo tanto, si ampliamos el dominio de definición de

a

, es decir

, y se cumple que

(10)

existen y son continuas en el conjunto abierto convexo ${\textstyle G}$ , entonces, por el teorema de la continuidad de una función solamente si sus derivadas parciales son continuas (Rudin, 1980, p. 236), tendremos que ${\textstyle f\in C'(G)}$ y por lo tanto ${\textstyle f\in C'(F)}$ (definiendo las derivadas por derecha y por izquierda en los respectivos extremos ${\textstyle \alpha _{i}}$ y ${\textstyle \alpha _{d}}$ ).

Si además, dados

y

fijos, se cumple

(11)

para todo ${\textstyle x'\in \mathbb {R} }$ , entonces podemos definir a la función

(12)

siendo con ello la derivada

(13)

continua en ${\textstyle \mathbb {R} }$ , i.e., por el teorema del valor intermedio, claramente ${\textstyle {u'}_{t_{r},x_{r}}(x')>0}$ ó ${\textstyle {u'}_{t_{r},x_{r}}(x')<0}$ (pero no ambos) para todo ${\textstyle x'\in \mathbb {R} }$ . De lo anterior, usando el teorema de la función estrictamente monótona (Lang, 1990, p. 60) se deduce que ${\textstyle u_{t_{r},x_{r}}}$ es estrictamente monótona en ${\textstyle \mathbb {R} }$ para todo par ${\textstyle (t,x)\in H=(\beta _{i},\beta _{d})\times \mathbb {R} }$ . En particular ${\textstyle u_{t_{r},x_{r}}}$ es estrictamente monótona en ${\textstyle \mathbb {R} }$ para todo ${\textstyle (t,x)\in I=[t_{0},t_{f}]\times \mathbb {R} }$ .

Y si también se cumple que para

y

fijos existen

y

, con

(14)

tales que

(15)

es decir

(16)

entonces, usando una vez más el teorema de valor intermedio, se puede demostrar que existe un único ${\textstyle {x'}_{r}}$ , con ${\textstyle {x'}_{i_{r}}{<x'}x'_{<}x'_{d_{r}}}$ , que satisface ${\textstyle u_{t_{r},x_{r}}{(x'}_{r})=0}$ , o lo que es lo mismo ${\textstyle {f(t_{r},x_{r},x'}_{r})=0}$ . En particular lo anterior es cierto para ${\textstyle t\in [t_{0},t_{f}]}$ .

Teorema 4: Cosiderando los puntos del teorem anterior, y observando que la ecuación ${\textstyle f(t,x,x')=0}$ definida en ${\textstyle G}$ determina implícitamente a ${\textstyle x'=g(t,x)}$ (que es la función que no podemos despejar), entonces, de acuerdo al punto 4. de dicho teorema y utilizando el teorema de la función implícita, se demuestra que para cada par ${\textstyle (t_{r},x_{r})\in H}$ existe un ${\textstyle {x'}_{r}\in \mathbb {R} }$ que satisface ${\textstyle {f(t_{r},x_{r},x'}_{r})=0}$ , de tal forma que para dicha triada ${\textstyle {(t_{r},x_{r},x'}_{r})}$ se cumple lo siguiente (es decir, en cada punto ${\textstyle (t_{r},x_{r})}$ del dominio ${\textstyle H}$ para ${\textstyle g}$ ):

${\textstyle {x'}_{r}=g(r_{r},y_{r})}$ es función monovaluada.
${\textstyle {x'}_{r}=g(r_{r},y_{r})}$ es continua y con primera derivada continua.
${\textstyle {\frac {\partial g}{\partial x}}|_{t_{r},x_{r}}=-{\frac {{\frac {\partial f}{\partial x}}|_{t_{r},x_{r}}}{{\frac {\partial f}{\partial x'}}|_{t_{r},x_{r}}}}}$ .

Corolario 1: En particular, el teorema anterior es cierto para el dominio restringido ${\textstyle I}$ para ${\textstyle g}$ .

Teorema 5: Utilizando el teorema de la derivada parcial para la condición de Lipschitz [1] y el punto 3. del teorema (4) resulta evidente que si existe una constante ${\textstyle L>0}$ que satisface

(17)

para toda ${\textstyle (t,x)\in I}$ , entonces ${\textstyle g}$ satisface una condición de Lipschitz sobre ${\textstyle I}$ en la variable ${\textstyle x}$ y con constante de Lipschitz ${\textstyle L}$ .

Teorema 6: Ahora, haciendo uso del teorema del problema de valor inicial bien planteado (Burden y Faires, 1996, p. 242), si la función ${\textstyle g}$ definida implícitamente es continua en ${\textstyle I}$ y satisface una condición de Lipschitz en la variable ${\textstyle x}$ sobre ${\textstyle I}$ , entonces el problema de valor inicial

(18)

está bien planteado.

3.1.3 Análisis del error del método de Euler-bisección.

En esta subsección se hará un análisis particular para el error de ${\textstyle {\tilde {x}}}$ respecto a ${\textstyle x}$ , su orden y el error óptimo, para el método de Euler-bisección, suponeindo que se cumplen las hipótesis de la subsección anterior.

Teorema 7: Dada la tolerancia ${\textstyle \tau (h)}$ definida en (7), así como los extremos ${\textstyle t_{0}}$ y ${\textstyle t_{f}}$ , entonces es claro que la subrutina de bisección se detendrá en cuanto se cumpla que ${\textstyle |{\tilde {x}}'-x'|\leq {\frac {t_{f}-t_{0}}{2^{N(h)}}}\leq \tau }$ , para algún ${\textstyle N\in \mathbb {N} _{0}}$ , donde ${\textstyle N(h)}$ no ha de depender de ${\textstyle t}$ , ${\textstyle x}$ o ${\textstyle x'}$ y por lo tanto siempre valdrá lo mismo para un ${\textstyle h}$ dado. Por lo tanto podemos expresar a dicho error como

(19)

donde ${\textstyle \delta (h)}$ tampoco dependerá de ${\textstyle t}$ , ${\textstyle x}$ o ${\textstyle x'}$ y por lo tanto será constante dado un valor fijo para ${\textstyle h}$ . En consecuencia tendremos que ${\textstyle -\delta <{\tilde {x}}'-x'<\delta }$ , o lo que es lo mismo, ${\textstyle g(t,x)-\delta <{\tilde {x}}'<g(t,x)+\delta }$ . Por ello, al emplear el método de Euler-biseccion tendremos la expresión

lo cual equivale a

{\begin{aligned}{\tilde {x}}_{0}&=x_{0}+(\delta _{-1}=0)\\{\tilde {x}}_{n+1}&={\tilde {x}}_{n}+hg(t_{n},{\tilde {x}}_{n})+(h\delta _{n}:=\Delta _{n}),{\hbox{ para }}n=0,1\ldots N-1\\\end{aligned}}

(20)

con ${\textstyle \phi =g+\delta _{n}}$ y ${\textstyle 0\leq |\delta _{n}|<\delta \leq \tau }$ , y por ende

(21)

La anterior es una ecuación en diferencias como la que corresponde al método de Euler perturbado [1], con una perturbación ${\textstyle h\delta _{n}=\Delta _{n}}$ , para ${\textstyle n=0,\ldots ,N-1}$ .

Ahora deduciremos el siguiente teorema.

Teorema 8: Empleando la fórmula del teorema (2) y el teorema (4) podemos expresar a ${\textstyle x''}$ como

(22)

Además, si existe una constante ${\textstyle M}$ con la propiedad ${\textstyle |x''|\leq M}$ , para alguna constate ${\textstyle M>0}$ y ${\textstyle t\in [t_{0},t_{f}]}$ , entonces

(23)

para todo ${\textstyle t\in [t_{0},t_{f}]}$ .

Observación 2: En el teorema anterior, en la expresión (23) aparece ${\textstyle x'}$ . Sin embargo, si dicha ${\textstyle x'}$ no se puede eliminar de la expresión por simplificación algebraica, entonces, una vez que ya se ha demostrado la unicidad en la solución de la ecuación, si el sistema físico nos da información extra respecto a un acotamiento para la velocidad ( ${\textstyle x'}$ ), entonces la ecuación modelo debe poseer el mismo acotamiento para ${\textstyle x'}$ , ya que la ecuación modelo y el sistema físico se corresponden en sus valores siempre que la ecuación con condiciones iniciales sea única.

Ahora enunciaremos el teorema de la cota del error para ${\textstyle {\tilde {x}}}$

Teorema 9: Usando el teorema del acotamiento del error global (Burden et al., 1996, p. 248), la fórmula (23), el teorema (7) y el teorema del error global para el método de Euler perturbado (Burden et al., 1996, p. 251), podemos obtener la siguiente cota para el error, en su iteración n-ésima, de la solución numérica respecto a la exacta

(24)

donde ${\textstyle L}$ es la constante de Lipschitz para ${\textstyle x'=g(t,x)}$ Además, el valor óptimo para ${\textstyle h}$ (el mínimo error posible) se presenta para un ${\textstyle h}$ aproximado a ${\textstyle h={\sqrt {2\Delta /M}}}$ , o, despejando a ${\textstyle \Delta }$ , cuando ${\textstyle \Delta ={\frac {M}{2}}h^{2}}$ , es decir, cuando

(25)

tomando entonces la expresión (19) la forma

(26)

Teorema 10: Usando la definición del error de truncamiento local (Burden et al., 1996, p. 254), el teorema (7) y suponiendo que ${\textstyle x''\leq M}$ para ${\textstyle t\in [t_{0},t_{f}]}$ , podemos observar que el error de truncamiento local para el método de Euler-bisección es ${\textstyle e_{n+1}(h)={\frac {x_{n+1}-x_{n}}{h}}-{{\tilde {x}}'}_{=}={\frac {x_{n+1}-x_{n}}{h}}-g(t_{n},x_{n})-\delta _{n}={\frac {h}{2}}x''(\xi )-\delta _{n}\leq {\frac {h}{2}}M-\delta _{n}}$ , por lo que al aplicar el valor absoluto nos quedará ${\textstyle |e_{n+1}(h)|=|{\frac {h}{2}}x''(\xi )-\delta _{n}|\leq |{\frac {h}{2}}x''(\xi )|+|\delta _{n}|<{\frac {h}{2}}M+\delta \leq {\frac {h}{2}}M+\tau }$ . En conclusión, obtenemos el siguiente acotamiento para el error de truncamiento local

(27)

donde vemos que dicho acotamiento no depende de la iteración ${\textstyle (n+1)}$ -ésima en la que estemos, ni tampoco de ${\textstyle t}$ , ${\textstyle x}$ ni ${\textstyle x'}$ .

Teorema 11: Del teorema anterior vemos que el método de Euler-biseccion es de orden lineal o menor, dependiendo de cómo esté definida la función ${\textstyle \tau (h)}$ . Así, si ${\textstyle \tau }$ es constante, el método es de orden cero, y ello significa que el error ${\textstyle e}$ no cambia, sin importa que hagamos más pequeña a ${\textstyle h}$ . Por ello, lo conveniente es definir a

(28)

de esa forma el método será por lo menos lineal. Además, es fácil ver que esta definición para ${\textstyle \tau }$ es compatible con la dada en el teorema (9) para el error mínimo, donde ${\textstyle C=M/2}$ , i.e.

(29)

es el valor óptimo para la tolerancia, el cual nos dará, usando la fórmula (10), un error mínimo de

(30)

Observación 3: Las fórmulas (29) y (30) se corresponden bellamente con las fórmulas (25) y (26), respectivamente, si desarrollamos la exponencial en su serie de Maclaurin.

Observación 4: Ahora ya se puede comenzar a dar respuesta a la pregunta de la subsección pirmera del por qué es conveniente definir a ${\textstyle \tau =\tau (h)}$ .

3.1.4 Análisis de estabilidad, consistencia y convergencia del método de Euler-bisección

Ahora se hará el análisis de estabilidad, consistencia y convergencia para el método de Euler-bisección suponiendo que se cumplen todas las condiciones de la subsección anterior.

Teorema 12: Empleando la definición de consistencia de un método de ecuación en diferencias (Burden et al., 1996, p. 312), la fórmula (10), la definición de punto adherido o punto límite, el teorema de compresión (Lang, 1990, p. 41) (teorema del emparedado) y definiendo a ${\textstyle \tau }$ como ${\textstyle \tau =Ch}$ , de acuerdo a (11), concluimos que ${\textstyle \lim _{h\rightarrow 0}|e_{n+1}(h)|=0}$ , por lo que

(31)

y en consecuencia el método es consistente.

Teorema 13: Ahora, empleando la definición de convergencia para un método de ecuación en diferencias [1], y la fórmula (26), obtendremos, de manera análoga al teorema anterior, ${\textstyle lim_{h\rightarrow 0}|x_{n}-{\tilde {x}}_{n}|=0}$ , es decir

(32)

i.e. el método es convergente.

Teorema 14: Considerando ahora el teorema (1), la subrutina de bisección y el problema perturbado mostrado en (20), entonces es obvio que ${\textstyle \phi (t_{n},{\tilde {x}}_{n};h)=biseccion(t_{n},{\tilde {x}}_{n};h,\alpha _{i},\alpha _{d})=biseccion(t_{n},{\tilde {x}}_{n};h)=g+\delta _{n}={{\tilde {x}}'}_{n}}$

Teorema 15: Retomando el teorema anterior y empleando la condición de Lipschitz para ${\textstyle g}$ , así como la fórmula (21), y la expresión (11), tendremos para ${\textstyle \phi (t,x;h)}$ que ${\textstyle |\phi (t,x,h)-\phi (t,y,h)|=|{\tilde {x}}'-{\tilde {y}}'|}$ $=|g(t,x)+{\tilde {\delta }}(t,x,h)-g(t,y)-{\tilde {\delta }}(t,y,h)|\leq |g(t,x)-g(t,y)|+|{\tilde {\delta }}(t,x,h)-{\tilde {\delta }}(t,y,h)|$ $\leq L|x-y|+|{\tilde {\delta }}(t,x,h)|+|{\tilde {\delta }}(t,y,h)|<L|x-y|+2\tau =L|x-y|+2Ch$ , donde hemos hecho la transición ${\textstyle \delta _{n}\rightarrow {\tilde {\delta }}}$ para el caso continuo, resultando la siguiente desigualdad

(33)

donde, del lado derecho de la última ecuación no podemos deshacernos del término ${\textstyle 2Ch}$ . Sin embargo, debido a que ya se demostró que el problema está bien planteado si cumple el criterio dado en (6), además de la consistencia y convergencia, entonces es de esperarse que para un ${\textstyle h}$ razonablemente pequeño, dicho término se puede tomar como equivalente a pequeños errores de redondeo de computadora, y por ende que el método se comporte como el de Euler ligeramente perturbado, siendo entonces un método estable.

Observación 5: Desafortunadamente, para este método no pude completar la prueba final que demostrara que ${\textstyle \phi }$ es una función que satisface la condición de Lipschitz para ${\textstyle x}$ , y con ello que el método es estable. No obstante dí los argumentos de que es un problema bien planteado para tratar de justificar esta última prueba.

4 Análisis rápido de los demás métodos híbridos para el caso de una ecuación individual de orden uno

Ahora abordaremos de manera rápida y práctica el problema de consistencia, convergencia y estabilidad de las demás combinaciones de métodos híbridos.

Consideremos primeramente que el análisis de la sección 3.1.2, referente al problema bien planteado se aplica de manera general para ecuaciones implícitas de la forma ${\textstyle f(t,x,x')}$ , sin importar qué combinación de métodos usemos.

En segundo lugar, en este artículo se omitirá el análisis del error de los demás métodos, dejándolo para futuros trabajos.

Y por último, respecto al análisis de estabilidad, consistencia y convergencia de los otros métodos, solo argumentaré algo análogo a lo dicho en el teorema (15) y en la observación (5), en cuanto a que mis métodos híbridos se pueden considerar como pequeñas perturbaciones al problema de valor inicial (para ${\textstyle h}$ suficientemente pequeña) empleando los métodos convencionales de solución de ecuaciones diferenciales, como se observa en la fórmula (20), (donde la perturbación es ${\textstyle h\delta _{n}=\Delta }$ ) pues solo se calcula de manera aproximada el valor de ${\textstyle x'}$ por métodos numéricos algebraicos, lo que nos va agregando un error extra en cada iteración. Mas como para todos esos métodos convencionales ya se han hecho los respectivos análisis, al tener un problema bien planteado significa que las soluciones dadas por mis métodos tendrán un pequeño error respecto a las soluciones mostradas por tales métodos estándar y por lo tanto también un pequeño error aceptable respecto a la solución exacta si ${\textstyle h}$ es muy pequeño.

5 Análisis gráficos del método de Euler-bisección

Ahora se procederá a hacer el análisis gráfico para el método de Euler-bisección, tomando como modelo el problema de caída libre con friccón laminar (bajas velocidades), por lo que la fuerza de fricción es proporcional a la velocidad y en sentido opuesto [5].

Cabe señalar que aunque este modelo se puede resolver por métodos estándar e incluso analíticamente, será utilizado justamente para evaluar todo lo afirmado en las secciones anteriores.

La ecuación diferencial con condiciones iniciales ha de ser entonces

(34)

donde ${\textstyle v}$ indica la velocidad del cuerpo, ${\textstyle v_{0}}$ es su velocidad inicial, ${\textstyle m}$ su masa, ${\textstyle g=9.8m/s^{2}}$ es la aceleración de la gravedad en unidades S.I., ${\textstyle k}$ es la constante de fricción y hemos reducido el orden de la ecuación con el cambio de variable ${\textstyle v=x'}$ .

Para este problema en particular elegimos ${\textstyle v_{0}=0}$ , ${\textstyle m=1}$ , y ${\textstyle k=.1}$ .

Además, el tiempo irá de ${\textstyle 0\leq t\leq 100}$ . También tomaremos un tamaño de paso de ${\textstyle h=.1}$ .

Ahora, en aras de la brevedad solo diremos que todas las condiciones para un problema bien planteado se cumplen (el lector interesado puede verificarlo), siendo la constante de Lipschitz ${\textstyle L=k/m}$ (para ${\textstyle v}$ en ${\textstyle g(t,v)}$ ).

Y en lo referente al análisis del error, de acuerdo al sistema físico que modelamos la aceleración máxima se da al inicio, cuando la velocidad inicial es cero y por lo tanto la fuerza de fricción también es cero. Y dicha aceleración máxima ha de ser igual a ${\textstyle |g|=9.8}$ .

Así que de acuerdo a la fórmula (23), podemo ver ${\textstyle |v''|=(k/m)|v'|\leq .98=M}$ , siendo por lo tanto el valor del error óptimo ${\textstyle \tau =(M/2)h=.049}$ (según (25)).

Con ello ya se pueden hacer los análisis respectivos de cotas del error y ver que el método tiene una convergencia de orden lineal, de acuerdo a (26).

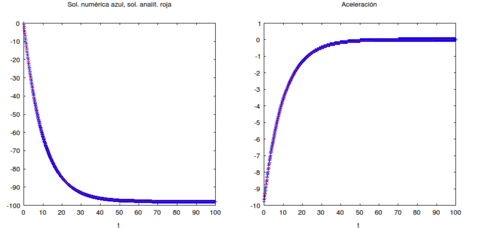
A continuación se presentan los gráficos correspondientes, donde se puede observar que se cumple todo lo señalado.

Figure 1:

¹

Figure 2:

²

(¹) El gráfico izquierdo es para la velocidad del cuerpo que cae, el derecho para su aceleración. El eje horizontal corresponde al tiempo. Se muestra en rojo la solución analítica y en azul la numérica; puede verse que prácticamente se traslapan.

(²) En el gráfico izquierdo aparece la derivada de la aceleración, es decir $v''$ , en el derecho el error global ${\tilde {v}}-v$

6 Sistemas de ecuaciones diferenciales de orden $n$ 6 Sistemas de ecuaciones diferenciales de orden n {\displaystyle n}

6.1 Explicación breve del algoritmo

En esta sección se explicará rápidamente cómo se desarrollan los métodos más generales de solución de sistemas de ${\textstyle m}$ ecuaciones diferenciales con ${\textstyle m}$ funciones incógnitas de ${\textstyle n}$ -ésimo orden. El respectivo análisis numérico se dejará para futuros trabajos.

Primeramente habrá de señalarse que todo sistema de ecuaciones diferenciales de orden ${\textstyle n}$ puede transformarse en un sistema equivalente de orden uno. Una vez transformado, se aplican métodos semejantes a los del caso de una sola ecuación de orden uno, como se verá a continuación.

Al considerar las condiciones iniciales, el sistema se transforma en un sistema algebraico para las variables incógnitas derivadas, el cual se puede resolver mediante métodos de resolución de sistemas de ecuaciones algebraicas, tales como punto fijo multivariable o Newton-Raphson multivariable. Una vez obtenidos los valores aproximados para las funciones derivadas, se procede a aplicar cualquier método estándar de solución numérica de sistemas de ecuaciones diferenciales, pero con un pequeño error en el cálculo de las funciones ${\textstyle g}$ para las derivadas (problema perturbado). Una vez aplicados los métodos estándar se obtiene el valor aproximado de las variables dependientes en ${\textstyle t_{1}}$ . Y el proceso se repite hasta llegar al ${\textstyle t_{f}}$ .

6.2 Gráficos del método generalizado aplicado a las ecuaciones de campo relativistas de las estrellas de bosones

La métrica para una estrella de bosones sin dependencia temporal (objeto compacto, esféricamente simétrico, estático) es [6]

(35)

de la cual se deducen, usando el formalismo de la geometría diferencial, las siguientes ecuaciones de Einstein [6]

(36)

(37)

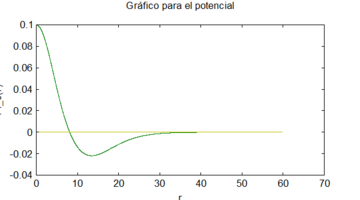
Además, elegimos un potencial de la forma ${\textstyle V=m^{2}|\phi |^{2}+{\frac {\lambda }{2}}|\phi |^{4}}$ [7,8], siendo ${\textstyle \phi =\phi _{0}(r)e^{-i\omega t}}$ . Por otro lado, la ecuación de la conservación de la energía ${\textstyle \nabla _{\nu }T_{\mu }^{\nu }}$ se reduce a la ecuación de Klein-Gordon ${\textstyle \left(\Box -{\frac {dV}{d|\phi |^{2}}}\right)\phi =0}$ , de lo que se obtiene la tercera ecuación de Einstein

(38)

donde ${\textstyle a,\alpha }$ y ${\textstyle \phi _{0}}$ dependen solamente del radio ${\textstyle r}$ .

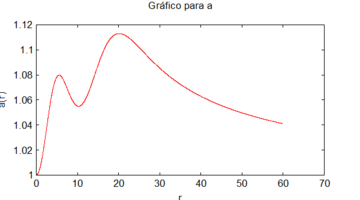
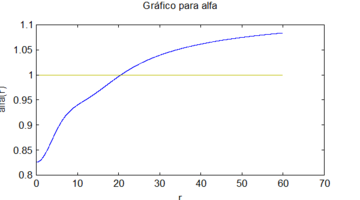
La solución numérica de este sistema usando mis métodos con las condiciones iniciales ${\textstyle a(0)=1}$ , ${\textstyle \phi _{0}(0)=.1}$ y ${\textstyle \alpha (0)=0.908710}$ , origina los siguientes gráficos

Figure 3: Gráfico para

vs

.

Figure 4: Gráfico para

vs

.

Figure 5: Gráfico para

vs

.

¹

(¹) Estos gráficos se corresponden muy bien con los obtenidos usando métodos numéricos tradicionales, como se puede apreciar al compararlos con [9].

7 Conclusiones y futuros trabajos

Los métodos numéricos alternativos para resolver ecuaciones diferenciales con condiciones iniciales, desarrollados en este trabajo, son útiles para los casos en que no se puede despejar explícitamente a la funciones derivadas. Además, en general pasaron todas las pruebas del análisis numérico (solo con ciertos detalles para la prueba de estabilidad) y se determinaron cotas del error, las cuales, los ejemplos aquí expuestos las satisfacen muy bien. En particular me enfoqué en el método de Euler-bisección, pero en futuros trabajos se desarrollarán otras combinaciones de métodos, así como los correspondientes métodos numéricos no estándar para ecuaciones diferenciales en derivadas parciales.

BIBLIOGRAPHY

[1] R. L. Burden y J. D. Faires, ``Análisis Numérico", Segunda edición, Grupo Editorial Iberoamérica, Ciudad de México, México, (1996).

[2] R. Gómez, D. Escobar, E. A. Gómez, J. L. Guerrero, J. M.M A. Gutiérrez, M. A. Hernández, A. P. Puerto y L. M. Sandoval, ``Elementos de métodos numéricos para ingeniería", Primera edición, Mc Graw Hill, Ciudad de México, México, (2002).

[3] W. Rudin, ``Principios de Análisis Matemático", Tercera edición, McGraw Hill, Edo. de México, México, (1980).

[4] S. Lang, ``Introducción al Análisis Matemático", Primera edición, Addison-Wesley Iberoaméricana, Ciudad de México, México, (1990).

[5] M. R. Spiegel, “Theoretical Mechanics”, Segunda edición, Schaum's Outline Series, McGraw-Hill, Estados Unidos de América, (1967).

[6] C. Rodríguez, ``Solución a las ecuaciones de Einstein para las estrellas de bosones usando el método de álgebras y simetrías”, Tesis de Maestría, Universidad de Guadalajara, Ameca, México, (2017).

[7] F. S. Guzmán, ``The three dinamical fates of Boson Stars”, Revista Mexicana de Física, pp. 321-326, (2009).

[8] F. E. Schunck y D. F. Torres, ``Boson stars with generic self-interactions”, arXiv:gr-qc/9911038v1, (1999).

[9] A. Bernal, ``Estudio Dinámico de Campos Escalares Autogravitantes”, Tesis Doctoral, CINVESTAV, México, (2007).

@@ Line 163: / Line 163: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: left;"
 <ol>
-<li> '''1.''' <math> {\tilde{x}'}_{0} = Biseccion(t_{0},\tilde{x}_{0},\alpha _i,\alpha _d,\tau ) </math></li>
+<li> '''-''' <math> {\tilde{x}'}_{0} = Biseccion(t_{0},\tilde{x}_{0},\alpha _i,\alpha _d,\tau ) </math></li>
-<li> '''2.''' para  <math> (n = 0 \hbox{ hasta } N-1) </math> </li>
+<li> '''-''' para  <math> (n = 0 \hbox{ hasta } N-1) </math> </li>
     '''a)'''   <math> t_{n+1} = t_n + h </math>
     '''b)'''   <math> \tilde{x}_{n+1} = \tilde{x}_n + {\tilde{x}'}_n h </math>
     '''c)'''   <math> \tau = \tau (h) </math>
     '''d)'''   <math>{\tilde{x}'}_{n+1} = Biseccion(t_{n+1},\tilde{x}_{n+1},\alpha _i,\alpha _d,\tau ) </math>
-<li>'''3.'''  fin</li>
+<li>'''-'''  fin</li>
 |}
 </ol>
@@ Line 271: / Line 270: @@
 | style="text-align: center;" | <math>
-\frac{\partial f}{\partial x'}|_{t_r,x_r} \neq 0 </li>
+\frac{\partial f}{\partial x'}|_{t_r,x_r} \neq 0
-</math>
+</math></li>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (11)
@@ Line 416: / Line 415: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>0 \leq |\tilde{x}' - x'| < \frac{t_f - t_0}{2^{N(h)} } =: \delta (h) = \tau (h) - \epsilon (h) \leq \tau (h), \hbox{ con } 0 \leq \epsilon < \tau /2,     </math>
+| style="text-align: center;" | <math>0 \leq |\tilde{x}' - x'| < \frac{t_f - t_0}{2^{N(h)} } =: \delta (h) = \tau (h) - \epsilon (h) \leq \tau (h), \hbox{ con } 0 \leq \epsilon < \tau /2   </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (19)
@@ Line 428: / Line 427: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math> \begin{align} \tilde{x}_0 & = x_0, \\
+| style="text-align: center;" | <math> \begin{align} \tilde{x}_0 & = x_0 \\
 \tilde{x}_{n+1} & = \tilde{x}_n + h {\tilde{x}'}_n        \end{align} </math>
 |}
@@ Line 441: / Line 440: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>\begin{align} \tilde{x}_0 & = x_0 + (\delta _{-1} = 0), \\
+| style="text-align: center;" | <math>\begin{align} \tilde{x}_0 & = x_0 + (\delta _{-1} = 0)\\
-\tilde{x}_{n+1} & = \tilde{x}_n + h g(t_n,\tilde{x}_n) + (h \delta _n := \Delta _n), \hbox{ para } n = 0,1 \ldots N-1, \\        \end{align}     </math>
+\tilde{x}_{n+1} & = \tilde{x}_n + h g(t_n,\tilde{x}_n) + (h \delta _n := \Delta _n), \hbox{ para } n = 0,1 \ldots N-1 \\        \end{align}     </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (20)
@@ Line 455: / Line 454: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>0 \leq |\Delta _n| = h |\delta _n| <  h \delta \leq h \tau := \Delta{.}  </math>
+| style="text-align: center;" | <math>0 \leq |\Delta _n| = h |\delta _n| <  h \delta \leq h \tau := \Delta </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (21)
@@ Line 471: / Line 470: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>x'' = \frac{-\frac{\partial f}{\partial t} -\frac{\partial f}{\partial x} x'}{\frac{\partial f}{\partial x'}}.     </math>
+| style="text-align: center;" | <math>x'' = \frac{-\frac{\partial f}{\partial t} -\frac{\partial f}{\partial x} x'}{\frac{\partial f}{\partial x'}}     </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (22)
@@ Line 484: / Line 483: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>|x''| = | \frac{\frac{\partial f}{\partial t} + \frac{\partial f}{\partial x} x'}{\frac{\partial f}{\partial x'}} | \leq M,     </math>
+| style="text-align: center;" | <math>|x''| = | \frac{\frac{\partial f}{\partial t} + \frac{\partial f}{\partial x} x'}{\frac{\partial f}{\partial x'}} | \leq M     </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (23)
@@ Line 503: / Line 502: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>|x_n - \tilde{x}_n| \leq \frac{1}{L} \left(\frac{h M}{2} + \frac{\Delta }{h} \right)(e^{L(t_n - t_0)} - 1) = \frac{1}{L} \left(\frac{h M}{2} + \tau (h) \right)(e^{L(t_n - t_0)} - 1),          </math>
+| style="text-align: center;" | <math>|x_n - \tilde{x}_n| \leq \frac{1}{L} \left(\frac{h M}{2} + \frac{\Delta }{h} \right)(e^{L(t_n - t_0)} - 1) = \frac{1}{L} \left(\frac{h M}{2} + \tau (h) \right)(e^{L(t_n - t_0)} - 1)          </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (24)
 |}
-donde <math display="inline">L</math> es la constante de Lipschitz para <math display="inline">x' = g(t,x)</math>    Además, el valor óptimo para <math display="inline">h</math> (el mínimo error posible) se presenta para un <math display="inline">h</math> aproximado a <math display="inline">h = \sqrt{2 \Delta / M}</math>, o, despejando a <math display="inline">Delta</math>, cuando <math display="inline">\Delta = \frac{M}{2} h^2</math>, es decir, cuando
+donde <math display="inline">L</math> es la constante de Lipschitz para <math display="inline">x' = g(t,x)</math>    Además, el valor óptimo para <math display="inline">h</math> (el mínimo error posible) se presenta para un <math display="inline">h</math> aproximado a <math display="inline">h = \sqrt{2 \Delta / M}</math>, o, despejando a <math display="inline">\Delta</math>, cuando <math display="inline">\Delta = \frac{M}{2} h^2</math>, es decir, cuando
 <span id="eq-25"></span>
@@ Line 516: / Line 515: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>\tau = \frac{M}{2} h \approx \delta ,    </math>
+| style="text-align: center;" | <math>\tau = \frac{M}{2} h \approx \delta     </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (25)
@@ Line 555: / Line 554: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>\tau = C \cdot h,  </math>
+| style="text-align: center;" | <math>\tau = C \cdot h  </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (28)
@@ Line 601: / Line 600: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>\lim _{h \rightarrow 0}  \max _{1 \leq n \leq N} |e_n(h)| = 0,  n = 1,2, \dots , N,    </math>
+| style="text-align: center;" | <math>\lim _{h \rightarrow 0}  \max _{1 \leq n \leq N} |e_n(h)| = 0,  n = 1,2, \dots , N    </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (31)
@@ Line 615: / Line 614: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>\lim _{h \rightarrow 0}  \max _{1 \leq n \leq N} |x_n - \tilde{x}_n| = 0,  n = 1,2, \dots , N,    </math>
+| style="text-align: center;" | <math>\lim _{h \rightarrow 0}  \max _{1 \leq n \leq N} |x_n - \tilde{x}_n| = 0,  n = 1,2, \dots , N    </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (32)
@@ Line 631: / Line 630: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>|\phi (t,x,h) - \phi (t,y,h)| < L|x-y| + 2 C h,    </math>
+| style="text-align: center;" | <math>|\phi (t,x,h) - \phi (t,y,h)| < L|x-y| + 2 C h    </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (33)
@@ Line 664: / Line 663: @@
 |-
 | style="text-align: center;" | <math>\begin{align} f(t,v,v') & = m v' + k v + m g= 0\\
-v(0) & = v_0,    \end{align}     </math>
+v(0) & = v_0    \end{align}     </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (34)
@@ Line 731: / Line 730: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>ds^2 = - \alpha (r)^2 dt^2+ a(r)^2 dr^2 + r^2 d\theta ^2 + r^2 \sin ^2(\theta ) d\varphi ^2,   </math>
+| style="text-align: center;" | <math>ds^2 = - \alpha (r)^2 dt^2+ a(r)^2 dr^2 + r^2 d\theta ^2 + r^2 \sin ^2(\theta ) d\varphi ^2   </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (35)
@@ Line 744: / Line 743: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>\frac{a_{,r}}{a} + \frac{\alpha _{,r}}{\alpha } = \frac{k_{0}}{2} r \frac{a^2 \omega ^2 \phi _{0}^2}{\alpha ^2} + \frac{k_{0}}{2} r \phi _{0,r}^2,   </math>
+| style="text-align: center;" | <math>\frac{a_{,r}}{a} + \frac{\alpha _{,r}}{\alpha } = \frac{k_{0}}{2} r \frac{a^2 \omega ^2 \phi _{0}^2}{\alpha ^2} + \frac{k_{0}}{2} r \phi _{0,r}^2   </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (36)
@@ Line 755: / Line 754: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>\frac{a_{,r}}{a} - \frac{\alpha _{,r}}{\alpha } = \frac{k_{0}}{2} r a^2 \phi _{0}^2 m^2 + \frac{k_{0}}{4} r \lambda a^2 \phi _{0}^4 + \frac{1-a^2}{r}.  </math>
+| style="text-align: center;" | <math>\frac{a_{,r}}{a} - \frac{\alpha _{,r}}{\alpha } = \frac{k_{0}}{2} r a^2 \phi _{0}^2 m^2 + \frac{k_{0}}{4} r \lambda a^2 \phi _{0}^4 + \frac{1-a^2}{r}  </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (37)
@@ Line 768: / Line 767: @@
 {| style="text-align: left; margin:auto;width: 100%;"
 |-
-| style="text-align: center;" | <math>\phi _{0,rr} + \phi _{0,r} \left(\frac{2}{r} + \frac{\alpha _{,r}}{\alpha } - \frac{a_{,r}}{a} \right)+ \omega ^2 \phi _{0} \frac{a^2}{\alpha ^2}  - a^2 (m^2 + \lambda \phi _{0}^2)  \phi _{0} = 0 \textrm{,}   </math>
+| style="text-align: center;" | <math>\phi _{0,rr} + \phi _{0,r} \left(\frac{2}{r} + \frac{\alpha _{,r}}{\alpha } - \frac{a_{,r}}{a} \right)+ \omega ^2 \phi _{0} \frac{a^2}{\alpha ^2}  - a^2 (m^2 + \lambda \phi _{0}^2)  \phi _{0} = 0    </math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (38)

Latest revision as of 10:43, 28 November 2017