(Created page with "==MODELADO PARAMÉTRICO MEDIANTE PROGRAMACIÓN VISUAL EN EL DISEÑO Y ANÁLISIS ESTRUCTURAL DE EDIFICIOS== '''Eugenio Muttio Departamento de Ingeniería Civil Universida...") |
|||
| Line 111: | Line 111: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>{\big[\mathbf{K}\big]\big[\mathbf{D}\big]= \big[\mathbf{F}\big]} </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (1) | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
Revision as of 10:55, 10 November 2017
MODELADO PARAMÉTRICO MEDIANTE PROGRAMACIÓN VISUAL EN EL DISEÑO Y ANÁLISIS ESTRUCTURAL DE EDIFICIOS
Eugenio Muttio
Departamento de Ingeniería Civil
Universidad de Guanajuato
Juárez 77, Zona Centro 36000, Guanajuato, México
e-mail: ej.muttiozavala@ugto.mx Salvador Botello, Maximino Tapia
Departamento de Ciencias de la Computación
Centro de Investigación en Matemáticas CIMAT
Jalisco s/n, Valenciana 36023, Guanajuato, México
e-mail: botello@cimat.mx,max@cimat.mx
Resumen
Durante siglos se ha definido un procedimiento estandarizado para la representación de información en la industria de la construcción, el cual se basa en el trazo de planos en un sustrato como lo es el papel. La llegada de las computadoras revolucionó la forma en que se realizaba cualquier trabajo donde se requirieran cálculos. Pero también cuando se desarrolló la comunicación gráfica entre el humano y la computadora, como lo son los primeros sistemas de diseño asistido por computadora (CAD), la realización de trazos tuvo una mejora indiscutible. Sin embargo ahora nos encontramos en una nueva revolución, la cual está basada en la eficiencia y reducción de tiempo debido a la gran competencia que existe en las oficinas de Arquitectura e Ingeniería. Además, la complejidad del diseño y análisis estructural se está volviendo un problema de conceptualización geométrica, de múltiple solución y de comportamientos estructurales sensibles a las propuestas cambiantes. El diseño paramétrico consiste en la utilización de algoritmos para generar relaciones geométricas que permitan no sólo llegar a una propuesta, sino dar origen a todo el rango de posibles soluciones, controlados por un conjunto de parámetros que pueden determinarse por el proyectista. El presente trabajo tiene por objetivo mostrar el desarrollo de una aplicación computacional que permita definir parámetros para estructurar una edificación, que pueda obtener un campo de soluciones en poco tiempo, obtener un propuesta óptima en cuanto a su resistencia mecánica, su disposición topológica y que satisfaga las necesidades arquitectónicas solicitadas.
Palabras Clave. Diseño Paramétrico, Geometría, Análisis Estructural, Edificaciones, Arquitectura, Ingeniería
Parametric Modeling Through Visual Programming in Structural Design and Analysis of Buildings
Abstract
For centuries, it has defined a standard procedure used for representation of construction industry information, which is based in drawing over paper. Arrival of computers revolutionized the way in which any work was made where calculations were required. But also when the graphic communication between the human and computers was developed, such as computer assisted design (CAD), the planning process had a indisputable improvement. However, now we are involved a new revolution, which is based in efficiency and time reduction due the great competition that exists among Architecture and Engineering offices. Besides that, design complexity and structural analysis is becoming a geometric conceptualization problem, with multiple solutions and sensitive structural behavior to changing proposals. Parametric design offers a new optimization alternative generating mathematical and geometric relationships that allow not a unique design, but a wide range of possible solutions controlled by a set of parameters which can be modified by the designer. This paper describes the scope of parametric design, and also the development of a computational tool that allows define a structural configuration by a set of parameters, which denotes a time decrease generating structural solutions, and also it proves the benefit of obtain an optimal proposal by mechanical strength, topological configuration and satisfy architectural needs.
Evolución del Proceso de Planeación
![Contexto Histórico. Plano que muestra el diseño arquitectónico de la iglesia de St. James en West Littleton, Inglaterra. Realizado en el año 1874 [2].](/wd/images/thumb/d/d3/Draft_Muttio_354740128-2_1_1_old_plans_1.png/525px-Draft_Muttio_354740128-2_1_1_old_plans_1.png)
|
| Figura 1: Contexto Histórico. Plano que muestra el diseño arquitectónico de la iglesia de St. James en West Littleton, Inglaterra. Realizado en el año 1874 [2]. |
Es inherente en un proceso de planeación la realización de un boceto inicial para marcar de manera general un camino a seguir para desarrollar un proyecto en específico. Al proponer un proyecto en la construcción es necesario realizar un plano arquitectónico, estructural, mecánico o cualquiera que sea indispensable para definir íntegramente el objetivo. Desde hace siglos se definió un estándar en cuanto a los elementos que debe presentar un plano. En la imagen 1 se observa un plano arquitectónico de 1874, éstos se caracterizan por mostrar los detalles finales de las construcciones, por ejemplo aquí se muestra el acabado final de la iglesia, y en la parte superior se muestra la distribución de espacios. Posteriormente se presentó la revolución de las computadoras y hasta la década de 1960's la interacción entre las computadoras era de forma numérica y de información escrita en papel. En esa década Ivan Sutherland desarrolló un sistema gráfico entre los humanos y la computadora, el cual era una forma de comunicación que permitía al usuario trazar figuras sobre una pantalla instalada en la computadora denominada que fue diseñada en 1956. Pero no fue hasta la década de los 80’s que las computadoras fueron más accesibles y se desarrolló el primer sistema comercial de dibujo asistido por computadora o CAD y rápidamente fue adoptado. Aún cuando la modelación de sólidos fue posible durante la misma época, los recursos computacionales no fueron suficientes para generar modelos tridimensionales eficientes que fueran sencillos de manejar por arquitectos y que a su vez afrontaran la necesidad del tiempo en los proyectos. Por ello se recurrió a continuar con el mismo estándar propuesto en el dibujo bidimensional.
Planeación Mediante Parámetros
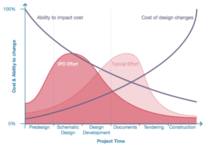
Paulson en 1976 propone que las decisiones importantes de diseño se realicen al principio del proyecto, y mediante una curva que trazó muestra que si el esfuerzo de diseño es mayor en la primer etapa, los cambios en etapas posteriores serán menos costosos [1]. Macleamy propone que las decisiones de diseño de un proyecto se deben concentrar en el inicio del mismo. Se debe recabar la suficiente experiencia para poder utilizar el mayor esfuerzo de planeación y diseño en la primer etapa, ya que en ese punto los cambios son menos costosos que al final de la ejecución del proyecto. A esto se le conoce como “Front-Loading” o por su traducción “Carga Inicial”, y los menciona Macleamy junto con los siguientes dos conceptos: “Entrega de Proyecto Integral” o IPD (por sus siglas en inglés), que fusiona de manera estipulada las partes de proyectos para dar pie a los diseñadores sobre soluciones que pueden realizar en el principio del proyecto y que pueden ser viables desde el inicio.
Samuel Geisberg alienta a la exploración del diseño mediante parámetros diciendo, “El objetivo es crear un sistema paramétrico que pueda ser suficientemente flexible para alentar al ingeniero y que fácilmente considere una diversidad de diseños. El costo de hacer cambios de diseño debería ser tan cercano a cero como sea posible.” (citado por Davis [1])
Si los cambios pueden ser anticipados, el modelo puede se construido únicamente con los parámetros necesarios para alojar dichos cambios. El problema existe cuando un cambio no es anticipado, entonces el diseñador debe adaptar la modificación realizando algún cambio en las funciones o variables clave del modelo. Es entonces que la tarea de construir un modelo mediante parámetros puede ser muy desafiante y más aún cuando el modelo es complejo, como lo puede ser una edificación integral [9]. Si el problema es definir las variables clave con anticipación, la solución más obvia es proveer mucha flexibilidad desde el inicio. Pero el uso de parámetros vienen con un costo, se requiere mucho trabajo anticipado planear y anticipar todos los deseos de un diseñador, además el modelo se vuelve tan complejo que su utilización no es práctica.
“El desafío de construir un modelo paramétrico es desenredar las interdependencias creadas por los diferentes requisitos y encontrar un conjunto de reglas que sean sencillas y que permanezcan lo suficientemente flexible para adaptarse a cualquier caso.” [8]
Por otra parte, un modelo paramétrico puede ser tan único cómo sea planteado, y no por el hecho del uso de parámetros (ya que todo diseño por simple definición, tiene parámetros asociados), no porque cambia (otras representaciones del diseño tienen la habilidad de cambio), y no porque se considera como una herramienta o estilo de arquitectura. Un modelo paramétrico es único no por lo que hace, sino por cómo fue creado. Un modelo paramétrico es creado por un diseñador explícitamente mediante reglas que indicarán como los resultados se derivan de un conjunto de valores iniciales o parámetros.
Diseño Paramétrico Computacional
El diseño paramétrico pretende obtener mayor eficiencia en cuanto al manejo de la información y ofrece una opción moderna a los procesos tradicionales. Según la Enciclopedia Concisa de las Matemáticas [11], paramétrico significa “Conjunto de ecuaciones que expresan un conjunto de cantidades a partir de funciones explícitas de un número de variables independientes, conocidas como “parámetros””. Dicha definición matemática puede ser llevada al contexto que estamos manejando, por lo que Davis menciona que “Un modelo paramétrico es un conjunto de ecuaciones que expresan un modelo geométrico a partir de funciones explícitas de un número de parámetros” [1]. Debido a la complejidad de las herramientas utilizadas por los diseñadores para modelar geometrías en tres dimensiones se buscaron alternativas que permitieran desarrollar modelos más rápidamente y con un esfuerzo menor. Entonces, utilizando la representación de formulaciones algebraicas para generar sólidos primitivos (p. ej. cilindros o cubos), combinados con operaciones como la unión, intersección y sustracción mediante funciones, se obtiene una representación compacta y fácil de editar [requicha_1980] (citado por Sacks [sacks_2003]). Las reglas impuestas en el diseño paramétrico actuaron como restricciones y éstas fueron añadidas a los primeros modeladores paramétricos de sólidos. Los sistemas paramétricos no solo generan formas representados en imágenes, sino que las restricciones y reglas utilizadas para generarlas también son mantenidas en todo momento como parte integral del modelo.
Programación Visual en el Diseño Paramétrico
![Data Flow Computing. Obtención de una geometría simple (línea) mediante un DAG. Figura adaptada de [1].](/wd/images/thumb/e/e5/Draft_Muttio_354740128-2_2_10_DAGlinea.png/1048px-Draft_Muttio_354740128-2_2_10_DAGlinea.png)
|
| Figura 3: Data Flow Computing. Obtención de una geometría simple (línea) mediante un DAG. Figura adaptada de [1]. |
Aunque hay claras diferencias entre hacer arquitectura y programar un software, la logística de tareas en ambos casos debe ser bien analizada para poder hacer más eficiente un trabajo. La programación que se requiere en un campo como lo es el diseño de edificaciones, tanto arquitectónico como estructural, es preferida dentro de ambientes donde se pueda resolver el problema de manera integral junto con el desarrollo del proyecto. David Rutten, desarrollador de Grasshopper (modelador paramétrico) menciona: “cualquier persona involucrada en algún trabajo que escriba instrucciones que posteriormente serán ejecutadas por una computadora, máquina o incluso una entidad biológica, puede decirse que se encuentra programando” [4] (citado por Davis [1]). La clave y el primer obstáculo que encontramos en la programación, es que debemos de confiar en alguna forma de abstracción para comunicarnos efectivamente con nuestra computadora. Esto nos da la opción de escoger el lenguaje que nos permita desarrollar nuestra aplicación, se escribe un conjunto de instrucciones que se traducen a la computadora. El funcionamiento de la programación visual se basa en el “Data Flow Computing”. En cuestión práctica, la programación visual es muy sencilla de aprender y la propuesta es acercarla a las áreas como Arquitectura o Ingeniería Civil para crear códigos visuales que permitan una optimización en procesos que se deben realizar cíclicamente o que son tediosos de realizar. En cuestión computacional, es muy interesante esta nueva metodología ya que en lugar de re-calcular cada operación geométrica, los gráficos con los que se construye el código, denominados “Gráficos Acíclicos Dirigidos” o simplemente DAG (por sus siglas en inglés) vistos en la figura 4, son actualizados de acuerdo a un criterio definido por el procesador de la computadora. Entonces cuando un nodo tiene una modificación en algún parámetro, el modelo se actualiza propagando los cambios a lo largo de la red para actualizar todos los nodos conectados posteriores. La estructura general de un DAG consta de módulos representados por cajas, denominados nodos, que hacen alguna función, en las que destacan las funciones geométricas en los ambientes de programación visual para arquitectos o diseñadores, los cuales tienen una entrada (input) en el caso más simple o más, de la misma manera constan de una o más salidas (outputs).
|
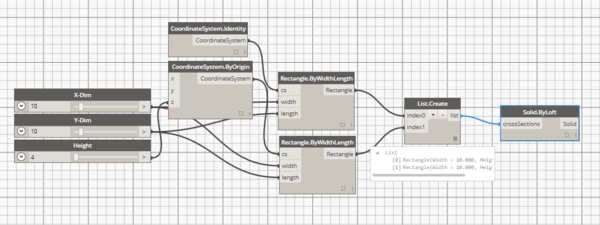
| Figura 4: Procedimiento para generar un DAG. Red de conexiones paramétricas o DAG para generar el sólido prismático, |
Al nodo que alimenta se le conoce como “nodo padre”, en cuanto al nodo que recibe información para ejecutarse se le conoce como “nodo hijo”. Esta característica la podemos observar en el DAG de la figura 3, donde se utilizan dos nodos “punto” los cuales dan como resultado un conjunto coordenadas en un espacio geométrico, éstos proveen de información a otro nodo “línea” que necesita de un punto inicial y uno final para poder ejecutarse, al hacer la conexión correcta podemos observar un elemento geométrico que ha sido generado mediante dicha relación. El modelador utilizado en este trabajo es Dynamo Studio, el cual es un software de parametrización con una interfaz de programación visual que conecta el diseño computacional con la modelación de información de construcción (BIM por sus siglas en inglés). Con Dynamo, los usuarios pueden crear scripts para construir, modificar e intercambiar información de acuerdo a sus necesidades. Un ejemplo de su funcionamiento es el mostrado en las figuras 4 y 5 en done la primer imagen denota la red DAG que se encarga de dar las instrucciones para generar un sólido rectangular prismático, pero debido a las características comentadas, es posible generar toda una familia de modelos al modificar algún parámetro de esta red, es lo que se muestra en la figura 5, al generar con el mismo “programa visual” diferentes prismas.

|

|

| |
| Figura 5: Procedimiento para generar un DAG. Diferentes modelos prismáticos, los cuales varían en el parámetro de dimensión vertical. | |
Parametrización en el Análisis de Edificios
El análisis estructural utiliza propiedades mecánicas de materiales además de formulaciones matemáticas para crear relaciones geométricas y topológicas de la configuración que presenta la estructura. El objetivo es conocer el comportamiento del edificio en conjunto y realizar una verificación mediante un código de construcción para garantizar la seguridad. El procedimiento seleccionado es el método matricial de las rigideces, el cual necesita de cierta información para poder ordenar ecuaciones en sistemas matriciales, que posteriormente serán resueltos en conjunto utilizando una matriz de rigidez ensamblada (ec. 1) para conocer los desplazamientos a los que está sometida la estructura [5]. Al trabajar en un sistema 3D se decidió utilizar el tipo de matriz “marco tridimensional”, por lo tanto el sistema de ecuaciones está en función de propiedades geométricas de la barra (, , , , ) y propiedades del material utilizado (, ). Así se obtiene una relación entre los desplazamientos lineales () y rotacionales () que sufre el elemento estructural, respecto a las fuerzas y momentos aplicados (, ). El sistema ensamblado a resolver se representa con el siguiente arreglo matricial:
|
|
(1) |
Donde:
- : Matriz de rigidez ensamblada.
- : Vector de fuerzas en sistema de coordenadas global.
- : Vector de desplazamientos. Solución del sistema lineal de ecuaciones.
Módulos de Estructuración y Análisis
El propósito de este trabajo fue desarrollar funciones “nodo” que puedan ser utilizadas para para proponer una configuración estructural, además poder analizar y realizar la verificación de resistencia mediante el paradigma de programación visual. El procedimiento considerado se enlista a continuación:

|

|
| (a) | (b) |

| |
| (c) | |
| Figura 6: Funcionamiento. Estructuración utilizando un sólido prismático rectangular. | |
|
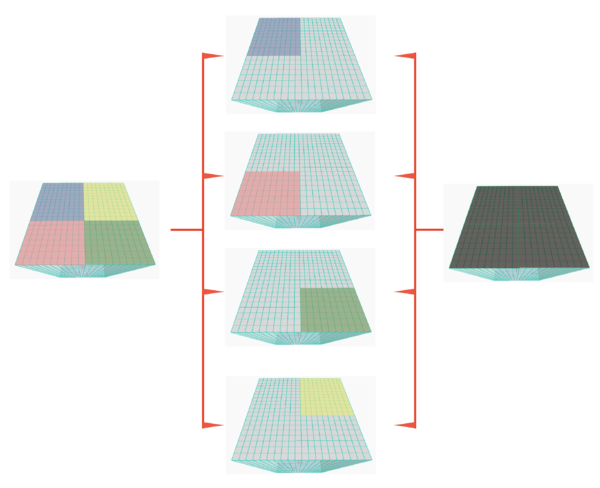
| Figura 7: Programación en paralelo. Reducción en tiempo de actualización. |
- Generar un sólido tridimensional. El tipo de edificaciones objetivo en este trabajo son las denominadas “Edificaciones Torre”. Y aunque los modelos 3D que servirán como materia prima para los módulos de estructuración pueden ser de distinto origen, para efecto de mostrar la funcionalidad de la programación visual se modelaron distintas edificaciones experimentales utilizando diagramas DAG dentro de un sistema paramétrico. Ver figura 6 a).
- Proponer una configuración estructural. Utilizando una retícula, se propone la ubicación de las columnas y vigas que darán soporte a la edificación. Ver figura 6 b).
- Estructuración. Un algoritmo estructura y prepara la información (material, geometría, topología) para el análisis. Esta estructuración se ajusta a la forma que tiene el sólido tridimensional y al estar en un ambiente de programación visual se pueden obtener distintas soluciones al cambiar parámetros de la propuesta estructural, ver figura 6 c). Además es importante mencionar que debido a que estos módulos están pensados para usarse en computadoras de escritorio con características medias, se implementó programación en paralelo para reducir la latencia o actualización por cada ejecución de código visual, teniendo como resultado un porcentaje de tiempo de tan solo el respecto al tiempo inicial. La forma de implementar esto se muestra en la figura 7 en donde se tuvo que hacer una división de la retícula mediante regiones, las cuales se separan para realizar los cálculos geométricos simultáneamente por cada núcleo de la computadora y posteriormente se unen y ordenan para garantizar la continuidad de la estructura.
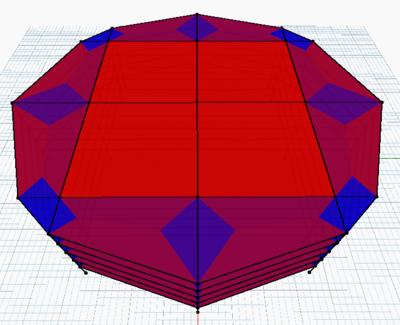
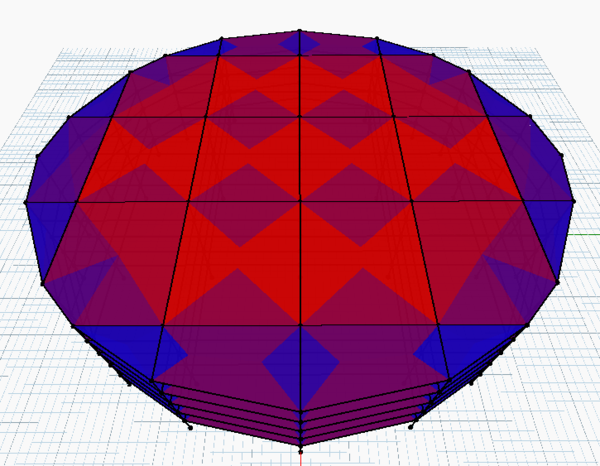
- Distribución de fuerzas. El método utilizado es de carácter geométrico y sólo requiere de un parámetro del usuario, cuyo valor es la magnitud de la sobrecarga asignada a cada nivel de la edificación. Sin embargo, estos métodos geométricos de distribución de áreas dependen de la forma del área de la losa, por lo que un algoritmo la identifica y asigna la función indicada de acuerdo a su tipo distribución. Además de que al poder modificar parámetros, la configuración estructural cambia y por tanto también la distribución de manera automática como se observa en la figura 8.
- Análisis estructural y verificación de resistencia. Al usar la información preparada por el nodo anterior, se realiza el análisis estructural utilizando el software MECA, el cual se encarga del cálculo numérico y posteriormente hace una verificación de resistencia de acuerdo al tipo de material utilizado para la sección transversal de cada barra.
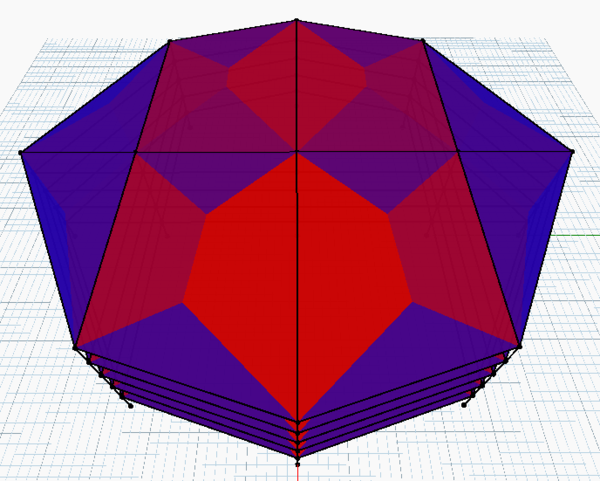
- Comportamiento estructural. A partir de los resultados del software MECA, se transfiere esta información a un módulo que sirve de post-proceso para ver de manera gráfica y con un código de color la resistencia de cada elemento estructural.
|
|
| (a) | (b) |
| |
| (c) | |
| Figura 8: Funcionamiento. Distribución de cargas en losas. | |
Resultados y Conclusiones

|
| Figura 9: Resultados. Distintas soluciones de estructuración mediante la modificación de un parámetro, se observa la distribución de cargas y la resistencia en cada barra. |
El resultado principal de este trabajo hasta este punto es un conjunto de módulos que están dentro de un contexto de la programación visual, los cuales se encuentran ya incluidos dentro de una librería de un software paramétrico y pudieran ser distribuidos para ser utilizados como herramienta para Ingeniería Estructural. En cuanto al producto que se genera por este conjunto de módulos es la estructuración de una edificación que puede tener distintas formas y además obtener un gran número de soluciones que beneficien la propuesta de un proyecto arquitectónico y estructural, se muestra un ejemplo de esto en la figura 9 ya que se tiene una edificación de forma “orgánica” controlada por parámetros que definen las dimensiones en distintos puntos del modelo tridimensional. Entonces se ve el primer modelo, la configuración estructural con la distribución de cargas en losas en la imagen central y en la tercer imagen se ve la verificación de resistencia, donde las barras que se presentan en color rojo están más cerca de fallar. Ahora al mover un solo parámetro en la dimensión superior del sólido, automáticamente la información se transmite a todos los nodos mediante las conexiones, se adapta la estructura al cambio, se hace el análisis estructural y la verificación de resistencia. De esta manera es más sencillo que un usuario pueda proponer múltiples soluciones hasta encontrar la configuración óptima para una edificación. En el proceso de planeación dentro de la industria de la construcción se han tenido distintos avances que han facilitado la realización de los trabajos involucrados. Sin embargo se considera la primer revolución en esta área el uso del CAD, ya que se pasó de un trazo en papel al uso de la computadora. Ahora la problemática no solamente es poder presentar un proyecto de arquitectura o ingeniería, sino que debe ser un proyecto integral en el menor tiempo posible debido a la gran competencia que existe. Entonces, la logística se ha vuelto una parte fundamental de la construcción de edificaciones. Por ello ahora la segunda revolución CAD es el modelado de sólidos paramétricos utilizando sistemas de información BIM. En la práctica tradicional se busca la manera de que el diseño propuesto funcione, y por tal motivo algunos proyectos son sobre-diseñados o con otras palabras, su resistencia es por mucho más alta que las solicitaciones. El diseño estructural paramétrico permite realizar una optimización para evitar esto y además presenta una reducción de tiempo y esfuerzo. El diseñador estructural puede proponer muchas soluciones a una edificación y hacer una selección de acuerdo a la más adecuada para el proyecto. Herramientas como ésta ofrecen alternativas que mejoran el desempeño de un proyectista a la hora de proponer soluciones estructurales y que además permite la modificación de parámetros en corto tiempo para adecuarse a los cambios repentinos del mismo. Estos resultados nos permiten imaginar en la gama de posibilidades de una sola edificación, o incluso tener la capacidad de brindar múltiples soluciones a edificaciones que son modificadas en el transcurso de la fase de planeación. Permitiendo al ingeniero tener mayor versatilidad en las propuestas realizadas.
BIBLIOGRAFÍA
[1] D. Davis, “Modelled on Software Engineering: Flexible Parametric Models in the Practice of Architecture”, Tesis para obtener el grado de doctor, RMIT University, (2013)
[2] St James West Littleton, Tombs and Memorials Conservation Project, Recuperado de http://www.stjamesmonuments.org/Plans.php
[3] A. Requicha, “Representations of rigid solids: theory, methods and systems”, ACM Computer Survey, 12, pp. 437 – 466, (1980)
[4] D. Rutten, “Programming, Conflicting Perspectives”, I Eat Bugs For Breakfast, Published 1 April, http:// ieatbugsforbreakfast.wordpress.com/2012/04/01/ programming-conflicting-perspectives/, (2012)
[5] J. Salazar, “Metodología Educativa de la Materia Análisis Estructural 2”, Tesis para obtener el grado de ingeniero, Universidad de Guanajuato, pp. 17-34, México, (2013)
[6] R. Sacks, C. Eastman y G. Lee, “Parametric 3D modeling in building construction with examples from precast concrete”, Automation in Construction, 13, pp. 291-312, United States Of America, (2003)
[7] R. Sacks y R. Barak, “Impact of three-dimensional parametric modeling of buildings on productivity in structural engineering practice”, Automation in Construction, 17, pp. 439-442, Israel, (2007)
[8] F. Scheurer y H. Stehling, “Lost in Parameter Space ?”, Architectural Design 81 (4): 70-79, (2011)
[9] R. Smith, “Technical Notes From Experiences and Studies in Using Parametric and BIM Architectural Software”, Published 4 March, http://www.vbtllc.com/images/ VBT TechnicalNotes.pdf, (2007)
[10] I. Sutherland, “Sketchpad, a man-machine graphical communication system.”, Spring Joint Computer Conference, (1963)
[11] E. Weisstein, “CRC Concise Encyclopedia of Mathematics”, Second edition, Boca Raton: Chapman & amp; Hall/CRC, (2003)
Document information
Published on 14/11/17
Submitted on 14/11/17
Volume 1, 2017
Licence: CC BY-NC-SA license