| (26 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | + | ==Abstract== | |
| − | + | Civil engineering constructions like pedestrian footbridges are structures increasingly slender, ambitious and complex in which the dynamic effects caused by the loads to which they are subjected (pedestrians) may induce service problems and / or significant or repetitive amplifications of the efforts and deformations. This fact together with the current social demands related to the perception and comfort raise the need to integrate the analysis and computer-aided design in the evaluation of the vibrations generated by the loads this type of structures supports. In the specific case of finite element commercial programs, their use has not proliferated as much as in other engineering fields due to the existence of simplified methodologies in numerous national and international guidelines and regulations and the difficulty of making realistic models in the case of complex structures. However, the knowledge generated by the analysis of this type of numerical models would be especially useful in the earlier phases of the design of similar structures, so much initial as of the necessary modifications to solve existing dynamic problems, since it is in these stages when the best solution could be applied from both a technical and an economic point of view. This article describes the process of generation and updating of the mechanical finite element model (FEM) of a footbridge in service and the simulation of two types of load: an excitation generated by a shaker and a pedestrian load, contrasting the results generated by the numerical model with those obtained experimentally. | |
==Resumen== | ==Resumen== | ||
| Line 10: | Line 9: | ||
''Palabras clave'': Pasarela peatonal, vibraciones, elementos finitos, ajuste modelo mecánico. | ''Palabras clave'': Pasarela peatonal, vibraciones, elementos finitos, ajuste modelo mecánico. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==1. Introducción== | ==1. Introducción== | ||
| Line 56: | Line 50: | ||
|} | |} | ||
| − | siendo | + | siendo <math display="inline"> f_{Xi}</math> el parámetro experimental y <math display="inline"> f_{Ai}</math> el parámetro calculado. |
Para medir la correlación entre los modos normalizados respecto a la matriz de masa experimentales y los obtenidos mediante el modelo en ANSYS se ha empleado el criterio de confianza modal (MAC según la abreviatura de su denominación en inglés) que proporciona una medida del grado de linealidad entre estimaciones de los modos de vibración originados desde diferentes fuentes <span id='cite-Marcador20'></span>[[#Marcador20|[16]]]. Se define como un escalar y su expresión se muestra a continuación: | Para medir la correlación entre los modos normalizados respecto a la matriz de masa experimentales y los obtenidos mediante el modelo en ANSYS se ha empleado el criterio de confianza modal (MAC según la abreviatura de su denominación en inglés) que proporciona una medida del grado de linealidad entre estimaciones de los modos de vibración originados desde diferentes fuentes <span id='cite-Marcador20'></span>[[#Marcador20|[16]]]. Se define como un escalar y su expresión se muestra a continuación: | ||
| Line 70: | Line 64: | ||
|} | |} | ||
| − | siendo | + | siendo <math display="inline"> \Psi_{X}</math> el modo de vibración experimental y <math display="inline"> \Psi_{A}</math> el modo de vibración calculado, donde la notación <math display="inline">\{\}^{X}</math> significa transpuesta compleja conjugada (matriz hermítica). |
===2.2. Simulación de cargas=== | ===2.2. Simulación de cargas=== | ||
| Line 106: | Line 100: | ||
En el caso que estamos analizando, consideramos la actividad de caminar/marcha (contacto continuo con el suelo), estableciendo una frecuencia de paso en torno a 1.8 Hz. | En el caso que estamos analizando, consideramos la actividad de caminar/marcha (contacto continuo con el suelo), estableciendo una frecuencia de paso en torno a 1.8 Hz. | ||
| − | Se ha estimado que con <math display="inline">n=3</math> se obtiene una precisión adecuada, siendo los valores de los coeficientes los siguientes: <math display="inline">G_0</math>= 700 N, <math display="inline">G_1= 0,4 G_0</math>, <math display="inline">G_2=G_3\ | + | Se ha estimado que con <math display="inline">n=3</math> se obtiene una precisión adecuada, siendo los valores de los coeficientes los siguientes: <math display="inline">G_0</math>= 700 N, <math display="inline">G_1= 0,4 G_0</math>, <math display="inline">G_2=G_3\approx 0,1 G_0</math>, <math display="inline">\varphi_2=\varphi_3 \approx \pi /2</math>. |
==3. Resultados numéricos y discusión== | ==3. Resultados numéricos y discusión== | ||
| Line 421: | Line 415: | ||
En el caso de la masa modal del tercer modo se ajustó a un valor de 18057 kg que corresponde aproximadamente al valor máximo que se ha obtenido en las estimaciones experimentales (tablas 2, 3 y 4). La diferencia en porcentaje con respecto al resto de las estimaciones no supera el 6%. | En el caso de la masa modal del tercer modo se ajustó a un valor de 18057 kg que corresponde aproximadamente al valor máximo que se ha obtenido en las estimaciones experimentales (tablas 2, 3 y 4). La diferencia en porcentaje con respecto al resto de las estimaciones no supera el 6%. | ||
| − | En la tabla 6 se indican los valores resultantes de la comparación entre los modos normalizados respecto a la matriz de masa del modelo en ANSYS y los experimentales obtenidos en <span id='cite-Marcador13'></span>[[#Marcador13|[6 | + | En la tabla 6 se indican los valores resultantes de la comparación entre los modos normalizados respecto a la matriz de masa del modelo en ANSYS y los experimentales obtenidos en <span id='cite-Marcador13'></span>[[#Marcador13|[6,7]]]. |
| Line 613: | Line 607: | ||
Las aceleraciones que se emplean de referencia se extraen de registros de aceleraciones verticales que corresponden al tránsito peatonal de hasta 10 individuos<span id="fnc-1">[[#fn-1|<sup>1</sup>]]</span>. | Las aceleraciones que se emplean de referencia se extraen de registros de aceleraciones verticales que corresponden al tránsito peatonal de hasta 10 individuos<span id="fnc-1">[[#fn-1|<sup>1</sup>]]</span>. | ||
| + | |||
| + | <div class="auto" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> | ||
| + | <math display="inline">{}^1</math> La influencia de la masa de los peatones en el factor de amortiguamiento del modelo de la estructura no se tiene en cuenta puesto que representa un valor menor al 5% de la masa total de la pasarela <span id='cite-Marcador21_b'></span>[[#Marcador21_b|[22]]].</div> | ||
| + | |||
La simulación de dicha solicitación sobre la pasarela se realiza empleando el programa Mathematica y se obtienen las respuestas dinámicas en aquellos puntos donde tenemos registros experimentales para poder comparar posteriormente ambos resultados. | La simulación de dicha solicitación sobre la pasarela se realiza empleando el programa Mathematica y se obtienen las respuestas dinámicas en aquellos puntos donde tenemos registros experimentales para poder comparar posteriormente ambos resultados. | ||
| Line 618: | Line 616: | ||
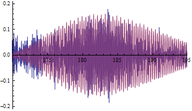
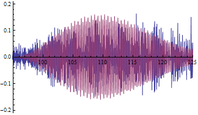
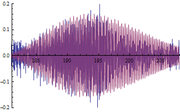
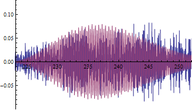
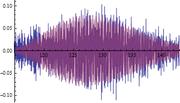
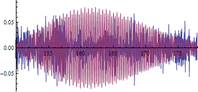
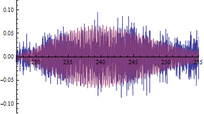
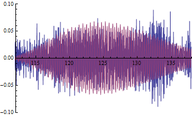
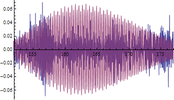
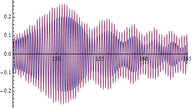
A continuación se muestran algunos ejemplos de las comparativas obtenidas entre respuestas dinámicas en forma de aceleraciones del modelo numérico y las registradas experimentalmente (figuras 16, 17 y 18): | A continuación se muestran algunos ejemplos de las comparativas obtenidas entre respuestas dinámicas en forma de aceleraciones del modelo numérico y las registradas experimentalmente (figuras 16, 17 y 18): | ||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;max-width: auto;" | |
| − | + | ||
|- | |- | ||
| − | | [[Image:draft_Samper_899487275-image30.png|192px]] | + | |[[Image:draft_Samper_899487275-image30.png|192px]] |
| − | | [[Image:draft_Samper_899487275-image31.png | + | |[[Image:draft_Samper_899487275-image31.png|198px]] |
| + | |[[Image:draft_Samper_899487275-image32.png|180px]] | ||
| + | |-style="text-align: center; font-size: 75%;" | ||
| + | |a) Ejemplo 1 | ||
| + | |b) Ejemplo 2 | ||
| + | |c) Ejemplo 3 | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
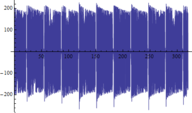
| + | | colspan="3" style="padding-top:10px;" | '''Figura 16.''' Respuestas dinámicas (aceleraciones) del modelo (color rojo) y registro experimental (color azul) en el punto <math display="inline">X=36.6</math> m de la pasarela. Abscisas en s y ordenadas en <math display="inline">m/s_2</math>. | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;max-width: auto;" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | [[Image:draft_Samper_899487275-image33.png|192px]] | + | |[[Image:draft_Samper_899487275-image33.png|192px]] |
| − | | [[Image:draft_Samper_899487275-image34.png | + | |[[Image:draft_Samper_899487275-image34.png|180px]] |
| + | |[[Image:draft_Samper_899487275-image35-c.png|198px]] | ||
| + | |-style="text-align: center; font-size: 75%;" | ||
| + | |a) Ejemplo 1 | ||
| + | |b) Ejemplo 2 | ||
| + | |c) Ejemplo 3 | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
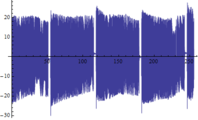
| + | | colspan="3" style="padding-top:10px;" | '''Figura 17.''' Respuestas dinámicas (aceleraciones) del modelo (color rojo) y registro experimental (color azul) en el punto <math display="inline">X=73.5</math> m de la pasarela. Abscisas en s y ordenadas en <math display="inline">m/s_2</math>. | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;max-width: auto;" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | [[Image:draft_Samper_899487275-image36.png|204px]] | + | |[[Image:draft_Samper_899487275-image36.png|204px]] |
| − | | [[Image:draft_Samper_899487275-image37.png | + | |[[Image:draft_Samper_899487275-image37.png|192px]] |
| + | |[[Image:draft_Samper_899487275-image38-c.png|174px]] | ||
| + | |-style="text-align: center; font-size: 75%;" | ||
| + | |a) Ejemplo 1 | ||
| + | |b) Ejemplo 2 | ||
| + | |c) Ejemplo 3 | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
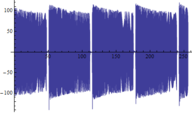
| + | | colspan="3" style="padding-top:10px;" | '''Figura 18.''' Respuestas dinámicas (aceleraciones) del modelo (color rojo) y registro experimental (color azul) en el punto <math display="inline">X=86.8</math> m de la pasarela. Abscisas en s y ordenadas en <math display="inline">m/s_2</math>. | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Siendo conscientes de las limitaciones del modelo de flujo peatonal y de la variabilidad de los registros experimentales de este tipo de aceleraciones, la finalidad del análisis de estos resultados es comprobar que los obtenidos numéricamente son del mismo orden de magnitud que los reales y que la estructura modelizada completa simula con adecuada precisión este tipo de solicitación. Tal y como puede desprenderse de las figuras anteriores (figuras 16, 17 y 18) los valores máximos alcanzados analíticamente son similares a los experimentales, situándose las mayores diferencias en torno al 20% en la mayoría de los casos. | Siendo conscientes de las limitaciones del modelo de flujo peatonal y de la variabilidad de los registros experimentales de este tipo de aceleraciones, la finalidad del análisis de estos resultados es comprobar que los obtenidos numéricamente son del mismo orden de magnitud que los reales y que la estructura modelizada completa simula con adecuada precisión este tipo de solicitación. Tal y como puede desprenderse de las figuras anteriores (figuras 16, 17 y 18) los valores máximos alcanzados analíticamente son similares a los experimentales, situándose las mayores diferencias en torno al 20% en la mayoría de los casos. | ||
| Line 692: | Line 690: | ||
<span id='Marcador12'></span>[5] J. De Sebastián, Análisis del Estado Límite de Servicio y Control de Vibraciones en pasarelas peatonales, Tesis Doctoral, Universidad de Valladolid, 2014. | <span id='Marcador12'></span>[5] J. De Sebastián, Análisis del Estado Límite de Servicio y Control de Vibraciones en pasarelas peatonales, Tesis Doctoral, Universidad de Valladolid, 2014. | ||
| − | <span id='Marcador13'></span>[6] M. Cacho-Pérez, N. Frechilla, A. Lorenzana, Estimación de las masas modales de una estructura en servicio mediante transformación en el espacio de estados, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 33(1) (2017) 123-128. DOI: | + | <span id='Marcador13'></span>[6] M. Cacho-Pérez, N. Frechilla, A. Lorenzana, Estimación de las masas modales de una estructura en servicio mediante transformación en el espacio de estados, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 33(1) (2017) 123-128. DOI: https://doi.org/10.1016/j.rimni.2016.02.002 |
| − | <span id='Marcador14'></span>[7] M. Cacho-Pérez, N. Frechilla, A. Lorenzana, Estimación de parámetros modales de estructuras civiles a partir de la función de respuesta en frecuencia, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. ( | + | <span id='Marcador14'></span>[7] M. Cacho-Pérez, N. Frechilla, A. Lorenzana, Estimación de parámetros modales de estructuras civiles a partir de la función de respuesta en frecuencia, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 33 (3-4) (2017) 197-203. DOI: http://doi.org/10.1016/j.rimni.2016.02.001. |
<span id='Marcador8_b'></span>[8] B. Caesar, Updating system matrices using modal test data, Procedings of the 5th International Modal Analysis Conference, London. (1987) 453-459. | <span id='Marcador8_b'></span>[8] B. Caesar, Updating system matrices using modal test data, Procedings of the 5th International Modal Analysis Conference, London. (1987) 453-459. | ||
Latest revision as of 13:54, 6 September 2017
Abstract
Civil engineering constructions like pedestrian footbridges are structures increasingly slender, ambitious and complex in which the dynamic effects caused by the loads to which they are subjected (pedestrians) may induce service problems and / or significant or repetitive amplifications of the efforts and deformations. This fact together with the current social demands related to the perception and comfort raise the need to integrate the analysis and computer-aided design in the evaluation of the vibrations generated by the loads this type of structures supports. In the specific case of finite element commercial programs, their use has not proliferated as much as in other engineering fields due to the existence of simplified methodologies in numerous national and international guidelines and regulations and the difficulty of making realistic models in the case of complex structures. However, the knowledge generated by the analysis of this type of numerical models would be especially useful in the earlier phases of the design of similar structures, so much initial as of the necessary modifications to solve existing dynamic problems, since it is in these stages when the best solution could be applied from both a technical and an economic point of view. This article describes the process of generation and updating of the mechanical finite element model (FEM) of a footbridge in service and the simulation of two types of load: an excitation generated by a shaker and a pedestrian load, contrasting the results generated by the numerical model with those obtained experimentally.
Resumen
Obras de ingeniería civil como las pasarelas peatonales son estructuras cada vez más esbeltas, ambiciosas y complejas en las que los efectos dinámicos producidos por las solicitaciones a las que están sometidas (peatones) pueden inducir problemas de servicio y/o amplificaciones importantes o repetitivas de los esfuerzos y deformaciones. Ésto junto con las actuales demandas sociales relativas a la percepción y confort suscitan la necesidad de integrar el análisis y diseño asistido por ordenador en la evaluación de las vibraciones generadas por las cargas a las que están sometidas. El empleo de los programas comerciales de elementos finitos no ha proliferado tanto como en otros campos de la ingeniería por la existencia de metodologías simplificativas en numerosas guías y normativas nacionales e internacionales y por la dificultad de hacer modelos realistas en el caso de estructuras complejas. Sin embargo, el conocimiento generado por el análisis de este tipo de modelos numéricos resultaría especialmente útil en las fases más tempranas del diseño de estructuras similares, tanto inicial como de las modificaciones necesarias para solucionar problemas dinámicos existentes, ya que es en estas etapas cuando se podría aplicar la mejor solución desde un punto de vista técnico y económico. En el presente artículo se describe el proceso de generación y ajuste del modelo mecánico de una pasarela actualmente en servicio y la simulación de la solicitación de dos tipos de carga: una excitación generada por un shaker y una carga peatonal, contrastando los resultados generados mediante el modelo numérico con los obtenidos experimentalmente.
Palabras clave: Pasarela peatonal, vibraciones, elementos finitos, ajuste modelo mecánico.
1. Introducción
El diseño y construcción de un gran número de obras de ingeniería industrial y civil ya no está apenas limitada por los materiales –cada vez más resistentes- y los sistemas constructivos –cada vez con mayor componente tecnológico- lo que ha provocado que en la actualidad éstas sean más esbeltas, ambiciosas y complejas.
Este hecho, junto con las actuales demandas sociales relativas a la percepción y confort suscitan la necesidad de integrar el análisis y diseño asistido por ordenador en la evaluación de la respuesta dinámica de estructuras esbeltas que son las más susceptibles de sufrir movimientos o vibraciones significativas.
Un caso particularmente relevante es el de las pasarelas peatonales, ya que generalmente son propensas a ser excitadas por las personas que las ocupan, pudiendo los efectos dinámicos producidos inducir, además de problemas de servicio, amplificaciones importantes y repetitivas de los esfuerzos y deformaciones que pueden afectar a la seguridad resistente o la vida a fatiga de la estructura.
Aunque las normativas recogen diversos criterios de evaluación de estos fenómenos, también reflejan la dificultad de evaluar con precisión el comportamiento dinámico de las estructuras, exigiendo en algunos casos un estudio dinámico riguroso.
La simulación mediante programas basados en el análisis de elementos finitos es una de las herramientas de cálculo con mayor profusión ya que los actuales softwares son muy competitivos respecto al ahorro de tiempo y costes. Sin embargo en el caso del análisis dinámico de estructuras no ha proliferado tanto debido a la existencia de normativas y guías nacionales e internacionales [1-3] que proporcionan metodologías simplificativas, que siendo útiles para la acotación del problema dinámico no ofrecen la enorme versatilidad del análisis numérico.
En general las predicciones logradas con el uso de modelos analíticos, especialmente en el caso de estructuras complejas como el que nos ocupa, difieren de los resultados obtenidos mediante ensayos experimentales por lo que es necesario efectuar un ajuste del modelo de elementos finitos (denominado en inglés FEM Updating), mejorando las hipótesis efectuadas y aproximando sus propiedades a las de la estructura real. Aunque los datos experimentales poseen errores que puedan provocar una baja correlación entre éstos y las predicciones, la teoría de ajuste de modelos supone que los principales causantes del desacuerdo teórico experimental son los errores en el modelo [4].
En el caso que nos ocupa se emplean los resultados experimentales procedentes de un análisis modal operacional, en inglés Operational Modal Analysis (OMA), realizado en la pasarela completa y un análisis modal clásico, del inglés Experimental Modal Analysis (EMA), realizado en el vano más sensible a excitaciones dinámicas producidas por humanos (vano 2), para conseguir que nuestro modelo numérico se ajuste lo mejor posible a la realidad. Los parámetros modales que identifican el comportamiento dinámico de la pasarela objeto de estudio (pasarela del Museo de la Ciencia de Valladolid) se han obtenido en estudios anteriores [5-7].
Una vez ajustado el modelo analítico (creado mediante el software de elementos finitos ANSYS) se han obtenido las respuestas dinámicas simuladas, en forma de aceleraciones, al aplicar la excitación generada durante el EMA y una carga peatonal según el modelo convencional de flujo de peatones [1]. Los resultados numéricos se han contrastado con los experimentales a fin de validar el comportamiento dinámico de la estructura modelizada.
El presente artículo se ha organizado del siguiente modo: en primer lugar, tras esta introducción, se resume la metodología empleada. A continuación en el tercer epígrafe se describe la pasarela estudiada, los parámetros modales que identifican su comportamiento dinámico y los procesos de modelización y ajuste de la estructura. En el cuarto apartado se presentan ejemplos de la respuesta dinámica simulada, y se comparan con la registrada experimentalmente para finalmente presentar las principales conclusiones que se deducen de este trabajo.
2. Metodología
2.1. Modelización y ajuste
La metodología seguida en el presente trabajo ha consistido en primer lugar en la modelización de la pasarela, partiendo de la geometría de proyecto, mediante el programa de elementos finitos ANSYS y procediendo posteriormente a su ajuste empleando para ello un esquema iterativo que permitió analizar y seleccionar aquellos parámetros físicos cuyo efecto era más relevante para tal fin. Respecto al ajuste del modelo mecánico (conocido como FEM Updating en la terminología inglesa), varios autores [8-15] han publicado y comparado varias técnicas sin alcanzarse ningún acuerdo sobre la existencia de un procedimiento general que pueda aplicarse a todos los casos, por lo que la elección ha dependido de los parámetros seleccionados.
Ésta se ha realizado en función de los parámetros modales extraídos de las campañas experimentales, empleando como referencia las frecuencias y las formas modales en el caso de la pasarela completa y complementándolo con las masas modales y/o modos normalizados respecto a la matriz de masa.
Dentro de los métodos iterativos de ajuste, se ha utilizado una aproximación para correlacionar el modelo experimental y el modelo matemático que consiste en la comparación entre las frecuencias naturales [16], pudiéndose la diferencia en porcentaje () expresarse tal y como se muestra a continuación:
|
|
(1) |
siendo el parámetro experimental y el parámetro calculado.
Para medir la correlación entre los modos normalizados respecto a la matriz de masa experimentales y los obtenidos mediante el modelo en ANSYS se ha empleado el criterio de confianza modal (MAC según la abreviatura de su denominación en inglés) que proporciona una medida del grado de linealidad entre estimaciones de los modos de vibración originados desde diferentes fuentes [16]. Se define como un escalar y su expresión se muestra a continuación:
|
|
(2) |
siendo el modo de vibración experimental y el modo de vibración calculado, donde la notación significa transpuesta compleja conjugada (matriz hermítica).
2.2. Simulación de cargas
Una vez ajustado el modelo se ha estudiado el comportamiento del mismo ante dos escenarios reales diferentes. El primero de ellos ha consistido en la simulación de las fuerzas generadas durante el EMA realizado en el vano más susceptible a las vibraciones (vano 2). En el segundo supuesto se ha simulado el tránsito peatonal a lo largo de toda la pasarela. En ambos casos el objetivo es obtener la respuesta dinámica en forma de aceleraciones del modelo numérico y poder comparar los resultados con los registrados experimentalmente con el fin de validarlo.
Para simular el efecto de varios peatones (solicitación del segundo escenario estudiado) se ha empleado el modelo convencional que considera que la respuesta de un flujo de peatones (sin ninguna sincronización particular) se obtiene multiplicando el efecto de un solo peatón por un factor igual a , siendo N el número de peatones presentes en la pasarela en un momento determinado [1]. La velocidad del peatón se ha considerado igual a 0.9 veces la frecuencia de paso en Hz.
La fuerza de excitación generada por un solo peatón (movimiento rítmico al caminar) se ha expresado matemáticamente mediante una serie de Fourier de la forma:
|
|
(3) |
donde
= fuerza estática (componente vertical del peso de un peatón)
= amplitud del primer armónico
= amplitud del i-ésimo armónico
= Frecuencia o cadencia de la actividad expresada en Herzios (Hz).
= ángulo de desfase del i-ésimo armónico respecto al primero
= número de armónicos
En el caso que estamos analizando, consideramos la actividad de caminar/marcha (contacto continuo con el suelo), estableciendo una frecuencia de paso en torno a 1.8 Hz.
Se ha estimado que con se obtiene una precisión adecuada, siendo los valores de los coeficientes los siguientes: = 700 N, , , .
3. Resultados numéricos y discusión
3.1. Resultados del análisis modal experimental
La Pasarela del Museo de la Ciencia es una estructura en servicio situada en Valladolid sobre el río Pisuerga (figura 1). Fue inaugurada en 2004 y tiene una longitud total de 234 metros repartidos en cuatro vanos: tres formados por barras metálicas de 51, 111 y 21 metros de luz (vano 2, 3 y 4 respectivamente), y uno de hormigón de 45 metros (vano 1). Éste último es muy rígido por lo que no se considera en el análisis objeto del presente trabajo. La tipología resistente de los vanos metálicos es de entramado triangulado de barras tubulares con sección pretensado formado por un conjunto de cables longitudinales y transversales en el vano 3 (figuras 2 y 3).

|
| Figura 1. Pasarela del Museo de la Ciencia. Vista general. |

|
| Figura 2. Pasarela del Museo de la Ciencia. Vista del vano 3. |

|
| Figura 3. Pasarela del Museo de la Ciencia. Detalle del pretensado perimetral en el vano 3. |
En el trabajo de investigación llevado a cabo por J. de Sebastián Sanz [5] se monitorizaron durante varios meses las aceleraciones verticales y laterales en el centro de cada uno de los tres vanos metálicos de la pasarela observándose que los niveles de vibración en la dirección lateral eran considerablemente menores que en la dirección vertical y que el nivel de vibraciones del vano 2 era notablemente mayor que el del vano 3. Más adelante se identificaron mediante un OMA los parámetros dinámicos de la estructura a partir de los registros de aceleración en dirección vertical monitorizados a lo largo de los tres vanos metálicos de la pasarela. Dichos parámetros modales se obtuvieron mediante el programa comercial ARTeMIS empleando tres algoritmos en el dominio de la frecuencia (FDD (Frequency Domain Decomposition), EFDD (Enhanced Frequency Domain Decomposition) y CFDD (Curve-Fit Frequency Domain Decomposition)) [17-19]. Éstos se recogen en la tabla 1 para los primeros cuatro modos de vibración:
| FDD | EFDD | CFDD |
| Frecuencia (Hz) | Frecuencia (Hz) | Frecuencia (Hz) |
| 1.245 | 1.243 | 1.257 |
| 2.759 | 2.763 | 2.765 |
| 3.516 | 3.514 | 3.515 |
| 4.785 | 4.792 | 4.792 |
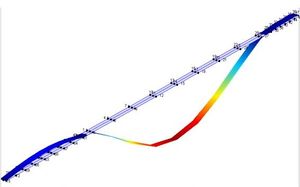
Los cuatro primeros modos de flexión de la pasarela completa se presentan a continuación.
|
|
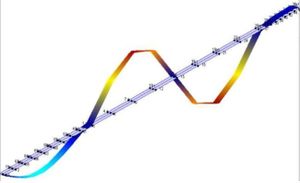
| (a) Primer modo | (b) Segundo modo unilateral |
|

|
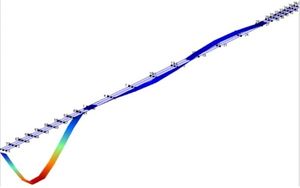
| (c) Tercer modo | (d) Cuarto modo |
| Figura 4. Primeros cuatro modos verticales de vibración obtenidos experimentalmente. | |
Debido a la mayor susceptibilidad del vano 2 de la pasarela, se realizó un EMA en el mismo identificando, entre otros, la masa modal vertical mediante el programa comercial OROS Modal 2. Se realizaron asimismo en este mismo estudio varias estimaciones de dicha masa modal empleando diferentes algoritmos, presentándose en la tabla 2 los resultados obtenidos [5].
| Método | Masa Modal (kg) |
| Programa OROS | 16983 |
| Algoritmo en frecuencia | 17950 |
| Algoritmo en el tiempo | 18060 |
| Ajuste de la FRF | 17900 |
| Aumento de la respuesta | 17500 |
Posteriormente empleando los registros del EMA realizado en el vano 2 se calcularon las masas modales y los modos normalizados asociados a cada modo de vibración de dicho vano mediante dos técnicas de escalado. Ambas parten de la información obtenida al aplicar el método de identificación de subespacios estocásticos, en inglés Stochastic Subspace Identification (SSI), consistiendo la primera de ellas en la resolución de un problema simétrico de valores propios y la segunda en el escalado de los modos de vibración a partir de la estimación de los residuos de la descomposición en fracciones parciales de la función de respuesta en frecuencia (FRF) de las mediciones [6,7]. Aplicando ambas técnicas se calcularon las masas modales y los valores de los modos normalizados respecto a la matriz de masa en las coordenadas L/3, L/2 y 2L/3 del vano 2 (L=51 m).
En la tabla 3 se indican los modos de vibración normalizados y la masa modal del modo vertical 3 de la pasarela estimado mediante el problema simétrico de valores propios expresado en el espacio de estados (método 1) [6].
| Masa modal (kg) | Coordenadas | |||
| L/3 | L/2 | 2L/3 | ||
| Valor medio | 17605.0 | 0.0039 | 0.0075 | 0.0058 |
| Desviación típica | 1028.0 | 0.0001 | 0.0002 | 0.0002 |
| Masa modal (kg) | Coordenadas | |||
| L/3 | L/2 | 2L/3 | ||
| Valor medio | 17814.9 | 0.0039 | 0.0075 | 0.0045 |
| Desviación típica | 952.9 | 0.0001 | 0.0002 | 0.0001 |
En la tabla 4 se indican los modos de vibración normalizados y la masa modal del modo vertical 3 de la pasarela mediante escalado a partir de la estimación de los residuos de la descomposición en fracciones parciales de la Función de Respuesta en Frecuencia (FRF) de las mediciones (método 2) [7].
3.2. Generación del modelo de la pasarela
La estructura del tramo metálico de la pasarela (vanos 2, 3 y 4) consiste en una celosía tubular tridimensional de sección transversal hexagonal (figura 5), que en el vano 3 se sitúa en el interior de otra celosía formada por cables pretensados longitudinales y transversales. Ambas celosías se enlazan mediante radios tubulares que permiten mantener la forma de los cables y aumentar su excentricidad en el centro del vano. La sección transversal es un hexágono irregular cuya inclinación y dimensiones cambian a lo largo del puente [20].
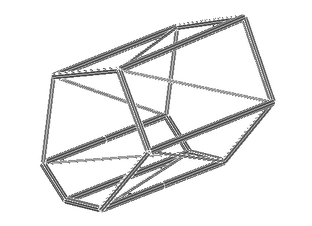
|
| Figura 5. Celosía tubular tridimensional de sección transversal hexagonal. |
En cuanto al pretensado transversal, cada sección hexagonal del vano 3 (son 15) consta de un tendón periférico en forma de hexágono, cuyos vértices son los extremos de los seis radios. El pretensado longitudinal consta de seis tendones que pasan por los extremos de los radios de las secciones transversales [21]. Se ha modelizado la estructura de forma que los nudos que conforman tanto el hexágono exterior como el interior, sean coplanarios (figura 6).
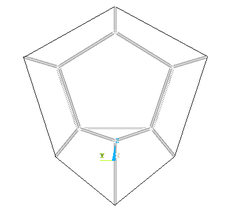
|
| Figura 6.Sección transversal y pretensado del vano 3. |
La estructura principal está formada por perfiles tubulares de sección circular (figura 7). El diámetro de los perfiles longitudinales es de 273 mm y las diagonales son perfiles de diámetro 135 mm. Los montantes y radios son perfiles tubulares de sección cuadrada de dimensiones 200 mm x 200 mm.
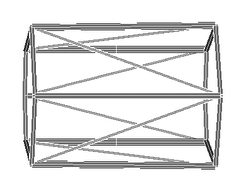
|
| Figura 7. Estructura principal. |
Las secciones de la estructura del tablero (figura 8), constituida por travesaños y arriostramientos, son cuadradas de dimensiones 120 mm x 100 mm y 120 mm x 120 mm respectivamente.
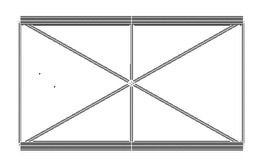
|
| Figura 8. Estructura del tablero. |
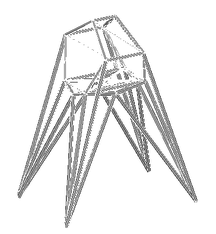
Los apoyos centrales son dos torres constituidas por celosías resueltas también con perfiles tubulares de 355 mm de diámetro (figura 9).
|
| Figura 9. Apoyo central. |
En cuanto a las propiedades del acero se ha considerado un módulo de elasticidad de 2,1·1011 N/m2, un coeficiente de Poisson igual a 0,3 y una densidad de 7.700 Kg/m3.
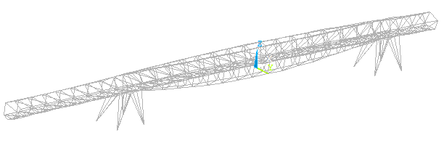
La modelización de la estructura se ha realizado mediante el programa ANSYS empleando dos tipos de elementos: BEAM188 para simular los perfiles tubulares, definiendo para cada tipo las secciones indicadas anteriormente y LINK180 para los tendones de pretensado (figura 10). En el caso del pretensado longitudinal se ha impuesto que los movimientos en la dirección lateral y vertical de los nudos que lo modelizan sean iguales a los de los nudos que representan los extremos de los radios de las secciones transversales. La fuerza de pretensado se ha modelizado mediante el comando INISTATE.
La principal dificultad en la definición geométrica de la pasarela ha sido la modelización del pretensado, principalmente por la elección del tipo de elemento y de las conexiones de éste con el resto de la estructura con el fin de que la transmisión de esfuerzos se realizara de forma realista.
En cuanto a los apoyos, la estructura se considera apoyada en las torres centrales y empotrada en los extremos del tablero. Las bases de las torres se suponen empotradas.
|
| Figura 10. Vista general del modelo completo de la pasarela en ANSYS. |
3.3. Ajuste del modelo de la pasarela
Para el ajuste del modelo de la pasarela se emplearon todos los datos experimentales expuestos en los estudios anteriores [5] que afectaban a los cuatro primeros modos verticales de vibración de la pasarela completa, esto es, las frecuencias y las formas modales de dichos modos y la masa modal y los modos normalizados del tercer modo de vibración.
Se empleó un esquema iterativo que nos permitió analizar y seleccionar aquellos parámetros físicos cuyo efecto era más relevante para que las frecuencias y las formas modales de nuestro modelo se aproximaran lo más posible a las obtenidas experimentalmente. En nuestro caso se comprobó que la masa era la variable que mayor influencia tenían en el ajuste una vez modelizada la geometría de la estructura.
En el caso de la masa, ha sido la principal variable que ha afectado al ajuste del tercer modo vertical, no sólo de la frecuencia y la forma modal sino también de su masa modal.
Se ha seleccionado para el análisis modal realizado el método de Block Lanczos y se han obtenido los primeros cuatro modos verticales, que a continuación se reflejan.

|
| a) Primer modo: f1 = 1.224 Hz |
|
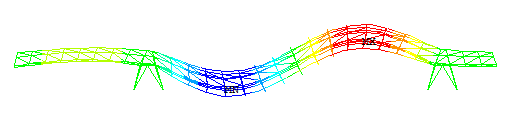
| b) Segundo modo: f2 = 2.842 Hz |
|
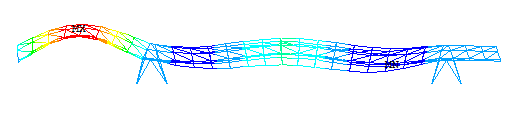
| c) Tercer modo: f3 = 3.662 Hz |
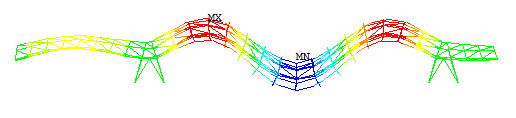
|
| d) Cuarto modo: f4 = 4.914 Hz |
| Figura 11. Modos verticales obtenidos con el modelo en ANSYS. |
Tal y como puede observarse la correspondencia entre las formas modales del modelo en ANSYS (figura 11) y las del OMA (figura 4) es buena.
En la tabla 5 se comparan los resultados del modelo numérico con los obtenidos experimentalmente (tabla 1).
| Modo | fMEF
(Hz) |
│fMEF – fFDD│/fMEF
(%) |
│fMEF – fEFDD│/fMEF
(%) |
│fMEF – fCFDD│/fMEF
(%) |
| 1 | 1.224 | 1.72 | 1.55 | 2.70 |
| 2 | 2.842 | 2.92 | 2.78 | 2.71 |
| 3 | 3.662 | 3.99 | 4.04 | 4.01 |
| 4 | 4.914 | 2.63 | 2.48 | 2.48 |
En todos los casos se obtienen diferencias menores del 5% lo que indica una buena correspondencia del modelo.
En el caso de la masa modal del tercer modo se ajustó a un valor de 18057 kg que corresponde aproximadamente al valor máximo que se ha obtenido en las estimaciones experimentales (tablas 2, 3 y 4). La diferencia en porcentaje con respecto al resto de las estimaciones no supera el 6%.
En la tabla 6 se indican los valores resultantes de la comparación entre los modos normalizados respecto a la matriz de masa del modelo en ANSYS y los experimentales obtenidos en [6,7].
| Técnica de obtención de los modos normalizados | Coordenadas | MAC | ||
| L/3 | L/2 | 2L/3 | ||
| Modelo ANSYS | 0.0069 | 0.0074 | 0.0055 | |
| Método 1 | 0.0039 | 0.0075 | 0.0058 | 0.938 |
| Método 2 | 0.0039 | 0.0075 | 0.0045 | 0.944 |
Los resultados son cercanos a la unidad lo que nos indica una buena correspondencia entre modos.
4. Análisis dinámico y validación del modelo
Una vez ajustado el modelo de elementos finitos de la pasarela, se obtienen los modos normalizados de los cuatro primeros modos de vibración y, con el resto de los parámetros modales, se procede a simular diferentes fuerzas de excitación para obtener su respuesta, en forma de aceleraciones. El objetivo es poder comparar los resultados con los obtenidos experimentalmente con el objetivo de validar la modelización. Para obtener la respuesta dinámica del modelo se emplearon los valores medios de los coeficientes de amortiguamiento obtenidos experimentalmente en [5] correspondientes a dichos modos. Estos coeficientes se muestran en la tabla 7.
| Modo | Amortiguamiento Método EFDD (%) | Amortiguamiento Método CFDD (%) |
| 1 | 1.173 | 1.233 |
| 2 | 0.563 | 0.914 |
| 3 | 0.447 | 0.436 |
| 4 | 0.345 | 0.327 |
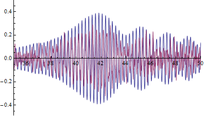
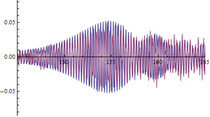
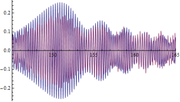
Para validar el comportamiento dinámico observado en el vano 2 del modelo se simularon las fuerzas generadas durante el EMA y se calcularon las aceleraciones en los mismos puntos en los que se obtuvieron mediciones experimentales (L/3, L/2 y 2L/3 del vano 2 siendo L=51). A continuación, se muestran algunos ejemplos de fuerzas simuladas (figura 12) y de las comparativas entre las respuestas experimentales y las obtenidas numéricamente (figuras 13, 14 y 15).
|
|
|
| a) Ejemplo 1 | b) Ejemplo 2 | c) Ejemplo 3 |
| Figura 12. Fuerzas de excitación generadas durante el EMA (abscisas en s y ordenadas en N). | ||
|
|
|
| a) Ejemplo 1 | b) Ejemplo 2 | c) Ejemplo 3 |
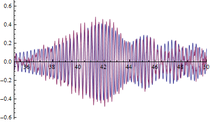
| Figura 13. Respuesta experimental (en rojo) y respuesta numérica (en azul) en m (L/3 del vano 2). Abscisas en s y ordenadas en . | ||
|
|
|
| a) Ejemplo 1 | b) Ejemplo 2 | c) Ejemplo 3 |
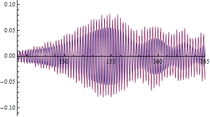
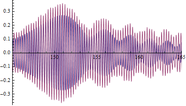
| Figura 14. Respuesta experimental (en rojo) y respuesta numérica (en azul) en m (L/2 del vano 2). Abscisas en s y ordenadas en . | ||
|
|
|
| a) Ejemplo 1 | b) Ejemplo 2 | c) Ejemplo 3 |
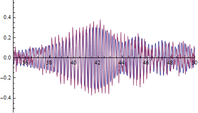
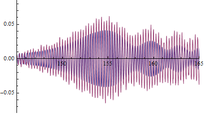
| Figura 15. Respuesta experimental (en rojo) y respuesta numérica (en azul) en m (2L/3 del vano 2). Abscisas en s y ordenadas en . | ||
| Prueba | Cota | Numérica | Experimental | Diferencia (%) |
| 1 | L/3 | 0,389 | 0,290 | 25,6 |
| L/2 | 0,413 | 0,486 | 14,9 | |
| 2L/3 | 0,308 | 0,380 | 19,1 | |
| 2 | L/3 | 0,052 | 0,050 | 4,8 |
| L/2 | 0,056 | 0,083 | 32,7 | |
| 2L/3 | 0,041 | 0,062 | 33,2 | |
| 3 | L/3 | 0,257 | 0,200 | 22,2 |
| L/2 | 0,273 | 0,359 | 24,0 | |
| 2L/3 | 0,203 | 0,271 | 25,1 |
Como puede observarse en la tabla 8, donde se muestran las aceleraciones máximas obtenidas tanto numérica como experimentalmente, las respuestas del modelo son ligeramente inferiores salvo a L/3 del vano 2, que son algo superiores debido a que el modo normalizado del modelo en esa coordenada es también superior al obtenido experimentalmente. En el resto de los casos las diferencias son probablemente consecuencia de que el modelo sólo tiene en cuenta la fuerza de excitación aplicada y no el resto de las cargas ambientales que pudieran existir. Las diferencias son más notables y variables en el caso de que la fuerza artificial aplicada es menor y por tanto el peso en la respuesta de las cargas ambientales es mayor, lo que corroboraría la hipótesis anterior. Tal y como queda reflejado en la tabla anterior (tabla 8) las diferencias en el valor máximo de las aceleraciones se encuentran en torno al 25% lo que indica que la correspondencia entre la respuesta del modelo y la experimental es buena.
Para estudiar el comportamiento del modelo completo se ha procedido a simular la principal solicitación a la que están sometidas este tipo de estructuras, esto es, el tránsito peatonal, para comparar la respuesta obtenida con la registrada experimentalmente en varios puntos de la pasarela y así verificar el comportamiento de la estructura completa.
Las aceleraciones que se emplean de referencia se extraen de registros de aceleraciones verticales que corresponden al tránsito peatonal de hasta 10 individuos1.
La simulación de dicha solicitación sobre la pasarela se realiza empleando el programa Mathematica y se obtienen las respuestas dinámicas en aquellos puntos donde tenemos registros experimentales para poder comparar posteriormente ambos resultados.
A continuación se muestran algunos ejemplos de las comparativas obtenidas entre respuestas dinámicas en forma de aceleraciones del modelo numérico y las registradas experimentalmente (figuras 16, 17 y 18):
Siendo conscientes de las limitaciones del modelo de flujo peatonal y de la variabilidad de los registros experimentales de este tipo de aceleraciones, la finalidad del análisis de estos resultados es comprobar que los obtenidos numéricamente son del mismo orden de magnitud que los reales y que la estructura modelizada completa simula con adecuada precisión este tipo de solicitación. Tal y como puede desprenderse de las figuras anteriores (figuras 16, 17 y 18) los valores máximos alcanzados analíticamente son similares a los experimentales, situándose las mayores diferencias en torno al 20% en la mayoría de los casos.
5. Conclusiones
A la vista de los resultados obtenidos se puede llegar a la conclusión de que el modelo de elementos finitos representa de forma bastante precisa los parámetros modales de la estructura a pesar de la complejidad geométrica de la misma.
En el caso de la respuesta dinámica se obtienen buenos resultados considerando la multitud de factores –y errores inherentes a ellos- que intervienen tanto en la obtención de los resultados numéricos como los experimentales (en especial en el caso del tránsito peatonal). Se ha podido comprobar que si la geometría de partida es realista y completa el ajuste únicamente de las frecuencias y formas modales proporciona una precisión adecuada del modelo.
Una vez validado, este modelo nos permitirá estudiar los diferentes factores que provocan la susceptibilidad a las vibraciones de la pasarela para, por ejemplo, contemplar diferentes alternativas de diseño y/o predecir su comportamiento ante diferentes solicitaciones durante las diversas fases del Proyecto. Asimismo se puede emplear el conocimiento generado en el presente estudio en las fases de diseño de otros casos similares, reduciendo de este modo las inversiones que serían necesarias implantar para solucionar efectos dinámicos no deseados en etapas más tardías que habitualmente son mucho más elevadas. Este análisis puede abrir nuevas líneas de investigación que pueden ser recogidas en futuras publicaciones.
Todo ello contribuirá a una mejor compresión del comportamiento dinámico de este tipo de estructuras favoreciendo asimismo la proliferación del uso de este tipo de herramientas y así ayudar a los proyectistas y a las administraciones responsables de su diseño y mantenimiento.
Agradecimientos
Este trabajo ha sido realizado en parte con la financiación aportada al proyecto de investigación BIA2011-28493-C02-02 por el programa de apoyo a Proyectos de Investigación Fundamental No Orientada (PIFNO) del Ministerio de Ciencia.
Los autores agradecen al Ayuntamiento de Valladolid y al Museo de la Ciencia su apoyo en las pruebas de campo.
Bibliografía
[1] P. Charles, W. Hoorpah, Technical guide – footbridges - Assessment of vibrational behavior of footbridges under pedestrian loading, Service d´Etudes Techniques des Routes et Autoroutes (SETRA), Paris, 2006.
[2] FIB. Bulletin 32. Guidelines for the design of footbridges. Fédération internationale du béton (FIB), 2005.
[3] M. Feldmann, C. Heinemeyer, M. Lukic, Design of Footbridges. Guideline. Human Induced Vibrations of Steel Structure (Hivoss), Hivoss-RFS2-CT-2007-00033, 2008.
[4] J. E. Mottershead, M.I. Friswell, Model updating in structural dynamics: A survey, Journal of Sounds and Vibration. 167(2) (1993) 347-375.
[5] J. De Sebastián, Análisis del Estado Límite de Servicio y Control de Vibraciones en pasarelas peatonales, Tesis Doctoral, Universidad de Valladolid, 2014.
[6] M. Cacho-Pérez, N. Frechilla, A. Lorenzana, Estimación de las masas modales de una estructura en servicio mediante transformación en el espacio de estados, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 33(1) (2017) 123-128. DOI: https://doi.org/10.1016/j.rimni.2016.02.002
[7] M. Cacho-Pérez, N. Frechilla, A. Lorenzana, Estimación de parámetros modales de estructuras civiles a partir de la función de respuesta en frecuencia, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 33 (3-4) (2017) 197-203. DOI: http://doi.org/10.1016/j.rimni.2016.02.001.
[8] B. Caesar, Updating system matrices using modal test data, Procedings of the 5th International Modal Analysis Conference, London. (1987) 453-459.
[9] S. R. Ibrahim, A.A. Saafan, Correlation of analysis and test in modelling of structures assessment and review. Procedings of the 5th International Modal Analysis Conference, London. (1987) 1651-1660.
[10] W. Heylen, P. Sas, Review of model optimisation techniques, Procedings of the 5th International Modal Analysis Conference, London. (1987) 1177-1182.
[11] H. G. Natke, Updating computational models in the frequency domain based on measured data: A Survey, Probabilistic Engineering Mechanics. 4 (1988) 28-35.
[12] M. Imregun, W.J. Visser, A review of model updating techniques, The Shock and Vibration Digest. 23(1) (1991) 9-20.
[13] J.E.Mottershead, M.I. Friswell, Model updating in structural dynamics: A survey, Journal of Sounds and Vibration. 167(2) (1993) 347-375.
[14] M.I. Friswell, J.E. Mottershead, Finite Element Model Updating in Structural Dynamics, Kluwer Academic publishers, 1995.
[15] W. Vélez, D. Gómez, P. Thomson, Ajuste de Modelos de Elementos Finitos, Dyna. 76(158) (2009) 177-189.
[16] S. Ziaei Rad, Methods for Updating Numerical Models in Structural Dynamics, Tesis, University of London, 1997.
[17] R. Brincker, L. Zhang, P. Andersen, (2000, February), Modal identification from ambient responses using frequency domain decomposition, Proceedings. of the 18 International Modal Analysis Conference (IMAC), San Antonio, Texas. (2000).
[18] S. Gade, N. Møller, H. Herlufsen, H. Konstantin-Hansen, Frequency domain techniques for operational modal analysis, 1st IOMAC Conference. (2005).
[19] N.J. Jacobsen, P. Andersen, R. Brincker, Applications of frequency domain curve-fitting in the EFDD technique, Proceedings IMAC XXVI Conference. (2008).
[20] J. Martínez Calzón, R. Moneo Vallés, E. De Teresa Trilla, (2007) Pasarela del Museo de la Ciencia sobre el río Pisuerga (Valladolid), Boletín Informativo Construber. 8 (2007) 10-13.
[21] P. Ladret, A. González, Pretensado exterior en la pasarela del Museo de la Ciencia en Valladolid, Informes de la Construcción, 57(497) (2005).
[22] C. Maraveas, Z.C. Fasoulakis and K.D: Tsavdaridis, A review of Human Induced Vibrations on Footbridges, American Journal of Engineering and Applied Sciences. 8(4) (2015) 422-433.
Document information
Published on 03/01/18
Accepted on 26/06/17
Submitted on 27/04/17
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.8.004
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?