| (15 intermediate revisions by 2 users not shown) | |||
| Line 43: | Line 43: | ||
|} | |} | ||
| − | donde ''R''<sub>F</sub> es el índice de riesgo físico y F es el coeficiente de agravamiento. El índice de riesgo físico está relacionado con las pérdidas esperadas debido a la fragilidad de los elementos expuestos a la acción sísmica. El coeficiente de agravamiento F está relacionado con la capacidad socio-económica y de resiliencia de una comunidad expuesta. El riesgo físico | + | donde ''R''<sub>F</sub> es el índice de riesgo físico y F es el coeficiente de agravamiento. El índice de riesgo físico está relacionado con las pérdidas esperadas debido a la fragilidad de los elementos expuestos a la acción sísmica. El coeficiente de agravamiento F está relacionado con la capacidad socio-económica y de resiliencia de una comunidad expuesta. El riesgo físico <math display="inline">R_F</math> se obtiene en la ecuación 2 como suma ponderada de unos ''factores de riesgo físico <math display="inline">F_{RF_i}</math> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 55: | Line 55: | ||
|} | |} | ||
| − | siendo | + | siendo <math display="inline">w_{RF_i}</math> los coeficientes de ponderación de cada factor y'' p'' el número total de factores considerados para el riesgo físico. Los ''p'' coeficientes <math display="inline">w_{RF_i}</math> suman 1 y se determinan utilizando el Proceso Analítico Jerárquico (PAJ) [19]. Los factores de riesgo <math display="inline">F_{RF_i}</math> dependen de la información disponible (descriptores) referente a evaluación de potenciales perdidas (humanas, económicas o daño físico en diferentes tipos de estructuras e infraestructuras). |
| − | La metodología propuesta en este artículo parte del cálculo de un índice de riesgo físico debido a una posible amenaza natural Hi <math display="inline">\left( {RF}_{{H}_{i}}\right)</math> . Según las evaluaciones de riesgo disponibles es posible que los factores de riesgo | + | La metodología propuesta en este artículo parte del cálculo de un índice de riesgo físico debido a una posible amenaza natural Hi <math display="inline">\left( {RF}_{{H}_{i}}\right)</math> . Según las evaluaciones de riesgo disponibles es posible que los factores de riesgo <math display="inline">F_{RF_i}</math> se basen en valores numéricos resultantes de dichas evaluaciones o que sea necesario recurrir a la opinión de expertos. |
===2.1. Evaluación con base en resultados numéricos de evaluaciones de riesgo=== | ===2.1. Evaluación con base en resultados numéricos de evaluaciones de riesgo=== | ||
| Line 116: | Line 116: | ||
* Identificar las amenazas naturales que pueden afectar a dicha zona (''Hi'' con <math display="inline">i\leq 3)</math>. | * Identificar las amenazas naturales que pueden afectar a dicha zona (''Hi'' con <math display="inline">i\leq 3)</math>. | ||
| − | * Obtener información de los niveles de riesgo físico y de pertenencia | + | * Obtener información de los niveles de riesgo físico y de pertenencia para la ponderación de dichos niveles con base en estudios existentes o, de ser necesario, con la opinión de expertos en evaluación del riesgo físico debido a cada amenaza natural considerada. En caso de contar con varias y diferentes opiniones por amenaza, se ponderan éstas para tener un solo nivel de riesgo físico <math display="inline">{\, (NR}_{{F}_{i}})</math> promedio y un nivel de pertenencia <math display="inline">\left( {\alpha}_{i}\right)</math> promedio por amenaza; dichos valores representan las variables de entrada de la metodología: <math display="inline">{\, Ei=(NR}_{{F}_{i}};\, {\alpha}_{i})</math> con <math display="inline">i\leq 3</math>. |
* Esta información de entrada se procesa mediante el uso de un mecanismo de inferencia difusa aplicable a modelos lingüísticos, utilizando reglas del tipo Si-Entonces del tipo Mamdani. | * Esta información de entrada se procesa mediante el uso de un mecanismo de inferencia difusa aplicable a modelos lingüísticos, utilizando reglas del tipo Si-Entonces del tipo Mamdani. | ||
| Line 136: | Line 136: | ||
Dependiendo de la información disponible en la zona urbana a estudiar, el riesgo físico debido a una determinada amenaza natural <math display="inline">\left( {R}_{{F}_{Hi}}\right)</math> , se puede estimar mediante una evaluación numérica, o mediante una evaluación basada en la opinión de expertos locales en las diferentes amenazas <math display="inline">{H}_{i}</math>. | Dependiendo de la información disponible en la zona urbana a estudiar, el riesgo físico debido a una determinada amenaza natural <math display="inline">\left( {R}_{{F}_{Hi}}\right)</math> , se puede estimar mediante una evaluación numérica, o mediante una evaluación basada en la opinión de expertos locales en las diferentes amenazas <math display="inline">{H}_{i}</math>. | ||
| − | En la evaluación basada en la opinión de expertos es necesario informar a los encuestados sobre la evaluación que se espera realizar de modo que sus respuestas tengan mayor grado de pertenencia en el nivel de riesgo que éstos seleccionen. Los expertos en una determinada amenaza natural, suministraran las calificaciones lingüísticas correspondientes a las tres afectaciones que debe dar cuenta el riesgo físico, <math display="inline">{R}_{{F}_{{H}_{i}}}</math>, (''daño predominante en edificios'', que varía con la amenaza, ''afectación en la población'', y ''afectación en las líneas vitales'') basándose en las cinco calificaciones lingüísticas establecidas: muy bajo (N<sub>1</sub>), bajo (N<sub>2</sub>), medio (N<sub>3</sub>), alto (N<sub>4</sub>) y muy alto (N<sub>5</sub>) (Tabla 1). Posteriormente, dicha información suministrada se procesa, utilizando la teoría de conjuntos difusos, para estimar el posible nivel de <math display="inline">{R}_{{F}_{{H}_{i}}}</math>; mediante un proceso de desfusificación, el valor numérico del riesgo físico debido a la amenaza natural | + | En la evaluación basada en la opinión de expertos es necesario informar a los encuestados sobre la evaluación que se espera realizar de modo que sus respuestas tengan mayor grado de pertenencia en el nivel de riesgo que éstos seleccionen. Los expertos en una determinada amenaza natural, suministraran las calificaciones lingüísticas correspondientes a las tres afectaciones que debe dar cuenta el riesgo físico, <math display="inline">{R}_{{F}_{{H}_{i}}}</math>, (''daño predominante en edificios'', que varía con la amenaza, ''afectación en la población'', y ''afectación en las líneas vitales'') basándose en las cinco calificaciones lingüísticas establecidas: muy bajo (N<sub>1</sub>), bajo (N<sub>2</sub>), medio (N<sub>3</sub>), alto (N<sub>4</sub>) y muy alto (N<sub>5</sub>) (Tabla 1). Posteriormente, dicha información suministrada se procesa, utilizando la teoría de conjuntos difusos, para estimar el posible nivel de <math display="inline">{R}_{{F}_{{H}_{i}}}</math>; mediante un proceso de desfusificación, el valor numérico del riesgo físico debido a la amenaza natural <math display="inline">{H}_{i}</math>, el cual debe tener un nivel de pertenencia mayor o igual a 0.50. |
<div class="center" style="font-size: 75%;">'''Tabla 1'''. Descripción de los cinco niveles de riesgo físico utilizados para cada descriptor</div> | <div class="center" style="font-size: 75%;">'''Tabla 1'''. Descripción de los cinco niveles de riesgo físico utilizados para cada descriptor</div> | ||
| Line 194: | Line 194: | ||
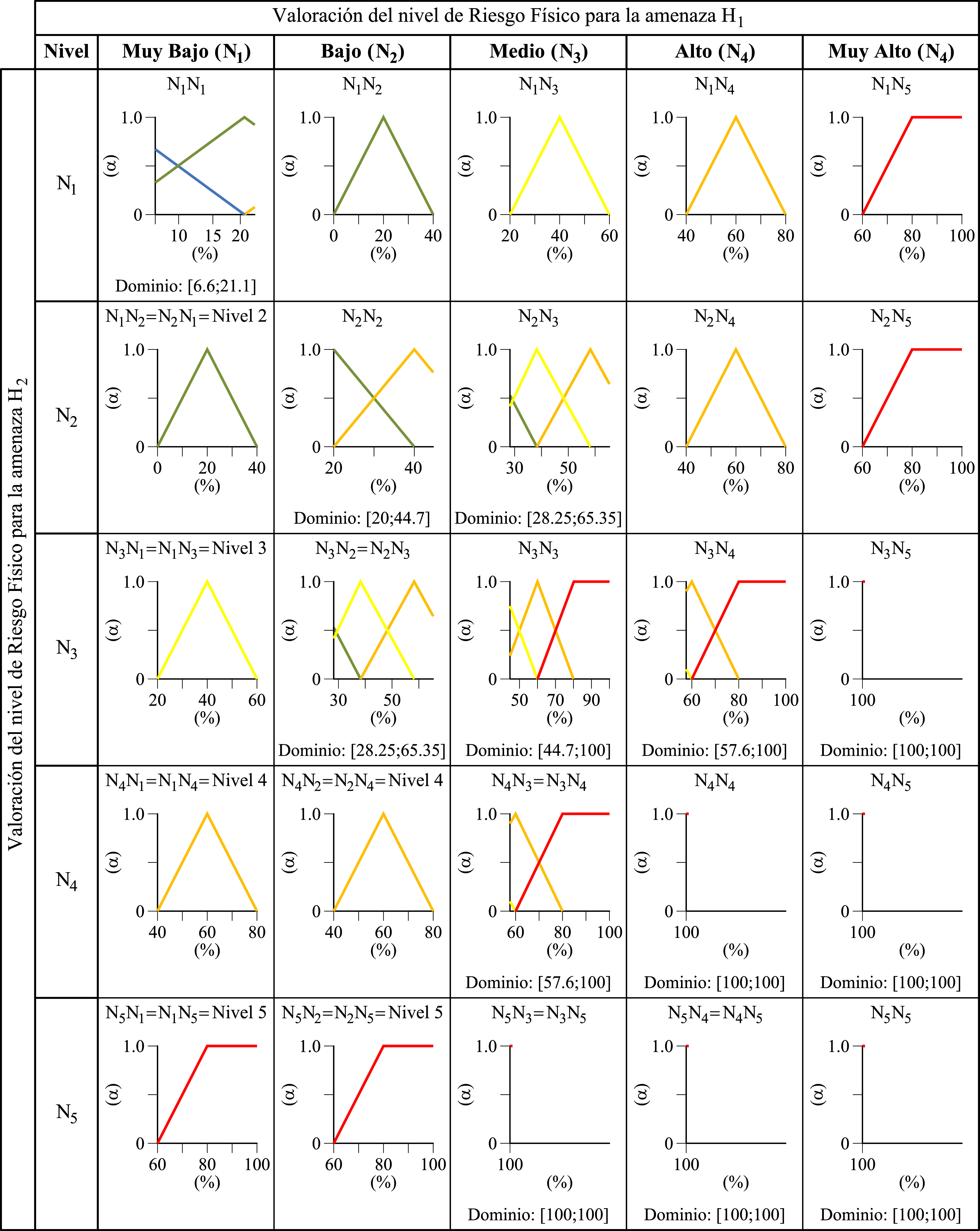
Teniendo en cuenta que, numéricamente, el índice de riesgo físico, así como sus factores contribuyentes, pueden variar entre cero y uno, se definen cinco calificaciones lingüísticas, en las que, por comodidad de manipulación, su dominio se expresa en %RF. Así el valor numérico de riesgo físico estará asociado a un % de riesgo, y con ese porcentaje se entra en el dominio del criterio establecido para los niveles de riesgo y se selecciona el nivel que presente mayor nivel de pertenencia. | Teniendo en cuenta que, numéricamente, el índice de riesgo físico, así como sus factores contribuyentes, pueden variar entre cero y uno, se definen cinco calificaciones lingüísticas, en las que, por comodidad de manipulación, su dominio se expresa en %RF. Así el valor numérico de riesgo físico estará asociado a un % de riesgo, y con ese porcentaje se entra en el dominio del criterio establecido para los niveles de riesgo y se selecciona el nivel que presente mayor nivel de pertenencia. | ||
| − | Se definen las funciones de pertenencia en un rango entre 0% y 100% para los 5 niveles de riesgo preestablecidos marcando como puntos de cruce (crossover) 10%, 30%, 50% y 70% (puntos con =0.5 en la Figura 6 superior). Por otro lado, se tiene una función de trasformación genérica tipo S entre 0 y 100% como puntos mínimo y máximo respectivamente (Figura 6 inferior). Los grados de pertenencia para los porcentajes marcados como puntos de cruce servirán para definir los niveles de riesgo para los diferentes componentes (0.02, 0.18, 0.50, 0.82 y 1.0 en la Figura 6 inferior). | + | Se definen las funciones de pertenencia en un rango entre 0% y 100% para los 5 niveles de riesgo preestablecidos marcando como puntos de cruce (crossover) 10%, 30%, 50% y 70% (puntos con <math display="inline">\alpha = 0.5</math> en la Figura 6 superior). Por otro lado, se tiene una función de trasformación genérica tipo S entre 0 y 100% como puntos mínimo y máximo respectivamente (Figura 6 inferior). Los grados de pertenencia para los porcentajes marcados como puntos de cruce servirán para definir los niveles de riesgo para los diferentes componentes (0.02, 0.18, 0.50, 0.82 y 1.0 en la Figura 6 inferior). |
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| Line 236: | Line 236: | ||
===3.2. Mecanismo de Inferencia=== | ===3.2. Mecanismo de Inferencia=== | ||
| − | En el proceso de inferencia es indispensable establecer reglas del tipo ''Si-entonces'', las cuales dependen de la naturaleza del problema a resolver. Las reglas son estructuras lógicas de decisión que permiten, entre otras cosas, transformar unos “valores” de entrada conocidos como antecedentes que son premisas o condiciones que han de cumplirse, en un “valor” de salida el cual se denomina consecuencia La metodología propuesta utiliza un proceso de inferencia en el que las reglas que se emplean tienen una estructura lógica de múltiples entradas y una única salida, denominado modelo tipo MISO (''Multiple Input-Simple Output''). Concretamente, las entradas que deben cumplirse, son los niveles de riesgo físico <math display="inline">\left( {N}_{{RF}_{Hi}}\right)</math> suministrados para cada amenaza natural (H<sub>i</sub>) con'' i=1…m'', siendo ''m'' el número total de amenazas a considerar; y la variable lingüística que define el posible nivel de riesgo físico de entre los cinco niveles propuestos <math display="inline">\left( {N}_{j},\, j=\right. </math><math>\left. 1,\cdots ,5\right)</math> (Figura 6 superior). | + | En el proceso de inferencia es indispensable establecer reglas del tipo ''Si-entonces'', las cuales dependen de la naturaleza del problema a resolver. Las reglas son estructuras lógicas de decisión que permiten, entre otras cosas, transformar unos “valores” de entrada conocidos como antecedentes que son premisas o condiciones que han de cumplirse, en un “valor” de salida el cual se denomina consecuencia. La metodología propuesta utiliza un proceso de inferencia en el que las reglas que se emplean tienen una estructura lógica de múltiples entradas y una única salida, denominado modelo tipo MISO (''Multiple Input-Simple Output''). Concretamente, las entradas que deben cumplirse, son los niveles de riesgo físico <math display="inline">\left( {N}_{{RF}_{Hi}}\right)</math> suministrados para cada amenaza natural (H<sub>i</sub>) con'' i=1…m'', siendo ''m'' el número total de amenazas a considerar; y la variable lingüística que define el posible nivel de riesgo físico de entre los cinco niveles propuestos <math display="inline">\left( {N}_{j},\, j=\right. </math><math>\left. 1,\cdots ,5\right)</math> (Figura 6 superior). |
En la metodología propuesta, los ''antecedentes'' de las reglas del tipo ''Si-Entonces ''los constituyen el número de amenazas (''m'') a considerar en la zona urbana a estudiar y sus respectivas valoraciones de nivel de riesgo físico <math display="inline">\left( {N}_{{RF}_{Hi}},\, \forall \, i=\right. </math><math>\left. 1,\cdots ,5\right)</math> . La consecuencia corresponde a una valoración del riesgo multiamenaza. | En la metodología propuesta, los ''antecedentes'' de las reglas del tipo ''Si-Entonces ''los constituyen el número de amenazas (''m'') a considerar en la zona urbana a estudiar y sus respectivas valoraciones de nivel de riesgo físico <math display="inline">\left( {N}_{{RF}_{Hi}},\, \forall \, i=\right. </math><math>\left. 1,\cdots ,5\right)</math> . La consecuencia corresponde a una valoración del riesgo multiamenaza. | ||
| − | El sistema de inferencia difuso adaptado en la metodología propuesta parte de los valores del cociente entre los valores de pertenencia definidos como los puntos de crossover (=0.5) para cada nivel de riesgo en los límites superiores. En la Tabla 3 pueden verse los valores de los cocientes para el caso de dos amenazas naturales. Estos cocientes sugieren de alguna manera las veces que un nivel inferior requiere ser multiplicado para lograr un nivel superior. Por ejemplo, el cociente entre el nivel N<sub>2</sub> y nivel N<sub>1</sub> es 9 (0.18/0.02 = 9), lo cual indica que el nivel N<sub>2</sub> es, aproximadamente, equivalente a 9 veces el nivel N<sub>1</sub>. | + | El sistema de inferencia difuso adaptado en la metodología propuesta parte de los valores del cociente entre los valores de pertenencia definidos como los puntos de crossover (<math display="inline">\alpha =0.5</math>) para cada nivel de riesgo en los límites superiores. En la Tabla 3 pueden verse los valores de los cocientes para el caso de dos amenazas naturales. Estos cocientes sugieren de alguna manera las veces que un nivel inferior requiere ser multiplicado para lograr un nivel superior. Por ejemplo, el cociente entre el nivel N<sub>2</sub> y nivel N<sub>1</sub> es 9 (0.18/0.02 = 9), lo cual indica que el nivel N<sub>2</sub> es, aproximadamente, equivalente a 9 veces el nivel N<sub>1</sub>. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> | ||
| Line 300: | Line 300: | ||
:* Se toma el centroide de la calificación de riesgo más bajo (Figura 6 superior) y se calcula su nivel de pertenencia en la función de la Figura 6 inferior. | :* Se toma el centroide de la calificación de riesgo más bajo (Figura 6 superior) y se calcula su nivel de pertenencia en la función de la Figura 6 inferior. | ||
| − | :* El valor calculado en el paso anterior se suma a los valores correspondientes a los extremos del intervalo de riesgo físico en el que se define el nivel más alto calificado. Los valores así resultantes se convierten a porcentajes de riesgo físico mediante la función de transformación (Figura 6 inferior) | + | :* El valor calculado en el paso anterior se suma a los valores correspondientes a los extremos del intervalo de riesgo físico en el que se define el nivel más alto calificado. Los valores así resultantes se convierten a porcentajes de riesgo físico mediante la función de transformación (Figura 6 inferior). |
Con los valores extremos del intervalo resultante en el paso anterior, se entra en la Figura 6 superior, este intervalo determina el criterio para definir la consecuencia de la regla. Este procedimiento se repite para las diferentes combinaciones de dos entradas de niveles de riesgo físico, obteniendo las consecuencias de la Tabla 4 de doble entrada, esta tabla puede encontrase en [26] para el caso de tres amenazas naturales. La salida de la regla <math display="inline">F(y)</math>, representa una variable difusa o un conjunto de éstas que permiten definir el nivel de riesgo físico resultante (Figura 8). | Con los valores extremos del intervalo resultante en el paso anterior, se entra en la Figura 6 superior, este intervalo determina el criterio para definir la consecuencia de la regla. Este procedimiento se repite para las diferentes combinaciones de dos entradas de niveles de riesgo físico, obteniendo las consecuencias de la Tabla 4 de doble entrada, esta tabla puede encontrase en [26] para el caso de tres amenazas naturales. La salida de la regla <math display="inline">F(y)</math>, representa una variable difusa o un conjunto de éstas que permiten definir el nivel de riesgo físico resultante (Figura 8). | ||
| − | En el proceso de inferencia se debe estimar el grado de disparo < | + | En el proceso de inferencia se debe estimar el grado de disparo <math display="inline">\tau_1</math> de cada regla (Figura 8) que en este caso se obtiene como el máximo grado o nivel de pertenencia, <math display="inline">\alpha_i</math> (''i=1,⋯,m''), con que cada experto califica el nivel de riesgo físico para las amenazas consideradas. |
<br/> | <br/> | ||
| Line 318: | Line 318: | ||
===3.3. Desfusificación=== | ===3.3. Desfusificación=== | ||
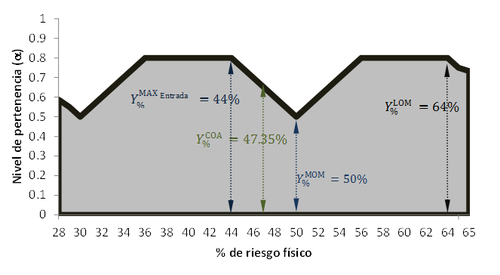
| − | Una vez obtenida la salida difusa, ''F(y)'', y el grado de disparo, se trunca el área definida en el intervalo de la salida por el valor de | + | Una vez obtenida la salida difusa, ''F(y)'', y el grado de disparo, <math display="inline">\tau</math>, se trunca el área definida en el intervalo de la salida por el valor de <math display="inline">\tau</math> y se realiza el proceso de desfusificación. Este proceso comprende dos etapas: en primer lugar, se obtiene la salida numérica expresada en porcentaje de riesgo físico, denominada <math display="inline">{{R}_{FmH}}^{\ast }</math>. El proceso de desfusificación considera como <math display="inline">{{R}_{FmH}}^{\ast }</math> el valor máximo entre los valores numéricos obtenidos a través de los métodos de desfusificación [29]: COA (''centroide of area''), MOM (''middle of maximum),'' LOM (''largest of máximum'') y el máximo valor del porcentaje de riesgo físico <math display="inline">{(\%R}_{FHi}</math>) que resulta de transformar las entradas de los expertos (<math display="inline">{R}_{FHi}</math>) (Ver ejemplo Figura 8). |
En segundo lugar, se transforma <math display="inline">{{R}_{FmH}}^{\ast }</math> a un valor numérico de riesgo físico mediante la función dada en la Figura 6, y así, obtener el índice de riesgo físico multiamenaza <math display="inline">\left( {R}_{FmH}\right)</math> . | En segundo lugar, se transforma <math display="inline">{{R}_{FmH}}^{\ast }</math> a un valor numérico de riesgo físico mediante la función dada en la Figura 6, y así, obtener el índice de riesgo físico multiamenaza <math display="inline">\left( {R}_{FmH}\right)</math> . | ||
| Line 335: | Line 335: | ||
Mérida, con una población de menos de 250 mil habitantes, es la capital del Estado de Mérida y del Municipio del Libertador. La ciudad está conformada por 12 de las 15 parroquias del municipio El Libertador: Arias, Milla, Osuna Rodríguez, Juan Rodríguez Suárez, Jacinto Plaza Lasso de Vega, Caracciolo Parra Pérez, Mariano Picón Salas and Antonio Spinetti Dini, El Llano, Sagrario and Domingo Peña. El estado de Mérida se encuentra dentro de una zona de alta sismicidad, definida como de alto peligro sísmico, zona 4 y 5 según la clasificación sísmica de la norma sismorresistente de Venezuela, la cual divide al país en siete zonas de diferente amenaza sísmica [32]. Por debajo de la ciudad pasa la mayor falla tectónica activa del occidente de Venezuela. La falla de Boconó que forma parte de la Placa Suramericana [33]. | Mérida, con una población de menos de 250 mil habitantes, es la capital del Estado de Mérida y del Municipio del Libertador. La ciudad está conformada por 12 de las 15 parroquias del municipio El Libertador: Arias, Milla, Osuna Rodríguez, Juan Rodríguez Suárez, Jacinto Plaza Lasso de Vega, Caracciolo Parra Pérez, Mariano Picón Salas and Antonio Spinetti Dini, El Llano, Sagrario and Domingo Peña. El estado de Mérida se encuentra dentro de una zona de alta sismicidad, definida como de alto peligro sísmico, zona 4 y 5 según la clasificación sísmica de la norma sismorresistente de Venezuela, la cual divide al país en siete zonas de diferente amenaza sísmica [32]. Por debajo de la ciudad pasa la mayor falla tectónica activa del occidente de Venezuela. La falla de Boconó que forma parte de la Placa Suramericana [33]. | ||
| − | La ciudad de Mérida puede verse afectada por diversas amenazas naturales, como la sísmica [22,34] y la amenaza debido a movimientos de ladera [35]. Para establecer el riesgo físico multiamenaza de la ciudad, debido a dos amenazas naturales: la sísmica (''H<sub>1</sub>'') y por movimientos de ladera (''H<sub>2</sub>''), se aplicó la metodología propuesta de evaluación del riesgo físico multiamenaza (''Hm''). Para ello, se emplearon encuestas realizadas a expertos locales que proporcionaron información de los diferentes niveles de daños físicos que afectarían los elementos expuestos | + | La ciudad de Mérida puede verse afectada por diversas amenazas naturales, como la sísmica [22,34] y la amenaza debido a movimientos de ladera [35]. Para establecer el riesgo físico multiamenaza de la ciudad, debido a dos amenazas naturales: la sísmica (''H<sub>1</sub>'') y por movimientos de ladera (''H<sub>2</sub>''), se aplicó la metodología propuesta de evaluación del riesgo físico multiamenaza (''Hm''). Para ello, se emplearon encuestas realizadas a expertos locales que proporcionaron información de los diferentes niveles de daños físicos que afectarían los elementos expuestos en las diferentes parroquias de la ciudad y el nivel de pertenencia (valor numérico comprendido en un rango de 0.5 a 1.0). Dicha información se procesó para establecer el nivel de riesgo físico debido a cada una de las dos amenazas naturales consideradas. |
| − | La Tabla 5 presenta los valores de nivel de riesgo sísmico identificados por los expertos para los tres tipos de afectación (daño predominante, afectación en la población y en líneas vitales) siguiendo los criterios de la Tabla 1; así como los resultados obtenidos para el riesgo sísmico para las parroquias de Mérida siguiendo el proceso explicado en la sección 2.2 de este artículo: un índice de riesgo físico RF, el nivel de riesgo correspondiente y el nivel de pertenencia a éste. Para la definición de la afectación en la población y en líneas vitales se tuvieron en cuenta además los criterios complementarios de la | + | La Tabla 5 presenta los valores de nivel de riesgo sísmico identificados por los expertos para los tres tipos de afectación (daño predominante, afectación en la población y en líneas vitales) siguiendo los criterios de la Tabla 1; así como los resultados obtenidos para el riesgo sísmico para las parroquias de Mérida siguiendo el proceso explicado en la sección 2.2 de este artículo: un índice de riesgo físico RF, el nivel de riesgo correspondiente y el nivel de pertenencia a éste. Para la definición de la afectación en la población y en líneas vitales se tuvieron en cuenta además los criterios complementarios de la Tabla 6. |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> | ||
| Line 577: | Line 577: | ||
|} | |} | ||
| − | Se calcula el riesgo multiamenaza para las parroquias de la ciudad de Mérida aplicando el sistema de inferencia propuesto tomando como base los niveles de riesgo sísmico y por movimiento de ladera, así como el nivel de pertenencia de cada uno ( | + | Se calcula el riesgo multiamenaza para las parroquias de la ciudad de Mérida aplicando el sistema de inferencia propuesto tomando como base los niveles de riesgo sísmico y por movimiento de ladera, así como el nivel de pertenencia de cada uno (Tabla 5 y Figura 10). La Figura 11 muestra para cada parroquia de la ciudad de Mérida el nivel de riesgo físico multiamenaza (sísmica y movimientos de ladera) y su respectivo nivel de pertenencia (valor numérico junto al nombre de la parroquia). Las parroquias que presentan el mayor nivel de riesgo físico multiamenaza (''nivel muy alto'') son aquellas que tenían al menos uno de los dos niveles de riesgo físico particular (H1 y H2) como muy alto, o cuando los niveles de riesgo físico de la amenaza sísmica y movimientos de ladera son nivel ''alto'' y ''medio'', respectivamente. |
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| Line 862: | Line 862: | ||
==Agradecimientos== | ==Agradecimientos== | ||
| − | + | Los autores agradecen el apoyo del Ministerio de Economía y Competitividad de España en los proyectos "Desprendimientos en escarpes rocosos: cualificación del riesgo y su prevención- RockRisk"(BIA2013-42582-P) y “Evaluación de la Vulnerabilidad y el Riesgo de Zonas Urbanas Expuestas a Amenazas Naturales y Antrópicas-EZUANA” (BIA2016-78544-R). | |
==Referencias== | ==Referencias== | ||
Latest revision as of 11:59, 7 July 2017
Resumen
Una zona urbana puede estar expuesta a diferentes amenazas naturales, para evaluar de forma conjunta el riesgo potencial ante éstas se ha desarrollado una metodología de evaluación cualitativa del riesgo físico multiamenaza utilizando un sistema de inferencia difuso, denominada MuHRA por sus siglas en inglés MUlti-Hazard physical Risk Assessment. Esta metodología se fundamenta en la teoría de conjuntos difusos y se apoya en información de encuestas a expertos en riesgos naturales, es aplicable a un máximo de tres amenazas naturales y utiliza cinco niveles de riesgo: muy bajo, bajo, medio, alto, muy alto. MuHRA considera que el riesgo físico en una zona urbana debido a una determinada amenaza debe dar cuenta de al menos tres afectaciones: daño predominante que varía con el tipo de amenaza; afectación de la población, y afectación en las líneas vitales. Dependiendo de la información disponible en la zona urbana a evaluar se establece el riesgo físico de cada amenaza particular, bien mediante una evaluación basada en la opinión de expertos o bien en una más detallada, que posteriormente se combinan y sintetizan en un único índice de riesgo físico multiamenaza (RFmh).
Para mostrar la aplicación de la metodología MuHRA se evaluó en la ciudad de Mérida-Venezuela el posible riesgo multiamenaza considerando tanto la amenaza sísmica como la amenaza por movimientos de ladera. Con esta aplicación se comprueba la versatilidad y robustez de la metodología, que puede adaptarse según la información disponible en cada caso de estudio.
Palabras claves: Riesgo multiamenaza, evaluación multiamenaza, conjuntos difusos, evaluación de riesgo de desastre, sistemas de inferencia difusos
Abstract
The urban areas may be exposed to different natural hazards; in order to jointly evaluate the potential risk, this article proposes a methodology for the qualitative assessment of the multi-hazard physical risk by using a fuzzy inference system called MuHRA by its abbreviations MUlti-Hazard Physical risk assessment. This methodology is based on the fuzzy sets theory and uses expert opinions. It is applicable to the risk evaluation involving a maximum of three natural hazards and uses five levels of risk: very low, low, medium, high and very high. The proposed methodology considers the physical risk in an urban area involving at least three potential effects: predominant damage that varies with the type of hazard; impact on the population, and damage in lifelines. According to the available information for the urban area to be assessed, the physical risk to a natural hazard can be evaluated, either through expert opinion or a more detailed assessment, and then they are combined and synthesized into a single multi-hazard physical risk index (RFmh).
The MuHRA methodology is applied to the multi-hazard risk evaluation for the city Merida-Venezuela considering both, the seismic hazard and the landslides. This application shows the versatility and robustness of the methodology, which can be adapted according to the information available in each case study.
1. Introducción
La evaluación del riesgo físico debido a diferentes amenazas naturales individuales proporciona información de gran importancia para las sociedades que debería ser incluida en el ordenamiento territorial, la planificación urbana (tanto en nuevas zonas urbanas como en las ya existentes) y la gestión del riesgo de desastres. Estas evaluaciones pretenden obtener resultados que sean de ayuda a la toma de decisiones en todos los niveles de gobierno (local, regional y nacional), proporcionando una base razonable para el desarrollo de planes y políticas de mitigación, preparación, respuesta y recuperación.
A nivel mundial, existen diferentes metodologías orientadas a la evaluación del riesgo físico en zonas urbanas debido a una amenaza determinada. En el caso de las amenazas sísmicas existen metodologías desarrolladas en Estados Unidos: el ATC-13 [1], RADIUS [2] y HAZUS [3]; en Europa: RISK-UE [4], LESSLOSS [5], SYNER-G [6], UPStrat-MAFA [7]; y a nivel internacional la fundación GEM (2014) [8] y la plataforma probabilista para la evaluación del riesgo de desastre CAPRA [9,10]
Sin embargo, muchas de estas zonas urbanas se encuentran amenazadas por diferentes tipos de eventos, que pueden ocurrir de forma individual o simultánea. En estos casos es necesaria una evaluación del riesgo dentro de un marco global que abarque todas las amenazas posibles. En estos casos en que se quiere evaluar el riesgo físico de zonas urbanas debido a diferentes amenazas naturales se cuenta con menos metodologías cuantitativas, debido a las diferentes características que presentan cada una y por tanto los diferentes métodos que requieren para su estudio. Chen et al (2016) [11] menciona una serie de metodologías de evaluación multiamenaza del riesgo a diferentes escalas de análisis desarrolladas en la última década. Entre ellas cabe destacar las metodologías numéricas propuestas en los proyectos Hazus-MH [3] y en CAPRA [10]. Concretamente, Hazus-MH cuenta con módulos de evaluación para el riesgo físico debido a amenazas naturales, como terremotos, inundaciones y huracanes. HAZUS-MH permite también incluir en la evaluación diferentes tipos de pérdidas y/o daños tanto directos como indirectos, según los alcances de cada modelo y amenaza (terremotos basándose en ATC-13[1], FEMA-154 [12], FEMA-155 [13], huracanes, inundaciones [3]).
CAPRA [10,14] es una metodología y una plataforma integrada por una serie de herramientas para la evaluación y comunicación de riesgo en diferentes niveles territoriales Este modelo permite la evaluación de pérdidas en elementos expuestos utilizando métricas probabilistas tales como la curva de probabilidad de excedencia, la pérdida anual esperada y la pérdida máxima probable; medidas útiles para análisis del riesgo multiamenaza involucrando amenazas naturales como huracanes, terremotos, actividad volcánica, inundaciones, tsunamis y deslizamientos del terreno.
La estimación del riesgo físico en una zona urbana, usando metodologías tradicionales basadas en el análisis numérico, es una tarea muy compleja y requiere gran cantidad de información que normalmente no está disponible. Los modelos lingüísticos de sistemas difusos, son la base para el modelado cualitativo capaz de describir el comportamiento de diferentes aspectos de sistemas usando un lenguaje natural. Asimismo, éstos se apoyan en reglas del tipo Si-Entonces, en mecanismos de razonamiento difuso, y las variables tienen etiquetas lingüísticas [15].
En tal sentido, este artículo propone una metodología versátil y alternativa para la evaluación multiamenaza del riesgo sísmico, basada en la teoría de conjuntos difusos, denominada MuHRA, por sus siglas en inglés Multi-Hazard physical Risk Assessment. Dicha metodología estima simultáneamente los daños físicos que pueden producirse por diferentes amenazas naturales, hasta un máximo de tres, y los sintetiza en un único nivel riesgo, al que puede asociarse un índice de riesgo físico multiamenaza ( ). Disponer de una estimación de riesgo que involucre múltiples amenazas puede resultar de gran utilidad para los responsables de la gestión del riesgo, ya que identifica de forma rápida y sencilla las áreas de la zona urbana que requieren un estudio más detallado.
MuHRA utiliza la opinión de expertos con amplia experiencia en la evaluación del riesgo en zonas urbanas bajo la acción de una amenaza particular y permite evaluar de forma más rápida el riesgo físico multiamenaza con un esfuerzo de cálculo menor respecto a las metodologías cuantitativas existentes. Especialmente en las zonas urbanas en que la información disponible es insuficiente para una evaluación numérica más completa. A continuación, se detallan fundamentos y aspectos esenciales de la metodología MuHRA propuesta.
2. Evaluación del riesgo físico debido a una amenaza natural
Carreño [16,17] desarrolló un método alternativo para la evaluación del riesgo urbano, a partir del modelo de Cardona [18], en donde el riesgo urbano se evalúa mediante indicadores compuestos o índices. La estimación de daños y pérdidas potenciales, obtenidas de diferentes escenarios de perdidas es la información básica para la evaluación de un índice de riesgo físico en cada unidad de análisis. El riesgo físico total, en este caso de origen sísmico, se calcula según la ecuación 1 mediante un índice denominado USRi (por sus siglas en inglés Urban Seismic Risk index):
|
donde RF es el índice de riesgo físico y F es el coeficiente de agravamiento. El índice de riesgo físico está relacionado con las pérdidas esperadas debido a la fragilidad de los elementos expuestos a la acción sísmica. El coeficiente de agravamiento F está relacionado con la capacidad socio-económica y de resiliencia de una comunidad expuesta. El riesgo físico se obtiene en la ecuación 2 como suma ponderada de unos factores de riesgo físico
|
siendo los coeficientes de ponderación de cada factor y p el número total de factores considerados para el riesgo físico. Los p coeficientes suman 1 y se determinan utilizando el Proceso Analítico Jerárquico (PAJ) [19]. Los factores de riesgo dependen de la información disponible (descriptores) referente a evaluación de potenciales perdidas (humanas, económicas o daño físico en diferentes tipos de estructuras e infraestructuras).
La metodología propuesta en este artículo parte del cálculo de un índice de riesgo físico debido a una posible amenaza natural Hi . Según las evaluaciones de riesgo disponibles es posible que los factores de riesgo se basen en valores numéricos resultantes de dichas evaluaciones o que sea necesario recurrir a la opinión de expertos.
2.1. Evaluación con base en resultados numéricos de evaluaciones de riesgo
Existen diferentes metodologías para la evaluación del riesgo, definido como las pérdidas potenciales en elementos expuestos debido a una amenaza natural, ellas pueden ser deterministas o probabilistas según el enfoque que utilicen. Para una amenaza sísmica podrían usarse metodologías como las propuestas en HAZUS [3], ATC-13 [1], PAHO [20], en RISKUE [4] y CAPRA [9,10], entre otras. Estas metodologías pueden evaluar el riesgo en términos de la proporción de daños potencial en los elementos expuestos (un edificio o conjunto de éstos, hospitales, líneas vitales, población humana, entre otros), así como también utilizando métricas probabilistas como la prima pura de riesgo (Pure Premium Rate).
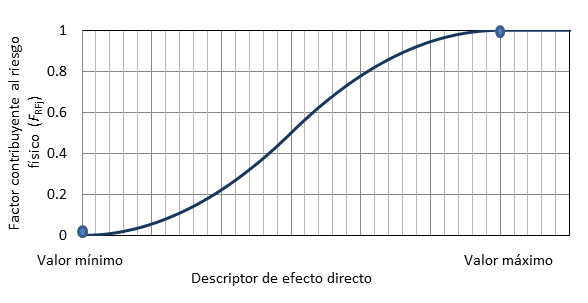
Basándose en los resultados obtenidos con las metodologías anteriores se estandariza el valor bruto de los descriptores de riesgo mediante funciones de transformación que los convierten en valores conmensurables y que tienen el patrón que se muestra en la Figura 1. Con estas funciones se calculan los factores de riesgo físico, FRFj, a partir de sus correspondientes descriptores. Más información sobre esta metodología puede consultarse en [17,21,22].
| Figura 1. Función de transformación de un indicador de daño físico. |
El uso de una determinada representación de los indicadores de efectos directos en los elementos expuestos a una amenaza natural está sujeto, entre otros a: la disponibilidad de información existente de la zona, el juicio del valor de los expertos evaluadores del riesgo físico, la exactitud y la precisión que se desee alcanzar. Sin embargo, independientemente de la representación que se emplee, en una evaluación numérica del riesgo físico, se utilizan funciones de transformación para obtener los factores contribuyentes del riesgo físico a partir de los descriptores de los posibles efectos directos que se esperan.
Esta metodología ha sido utilizada en la evaluación del riesgo para diferentes zonas urbanas como: Barcelona, España [22,23,24]; Bogotá y Medellín, Colombia [17,25]; y Mérida, Venezuela [22,26], entre otras.
2.2. Evaluación con base en opinión de expertos
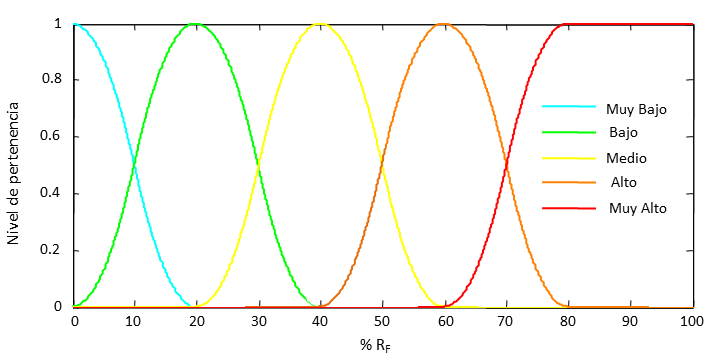
Los efectos directos pueden estimarse mediante la opinión de expertos que tengan una amplia experiencia en relación con el riesgo en la zona urbana bajo la acción de una amenaza particular. En este tipo de evaluación se utilizan calificaciones lingüísticas para definir niveles tanto de daño potencial como de riesgo físico [27,28]. Los niveles de daño de los diferentes efectos directos esperados tienen correspondencia con un conjunto difuso de factores contribuyentes al riesgo. En la Figura 2 se muestran cinco funciones de pertenencia de los niveles para los factores contribuyentes al riesgo, los cuales son: muy bajo, bajo, medio, alto y muy alto. El nivel de pertenencia toma valores entre 0 y 1, siendo: 1, la certeza absoluta, mientras que 0 índica certeza nula.
 |center|600px]] |center|600px]]
|
| Figura 2. Conjuntos difusos de los factores contribuyentes de riesgo físico. |
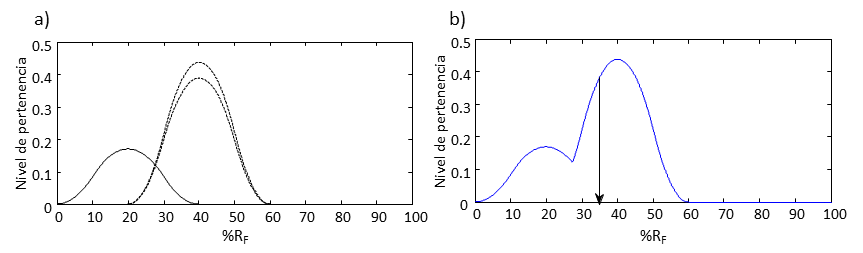
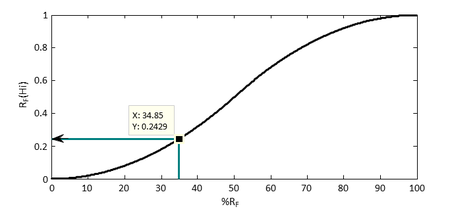
Mediante la aplicación de operaciones de conjuntos difusos y la ecuación 1 se obtiene el riesgo físico debido a la amenaza . Para lo cual, se asigna un peso de participación a cada factor asociado al descriptor de riesgo físico (efecto directo) establecido, mediante el Proceso Analítico Jerárquico (PAJ). Mediante la opinión de expertos se establece el nivel de daño de los diferentes factores contribuyentes al riesgo para el efecto directo seleccionado. Luego, se multiplica cada función de pertenencia del factor contribuyente al riesgo por su peso de participación (ver ejemplo para tres factores contribuyentes en figura 3). Posteriormente, se obtiene la envolvente de las funciones de pertenencia resultantes, para establecer el centroide del área resultante, que permite establecer el % de riesgo físico (%RF) (ver ejemplo con valor 34.84% en Figura 3) y a través de la función de transformación planteada se transforma el valor de %RF a valor numérico de riesgo (RF=0.2429 en el ejemplo de la Figura 4). Y así se obtiene el valor numérico de riesgo físico debido a la amenaza .
| Figura 3. Operaciones de conjuntos difusos para obtener del valor numérico de porcentaje de riesgo físico, RF: (izquierda) funciones de pertenencia de tres factores contribuyentes al riesgo y (derecha) obtención del valor del centroide del área de la función envolvente (34.84%). |
|
| Figura 4. Función de transformación del % RF a valor numérico de riesgo físico para la amenaza Hi. |
Con este valor de porcentaje de riesgo físico se puede obtener el nivel de riesgo correspondiente de entre los cinco establecidos en la Figura 2, buscando la función en la que tiene mayor pertenencia.
3. Metodología propuesta de evaluación del riesgo multiamenaza
La metodología que se propone para la evaluación multiamenaza del riesgo (de hasta tres amenazas naturales) denominada MuHRA, está basada en la teoría de conjuntos difusos y utiliza la opinión de expertos basándose en 5 calificaciones lingüísticas que son: muy bajo, bajo, medio, alto y muy alto.
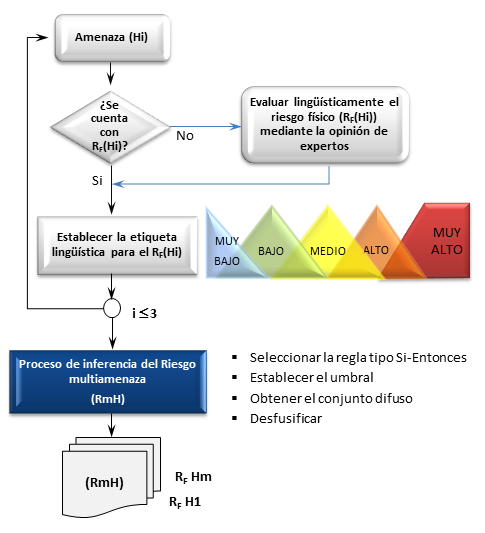
Para aplicar la metodología propuesta, en una zona urbana determinada, se deben seguir los siguientes pasos (ver Figura 5):
- Identificar las amenazas naturales que pueden afectar a dicha zona (Hi con .
- Obtener información de los niveles de riesgo físico y de pertenencia para la ponderación de dichos niveles con base en estudios existentes o, de ser necesario, con la opinión de expertos en evaluación del riesgo físico debido a cada amenaza natural considerada. En caso de contar con varias y diferentes opiniones por amenaza, se ponderan éstas para tener un solo nivel de riesgo físico promedio y un nivel de pertenencia promedio por amenaza; dichos valores representan las variables de entrada de la metodología: con .
- Esta información de entrada se procesa mediante el uso de un mecanismo de inferencia difusa aplicable a modelos lingüísticos, utilizando reglas del tipo Si-Entonces del tipo Mamdani.
- Finalmente, a partir de los conjuntos difusos resultantes, se obtiene el valor numérico del riesgo físico multiamenaza mediante un proceso de desfusificación.
| Figura 5. Flujo de trabajo de aplicación de la metodología MuHRA. |
3.1. Criterio de evaluación lingüística del riesgo físico
Al igual que otros autores [16,17,18], la metodología MuHRA considera que el riesgo físico para los casos en los que se considera una sola amenaza natural cualquiera, es estimado como la suma ponderada de diferentes factores mensurables de riesgo físico , y éstos a su vez, dependen de descriptores asociados a los daños físicos que se generan por la amenaza natural en la zona urbana a estudiar. En forma general, dichos descriptores se transforman a factores mensurables de riesgo físico , mediante funciones de transformación como se indica en la sección 2.1 [22].
Dependiendo de la información disponible en la zona urbana a estudiar, el riesgo físico debido a una determinada amenaza natural , se puede estimar mediante una evaluación numérica, o mediante una evaluación basada en la opinión de expertos locales en las diferentes amenazas .
En la evaluación basada en la opinión de expertos es necesario informar a los encuestados sobre la evaluación que se espera realizar de modo que sus respuestas tengan mayor grado de pertenencia en el nivel de riesgo que éstos seleccionen. Los expertos en una determinada amenaza natural, suministraran las calificaciones lingüísticas correspondientes a las tres afectaciones que debe dar cuenta el riesgo físico, , (daño predominante en edificios, que varía con la amenaza, afectación en la población, y afectación en las líneas vitales) basándose en las cinco calificaciones lingüísticas establecidas: muy bajo (N1), bajo (N2), medio (N3), alto (N4) y muy alto (N5) (Tabla 1). Posteriormente, dicha información suministrada se procesa, utilizando la teoría de conjuntos difusos, para estimar el posible nivel de ; mediante un proceso de desfusificación, el valor numérico del riesgo físico debido a la amenaza natural , el cual debe tener un nivel de pertenencia mayor o igual a 0.50.
| Descriptores de riesgo físico | ||||
| Niveles
|
Daño predominante (área destruida)
|
Afectación en la población
|
Afectación en la infraestructura de las líneas vitales | |
| Muy bajo
(N1) |
< 2% del área construida. | < 4% de la población. | <5% de la infraestructura. Daños mínimos, localizados en algunos elementos que normalmente no necesitan reparación para mantener su operatividad | |
| Bajo
(N2) |
Del 2% a 6% del área construida | Del 4% al 13% de la población | Del 5% al 15% de la infraestructura. Daños significativos localizados en bastantes elementos, que deben repararse. | |
| Medio
(N3) |
Del 6% a 10%º del área construida. | Del 13% al 21 de la población. | Del 15% al 25% de la infraestructura. Daños generales, es necesario efectuar reparaciones importantes. | |
| Alto
(N4) |
Del 10% a 14% del área construida. | Del 21% al 30 de la población. | Del 25% al 35% de la infraestructura. Daños graves que pueden interrumpir la operatividad de los elementos. Se deben reparar, sustituir o derribar. | |
| Muy Alto
(N5) |
> 14% del área construida | >30% de la población | >35% de la infraestructura, Daños muy graves, destrucción de elementos e inutilidad total de las líneas vitales. | |
Teniendo en cuenta que, numéricamente, el índice de riesgo físico, así como sus factores contribuyentes, pueden variar entre cero y uno, se definen cinco calificaciones lingüísticas, en las que, por comodidad de manipulación, su dominio se expresa en %RF. Así el valor numérico de riesgo físico estará asociado a un % de riesgo, y con ese porcentaje se entra en el dominio del criterio establecido para los niveles de riesgo y se selecciona el nivel que presente mayor nivel de pertenencia.
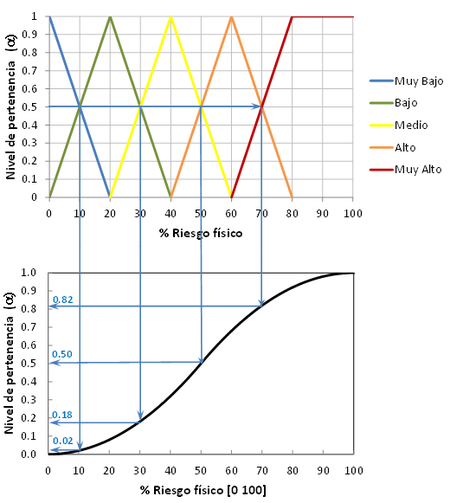
Se definen las funciones de pertenencia en un rango entre 0% y 100% para los 5 niveles de riesgo preestablecidos marcando como puntos de cruce (crossover) 10%, 30%, 50% y 70% (puntos con en la Figura 6 superior). Por otro lado, se tiene una función de trasformación genérica tipo S entre 0 y 100% como puntos mínimo y máximo respectivamente (Figura 6 inferior). Los grados de pertenencia para los porcentajes marcados como puntos de cruce servirán para definir los niveles de riesgo para los diferentes componentes (0.02, 0.18, 0.50, 0.82 y 1.0 en la Figura 6 inferior).
|
| Figura 6. Definición de rangos de los niveles de riesgo para una función de transformación. |
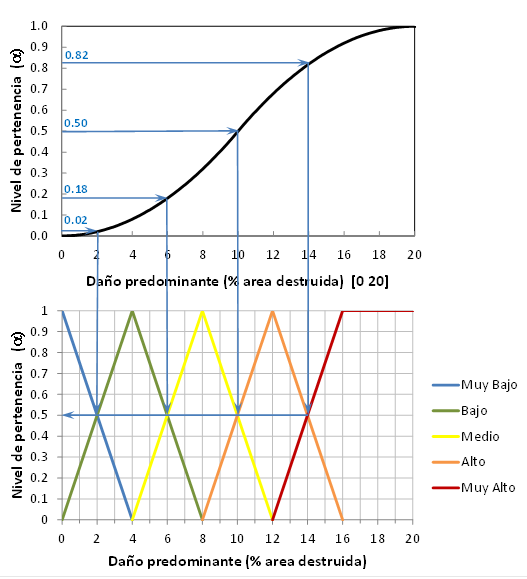
La Figura 7 presenta un ejemplo de la definición de niveles de riesgo para el caso de daño predominante, que utiliza la función de trasformación para área destruida utilizada por [22]. Las definiciones de los niveles de riesgo de la Tabla 1 se basan en análisis similares utilizando las funciones de trasformación definidas por los parámetros de la Tabla 2, las cuales fueron construidas con base en opinión de expertos y propuestas por [17,22].
|
| Figura 7. Rangos definidos para los niveles de riesgo correspondientes al daño predominante. |
| Descriptor de riesgo físico | Xmin | Xmax |
| Área destruida | 0% | 20% |
| Afectación a la población | 0% | 425 por cada 1000 habitantes |
| Afectación líneas vitales | 0% | 50% |
3.2. Mecanismo de Inferencia
En el proceso de inferencia es indispensable establecer reglas del tipo Si-entonces, las cuales dependen de la naturaleza del problema a resolver. Las reglas son estructuras lógicas de decisión que permiten, entre otras cosas, transformar unos “valores” de entrada conocidos como antecedentes que son premisas o condiciones que han de cumplirse, en un “valor” de salida el cual se denomina consecuencia. La metodología propuesta utiliza un proceso de inferencia en el que las reglas que se emplean tienen una estructura lógica de múltiples entradas y una única salida, denominado modelo tipo MISO (Multiple Input-Simple Output). Concretamente, las entradas que deben cumplirse, son los niveles de riesgo físico suministrados para cada amenaza natural (Hi) con i=1…m, siendo m el número total de amenazas a considerar; y la variable lingüística que define el posible nivel de riesgo físico de entre los cinco niveles propuestos (Figura 6 superior).
En la metodología propuesta, los antecedentes de las reglas del tipo Si-Entonces los constituyen el número de amenazas (m) a considerar en la zona urbana a estudiar y sus respectivas valoraciones de nivel de riesgo físico . La consecuencia corresponde a una valoración del riesgo multiamenaza.
El sistema de inferencia difuso adaptado en la metodología propuesta parte de los valores del cociente entre los valores de pertenencia definidos como los puntos de crossover () para cada nivel de riesgo en los límites superiores. En la Tabla 3 pueden verse los valores de los cocientes para el caso de dos amenazas naturales. Estos cocientes sugieren de alguna manera las veces que un nivel inferior requiere ser multiplicado para lograr un nivel superior. Por ejemplo, el cociente entre el nivel N2 y nivel N1 es 9 (0.18/0.02 = 9), lo cual indica que el nivel N2 es, aproximadamente, equivalente a 9 veces el nivel N1.
| Muy bajo (N1) | Bajo (N2) | Medio (N3) | Alto (N4) | Muy Alto (N5) | |
| Muy bajo (N1) | 1 | 0.11 | 0.04 | 0.02 | 0.02 |
| Bajo (N2) | 9 | 1.00 | 0.36 | 0.22 | 0.18 |
| Medio (N3) | 25 | 2.78 | 1.00 | 0.61 | 0.50 |
| Alto (N4) | 41 | 4.56 | 1.64 | 1.00 | 0.82 |
| Muy alto (N5) | 50 | 5.56 | 2.00 | 1.22 | 1 |
Partiendo del cociente mencionado se definen 2 posibles casos:
- 1. Si el cociente toma un valor menor o igual a 1/3, o mayor o igual a 3 (celdas en gris de la Tabla 3), se toma como consecuencia el nivel superior de riesgo físico.
- 2. En caso de que el cociente tenga un valor entre 1/3 y 3 (celdas en blanco en la Tabla 3), la consecuencia se obtiene mediante contribuciones de las distintas variables lingüísticas del nivel de riesgo físico. En el este caso, el sistema de inferencia sigue el siguiente procedimiento:
- Se ordenan ascendentemente los niveles de riesgo físico para las diferentes amenazas incluidas en la evaluación.
- Se toma el centroide de la calificación de riesgo más bajo (Figura 6 superior) y se calcula su nivel de pertenencia en la función de la Figura 6 inferior.
- El valor calculado en el paso anterior se suma a los valores correspondientes a los extremos del intervalo de riesgo físico en el que se define el nivel más alto calificado. Los valores así resultantes se convierten a porcentajes de riesgo físico mediante la función de transformación (Figura 6 inferior).
Con los valores extremos del intervalo resultante en el paso anterior, se entra en la Figura 6 superior, este intervalo determina el criterio para definir la consecuencia de la regla. Este procedimiento se repite para las diferentes combinaciones de dos entradas de niveles de riesgo físico, obteniendo las consecuencias de la Tabla 4 de doble entrada, esta tabla puede encontrase en [26] para el caso de tres amenazas naturales. La salida de la regla , representa una variable difusa o un conjunto de éstas que permiten definir el nivel de riesgo físico resultante (Figura 8).
En el proceso de inferencia se debe estimar el grado de disparo de cada regla (Figura 8) que en este caso se obtiene como el máximo grado o nivel de pertenencia, (i=1,⋯,m), con que cada experto califica el nivel de riesgo físico para las amenazas consideradas.
|
3.3. Desfusificación
Una vez obtenida la salida difusa, F(y), y el grado de disparo, , se trunca el área definida en el intervalo de la salida por el valor de y se realiza el proceso de desfusificación. Este proceso comprende dos etapas: en primer lugar, se obtiene la salida numérica expresada en porcentaje de riesgo físico, denominada . El proceso de desfusificación considera como el valor máximo entre los valores numéricos obtenidos a través de los métodos de desfusificación [29]: COA (centroide of area), MOM (middle of maximum), LOM (largest of máximum) y el máximo valor del porcentaje de riesgo físico ) que resulta de transformar las entradas de los expertos () (Ver ejemplo Figura 8).
En segundo lugar, se transforma a un valor numérico de riesgo físico mediante la función dada en la Figura 6, y así, obtener el índice de riesgo físico multiamenaza .
|
| Figura 8. Salida difusa F(y) del nivel de riesgo físico (área gris) y las salidas numéricas de porcentaje de riesgo físico, desfusificados (flechas verticales). |
4. Aplicación a la ciudad de Mérida-Venezuela
La ciudad de Mérida se encuentra en la parte noroeste de Venezuela, ubicada en la parte central de la cordillera andina venezolana. Está asentada sobre una meseta alargada dentro de un valle aluvial (sedimentos cuaternarios), limitada por dos cordilleras: la Sierra Nevada al sureste, y la Sierra de la Culata al Noroeste y atravesada por los ríos Albarregas y Chama [30,31].
Mérida, con una población de menos de 250 mil habitantes, es la capital del Estado de Mérida y del Municipio del Libertador. La ciudad está conformada por 12 de las 15 parroquias del municipio El Libertador: Arias, Milla, Osuna Rodríguez, Juan Rodríguez Suárez, Jacinto Plaza Lasso de Vega, Caracciolo Parra Pérez, Mariano Picón Salas and Antonio Spinetti Dini, El Llano, Sagrario and Domingo Peña. El estado de Mérida se encuentra dentro de una zona de alta sismicidad, definida como de alto peligro sísmico, zona 4 y 5 según la clasificación sísmica de la norma sismorresistente de Venezuela, la cual divide al país en siete zonas de diferente amenaza sísmica [32]. Por debajo de la ciudad pasa la mayor falla tectónica activa del occidente de Venezuela. La falla de Boconó que forma parte de la Placa Suramericana [33].
La ciudad de Mérida puede verse afectada por diversas amenazas naturales, como la sísmica [22,34] y la amenaza debido a movimientos de ladera [35]. Para establecer el riesgo físico multiamenaza de la ciudad, debido a dos amenazas naturales: la sísmica (H1) y por movimientos de ladera (H2), se aplicó la metodología propuesta de evaluación del riesgo físico multiamenaza (Hm). Para ello, se emplearon encuestas realizadas a expertos locales que proporcionaron información de los diferentes niveles de daños físicos que afectarían los elementos expuestos en las diferentes parroquias de la ciudad y el nivel de pertenencia (valor numérico comprendido en un rango de 0.5 a 1.0). Dicha información se procesó para establecer el nivel de riesgo físico debido a cada una de las dos amenazas naturales consideradas.
La Tabla 5 presenta los valores de nivel de riesgo sísmico identificados por los expertos para los tres tipos de afectación (daño predominante, afectación en la población y en líneas vitales) siguiendo los criterios de la Tabla 1; así como los resultados obtenidos para el riesgo sísmico para las parroquias de Mérida siguiendo el proceso explicado en la sección 2.2 de este artículo: un índice de riesgo físico RF, el nivel de riesgo correspondiente y el nivel de pertenencia a éste. Para la definición de la afectación en la población y en líneas vitales se tuvieron en cuenta además los criterios complementarios de la Tabla 6.
| Parroquia | Daño predominante | Afectación en la población | Afectación en líneas vitales | %RF | RF | Nivel de riesgo | Pertenencia |
| Antonio Spinetti Dini | 5 | 5 | 3 | 75.565 | 0.881 | Muy alto | 0.90 |
| Arias | 5 | 5 | 5 | 84.725 | 0.953 | Muy alto | 1.00 |
| Caracciolo Parra Pérez | 3 | 2 | 2 | 29.329 | 0.172 | Bajo | 0.57 |
| Domingo Peña | 3 | 4 | 5 | 58.695 | 0.659 | Alto | 0.99 |
| El Llano | 3 | 2 | 3 | 29.329 | 0.172 | Bajo | 0.57 |
| Jacinto Plaza | 5 | 5 | 4 | 80.248 | 0.922 | Muy alto | 1.00 |
| Juan Rodríguez Suárez | 4 | 3 | 4 | 49.329 | 0.487 | Medio | 0.57 |
| Lasso de la Vega | 3 | 2 | 3 | 29.329 | 0.172 | Bajo | 0.57 |
| Mariano Picón Salas | 3 | 4 | 4 | 50.671 | 0.513 | Alto | 0.57 |
| Milla | 4 | 3 | 5 | 57.678 | 0.642 | Alto | 0.97 |
| Osuna Rodríguez | 3 | 5 | 3 | 68.114 | 0.797 | Alto | 0.67 |
| Sagrario | 3 | 4 | 5 | 58.695 | 0.659 | Alto | 0.99 |
| Peso | 0.39 | 0.44 | 0.17 | - | - | - | - |
| Descriptores de riesgo físico | ||
| Niveles | Afectación en la población | Afectación en las líneas vitales |
| Muy bajo
(N1) |
< 4% de la población
Contempla (en ‰): fallecidos (<5), heridos (< 7), personas sin hogar (< 30). |
<5% de la infraestructura.
Sistema de tuberías de agua potable: 0 a 1 rotura por km. |
| Bajo
(N2) |
Del 4% al 13% de la población
Contempla (en ‰): fallecidos (5 a 15), heridos (7 a 23), personas sin hogar (30 a 90). |
Del 5% al 15% de la infraestructura.
Sistema de tuberías de agua potable: 1 a 3 roturas por km |
| Medio
(N3) |
Del 13% al 21 de la población
Contempla (en ‰): fallecidos (15 a 25), heridos (23 a 38), personas sin hogar (90 a 150) |
Del 15% al 25% de la infraestructura.
Sistema de tuberías de agua potable: 3 a 5 roturas por km. |
| Alto
(N4) |
Del 21% al 30 de la población
Contempla (en ‰): fallecidos (25 a 35), heridos (38 a 53), personas sin hogar (150 a 210). |
Del 25% al 35% de la infraestructura.
Sistema de tuberías de agua potable: 5 a 7 roturas por km. |
| Muy Alto
(N5) |
>30% de la población
Contempla (en ‰): fallecidos (>35), heridos (>53), persona sin hogar (>210). |
>35% de la infraestructura,
Sistema de tuberías de agua potable: más de 7 roturas por km. |
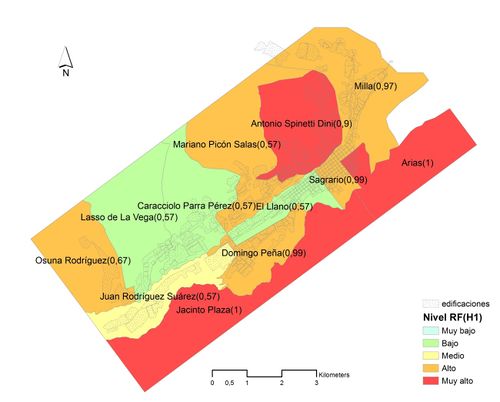
En la Figura 9 se muestra para cada parroquia de la ciudad de Mérida tanto el nivel de riesgo físico sísmico como el nivel de pertenencia a dicho nivel (dos últimas columnas de la Tabla 5).
|
| Figura 9. Riesgo físico sísmico y valor de pertenencia para cada parroquia en valor numérico (evaluación basada en opinión de expertos). |
La respuesta de los expertos en relación a las amenazas como movimientos de ladera es difícil de realizar por divisiones administrativas, ya que dichos eventos se producen en zonas del territorio que pueden afectar de forma muy diferente a las edificaciones de una misma parroquia en función de su cercanía a dicho evento. Por ello, para el caso de riesgo por movimientos de ladera, los expertos consultados calificaron el nivel de riesgo para diferentes sectores de la ciudad identificados geomorfológicamente. Posteriormente se calculó un nivel medio de riesgo para cada parroquia (Figura 10) ponderando los diferentes niveles de riesgo físico calificados, en función del porcentaje de su área para cada una de las parroquias.
Las zonas que presentan mayor nivel de riesgo físico a movimientos de ladera se encuentran en la parroquia Jacinto Plaza y el gran sub-sector denominado la otra banda al norte del río Albarregas. Estos resultados son coherentes con las zonas identificadas como susceptibles a movimientos de ladera en el mapa de susceptibilidad propuesto por Ramírez y Saito [35].
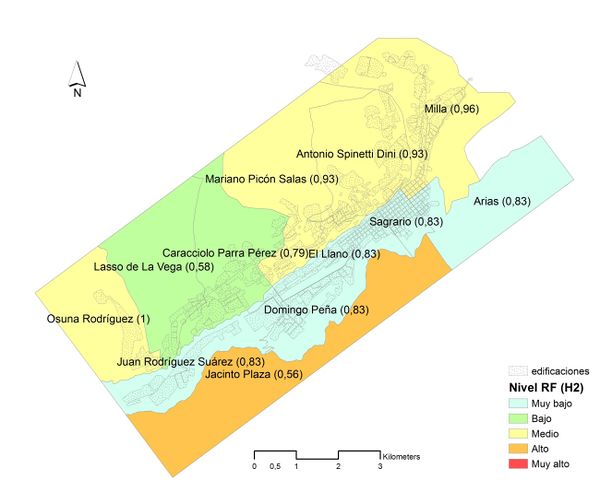
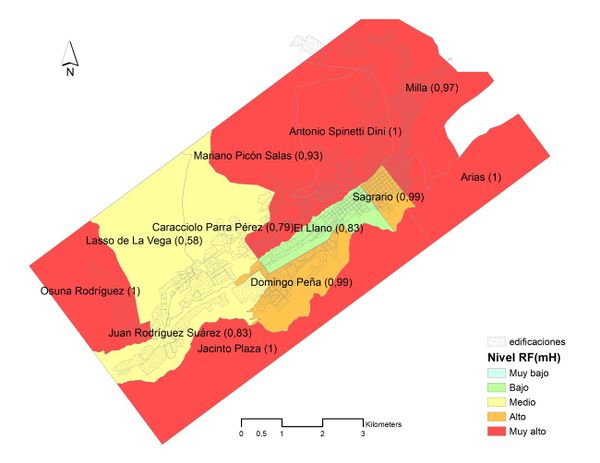
Se calcula el riesgo multiamenaza para las parroquias de la ciudad de Mérida aplicando el sistema de inferencia propuesto tomando como base los niveles de riesgo sísmico y por movimiento de ladera, así como el nivel de pertenencia de cada uno (Tabla 5 y Figura 10). La Figura 11 muestra para cada parroquia de la ciudad de Mérida el nivel de riesgo físico multiamenaza (sísmica y movimientos de ladera) y su respectivo nivel de pertenencia (valor numérico junto al nombre de la parroquia). Las parroquias que presentan el mayor nivel de riesgo físico multiamenaza (nivel muy alto) son aquellas que tenían al menos uno de los dos niveles de riesgo físico particular (H1 y H2) como muy alto, o cuando los niveles de riesgo físico de la amenaza sísmica y movimientos de ladera son nivel alto y medio, respectivamente.
|
| Figura 11. Riesgo físico multiamenaza y valor de pertenencia para cada parroquia en valor numérico (evaluación con opinión de expertos). |
En la Tabla 7 se presenta los resultados de la evaluación lingüística del riesgo físico, mostrando el nivel de riesgo físico para cada parroquia de la ciudad, y su respectivo nivel de pertenencia , tanto para una amenaza sísmica (H1), como para la amenaza movimientos de ladera (H2) y multiamenaza (mH). Se observa que, en general el riesgo físico multiamenaza presenta un nivel de riesgo físico mayor o igual al mayor nivel de riesgo físico particular de las amenazas naturales H1 y H2. Las parroquias con nivel muy alto de riesgo físico para cualquiera de las dos amenazas naturales (H1 y H2) presentan igual nivel para el riesgo físico multiamenaza.
Se sube un nivel de riesgo físico multiamenaza cuando el riesgo físico particular de las amenazas H1 y H2 es igual al nivel 2 (Caracciolo Parra y Lasso de la Vega presentan un nivel 3 en el ) o cuando los niveles de riesgo físico particulares de las amenazas H1 y H2 son nivel 4 y nivel 3, respectivamente (Mariano Picón Salas, Milla y Osuna Rodríguez presentan un nivel 5 en el RF (mH)).
Por otra parte se evidencia que en algunas parroquias de la ciudad el nivel de riesgo físico debido a movimientos de ladera no altera el nivel de riesgo físico sísmico, cuando se consideran ambos amenazas naturales; así que, la amenaza sísmica generará el mayor riesgo físico en las parroquias: Arias1, Domingo Peña, El Llano, Juan Rodríguez Suárez y Sagrario.
| Zonas urbanas de la ciudad de Mérida |
Evaluación lingüística del riesgo físico debido a: | |||||
| Amenaza Sísmica (H1) |
Movimientos de ladera (H2) |
Multiamenaza H1 y H2 (mH) | ||||
| Parroquia | Nivel RF (H1) |
Pertenencia α |
Nivel RF (H2) |
Pertenencia α |
Nivel RF (mH) |
Pertenencia α |
| Antonio Spinetti Dini | 5 | 0.90 | 3 | 0.93 | 5 | 1.00 |
| Arias | 5 | 1.00 | 1 | 0.83 | 5 | 1.00 |
| Caracciolo Parra Pérez | 2 | 0.57 | 2 | 0.79 | 3 | 0.79 |
| Domingo Peña | 4 | 0.99 | 1 | 0.83 | 4 | 0.99 |
| El Llano | 2 | 0.57 | 1 | 0.83 | 2 | 0.83 |
| Jacinto Plaza | 5 | 1.00 | 4 | 0.56 | 5 | 1.00 |
| Juan Rodríguez Suárez | 3 | 0.57 | 1 | 0.83 | 3 | 0.83 |
| Lasso de la Vega | 2 | 0.57 | 2 | 0.58 | 3 | 0.58 |
| Mariano Picón Salas | 4 | 0.57 | 3 | 0.93 | 5 | 0.93 |
| Milla | 4 | 0.97 | 3 | 0.96 | 5 | 0.97 |
| Osuna Rodríguez | 4 | 0.67 | 3 | 1.00 | 5 | 1.00 |
| Sagrario | 4 | 0.99 | 1 | 0.83 | 4 | 0.99 |
5. Comparación teniendo en cuenta evaluaciones más completas
Para el caso del riesgo sísmico en Mérida, se cuenta con una evaluación previa, realizada por los autores, que no está basada en la opinión de expertos. El riesgo sísmico de la ciudad es estudiado teniendo en cuenta dos intensidades macro sísmicas (VI y IX), completando la evaluación realizada por Castillo [34,36], y siguiendo las metodologías de HAZUS-99 [22,26]. La evaluación de Jaramilo et al [22] no incluye a la parroquia Jacinto Plaza, de la cual no se contaba con información suficiente sobre la tipología estructural existente. En esta sección se presenta una evaluación de riesgo multiamenaza que tiene en cuenta los niveles de riesgo sísmico resultantes de [22] (sismo intensidad IX) y la evaluación de riesgo por movimientos de ladera con base en opinión de expertos incluida en la sección anterior.
Tomando como base la evaluación de riesgo sísmico mencionada [22], se obtuvo un nivel de riesgo sísmico y la pertenencia al mismo para cada una de las parroquias de la ciudad teniendo en cuenta los niveles definidos en la figura 6a. La Tabla 8 presenta también los resultados obtenidos para el riesgo multiamenaza aplicando la metodología propuesta. Excepto, en el caso de la parroquia Jacinto Plaza para la cual no se dispone de una evaluación detallada del riesgo sísmico.
| Riesgo sísmico
(Intensidad IX) |
Riesgo por Movimiento de ladera | RIESGO
MULTIAMENAZA | ||||
| Parroquia | Nivel | Pertenencia | Nivel | Pertenencia | Nivel | Pertenencia |
| Antonio Spinetti Dini | 4 | 0.67 | 3 | 0.93 | 5 | 0.93 |
| Arias | 5 | 0.56 | 1 | 0.83 | 5 | 1.00 |
| Caracciolo Parra Pérez | 4 | 0.84 | 2 | 0.79 | 4 | 1.00 |
| Domingo Peña | 5 | 0.88 | 1 | 0.83 | 5 | 1.00 |
| El Llano | 5 | 0.64 | 1 | 0.83 | 5 | 1.00 |
| Jacinto Plaza | - | - | 4 | 0.56 | - | - |
| Juan Rodríguez Suárez | 2 | 0.62 | 1 | 0.83 | 2 | 1.00 |
| Lasso de la Vega | 2 | 0.78 | 2 | 0.58 | 3 | 0.78 |
| Mariano Picón Salas | 2 | 0.75 | 3 | 0.93 | 4 | 0.93 |
| Milla | 5 | 0.75 | 3 | 0.96 | 5 | 1.00 |
| Osuna Rodríguez | 4 | 0.65 | 3 | 1.00 | 5 | 1.00 |
| Sagrario | 5 | 0.88 | 1 | 0.83 | 5 | 1.00 |
La aplicación de la metodología teniendo en cuenta las dos evaluaciones de riesgo físico obtiene resultados coherentes en ambos casos con los niveles de riesgo de las amenazas individuales. Comparando los resultados obtenidos en las Tablas 7 y 8 se observan lo siguiente:
Las dos evaluaciones presentan los mismos resultados para el nivel de riesgo multiamenza en 6 parroquias de la ciudad. Tres de ellas (Arias, Lasso de la Vega y Osuna Rodríguez) presentaban el mismo nivel de riesgo sísmico en las dos evaluaciones. Las tres restantes (Antonio Spinetti Dini, Milla y Osuna Rodriguez) presentaron el mismo nivel de riesgo multiamenza a pesar de que el nivel de riesgo sísmico en la evaluación detallada varía un nivel con respecto a la obtenida con la opinión de expertos. Las parroquias Antonio Spinetti Dini, Arias, Milla y Osuna Rodríguez mantienen en nivel muy alto de riesgo multiamenaza en las dos evaluaciones.
Los resultados entre las dos evaluaciones varían en un nivel el riesgo multiamenaza para las parroquias Caracciolo Parra Pérez, Domingo Peña, Juan Rodríguez Suarez, Mariano Picón Salas y Sagrario.
La parroquia Caracciolo Parra Pérez pasa de un nivel de riesgo multiamenaza medio con la opinión de expertos a un nivel alto cuando se tiene en cuenta la evaluación detallada del riesgo sísmico. Según la evaluación detallada del riesgo sísmico resultó dos niveles mayor (Alto), seguramente debido a que en esta parroquia se encuentra un importante porcentaje de edificios con sistemas estructurales más vulnerables [34].
Domingo Peña y Sagrario pasaron de un nivel alto a uno muy alto de riesgo multiamenaza, esto debido al mismo cambio entre las evaluaciones de riesgo sísmico consideradas.
Juan Rodríguez Suarez y Mariano Picón Salas presentaron una baja en el nivel de riesgo cuando se tuvo en cuenta la evaluación detallada del riesgo sísmico. En la primera, paso de un nivel medio y un nivel bajo; mientras que en la segunda pasó de un nivel de riesgo multiamenaza muy alto a un nivel alto debido al cambio en el nivel de riesgo sísmico de alto a bajo debido a que la evaluación detallada (Jaramillo, 2014) identifica edificios de hormigón armado menos vulnerables como la tipología predominante en esta parroquia.
EL Llano presentó el cambio más notable pasando de un nivel bajo a uno muy alto de riesgo multiamenaza. Este cambio debido directamente a la misma variación en el nivel de riesgo sísmico identificado. Concretamente en esta parroquia la evaluación detallada identifica efectos de suelo que hacen que se presente medio grado más de intensidad, que afecta a un 60% de las edificaciones del Llano [26].
6. Conclusiones
Este artículo propone una metodología para evaluar el riesgo físico multiamenaza en una zona urbana (MuHRA) basada en el uso de un mecanismo de inferencia difusa utilizando reglas del tipo Si-Entonces del tipo Mamdani. Esta metodología permite estimar de una manera versátil el riesgo físico, considerando hasta un máximo de tres amenazas naturales en cualquier zona urbana; y busca ser un primer paso en la evaluación del riesgo multiamenaza útil para los tomadores de decisiones en la gestión integral del riesgo de desastres naturales.
La metodología propuesta es especialmente útil en los casos en que la información disponible es insuficiente para realizar una evaluación del riesgo multiamenaza. El riesgo físico para cada amenaza natural puede estimarse con los niveles de daño potencial sobre tres tipos de elementos expuestos considerados: área predominante, daño a la población y daño a las líneas vitales. Las variables de entrada de MuHRA, se pueden obtener de cualquiera de dos maneras siguientes: 1) una evaluación numérica parcial del riesgo físico de cada amenaza natural a considerar, si se dispone de información suficiente; 2) una evaluación basada en las opiniones de expertos locales de dichas amenazas, situación más frecuente.
Se aplicó la metodología propuesta a la ciudad de Mérida (Venezuela), donde se contaba con una evaluación más detallada de riesgo sísmico y con información sobre la susceptibilidad de movimientos de ladera. Aprovechando esta situación, fue posible aplicar la metodología utilizando únicamente la opinión de expertos, y en el caso del riesgo sísmico, involucrando los resultados de otras evaluaciones cuantitativas más detalladas. El primer beneficio del primer caso fue la estimación del riesgo sísmico de la parroquia Jacinto Plaza, la cual no había sido incluida en la evaluación detallada debido a la falta de información sobre los elementos expuestos en la zona.
Los resultados de las dos evaluaciones (solo opinión de expertos, e incluyendo evaluaciones más detalladas) fueron comparados para probar la versatilidad y robustez de la metodología, que puede adaptarse según la información disponible en cada caso de estudio.
La respuesta de los expertos en relación a las amenazas como movimientos de ladera es difícil de realizar por divisiones administrativas, ya que dichos eventos se producen en zonas del territorio que pueden afectar de forma muy diferente a las edificaciones de una misma parroquia en función de su cercanía a dicho evento. La adecuación de la respuesta a la afectación por parroquia requiere de efectuar una ponderación de los diferentes niveles de riesgo físico debido a movimientos de ladera, que se encuentren en una determinada división administrativa, en función del porcentaje relativo de las diferentes zonas del territorio que ocupan la división administrativa. Esta misma situación puede surgir con otras amenazas muy focalizadas en un determinado territorio como es el caso de los tsunamis.
Agradecimientos
Los autores agradecen el apoyo del Ministerio de Economía y Competitividad de España en los proyectos "Desprendimientos en escarpes rocosos: cualificación del riesgo y su prevención- RockRisk"(BIA2013-42582-P) y “Evaluación de la Vulnerabilidad y el Riesgo de Zonas Urbanas Expuestas a Amenazas Naturales y Antrópicas-EZUANA” (BIA2016-78544-R).
Referencias
[1] ATC-13 (1985). Earthquake damage evaluation data for California, ATC-13. Redwook City, California: Applied Technology Council. 492.
[2] RADIUS (2000). Risk Assessment tools for DIagnosis of Urban areas against Seismic Disasters. http://www.geohaz.org/projects/radius.html. Último acceso 30 de septiembre 2010
[3] FEMA (2011). Getting started with HAZUS-MH 2.1. Tech. rep. U.S. Department of Homeland Security, Federal Emergency Management Agency. Disponible en http://www.fema.gov/library/viewrecord.do?id=5120 Último acceso 2 de noviembre 2016
[4] Mouroux, P., Bertrand, E., Bour, M., Le Brun, B, Depinois, S., Masure, P. (2004). The european Risk-UE project: an advanced approach to Earthquake risk scenarios. Vancouver, B.C., Canada: 13th World Conference on Earthquake Engineering. http://www.iitk.ac.in/nicee/wcee/article/13_3329.pdf. Último acceso 28 de septiembre 2010
[5] Calvi, G.M., Pinho, R. (2004). LESSLOSS. A European Integrated Project on Risk Mitigation for Earthquakes and Landslides, Report 2004/02, European School for Advanced Studies in Reduction of Seismic Risk (ROSE School), ISBN: 88-7358-020-3 Pavia, Italy.
[6] Pitilakis, K., Crowley, H., Kaynia, A.M. (2014). SYNER-G: Typology Definition and Fragility Functions for Physical Elements at Seismic Risk. Springer. Geotechnical, Geological and Earthquake Engineering. Vol 27. ISBN: 978-94-007-7871-9 (Print) 978-94-007-7872-6 (Online)
[7] UPStrat-MAFA (2012) Urban disaster prevention strategies using MAcroseismic Fields and Fault Sources (UPStrat-MAFA – EU Project Num. 230301/2011/613486/SUB/A5), DG ECHO Unit A. http://upstrat-mafa.ov.ingv.it/UPStrat/ Último acceso 1 de abril 2016
[8] Silva, V., Crowley, H., Pagani, M., Monelli, D., Pinho, R. (2014). Development of the OpenQuake engine, the Global Earthquake Model’s open-source software for seismic risk assessment. Natural Hazards 72:1409–142 doi:10.1007/s11069-013-0618-x
[9] CAPRA (2012). CAPRA Probabilistic Risk Assessment Initiative. http://www.ecapra.org Último acceso 27 de julio 2012
[10] Cardona, O.D., Ordaz, M., Yamin, L., Barbat, A. (2011). Enfoque integral para la evaluación probabilista del riesgo (CAPRA): Iniciativa internacional para la efectividad de la gestión del riesgo de desastre. 4° Congreso Nacional de Ingeniería Sísmica (4CNIS). Granada, España.
[11] Chen L., van Westen C.J., Hussin H., Ciurean R.L, Turkington T., Chavarro-Rincon D., Shrestha D.P. (2016). Integrating expert opinion with modelling for quantitative multi-hazard risk assessment in the Eastern Italian Alps. Geomorphology 273, 150-167. Doi: http://dx.doi.org/10.1016/j.geomorph.2016.07.041
[12] FEMA-154 (2002). Rapid Visual Screening of Buildings for Potential Seismic Hazards: A Handbook, Second Edition. Prepared by the Applied Technology Council for the Federal Emergency Management Agency, Washington D.C., FEMA 154 Report.
[13] FEMA-155 (2002). Rapid Visual Screening of Building for Potencial Seismic Hazards: Supporting Documentation. Second Edition. National Earthquake Hazards Reduction Program, 117pp
[14] Cardona, O.D., Ordaz, M., Reinoso, E., Yamín, L., Barbat, A.H. (2010). Comprehensive approach for probabilistic risk assessment (CAPRA): International initiative for disaster risk management effectiveness. International Symposium on Reliability Engineering and Risk Management. Beijing, China.
[15] Yager, R.R., Filev, D.P. (1994). Essentials of fuzzy modeling and control. New york: John Wiley & Sons.
[16] Carreño (2006). Técnicas innovadoras para la evaluación del riesgo sísmico y su gestión en centros urbanos: Acciones ex ante y ex post. Tesis doctoral. Universitat Politècnica de Catalunya, Barcelona. Disponible en: http://www.tesisenred.net/handle/10803/6241
[17] Carreño M.L., Cardona O.D., Barbat A.H. (2007). “Urban seismic risk evaluation: A holistic approach”. Natural Hazards 40: 137-172, Springer.
[18] Cardona O.D. (2001). Estimación holística del riesgo sísmico utilizando sistemas dinámicos completos. Tesis Doctoral, Universitat Politècnica de Cataluña, Barcelona. Disponible en: [http http]://www.tdx.cat/handle/10803/6219
[19] Saaty, T.L. (2001). Decision Making for Leaders the Analytic Hierarchy Process for decisions in a Complex World, Pittsburgh RWS, USA.
[20] PAHO (1998). Manual para la Mitigación de Desastres Naturales en Sistemas Rurales de Agua Potable y alcantarillado sanitario-Guías para el análisis de vulnerabilidad. Organización Panamericana de la Salud (OPS) / Pan American Health Organization (PAHO), 110p. Consultado el día 16/03/2010. Disponible en: http://cidbimena.desastres.hn y http://www.crid.or.cr/digitalizacion/pdf/spa/doc9816/doc9816.htm.
[21] Barbat A.H., Carreño M.L., Cardona O.D., Marulanda M.C. (2011). “Evaluación holística del riesgo sísmico en zonas urbanas” Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 27: 3-27.
[22] Jaramillo N., Carreño M.L., Lantada N. (2016). Evaluation of the social context integrated into the study of seismic risk for urban areas. International Journal of Disaster Risk Reduction. 17:185-198.
[23] Marulanda, M.C., Cardona, O.D., Barbat, A.H. (2009). Robustness of the holistic seismic risk evaluation in urban centers using the USRi. Natural Hazards, 49, 501–516
[24] Carreño, M.L., Barbat, A. H., Cardona, O.D., Marulanda, M.C. (2014). Holistic Evaluation of Seismic Risk in Barcelona, en Assessment of vulnerability to Natural Hazards: A European Perspective. Editado por: Alexander D., Birkmann J., Kienberger S. Editorial.
[25] Salgado-Gálvez M.A., Zuloaga Romero D., Velásquez C.A., Carreño M.L., Cardona O.D., Barbat A.H. (2016). Urban seismic risk index for Medellín, Colombia, based on probabilistic loss and casualties estimations. Natural Hazards 80:1995–2021.
[26] Jaramillo N. (2014) Evaluación holística del riesgo sísmico en zonas urbanas y estrategias para su mitigación. Aplicación a la ciudad de Mérida-Venezuela. Tesis doctoral, Universitat Politècnica de Catalunya, Barcelona. Disponible en: http://www.tdx.cat/handle/10803/279216
[27] Carreño M.L., Cardona O.D., Barbat A.H. (2012). New methodology for urban seismic risk assessment from a holistic perspective. Bulletin of Earthquake Engineering. 10(2):547-565.
[28] Carreño M.L., Barbat A.H., Cardona O.D. (2014). Método numérico para la evaluación holística del riesgo sísmico utilizando la teoría de conjuntos difusos. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 3: 25-34.
[29] Naaz, S., Alam, A., Biswas, R. (2011). Effect of different defuzzification methods in a fuzzy based load balancing application. IJCSI-International Journal of Computer Science Issues, 8(5).
[30] Ministerio de Obras Públicas (1976). Microzonificación sísmica de la meseta de Mérida (Vol. I y II). Caracas, Venezuela: Publicaciones Técnicas, Ministerio de Obras Públicas, Dirección General de Desarrollo Urbanístico, Secretaría Técnica.
[31] Gutiérrez, J. (2008) Actualización del mapa geológico del área metropolitana de Mérida-Venezuela, in: Proceedings of the 33rd IGC International Geological Congress, 6–14August 2008, Oslo, Norway.
[32] COVENIN (2001). Edificaciones Sismorresistentes. Norma COVENIN 1756:2.001. Venezuela.
[33] Funvisis (2000), Mapa de fallas cuaternarias de Venezuela, 2000. Disponible en: http://www.funvisis.gob.ve/archivos/mapas/fallas_activas.pdf. Último acceso 21 octubre 2015
[34] Castillo A., López-Almansa F., Pujades L.G. (2011), Seismic risk analysis of urban non- engineered buildings: application to an informal settlement in Merida, Venezuela, Natural Hazards 59 (2011) 891–916, Doi: http://dx.doi.org/10.1007/
[35] Ramírez, N., Saito, S.M. (2011). Zonificación de áreas susceptibles a los movimientos en masa: terraza de la Ciudad de Mérida y sus alrededores. Anais XV Simpósio Brasileiro de Sensoriamento Remoto - SBSR-, (págs. 4609-4616). Curitiba, PR, Brasil.
[36] Castillo, A. (2005) Seismic risk scenarios for buildings in Mérida. Venezuela. Detailed vulnerability assessment for non-engineering housing. Tesis doctoral, Universitat Politècnica de Catalunya, Barcelona. Disponible en: [http http]://www.tdx.cat/handle/10803/6537
Document information
Published on 03/01/18
Accepted on 06/06/17
Submitted on 14/12/16
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.7.001
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?